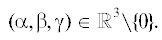Доклады Российской академии наук. Математика, информатика, процессы управления, 2021, T. 496, № 1, стр. 73-78

1. СУБРИМАНОВЫ ФАКТОР-СТРУКТУРЫ

Все алгебры Ли в данной работе рассматриваются над полем $\mathbb{R}$.

Определение 1. Нильпотентная алгебра Ли $\mathfrak{g}$ называется  алгеброй Карно, если:

1) она градуирована:

2) порождена первой компонентой:

Соответствующая связная односвязная группа Ли называется  группой Карно.

Условия 1) и 2) эквивалентны условию

Определение 2.   Вектором роста алгебры Карно $\mathfrak{g}$ называется вектор

Вектор $({{n}_{1}},\; \ldots ,\;{{n}_{s}})$ есть вектор роста левоинвариантного распределения на группе Ли алгебры Ли $\mathfrak{g}$, порожденного подпространством ${{\mathfrak{g}}^{{(1)}}} \subset \mathfrak{g}$.

Пусть $M$ есть гладкое многообразие. Субриманова структура на M [1] есть пара $(\Delta ,g)$, состоящая из векторного распределения $\Delta \subset TM$ и скалярного произведения $g$ в Δ.

Пусть G  –  группа Ли и $\mathfrak{g}$ – ее алгебра Ли. Левоинвариантная СР структура на группе Ли G состоит из левоинвариантного распределения на G и левоинвариантного скалярного произведения в распределении. Такая структура задается подпространством $\Delta \subset \mathfrak{g}$ и скалярным произведением g в $\Delta $. В этом случае будем говорить, что $(\Delta ,g)$ есть СР структура в алгебре $\mathfrak{g}$.

Левоинвариантные СР структуры на группах Карно возникают как нильпотентные аппроксимации общих СР структур на гладких многообразиях [1].

Определение 3. Пусть $(\Delta ,g)$ есть СР структура в алгебре Ли $\mathfrak{g}$, и пусть $\mathfrak{i} \subset \mathfrak{g}$ есть такой идеал, что $\Delta \cap \mathfrak{i} = {\text{\{ }}0{\text{\} }}$. Пусть $\tilde {\mathfrak{g}} = \mathfrak{g}{\text{/}}\mathfrak{i}$ есть фактор-алгебра, а $\pi $: $\mathfrak{g} \to \tilde {\mathfrak{g}}$ – каноническая проекция. Положим $\tilde {\Delta } = \pi (\Delta )$ и $\tilde {g}(\pi (X),\pi (Y)) = g(X,Y)$ для $X,Y \in \Delta $. Тогда ($\tilde {\Delta }$, $\tilde {g}$) есть СР структура в $\tilde {\mathfrak{g}}$, которую будем называть фактор-структурой СР структуры $(\Delta ,g)$.

Пример 1. Пусть ${{\mathfrak{g}}^{5}}$ есть свободная нильпотентная алгебра Ли с двумя образующими, глубины 3 (алгебра Картана) – это алгебра Карно с вектором роста (2, 3, 5). Существует базис ${{\mathfrak{g}}^{5}} = {\text{span}}$(X₁, ..., X₅), в котором ненулевые скобки Ли суть

Рассмотрим СР структуру $(\Delta ,g)$ в ${{\mathfrak{g}}^{5}}$ с ортонормированным репером $({{X}_{1}},{{X}_{2}})$ [8]. Последовательно выбирая в качестве идеала $i \subset {{\mathfrak{g}}^{5}}$ подпространства $\mathbb{R}{{X}_{5}}$, ${\text{span}}({{X}_{4}},{{X}_{5}})$, ${\text{span}}({{X}_{3}},{{X}_{4}},{{X}_{5}})$, получим СР фактор-структуры в алгебре Энгеля (вектор роста (2, 3, 4)) [7], алгебре Гейзенберга (вектор роста (2, 3)) [2] и в двумерной коммутативной алгебре ${{\mathbb{R}}^{2}}$ (вектор роста $(2)$).

Пример 2. Пусть ${{\mathfrak{g}}^{8}}$ есть свободная нильпотентная алгебра Ли с двумя образующими, глубины 4 – это алгебра Карно с вектором роста (2, 3, 5, 8), назовем ее нильпотентной (2, 3, 5, 8)-алгеброй. Существует базис ${{\mathfrak{g}}^{8}} = {\text{span}}({{X}_{1}},\; \ldots ,\;{{X}_{8}})$, в котором ненулевые скобки Ли суть

Рассмотрим СР структуру $(\Delta ,g)$ в ${{\mathfrak{g}}^{8}}$ с ортонормированным репером $({{X}_{1}},{{X}_{2}})$ [9–11]. Легко видеть, что эта СР структура – единственная, с точностью до автоморфизма алгебры Ли, СР структура в ${{\mathfrak{g}}^{8}}$ ранга 2, удовлетворяющая условию Lie(Δ) = = ${{\mathfrak{g}}^{8}}$, назовем ее нильпотентной СР (2, 3, 5, 8)-структурой. Будем далее использовать двойственный базис в коалгебре Ли $({{\mathfrak{g}}^{8}}){\text{*}}$:

Цель данной работы – описать для структуры $(\Delta ,g)$ все СР фактор-структуры для двумерных идеалов $\mathfrak{i} \subset {{\mathfrak{g}}^{8}}$. Это в точности нильпотентные СР структуры с вектором роста (2, 3, 5, 6).

Легко видеть, что двумерное подпространство $\mathfrak{i} \subset {{\mathfrak{g}}^{8}}$ есть идеал тогда и только тогда, когда $\mathfrak{i} \subset Z(\mathfrak{g}) = {\text{span}}({{X}_{6}},{{X}_{7}},{{X}_{8}})$. Поэтому любая фактор-алгебра ${{\mathfrak{g}}^{8}}{\text{/}}\mathfrak{i}$ по двумерному идеалу $\mathfrak{i}$ есть алгебра Карно с вектором роста (2, 3, 5, 6). Опишем такие алгебры.

2. АЛГЕБРЫ КАРНО С ВЕКТОРОМ РОСТА (2, 3, 5, 6)

Теорема 1. (1) В любой алгебре Карно $\mathfrak{g}$ с вектором роста (2, 3, 5, 6) можно выбрать базис $\mathfrak{g} = {\text{span}}({{X}_{1}}, \ldots ,{{X}_{6}})$, в котором все ненулевые скобки Ли имеют вид

(2) Любые две алгебры Карно с вектором роста (2, 3, 5, 6), имеющие пропорциональные тройки $(\alpha ,\beta ,\gamma )$ в (6), изоморфны между собой. Будем поэтому обозначать такие алгебры как $\mathfrak{g}_{{\alpha :\beta :\gamma }}^{6}$, $(\alpha :\beta :\gamma ) \in \mathbb{R}{{P}^{2}}$.

(3) Имеет место изоморфизм алгебр Ли

Каждому базису в алгебре $\mathfrak{g}_{{\alpha :\beta :\gamma }}^{6}$ с таблицей умножения (5), (6) соответствует квадратичная форма $Q(x,y) = \alpha {{x}^{2}} + 2\beta xy + \gamma {{y}^{2}}$. В зависимости от знака ее дискриминанта s = ${\text{sgn}}(\alpha \gamma - {{\beta }^{2}}) \in {\text{\{ }}0,\; \pm {\kern 1pt} 1{\text{\} }}$ будем называть алгебру $\mathfrak{g}_{{\alpha :\beta :\gamma }}^{6}$:

– параболической при s = 0,

– эллиптической при s = 1,

– гиперболической при ${\mathbf{s}} = - 1$.

Замечание 1. Отметим топологию множеств троек $(\alpha :\beta :\gamma ) \in \mathbb{R}{{P}^{2}}$, в зависимости от числа ${\mathbf{s}} = {\text{sgn}}(\alpha \gamma - {{\beta }^{2}})$:

Топологически A_P есть окружность, A_E есть открытый диск, а ${{A}_{H}} = \mathbb{R}{{P}^{2}}{\backslash }({{A}_{P}} \cup {{A}_{E}})$ есть проективная плоскость с вырезанной дыркой, т.е. лента Мёбиуса.

Приведем несколько примеров алгебр Карно с вектором роста (2, 3, 5, 6), вместе с ненулевыми скобками Ли в соответствующем базисе. Напомним также обозначения ${{N}_{{6,2, * }}}$ этих алгебр, используемые в работах [12, 13]. В диссертации М.-П. Гонг [12] получена классификация нильпотентных алгебр Ли размерности $ \leqslant 7$, а в препринте Э. Ле Донне и Ф. Трипальди [13] описаны все алгебры Карно размерности $ \leqslant 7$.

Пример 3. Параболическая алгебра $\mathfrak{g}_{{1:0:0}}^{6}$ = = N_{6, 2, 7} = span(X₁, ..., X₆),

Пример 4. Гиперболическая алгебра $\mathfrak{g}_{{1:0:( - 1)}}^{6}$ = = N_{6, 2, 5} = span(X₁, ..., X₆),

Пример 5. Эллиптическая алгебра $\mathfrak{g}_{{1:0:1}}^{6}$ = = N_{6, 2, 5a} = span(X₁, ..., X₆),

Теорема 2. (1) Алгебры $\mathfrak{g}_{{1:0:0}}^{6}$, $\mathfrak{g}_{{1:0:( - 1)}}^{6}$, $\mathfrak{g}_{{1:0:1}}^{6}$ попарно неизоморфны. Любая алгебра $\mathfrak{g}_{{\alpha :\beta :\gamma }}^{6}$, $(\alpha :\beta :\gamma ) \in \mathbb{R}{{P}^{2}}$, изоморфна одной из этих алгебр.

(2) Число ${\mathbf{s}} = {\text{sgn}}(\alpha \gamma - {{\beta }^{2}}) \in {\text{\{ }}0,\; \pm {\kern 1pt} 1{\text{\} }}$ есть инвариант алгебры Карно $\mathfrak{g}$, будем называть его сигнатурой алгебры $\mathfrak{g}$.

(3) Алгебры $\mathfrak{g}_{{\alpha :\beta :\gamma }}^{6}$ различаются сигнатурой ${\mathbf{s}}$:

Таким образом, сигнатура ${\mathbf{s}} \in {\text{\{ }}0,\; \pm {\kern 1pt} 1{\text{\} }}$ есть инвариант, различающий три класса изоморфизма алгебр $\mathfrak{g}_{{\alpha :\beta :\gamma }}^{6}$.

Замечание 2. Пункт (1) теоремы 2 доказан впервые в работе Э. Ле Донне и Ф. Трипальди [13]. Нами он доказан независимо, вместе с алгоритмом приведения таблицы умножения в (2, 3, 5, 6)-алгебре к нормальной форме примеров 3–5.

Для отыскания замены базиса в алгебре $\mathfrak{g} = \mathfrak{g}_{{\alpha :\beta :\gamma }}^{6}$, приводящей его к одной из нормальных форм примеров 3–5, достаточно привести квадратичную форму $Q(x,y) = \alpha {{x}^{2}} + 2\beta xy + \gamma {{y}^{2}}$ к сумме квадратов, применить эту замену к базису $({{X}_{1}},{{X}_{2}})$ пространства ${{\mathfrak{g}}^{{(1)}}}$, и нормировать вектор ${{X}_{6}}$, порождающий пространство ${{\mathfrak{g}}^{{(4)}}}$.

3. НИЛЬПОТЕНТНЫЕ (2, 3, 5, 6)-РАСПРЕДЕЛЕНИЯ И СУБРИМАНОВЫ СТРУКТУРЫ

Определение 4. Пусть $\mathfrak{g}$ есть алгебра Карно с вектором роста (2, 3, 5, 6). Будем называть нильпотентной субримановой (2, 3, 5, 6)-структурой субриманову структуру $(\Delta ,g)$ в $\mathfrak{g}$, удовлетворяющую условиям:

или, что эквивалентно, равенству Δ ⊕ ${{\mathfrak{g}}^{{(2)}}}$ ⊕ ⊕ ${{\mathfrak{g}}^{{(3)}}} \oplus {{\mathfrak{g}}^{{(4)}}}$ = $\mathfrak{g}$. Соответствующую плоскость $\Delta \subset \mathfrak{g}$ будем называть  нильпотентным (2, 3, 5, 6)-распределением в $\mathfrak{g}$.

Вектор (2, 3, 5, 6) есть вектор роста левоинвариантного распределения на группе Ли $G$ алгебры Ли $\mathfrak{g}$, заданного плоскостью $\Delta \subset \mathfrak{g}$.

Теорема 3. Пусть $\mathfrak{g}$ есть алгебра Карно с вектором роста (2, 3, 5, 6) сигнатуры ${\mathbf{s}} \in {\text{\{ }}0,\; \pm {\kern 1pt} 1{\text{\} }}$. Для любого нильпотентного (2, 3, 5, 6)-распределения $\Delta \subset \mathfrak{g}$ существует репер $\Delta = {\text{span}}({{X}_{1}},{{X}_{2}})$, для которого выполняются следующие соотношения:

Теорема 4. Пусть $\mathfrak{g}$ есть алгебра Карно с вектором роста (2, 3, 5, 6). Для любой нильпотентной СР (2, 3, 5, 6)-структуры в алгебре $\mathfrak{g}$ существует ортонормированный репер $({{X}_{1}},{{X}_{2}})$ и число $\nu \in $ [–1, 1], для которых выполняются следующие соотношения:

Будем называть число $\nu \in [ - 1,\;1]$ из равенств (12) каноническим параметром СР структуры ($\Delta ,g)$. Легко видеть, что $\nu $ равно отношению меньшего по модулю собственного значения квадратичной формы Q к большему собственному значению. Более того, ${\mathbf{s}} = {\text{sgn}}\nu $.

Теорема 5. Канонический параметр $\nu \in $ [–1, 1] есть инвариант нильпотентной СР (2, 3, 5, 6)-структуры.

Пусть $(\Delta ,g)$ – СР структура на многообразии $M$. Соответствующее СР расстояние d [1] превращает M в метрическое пространство. Напомним, что изометрия между метрическими пространствами $(M,d)$ и $(\tilde {M},\tilde {d})$ – это такое отображение $F$: $M \to \tilde {M}$, что

Метрической группой [15] называется группа Ли с левоинвариантным расстоянием, индуцирующим топологию многообразия на этой группе. В частности, любая группа Карно есть метрическая группа. В работе В. Кивиоя и Э. Ле Донне [15] доказано, что:

любая изометрия между метрическими группами есть аналитическое отображение,

любая изометрия между связными нильпотентными метрическими группами есть аффинное отображение (т.е. композиция левого сдвига и изоморфизма).

В следующей теореме получена классификация левоинвариантных СР (2, 3, 5, 6)-структур с точностью до изометрий соответствующих групп Карно.

Теорема 6. Пусть $\mathfrak{g}$ и $\tilde {\mathfrak{g}}$ – нильпотентные (2, 3, 5, 6)-алгебры Карно, и пусть $G$ и $\tilde {G}$ – соответствующие группы Карно. Пусть $(\Delta ,g)$ и $(\tilde {\Delta },\tilde {g})$ – нильпотентные СР (2, 3, 5, 6)-структуры в $g$ и $\tilde {\mathfrak{g}}$, $\nu $ и $\tilde {\nu }$ – соответствующие канонические параметры, а $d$ и $\tilde {d}$ – соответствующие левоинвариантные СР метрики на $G$ и $\tilde {G}$.

Метрические пространства $(G,d)$ и $(\tilde {G},\tilde {d})$ изометричны тогда и только тогда, когда $\nu = \tilde {\nu }$.

Теорема 7. Пусть $\mathfrak{g} = {{\mathfrak{g}}^{8}}$ есть (2, 3, 5, 8)-алгебра из примера 2 с базисом $({{X}_{1}}, \ldots ,{{X}_{8}})$ согласно (3), (4), и пусть ($\Delta ,g)$ есть СР структура в $\mathfrak{g}$ с ортонормированным репером $({{X}_{1}},{{X}_{2}})$. Пусть $\mathfrak{i}$ = = $ker\omega \cap Z(\mathfrak{g})$, $\omega = \alpha {{\omega }_{6}} + \beta {{\omega }_{7}} + \gamma {{\omega }_{8}} \ne 0$, есть любое 2-мерное подпространство в $Z(\mathfrak{g})$. Тогда СР фактор-структура $(\tilde {\Delta },\tilde {g})$ есть одна из СР (2, 3, 5, 6)-структур в $\tilde {\mathfrak{g}} = \mathfrak{g}{\text{/}}\mathfrak{i}$:

(1) в параболическом случае ${\mathbf{s}} = 0$ выполнено $\tilde {\mathfrak{g}} \cong \mathfrak{g}_{{1:0:0}}^{6}$,

(2) в гиперболическом случае ${\mathbf{s}} = - 1$ выполнено $\tilde {\mathfrak{g}} \cong \mathfrak{g}_{{1:0:( - 1)}}^{6}$,

(3) в эллиптическом случае ${\mathbf{s}} = 1$ выполнено $\tilde {\mathfrak{g}} \cong \mathfrak{g}_{{1:0:1}}^{6}$.

Обратно, любая нильпотентная (2, 3, 5, 6)-структура в каждой из этих алгебр реализуется как фактор-структура нильпотентной (2, 3, 5, 8)-структуры $(\Delta ,g)$.

Замечание 3. В работе Н. Боизо и Ж.-П. Го-тье [14] рассмотрена СР структура в эллиптической алгебре $\mathfrak{g}_{{1:0:1}}^{6}$ с каноническим параметром ν = 1. Доказано, что для этой структуры вертикальная подсистема гамильтоновой системы принципа максимума Понтрягина [1] интегрируема по Лиувиллю. В работе [11] эта гамильтонова система проинтегрирована.

4. ФУНКЦИИ КАЗИМИРА И СИМПЛЕКТИЧЕСКИЕ СЛОЕНИЯ

Напомним некоторые базовые понятия симплектической геометрии. Пусть $\mathfrak{g}$ – алгебра Ли, а $\mathfrak{g}{\text{*}}$ – коалгебра Ли (двойственное пространство к $\mathfrak{g}$). Любая функция $h \in {{C}^{\infty }}(\mathfrak{g}*)$ называется гамильтонианом. Для любых гамильтонианов f, g определена скобка Пуассона

Функцией Казимира (на подмногообразии $M \subset \mathfrak{g}{\text{*}}$) называется любой гамильтониан f, коммутирующий в смысле скобки Пуассона со всеми гамильтонианами:

Симплектическим слоением на $\mathfrak{g}{\text{*}}$ называется разбиение $\mathfrak{g}{\text{*}}$ на симплектические листы $L(\lambda )$ — орбиты коприсоединенного действия группы Ли $G$ алгебры Ли $\mathfrak{g}$ в коалгебре $\mathfrak{g}{\text{*}}$:

Рангом скобки Пуассона {⋅, ⋅} в точке $\lambda \in \mathfrak{g}{\text{*}}$ называется размерность симплектического листа, проходящего через точку $\lambda $, обозначение: ${\text{rank}}(\lambda )$. Симплектические листы и функции Казимира – инварианты гамильтонова векторного поля

для любого гамильтониана h, поэтому они важны для анализа левоинвариантных гамильтонианов на группе Ли алгебры Ли $\mathfrak{g}$, в частности, для исследования левоинвариантных задач оптимального управления на этой группе Ли.

Опишем для коалгебр $\mathfrak{g}{\text{*}}$ всех алгебр Карно $\mathfrak{g}$ с вектором роста (2, 3, 5, 6) их функции Казимира и симплектические слоения. В каждой из алгебр $\mathfrak{g} = \mathfrak{g}_{{1:0:0}}^{6}$, $\mathfrak{g}_{{1:0:( - 1)}}^{6}$, $\mathfrak{g}_{{1:0:1}}^{6}$ будем использовать канонический базис $\mathfrak{g} = {\text{span}}({{X}_{1}},\; \ldots ,\;{{X}_{6}})$ согласно примерам 3–5, а также соответствующие линейные гамильтонианы ${{h}_{1}},\; \ldots ,\;{{h}_{6}} \in \mathfrak{g}{\text{**}}$, ${{h}_{i}}(\lambda ) = \left\langle {\lambda ,{{X}_{i}}} \right\rangle $. В каждом случае ниже симплектический лист $L(\lambda )$ есть компонента связности совместных поверхностей уровня функций Казимира на соответствующих подмногообразиях в $\mathfrak{g}{\text{*}}$.

ЗАКЛЮЧЕНИЕ

В работе получены следующие результаты.

Описаны алгебры Карно с вектором роста (2, 3, 5, 6) – фактор-алгебры свободной нильпотентной алгебры Карно ${{\mathfrak{g}}^{8}}$ с двумя образующими, глубины 4. Ранее было известно, что существуют три нормальные формы таких алгебр – параболическая, гиперболическая и эллиптическая. Отыскан различающий эти алгебры инвариант – сигнатура ${\mathbf{s}} \in {\text{\{ }}0,\; \pm {\kern 1pt} 1{\text{\} }}$, и описана замена базиса, приводящая таблицу умножения в нем к одной из трех нормальных форм.

Исследованы левоинвариантные субримановы структуры с вектором роста (2, 3, 5, 6) – фактор-структуры (единственной) субримановой структуры с вектором роста (2, 3, 5, 8) по двумерному подпространству центра алгебры ${{\mathfrak{g}}^{8}}$. Получена классификация (2, 3, 5, 6)-структур с точностью до изометрий: все они однозначно параметризуются каноническим параметром $\nu \in {\text{\{ }}0,\; \pm {\kern 1pt} 1{\text{\} }}$, таким что ${\mathbf{s}} = {\text{sgn}}\nu $. Также получена классификация левоинвариантных (2, 3, 5, 6)-распределений: в каждой из (2, 3, 5, 6)-алгебр (параболической, гиперболической, эллиптической) существует единственное такое распределение, с точностью до изоморфизма.

Для каждой алгебры Карно $\mathfrak{g}$ с вектором роста (2, 3, 5, 6) вычислены ранг скобки Пуассона, функции Казимира и симплектическое слоение в коалгебре Ли $\mathfrak{g}{\text{*}}$.

БЛАГОДАРНОСТИ

Авторы благодарны Л.В. Локуциевскому за ценные замечания по содержанию работы.