Доклады Российской академии наук. Математика, информатика, процессы управления, 2021, T. 496, № 1, стр. 5-9

Неоднократно возникал общий вопрос: можно ли реализовать интегрируемую гамильтонову систему с двумя степенями свободы (ИГС) с помощью одной биллиардной системы сразу на всем фазовом 4-многообразии M⁴?

Как известно, многие ИГС из механики и физики и их аналоги на алгебрах Ли ранее удалось охарактеризовать “кодом” – инвариантами Фоменко–Цишанга [1] слоений Лиувилля системы в ограничении на упорядоченный (по возрастанию энергии H) набор изоэнергетических 3-поверхностей Q³, представляющих регулярные зоны энергии системы (см. [1–3]).

Такие системы были затем реализованы c помощью нескольких биллиардов (см. [4–6]): для регулярной зоны энергии системы (любой Q³ из нее) подбирался свой биллиард с таким же инвариантом Фоменко–Цишанга. Так, для геодезических потоков римановых метрик (например, на кониках [7]) и для введенных В.В. Ведюшкиной биллиардов на CW-комплексах (биллиардных книжек [8] и топологических биллиардов [9]) энергия частицы $H = {{\left| {v} \right|}^{2}}$ являлась лишь масштабным параметром. Эти классы оказались важны для приложений.

Добавление к биллиарду или геодезическому потоку на 2-поверхности потенциала, делая нетривиальной зависимость топологии слоения от энергии, меняет не только “код” системы, но и ее иные, чисто четырехмерные инварианты. Среди них – топологию ее 4-особенностей. Многие ИГС содержат 4-особенности, как невырожденные (классифицированы Н.Т. Зунгом, см. [1]), так и вырожденные (см. [10] для параболических особенностей). Их изучение – отдельная непростая тема. Инварианты систем с потенциалами изучались в [11–13]. В то же время добавление потенциала, например, к локально евклидовому биллиарду, усложняет траектории материальной частицы – они перестают быть прямолинейными. Мы же хотим реализовать ИГС биллиардами с классическим движением частицы по геодезическим.

Требуется найти класс локально плоских биллиардов, подходящий для реализации “кода” ИГС, т.е. топологии ее слоений Лиувилля (замыканий ее решений) во всех регулярных зонах энергии, причем не вводя потенциалы и без дополнительных условий на четырехмерную топологию системы.

Ответ оказался положительным: А.Т. Фоменко предложил новый класс биллиардов – силовые (или эволюционные) биллиарды. В них с изменением скорости шара (“силы” удара о стенку-границу) может меняться как топология биллиардного стола, так и закон отражения шара. Следующие определения введены А.Т. Фоменко.

Определение 1. Носителем силового биллиарда назовем конечный связный двумерный локально-плоский (с евклидовой метрикой внутри  2-клеток)  клеточный  комплекс  X.  Его 2-листы L_i гомеоморфны замкнутым односвязным областям R² и ограничены кусочно-гладкой кривой. Ее углы излома равны π/2. Склейка нескольких 2-листов происходит по изометрии их общей гладкой граничной дуги (корешка книжки).

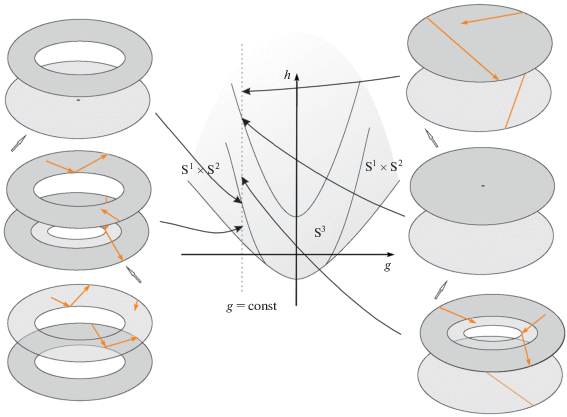
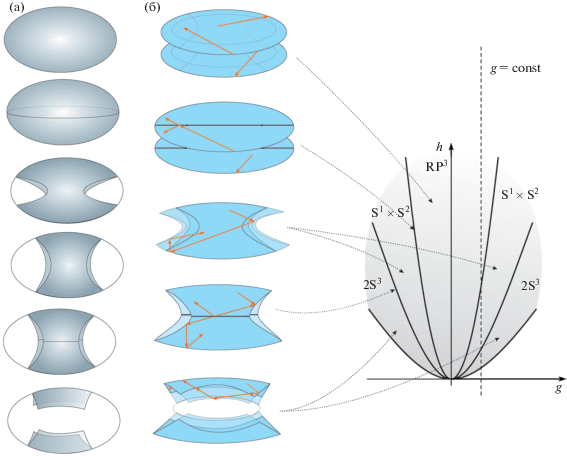
Определение 2.  Для каждого значения параметра-энергии H = h ≥ 0 рассмотрим в носителе X замкнутый подкомплекс X(h), возможно не связный. Назовем его состоянием силового биллиарда, отвечающим значению h. При этом X(h₁) ⊆ X(h₂) для любых h₁< h₂ и X = ∪X(h) по всем h. Тем самым с ростом h состояние X(h) “разрастается”. На рис. 1а состояния силового биллиарда изображены как подмножества эллипсоида E².

Рис. 1.

Реализация случая Эйлера силовых биллиардов: а – состояния силового биллиарда как подмножества эллипсоида, б – состояния силового биллиарда как плоские области и бифуркационная диаграмма интеграла площадей и энергии системы Эйлера.

Определение 3. Конечное количество значений h = 1, …, N энергии H, при которых меняется топология стола или закон отражения–преломления на ребрах границы, назовем особыми (сингулярными), а остальные – регулярными. Напомним, что 1-ребрами (корешками) биллиарда X(h) являются дуги софокусных квадрик- или концентрических окружностей. На рис. 1б особые значения 1 и 2 энергии соответствуют двум переходам (между состояниями).

Определение 4. Закон отражения–преломления на ребре-корешке r в состоянии X(h) обозначим через Z(h, r). Он задается циклической перестановкой на n листах, склеиваемых по ребру r, и определяет динамику частицы после удара о границу. Пусть Z(h) = {Z(h, r)} – набор таких законов – есть кусочно-постоянная функция энергии, изменения которой могут быть лишь при особых значениях h.

Определение 5. Разрешим ребрам-корешкам состояния X(h) гладко меняться в классе софокусных квадрик без вырождений. Как известно из теории интегрируемых биллиардов [14], это задает эквивалентные биллиарды [4]. При особых h ребра могут склеиваться с другими ребрами, вырождаться или превращаться в отрезки фокусных прямых. Склейка листов вдоль границ происходит вдоль дуги одной и той же квадрики. На “новом корешке” появляется новый цикл-перестановка. В момент скачка мы разрешаем биллиардам менять свой класс эквивалентности. Например, сегмент границы при особом h может лечь на фокальную прямую или “сложиться пополам”. Скачком угол π/2 может стать равным π. Разрешается склеивать в граничных точках корешки одного состояния X(h), если они легли на одну граничную дугу, т.е. если угол между ними стал равен π. В круговых биллиардах граничные окружности могут стягиваться в точки.

Так, на рис. 1б при каждом из двух особых значениях h соответствующее ребро r становится “проницаемым” (“прозрачным”). После этого биллиардный шар начинает проходить сквозь него, а до этого – он отражался. При этом пара тождественных перестановок на эллиптических дугах меняется на транспозиции на отрезке фокальной прямой.

Определение 6. Итак, носитель X мы считаем неизменным, “неподвижным”. В нем “разрастаются” состояния X(h), причем X совпадает с последним состоянием X(N). Интегрируемую систему с двумя степенями свободы, задаваемую динамикой биллиардного шара на меняющихся состояниях X(h), назовем силовым (эволюционным) биллиардом.

Пусть h – регулярное значение энергии из некоего интервала D_i = (i, i + 1). Соответствующий биллиард-состояние обозначим через X(D_i).

Определение 7. Точкой фазового комплекса TX(D_i) является пара $(x,{v})$, где x – точка биллиардного стола X(D_i), а ${v}$ – вектор скорости материальной частицы в точке x. Когда точка x оказывается на границе листа L_i, соседствующего с листом L_k, то склейка соответствующих пар $(x,{v})$ и $(x,w)$ происходит по закону отражения–преломления Z(h, r), действующего на данном ребре r при данном h.

Определение 8. Регулярной изоэнергетической 3-поверхностью Q_h назовем подмножество в четырехмерном фазовом комплексе TX(D_i), задаваемое уравнением: H = h; т.е. “уровень постоянной энергии”. Для интегрируемых биллиардных книжек регулярные Q_h являются топологическими 3-многообразиями [15].

Рассмотрим знаменитый случай Эйлера (1750) динамики тяжелого твердого тела, закрепленного в центре масс [1]. Он обладает первым интегралом, квадратичным по компонентам импульса. Топология симплектического листа $M_{g}^{4}$ системы не зависит от выбора ненулевого значения g интеграла площадей f₂. На рис. 1б справа $M_{g}^{4}$ соответствует прообраз вертикальной прямой при отображении (f₂, H). Особые изоэнергетические Q отображаются в точки трех парабол. Каждой 2-области приписан класс гомеоморфности прообраза любой ее точки – регулярной $Q_{{g,h}}^{3}$.

Построим силовой биллиард для такого $M_{g}^{4}$, см. рис. 1. Его носитель склеен из двух областей, ограниченных эллипсом, и гомеоморфен 2-эллипсоиду E². Состояния биллиарда изображены на рис. 1а как подмножества E² и на рис. 1б как склейка плоских областей. Состояния с меньшей энергией изображены ниже, с большей – выше. Начальным (стартовым) состоянием является несвязный биллиард, не имеющий общих точек с фокальной прямой (внизу). Он гомеоморфен двум дискам и реализует систему Эйлера на паре 3-сфер 2S³. Затем он превращается в кольцо, реализующее произведение 2-сферы и окружности S¹ × S². Затем кольцо превращается в сферу (эллипсоид), и реализует проективное пространство RP³. На рис. 1б также показаны траектории биллиардного шара и склейка корешков. Интегрируемость биллиарда в каждый момент эволюции следует из принадлежности его стенок дугам софокусных квадрик.

Теорема 1. Построенный интегрируемый силовой биллиард, носитель которого гомеоморфен эллипсоиду, реализует (в смысле лиувиллевой эквивалентности) интегрируемый случай Эйлера сразу на всем фазовом многообразии $M_{g}^{4}$, т.е. на всех его регулярных изоэнергетических 3-поверхностях для всех регулярных значений g и h.

Случай Лагранжа, допускающий линейный интеграл, описывает движение осесимметричного тяжелого твердого тела с закрепленной точкой на оси симметрии. Известно, что в зависимости от значений параметров, существует четыре типа бифуркационных диаграмм, см. [1]. Оказалось, что здесь есть ровно пять различных типов симплектических 4-листов. Для всех них мы обнаружили силовые биллиарды. На рис. 2 показан один из них.

Рис. 2.

Силовой биллиард реализует симплектический лист системы Лагранжа.

Теорема 2. Интегрируемый случай Лагранжа на каждом своем регулярном симплектическом 4-листе $M_{g}^{4}$ реализуется (в смысле лиувиллевой эквивалентности) одним из построенных нами пяти силовых биллиардов, у которых биллиарды–состояния ограничены концентрическими окружностями (и потому интегрируемы в каждый момент эволюции).

Продеформируем семейство софокусных эллипсов и гипербол в семейство концентрических окружностей и радиальных лучей (устремляя фокусы друг к другу).

Теорема 3. Указанная деформация софокусных биллиардов в круговые переводит силовой биллиард, реализующий случай Эйлера, в новый силовой биллиард, полный набор лиувиллевых слоений которого совпадает с полным набором лиувиллевых слоений случая Лагранжа (для всех его трех типов изоэнергетических 3-поверхностей). Такие системы мы называем “биллиардно эквивалентными”.

Обнаруженное “превращение” случая Эйлера в случай Лагранжа не переводит симплектический лист случая Эйлера в какой-либо из пяти типов симплектических листов случая Лагранжа. Оно устроено сложнее. Именно это не позволяло ранее заметить превращение этих систем друг в друга. Тем не менее, оказалось, что полный набор лиувиллевых слоений случая Эйлера превращается в полный набор лиувиллевых слоений случая Лагранжа. Сначала потребовалось обнаружить в случае Эйлера “скрытые софокусные квадрики”, а в случае Лагранжа – “скрытые концентрические окружности”. В итоге, именно деформация софокусных квадрик в окружности (при слиянии фокусов) и “превращает” случай Эйлера в случай Лагранжа.

Также мы обнаружили силовые биллиарды, реализующие интегрируемый случай Горячева–Чаплыгина–Сретенского одновременно в нескольких регулярных зонах энергии.