Доклады Российской академии наук. Математика, информатика, процессы управления, 2021, T. 497, № 1, стр. 12-17

В задаче поиска безусловного минимума рассматриваются функции $f(.)$, определенные и достаточно гладкие в окрестности $U(x{\kern 1pt} *)$ точки минимума функции n вещественных переменных. Всюду далее множество точек минимума функции f обозначается как $X{\kern 1pt} * = {\text{Arg}}\min f$ и предполагается непустым. Необходимое условие минимума функции f в точке x* задается равенством $f{\kern 1pt} '(x{\kern 1pt} *) = 0,$ при этом матрица вторых производных функции в точке минимума является положительно полуопределенной. Следует отметить, что исследованиям по методу Ньютона посвящено значительное число научных работ, среди которых укажем [2–6]. Со многими работами можно ознакомиться в обзорной статье [1]. В данной работе показывается, что несмотря на возможную вырожденность матрицы Гессе в точке x*, в окрестности этой точки градиент целевой функции принадлежит образу ее второй производной и, следовательно, ньютоновская система относительно направления спуска разрешима в точках этой окрестности. Это топологическое свойство выпуклости и экстремальности позволяет по-новому взглянуть на численные методы ньютоновского типа и обосновать скорость сходимости этих методов без обременительного предположения относительно невырожденности матрицы Гессе в точке x*. Для задачи безусловной оптимизации получены свойства, уточняющие неравенство Лоясевича [7, 8]. Именно, неравенство обобщено для всего спектра производных до определенного порядка. В работе рассматриваются функции, производные которых равномерно по аргументу и в совокупности по порядку ограничены в некоторой окрестности $U(x{\kern 1pt} *)$ точки x*, т.е. для данной окрестности существует положительная константа M такая, что значения производных любого порядка не превосходят по абсолютному значению эту константу. Кроме того, объектом рассмотрения в работе будут достаточно гладкие в окрестности точки минимума функции, т.е. функции, имеющие неограниченное число порядков производных. Всюду далее без ограничения общности считаем $f(x{\kern 1pt} *) = 0$ и обозначаем ${{f}^{{(0)}}}(x) = f(x).$ Для функции одной переменной справедлива

Лемма 1. Если x* – точка изолированного локального минимума достаточно гладкой в $U(x{\kern 1pt} *)$ функции $f{\kern 1pt} :\;R \to R$, производные которой равномерно по аргументу и в совокупности по порядку ограничены в некоторой окрестности $U(x{\kern 1pt} *)$, то существует четная степень 2p, $p = {{p}_{f}} \in \mathbb{N}$, для которой справедливы неравенства

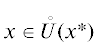при всех , где положительные константы ${{C}_{k}} = {{C}_{{k,f}}}$, $k = 0,1,2, \ldots ,2p - 1$, не зависят от $x.$

Доказательство. Поскольку x* – точка локального минимума функции f, то $f{\kern 1pt} '(x{\kern 1pt} *) = 0.$ Сначала покажем, что в условиях леммы невозможна ситуация, когда производные ${{f}^{{(k)}}}(x{\kern 1pt} *) = 0$ при любом порядке $k,k = 1,2, \ldots $ Действительно, в этом случае для фиксированной точки x = x* + + $t \in U(x{\kern 1pt} *)$ в силу ограниченности производных в окрестности x* из формулы Тейлора при нулевых производных до любого фиксированного порядка $k$ следует неравенство ${\text{|}}f{\kern 1pt} '(x{\kern 1pt} * + \;\theta t){\text{|}} \leqslant \tfrac{{M{{{({\text{|}}\theta t{\text{|}})}}^{k}}}}{{k!}}$, где M – обозначенная выше верхняя грань для множества значений производных функции f в указанной окрестности и $\theta \in (0,1).$ Отсюда и из условия изолированности локального минимума x* значение $f(x{\kern 1pt} {\text{*}} + t) = \int\limits_0^1 {f{\kern 1pt} '(x{\kern 1pt} {\text{*}} + \theta t)d\theta } \leqslant \frac{M}{{(k + 1)!}}$. При достаточно больших k это означает противоречие с возможным предположением $f(x) \ne 0$, $x \ne x{\kern 1pt} *$, что противоречит изолированности локального минимума x*. Следовательно, существует конечное k > 1: ${{f}^{{(k)}}}(x{\kern 1pt} *) \ne 0$, ${{f}^{{(l)}}}(x{\kern 1pt} *) = 0$, $l = 1,2, \ldots ,k - 1$. При этом порядок k может быть только четным: k = 2p, $p \in \mathbb{N}$ и ${{f}^{{(2p)}}}(x{\kern 1pt} *) > 0$, поскольку x* – точка локального минимума функции f. Теперь для завершения доказательства достаточно обозначить через C₀ значение $\tfrac{1}{{(2p + 1)!}}{{f}^{{(2p)}}}(x{\kern 1pt} *)$, тогда из формулы Тейлора и ограниченности производной порядка 2p + 1 в окрестности $U(x{\kern 1pt} *)$ будет вытекать первое неравенство леммы. Разложение в окрестности x* по формуле Тейлора производной ${{f}^{{(k)}}}(x)$ дает остальные неравенства леммы при любом k, k = 1, 2, ..., 2p – 1, если через C_k обозначить $\tfrac{1}{{(2p + 1 - k)!}}{{f}^{{(2p)}}}(x{\kern 1pt} *)$.

Следствие 1. При выполнении условий леммы 1 функция f локально выпукла.

Действительно, если ${{f}^{{(2)}}}(x{\kern 1pt} *) > 0$, то в малой окрестности x* вторая производная будет оставаться положительной, что означает локальную выпуклость f(x). Если же ${{f}^{{(2)}}}(x{\kern 1pt} *) = 0$, то, как показано в лемме 1, ${{f}^{{(2p)}}}(x{\kern 1pt} *) > 0$ для некоторого $p\, = \,{{p}_{f}}\, \in \,\mathbb{N}$, $p > 1$, и при этом ${{f}^{{(k)}}}(x{\kern 1pt} *) = 0$, k = 1, $2, \ldots ,2p - 1$. Тогда ${{f}^{{(2)}}}(x) \geqslant {{C}_{2}}{{(x - x{\kern 1pt} *)}^{{2p - 2}}}$ для любого $x \in U(x{\kern 1pt} *)$, положительная константа ${{C}_{2}}$ определена ранее в лемме 1. Последнее неравенство также означает локальную выпуклость f.

Для функции n переменных производную k-го порядка по направлению h в точке x будем обозначать как $f_{h}^{{(k)}}(x).$

Следствие 2. Если достаточно гладкая функция $f{\kern 1pt} :\;{{R}^{n}} \to R$, производные которой равномерно по аргументу и в совокупности по порядку ограничены в некоторой окрестности $U(x{\kern 1pt} *)$ изолированной точки минимума $x{\kern 1pt} *$, то для каждого $h \in {{R}^{n}}{\kern 1pt} :\;{\text{||}}h{\text{||}}$ = 1, существует четная степень $2{{p}_{{h,f}}},{{p}_{{h,f}}} \in \mathbb{N}$, для которой справедливы неравенства ${{f}^{{(2{{p}_{{h,f}}})}}}(x{\kern 1pt} *)$ > 0, ${{f}^{{(k)}}}(x{\kern 1pt} *)$ = 0, $\tfrac{{{{f}^{{(k)}}}(x{\kern 1pt} *\, + \,th)}}{{{{t}^{{2{{p}_{{h,f}}} - k}}}}}\, \geqslant \,{{C}_{k}}$, $k\, = \,0,1,2, \ldots ,2{{p}_{{h,f}}}\, - \,1$ при всех $t\, \in \,(0$, δ_h], где положительные константы ${{C}_{k}} = {{C}_{{k,h,f}}}$, k = = 0, 1, 2, ..., $2{{p}_{{h,f}}}$ – 1, не зависят от $t,x{\kern 1pt} * + \;{{\delta }_{h}} \in U(x{\kern 1pt} *)$, при этом сама функция локально выпукла вдоль направления $h.$

Здесь элемент $p = {{p}_{{h,f}}} \in \mathbb{N}$ определяется направлением $h,{\text{||}}h{\text{||}} = 1$ и не зависит от малых t, для которых $x{\kern 1pt} * + \;{{\delta }_{h}} \in U(x{\kern 1pt} *)$, но значение ${{\delta }_{h}} > 0$ зависит от h и в общем случае эта величина может быть бесконечно малой относительно h. Далее в лемме 2 будет показано, что для случая выпуклой функции f можно гарантировать существование верхней границы для величины ${{p}_{{h,f}}} \in \mathbb{N}$ и положительной нижней границы для δ_h на множестве векторов $h{\kern 1pt} :\;{\text{||}}h{\text{||}} = 1$.

Из леммы 1 вытекает, что в точках достаточно малой выколотой окрестности решения корректно определен оператор Ньютона ψ(x) = x – ‒ ${{f}^{{(2)}}}{{(x)}^{{ - 1}}}f{\kern 1pt} '(x).$ Для случая произвольной размерности пространства Rⁿ лемма 1 означает выпуклость функции f вдоль любой прямой, проходящей через точку x*, при условии достаточной гладкости функции на пересечении прямой и окрестности $U(x{\kern 1pt} *)$. Кроме того, для любой прямой, проходящей через точку x* вдоль вектора $h,$ справедливо неравенство $f_{h}^{{(2m)}}(x{\kern 1pt} *) \geqslant {{C}_{2}}$ для некоторой степени $2p,p = {{p}_{h}} \in \mathbb{N}$ и некоторой константы ${{C}_{2}} = {{C}_{{2,h}}} > 0.$ Неравенство Лоясевича гарантирует выполнимость данного неравенства в случае аналитичности в окрестности $U(x{\kern 1pt} *)$ функции при некоторых p, C₂, не зависящих от h. Выпуклость в указанной окрестности функции позволяет требовать лишь достаточную гладкость функции и получить свойство “устойчивости” неравенства Лоясевича, что расширяет область применения метода Ньютона. Имеет место

Лемма 2. Если выпуклая достаточно гладкая функция $f{\kern 1pt} :\;{{R}^{n}} \to R$, производные которой равномерно по аргументу и в совокупности по порядку ограничены в некоторой окрестности $U(x{\kern 1pt} *)$ изолированной точки минимума x*, то существует четная степень $2p,\;p = {{p}_{f}} \in \mathbb{N}$, константа $C = {{C}_{f}} > 0$ и величина $\delta = {{\delta }_{f}} > 0,$ для которых

при всех $h{\kern 1pt} :\;{\text{||}}h{\text{||}} = 1,\;t \in (0,\delta ]$.

Доказательство. Докажем существование такого $p = {{p}_{f}} \in \mathbb{N}$, обладающего свойством: если $f_{h}^{{(i)}}(x{\kern 1pt} *) = 0$, $i = 0,1,2,...,2p{\kern 1pt} '(h) - 1$, $f_{h}^{{(2p'(h))}}(x{\kern 1pt} *)$ > 0, то $p{\kern 1pt} '(h) \leqslant p$. Предположим противное, тогда для  некоторых последовательностей ${{h}_{k}}{\kern 1pt} :\;{\text{||}}{{h}_{k}}{\text{||}} = 1$, ${{t}_{k}}{\kern 1pt} :\;{{t}_{k}} \to + 0$ имеет место неравенство f(x* + t_kh_k) < < ${{C}_{k}}{{t}^{{{{m}_{k}}}}}$, где ${{C}_{k}} > 0$ – элементы некоторой ограниченной, а ${{m}_{k}} \in \mathbb{N}$ – возрастающей последовательностей. Без ограничения общности можно считать, что ${{h}_{k}} \to h$, ${{C}_{k}} \to C$, $k \to \infty $. Обозначим ${\text{conv}}\{ {{h}_{k}},{{h}_{{k + 1}}},{{h}_{{k + 2}}},...,{{h}_{{k + n}}}\} $ через ${{V}_{k}}.$ В случае ${\text{dim}}{{V}_{k}}$ < n указанный набор векторов изменяется путем прибавления к $n - {\text{dim}}{{V}_{k}}$ векторам линейно независимых приращений длины порядка ${{C}_{k}}{{t}^{{2p}}}$, ${{C}_{k}} \to 0$, $k \to \infty $, после чего можно считать ${\text{dim}}{{V}_{k}}$ = n. Пусть далее $h{{{\text{'}}}_{k}} \in {\text{int}}{{V}_{k}}$, ${{h}_{k}}{\text{''}} = h + {{\alpha }_{k}}(h{{{\text{'}}}_{k}} - h)$, ${{\alpha }_{k}} \in (0$, 1), ${{\alpha }_{k}} = {\text{inf}}\{ \alpha > 0{\kern 1pt} :\;h + \alpha (h{{{\text{'}}}_{k}} - h) \in {{V}_{k}}\} $. Из выпуклости и непрерывности f следует f(x* + t_k${{h}_{k}}{\text{''}}$) ≤ $2C{{t}^{{{{m}_{k}}}}}$. С другой стороны, из леммы 1 следует, что для некоторого $p = {{p}_{h}} \in \mathbb{N}$ существует степень $k \in \mathbb{N}$, $k \leqslant p$, для которой производная $f_{h}^{{(2k)}}(x{\kern 1pt} *) \geqslant {{C}_{2}} > 0$ для некоторого ${{C}_{2}} > 0.$ Поскольку ${{h}_{k}}{\text{''}} \to h$, $k \to \infty $, то при достаточно больших номерах k будут выполняться неравенства $f(x{\kern 1pt} * + {{t}_{k}}{{h}_{k}}{\text{''}}) \geqslant {{C}_{2}}{{t}^{{2k}}}$, что противоречит предположению.

Следствие 3. Из доказательства леммы 2 следует существование степени $2p,\;p = {{p}_{f}} \in \mathbb{N}$, а также констант ${{C}_{k}} = {{C}_{{k,f}}}$, $k = 1,2,...,2p{\kern 1pt} '\; - 1$, для которых

при этом $p{\kern 1pt} ' = p{\kern 1pt} '(h) \leqslant p$ при всех $h{\kern 1pt} :\;{\text{||}}h{\text{||}} = 1$.

Для точки $x = x{\kern 1pt} * + \;th \in U(x{\kern 1pt} *)$, ${\text{||}}h{\text{||}} = 1$ определим базис $G = G(h) = \{ {{g}_{1}},{{g}_{2}},...,{{g}_{n}}\} $ пространства Rⁿ и соответствующий индекс $q = q(h)$ следующим образом. Рассмотрим матрицы

Тогда в точке $x = x{\kern 1pt} * + \;th$ для достаточно гладкой функции f справедливы соотношения

Далее определим номер ${{k}_{1}} \geqslant 2$ как минимальный среди тех номеров k, для которых одномерное пространство ${{L}_{1}} = {{L}_{{{{k}_{1}}}}} = Lin\{ {{a}_{k}}h\} \ne \{ 0\} $. Прямую L₁ переобозначим через L¹, вектор ${{g}_{1}}$ определим как $\tfrac{{{{a}_{{{{k}_{1}}}}}h}}{{{\text{||}}{{a}_{{{{k}_{1}}}}}h{\text{||}}}}$ и далее номер ${{k}_{2}} > {{k}_{1}}$ определим как минимальный номер k, для которого $Lin\{ {{a}_{k}}h\} $ не содержится в ${{L}^{1}}.$ Тогда ${{L}_{{{{k}_{2}}}}} = Lin\{ {{a}_{{{{k}_{2}}}}}h\} $, ${\text{dim}}({{L}_{{{{k}_{2}}}}} \oplus {{L}^{1}}) = 2$, одномерное подпространство L₂ определяется как $P{{r}_{{{{{({{L}^{1}})}}^{ \bot }}}}}{{L}_{{{{k}_{2}}}}}$, вектор ${{g}_{2}}$ определяется как нормированный вектор $P{{r}_{{{{L}_{2}}}}}{{a}_{{{{k}_{2}}}}}h.$ При этом $P{{r}_{{{{L}_{2}}}}}({{a}_{{{{k}_{2}}}}}h) \subseteq P{{r}_{{{{L}_{2}}}}}Im{{a}_{{{{k}_{2}}}}}.$ Далее пространство L² определим ${{L}^{1}} \oplus {{L}_{2}}$. Далее для каждого $j = 3,4,...,q = q(h)$ аналогично определяются прямые ${{L}_{j}} = P{{r}_{{{{{({{L}^{{j - 1}}})}}^{ \bot }}}}}{{L}_{{{{k}_{j}}}}}$, $j = 3,4,...,q$ и соответствующие единичные векторы g_j, $j = 1,2,...,q.$ Номер q = q(h) = $\dim Lin\{ {{a}_{1}}h,{{a}_{2}}h,...\} \leqslant n$, прямая сумма ${{L}^{{j - 1}}} \oplus {{L}_{j}}$ обозначается как L^j и является подпространством в ${{R}^{n}}$ размерности j. На конечном этапе построено подпространство L^q размерности $q = q(h) \leqslant n.$ Обозначим ортогональное дополнение подпространства L^q через $H{\kern 1pt} :\;H = {{({{L}^{q}})}^{ \bot }}$ в случае q < n и $H = \{ 0\} $ при q = n. Определим базис $G(h)$ пространства ${{R}^{n}}$ как набор построенных единичных взаимно ортогональных векторов ${{g}_{1}},{{g}_{2}},...,{{g}_{q}}$, направленных вдоль построенных ортогональных прямых ${{L}_{l}},l = 1,2,...,q$, и произвольного ортогонального базиса ${{g}_{{q + 1}}},{{g}_{{q + 2}}},...,{{g}_{n}}$ подпространства H.

Справедлива

Теорема 1. Если для достаточно гладкой функции $f{\kern 1pt} :\;{{R}^{n}} \to R$ производные равномерно по аргументу и в совокупности по порядку ограничены в некоторой окрестности $U(x{\kern 1pt} *)$ изолированной точки минимума x*, то для любого фиксированного $h{\kern 1pt} :\;{\text{||}}h{\text{||}} = 1$ система

разрешима относительно s при достаточно малых t.

Доказательство. Решение системы s в базисе $G$ при любом фиксированном векторе h определим покоординатно следующим образом. Положим $P{{r}_{H}}s = 0,$ далее координата s_q в соответствии с (1) определяется из условия

$P{{r}_{{{{L}_{q}}}}}(({{k}_{q}} - 1){{a}_{{{{k}_{q}}}}}{{t}^{{{{k}_{q}} - 2}}}s)$ = $P{{r}_{{{{L}_{q}}}}}f{\kern 1pt} '(x)$ = $P{{r}_{{{{L}_{q}}}}}\sum\limits_{k \geqslant {{k}_{q}}} {{{a}_{k}}h{{t}^{{k - 1}}}} $.

При этом s_q = $\frac{{P{{r}_{{{{L}_{q}}}}}ht}}{{{{k}_{q}} - 1}} + o(t)$. Подстановка координаты s_q в систему (2) позволяет получить координату s_{q – 1} = $\frac{{P{{r}_{{{{L}_{{q - 1}}}}}}ht}}{{{{k}_{{q - 1}}} - 1}} + o(t)$. Далее последовательно определяются координаты ${{s}_{l}},l = q - 2,q - 3,...,1$. Решение системы (2), вообще говоря, не единственно, но из (1) следует, что координаты любого решения s в базисе $G = G(h)$ имеют вид

Замечание 1. Для получения единственного решения системы (2) определим задачу

решение которой существует при каждом фиксированном h при всех достаточно малых $t,$ при условиях, указанных в теореме 1. При этом длина интервала для $t$, в пределах которого решение существует, зависит от h.

Пример 1. Для невыпуклой функции f(x) = = $x_{1}^{4} + {{({{x}_{2}} - x_{1}^{2})}^{2}}$ вывод теоремы 1 нарушается для точек параболы ${{x}_{2}} = x_{1}^{2}.$ Таким образом, длина интервала, для которого имеет место теорема 1, стремится к нулю по мере приближения вектора h к (1, 0).

Далее будет показано, что в случае выпуклой функции можно указать общий для всех векторов единичной сферы радиус окрестности переменной $t,$ в пределах которой задача (4) разрешима. Из вида целевой функции задачи (4) следует, что ее решение $s = {{f}^{{(2)}}}{{(x)}^{ + }}f'(x),$ где ${{(.)}^{ + }}$ означает псевдообратный оператор на своем образе. Координаты решения этой задачи в базисе $G$ удовлетворяют условию $P{{r}_{H}}s = 0.$

Теорема 2. При выполнении условий леммы 2 при всех $x$, достаточно близких к $x{\kern 1pt} *$, задача (4) разрешима и ее решение удовлетворяет условиям

где степень $2p$ определена в лемме 2, константы ${{M}_{1}} = {{M}_{{1,f}}}$, ${{M}_{2}} = {{M}_{{2,f}}} > 0$ не зависят от $x$.

Доказательство. Из леммы 2 и (1) следует, что при всяком $h{\kern 1pt} :\;{\text{||}}h{\text{||}}$ = 1 номера k_j, определяющие базис G, удовлетворяют условию: существует индекс ${{l}_{1}} \in \{ {{k}_{1}},{{k}_{1}} + 1,...,2p\} $, для которого ${{a}_{{{{l}_{1}}}}}{{[h]}^{2}} \geqslant C$ > 0, степень 2p определена в лемме 2 и от $h$ не зависит, константа C > 0 также не зависит от h и определяется в следствии 3. Последнее неравенство эквивалентно условию $\tfrac{{{{a}_{{{{l}_{1}}}}}{{{[h]}}^{2}}}}{{{{l}_{1}} - 1}} \geqslant {{C}_{1}}{{t}^{{2p}}}$ при малых t. Обозначая $\tfrac{C}{{2p - 1}}$ через ${{M}_{1}},$ получим неравенство в утверждении теоремы. Аналогично из следствия 3 получается и второе неравенство.

Следствие 4. При выполнении условий леммы 2 для выпуклой функции f при всех x, достаточно близких к x*, имеет место разрешимость относительно s системы

что равносильно справедливости включениянезависимо от величины ранга матрицы ${{f}^{{(2)}}}(x).$

Далее будем обозначать множество $\{ x \in {{R}^{n}}$: $f(x) \leqslant f(x{\kern 1pt} *) + \varepsilon \} $ как $X_{\varepsilon }^{*}$, диаметр множества A как ${\text{diam}}A.$ Справедлива

Теорема 3. При выполнении условий леммы 2 существует натуральное p и константа $\bar {C} < \infty $, для которых справедливо неравенство

Замечание 2. Указанные ранее свойства справедливы в предположении, что множество точек минимума функции f(x) представляет изолированную точку. Если отказаться от данного предположения, то при выполнении остальных предположений теоремы 1 справедливо представление

где $L$ – собственное подпространство Rⁿ, которое определяется условием ${{f}^{k}}(x{\text{*}}){{[h]}^{k}} = 0$ для всякого натурального k.

Из теоремы 1 не следует положительная определенность матрицы ${{f}^{{(2)}}}(x)$ в окрестности точки минимума x*. Тем не менее она гарантирует применимость метода Ньютона для поиска точки минимума гладкой функции при условии подходящей начальной точки, поскольку задача (1) позволяет получить вектор перехода в итерационной схеме без предположения выпуклости целевой функции. Кроме того, в данном случае удается получить монотонность по аргументу метода Ньютона, а при более сильных предположениях – линейную скорость сходимости. В случае же выпуклости целевой функции полученной свойство справедливо без дополнительных предположений.

Рассмотрим сначала применение результата теоремы 1 для доказательства монотонности по аргументу схемы метода Ньютона. Именно, определим оператор Ньютона ψ(x, s) = $x - {{f}^{{(2)}}}{{(x)}^{ + }}f{\kern 1pt} '(x)$, где ${{f}^{{(2)}}}{{(x)}^{ + }}f{\kern 1pt} '(x) = s$ – решение задачи (4). Из процесса построения решения s в теореме 1 и замечания к теореме следует, что для любого фиксированного $h{\kern 1pt} :\;{\text{||}}h{\text{||}} = 1$, при достаточно малых значениях t данный оператор корректно определен без предположения выпуклости функции f. Для получения оценки скорости сходимости дополнительно к предположениям теоремы 1 естественно определяется следующее свойство.

Определение 1. Функция f слабо регулярна в точке x*, если существует константа  $d = {{d}_{f}}$ > 0, для которой $\mathop {\max }\limits_{j \leqslant q} {\text{|}}{{h}_{j}}{\text{|}} \geqslant d$ для всякого $h,{\text{||}}h{\text{||}} = 1$. Здесь, как и ранее, $q = q(h) = \dim Lin\{ {{a}_{2}}h,{{a}_{3}}h,...\} $, h_j – координата вектора h с номером j в базисе G.

Теорема 4. Если функция f слабо регулярна в точке x*, то при выполнении условий теоремы 1 существует $\lambda \in (0,1),$ для которого

||ψ(x* + th, $s) - x{\kern 1pt} *{\text{||}} \leqslant \lambda t$

при всех достаточно малых t.

Доказательство. Для любого решения системы (1) в силу предположения слабой регулярности в точке x* существует номер  j, для которого ${\text{||}}P{{r}_{{{{L}_{{{{k}_{j}}}}}}}}h{\text{||}} > d$. Отсюда

Замечание 3. Полученное неравенство не означает линейной сходимости метода Ньютона, поскольку знаменатель $\lambda ,$ который участвует в оценке, вообще говоря, зависит от h. В случае выпуклой функции полученный результат справедлив в более сильном виде: ${\text{||}}\psi (x,s) - x{\kern 1pt} *{\text{||}} \leqslant \lambda {\text{||}}x - x{\kern 1pt} *{\text{||}}$ при всех x из достаточно малой окрестности x*, поскольку для выпуклых функций справедливо следующее свойство.

Определение 2. Функция  f  равномерно регулярна в точке x*, если существуют номер $m = {{m}_{f}} \in \mathbb{N}$ и константа $d = {{d}_{f}} > 0$, для которых найдется индекс $j\, \leqslant \,q{\text{:}}\,\,{{k}_{j}}\, \leqslant \,m$, такой что ${\text{||}}P{{r}_{{{{L}_{j}}}}}h{\text{||}} \geqslant d$.

Имеет место

Теорема 5. Если функция f равномерно регулярна в точке x*, то при выполнении условий теоремы 1 существует $\lambda \in (0,1),$ для которого ||ψ(x, s) – – $x{\kern 1pt} *{\text{||}} \leqslant \lambda {\text{||}}x$ – x*|| при всех x из достаточно малой окрестности x*.

Доказательство. Из теоремы 4 следует, что полученный знаменатель $\lambda = \lambda (h)$ ограничен сверху равномерно по h, ||h|| = 1:  λ(h) = 1 – $\tfrac{d}{{{{k}_{j}} - 1}} \leqslant \lambda {\kern 1pt} '$ < 1, где $j{\kern 1pt} :\;{{k}_{j}} \leqslant m.$ Такой номер j существует, как показано в теореме 1. Кроме того, из условия равномерной регулярности следует, что ${\text{||}}h_{H}^{ \bot }{\text{||}} > d$ для некоторого $d > 0$, не зависящего от h, где h_A – проекция вектора $h$ на подпространство A. Отсюда следует оценка для знаменателя λ, не зависящая от $h.$

Замечание 4. Из леммы 2 следует, выпуклая функции равномерно регулярна в точке $x{\kern 1pt} *$: ${{k}_{j}} = {{k}_{j}}(h) \leqslant m = 2p$, ${\text{||}}h{\text{||}} = 1$. Условие равномерной регулярности является необходимым и достаточным условием линейной скорости сходимости метода Ньютона при выполнении условий теоремы 1 без предположения о выпуклости функции $f.$ Итерационная схема метода Ньютона имеет вид

а оценка скорости сходимости метода будет линейная: при начальном приближении, достаточно близком к решению x* в случае равномерно регулярной в точке минимума функции f.

Следствие 5. При выполнении условий теоремы 2 для выпуклой функции скорость сходимости итерационной схемы метода Ньютона является линейной при любом выборе начальной точки x из достаточно малой окрестности решения. Действительно, из теоремы 2 следует, что выпуклая функция является равномерно регулярной в решении x*, откуда вытекает линейная оценка скорости сходимости.

Для получения сходимости метода Ньютона с более высокой скоростью, чем линейная, рассмотрим модифицированный оператор ${{\psi }_{1}}(x,s),$ покоординатная запись которого в базисе G представляет собой ${{\psi }_{1}}{{(x,s)}_{j}} = x - ({{k}_{j}} - 1){{s}_{j}}$, $j = 1,2$, ..., q; ${{\psi }_{1}}{{(x,s)}_{H}} = {{x}_{H}} - g(x,h)$, где вектор-функция g(x, h): $H \to H,s = {{f}^{{(2)}}}{{(x)}^{ + }}f{\kern 1pt} '(x)$. Оператор ${{\psi }_{1}}{{(x,s)}_{H}}$ позволяет определить модифицированную схему Ньютона ${{x}_{{k + 1}}}$ = ${{\psi }_{1}}({{x}_{k}},{{s}_{k}})$. Из теоремы 1 следует

Теорема 6. Модифицированная схема Ньютона гарантирует сверхлинейную оценку скорости сходимости при хорошем начальном приближении в том и только в том случае, когда функция $g(x,h)$ удовлетворяет условию ${\text{||}}g(x,h) - {{h}_{H}}{\text{||}} = o(t)$.

ИСТОЧНИК ФИНАНСИРОВАНИЯ

Исследование выполнено при финансовой поддержке Российского научного фонда (проект № 21-71-30005).