Доклады Российской академии наук. Математика, информатика, процессы управления, 2021, T. 499, № 1, стр. 73-77
ОПТИМАЛЬНАЯ ТРАЕКТОРИЯ НАБЛЮДАТЕЛЯ, ОТСЛЕЖИВАЮЩЕГО ДВИЖЕНИЕ ОБЪЕКТА С ПОРАЖАЮЩИМ УСТРОЙСТВОМ
Академик РАН В. И. Бердышев 1, *
1 Институт математики и механики
им. Н.Н. Красовского Уральского отделения
Российской академии наук
Екатеринбург, Россия
* E-mail: bvi@imm.uran.ru
Поступила в редакцию 23.03.2021
После доработки 27.04.2021
Принята к публикации 28.04.2021
Аннотация
Телесный наблюдатель f, отслеживающий двигающегося по заданной траектории $\mathcal{T}$ объекта t со скоростным поражающим устройством, вынужден скрываться за выпуклые фрагменты окружающей среды. Предлагается способ построения траектории ${{\mathcal{T}}_{f}}$ наблюдателя, обеспечивающей возможность следить за движением объекта на возможно бóльшей части траектории $\mathcal{T}$. В предположении ухода наблюдателя в укрытие по ${{\mathcal{T}}_{f}}$ на постоянной максимальной скорости, объект t выбирает оптимальный скоростной режим движения на своей траектории.
1. В заданном коридоре $Y \subset {{\mathbb{R}}^{3}}$, граница которого гомеоморфна сфере, движется объект t со скоростным поражающим мини-объектом m. В ${{\mathbb{R}}^{3}}$ имеется множество G, $G \cap Y = \emptyset $, являющееся замыканием открытого множества, препятствующее видимости и движению. Наблюдатель f, недружественный по отношению к объекту t, опасаясь мини-объекта, располагается вблизи выпуклых фрагментов границы $\partial G$ множества G. Такой фрагмент, далее обозначаемый через S, должен обеспечить возможность наблюдателю укрыться от m. Скорость ${{{v}}_{m}}$ мини-объекта m существенно превосходит скорости ${{{v}}_{f}},{{{v}}_{t}}$ наблюдателя и объекта, при этом ${{{v}}_{t}} \geqslant {\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{v} } > 0$, где ${\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{v} }$ – минимальная скорость объекта.
Пусть объект t, двигающийся по своей траектории $\mathcal{T} \subset Y$, проходя точку ${{t}_{0}} \in \mathcal{T}$, обнаружил наблюдателя $f \notin Y$, демаскировавшего себя. Учитывая возможность немедленного запуска мини-объекта, наблюдатель занимает исходное для движения положение f0, имея точку ${{t}_{0}}$ в зоне видимости и рассчитывая уйти в укрытие за время $\bar {\tau } = \mathcal{R}{\text{/}}{{{v}}_{m}}$, где $\mathcal{R} = \left\| {{{f}_{0}} - {{t}_{0}}} \right\|{\text{\;}}$. Одновременно с перемещением из начального положения f0 в укрытие наблюдатель продолжает по мере возможности следить за движением объекта t. В предлагаемой модели объект и мини-объект m изображаются точками, а наблюдатель – шаром ${{V}_{\varepsilon }}\left( f \right)$ радиуса $\varepsilon > 0$, в центре f которого расположено средство наблюдения. Попадание мини-объекта в шар ${{V}_{\varepsilon }}\left( f \right)$ означает гибель наблюдателя.
Траектория объекта – это кривая $\mathcal{T} \subset Y$ (маршрут) в совокупности со скоростным режимом ${{{v}}_{t}}$ движения объекта по ней. Требуется выяснить возможности наблюдателя следить за объектом в безопасном для себя режиме, а объекта – уклониться от наблюдения на участке траектории от момента $\tau = 0$ прохождения объектом точки ${{t}_{0}}$ до момента $\bar {\tau }$ полного укрытия наблюдателя.
В данной работе предлагается траектория ${{\mathcal{T}}_{f}}$ наблюдателя, позволяющая ему следить за движением объекта $t$ на максимально длинном, начинающимся в точке ${{t}_{0}}$ участке траектории $\mathcal{T}$. Кроме того, указывается оптимальная для объекта t тактика выбора скорости ${{{v}}_{t}}$ на временном участке $\left[ {0,\bar {\tau }} \right]$.
Задачам движения объектов в среде с препятствиями посвящена, например, работа [1], см. также [2, 3].
2. Фрагмент S – связная открытая на $\partial G$ выпуклая поверхность: в каждой ее точке существует опорная к S плоскость, относительно которой S расположена по одну сторону. Наблюдатель f выбирает фрагмент S и свое начальное положение f0 так, чтобы:
1) расстояние $\rho \left( {{{t}_{0}},S} \right)$ было достаточно большим для обеспечения наблюдателю возможности укрыться от мини-объекта, стартовавшего из точки ${{t}_{0}}$;
2) ${\text{inf\;}}\left\{ {{\text{||}}x - y{\text{||:\;}}x \in S,{\text{\;}}y \in Y} \right\} > \varepsilon $;
3) существовал шар ${{V}_{\varepsilon }}(\bar {f})$, удовлетворяющий включению
(1)
${{V}_{\varepsilon }}\left( {\bar {f}} \right) \subset {\text{co}}({{t}_{0}},S){{\backslash conv}}\left( {{{t}_{0}} \cup S} \right),$4) время $\bar {\tau }$ на процесс перехода наблюдателя в положение ${{V}_{\varepsilon }}\left( {\bar {f}} \right):~{{V}_{\varepsilon }}\left( {{{f}_{\tau }}} \right):0 \leqslant \tau \leqslant \bar {\tau }$, было бы не больше, чем $\mathcal{R}{\text{/}}{{{v}}_{m}}$, где ${{f}_{{\bar {\tau }}}} = \bar {f}$, далее предполагается, что $\bar {f}$ – ближайшая к ${{f}_{0}}$ из точек, удовлетворяющих включению (1);
5) существует плоскость Q, содержащая точку ${{t}_{0}}$, опорная к S в некоторой точке $s \in S$, при этом S и точка ${{y}_{s}} \in Y$, ближайшая к s, расположены по разные стороны от Q.
Объект t движется через точку ${{t}_{0}}$ в сторону точки ${{y}_{{\text{s}}}}$. Траектория движения центра шара ${{V}_{\varepsilon }}\left( {{{f}_{\tau }}} \right)$ при переходе из положения ${{V}_{\varepsilon }}\left( {{{f}_{0}}} \right)$ в положение ${{V}_{\varepsilon }}\left( {{{f}_{{\bar {\tau }}}}} \right)$ обозначается через ${{\mathcal{T}}_{f}}$. Естественно предположить, что $\rho \left( {{{f}_{\tau }},S} \right) = \varepsilon $ $\left( {0 \leqslant \tau \leqslant \bar {\tau }} \right)$ и наблюдатель движется по ${{\mathcal{T}}_{f}}$ с постоянной максимальной скоростью ${{{v}}_{f}}$. Ради простоты будем предполагать, что поверхность S строго выпукла, т.е. не содержит прямолинейных отрезков. Нам понадобится лишь часть поверхности S, расположенная между Q и параллельной ей плоскостью $\bar {Q}$, содержащей точку $\bar {f}$, и все построения будут производиться “выше” плоскости $\bar {Q}$. Пусть
Лемма 1. Отображения $\tau \, \to \,{{K}_{\tau }}~\, \cap \,{{V}_{R}}(s)$, $\tau \, \to \,{{\mathcal{K}}_{\tau }}$ ∩ VR(s) непрерывны по Хаусдорфу, где R = = ${\text{||}}{{t}_{0}} - {{f}_{0}}{\text{||}}$.
3. Пусть ${{S}_{\varepsilon }}$ – часть поверхности $\{ x:~\rho (x,S) = \varepsilon \} $, невидимая из точки ${{t}_{0}}$, расположенная между плоскостями $Q,~\bar {Q}$. Определим на ${{S}_{\varepsilon }}$ систему координат $\left\{ {\left( {h,\varphi } \right)} \right\}$ так, что ее ось – луч с началом в центре отрезка $Z \cap \,~\overline {Q~} \cap \,~{\text{conv}}S$, содержащий точку s, где Z – плоскость, натянутая на точки ${{t}_{0}},~s,~\bar {f}$; “широта” h определяется положением плоскости ${{Q}_{h}} = \left( {1 - h} \right)\bar {Q} + hQ$, $0 \leqslant h \leqslant 1$, $\left( {h,\varphi } \right) \in {{Q}_{h}}$; “долгота” φ – величина угла, на который следует повернуть вокруг оси плоскость Z до поглощения точки $(h,\varphi )$.
В простейшем случае, когда ${{\mathcal{T}}_{f}} \subset Z$, справедливо соотношение ${{\mathcal{K}}_{{\tau '}}} \subset {{\mathcal{K}}_{{\tau ''}}}$ $\left( {\tau ' \leqslant \tau ''} \right)$, из которого следует, что для близких к нулю τ начальная часть траектории $\mathcal{T}$ содержится в $\mathcal{K}_{\tau }^{^\circ }$ и, значит, не видна наблюдателю ${{f}_{\tau }}$, где $\mathcal{K}^\circ $ – внутренность множества $\mathcal{K}$. От этого недостатка можно избавиться, изменив начальную часть траектории ${{\mathcal{T}}_{f}}$. Если наблюдатель из начальной точки f0 пройдет участок ${{f}_{\varphi }} = \left( {1,\varphi } \right)$, $0 \leqslant \varphi \leqslant \delta $, при малом δ, то весь отрезок $\left[ {s,{{t}_{0}}} \right]$ и начальная часть траектории $\mathcal{T}$ окажутся вне множества $\mathcal{K}_{{{{f}_{\varphi }}}}^{^\circ }$ и будут видны наблюдателю ${{f}_{\varphi }}$.
4. Поскольку $\bar {f}$ – ближайшая к f0 точка из ${{S}_{\varepsilon }}$, удовлетворяющая включению (1), то для любой траектории
(2)
${{\mathcal{T}}_{f}} = \{ {{f}_{\tau }}{\text{:}}~~0 \leqslant \tau \leqslant \bar {\tau },~~{{f}_{{\bar {\tau }}}} = \bar {f}\} \subset {{S}_{\varepsilon }},$(3)
${{\bar {\tau }}_{f}} = \frac{{\left| {{{\mathcal{T}}_{f}}} \right|}}{{{{{v}}_{f}}}} \leqslant {{\tau }_{m}} = \frac{{\rho \left( {{{t}_{0}},W} \right)}}{{{{{v}}_{m}}}},$Из условия (1) следует, что $\mathcal{K}_{{\bar {f}}}^{^\circ }$ содержит отрезок $(s,{{t}_{0}}]$ и начальную часть траектории $\mathcal{T}$. Пусть $\tilde {t} \in \mathcal{T}$ – ближайшая к ${{t}_{0}}$ точка из пересечения $\mathcal{T} \cap {{k}_{{\bar {f}}}}$. Далее через $\mathcal{T}$ будем обозначать участок траектории объекта между точками ${{t}_{0}}$ и $\tilde {t}$.
Задача наблюдателя – поиск траектории 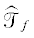 , удовлетворяющей условиям (3)–(4), которая позволит отслеживать движение объекта
на возможно бóльшей части траектории $\mathcal{T}$.
, удовлетворяющей условиям (3)–(4), которая позволит отслеживать движение объекта
на возможно бóльшей части траектории $\mathcal{T}$.
5. Вначале рассмотрим частный случай, когда S является выпуклым конусом с вершиной s и, значит, конус ${{K}_{\tau }}$ является частью двугранного угла с гранями, касающимися боковой поверхности конуса S. Введем отображение траектории $\mathcal{T}$ на поверхность ${{S}_{\varepsilon }}$:
(4)
$z \to f\left( z \right):s \in \left[ {z,f\left( z \right)} \right]~~~\left( {z \in \mathcal{T},~f\left( z \right) \in {{S}_{\varepsilon }}} \right),$Наложим на $\mathcal{T}$ дополнительное условие:
(Е) Для любой точки $z \in \mathcal{T}$ выполняется соотношение ${{K}_{{f\left( z \right)}}} \cap \mathcal{T} = z$.
При этом условии отображение (4) гомеоморфно. Класс кривых, удовлетворяющих условию (Е), достаточно широк. В частности, он содержит прямолинейные траектории, не содержащиеся в плоскости Z. Условие (Е) гарантирует наблюдателю f видимость всей траектории $\mathcal{T}$ при движении по траектории $\mathcal{T}_{f}^{*}$. Но f хотел бы наблюдать движение объекта на максимально протяженном участке. Далее через ${{\mathcal{T}}_{f}}\left( {f{\kern 1pt} '~,f{\kern 1pt} ''} \right)$ обозначается часть траектории ${{\mathcal{T}}_{f}}$ между точками $f'$ и $f''$.
Пусть $t \in \mathcal{T}$, $f = f\left( t \right)$. Определим верхнюю грань
(5)
$\hat {\rho }\, = \,\left\{ {\mathop {\sup }\limits_{t \in \mathcal{T}} \rho ({{t}_{0}},t)\,:\,f(t)\, \in \,\mathcal{T}_{f}^{*},~\frac{{\rho ({{f}_{0}},f)\, + \,d(f,\bar {f})}}{{{{{v}}_{f}}}}\, \leqslant \,{{\tau }_{m}}} \right\},$Поскольку $\mathcal{T} \subset K_{{\bar {f}}}^{^\circ }$, то $\hat {f} \ne \bar {f}$. Искомую траекторию ${{\hat {\mathcal{T}}}_{f}}$ составим из двух дуг:
первая является замыканием части траектории $\mathcal{T}_{f}^{*}$ (см. рис. 1), ограниченной точками f0 и $\hat {f}$, т.е. $\mathcal{T}_{f}^{1} = \mathcal{T}_{f}^{*}({{f}_{0}},~\hat {f})$, вторая – кратчайшая кривая на поверхности ${{S}_{\varepsilon }}$, соединяющая точки $\hat {f}$ и $\bar {f}$.Рис. 1.
Оптимальная траектория наблюдателя. На рисунке плоскости $Q,~\bar {Q},~Z$, траектория $\mathcal{T}$, граница ${{k}_{{\bar {\tau }}}}$ конуса ${{K}_{{\bar {\tau }}}}$ и поверхность ${{S}_{\varepsilon }}$ изображены сплошными линиями, поверхность S – штриховой, оптимальная траектория 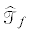 – пунктирной линиями.
– пунктирной линиями.
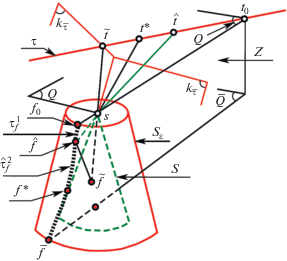
Двигаясь по траектории $\mathcal{T}_{f}^{1}$, наблюдатель видит всю траекторию $\mathcal{T}$ объекта. Переход наблюдателя $f = \left( {h,\varphi } \right)$ на дугу $\mathcal{T}_{f}^{2}$ и дальнейшее движение в сторону точки $\bar {f}$ влечет уменьшение широты h и возникновение невидимого наблюдателем участка $\mathcal{T} \cap \mathcal{K}_{f}^{^\circ }$. При стремлении наблюдателя f к $\bar {f}$ множество ${{\mathcal{K}}_{f}} \cap {{V}_{R}}\left( s \right)$ сходится к ${{\mathcal{K}}_{{\bar {f}}}} \cap {{V}_{R}}\left( s \right)$ в метрике Хаусдорфа (см. лемму 1). По построению множество $\mathcal{K}_{{\bar {f}}}^{^\circ }$ содержит траекторию $\mathcal{T}$. Поэтому существует позиция $f* = {{f}_{{\tau *}}} \in \mathcal{T}_{f}^{2}$ такая, что для всех последующих позиций $f,~~f \to \bar {f}$, дуга траектории $\mathcal{T}$ от ${{t}_{0}}$ до некоторой точки ${{t}_{f}} \in \mathcal{T}$ содержится в $\mathcal{K}_{f}^{^\circ }$, т.е. лежит вне зоны видимости наблюдателя, и при этом $\rho \left( {{{t}_{f}},{{k}_{{\bar {\tau }}}}} \right) \to 0$ (при $f \to \bar {f}$). Отсюда, в частности, следует, что часть траектории $\mathcal{T}$ от $t* = z\left( {f{\text{*}}} \right)$ до точки $\tilde {t}$ не удовлетворяет условию (Е) и, как уже отмечалось, $\hat {f} \ne \bar {f}$, где z(f) – обратное к (4) отображение.
Объект t, предполагая, что наблюдатель намерен двигаться по приведенной выше траектории 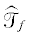 с постоянной максимальной скоростью, и стремясь сократить длину траектории, пройденной
под наблюдением, будет придерживаться следующей тактики движения.
с постоянной максимальной скоростью, и стремясь сократить длину траектории, пройденной
под наблюдением, будет придерживаться следующей тактики движения.
Вариант 1. Во временном промежутке $\left[ {0,\tau {\text{*}}} \right]$ объект движется с минимальной скоростью, преодолев расстояние ${\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{v} } \cdot \tau {\text{*}}$ под наблюдением. В момент τ* участок траектории $\mathcal{T}$ от ${{t}_{0}}$ до точки ${{t}_{f}}$ попадает в невидимую наблюдателем зону, в которой объект продолжает свое движение, учитывая, что ${{t}_{f}} \to \tilde {t}$, и преодолевает расстояние $\left| \mathcal{T} \right| - {\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{v} } \cdot \tau {\text{*}}$ вне зоны наблюдения.
Вариант 2. Объект движется вместе с точкой $z\left( f \right)$ на участке от ${{t}_{0}}$ до $\hat {t}$ под наблюдением. Для позиции $f\left( t \right)$ при $t \in z(\mathcal{T}_{f}^{2})$ выполняется соотношение $\mathcal{K}_{{f\left( t \right)}}^{^\circ } \cap \mathcal{T} \ne \emptyset $, поэтому объект в дальнейшем движется, включившись в множество $\mathcal{K}_{{f\left( t \right)}}^{^\circ }$, и пройдет вне наблюдения участок длины $\left| \mathcal{T} \right| - \rho (\hat {t},{{t}_{0}})$.
Установлены следующие утверждения.
Лемма 2. Пусть S – выпуклая коническая поверхность с вершиной $s$, $\tilde {t}$ – ближайшая к ${{t}_{0}}$ точка из пересечения траектории объекта с ${{k}_{{\bar {\tau }}}}$, $\mathcal{T}$ – часть траектории объекта, ограниченная точками ${{t}_{0}}$ и $\tilde {t}$; точка $\hat {t}$ доставляет верхнюю грань (5) ${{f}_{{\hat {\tau }}}} = \hat {f} = f(\hat {t})$ (см. (4)); 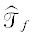 – траектория наблюдателя, заданная равенством (6).
– траектория наблюдателя, заданная равенством (6).
Тогда
1) для любого $\tau \in \left[ {0,\hat {\tau }} \right]$ траектория $\mathcal{T}$ видна наблюдателю ${{f}_{\tau }}$;
2) $\mathcal{K}_{\tau }^{^\circ } \cap \mathcal{T} \ne \emptyset $ для любого $\tau \in \left( {\hat {\tau },\bar {\tau }} \right]$;
3) существует $\tau * \in \left( {\hat {\tau },\bar {\tau }} \right)$ такой, что для любого $\tau \in \left( {\tau {\text{*}},\bar {\tau }} \right)$ найдется точка ${{t}_{\tau }}$, удовлетворяющая условиям ${{t}_{\tau }} \to \tilde {t}$ при $\tau \to \bar {\tau }$, и отрезок траектории $\mathcal{T}$ от до ${{t}_{\tau }}$ содержится в $\mathcal{K}_{\tau }^{^\circ }$.
Теорема. Пусть выполняются условия леммы 2. Тогда существуют $\tau {\text{*}} \in \left( {\hat {\tau },\bar {\tau }} \right)$ и скоростной режим движения объекта по траектории $\mathcal{T}$ (см. варианты 1, 2), позволяющий пройти вне наблюдения концевой участок траектории $\mathcal{T}$ длины
6. В общем случае, когда S – выпуклая поверхность, найдем
Находясь в любой позиции $f \in \mathcal{T}_{f}^{*}$, наблюдатель видит всю траекторию $\mathcal{T}$, так как $\mathcal{K}_{f}^{^\circ } \cap \mathcal{T} = \emptyset $. Используя изложенный выше способ, построим траекторию 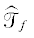 (см. (6)). Движение по ней на максимальной скорости гарантирует наблюдателю возможность
следить за движением объекта на участке траектории $\mathcal{T}$ от ${{t}_{0}}$ до точки ${\text{min}}\{ {\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{v} } \cdot \tau {\text{*}},\rho ({{t}_{0}},\hat {t})\} $ (при оптимальном выборе объектом варианта тактики движения).
(см. (6)). Движение по ней на максимальной скорости гарантирует наблюдателю возможность
следить за движением объекта на участке траектории $\mathcal{T}$ от ${{t}_{0}}$ до точки ${\text{min}}\{ {\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{v} } \cdot \tau {\text{*}},\rho ({{t}_{0}},\hat {t})\} $ (при оптимальном выборе объектом варианта тактики движения).
Список литературы
Лю В. Методы планирования пути в среде с препятствиями (обзор) // Математика и мат. моделирование. 2018. № 1. С. 15–58.
Красовский Н.Н., Субботин А.И. Позиционные дифференциальные игры. М.: Наука, 1974. 456 с.
Бердышев В.И., Костоусов В.Б. Визуальные характеристики наблюдения и оптимальные траектории. Ин-т математики и механики им. Н.Н. Красовского УрО РАН. Новосибирск: Изд-во СО РАН, 2021. 250 с.
Дополнительные материалы отсутствуют.
Инструменты
Доклады Российской академии наук. Математика, информатика, процессы управления