Доклады Российской академии наук. Математика, информатика, процессы управления, 2021, T. 500, № 1, стр. 62-66

КОРРЕКТНАЯ РАЗРЕШИМОСТЬ И ЭКСПОНЕНЦИАЛЬНАЯ УСТОЙЧИВОСТЬ РЕШЕНИЙ ВОЛЬТЕРРОВЫХ ИНТЕГРО-ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ

Н. А. Раутиан^1, *

¹ Московский государственный университет имени М.В. Ломоносова, Московский центр фундаментальной и прикладной математики
Москва, Россия

^* E-mail: nrautian@mail.ru

Поступила в редакцию 08.07.2021
После доработки 08.07.2021
Принята к публикации 18.08.2021

DOI: 10.31857/S268695432105012X

Полный текст (PDF)

Аннотация

Работа посвящена исследованию абстрактных интегро-дифференциальных уравнений, являющихся операторными моделями задач теории вязкоупругости. В качестве ядер интегральных операторов могут быть рассмотрены, в частности, суммы убывающих экспонент или суммы функций Работнова с положительными коэффициентами, имеющие широкое применение в теории вязкоупугости. Приводится метод сведения исходной начальной задачи для модельного интегро-дифференциального уравнения с операторными коэффициентами в гильбертовом пространстве к задаче Коши для дифференциального уравнения первого порядка. Установлено экспоненциальное убывание решений при известных предположениях для ядер интегральных операторов. На основе полученных результатов установлена корректная разрешимость исходной начальной задачи для вольтеррова интегро-дифференциального уравнения с соответствующими оценками решения.

Ключевые слова: вольтерровы интегро-дифференциальные уравнения, линейные дифференциальные уравнения в гильбертовых пространствах, экспоненциальная устойчивость

В статье будет рассмотрено абстрактное интегро-дифференциальное уравнение с операторными коэффициентами в гильбертовом пространстве и представлена общая схема исследования, которую можно применить ко многим другим линейным моделям, содержащим вольтерровы интегральные операторы.

Указанное абстрактное интегро-дифференциальное уравнение может быть реализовано как интегро-дифференциальное уравнение в частных производных, возникающее в теории линейной вязкоупругости (см. [1–6]). К рассматриваемому классу уравнений относятся также интегро-дифференциальные уравнения Гуртина–Пипкина, описывающие процесс распространения тепла в средах с памятью (см. [7, 8]). Кроме того, указанные уравнения возникают в задачах усреднения в многофазных средах (закон Дарси) (см. [9]). В качестве ядер интегральных операторов могут быть рассмотрены, в частности, суммы убывающих экспонент или суммы дробно-экспоненциальных функций (функций Работнова) с положительными коэффициентами, имеющие широкое применение в теории вязкоупругости (см. [10]).

Представленные в данной работе результаты базируются на подходе, связанном с исследованием линейных дифференциальных уравнений в банаховых пространствах (см. [11, 12]), и являются продолжением и развитием исследований, опубликованных в работах [13, 14], посвященных спектральному анализу оператор-функций, являющихся символами вольтерровых интегро-дифференциальных уравнений.

Следует отметить, что существуют и другие подходы для описания колебаний неоднородных многофазных сред. В качестве примера можно привести подход, связанный с применением эллиптических функционально-дифференциальных уравнений, изложенный в работе [15].

1. ОПРЕДЕЛЕНИЯ, ОБОЗНАЧЕНИЯ И ПОСТАНОВКА ЗАДАЧИ

Пусть H – сепарабельное гильбертово пространство, A – самосопряженный положительный оператор $A{\text{*}} = A \geqslant {{\kappa }_{0}}I$ $({{\kappa }_{0}} > 0)$, действующий в пространстве H. Пусть $B$ – самосопряженной неотрицательный оператор, действующий в пространстве H с областью определения $D\left( B \right)$, такой, что $D(A) \subseteq D(B)$, удовлетворяющий неравенству $\left\| {Bx} \right\| \leqslant \kappa \left\| {Ax} \right\|$, $\kappa > 0$ для любого $x \in Dom\left( A \right)$, I – тождественный оператор в пространстве H.

Рассмотрим следующую задачу для интегро-дифференциального уравнения второго порядка на положительной полуоси ${{\mathbb{R}}_{ + }} = (0,\infty )$:

(1)

$\begin{gathered} \frac{{{{d}^{2}}u(t)}}{{d{{t}^{2}}}} + \left( {A + B} \right)u(t) - \int\limits_0^t {{K}_{1}}(t - s)Au(s)ds - \\ - \,\int\limits_0^t {{K}_{2}}(t - s)Bu(s)ds = f(t), \\ t \in {{\mathbb{R}}_{ + }}, \\ \end{gathered} $

(2)

$u( + 0) = {{\varphi }_{0}},\quad {{u}^{{(1)}}}( + 0) = {{\varphi }_{1}}.$

Предположим, что ядра интегральных операторов ${{K}_{i}}(t),$ $i = 1,2$, имеют следующее представление:

(3)

${{K}_{i}}(t) = \int\limits_0^{ + \infty } {{e}^{{ - t\tau }}}d{{\mu }_{i}}(\tau ),\quad i = 1,2,$

где $d{{\mu }_{i}}$ (i = 1, 2) – положительные меры, которым соответствуют возрастающие, непрерывные справа функции распределения ${{\mu }_{i}}$, соответственно. Интеграл понимается в смысле Стилтьеса. Кроме того, будем считать, что выполнены условия

(4)

$\int\limits_0^{ + \infty } \,\frac{{d{{\mu }_{i}}(\tau )}}{\tau } < 1,\quad i = 1,2.$

Положим

(5)

${{A}_{0}}: = \left( {1 - \int\limits_0^{ + \infty } \,\frac{{d{{\mu }_{1}}(\tau )}}{\tau }} \right)A + \left( {1 - \int\limits_0^{ + \infty } \,\frac{{d{{\mu }_{2}}(\tau )}}{\tau }} \right)B.$

Замечание 1. Из свойств операторов A и $B$ и неравенства Гайнца (см. [11]) следует, что оператор ${{A}_{0}}$, является обратимым, операторы Q₁ := := ${{A}^{{1/2}}}A_{0}^{{ - 1/2}}$, ${{Q}_{2}}: = {{B}^{{1/2}}}A_{0}^{{ - 1/2}}$ – допускают ограниченное замыкание в H, $A_{0}^{{ - 1}}$ – ограниченный оператор.

Превратим область определения $D(A_{0}^{\beta })$ оператора $A_{0}^{\beta }$, $\beta > 0$ в гильбертово пространство H_β, введя на $D(A_{0}^{\beta })$ норму ${\text{||}} \cdot \,{\text{|}}{{{\text{|}}}_{\beta }} = {\text{||}}A_{0}^{\beta }\, \cdot \,{\text{||}}$, эквивалентную норме графика оператора $A_{0}^{\beta }$.

Определение 1. Будем называть век-тор функцию $u(t)$ классическим решением задачи (1), (2), если $u(t) \in {{C}^{2}}({{\mathbb{R}}_{ + }},H)$, $Au(t),\;Bu(t) \in C({{\mathbb{R}}_{ + }},H)$, $u(t)$ удовлетворяет уравнению (1) для каждого значения $t \in {{\mathbb{R}}_{ + }}$ и начальному условию (2).

2. СВЕДЕНИЕ ИСХОДНОЙ ЗАДАЧИ К ДИФФЕРЕНЦИАЛЬНОМУ УРАВНЕНИЮ ПЕРВОГО ПОРЯДКА

Применим формулу интегрирования по частям к интегралам в левой части уравнения (1) и заметим, что $A = A_{0}^{{1/2}}Q_{1}^{ * }{{Q}_{1}}A_{0}^{{1/2}}$, $B = A_{0}^{{1/2}}Q_{2}^{ * }{{Q}_{2}}A_{0}^{{1/2}}$. Введем новые переменные

${v}(t): = u{\kern 1pt} '(t),\quad {{\xi }_{0}}(t): = A_{0}^{{1/2}}u(t),$

(6)

$\begin{gathered} {{\xi }_{k}}(t,\tau ) = \int\limits_0^t \frac{{{{e}^{{ - (t - s)\tau }}}}}{{\sqrt \tau }}{{Q}_{k}}A_{0}^{{1/2}}\frac{{du(s)}}{{ds}}ds, \\ t > 0,\quad k = 1,2,\quad \tau \in \bigcup\limits_{k = 1}^2 \,{\text{supp}}d{{\mu }_{k}}. \\ \end{gathered} $

Введем следующее обозначение:

(7)

${{M}_{k}}(t): = \int\limits_0^{ + \infty } \frac{{{{e}^{{ - t\tau }}}d{{\mu }_{k}}(\tau )}}{\tau },\quad t \geqslant 0,\quad k = 1,2.$

Тогда задача (1), (2) формально может быть приведена к следующей начальной задаче для системы дифференциальных уравнений первого порядка:

(8)

$\begin{gathered} \frac{{d{v}(t)}}{{dt}} + A_{0}^{{1/2}}\left[ {{{\xi }_{0}}(t) + \sum\limits_{k = 1}^2 \int\limits_0^\infty \frac{1}{{\sqrt \tau }}Q_{k}^{ * }{{\xi }_{k}}(t,\tau )d{{\mu }_{k}}(\tau )} \right] = {{f}_{1}}(t), \\ \frac{{d{{\xi }_{0}}(t)}}{{dt}} = A_{0}^{{1/2}}{v}(t), \\ \frac{{d{{\xi }_{1}}(t,\tau )}}{{dt}} = \frac{1}{{\sqrt \tau }}{{Q}_{1}}A_{0}^{{1/2}}{v}(t) - \tau {{\xi }_{1}}(t,\tau ), \\ \frac{{d{{\xi }_{2}}(t,\tau )}}{{dt}} = \frac{1}{{\sqrt \tau }}{{Q}_{2}}A_{0}^{{1/2}}{v}(t) - \tau {{\xi }_{2}}(t,\tau ), \\ \end{gathered} $

где $t > 0$, $\tau \in \bigcup\limits_{k = 1}^2 \,{\text{supp}}\,d{{\mu }_{k}}$, f₁(t) := f(t) – (M₁(t)A + + ${{M}_{2}}(t)B){{\varphi }_{0}},$

(9)

$\begin{gathered} \mathop {\left. {{v}(t)} \right|}\nolimits_{t = 0} = {{\varphi }_{1}},\quad \mathop {\left. {{{\xi }_{0}}(t)} \right|}\nolimits_{t = 0} = A_{0}^{{1/2}}{{\varphi }_{0}}, \\ \mathop {\left. {{{\xi }_{k}}(t,\tau )} \right|}\nolimits_{t = 0} = 0,\quad k = 1,2. \\ \end{gathered} $

Теперь наша задача состоит в том, чтобы превратить систему уравнений (8), (9) в начальную задачу в некотором расширенном функциональном пространстве, в котором эта задача будет корректной, а также установить соответствие (не только формальное) между решением задачи (8), (9) и решением исходной задачи (1), (2).

3. ЗАДАЧА КОШИ В РАСШИРЕННОМ ФУНКЦИОНАЛЬНОМ ПРОСТРАНСТВЕ. ФОРМУЛИРОВКА РЕЗУЛЬТАТОВ

Через ${{\Omega }_{k}}$ обозначим пространства $L_{{{{\mu }_{k}}}}^{2}\left( {{{\mathbb{R}}_{ + }},H} \right)$ вектор-функций на полуоси ${{\mathbb{R}}_{ + }} = (0,\infty )$ со значениями в H, снабженные нормами

${\text{||}}u{\text{|}}{{{\text{|}}}_{{{{\Omega }_{k}}}}} = \mathop {\left( {\int\limits_0^{ + \infty } {\text{||}}u(s){\text{||}}_{H}^{2}d{{\mu }_{k}}(s)} \right)}\nolimits^{1/2} ,$

соответственно.

Рассмотрим сильно непрерывную мультипликативную полугруппу ${{L}_{k}}(t)$ в пространстве ${{\Omega }_{k}}$ (см. [12, c. 65]): ${{L}_{k}}(t)\xi (\tau ) = {{e}^{{t\tau }}}\xi (\tau ),$ $\xi (\tau ) \in {{\Omega }_{k}}$, t ≥ 0, $\tau \in {\text{supp}}{{\mu }_{k}}$. Известно, что линейный оператор ${{\mathbb{T}}_{k}}\xi (\tau ) = \tau \xi (\tau )$ в пространстве Ω_k с областью определения D(T_k) = $\left\{ {\xi \in {{\Omega }_{k}}{\text{:}}\,\,\tau \xi (\tau ) \in {{\Omega }_{k}}} \right\}$ является генератором полугруппы ${{L}_{k}}(t)$ (см. [12, c. 65]).

Введем операторы ${{\mathbb{B}}_{k}}{\text{:}}\,\,H \to {{\Omega }_{k}}$ и сопряженные операторы $\mathbb{B}_{k}^{ * }{\text{:}}\,\,{{\Omega }_{k}} \to H$ (k = 1, 2) следующим образом:

$\begin{gathered} {{\mathbb{B}}_{k}}{v} = \frac{1}{{\sqrt \tau }}{{Q}_{k}}{v},\quad \mathbb{B}_{k}^{ * }\xi (\tau ) = Q_{k}^{ * }\int\limits_0^\infty \frac{1}{{\sqrt \tau }}\xi (\tau )d{{\mu }_{k}}(\tau ), \\ k = 1,2,\quad \tau \in {\text{supp}}\,d{{\mu }_{k}}. \\ \end{gathered} $

Рассмотрим гильбертово пространство $\mathbb{H}$ = = $H \oplus H \oplus ( \oplus _{{k = 1}}^{2}{{\Omega }_{k}}),$ снабженное нормой

$\begin{gathered} \mathop {\left\| {({v},{{\xi }_{0}},{{\xi }_{1}}(\tau ),{{\xi }_{2}}(\tau ))} \right\|}\nolimits_\mathbb{H}^2 = {\text{||}}{v}{\text{||}}_{H}^{2} + \,{\text{||}}{{\xi }_{0}}{\text{||}}_{H}^{2} + \sum\limits_{k = 1}^2 {\text{||}}{{\xi }_{k}}(\tau ){\text{||}}_{{{{\Omega }_{k}}}}^{2}, \\ \tau \in \bigcup\limits_{k = 1}^2 \,{\text{supp}}\,d{{\mu }_{k}}, \\ \end{gathered} $

которое будем называть расширенным гильбертовым пространством.

Введем линейный оператор $\mathbb{A}$ в пространстве $\mathbb{H}$ с областью определения

$\begin{gathered} D(\mathbb{A}) = {\text{\{ }}({v},{{\xi }_{0}},{{\xi }_{1}}(\tau ),{{\xi }_{2}}(\tau )) \in \mathbb{H}:{v} \in {{H}_{{1/2}}}, \\ {{\xi }_{0}} + \mathbb{B}_{k}^{ * }{{\xi }_{k}}(\tau ) \in {{H}_{{1/2}}},{{\xi }_{k}}(\tau ) \in D({{T}_{k}}),k = 1,2{\text{\} }}, \\ \end{gathered} $

действующий следующим образом:

$\begin{gathered} \mathbb{A}{{({v},{{\xi }_{0}},{{\xi }_{1}}(\tau ),{{\xi }_{2}}(\tau ))}^{T}} = \\ = \left( { - A_{0}^{{1/2}}\left[ {{{\xi }_{0}} + \sum\limits_{k = 1}^2 \,\mathbb{B}_{k}^{ * }{{\xi }_{k}}(\tau )} \right],} \right. \\ {{\left. {_{{_{{_{{_{{_{{_{{_{{_{{_{{_{{_{{_{{}}}}}}}}}}}}}}}}}}}}}}}}A_{0}^{{1/2}}{v},{{B}_{k}}A_{0}^{{1/2}}v - {{\mathbb{T}}_{k}}{{\xi }_{k}}(\tau ),\,\,k = 1,2} \right)}^{T}}. \\ \end{gathered} $

Введем четырехкомпонентные векторы вида

$\begin{gathered} Z(t) = ({v}(t),{{\xi }_{0}}(t),{{\xi }_{1}}(t,\tau ),{{\xi }_{2}}(t,\tau )) \in \mathbb{H}, \\ z = ({{{v}}_{0}},{{\xi }_{{00}}},{{\xi }_{{10}}}(\tau ),{{\xi }_{{20}}}(\tau )) \in \mathbb{H}. \\ \end{gathered} $

Теперь мы можем переписать систему (8), (9) в виде дифференциального уравнения первого порядка в расширенном функциональном пространстве. Рассмотрим следующую задачу Коши в пространстве $\mathbb{H}$:

(10)

$\frac{d}{{dt}}Z(t) = \mathbb{A}Z(t),$

(11)

$Z(0) = z.$

Определение 2. Вектор Z(t) = $({v}(t),{{\xi }_{0}}(t)$, ${{\xi }_{1}}(t,\tau ),{{\xi }_{2}}(t,\tau )) \in \mathbb{H}$ называется классическим решением задачи (10), (11), если ${v}(t)$, ${{\xi }_{0}}(t) \in {{C}^{1}}((0, + \infty )$, H), ${{\xi }_{k}}(t,\tau ) \in {{C}^{1}}((0, + \infty ),H),$ k = 1, 2, по переменной t, для любого $\tau \in \bigcup\limits_{k = 1}^2 \,{\text{supp}}\,d{{\mu }_{k}}$, $Z(t) \in C([0, + \infty ),D(\mathbb{A}))$, вектор Z(t) удовлетворяет уравнению (10) для любого $t \in {{\mathbb{R}}_{ + }}$и начальному условию (11).

Определение 3 (см. [11]). Линейный оператор $\mathcal{A}$ c областью определения, плотной в гильбертовом пространстве, называется диссипативным, если ${\text{Re}}\left( {\mathcal{A}x,x} \right) \leqslant 0$ при $x \in D(\mathcal{A})$ и максимально диссипативным, если он диссипативен и не имеет нетривиальных диссипативных расширений.

Теорема 1. Пусть выполнены условия (4). Тогда оператор $\mathbb{A}$ в пространстве $\mathbb{H}$ с плотной областью определения $D(\mathbb{A})$ является максимально диссипативным.

Теорема 2. Пусть выполнены условия (4). Тогда линейный оператор $\mathbb{A}$ является генератором сжимающей C₀-полугруппы $S(t) = {{e}^{{t\mathbb{A}}}}$ в пространстве $\mathbb{H}$, при этом решение задачи (10), (11) представимо в виде $Z(t) = S(t)z,$ $t > 0,$ и для любого $z \in D(\mathbb{A})$ справедливо энергетическое равенство

(12)

$\begin{gathered} \frac{d}{{dt}}{\text{||}}S(t)z{\text{||}}_{\mathbb{H}}^{2} = \\ = - 2\left( {\int\limits_0^{ + \infty } \,\tau {\text{||}}{{\xi }_{1}}(t,\tau ){\text{||}}_{H}^{2}d{{\mu }_{1}}(\tau ) + \int\limits_0^{ + \infty } \,\tau {\text{||}}{{\xi }_{2}}(t,\tau ){\text{||}}_{H}^{2}d{{\mu }_{2}}(\tau )} \right). \\ \end{gathered} $

4. ЭКСПОНЕНЦИАЛЬНАЯ УСТОЙЧИВОСТЬ

Перед формулировкой теоремы об экспоненциальной устойчивости сформулируем следующее утверждение.

Утверждение 1. Существует такое $\gamma > 0$, что для всех $p > 0$ справедливо неравенство

(13)

$ - \int\limits_0^{ + \infty } \tau {{e}^{{ - p\tau }}}d{{\mu }_{k}}(\tau ) + \gamma \int\limits_0^{ + \infty } {{e}^{{ - p\tau }}}d{{\mu }_{k}}(\tau ) \leqslant 0,\quad k = 1,2.$

Приведем результат об экспоненциальной устойчивости полугруппы $S\left( t \right),t \geqslant 0$, в предположении, что H – сепарабельное вещественное гильбертово пространство.

Теорема 3. Пусть $S(t)z$ – решение задачи (10), (11) при $t > 0$ и выполнены условия (4). Тогда справедливо неравенство

(14)

$\mathop {\left\| {S(t)z} \right\|}\nolimits_\mathbb{H} \leqslant \sqrt 3 \mathop {\left\| z \right\|}\nolimits_\mathbb{H} {{e}^{{ - \omega t}}}$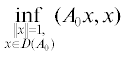

для любого $z \in \mathbb{H}{\text{.}}$ При этом $\omega = \mathop {\max }\limits_{\beta > 0} {{\omega }_{\beta }},$ ω_β = = $\frac{1}{6}min\left\{ {\frac{\gamma }{{{{\gamma }_{1}}(\beta )}};\frac{1}{{{{\gamma }_{2}}(a)}}} \right\},$

$\begin{gathered} {{\gamma }_{1}}(\beta ): = \mathop {\max }\limits_{k = 1,2} \left\{ {\frac{3}{{M(\beta )}}\left[ {(3 + {{M}_{k}}(\beta ) + \mathop {(2{{\lambda }_{0}})}\nolimits^{ - 1} ){\text{||}}Q_{k}^{{ - 1}}{\text{|}}{{{\text{|}}}^{2}}{{ + }_{{_{{_{{_{{_{{_{{_{{_{{}}}}}}}}}}}}}}}}}} \right.} \right. \\ \left. {_{{_{{_{{_{{_{{_{{_{{_{{_{{_{{_{{_{{}}}}}}}}}}}}}}}}}}}}}}}}\left. { + \,{{M}_{k}}(0)\left( {1 + \frac{2}{3}M(\beta )} \right)\mathop {{\text{||}}Q_{k}^{{}}{\text{||}}}\nolimits^2 } \right] + \frac{1}{2}} \right\}, \\ \end{gathered} $

${{\gamma }_{2}}(\beta ): = \frac{3}{{M(\beta )}}max\left\{ {1,\;\frac{2}{{{{\lambda }_{0}}}} \cdot \mathop {\max }\limits_{k = 1,2} \{ {\text{||}}Q_{k}^{{ - 1}}{\text{|}}{{{\text{|}}}^{2}}{{M}_{k}}(\beta )\} } \right\} + \frac{1}{{\sqrt {{{\lambda }_{0}}} }},$

где $\gamma > 0$ определяется неравенством (13), λ₀ = =

, $M(\beta ): = \sum\limits_{k = 1}^2 \,{{M}_{k}}(\beta ).$

5. КОРРЕКТНАЯ РАЗРЕШИМОСТЬ

Рассмотрим задачу Коши для неоднородного уравнения

(15)

$\frac{d}{{dt}}Z(t) = \mathbb{A}Z(t) + F(t),$

(16)

$Z(0) = z.$

Будем предполагать, что вектор-функция $F(t)$ имеет вид $F(t): = ({{f}_{1}}(t),0,0,0)$, f₁(t) = f(t) – (M₁(t)A + + ${{M}_{2}}(t)B){\kern 1pt} {{\varphi }_{0}},$ где ${{M}_{k}}(t)$, k = 1, 2, определяются формулами (7), вектор имеет вид $z = ({{\varphi }_{1}},A_{0}^{{1/2}}{{\varphi }_{0}}$, 0, 0).

Теорема 4. Пусть выполнены условия (4) и следующие условия:

1) вектор-функция $A_{0}^{{1/2}}f(t) \in C\left( {[0, + \infty ),H} \right)$ и векторы ${{\varphi }_{0}} \in {{H}_{{3/2}}},$ ${{\varphi }_{1}} \in {{H}_{{1/2}}};$ или

2) вектор-функция $f(t) \in {{C}^{1}}\left( {[0, + \infty ),H} \right),$ функции ${{M}_{k}}(t) \in {{C}^{1}}\left( {[0, + \infty )} \right),$ k = 1, 2, векторы ${{\varphi }_{0}} \in {{H}_{1}},$ ${{\varphi }_{1}} \in {{H}_{{1/2}}}.$

Тогда задача (15), (16) имеет единственное классическое решение Z(t) = $({v}(t),{{\xi }_{0}}(t),{{\xi }_{1}}(t,\tau )$, ξ₂(t, τ)), где ${v}(t): = u{\kern 1pt} '(t)$, ${{\xi }_{0}}(t): = A_{0}^{{1/2}}u(t)$, u(t) – классическое решение задачи (1), (2) и справедлива следующая оценка:

(17)

$\begin{gathered} E(t): = \frac{1}{2}(\mathop {\left\| {u{\kern 1pt} '(t)} \right\|}\nolimits_H^2 + \,{\text{||}}A_{0}^{{1/2}}u(t){\text{||}}_{H}^{2}) \leqslant \frac{1}{2}\mathop {\left\| {Z(t)} \right\|}\nolimits_\mathbb{H}^2 \leqslant \\ \leqslant d\left[ {(\mathop {\left\| {{{\varphi }_{1}}(t)} \right\|}\nolimits_H^2 + \,{\text{||}}A_{0}^{{1/2}}{{\varphi }_{0}}{\text{||}}_{H}^{2}){{ + }_{{_{{_{{_{{_{{_{{_{{_{{_{{_{{_{{_{{_{{_{{_{{}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}} \right. \\ \left. { + \,\mathop {\left( {\int\limits_0^t {\text{||}}\,f(s) - ({{M}_{1}}(s)A + {{M}_{2}}(s)B){{\varphi }_{0}}{\text{|}}{{{\text{|}}}_{H}}ds} \right)}\nolimits^2 } \right] \\ \end{gathered} $

с постоянной d, не зависящей от вектор-функции f и векторов φ₀, φ₁.

Если выполнены условия теоремы и H – сепарабельное вещественное гильбертово пространство, то для решения $Z(t) = ({v}(t),{{\xi }_{0}}(t),{{\xi }_{1}}(t,\tau ),{{\xi }_{2}}(t,\tau ))$, где ${v}(t): = u{\kern 1pt} '(t)$, ${{\xi }_{0}}(t): = A_{0}^{{1/2}}u(t)$, $u(t)$ – классическое решение задачи (1), (2), справедлива следующая оценка:

(18)

$\begin{gathered} E(t): = \frac{1}{2}(\mathop {\left\| {u{\kern 1pt} '(t)} \right\|}\nolimits_H^2 + \,{\text{||}}A_{0}^{{1/2}}u(t){\text{||}}_{H}^{2}) \leqslant \frac{1}{2}\mathop {\left\| {Z(t)} \right\|}\nolimits_\mathbb{H}^2 \leqslant \\ \leqslant d\left[ {(\mathop {\left\| {{{\varphi }_{1}}(t)} \right\|}\nolimits_H^2 + \,{\text{||}}A_{0}^{{1/2}}{{\varphi }_{0}}{\text{||}}_{H}^{2}){{e}^{{ - 2\omega t}}}{{ + }_{{_{{_{{_{{_{{_{{_{{_{{_{{_{{_{{_{{_{{_{{_{{}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}} \right. \\ \left. { + \,\mathop {\left( {\int\limits_0^t {{e}^{{ - \omega (t - s)}}}{\text{||}}f(s) - ({{M}_{1}}(s)A + {{M}_{2}}(s)B){{\varphi }_{0}}{\text{|}}{{{\text{|}}}_{H}}ds} \right)}\nolimits^2 } \right] \\ \end{gathered} $

с постоянной d, не зависящей от вектор-функции f и векторов φ₀, φ₁, и постоянной ω, определенной в формулировке теоремы 3.

Список литературы

Ильюшин А.А., Победря Б.Е. Основы математической теории термовязкоупругости. М.: Наука, 1970. 280 с.
Christensen R.M. Theory of viscoelasticity. An introduction. N.Y., L.: Academic Press, 1971. 364 p.
Kopachevsky N.D., Krein S.G. Operator Approach to Linear Problems of Hydrodynamics. V. 2: Nonself-adjoint Problems for Viscous Fluids // Operator Theory: Advances and Applications. Basel/Switzerland: Birkhauser Verlag, 2003. V. 146. 444 p.
Munoz Rivera J.E. Asymptotic behaviour in linear viscoelasticity // Quart. Appl. Math. 1994. V. 52. P. 629–648.
Amendola G., Fabrizio M., Golden J.M. Thermodynamics of Materials with memory. N.Y., Dordrecht; Heidelberg; L.: Springer. Theory and applications, 2012. 576 p.
Локшин А.А., Суворова Ю.В. Математическая теория распространения волн в средах с памятью. М.: Изд-во МГУ, 1982. 152 с.
Gurtin M.E., Pipkin A.C. General theory of heat conduction with finite wave speed // Arch. Rat. Mech. Anal. 1968. V. 31. P. 113–126.
Лыков А.В. Тепломассообмен: Справочник. 2-е изд., перераб. и доп. М.: Энергия, 1978. 480 с.
Санчес-Паленсия Э. Неоднородные среды и теория колебаний. М.: Мир, 1984.
Работнов Ю.Н. Элементы наследственной механики твердых тел. М.: Наука, 1977. 384 с.
Крейн С.Г. Линейные дифференциальные уравнения в банаховых пространствах. М.: Наука, 1967. 464 с.
Engel K.J., Nagel R. One-Parameter Semigroups for Linear Evolution Equations. N.Y.: Springer-Verlag, 2000. 586 p.
Vlasov V.V., Rautian N.A. Correct solvability and representation of solutions of volterra integrodifferential equations with fractional exponential kernels // Doklady Mathematics. 2019. V. 100. № 2. P. 467–471.
Vlasov V.V., Rautian N.A. A Study of Operator Models Arising in Problems of Hereditary Mechanics // Journal of Mathematical Sciences (N.Y.). 2020. V. 244. № 2. P. 170–182.
Skubachevskii A.L. Boundary-value problems for elliptic functional-differential equations and their applications // Russian Mathematical Surveys. 2016. V. 71. № 5. P. 801–906.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Доклады Российской академии наук. Математика, информатика, процессы управления

Архивы выпусков Информация о журнале Отправить рукопись в журнал