Доклады Российской академии наук. Математика, информатика, процессы управления, 2021, T. 500, № 1, стр. 55-61

ВВЕДЕНИЕ

Самоподобные замощения (тайлинги) компактных множеств широко изучались в литературе по геометрии, комбинаторике, теории чисел, гармоническому анализу и всплескам. В данной работе мы получим классификацию всех многогранных замощений и их особого вида – многогранных целых аттракторов. В разделе 1 будут даны формулировки основных результатов, в разделе 2 – краткие доказательства (подробные доказательства будут представлены в расширенном варианте данной статьи).

Определение 1. Компактное множество $G \subset {{\mathbb{R}}^{d}}$ положительной меры Лебега допускает тайлинг, если существует разбиение $G = \bigcup\limits_{i = 1}^N {{{T}_{i}}} $, в котором все множества ${{T}_{i}}$ являются параллельными сдвигами одного и того же компакта (тайла) и их попарные пересечения имеют меру нуль. Если тайл аффинно подобен G, то тайлинг называется самоподобным.

Как правило, множества, допускающие самоподобный тайлинг, имеют фрактальную структуру, что затрудняет их использование в приложениях. Естественная задача – найти и охарактеризовать простые (в том или ином смысле) множества, обладающие этим свойством. Например, многогранники или, более широко, многогранные множества. Многогранным множеством называется объединение конечного числа выпуклых многогранников. Каждый многогранник предполагается компактным и невырожденным (имеющим непустую внутренность). Кроме чисто геометрического интереса, этот вопрос важен в кристаллографии, при исследовании уточняющих алгоритмов (subdivision schemes), в теории приближений, при построении всплесков и других ортогональных систем в ${{L}_{2}}({{\mathbb{R}}^{d}})$, см. [1, 3, 4, 6, 9, 11] и ссылки в этих работах. В частности, тайлы являются основой для функций Хаара многих переменных. Поэтому, многогранные тайлы приводят к построению функций Хаара с носителями – многогранными множествами.

Первые результаты в этом направлении были получены Грехенигом и Мадих [2], которые охарактеризовали самоподобные тайлинги параллелепипедов и соответствующие базисы Хаара в ${{L}_{2}}({{\mathbb{R}}^{d}})$. Полная классификация операторов аффинного подобия и векторов сдвигов, порождающих тайлинги параллелепипедов, была получена в [13]. Вопрос классификации тайлов-многогранников исследовался в [9, 12, 13]. Несложно показать, что среди всех выпуклых многогранников (и даже среди выпуклых тел) только параллелепипед допускает самоподобный тайлинг. Для невыпуклых многогранников вопрос гораздо более сложен. В [13] было показано, что на двумерной плоскости невыпуклый многоугольник не может иметь самоподобного тайлинга. Случай большей размерности был оставлен в качестве открытой проблемы. В недавней работе [12] было показано, что если у самоподобного тайла есть выпуклый угол (т.е. пересечение с некоторым шаром является окрестностью вершины выпуклого конуса, не содержащего прямой линии), то данный тайл аффинно эквивалентен объединению целых сдвигов единичного куба. Поэтому, в случае когда многогранник имеет хотя бы один выпуклый угол, мы знаем его общий вид. Это, однако, не решает проблему полностью, поскольку не все многогранники данного вида допускают самоподобный тайлинг. Но главная сложность состоит в том, что не все многогранники имеют хотя бы один выпуклый угол. В качестве примера рассмотрим правильный тетраэдр в ${{\mathbb{R}}^{3}}$ и каждую из его вершин “вдавим внутрь”, сделав на ее месте ямку в виде тетраэдра. Что касается многогранных множеств, то они уже на двумерной плоскости могут не иметь выпуклых углов. Выпуклость в [12] существенна, и доказательство не проходит в общем случае. Таким образом, вопрос о многогранниках, допускающих самоподобный тайлинг, оставался открытым. С другой стороны, известны примеры несвязных многогранных множеств с самоподобным тайлингом [13]. Поэтому, разумно ставить задачу следующим образом:

Задача 1. Найти все многогранные множества в ${{\mathbb{R}}^{d}}$, допускающие самоподобный тайлинг.

Вторая задача сужает вопрос на один класс самоподобных тайлов – целых аттракторов. Целый аттрактор в ${{\mathbb{R}}^{d}}$ является аналогом единичного отрезка в системе счисления, определенной целой матрицей и системой целых векторов – “цифр”. Пусть дана d × d матрица M с целыми коэффициентами, а также множество векторов D = ${\text{\{ }}{{{\mathbf{s}}}_{i}}{\text{\} }}_{{i = 0}}^{{m - 1}} \subset {{\mathbb{Z}}^{d}}$, где $m = {\text{|det}}M{\text{|}}$. Матрица $M$ предполагается растягивающей, т.е. все ее собственные значения по модулю больше 1, а векторы ${{{\mathbf{s}}}_{i}}$ взяты из разных классов смежности ${{\mathbb{Z}}^{d}}{\text{/}}M{{\mathbb{Z}}^{d}}$, т.е., 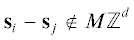при $i\, \ne \,j$. Таким образом, в ${{\mathbb{Z}}^{d}}$ задана M-адическая система счисления с цифрами s_i. Целым аттрактором называется множество G = $\left\{ {\sum\limits_{k = 1}^\infty {{{M}^{{ - k}}}{\mathbf{s}}(k)\,|\,{\mathbf{s}}(k)\, \in \,D} } \right\}$. Известно [2, 7], что $G$ – компакт, имеющий целую положительную меру и допускающий самоподобный тайлинг множествами ${{M}^{{ - 1}}}(G + {{{\mathbf{s}}}_{i}}),i = 0$, ..., m – 1. Характеристическая функция аттрактора φ(x) = ${{\chi }_{G}}({\mathbf{x}})$ удовлетворяет масштабирующему уравнению φ(x) = $\sum\limits_{i = 0}^{m - 1} {\varphi (M{\mathbf{x}} - {{{\mathbf{s}}}_{i}})} $. Этим объясняются многочисленные применения целых аттракторов в теории всплесков, теории приближений (subdivision schemes) и т.д. В частности, если мера $G$ равна единице, то функция φ порождает кратномасштабный анализ в ${{L}_{2}}({{\mathbb{R}}^{d}})$ [3, 10, 11].

Единичный куб в ${{\mathbb{R}}^{d}}$ является целым аттрактором, порожденным матрицей $M = 2I$, где I – единичная матрица, и 2^d цифрами $D = {\text{\{ }}({{s}_{1}}, \ldots ,{{s}_{d}})$, ${{s}_{i}} \in {\text{\{ }}0,1{\text{\} \} }}$. Тот же куб порождается и другими парами $(M,D)$. Например, при надлежащем выборе матрицы M, куб является целым аттрактором, задаваемым всего двумя цифрами. Системы счисления в ${{\mathbb{Z}}^{d}}$, имеющие в качестве аттрактора единичный куб или параллелепипед, исследовались, в частности, в [2, 13], в [13] дана полная классификация таких систем в ${{\mathbb{R}}^{d}}$. Вопрос – есть ли другие многогранные целые аттракторы в ${{\mathbb{R}}^{d}}$?

Задача 2. Найти все многогранные множества в ${{\mathbb{R}}^{d}}$, являющиеся целыми аттракторами.

Мы даем решения задач 1 и 2. В теореме 1 классифицированы все многогранные множества в ${{\mathbb{R}}^{d}}$, допускающие самоподобный тайлинг. В любой размерности таких множеств (не эквивалентных друг другу) бесконечно много. А с многогранными целыми аттракторами ситуация иная. Теорема 2 устанавливает, что все они – параллелепипеды.

1. ОСНОВНЫЕ РЕЗУЛЬТАТЫ

Мы рассматриваем самоподобный тайлинг $\mathcal{T} = {\text{\{ }}{{T}_{i}}{\text{\} }}_{{i = 1}}^{N}$ компактного множества $G$; для каждого тайла $T \in \mathcal{T}$ его подобие множеству $G$ задается аффинным преобразованием $A:T \to G$; все эти преобразования имеют одну и ту же линейную часть, заданную растягивающей матрицей M, и отличаются только сдвигами.

Многогранное множество в ${{\mathbb{R}}^{d}}$ – объединение конечного числа выпуклых невырожденных многогранников. Одномерные многогранные множества состоят из конечного числа отрезков. Все одномерные многогранные множества, допускающие самоподобный тайлинг, охарактеризованы в [5, 13]. Мы используем этот результат, поэтому приведем его полностью. Для натуральных чисел a, n, обозначим $\mathcal{S}(a,n) = {\text{\{ }}ka|k = 0, \ldots ,n - 1{\text{\} }}$. Это – арифметическая прогрессия длины $n$, начинающаяся с нуля, имеющая разность a. Для натурального числа r и положительных векторов ${\mathbf{a}},{\mathbf{n}} \in {{\mathbb{Z}}^{r}}$, обозначим $\mathcal{S}({\mathbf{a}},{\mathbf{n}}) = \mathcal{S}({{a}_{1}},{{n}_{1}}) + \ldots + \mathcal{S}({{a}_{r}},{{n}_{r}})$ – суммы по Минковскому арифметических прогрессий $\mathcal{S}({{a}_{i}},{{n}_{i}})$. Пару векторов ${\mathbf{a}},{\mathbf{n}} \in {{\mathbb{Z}}^{r}}$ назовем допустимой, если ${{a}_{1}} = {{n}_{1}} = 1$, и для каждого $i \geqslant 2$ выполнено: ${{a}_{i}} \geqslant 2,\,\,{{n}_{i}} \geqslant 2$ и a_i делится на ${{a}_{{i - 1}}}{{n}_{{i - 1}}}$. Следующий результат дает классификацию одномерных многогранных тайлов [13, теорема 7]:

Множество $G \subset \mathbb{R}$, являющееся объединением конечного числа отрезков, допускает самоподобный тайлинг тогда и только тогда, когда найдутся $r \in \mathbb{N}$ и допустимая пара векторов ${\mathbf{a}},{\mathbf{n}} \in {{\mathbb{Z}}^{r}}$ такая, что $G$ эквивалентно, с точностью до умножения на константу, множеству

Итак, множество $G$ эквивалентно объединению целых сдвигов единичного отрезка, заданному формулой (1). Общее число отрезков равно ${{n}_{1}} \cdots {{n}_{r}}$; случай одного отрезка соответствует r = 1. Теперь мы формулируем основной результат, классифицирующий многогранные самоподобные тайлы в ${{\mathbb{R}}^{d}}$.

Теорема 1. Многогранное множество в ${{\mathbb{R}}^{d}}$ допускает самоподобный тайлинг тогда и только тогда, когда оно аффинно эквивалентно прямому произведению d одномерных множеств вида (1). Каждое из этих d множеств порождено своей тройкой $(r,{\mathbf{a}},{\mathbf{n}})$, где $r \in \mathbb{N}$ и a, n – допустимая пара из ${{\mathbb{Z}}^{r}}$.

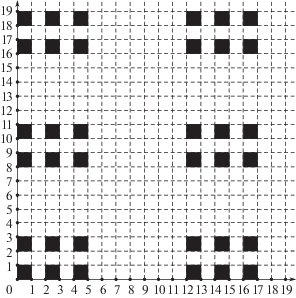
Замечание 1. Пример такого множества дан на рис. 1. Одно из множеств порождено тройкой $(3,(1,2,12),(1,3,2))$, а другое $(3,(1,2,8),(1,2,3))$. Соответствующие арифметические прогрессии получаются $(0),(0,2,4),(0,12)$ (их сумма дает множество по оси x), $(0),(0,2),(0,8,16)$ (их сумма дает множество по оси y).

Рис. 1.

Пример двумерного многогранного множества, допускающего самоподобный тайлинг.

Итак, все многогранные множества, допускающие самоподобный тайлинг, являются прямыми произведениями соответствующих одномерных множеств. Следовательно, каждое такое множество является дизъюнктным объединением единичных кубиков целочисленной решетки.

В частности, такой же вид должны иметь все многогранные целые аттракторы. Следующий результат, однако, показывает, что их семейство гораздо беднее и ограничивается параллелепипедами.

Теорема 2. Если целый аттрактор является многогранным множеством, то это – параллелепипед.

Схемы и основные шаги доказательств теорем 1 и 2 приведены в следующем параграфе.

2. НАБРОСКИ ДОКАЗАТЕЛЬСТВ

Короткий формат сообщения не позволяет изложить полные доказательства, это будет сделано в отдельной статье. Мы наметим план и подробнее остановимся на главных идеях.

Доказательство теоремы 1: краткое изложение. Доказательство мы разбили на несколько шагов, в каждом устанавливается одна лемма. Пусть $G \subset {{\mathbb{R}}^{d}}$ – многогранное множество, имеющее самоподобный тайлинг $\mathcal{T}$.

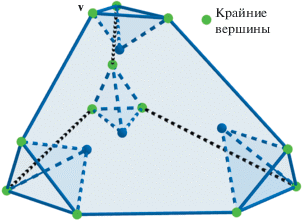
Шаг 1. Выпуклая оболочка ${\text{co}}\,(G)$ – выпуклый многогранник. Его вершины будем называть крайними вершинами множества $G$. В силу теоремы Крейна–Мильмана, у каждого многогранного множества есть крайние вершины, и их выпуклая оболочка содержит это множество. На рис. 2 проиллюстрированы крайние вершины у тетраэдра с “вдавленными” углами.

Рис. 2.

Крайние вершины тетраэдра с “вдавленными” вершинами.

Для произвольной крайней вершины ${\mathbf{v}}$, рассмотрим соответствующий угол K – пересечение множества $G$ с малым шаром с центром ${\mathbf{v}}$. Радиус шара будем предполагать настолько малым, насколько это необходимо. Тем же символом K будем обозначать коническую оболочку угла K, т.е. множество $\bigcup\nolimits_{\lambda > 0} \,\lambda K$. Это – невырожденный точечный (не содержащий прямой линии) конус, возможно, невыпуклый. Мы часто будем отождествлять угол с соответствующим конусом. Выпуклая оболочка ${\text{co}}\,(K)$ – угол многогранника ${\text{co}}\,(G)$. Конус ${\text{co}}\,(K)$ определяет частичный порядок в ${{\mathbb{R}}^{d}}$: ${\mathbf{x}} \leqslant {\mathbf{y}}$, если ${\mathbf{y}} - {\mathbf{x}} \in {\text{co}}\,(K)$. У каждого подмножества $S \subset {{\mathbb{R}}^{d}}$ есть не более одного минимального элемента x, для которого ${\mathbf{x}} \leqslant {\mathbf{y}}$ для всех ${\mathbf{y}} \in S$.

Лемма 1. Если многогранное множество $G$ имеет самоподобный тайлинг $\mathcal{T}$, то каждая его крайняя вершина ${\mathbf{v}} \in G$ содержится в единственном тайле $T \in \mathcal{T}$. Более того, ${\mathbf{v}}$ является также и крайней вершиной $T$, а углы множеств $T$ и $G$ в этой вершине совпадают.

Доказательство основано на том, что ${\mathbf{v}}$ – единственный минимальный элемент конуса ${\text{co}}\,(K)$, а значит, и единственный минимальный элемент $G$, поскольку $G$ содержится в этом конусе. Если бы два сдвига тайла $T$ содержали ${\mathbf{v}}$, то $T$ имело бы два минимальных элемента, что невозможно.

Шаг 2. Итак, каждая крайняя вершина $G$ покрыта единственным тайлом $T$, для которого она также является крайней вершиной. Это определяет отображение множества крайних вершин $G$ в множество крайних вершин $T$. Но поскольку $G$ и $T$ аффинно подобны, получаем отображение (возможно, не инъективное) множества крайних вершин $G$ в себя. Какая-то итерация этого отображения имеет неподвижную точку ${\mathbf{v}}$, причем (возможно, после дополнительных итераций) можно считать, что все грани угла ${\text{co}}\,(K)$ множества $G$ совпадают с соответствующими гранями того же угла в $T$. Мы будем называть крайнюю вершину множества $G$ неподвижной, если она совпадает с соответствующей вершиной покрывающего ее тайла $T$, и все соответствующие грани угла ${\text{co}}(K)$ в этой вершине у множеств $T$ и $G$ совпадают.

Лемма 2. У самоподобного тайлинга $\mathcal{T}$ многогранного множества $G$ всегда существует итерация ${{\mathcal{T}}^{n}}$ такая, что $G$ с тайлингом ${{\mathcal{T}}^{n}}$ имеет хотя бы одну неподвижную вершину.

Заметим, что если понятие крайней вершины зависит только от геометрии множества $G$, то неподвижная вершина зависит от тайлинга. Везде далее мы будем считать, что достаточное число итераций уже проделано, и ${\mathbf{v}}$ – неподвижная вершина $G$ с тайлингом $\mathcal{T}$, а размер тайла достаточно мал (насколько это необходимо). Угол множества $G$ (он же – угол T) в неподвижной вершине также будем называть неподвижным.

Шаг 3. Итак, множество $G$ с тайлингом $\mathcal{T}$ имеет хотя бы один неподвижный угол. Наша следующая цель – доказать, что этот угол выпуклый и простой (т.е. имеет ровно d ребер). Это будет сделано в несколько этапов – шаги 3–6. В начале мы установим следующую лемму, которая позволит свести задачу к меньшей размерности.

Лемма 3. Пусть многогранное множество $G$ имеет самоподобный тайлинг $\mathcal{T}$, и $T \in \mathcal{T}$ – тайл, содержащий неподвижный угол $K$. Тогда если $K$ содержит некоторую грань $L$ конуса ${\text{co }}(K)$, $1 \leqslant {\text{dim}}L \leqslant d - 1$, то все элементы T, пересекающие эту грань, являются сдвигами $T$ на векторы, параллельные $L$. Пересечения грани $L$ с тайлами из $T$ образуют самоподобный тайлинг множества $G \cap L$.

Таким образом, если неподвижный угол $K$ содержит какую-то грань своей выпуклой оболочки, то тайлинг $\mathcal{T}$ также определяет самоподобный тайлинг для пересечения $G$ с этой гранью.

Шаг 4. Теперь доказываем, что если неподвижный угол $K$ содержит какую-то грань $L$, ${\text{dim}}L$ = j, своей выпуклой оболочки, и эта грань простая (имеет ровно  j  ребер), то тайл T, содержащий $K$, содержит также $j$-мерный параллелепипед, вписанный в $L$.

Лемма 4. В условиях леммы 3 предположим, что $L$ является j-мерным простым конусом. На каждом его ребре отметим максимальный по включению отрезок, содержащий точку ${\mathbf{v}}$ и лежащий в $T$. Тогда $T$ содержит j-мерный параллелепипед, порожденный этими отрезками (т.е. являющийся их суммой по Минковскому).

Доказательство осуществляется по индукции относительно размерности j. Для j = 1 утверждение верно, поскольку угол всегда содержит ребра своей выпуклой оболочки, и соответствующий отрезок на этом ребре является одномерным параллелепипедом, который (по определению!) лежит в $T$. Переход $j - 1 \to j$ осуществляется так: по предположению индукции, для каждой $(j - 1)$-мерной грани L' конуса $L$ соответствующий $(j - 1)$-мерный параллелепипед $P' \subset $ L' содержится в $T$. Обозначим через ${\mathbf{a}}$ отрезок, содержащийся в оставшемся ребре конуса $L$. Тогда (по предположению индукции для одномерной грани L = = ${\text{span}}({\mathbf{a}})$) сдвиг $P' + {\mathbf{a}}$ содержится в соответствующем сдвиге T + a, и, следовательно, содержится в $G$. Если какая-то точка ${\mathbf{x}} \in P$ не покрывается тайлом T, то она должна содержаться в каком-то его сдвиге $T + {\mathbf{b}} \in \mathcal{T}$, причем ${\mathbf{b}} \ne {\mathbf{a}}$. Из этого следует, что сдвиг ребра ${\mathbf{a}}$, лежащий в $T + {\mathbf{b}} \in \mathcal{T}$, содержится в $P$. Значит, он пересекает одну из противоположных граней $P{\kern 1pt} '$ и $P{\kern 1pt} '\, + {\mathbf{a}}$ этого параллелепипеда. Последнее невозможно, поскольку тайл $T + {\mathbf{b}}$ не пересекает ни T, ни $T + {\mathbf{a}}$.

Шаг 5. Теперь мы устанавливаем главное вспомогательное утверждение. Несмотря на технический характер леммы, этот геометрический факт, возможно, не лишен и самостоятельного интереса.

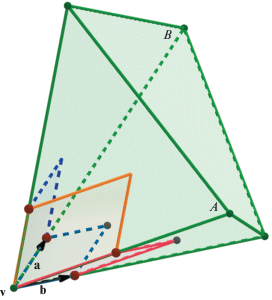
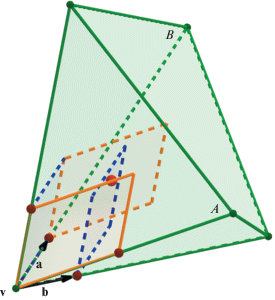
Лемма 5. Если выпуклый многогранный конус $C$ не является простым, но имеет простые фасады (т.е. гиперграни), то верно следующее: либо $C$ простой, либо для любого семейства векторов $\mathcal{V}$, исходящих из вершины конуса $C$ и идущих вдоль его ребер (один вектор на каждом ребре), найдется два фасада $A,B$ и два различных вектора ${\mathbf{a}},{\mathbf{b}} \in \mathcal{V}$, для которых параллелепипеды ${\mathbf{a}} + P(A)$ и ${\mathbf{b}} + P(B)$ имеют общую внутреннюю точку. Через $P(X)$ обозначен параллелепипед, порожденный векторами, лежащими на фасаде X.

В первом случае, если C – простой конус, параллелепипеды всех фасадов и их сдвиги на векторы семейства $\mathcal{V}$ образуют границу d-мерного параллелепипеда, лежащую в $T$.

Иллюстрация ко второму случаю леммы дана на рис. 3, 4.

Рис. 3.

“Лилия” – фигура из параллелепипедов, порожденных векторами на фасадах.

Рис. 4.

Пересечение параллелепипедов ${\mathbf{a}} + P(A)$ и ${\mathbf{b}} + P(B)$.

Шаг 6. Мы подошли к ключевому месту в доказательстве.

Лемма 6. Если многогранное множество допускает самоподобный тайлинг $\mathcal{T}$, и $K$ – его неподвижный угол, то для любого $j = 1, \ldots ,d$ этот угол содержит все j-мерные грани угла ${\text{co}}\,(K)$, и все эти грани простые.

При $j = d$ мы немедленно получаем, что $K = {\text{co}}\,(K)$ и что этот конус простой.

Следствие 1. Каждый неподвижный угол многогранного множества – выпуклый и простой.

Лемма 6 доказывается по индукции относительно j. Для j = 1 все выполнено, поскольку $K$ содержит все ребра конуса $K = {\text{co}}\,(K)$. Если утверждение верно для размерности $j - 1$, то у произвольной j-мерной грани $L$ конуса ${\text{co}}\,(K)$ все $(j - 1)$-мерные грани простые и содержатся в $K$. Возьмем на каждом ребре конуса $L$ по максимальному отрезку, лежащему в тайле $T$, и воспользуемся леммой 4. Получается, что на каждой $(j - 1)$-мерной грани конуса $L$ эти отрезки порождают параллелепипед, лежащий в $T$. Теперь применяем лемму 5 к конусу $C = L$ с простыми гранями. Если конус $L$ не простой, то найдется две грани и два отрезка, для которых два соответствующих сдвинутых параллелепипеда имеют общую внутреннюю точку. Последнее невозможно, поскольку в силу леммы 5 векторы сдвигов ${\mathbf{a}},{\mathbf{b}}$ различны и, следовательно, эти параллелепипеды принадлежат разным тайлам. Таким образом, имеет место первый случай леммы 5: конус $L$ простой, и $T$ содержит границу $j$-мерного параллелепипеда $P$ с углом $L$. Если множество точек $L$, не лежащих в $T$, непусто, то оно содержит открытый угол $S$ с вершиной ${\mathbf{v}}$. Если мы выбрали размер тайла $T$ достаточно малым, то мал будет и параллелепипед $P$, а значит $S$ пересечет его границу. Последнее невозможно, поскольку граница $P$ лежит в $L$.

Шаг 7. Каждый неподвижный угол множества $G$ выпуклый и простой (Следствие 1). Поскольку множество $G$ имеет хотя бы один неподвижный угол (лемма 2), оно имеет и выпуклый простой угол, а значит, согласно [12], $G$ эквивалентно объединению целых сдвигов единичного куба. Остается классифицировать все множества такого типа, допускающие самоподобный тайлинг.

Лемма 7. Если множество $G$ является объединением целых сдвигов единичного куба и допускает самоподобный тайлинг $\mathcal{T}$ с неподвижным углом $K$, то найдется подмножество $\mathcal{T}$, составляющее тайлинг некоторого прямоугольного параллелепипеда с углом $K$.

Шаг 8. Итак, множество $G$ является объединением целых сдвигов единичного куба и, поскольку оно подобно $T$, несколько сдвигов $G$ образуют тайлинг параллелепипеда. Следовательно, центры составляющих $G$ кубов образуют дискретный тайл для параллелепипеда, т.е. его целые сдвиги образуют дискретный параллелепипед. Тогда из [8] следует, что множество центров является прямым произведением одномерных множеств, каждое из которых составляет тайлинг отрезка. Поэтому $G$ является произведением одномерных множеств, состоящих из конечного числа отрезков и допускающих самоподобный тайлинг. Осталось воспользоваться классификацией таких одномерных множеств, данной в параграфе 2 [13, теорема 7].

Схема доказательства теоремы 2. Из теоремы 1 следует, что $G$ состоит из непересекающихся целых сдвигов единичного куба. Взяв достаточно большую итерацию самоподобного тайлинга $\mathcal{T}$, можно считать, что диаметр тайла меньше 1. Значит, один тайл не может пересекать несколько кубов, т.е. каждый тайл лежит в одном из кубов. Если $G$ состоит из более чем одного куба, то рассмотрим сдвиги тайла $T = {{M}^{{ - 1}}}G$, лежащие в двух фиксированных кубах. Несложно показать, что векторы ${\mathbf{s}} \in {{\mathbb{Z}}^{d}}$, для которых тайлы ${{M}^{{ - 1}}}(G + {\mathbf{s}})$ составляют первый куб, находятся в тех же классах смежности ${{\mathbb{Z}}^{d}}{\text{/}}M{{\mathbb{Z}}^{d}}$, что векторы ${\mathbf{s}} \in {{\mathbb{Z}}^{d}}$ для второго куба. Последнее невозможно, поскольку все эти векторы являются цифрами из D и должны принадлежать разным классам.