Доклады Российской академии наук. Математика, информатика, процессы управления, 2021, T. 500, № 1, стр. 35-39

Теоремы сравнения для эллиптических неравенств с младшими производными, учитывающие геометрию области

А. А. Коньков^1, *

¹ Московский государственный университет имени М.В. Ломоносова
Москва, Россия

Поступила в редакцию 08.07.2021
После доработки 08.07.2021
Принята к публикации 08.08.2021

DOI: 10.31857/S2686954321050209

Аннотация

Получены теоремы сравнения, позволяющие оценить сферический максимум решений квази-линейных эллиптических неравенств, содержащих младшие производные, через решения задачи Коши для обыкновенного дифференциального уравнения, правая часть которого зависит от геометрии области.

Ключевые слова: нелинейные эллиптические операторы, неограниченные области, емкость

Пусть $\Omega \ne \emptyset $ — открытое подмножество ${{\mathbb{R}}^{n}}$, $n \geqslant 2$. Положим ${{\Omega }_{{{{r}_{1}},{{r}_{2}}}}} = {\text{\{ }}x \in \Omega :{{r}_{1}} < {\text{|}}x{\text{|}} < {{r}_{2}}{\text{\} }}$ и ${{B}_{{{{r}_{1}},{{r}_{2}}}}}$ = = ${\text{\{ }}x \in {{\mathbb{R}}^{n}}{\text{:}}\,\,{{r}_{1}} < {\text{|}}x{\text{|}} < {{r}_{2}}{\text{\} }}$, $0 < {{r}_{1}} < {{r}_{2}}$. Через $B_{r}^{x}$ и $S_{r}^{x}$ обозначим открытый шар и сферу радиуса $r > 0$ с центром в точке x. В случае x = 0 пишем ${{B}_{r}}$ и ${{S}_{r}}$ вместо $B_{r}^{0}$ и $S_{r}^{0}$.

Будем рассматривать неравенства

(1)

${\text{div}}A(x,Du) + b(x){\text{|}}Du{{{\text{|}}}^{{p - 1}}} \geqslant 0\quad {\text{в}}\quad {{\Omega }_{{{{R}_{0}},{{R}_{1}}}}},$

где $0 \leqslant {{R}_{0}} < {{R}_{1}} \leqslant \infty $, $D = ({{\partial }_{{{{x}_{1}}}}}, \ldots ,{{\partial }_{{{{x}_{n}}}}})$ – оператор градиента и $p > 1$ – вещественное число. Считаем, что главная часть дифференциального оператора удовлетворяет условию равномерной эллиптичности

$\begin{gathered} {{C}_{1}}{\text{|}}\xi {{{\text{|}}}^{p}} \leqslant \xi A(x,\xi ), \\ {\text{|}}A(x,\xi ){\text{|}} \leqslant {{C}_{2}}{\text{|}}\xi {{{\text{|}}}^{{p - 1}}},\quad {{C}_{1}},{{C}_{2}} > 0, \\ \end{gathered} $

для почти всех x $ \in {{\Omega }_{{{{R}_{0}},{{R}_{1}}}}}$ и всех $\xi \in {{\mathbb{R}}^{n}}$, а коэффициент при младших производных b – неотрицательная функция, принадлежащая пространству ${{L}_{\nu }}({{\Omega }_{{{{R}_{0}},r}}})$ для всех $r \in ({{R}_{0}},{{R}_{1}})$, где $n < \nu \leqslant \infty $ при $p \leqslant n$ и $\nu = p$ при $p > n$.

Теоремы сравнения для неравенств (1), не содержащих младшие производные, получены в работе [2].

Решением (1) будем называть функцию u такую, что $u \in W_{p}^{1}({{\Omega }_{{{{R}_{0}},r}}}) \cap {{L}_{\infty }}({{\Omega }_{{{{R}_{0}},r}}})$ и A(x, Du) ∈ ∈ ${{L}_{{p/(p - 1)}}}({{\Omega }_{{{{R}_{0}},r}}})$ для любого $r \in ({{R}_{0}},{{R}_{1}})$ и при этом

$ - \int\limits_{{{\Omega }_{{{{R}_{0}},{{R}_{1}}}}}}^{} {A(x,Du)D\varphi dx} + \int\limits_{{{\Omega }_{{{{R}_{0}},{{R}_{1}}}}}}^{} {b(x){\text{|}}Du{{{\text{|}}}^{{p - 1}}}\varphi dx \geqslant 0} $

для всех неотрицательных φ ∈ $C_{0}^{\infty }({{\Omega }_{{{{R}_{0}},{{R}_{1}}}}})$ .

Говорим также, что

(2)

$u{{{\text{|}}}_{{{{B}_{{{{R}_{1}}}}}{{\backslash }}\overline {{{B}_{{{{R}_{0}}}}}} \cap \partial {{\Omega }_{{{{R}_{0}},{{R}_{1}}}}}}}} = 0,$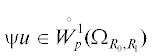

если

для всех $\psi \in C_{0}^{\infty }({{B}_{{{{R}_{0}},{{R}_{1}}}}}).$

Пусть $u$ – решение (1), (2). Обозначим

$M(r;u) = \mathop {{\text{ess}}\,{\text{sup}}}\limits_{{{S}_{r}} \cap \Omega } u,\quad r \in ({{R}_{0}},{{R}_{1}}),$

где ограничение u на ${{S}_{r}} \cap \Omega $ понимается в смысле следа, а ess sup берется по $(n - 1)$-мерной мере Лебега на сфере S_r. Если ${{S}_{r}} \cap \Omega = \emptyset $, то будем считать, что $M(r;u) = 0$.

Емкость компакта $K \subset \omega $ по отношению к открытому множеству $\omega \subset {{\mathbb{R}}^{n}}$ определяется равенством

${\text{cap}}(K,\omega ) = \mathop {inf}\limits_\varphi \int\limits_\omega ^{} {{\text{|}}D\varphi {{{\text{|}}}^{p}}dx,} $

где точная нижняя грань берется по всем функциям $\varphi \in C_{0}^{\infty }(\omega )$, равным тождественно единице в окрестности K. Емкость пустого множества считается равной нулю. В случае $\omega = {{\mathbb{R}}^{n}}$ пишем cap(K) вместо cap(K, ω).

Если p = 2 и $n \geqslant 3$, то cap(K) совпадает с хорошо известной винеровской емкостью [4].

Для любого $\varepsilon \in (0,1)$ величину

${\text{dia}}{{{\text{m}}}_{\varepsilon }}\omega = \sup \left\{ {r:\exists x \in \omega \frac{{{\text{cap}}(\overline {B_{r}^{x}} {{\backslash }}\omega ,B_{{2r}}^{x})}}{{{\text{cap}}(\overline {{{B}_{r}}} ,{{B}_{{2r}}})}} < \varepsilon } \right\}$

будем называть $\varepsilon $-существенным внутренним диаметром открытого множества $\omega \subset {{\mathbb{R}}^{n}}$ [5]. В случае $\omega = \emptyset $ полагаем diam_εω = 0.

Несложно увидеть, что diam_εω является монотонной функцией множества $\omega $ и вещественного числа $\varepsilon $. Другими словами, если ${{\omega }_{1}} \subset {{\omega }_{2}}$ и ${{\varepsilon }_{1}} \leqslant {{\varepsilon }_{2}}$, то $\mathop {{\text{diam}}}\nolimits_{{{\varepsilon }_{1}}} {{\omega }_{1}} \leqslant \mathop {{\text{diam}}}\nolimits_{{{\varepsilon }_{2}}} {{\omega }_{2}}.$

Под ${{\mathcal{L}}_{{\nu ,\varepsilon }}}(\omega )$, где $\omega $ – открытое подмножество ${{\mathbb{R}}^{n}}$, будем подразумевать пространство измеримых функций f таких, что

$\mathop {sup}\limits_{x \in \omega } {\text{||}}\,f\,{\text{|}}{{{\text{|}}}_{{{{L}_{\nu }}(\omega \cap B_{{\mathop {{\text{diam}}}\nolimits_\varepsilon \omega }}^{x})}}} < \infty .$

Норма в ${{\mathcal{L}}_{{\nu ,\varepsilon }}}(\omega )$ определяется равенством

${\text{||}}\,f\,{\text{|}}{{{\text{|}}}_{{{{\mathcal{L}}_{{\nu ,\varepsilon }}}(\omega )}}} = {\text{|}}{{B}_{1}}{{{\text{|}}}^{{ - \tfrac{1}{\nu }}}}\mathop {sup}\limits_{x \in \omega } {\text{||}}\,f\,{\text{|}}{{{\text{|}}}_{{{{L}_{\nu }}(\omega \cap B_{{\mathop {{\text{diam}}}\nolimits_\varepsilon \omega }}^{x})}}},$

где |B₁| – объем единичного шара в ${{\mathbb{R}}^{n}}$. В случае $f \in {{L}_{\infty }}(\omega )$, очевидно, имеем

(3)

${\text{||}}\,f\,{\text{|}}{{{\text{|}}}_{{{{\mathcal{L}}_{{\nu ,\varepsilon }}}(\omega )}}} \leqslant {{({\text{dia}}{{{\text{m}}}_{\varepsilon }}\omega )}^{{\tfrac{n}{\nu }}}}{\text{||}}\,f\,{\text{|}}{{{\text{|}}}_{{{{L}_{\infty }}(\omega )}}}.$

Предположим, что E – непустое открытое подмножество сферы S_r. Обозначим

${{\lambda }_{{\min }}}(E) = \mathop {\inf }\limits_{\psi \in C_{0}^{\infty }(E)} \frac{{\int\limits_E^{} {{\text{|}}\nabla \psi {{{\text{|}}}^{p}}d{{S}_{r}}} }}{{\int\limits_E^{} {{\text{|}}\psi {{{\text{|}}}^{p}}d{{S}_{r}}} }},$

где ${\text{|}}\nabla \psi {\text{|}} = {{({{g}^{{ij}}}{{\nabla }_{i}}\psi {{\nabla }_{j}}\psi )}^{{\frac{1}{2}}}},$ ${{g}^{{ij}}}$ – дуальный метрический тензор на сфере S_r, индуцированный евклидовой метрикой в ${{\mathbb{R}}^{n}}$, а $d{{S}_{r}}$ – элемент $(n - 1)$-мерного объема сферы ${{S}_{r}}$.

Согласно вариационному принципу ${{\lambda }_{{{\text{min}}}}}(E)$ является первым собственным значением спектральной задачи

${{\Delta }_{p}}w = - \lambda {\text{|}}w{{{\text{|}}}^{{p - 2}}}w\quad {\text{в}}\quad E,\quad \mathop {\left. w \right|}\nolimits_{\partial E} = 0,$

для оператора p-Лапласа–Бельтрами

${{\Delta }_{p}}w = {{\nabla }_{i}}({\text{|}}\nabla w{{{\text{|}}}^{{p - 2}}}{{g}^{{ij}}}{{\nabla }_{j}}w).$

Т е о р е м а 1. Пусть $\Lambda $ и q – неотрицательные измеримые функции такие, что

(4)

$\mathop {\left. \Lambda \right|}\nolimits_{[{{R}_{0}},\zeta {{R}_{0}}] \cap [{{R}_{0}},{{R}_{1}})} = 0$

и при этом

(5)

$\Lambda (r) \leqslant \mathop {inf}\limits_{t \in (r/\zeta ,r\zeta ),{{S}_{t}} \cap \Omega \ne \emptyset } {{\lambda }_{{\min }}}({{S}_{t}} \cap \Omega )$

(6)

$q(r) \geqslant {{({\text{dia}}{{{\text{m}}}_{\varepsilon }}{{\Omega }_{{r/\sigma ,r\sigma }}})}^{{1 - \frac{n}{\nu }}}}{\text{||}}b{\text{|}}{{{\text{|}}}_{{{{\mathcal{L}}_{{\nu ,\varepsilon }}}({{\Omega }_{{r/\sigma ,r\sigma }}})}}}$

для всех r $ \in ({{R}_{0}},{{R}_{1}})$, где $0 < \varepsilon < 1$, $\zeta > 1$ и $\sigma > 1$ – некоторые вещественные числа.

Предположим также, что $u$ – неотрицательное решение (1), (2), причем $M( \cdot ;u)$ – неубывающая функция на интервале $({{R}_{0}},{{R}_{1}})$ и

(7)

$M({{R}_{0}} + 0;u) > 0.$

Тогда для любого вещественного числа $a > p - 2$ найдутся постоянные $\gamma > 0$ и $k > 0$, зависящие только от a, $n$, $p$, $\varepsilon $, $\zeta $, $\sigma $, $\nu $, ${{C}_{1}}$, ${{C}_{2}}$, такие, что на промежутке $[{{R}_{0}},{{R}_{1}})$ существует решение задачи Коши

(8)

$\frac{1}{{{{r}^{{1 + a}}}}}\frac{d}{{dr}}\left( {{{r}^{{1 + a}}}\mathop {\left| {\frac{{dm}}{{dr}}} \right|}\nolimits^{p - 2} \frac{{dm}}{{dr}}} \right) = \gamma {{e}^{{ - kq(r)}}}\Lambda (r){\text{|}}m{{{\text{|}}}^{{p - 2}}}m,$

(9)

$m({{R}_{0}}) = M({{R}_{0}} + 0;u),\quad m'({{R}_{0}}) = 0,$

удовлетворяющее оценке

(10)

$M(r;u) \geqslant m(r) > 0$

для всех r ∈ (R₀, R₁).

З а м е ч а н и е 1. Если $n > p$, то в теореме 1 можно взять $a = n - 2$. В этом случае, в левой части (8) будем, очевидно, иметь радиальный оператор p-Лапласа.

Т е о р е м а 2. Пусть справедливы условия теоремы 1. Тогда для любого вещественного числа a > p – 2 найдутся постоянные $\gamma > 0$ и $k > 0$, зависящие только от $a$, $n$, $p$, $\varepsilon $, $\zeta $, $\sigma $, $\nu $, ${{C}_{1}}$, ${{C}_{2}}$, такие, что

(11)

$\begin{gathered} M(r;u) - M({{R}_{0}} + 0;u) \geqslant \\ \geqslant \int\limits_{{{R}_{0}}}^r {dt{{{\left( {\frac{\gamma }{{{{t}^{{1 + a}}}}}\int\limits_{{{R}_{0}}}^t {{{\xi }^{{1 + a}}}{{e}^{{ - kq(\xi )}}}\Lambda (\xi ){{M}^{{p - 1}}}(\xi ;u)d\xi } } \right)}}^{{\frac{1}{{p - 1}}}}}} \\ \end{gathered} $

для всех $r \in ({{R}_{0}},{{R}_{1}})$.

З а м е ч а н и е 2. Согласно (3) неравенство (6) будет выполнено, если $b \in {{L}_{\infty }}({{\Omega }_{{{{R}_{0}},r}}})$ и

$q(r) \geqslant {\text{dia}}{{{\text{m}}}_{\varepsilon }}{{\Omega }_{{r/\sigma ,r\sigma }}}\mathop {{\text{ess}}\,{\text{sup}}}\limits_{{{\Omega }_{{r/\sigma ,r\sigma }}}} b$

для всех $r \in ({{R}_{0}},{{R}_{1}})$.

Т е о р е м а 3. Теорема 1 остается в силе, если функция $\Lambda $ вместо (4) и (5) удовлетворяет условиям

(12)

$\mathop {\left. \Lambda \right|}\nolimits_{([{{R}_{0}},h{{R}_{0}}/(1 - \delta )] \cup [{{R}_{0}},\sigma {{R}_{0}}]) \cap [{{R}_{0}},{{R}_{1}})} = 0$

(13)

$\Lambda (r) \leqslant \mathop {inf}\limits_{{{\Omega }_{{r/h,rh}}}} \mu _{\delta }^{p} + {{r}^{{ - n}}}{\text{cap}}(\overline {{{B}_{{r{{\sigma }_{3}},r{{\sigma }_{2}}}}}} {{\backslash }}\Omega ,{{B}_{{r{{\sigma }_{4}},r{{\sigma }_{1}}}}})$

для всех $r \in ({{R}_{0}},{{R}_{1}})$, где

${{\mu }_{\delta }}(x) = \mathop {sup}\limits_{\xi \in (0,\delta |x|)} {{({{\xi }^{{1 - n}}}{\text{cap}}(\overline {B_{\xi }^{x}} {{\backslash }}\Omega ,B_{{2\xi }}^{x}))}^{{\tfrac{1}{{p - 1}}}}},$

а $1 < h$, $0 < \delta < min\left\{ {1 - \frac{1}{h},1 - {{\sigma }^{{ - \frac{1}{2}}}}} \right\}$ и $\frac{1}{\sigma } \leqslant {{\sigma }_{4}}$ < σ₃ < < σ₂ < ${{\sigma }_{1}} \leqslant 1$ – некоторые вещественные числа. При этом постоянные $\gamma > 0$ и $k > 0$ теперь будут зависеть только от $a$, $h$, $n$, $p$, $\delta $, $\varepsilon $, $\sigma $, $\nu $, ${{\sigma }_{1}}$, ${{\sigma }_{2}}$, ${{\sigma }_{3}}$, ${{\sigma }_{4}}$, ${{C}_{1}}$, ${{C}_{2}}$.

З а м е ч а н и е 3. Если дополнительно потребовать, чтобы

(14)

${{r}^{{p - n}}}{\text{cap}}(\overline {{{B}_{{r{{\sigma }_{3}},r{{\sigma }_{2}}}}}} {{\backslash }}\Omega ,{{B}_{{r{{\sigma }_{4}},r{{\sigma }_{1}}}}}) \geqslant \kappa $

для всех $r \in ({{R}_{0}},{{R}_{1}})$, где $\kappa > 0$ – вещественное число, то неравенство (13) будет справедливо для некоторой функции Λ, пропорциональной ${{({\text{dia}}{{{\text{m}}}_{\varepsilon }}{{\Omega }_{{r/{{h}^{2}},r{{h}^{2}}}}})}^{{ - p}}}$.

В самом деле, можно показать, что соотношение (14) влечет оценку

$\begin{gathered} \mathop {inf}\limits_{{{\Omega }_{{r/h,rh}}}} \mu _{\delta }^{p} + {{r}^{{ - n}}}{\text{cap}}(\overline {{{B}_{{r{{\sigma }_{3}},r{{\sigma }_{2}}}}}} {{\backslash }}\Omega ,{{B}_{{r{{\sigma }_{4}},r{{\sigma }_{1}}}}}) \geqslant \\ \geqslant C{{({\text{dia}}{{{\text{m}}}_{\varepsilon }}{{\Omega }_{{r/{{h}^{2}},r{{h}^{2}}}}})}^{{ - p}}} \\ \end{gathered} $

для всех $r \in ({{R}_{0}},{{R}_{1}})$, где постоянная C > 0 зависит только от $h$, $n$, $p$, $\delta $, $\varepsilon $, $\kappa $.

При ${{R}_{0}} \to + 0$ из теоремы 3 можно также получить емкостные оценки решения в окрестности граничной точки $0 \in \partial \Omega $, аналогичные [1, 6, 7].

Т е о р е м а 4. Пусть в предположениях теоремы 1 вместо (4) и (5) справедливы условия (12) и (13). Тогда для любого вещественного числа $a > p - 2$ найдутся постоянные $\gamma > 0$ и $k > 0$, зависящие только от $a$, $h$, $n$, $p$, $\delta $, $\varepsilon $, $\sigma $, $\nu $, ${{\sigma }_{1}}$, ${{\sigma }_{2}}$, ${{\sigma }_{3}}$, ${{\sigma }_{4}}$, ${{C}_{1}}$, ${{C}_{2}}$, такие, что для всех $r \in ({{R}_{0}},{{R}_{1}})$ имеет место неравенство (11).

Далее будем рассматривать неравенства

(15)

${\text{div}}A(x,Du) + b(x){\text{|}}Du{{{\text{|}}}^{{p - 1}}} \geqslant F(x,u)\quad {\text{в}}\quad {{\Omega }_{{{{R}_{0}},{{R}_{1}}}}}.$

Функция u называется решением (15), если $u \in W_{p}^{1}({{\Omega }_{{{{R}_{0}},r}}}) \cap {{L}_{\infty }}({{\Omega }_{{{{R}_{0}},r}}}),$ $A(x,Du) \in {{L}_{{p/(p - 1)}}}({{\Omega }_{{{{R}_{0}},r}}})$ и $F(x,u) \in {{L}_{{p/(p - 1)}}}({{\Omega }_{{{{R}_{0}},r}}})$ для любого $r \in ({{R}_{0}},{{R}_{1}})$ и при этом

$\begin{gathered} - \int\limits_{{{\Omega }_{{{{R}_{0}},{{R}_{1}}}}}}^{} {A(x,Du)D\varphi dx} + \int\limits_{{{\Omega }_{{{{R}_{0}},{{R}_{1}}}}}}^{} {b(x){\text{|}}Du{{{\text{|}}}^{{p - 1}}}\varphi dx \geqslant } \\ \geqslant \int\limits_{{{\Omega }_{{{{R}_{0}},{{R}_{1}}}}}}^{} {F(x,u)\varphi dx} \\ \end{gathered} $

для всех неотрицательных $\varphi \in C_{0}^{\infty }({{\Omega }_{{{{R}_{0}},{{R}_{1}}}}}).$

Объединяя теоремы 1–4 с результатами работы [3], приходим к следующим утверждениям.

Т е о р е м а 5. Пусть $\Lambda $ и $q$ – неотрицательные измеримые функции, удовлетворяющие условиям (4)–(6), а $f{\text{:}}\,\,[{{R}_{0}},{{R}_{1}}) \times (0,\infty ) \to [0,\infty )$ и l: [R₀, R₁) × × $(0,\infty ) \to [0,\infty )$ — локально ограниченные измеримые функции такие, что

(16)

$f(r,t - 0) = f(r,t)$

для всех $r \in ({{R}_{0}},{{R}_{1}})$, $t > 0$,

(17)

$f(r,{{t}_{1}}) \geqslant f(r,{{t}_{2}})$

для всех $r \in ({{R}_{0}},{{R}_{1}})$, ${{t}_{1}} \geqslant {{t}_{2}} > 0$,

(18)

$f(r,t) \leqslant \mathop {{\text{ess}}\,{\text{inf}}}\limits_{x \in {{\Omega }_{{r/\theta ,\theta r}}}} F(x,t)$

для всех $r \in ({{R}_{0}},{{R}_{1}})$, $t > 0$, и

(19)

$l(r) \geqslant \mathop {{\text{ess}}\,{\text{sup}}}\limits_{{{\Omega }_{{r/\theta ,\theta r}}}} b$

для всех $r \in ({{R}_{0}},{{R}_{1}})$, где $\theta > 1$ – некоторое вещественное число.

Предположим также, что $u$ – неотрицательное решение (15), (2), причем $M( \cdot ;u)$ – неубывающая функция на интервале $({{R}_{0}},{{R}_{1}})$ и выполнено условие (7).

Тогда для любых вещественных чисел $a > p - 2$ и $\alpha > 0$ найдутся постоянные $\beta > 0$, $\gamma > 0$ и $k > 0$, зависящие только от $a$, $n$, $p$, $\alpha $, $\varepsilon $, $\zeta $, $\theta $, $\sigma $, $\nu $, ${{C}_{1}}$, ${{C}_{2}}$, такие, что на промежутке $[{{R}_{0}},{{R}_{1}})$ существует решение уравнения

$\begin{gathered} \frac{1}{{{{r}^{{1 + a}}}}}\frac{d}{{dr}}\left( {{{r}^{{1 + a}}}\mathop {\left| {\frac{{dm}}{{dr}}} \right|}\nolimits^{p - 2} \frac{{dm}}{{dr}}} \right) + \alpha l(r)\mathop {\left| {\frac{{dm}}{{dr}}} \right|}\nolimits^{p - 2} \frac{{dm}}{{dr}} = \\ = \gamma (f(r,\beta m) + {{e}^{{ - kq(r)}}}\Lambda (r){\text{|}}m{{{\text{|}}}^{{p - 2}}}m), \\ \end{gathered} $

удовлетворяющее условию (9) и оценке (10).

П р и м е р 1. Пусть $u$ – решение задачи

$Lu \geqslant F(x,u)\quad {\text{в}}\quad {{B}_{{{{R}_{1}}}}} \cap \Omega ,\quad u{{{\text{|}}}_{{{{B}_{{{{R}_{1}}}}} \cap \partial \Omega }}} = 0,$

для которого справедливо соотношение (7), где

$L = \sum\limits_{i,j = 1}^n \frac{\partial }{{\partial {{x}_{i}}}}\left( {{{a}_{{ij}}}(x)\frac{{\partial u}}{{\partial {{x}_{j}}}}} \right) + \sum\limits_{i = 1}^n {{b}_{i}}(x)\frac{{\partial u}}{{\partial {{x}_{i}}}}$

есть равномерно эллиптический оператор с измеримыми коэффициентами. Согласно принципу максимума, $M( \cdot ;u)$ должна быть неубывающей функцией на интервале $({{R}_{0}},{{R}_{1}})$. Полагая

$b(x) = \mathop {\left( {\sum\limits_{i = 1}^n b_{i}^{2}(x)} \right)}\nolimits^{\frac{1}{2}} ,$

очевидно, получим, что $u$ является решением неравенства

${\text{div}}A(x,Du) + b(x){\text{|}}Du{\text{|}} \geqslant F(x,u)\quad {\text{в}}\quad {{B}_{{{{R}_{1}}}}} \cap \Omega ,$

где A(x, Du) = $({{A}_{1}}(x,Du), \ldots ,{{A}_{n}}(x,Du))$,

${{A}_{i}}(x,Du) = \sum\limits_{j = 1}^n {{a}_{{ij}}}(x)\frac{{\partial u}}{{\partial {{x}_{j}}}},\quad i = 1,2, \ldots ,n.$

Таким образом, для любых функций $\Lambda $, $q$, f и $l$, удовлетворяющих условиям (4)–(6), (16)–(19), и вещественных чисел $a > 0$ и $\alpha > 0$ найдутся постоянные $\beta > 0$, $\gamma > 0$ и $k > 0$, зависящие только от $a$, $n$, $\alpha $, $\varepsilon $, $\zeta $, $\theta $, $\sigma $, $\nu $ и от постоянных эллиптичности оператора $L$, такие, что на промежутке $[{{R}_{0}},{{R}_{1}})$ существует решение уравнения

(20)

$\begin{gathered} \frac{{{{d}^{2}}m}}{{d{{r}^{2}}}} + \left( {\frac{{1 + a}}{r} + \alpha l(r)} \right)\frac{{dm}}{{dr}} = \\ = \gamma \left( {f(r,\beta m) + {{e}^{{ - kq(r)}}}\Lambda (r)m} \right), \\ \end{gathered} $

удовлетворяющее условию (9) и оценке (10).

В случае $n > 2$, полагая $a = n - 2$ и α = 1, мы, очевидно, получим радиальную компоненту оператора $\Delta + l({\text{|}}x{\text{|}})D{\text{|}}x{\text{|}}D$ в левой части (20).

Т е о р е м а 6. В предположениях теоремы 5 для любых вещественных чисел a > p – 2 и $\alpha > 0$ найдутся постоянные $\beta > 0$, $\gamma > 0$ и $k > 0$, зависящие только от $a$, $n$, $p$, $\alpha $, $\varepsilon $, $\zeta $, $\theta $, $\sigma $, $\nu $, ${{C}_{1}}$, ${{C}_{2}}$, такие, что

(21)

$\begin{gathered} M(r;u) - M({{R}_{0}} + 0;u) \geqslant \\ \geqslant \int\limits_{{{R}_{0}}}^r \begin{gathered} dt\left( {\frac{\gamma }{{{{t}^{{1 + a}}}}}\int\limits_{{{R}_{0}}}^t {{{\xi }^{{1 + a}}}{{e}^{{ - \alpha \int\limits_\xi ^t {l(s)ds} }}}(f(\xi ,\beta M(\xi ;u)) + } } \right. \hfill \\ {{\left. {^{{^{{^{{^{{^{{^{{^{{^{{}}}}}}}}}}}}}}}} + \,{{e}^{{ - kq(r)}}}\Lambda (\xi ){{M}^{{p - 1}}}(\xi ;u))d\xi } \right)}^{{\frac{1}{{p - 1}}}}} \hfill \\ \end{gathered} \\ \end{gathered} $

для всех $r \in ({{R}_{0}},{{R}_{1}})$.

Т е о р е м а 7. Теорема 5 остается в силе, если функция $\Lambda $ вместо (4) и (5) удовлетворяет условиям (12) и (13). При этом постоянные $\beta > 0$, $\gamma > 0$ и $k > 0$ теперь будут зависеть только от $a$, $h$, $n$, $p$, $\alpha $, $\delta $, $\varepsilon $, $\theta $, $\sigma $, $\nu $, ${{\sigma }_{1}}$, ${{\sigma }_{2}}$, ${{\sigma }_{3}}$, ${{\sigma }_{4}}$, ${{C}_{1}}$, ${{C}_{2}}$.

Т е о р е м а 8. Пусть в предположениях теоремы 5 функция $\Lambda $ вместо (4) и (5) удовлетворяет условиям (12) и (13). Тогда для любых вещественных чисел $a > p - 2$ и $\alpha > 0$ найдутся постоянные $\beta > 0$, $\gamma > 0$ и $k > 0$, зависящие только от $a$, $h$, $n$, $p$, $\alpha $, $\delta $, $\varepsilon $, $\theta $, $\sigma $, $\nu $, ${{\sigma }_{1}}$, ${{\sigma }_{2}}$, ${{\sigma }_{3}}$, ${{\sigma }_{4}}$, ${{C}_{1}}$, ${{C}_{2}}$, такие, что для всех $r \in ({{R}_{0}},{{R}_{1}})$ имеет место неравенство (21).

Список литературы

Gariepy R., Ziemer W. A regularity condition at the boundary for solutions of quasilinear elliptic equations // Arch. Rat. Mech. Anal. 1977. V. 67. P. 25–39.
Коньков А.А. О теоремах сравнения для квазилинейных эллиптических неравенств, учитывающих геометрию области // Изв. РАН. Сер. Матем. 2014. Т. 78. 4. С. 123–174.
Kon’kov A.A. On comparison theorems for elliptic inequalities // J. Math. Anal. Appl. 2012. V. 388. P. 102–124.
Ландкоф Н.С. Основы современной теории потенциала. М.: Наука, 1966.
Мазья В.Г. Пространства С.Л.Соболева. Л.: Изд-во ЛГУ, 1985.
Мазья В.Г. О непрерывности в граничной точке решений квазилинейных эллиптических уравнений // Вестник ЛГУ. 1970. 13. Вып. 3. С. 42–55.
Мазья В.Г. О поведении вблизи границы решения задачи Дирихле для эллиптического уравнения второго порядка в дивергентной форме // Матем. заметки. 1967. Т. 2. Вып. 2. С. 209–220.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Доклады Российской академии наук. Математика, информатика, процессы управления

Архивы выпусков Информация о журнале Отправить рукопись в журнал