Доклады Российской академии наук. Математика, информатика, процессы управления, 2021, T. 501, № 1, стр. 95-97

1. Автономный объект t и недружественный наблюдатель  f движутся в пространстве ${{\mathbb{R}}^{3}}$, содержащем телесное замкнутое выпуклое множество G, препятствующее движению и видимости. Объект, следующий из начальной точки ${{t}_{*}}$ в конечную $t{\text{*\;}}({{t}_{*}},t{\text{*}} \notin G)$, обходит множество G по кратчайшей траектории $\mathcal{T} = {{\mathcal{T}}_{t}}$. Предполагается, что величины скоростей ${{V}_{t}},{{V}_{f}}$ объекта и наблюдателя одинаковы, а расстояние между позициями взаимно видимых $t = {{t}_{\tau }}$ и $f = {{f}_{\tau }}$ в каждый момент времени $\tau $ удовлетворяет неравенствам

при заданных δ и $K \geqslant 1$. Левое неравенство “обеспечивает” взаимную безопасность объекта и наблюдателя, а правое продиктовано желанием улучшить качество наблюдения.

Задача наблюдателя состоит в построении траектории ${{\mathcal{T}}_{f}}$, при движении по которой соблюдается неравенство (1) с возможно меньшим значением константы K, а наблюдатель ${{f}_{\tau }} \in {{\mathcal{T}}_{f}}$ может видеть движущийся объект ${{t}_{\tau }}$ на возможно бóльшей части траектории ${{\mathcal{T}}_{t}}$

При отсутствии ограничения на величину $\left| {{{V}_{f}}} \right|$ вектора скорости наблюдателя задача решается просто: так, двигаясь по траектории ${{\mathcal{T}}_{f}} = \left\{ {{{f}_{\tau }}} \right\}$, где ${{f}_{\tau }} = {{t}_{\tau }} - \delta \frac{{{{V}_{{{{t}_{\tau }}}}}}}{{\left| {{{V}_{{{{t}_{\tau }}}}}} \right|}}$, наблюдатель  f_τ отслеживает движение объекта ${{t}_{\tau }}$ на всей траектории ${{\mathcal{T}}_{t}}$, при этом ${\text{||}}{{t}_{\tau }} - {{f}_{\tau }}{\text{||}} = \delta $ и скорость наблюдателя ${{V}_{{{{f}_{\tau }}}}}$ зависит от ${{V}_{{{{t}_{\tau }}}}}$ и кривизны траектории ${{\mathcal{T}}_{t}}$. Отметим, что наблюдателю нецелесообразно двигаться непосредственно по ${{\mathcal{T}}_{t}}$ вслед за объектом по участкам строгой выпуклости траектории ${{\mathcal{T}}_{t}}$ и в окрестности ее угловых точек, опасаясь потерять объект t из виду. Поскольку траектория ${{\mathcal{T}}_{t}}$ является кратчайшей, а траектория ${{\mathcal{T}}_{f}}$ при условиях $\left| {{{V}_{t}}} \right| = \left| {{{V}_{f}}} \right|$, (1) таковой не является, то существует участок траектории ${{\mathcal{T}}_{t}}$, который преодолевается объектом вне зоны наблюдения за ${{t}_{\tau }}$.

В данной работе предлагается способ построения траектории ${{\mathcal{T}}_{f}}$, обеспечивающей неравенство (1) с константой K сколь угодно близкой к единице, и сколь угодно малую длину участка траектории ${{\mathcal{T}}_{t}}$, недоступного для наблюдения.

2. Так как ${{t}_{*}}$ и t* не содержатся в множестве $G$, то начальная и конечная части траектории $\mathcal{T}$ являются прямолинейным отрезками. Пусть это $[{{t}_{*}},\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{t} ]$ и $\left[ {t{\text{*}},\bar {t}} \right]$. Будем использовать обозначения:

${{P}_{{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{t} ~}}},~{{P}_{{\bar {t}}}}$ – плоскости, опорные к множеству G в точках $\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{t} $, $\bar {t}$ соответственно. Отметим, что ${{l}_{*}} \subset {{P}_{{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{t} ~}}}$, $~l{\text{*}} \subset {{P}_{{\bar {t}}}}$.

3. Пусть плоскости ${{P}_{{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{t} ~}}},~{{P}_{{\bar {t}}}}$ параллельны или пересекаются, $l = {{P}_{{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{t} ~}}} \cap ~{{P}_{{\bar {t}}}}$ и при этом

Двигаясь по траектории

наблюдатель ${{f}_{\tau }}$ имеет возможность видеть объект ${{t}_{\tau }} = \left( {{{f}_{\tau }} - b} \right) \in \mathcal{T}$, не меняя направление наблюдения b.

4. Рассмотрим случай, когда выполняются обратные к (2) неравенства (см. рис. 1). Далее $\widehat {t,t'}$ – дуга траектории $\mathcal{T}$, заключенная между точками $t,~t'$, а $\left| {\widehat {t,t'}} \right|$ – длина этой дуги. Определим последовательность точек ${{t}_{i}} \in \mathcal{T}$ и по ней последовательность точек ${{f}_{i}}$. Кусочно-линейная дуга с узлами ${{f}_{i}}$ будет далее включена в состав траектории ${{\mathcal{T}}_{f}}$.

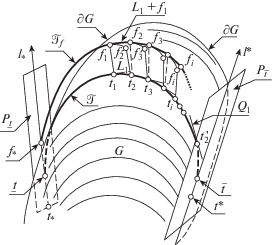
Поскольку траектория $\mathcal{T}$ является кратчайшей, то в каждой ее точке t существует (см., например, [1, 2]) пара касательных векторов. Через ${{L}_{i}}$ обозначим касательный вектор ${{V}_{{{{t}_{i}}}}}$ в точке ${{t}_{i}}$, являющийся вектором скорости объекта $t$. Дугу $\widehat {{{t}_{i}},{{t}_{{i + 1}}}}$ траектории $\mathcal{T}$ будем обозначать через Δ_i.

Точка ${{t}_{1}} \in \mathcal{T}$ такова, что касательный в ней к $\mathcal{T}$ вектор ортогонален лучу ${{l}_{*}}$. Положим ${{f}_{1}} = {{t}_{1}} + {{b}_{1}}$, где ${{b}_{1}} = b$ (см. (3)). В качестве начального участка траектории ${{\mathcal{T}}_{f}}$ возьмем дугу $(\widehat {\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{t} ,{{t}_{1}}}) + {{b}_{1}}$. Чтобы определить ${{t}_{2}} \in \widehat {{{t}_{1}},\bar {t}}$, найдем точку $t_{2}^{'} \in \widehat {{{t}_{1}},\bar {t}} \subset \mathcal{T}$ такую, что прямая ${{Q}_{1}}$, содержащая $t_{2}^{'}$ и параллельная вектору ${{b}_{1}}$, не пересекается с G°, где G° – внутренность множества $G$. Точка ${{t}_{2}}$ должна лежать на дуге $\widehat {{{t}_{1}},t_{2}^{'}}$ на малом расстоянии от ${{t}_{1}}$. Построим дугу $\widehat {{{f}_{1}},f_{2}^{'}}{\text{\;}} = {{\Delta }_{1}} + {{b}_{1}}$ и на луче ${{L}_{1}} + {{f}_{1}}$ отметим точку ${{f}_{2}}$, для которой ${\text{||}}{{f}_{1}} - {{f}_{2}}{\text{||}} = \left| {{{\Delta }_{1}}} \right|$. Непрерывное взаимнооднозначное отображение отрезка $[{{f}_{1}},{{f}_{2}}]$ на дугу $\widehat {{{t}_{1}},{{t}_{2}}}$ дает наблюдателю ${{f}_{\tau }} \in [{{f}_{1}},{{f}_{2}}]$ способ слежения за двигающимся объектом ${{t}_{\tau }}$. На этом завершается первый шаг. Легко проверить, что увеличение расстояния от ${{t}_{1}}$ до ${{t}_{2}}$ влечет рост величины ${\text{||}}{{f}_{2}} - {{t}_{2}}{\text{||}}$ и константы K в неравенстве (1). На втором шаге, по аналогии с первым, найдем точку $t_{3}^{'} \in \mathcal{T}$ такую, что прямая ${{Q}_{2}}$, содержащая точку $t_{3}^{'}$ и параллельная вектору ${{b}_{2}} = {{f}_{2}} - {{t}_{2}}$, не пересекается с G°. Точку ${{t}_{3}}$ возьмем на дуге $\widehat {{{t}_{2}},t_{3}^{'}}$ на малом расстоянии от точки ${{t}_{2}}$, и т.д. Увеличивая число шагов, строим последовательности $\left\{ {{{t}_{i}}} \right\} \in \mathcal{T}$, ${{t}_{i}} \to \bar {t}$, и $\left\{ {{{f}_{i}}} \right\}$, $\rho \left( {{{f}_{i}},{{P}_{{\bar {t}}}}} \right) \to 0$ $\left( {i \to \infty } \right)$. Траектория наблюдателя f имеет вид

Построенные последовательности ${{t}_{i}},~{{f}_{i}}~\left( {i = 1,2, \ldots } \right)$ удовлетворяют соотношениям

при этом последовательность ${\text{||}}{{t}_{i}} - {{f}_{i}}{\text{||}}$ возрастает. Справедлива

Теорема 1. Пусть $\left\{ {{{t}_{i}}} \right\}_{1}^{\infty } \subset \widehat {{{t}_{1}},\bar {t}}~$ – последовательность точек, построенная по указанному выше правилу, $\widehat {{{t}_{{i + 1}}},\bar {t}} \subset \widehat {{{t}_{i}},\bar {t}}$ $\left( {i = 1,2, \ldots } \right).$ Наблюдатель f, двигаясь по траектории ${{\mathcal{T}}_{f}}$ (4), имеет возможность следить за движением объекта $t = t\left( f \right)$ по $\mathcal{T}$, где $t\left( f \right) = f - {{b}_{1}}$ при $f \in (\widehat {\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{t} ,{{t}_{1}}}) + {{b}_{1}}$, и $t({{f}^{\lambda }}) \in {{\Delta }_{i}}$, ${\text{|}}\widehat {{{t}_{i}},t({{f}^{\lambda }})}{\text{|}} = \lambda \left| {{{\Delta }_{i}}} \right|$ при ${{f}^{\lambda }} = \left( {1 - \lambda } \right){{f}_{i}} + \lambda {{f}_{{i + 1}}}$ $\left( {0 \leqslant \lambda \leqslant 1} \right)$.

Число звеньев в (4) можно ограничить, проецируя точку f_j, при достаточно большом i на плоскость ${{P}_{{\bar {t}}}}$. Обозначим эту проекцию через $\bar {f}$. При движении по отрезку $[{{t}_{j}},\bar {t}]$ наблюдатель не контролирует объект, преодолевающий дугу $\widehat {{{f}_{j}},\bar {f}}$, но, передвигаясь по плоскости ${{P}_{{\bar {t}}}}$ из позиции ${{f}_{\tau }} = \bar {f}$, он отслеживает движение объекта по отрезку $\left[ {\bar {t},t{\text{*}}} \right]$.

Используя неравенства (5), (6), легко установить, что имеет место

Теорема 2. Пусть для любого номера $n = 1,2$, ... по указанному выше правилу построена упорядоченная сетка узлов $\{ t_{i}^{n}\} _{{i = 1}}^{{k\left( n \right)}} \subset \widehat {{{t}_{1}},\bar {t}}$, $t_{{k\left( n \right)}}^{n} \to \bar {t}$ при $k(n) \to \infty ,$ для которой

тогда для последовательности траекторий где $f_{i}^{n} = t_{i}^{n} + {{b}_{i}}$, выполняется соотношение