Доклады Российской академии наук. Математика, информатика, процессы управления, 2022, T. 502, № 1, стр. 52-57

ОПТИМИЗАЦИЯ КОЛЕБАНИЙ МЕХАНИЧЕСКИХ СИСТЕМ

Ю. Ф. Голубев^1, *

¹ Институт прикладной математики им. М.В. Келдыша Российской академии наук
Москва, Россия

Поступила в редакцию 02.09.2021
После доработки 22.11.2021
Принята к публикации 25.11.2021

EDN: LASLAL
DOI: 10.31857/S2686954322010040

Аннотация

Решается проблема управления колебаниями в окрестности положения равновесия склерономной механической системы с несколькими степенями свободы. Одна степень свободы не поддается непосредственному управлению, а остальные управляются сервоприводами. Предложен оригинальный метод поиска оптимального управления амплитудой колебаний по неуправляемой степени свободы за счет выбора управления законом изменения других степеней свободы. В число управляемых могут входить как позиционные, так и циклические координаты. По сравнению с принципом максимума Л.С. Понтрягина метод не содержит сопряженных переменных и дает существенное преимущество в уменьшении размерности анализируемой совокупной системы дифференциальных уравнений. На примере конкретной маятниковой системы продемонстрирована эффективность применения предложенного метода.

Ключевые слова: механическая система, колебания, амплитуда, управление, оптимизация

1. ПОСТАНОВКА ПРОБЛЕМЫ

Рассмотрим склерономную голономную механическую систему с кинетической энергией

$T = \frac{1}{2}\sum\limits_{i,j = 1}^n {{{a}_{{ij}}}{{{\dot {q}}}_{i}}{{{\dot {q}}}_{j}}} ,\quad n \geqslant 2,$

где n – число степеней свободы системы, q_i – обобщенные координаты, ${{\dot {q}}_{i}}$ – обобщенные скорости, а симметричная матрица $({{a}_{{ij}}})$ зависит от координат и положительно определена. Уравнения движения системы представим в форме уравнений Лагранжа 2-го рода

(1)

$\frac{d}{{dt}}\left( {\frac{{\partial T}}{{\partial {{{\dot {q}}}_{i}}}}} \right) - \frac{{\partial T}}{{\partial {{q}_{i}}}} = {{Q}_{i}},\quad i = 1,...,n,$

в которых $t$ – время, а позиционные обобщенные силы ${{Q}_{i}} = {{Q}_{i}}({{q}_{1}},...,{{q}_{n}})$ стационарны. Пусть первыми в наборе $({{q}_{1}},...,{{q}_{n}})$ идут s позиционных координат, а остальными – $(n - s)$ циклических координат. Пользуясь произволом в нумерации обобщенных координат, выделим первую обобщенную координату, обозначив ее буквой $x$. Остальные координаты переобозначим: ${{u}_{j}} = {{q}_{{j + 1}}}$, $j = 1,...,s - 1$ и ${{w}_{k}} = {{q}_{{s + k}}}$, $k = 1,...,n - s$, где ${\mathbf{u}} = ({{u}_{1}},...,{{u}_{{s - 1}}})$ – вектор позиционных координат, ${\mathbf{w}}\, = \,({{w}_{1}},...,{{w}_{{n - s}}})$ – вектор циклических координат, так что $\frac{{\partial T}}{{{{w}_{k}}}}\, \equiv \,0$, $\frac{{\partial {{Q}_{i}}}}{{\partial {{w}_{k}}}} = 0,$ $i = 1,...,n,$ $k = 1,...,n - s$. Кинетическая энергия примет вид

$Т = \frac{1}{2}\left[ {{{a}_{{11}}}{{{\dot {x}}}^{2}} + 2\dot {x}\left( {\sum\limits_{j = 1}^{s - 1} {{{a}_{{1,j + 1}}}{{{\dot {u}}}_{j}} + \sum\limits_{k = 1}^{n - s} {{{a}_{{1,s + k}}}{{{\dot {w}}}_{k}}} } } \right)} \right] + T{\kern 1pt} *,$

где s – число позиционных координат, включающее выделенную координату x, и

$\begin{gathered} T{\kern 1pt} {\text{*}}(x,{\mathbf{u}},{\mathbf{\dot {u}}},{\mathbf{\dot {w}}}) = \frac{1}{2}\left( {\sum\limits_{j,r = 1}^{s - 1} {{{a}_{{j + 1,r + 1}}}{{{\dot {u}}}_{j}}{{{\dot {u}}}_{r}}} + } \right. \\ \left. {\, + 2\sum\limits_{j = 1}^{s - 1} {\sum\limits_{k = 1}^{n - s} {{{a}_{{j + 1,k + s}}}{{{\dot {u}}}_{j}}{{{\dot {w}}}_{k}}} + \sum\limits_{k,r = 1}^{n - s} {{{a}_{{k + s,r + s}}}{{{\dot {w}}}_{k}}{{{\dot {w}}}_{r}}} } } \right). \\ \end{gathered} $

В системе (1) выделим уравнение для координаты x:

(2)

$\frac{d}{{dt}}\left( {{{a}_{{11}}}\dot {x} + \sum\limits_{j = 1}^{s - 1} {{{a}_{{1,j + 1}}}{{{\dot {u}}}_{j}}} + \sum\limits_{k = 1}^{n - s} {{{a}_{{1,s + k}}}{{{\dot {w}}}_{k}}} } \right) - \frac{{\partial T}}{{\partial x}} = F(x,{\mathbf{u}}),$

где ${\mathbf{u}} = ({{u}_{1}},...,{{u}_{{s - 1}}}) \in {{R}^{{s - 1}}}$, $F(x,{\mathbf{u}}) = {{Q}_{1}}(x,{{u}_{1}}, \cdots ,{{u}_{{s - 1}}})$. Примем координату x в качестве независимой переменной на участке ее монотонного изменения: $\dot {x} \ne 0$. Тогда уравнение (2) преобразуется к виду

(3)

$\dot {x}\frac{d}{{dx}}\left[ {f(x,{\mathbf{u}},{\mathbf{u}}{\kern 1pt} ',{\mathbf{w}}{\kern 1pt} ')\dot {x}} \right] - p(x,{\mathbf{u}},{\mathbf{u}}{\kern 1pt} ',{\mathbf{w}}{\kern 1pt} '){{\dot {x}}^{2}} = F(x,{\mathbf{u}}),$

где ${\mathbf{u}}{\kern 1pt} ' = \frac{{d{\mathbf{u}}}}{{dx}}$, ${\mathbf{w}}{\kern 1pt} ' = \frac{{d{\mathbf{w}}}}{{dx}}$ и

$f(x,{\mathbf{u}},{\mathbf{u}}{\kern 1pt} ',{\mathbf{w}}{\kern 1pt} ') = {{a}_{{11}}} + \sum\limits_{j = 1}^{s - 1} {{{a}_{{1,j + 1}}}u_{j}^{'}} + \sum\limits_{k = 1}^{n - s} {{{a}_{{1,s + k}}}w_{k}^{'}} ,$

$\begin{gathered} p(x,{\mathbf{u}},{\mathbf{u}}{\kern 1pt} ',{\mathbf{w}}{\kern 1pt} ') = \\ \, = \frac{1}{2}\left( {\frac{{\partial {{a}_{{11}}}}}{{\partial x}} + 2\sum\limits_{j = 1}^{s - 1} {\frac{{\partial {{a}_{{1,j + 1}}}}}{{\partial x}}u_{j}^{'} + } \,2\sum\limits_{k = 1}^{n - s} {\frac{{\partial {{a}_{{1,s + k}}}}}{{\partial x}}w_{k}^{'}} } \right) + \\ \, + \frac{{\partial T{\kern 1pt} {\text{*}}(x,{\mathbf{u}},{\mathbf{u}}{\kern 1pt} ',{\mathbf{w}}{\kern 1pt} ')}}{{\partial x}}. \\ \end{gathered} $

Будем считать, что векторы ${\mathbf{u}} = {\mathbf{u}}(x)$, ${\mathbf{\dot {w}}} = {\mathbf{\dot {w}}}(x)$ заданы, а их компоненты ограничены:

(4)

$\begin{gathered} \left| {u_{j}^{m} \leqslant {{u}_{j}}(x) \leqslant u_{j}^{M}} \right|,\quad j = 1,...,s - 1, \\ \left| {\dot {w}_{k}^{m} \leqslant {{{\dot {w}}}_{k}}(x) \leqslant \dot {w}_{k}^{M}} \right|,\quad k = 1,...,n - s. \\ \end{gathered} $

Эти вектор-функции будем рассматривать как сервосвязи, наложенные на систему. Обобщенные силы ${{Q}_{2}},...,{{Q}_{n}}$ следует выбирать так, чтобы указанные вектор-функции ${\mathbf{u}}(x)$, ${\mathbf{\dot {w}}}(x)$ были реализованы. Предположим, что это сделано, так что ограничения (4) удовлетворяются, и можно написать уравнение

(5)

$\begin{gathered} \int\limits_{{{x}_{0}}}^x {\lambda \left\{ {F(x,{\mathbf{u}}) + p(x,{\mathbf{u}},{\mathbf{u}}{\kern 1pt} ',{\mathbf{w}}{\kern 1pt} '){{{\dot {x}}}^{2}}\mathop - \limits_{_{{_{{}}}}} } \right.} \\ \, - \left. {\dot {x}\frac{d}{{dx}}\left[ {f(x,{\mathbf{u}},{\mathbf{u}}{\kern 1pt} ',{\mathbf{w}}{\kern 1pt} ')\dot {x}} \right]} \right\}dx = 0, \\ \end{gathered} $

где x₀ – начальное значение независимой переменной x, $\lambda (x,{\mathbf{u}},{\mathbf{u}}{\kern 1pt} ',{\mathbf{w}}{\kern 1pt} ')$ – произвольная функция. Уравнение (5) непосредственно следует из уравнения (3). Заметим, что если $f(x,{\mathbf{u}},{\mathbf{u}}{\kern 1pt} ',{\mathbf{w}}{\kern 1pt} ') \ne 0$, то уравнение (3) допускает интегрирующий множитель [1]. Выберем его в качестве $\lambda $:

(6)

$\begin{gathered} \lambda = f(x,{\mathbf{u}},{\mathbf{u}}{\kern 1pt} ',{\mathbf{w}}{\kern 1pt} ')\exp \left( { - \int\limits_{{{x}_{0}}}^x {\frac{{2p(x,{\mathbf{u}},{\mathbf{u}}{\kern 1pt} ',{\mathbf{w}}{\kern 1pt} ')}}{{f(x,{\mathbf{u}},{\mathbf{u}}{\kern 1pt} ',{\mathbf{w}}{\kern 1pt} ')}}dx} } \right), \\ f(x,{\mathbf{u}},{\mathbf{u}}{\kern 1pt} ',{\mathbf{w}}{\kern 1pt} ') \ne 0. \\ \end{gathered} $

Тогда равенство (5) можно преобразовать к виду

$\int\limits_{{{x}_{0}}}^x {\lambda F(x,{\mathbf{u}})dx} - \frac{1}{2}\left. {[{{{\dot {x}}}^{2}}f(x,{\mathbf{u}},{\mathbf{u}}{\kern 1pt} ',{\mathbf{w}}{\kern 1pt} ')\lambda (x,{\mathbf{u}},{\mathbf{u}}{\kern 1pt} ',{\mathbf{w}}{\kern 1pt} ')]} \right|_{{{{x}_{0}}}}^{x} = 0$

или

(7)

$\begin{gathered} \int\limits_{{{x}_{0}}}^x {\lambda F(x,{\mathbf{u}})dx} = \\ \, = \frac{1}{2}\left. {\left[ {f{\text{*}}(x,\dot {x},{\mathbf{u}},{\mathbf{\dot {u}}},{\mathbf{\dot {w}}})\lambda {\kern 1pt} *(x,\dot {x},{\mathbf{u}},{\mathbf{\dot {u}}},{\mathbf{\dot {w}}})} \right]} \right|_{{{{x}_{0}}}}^{x}, \\ \end{gathered} $

где

$f{\kern 1pt} {\text{*}}(x,\dot {x},{\mathbf{u}},{\mathbf{\dot {u}}},{\mathbf{\dot {w}}}) = {{a}_{{11}}}\dot {x} + \sum\limits_{j = 1}^{s - 1} {{{a}_{{1,j + 1}}}{{{\dot {u}}}_{j}}} + \sum\limits_{k = 1}^{n - s} {{{a}_{{1,s + k}}}{{{\dot {w}}}_{k}}} ,$

$\begin{gathered} \lambda {\kern 1pt} {\text{*}}(x,\dot {x},{\mathbf{u}},{\mathbf{\dot {u}}},{\mathbf{\dot {w}}}) = \\ \, = f{\kern 1pt} {\text{*}}(x,\dot {x},{\mathbf{u}},{\mathbf{\dot {u}}},{\mathbf{\dot {w}}})\exp \left( { - \int\limits_{{{x}_{0}}}^x {\frac{{2p(x,{\mathbf{u}},{\mathbf{u}}{\kern 1pt} ',{\mathbf{w}}{\kern 1pt} ')}}{{f(x,{\mathbf{u}},{\mathbf{u}}{\kern 1pt} ',{\mathbf{w}}{\kern 1pt} ')}}dx} } \right). \\ \end{gathered} $

В том случае, когда $\dot {x} = \dot {x}(x)$ обращается в нуль, интеграл в левой части равенства (7) становится несобственным из-за того, что при $\dot {x} = 0$ значения ${\mathbf{u}}{\kern 1pt} ' = {\mathbf{\dot {u}}}{\text{/}}\dot {x}$ и ${\mathbf{w}}{\kern 1pt} ' = {\mathbf{\dot {w}}}{\text{/}}\dot {x}$ могут стать бесконечно большими. Однако та же формула (7) показывает, что этот интеграл существует и принимает конечное значение. Заметим, что переменные $f{\kern 1pt} *$ и $\lambda {\kern 1pt} *$ не содержат отмеченной особенности. Кроме того,

(8)

$\begin{gathered} \hfill f{\kern 1pt} {\text{*}}\lambda {\kern 1pt} {\text{*}} = {{\left( {f{\kern 1pt} {\text{*}}(x,\dot {x},{\mathbf{u}},{\mathbf{\dot {u}}},{\mathbf{\dot {w}}})} \right)}^{2}} \times \\ \hfill \, \times \exp \left( { - \int\limits_{{{x}_{0}}}^x {\frac{{2p(x,{\mathbf{u}},{\mathbf{u}}{\kern 1pt} ',{\mathbf{w}}{\kern 1pt} ')}}{{f(x,{\mathbf{u}},{\mathbf{u}}{\kern 1pt} ',{\mathbf{w}}{\kern 1pt} ')}}dx} } \right) \geqslant 0. \\ \end{gathered} $

Предположим, что силовая функция

(9)

$U(x,{\mathbf{u}}( \cdot )) = \int\limits_{{{x}_{0}}}^x {F(\tau ,{\mathbf{u}}(\tau ))} d\tau $

имеет изолированный максимум по координате x для ${\mathbf{u}}(\tau ) \equiv 0$ и этот максимум остается изолированным, когда ${\mathbf{u}}(\tau )$ меняется. Будем рассматривать движение в окрестности этого максимума. Пусть начальные условия выбраны так, что равенство ${{\dot {x}}_{0}} = \dot {x}({{x}_{0}}) = 0$ выполнено, когда $x = {{x}_{0}}$. Назовем амплитудой колебаний величину J = x₁ – x₀, где ${{x}_{1}} > {{x}_{0}}$ – следующее значение координаты x, когда ${{\dot {x}}_{1}} = \dot {x}({{x}_{1}})$ обращается в ноль. В этом случае аргумент изолированного максимума силовой функции $U(x,{\mathbf{u}}( \cdot ))$ будет принадлежать отрезку $[{{x}_{0}},{{x}_{1}}]$. В общем случае этот аргумент может меняться в зависимости от выбранных вектор-функций ${\mathbf{u}}(x)$, ${\mathbf{\dot {w}}}(x)$. На концах отрезка должно быть выполнено

(10)

${{\dot {x}}_{0}} = {{\dot {x}}_{1}} = 0,$

а также

$f{\kern 1pt} {\text{*}}({{x}_{0}},{{\dot {x}}_{0}},{\mathbf{u}}({{x}_{0}}),{\mathbf{\dot {u}}}({{x}_{0}}),{\mathbf{\dot {w}}}({{x}_{0}})) = $

(11)

$\begin{gathered} \, = \sum\limits_{j = 1}^{s - 1} {{{a}_{{1,j + 1}}}{{{\dot {u}}}_{j}}({{x}_{0}})} + \sum\limits_{k = 1}^{n - s} {{{a}_{{1,s + k}}}{{{\dot {w}}}_{k}}({{x}_{0}}),} \\ f{\kern 1pt} {\text{*}}({{x}_{1}},{{{\dot {x}}}_{1}},{\mathbf{u}}({{x}_{1}}),{\mathbf{\dot {u}}}({{x}_{1}}),{\mathbf{\dot {w}}}({{x}_{1}})) = \\ \end{gathered} $

$\, = \sum\limits_{j = 1}^{s - 1} {{{a}_{{1,j + 1}}}{{{\dot {u}}}_{j}}} ({{x}_{1}}) + \sum\limits_{k = 1}^{n - s} {{{a}_{{1,s + k}}}{{{\dot {w}}}_{k}}({{x}_{1}}).} $

Требуется найти кусочно-непрерывные управления ${\mathbf{u}}(x)$, ${\mathbf{\dot {w}}}(x)$, при которых достигается максимум (минимум) функционала J.

Теперь рассмотрим обратное движение маятника и обозначим $\xi = - x$. Уравнение (2) принимает вид

(12)

$\begin{gathered} \frac{d}{{dt}}\left( {{{a}_{{11}}}\dot {\xi } - \sum\limits_{j = 1}^{s - 1} {{{a}_{{1,j + 1}}}{{{\dot {u}}}_{j}}} - \sum\limits_{k = 1}^{n - s} {{{a}_{{1,s + k}}}{{{\dot {w}}}_{k}}} } \right) - \\ \, - \frac{{\partial T}}{{\partial \xi }} = - F( - \xi ,{\mathbf{u}}). \\ \end{gathered} $

Уравнение (3) можно представить как

(13)

$\begin{gathered} \dot {\xi }\frac{d}{{d\xi }}[{{f}_{\xi }}( - \xi ,{\mathbf{u}},{\mathbf{u}}_{\xi }^{'},{\mathbf{w}}_{\xi }^{'})\dot {\xi }] - \\ \, - {{p}_{\xi }}( - \xi ,{\mathbf{u}},{\mathbf{u}}_{\xi }^{'},{\mathbf{w}}_{\xi }^{'}){{{\dot {\xi }}}^{2}} = - F( - \xi ,{\mathbf{u}}), \\ \end{gathered} $

где ${\mathbf{u}}_{\xi }^{'} = \frac{{d{\mathbf{u}}}}{{d\xi }}$, ${\mathbf{w}}_{\xi }^{'} = \frac{{d{\mathbf{w}}}}{{d\xi }}$ и

${{f}_{\xi }}( - \xi ,{\mathbf{u}},{\mathbf{u}}_{\xi }^{'},{\mathbf{w}}_{\xi }^{'}) = {{a}_{{11}}} - \sum\limits_{j = 1}^{s - 1} {{{a}_{{1,j + 1}}}u_{{j\xi }}^{'}} - \sum\limits_{k = 1}^{n - s} {{{a}_{{1,s + k}}}w_{{k\xi }}^{'}} ,$

$\begin{gathered} {{p}_{\xi }}( - \xi ,{\mathbf{u}},{\mathbf{u}}_{\xi }^{'},{\mathbf{w}}_{\xi }^{'}) = \\ \, = \frac{1}{2}\left( {\frac{{\partial {{a}_{{11}}}}}{{\partial \xi }} + 2\sum\limits_{j = 1}^{s - 1} {\frac{{\partial {{a}_{{1,j + 1}}}}}{{\partial \xi }}u_{{j\xi }}^{'} + \,} 2\sum\limits_{k = 1}^{n - s} {\frac{{\partial {{a}_{{1,s + k}}}}}{{\partial \xi }}w_{{k\xi }}^{'}} } \right) + \\ \, + \frac{{\partial T{\kern 1pt} *(x,{\mathbf{u}},{\mathbf{u}}{\kern 1pt} ',{\mathbf{w}}{\kern 1pt} ')}}{{\partial \xi }}. \\ \end{gathered} $

Следовательно, получаем

(14)

${{\lambda }_{\xi }} = {{f}_{\xi }}( - \xi ,{\mathbf{u}},{\mathbf{u}}_{\xi }^{'},{\mathbf{w}}_{\xi }^{'}){\text{exp}}\left( { - \int\limits_{{{\xi }_{0}}}^\xi {\frac{{2{{p}_{\xi }}( - \xi ,{\mathbf{u}},{\mathbf{u}}_{\xi }^{'},{\mathbf{w}}_{\xi }^{'})}}{{{{f}_{\xi }}( - \xi ,{\mathbf{u}},{\mathbf{u}}_{\xi }^{'},{\mathbf{w}}_{\xi }^{'})}}d\xi } } \right),$

и формулу (7) можно переписать следующим образом:

(15)

$\begin{gathered} \int\limits_{{{\xi }_{0}}}^\xi {{{\lambda }_{\xi }}F( - \xi ,{\mathbf{u}})d\xi } = \\ \, = - \frac{1}{2}\left. {[f_{\xi }^{*}( - \xi ,\dot {\xi },{\mathbf{u}},{\mathbf{\dot {u}}},{\mathbf{\dot {w}}})\lambda _{\xi }^{*}( - \xi ,\dot {\xi },{\mathbf{u}},{\mathbf{\dot {u}}},{\mathbf{\dot {w}}})]} \right|_{{{{\xi }_{0}}}}^{\xi }, \\ \end{gathered} $

где

$f_{\xi }^{*}( - \xi ,\dot {\xi },{\mathbf{u}},{\mathbf{\dot {u}}},{\mathbf{\dot {w}}}) = {{a}_{{11}}}\dot {\xi } - \sum\limits_{j = 1}^{s - 1} {{{a}_{{1,j + 1}}}{{{\dot {u}}}_{j}}} - \sum\limits_{k = 1}^{n - s + 1} {{{a}_{{1,s + k}}}{{{\dot {w}}}_{k}}} ,$

$\begin{gathered} \lambda _{\xi }^{*}( - \xi ,\dot {\xi },{\mathbf{u}},{\mathbf{\dot {u}}},{\mathbf{\dot {w}}}) = f_{\xi }^{*}( - \xi ,\dot {\xi },{\mathbf{u}},{\mathbf{\dot {u}}},{\mathbf{\dot {w}}}) \times \\ \, \times \exp \left( { - \int\limits_{{{\xi }_{0}}}^\xi {\frac{{2{{p}_{\xi }}( - \xi ,{\mathbf{u}},{\mathbf{u}}_{\xi }^{'},{\mathbf{w}}_{\xi }^{'})}}{{{{f}_{\xi }}( - \xi ,{\mathbf{u}},{\mathbf{u}}_{\xi }^{'},{\mathbf{w}}_{\xi }^{'})}}d\xi } } \right). \\ \end{gathered} $

Амплитуда колебаний имеет вид $J = {{\xi }_{1}} - {{\xi }_{0}}$, где ${{\xi }_{1}} > {{\xi }_{0}}$, ${{\dot {\xi }}_{0}} = \dot {\xi }({{\xi }_{0}}) = 0$, ${{\dot {\xi }}_{1}} = \dot {\xi }({{\xi }_{1}}) = 0$ и $\dot {\xi }(\xi ) \ne 0$, если $\xi \in ({{\xi }_{0}},{{\xi }_{1}})$. Требуется найти кусочно-непрерывные управления ${\mathbf{u}}(\xi )$, ${\mathbf{\dot {w}}}(\xi )$, при которых значение функционала J максимально (минимально).

2. ОПТИМАЛЬНОЕ РАСКАЧИВАНИЕ (УСПОКОЕНИЕ) КОЛЕБАНИЙ

Пусть λ определено формулой (6). Тогда справедливы следующие теоремы.

Теорема 1 (Принцип наилучшего раскачивания). Предположим, что движение системы описывается уравнением (2) и существуют две точки ${{x}_{0}}$ и ${{x}_{1}}$, причем ${{x}_{0}} < {{x}_{1}}$ и ${{\dot {x}}_{0}} = {{\dot {x}}_{1}} = 0$. Тогда

I. Необходимыми условиями оптимальности управлений ${\mathbf{u}} = {{{\mathbf{u}}}_{M}}(\tau )$, ${{{\mathbf{\dot {w}}}}_{M}}({{x}_{1}})$, которые, будучи стесненными ограничениями (4), обеспечивают максимум величины ${{x}_{1}}$, служат уравнения

(16)

$\begin{gathered} {{{\mathbf{u}}}_{M}}(x) = \arg \mathop {\max }\limits_{\mathbf{u}} \text{[}\chi (x,{{{\mathbf{u}}}_{М}},{\mathbf{u}}_{M}^{'},{\mathbf{w}}_{M}^{'})F(x,{\mathbf{u}})], \\ {{{{\mathbf{\dot {w}}}}}_{M}}({{x}_{1}}) = \arg \mathop {\min }\limits_{{\mathbf{\dot {w}}}} \left[ {\sum\limits_{k = 1}^{n - s} {{{a}_{{1,s + k}}}({{x}_{1}},{{{\mathbf{u}}}_{M}}){{{\dot {w}}}_{k}}} } \right], \\ \end{gathered} $

где $\chi = \lambda (x) \cdot {\text{sign[}}\lambda ({{x}_{1}} - 0)]$.

II. Необходимыми условиями оптимальности управлений ${\mathbf{u}} = {{{\mathbf{u}}}_{m}}(\tau )$, ${{{\mathbf{\dot {w}}}}_{m}}({{x}_{0}})$, которые, будучи стесненными ограничениями (4), обеспечивают минимум величины ${{x}_{0}}$, служат уравнения

(17)

$\begin{array}{*{20}{c}} {{{{\mathbf{u}}}_{m}}(x) = \arg \mathop {\min }\limits_{\mathbf{u}} \text{[}\chi (x,{{{\mathbf{u}}}_{m}},{\mathbf{u}}_{m}^{'},{\mathbf{w}}_{m}^{'})F(x,{\mathbf{u}})],} \\ {{{{{\mathbf{\dot {w}}}}}_{m}}({{x}_{0}}) = \arg \mathop {\max }\limits_{{\mathbf{\dot {w}}}} \left[ {\sum\limits_{k = 1}^{n - s} {{{a}_{{1,s + k}}}({{x}_{0}},{{{\mathbf{u}}}_{m}}){{{\dot {w}}}_{k}}} } \right],} \end{array}$

где $\chi = \lambda (x) \cdot {\text{sign}}[\lambda ({{x}_{0}} + 0)]$.

Теорема 2 (Принцип оптимального успокоения колебаний). Предположим, что движение системы описывается уравнениями (2) и имеются две точки x₀и x₁, такие, что ${{x}_{0}} < {{x}_{1}}$ ${{\dot {x}}_{0}} = {{\dot {x}}_{1}} = 0$. Тогда:

I. Необходимое условие оптимальности управлений ${\mathbf{u}} = {{{\mathbf{u}}}_{m}}(\tau )$, ${{{\mathbf{\dot {w}}}}_{m}}({{x}_{1}})$, которые при выполнении ограничений (4) обеспечивают минимум величины x₁, выражается равенствами

(18)

$\begin{array}{*{20}{c}} {{{{\mathbf{u}}}_{m}}(x) = \arg \mathop {\min }\limits_{\mathbf{u}} \text{[}\chi (x,{{{\mathbf{u}}}_{m}},{\mathbf{u}}_{m}^{'},{\mathbf{w}}_{m}^{'})F(x,{\mathbf{u}})],} \\ {{{{{\mathbf{\dot {w}}}}}_{m}}({{x}_{1}}) = \arg \mathop {\max }\limits_{{\mathbf{\dot {w}}}} \left[ {\sum\limits_{k = 1}^{n - s} {{{a}_{{1,s + k}}}({{x}_{1}},{{{\mathbf{u}}}_{m}}){{{\dot {w}}}_{k}}} } \right],} \end{array}$

где $\chi = \lambda (x) \cdot {\text{sign}}[\lambda {\kern 1pt} {\text{*}}({{x}_{1}} - 0)]$.

II. Необходимые условия оптимальности управлений ${\mathbf{u}} = {{{\mathbf{u}}}_{M}}(x)$, ${{{\mathbf{\dot {w}}}}_{M}}({{x}_{0}})$, которые при выполнении ограничений (4) обеспечивают максимум величины ${{x}_{0}}$, выражаются уравнениями

(19)

$\begin{array}{*{20}{c}} {{{{\mathbf{u}}}_{M}}(x) = \arg \mathop {\max }\limits_{\mathbf{u}} \left[ {\lambda (x,{{{\mathbf{u}}}_{M}},{\mathbf{u}}_{M}^{'},{\mathbf{w}}_{M}^{'})F(x,{\mathbf{u}})} \right],} \\ {{{{{\mathbf{\dot {w}}}}}_{M}}({{x}_{0}}) = \arg \mathop {\min }\limits_{{\mathbf{\dot {w}}}} \left[ {\sum\limits_{k = 1}^{n - s} {{{a}_{{1,s + k}}}({{x}_{0}},{{{\mathbf{u}}}_{M}}){{{\dot {w}}}_{k}}} } \right]{\text{,}}} \end{array}$

где $\chi = \lambda (x) \cdot {\text{sign}}[\lambda {\kern 1pt} *({{x}_{0}} + 0)]$.

Доказательство приведенных теорем достигается применением формул (7) и (15), а также с учетом того, что в уравнении (2) коэффициент ${{a}_{{11}}}$ > 0. Рассмотрим, например, утверждение I теоремы 1. В соответствии с общим принципом вариационного исчисления [2] множители λ и ${{\lambda }_{\xi }}$, входящие в формулы (7) и (15), играют вспомогательную роль и не участвуют в процессе оптимизации. Они служат лишь для тождественного преобразования уравнения движения. Пусть значение координаты $x = {{x}_{1}}$ соответствует максимально достижимому отклонению системы от положения равновесия, но первое равенство формулы (16) в какой-нибудь внутренней точке отрезка [${{x}_{0}}$, ${{x}_{1}}$] нарушено. Тогда, как следует из формулы (7), в этой точке можно за счет управления u, оставив значения других управлений неизменными, увеличить подынтегральную функцию в (7), а за счет этого увеличить значение скорости ${{\dot {x}}_{1}} > 0$. Тогда вырастет и новое значение координаты $x = {{x}_{1}}$, при котором скорость $\dot {x}$ сделается равной нулю. Полученное противоречие доказывает необходимость выполнения первого соотношения равенства (16). Второе соотношение равенства (16) аналогичным образом следует из того, что функции f * в (7), (11) линейно зависят от скоростей системы.

Для доказательства утверждения II теоремы 1 следует воспользоваться формулой (15) с последующей интерпретацией полученного результата в терминах независимой переменной x.

Теорема 2 является взаимной по отношению к теореме 1, и поэтому доказательство теоремы 2 вполне аналогично доказательству теоремы 1.

Подробное доказательство приведенных выше теорем с помощью метода первой вариации см. в [3].

3. ПРИМЕР. ДВУХЗВЕННЫЙ МАЯТНИК ПЕРЕМЕННОЙ ДЛИНЫ

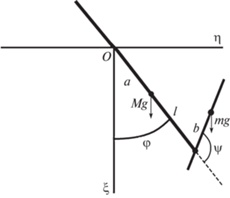
Двухзвенный маятник (рис. 1) состоит из двух стержней. Первый стержень прикреплен к неподвижной точке $O$. К этому стержню на расстоянии $l$ от его центра масс шарнирно прикреплен второй стержень. Обозначим $M$ массу первого стержня, $I$ − момент инерции первого стержня относительно его центра масс, $\varphi $ − угол отклонения первого стержня от нижнего направления вертикали. Центр масс первого стержня расположен на расстоянии $a(t)$ от точки $O$. Пусть $m$ − масса второго стержня, ${{I}_{2}}$ − момент инерции второго стержня относительно его центра масс, $b$ − расстояние от точки прикрепления второго стержня до его центра масс, $\psi $ − угол между вторым стержнем и продолжением первого стержня за точку соединения стержней, $g$ − ускорение силы тяжести. Угол $\psi $ и расстояние $a$ примем в качестве управления с целью раскачивания системы, ограничив их допустимые значения: ${{\psi }_{m}} \leqslant \psi \leqslant {{\psi }_{M}}$, ${{a}_{m}} \leqslant a \leqslant {{a}_{M}}$.

Рис. 1.

Двухзвенный маятник.

Представленная механическая система может служить упрощенной математической моделью как для человека, раскачивающегося на качелях, так и для гимнаста, раскачивающегося на перекладине.

Для описания движения выберем начало $O$ абсолютной системы координат в точке подвеса первого стержня, ось $O\xi $ направим вертикально вниз, ось $O\eta $ направим горизонтально в правую координатную полуплоскость. Координаты и скорости центра масс первого стержня примут вид

$\begin{gathered} {{\xi }_{1}} = a\cos \varphi ,\quad {{\eta }_{1}} = a\sin \varphi , \\ {{{\dot {\xi }}}_{1}} = - a\dot {\varphi }\sin \varphi + \dot {a}\cos \varphi , \\ {{\eta }_{1}} = a\dot {\varphi }\cos \varphi + \dot {a}\sin \varphi . \\ \end{gathered} $

Координаты и скорости центра масс второго стержня запишем следующим образом:

$\begin{gathered} {{\xi }_{2}} = (a + l)\cos \varphi + b\cos (\varphi + \psi ), \\ {{{\dot {\xi }}}_{2}} = - [(a + l)\dot {\varphi }\sin \varphi + b(\dot {\varphi } + \dot {\psi })\sin (\varphi + \psi )] + \dot {a}\cos \varphi , \\ {{\eta }_{2}} = (a + l)\sin \varphi + b\sin (\varphi + \psi ), \\ {{{\dot {\eta }}}_{2}} = (a + l)\dot {\varphi }\cos \varphi + b(\dot {\varphi } + \dot {\psi })\cos (\varphi + \psi ) + \dot {a}\sin \varphi . \\ \end{gathered} $

Найдем координаты центра масс системы:

$\begin{array}{*{20}{c}} {{{\xi }_{с}} = \frac{{aM + (a + l)m}}{{M + m}}\cos \varphi + \frac{{bm}}{{M + m}}\cos (\varphi + \psi ),} \\ {{{\eta }_{с}} = \frac{{aM + (a + l)m}}{{M + m}}\sin \varphi + \frac{{bm}}{{M + m}}\sin (\varphi + \psi ).} \end{array}$

Кинетический момент системы относительно точки $O$ имеет вид

$K = (I + M{{a}^{2}})\dot {\varphi } + {{I}_{c}}(\dot {\varphi } + \dot {\psi }) + m({{\xi }_{2}}{{\dot {\eta }}_{2}} - {{\eta }_{2}}{{\dot {\xi }}_{2}}).$

После преобразований получим

$\begin{array}{*{20}{c}} {K = [I + M{{a}^{2}} + m(a + l)(a + l + b\cos \psi )]\dot {\varphi } + } \\ {\, + \{ {{I}_{c}} + mb[(a + l)\cos \psi + b]\} (\dot {\varphi } + \dot {\psi }) - m\dot {a}b\sin \psi .} \end{array}$

Уравнение изменения кинетического момента запишем следующим образом:

(20)

$\begin{gathered} \frac{{d(f\dot {\varphi })}}{{dt}} = F(\varphi ,a,\psi ) = \\ \, = - g\{ [a(M + m) + lm]\sin \varphi + bm\sin (\varphi + \psi )\} , \\ \end{gathered} $

где

$\begin{gathered} f = [I + m(a + l)(a + l + b\cos \psi )] + \\ \, + \{ {{I}_{c}} + mb[(a + l)\cos \psi + b]\} (1 + \psi {\kern 1pt} ') - ma{\kern 1pt} 'b\sin \psi , \\ \end{gathered} $

а $\psi {\kern 1pt} '$, $a{\kern 1pt} '$ − производные по переменной $\varphi $. Из формулы (6) найдем $\lambda = f$.

Предположим, что $0 < b < a + l$. Применим утверждение I теоремы 1. Пусть ${{\varphi }_{0}} < 0$ есть левая граница отклонения по углу $\varphi $, а ${{\varphi }_{1}} > 0$ − соответственно правая граница, и пусть в начальный момент $\varphi = {{\varphi }_{0}}$. Из формулы (16) видим, что наилучший способ достичь максимума положительного полуколебания состоит в применении правила

(21)

$\begin{gathered} \psi = \left\{ {\begin{array}{*{20}{l}} {{{\psi }_{M}},\quad {\text{если}}\quad \varphi + {{\psi }_{M}} < - \frac{\pi }{2},{\text{ }}} \\ { - \frac{\pi }{2} - \varphi ,\quad {\text{если}}\quad \varphi + {{\psi }_{m}} \leqslant - \frac{\pi }{2} \leqslant \varphi + {{\psi }_{M}},} \\ {{{\psi }_{m}},\quad {\text{если}}\quad \varphi + {{\psi }_{m}} > - \frac{\pi }{2};{\text{ }}} \end{array}} \right. \\ a = \left\{ {\begin{array}{*{20}{c}} {{{a}_{M}},\quad {\text{если}}\quad \varphi < 0,} \\ {{{a}_{m}},\quad {\text{если}}\quad \varphi \geqslant 0.} \end{array}} \right. \\ \end{gathered} $

Из формулы для f видно, что при $0 < b < а + l$ в любом из перечисленных в формуле (21) случаев знак λ остается положительным.

Применим утверждение II теоремы 1. Пусть теперь в начальный момент $\varphi = {{\varphi }_{1}} > 0$. Тогда, напротив, требуется минимизировать значение ${{\varphi }_{0}}$ отрицательного полуразмаха. Из (17) заключаем, что наилучший режим для достижения минимума отклонения отрицательного полуразмаха состоит в применении формулы

(22)

$\begin{gathered} \psi = \left\{ {\begin{array}{*{20}{c}} {{{\psi }_{m}},\quad {\text{если}}\quad \varphi + {{\psi }_{m}} > \frac{\pi }{2},{\text{ }}} \\ {\frac{\pi }{2} - \varphi ,\quad {\text{если}}\quad \varphi + {{\psi }_{m}} \leqslant \frac{\pi }{2} \leqslant \varphi + {{\psi }_{M}},} \\ {{{\psi }_{M}},\quad {\text{если}}\quad \varphi + {{\psi }_{M}} < \frac{\pi }{2};{\text{ }}} \end{array}} \right. \\ a = \left\{ {\begin{array}{*{20}{c}} {{{a}_{m}},\quad {\text{если}}\quad \varphi < 0,} \\ {{{a}_{M}},\quad {\text{если}}\quad \varphi \geqslant 0.} \end{array}} \right. \\ \end{gathered} $

В итоге получается синтез управления для оптимального раскачивания двухзвенного маятника, а именно: после достижения максимального положительного отклонения качелей следует применять формулы (22); после достижения минимального отрицательного отклонения следует применять формулы (21), и так далее.

Из теоремы 2 выводится синтез управления для оптимального успокоения колебаний двухзвенного маятника, а именно: после достижения максимального положительного отклонения маятника следует применять формулы (21); после достижения минимального отрицательного отклонения следует применять формулы (22), и так далее.

Из уравнения (20) видим, что при $b = 0$ угол $\psi $ становится циклической координатой. Тогда, чтобы обеспечить раскачивание, достаточно воспользоваться правилами для циклических координат раздела 2. В том случае, когда $b > (a + l)$, параметр χ для значений ${\text{|}}\psi {\text{|}} > \arccos \left[ { - \frac{{a + l}}{b}} \right]$ в режиме $\varphi + \psi = \pm \frac{\pi }{2}$ может менять знак. Для того чтобы избежать этой неприятности, следует принять ограничения ${{\psi }_{m}} > - \arccos \left[ { - \frac{{a + l}}{b}} \right]$, ${{\psi }_{M}}\, < \,{\text{arccos}}\left[ { - \frac{{a + l}}{b}} \right]$.

В рассмотренном выше примере была применена теорема об изменении кинетического момента системы вместо уравнений Лагранжа второго рода. Применение этой теоремы к угловым координатам приводит к уравнениям, эквивалентным уравнениям Лагранжа, но содержащим меньше взаимно уничтожающихся слагаемых.

ЗАКЛЮЧЕНИЕ

Применение предложенных алгоритмов управления, получаемых из необходимых условий оптимальности (16)–(19), предполагает учет информации о моментах времени достижения экстремальных значений оптимизируемой координаты и информации о направлении соответствующего полуколебания. Условия оптимальности (16)–(19) не содержат сопряженных переменных в смысле принципа максимума Л.С. Понтрягина [4]. Это облегчает применение указанных условий для рассмотренного класса задач. Дополнительным преимуществом предложенного метода служит то, что закон оптимального управления получается непосредственно в виде зависимости от оптимизируемой координаты. Используя предложенные условия оптимальности, можно получить аналитические решения для некоторых новых нетривиальных модельных задач. Условия оптимальности управления амплитудой колебаний, предложенные в работе, упрощают решение соответствующих задач в многомерном пространстве управляющих функций по сравнению с известными методами. Они эффективны как для задач раскачивания, так и для задач успокоения колебаний.

Список литературы

Степанов В.В. Курс дифференциальных уравнений. Изд. 11, испр., обновл. М.: URSS, 2016. 512 с. ISBN 978-5-382-01622-1.
Охоцимский Д.Е., Энеев Т.М. Некоторые вариационные задачи, связанные с запуском искусственного спутника Земли. М.: Гос. Изд-во технико-теор. лит-ры. (Успехи физических наук. Т. 63, вып. 1а), 1957. С. 5–32.
Голубев Ю.Ф. Метод оптимального управления колебаниями механических систем // Препринт ИПМ им. М.В. Келдыша. 2021. № 33. 37 с. https://doi.org/10.20948/prepr-2021-33
Понтрягин Л.С., Болтянский В.Г., Гамкрелидзе Р.В., Мищенко Е.Ф. Математическая теория оптимальных процессов. М.: Наука, 1976. 393 с.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Доклады Российской академии наук. Математика, информатика, процессы управления

Архивы выпусков Информация о журнале Отправить рукопись в журнал