Доклады Российской академии наук. Математика, информатика, процессы управления, 2022, T. 505, № 1, стр. 56-62

1. ВВЕДЕНИЕ

Пусть $f(x) \in K[x]$ – свободный от квадратов многочлен степени $2g + 2$, $g \geqslant 0$, над полем K характеристики, отличной от 2. Дополнительно предположим, что старший коэффициент многочлена f является полным квадратом в мультипликативной группе $K{\kern 1pt} *$ поля $K$. Проблема периодичности непрерывных дробей элементов гиперэллиптических полей $\mathcal{L} = K(x)(\sqrt f )$, построенных в поле $K(({{x}^{{ - 1}}}))$, приобрела широкую известность еще с работ Абеля и Чебышева, и с тех пор проявлялась в различных разделах теории чисел, анализа и алгебраической геометрии. Современные результаты о периодичности непрерывной дроби $\sqrt f $ и эквивалентных условиях изложены в [1–3]. В частности, из этих результатов следует, что в поле $\mathcal{L}$ элемент $\sqrt f $ и его разложение в непрерывную дробь играют ключевую роль в вопросах, связанных с поиском фундаментальных единиц и рациональных точек кручения в якобиане гиперэллиптической кривой, заданной уравнением ${{y}^{2}}$ = = f(x).

Пусть теперь $f(x)$ – свободный от квадратов многочлен произвольной степени, и свободный член многочлена $f(x)$ является полным квадратом в группе $K{\kern 1pt} *$. В статье [4] доказано следующее утверждение: если для некоторого $s \in \mathbb{Z}$ непрерывная дробь элемента $\sqrt f {\text{/}}{{x}^{s}}$, построенная в K(x), квазипериодическая, то она периодическая. В статье [1] сформулирована естественная задача об исследовании периодичности непрерывной дроби элемента $\sqrt f $, построенной в поле формальных степенных рядов $K((x))$. А именно, в этой статье сформулирована проблема описания числовых полей K и многочленов $f(x) \in K[x]$, для которых элемент $\sqrt f $ имеет периодическую непрерывную дробь, построенную в поле $K((x))$. В статьях [1] и [5] эта проблема полностью решена для эллиптических полей над полем $K = \mathbb{Q}$ рациональных чисел. В [5] сформулирована гипотеза о конечности с точностью до естественного отношения эквивалентности многочленов $f(x)$ над числовыми полями $K$, являющимися расширениями поля $\mathbb{Q}$ ограниченной степени, с периодическим разложением элемента $\sqrt f $ в непрерывную дробь в поле $K((x))$. В статьях [7, 8] эта проблема решена для кубических многочленов $f(x)$, определенных над полями $K$, $[K:\mathbb{Q}] \leqslant 4$, а в случае $[K:\mathbb{Q}] = 2$ в [6, 7] дано явное описание таких пар $[K,f(x)]$, что $\deg f = 3$ и $\sqrt f $ имеет периодическое разложение в непрерывную дробь в поле $K((x))$.

Определим множество $S$, состоящее из двух сопряженных нормирований, которые определены на поле $\mathcal{L}$ и связаны с униформизующей $x$ поля $K(x)$. Мы продолжаем исследование периодических элементов вида $\sqrt f $, $f \in K[x]$ в случае квадратичных полей $K$ и $\deg f = 4$. Найдено полное описание таких свободных от квадратов многочленов $f$, что $\sqrt f $ имеет периодическое разложение в непрерывную дробь в поле формальных степенных рядов $K((x))$, а эллиптическое поле $K(x)(\sqrt f )$ обладает фундаментальной $S$-единицей степени $m$, $4 \leqslant m \leqslant 12$, $m \ne 11$.

2. ВСПОМОГАТЕЛЬНЫЕ УТВЕРЖДЕНИЯ

Для натуральных $n$ определим две последовательности многочленов ${{T}_{n}},{{Q}_{n}} \in \mathbb{Z}[x]$:

Из определения следует, что $\deg {{T}_{n}} = \left[ {\frac{n}{2}} \right]$, degQ_n = = $\left[ {\frac{{n - 1}}{2}} \right]$. Положим x = y², тогда справедливо тождество

Если подставить вместо y значение –y, то имеем ${{T}_{n}}({{y}^{2}}) - y{{Q}_{n}}({{y}^{2}}) = (1 - y{{)}^{n}}$. Отсюда получаем формулы, которые можно использовать как альтернативное определение многочленов ${{T}_{n}},\;{{Q}_{n}}$:

При любом $n \in \mathbb{N}$ многочлены ${{T}_{n}}(x)$ и ${{Q}_{n}}(x)$ взаимно просты и не имеют кратных корней.

Из (2) следует, что для любых $n,m \in \mathbb{N}$ справедливы тождества

Пусть K – числовое поле, и даны числа n, $m \in \mathbb{N}$. Из формул (3) следует, что, если у многочленов ${{T}_{n}}(x)$, ${{Q}_{n}}(x)$, ${{T}_{m}}(x)$ и ${{Q}_{m}}(x)$ нет корней в поле K, то у многочленов ${{T}_{{nm}}}(x)$ и ${{Q}_{{nm}}}(x)$ также нет корней в поле K.

3. МНОЖЕСТВО КОРНЕЙ ${{T}_{n}}(x)$ И ${{Q}_{n}}(x)$, НАД КВАДРАТИЧНЫМИ ПОЛЯМИ

В статье [9] были найдены все рациональные корни многочленов ${{T}_{n}}(x)$ и ${{Q}_{n}}(x)$, определенных в (1), при всех натуральных $n$: для многочленов ${{T}_{n}}(x)$, $n \in \mathbb{N}$, корнями могут быть только $x \in \{ - 1$, –1/3}, более точно, ${{T}_{{2(2k - 1)}}}( - 1) = 0$, ${{T}_{{3(2k - 1)}}}( - 1{\text{/}}3)$ = 0 при всех $k \in \mathbb{N}$, причем указанные корни имеют кратность один и других рациональных корней нет; для многочленов ${{Q}_{n}}(x)$, $n \in \mathbb{N}$, корнями могут быть только $x \in \{ - 3, - 1, - 1{\text{/}}3\} $, более точно, ${{Q}_{{3k}}}( - 3) = 0$, ${{Q}_{{4k}}}( - 1) = 0$, ${{Q}_{{6k}}}( - 1{\text{/}}3) = 0$ при всех $k \in \mathbb{N}$, причем указанные корни имеют кратность один и других рациональных корней нет.

Исследуем последовательности многочленов ${{T}_{n}}(x)$ и ${{Q}_{n}}(x)$, на наличие корней в квадратичных полях. Запишем явные выражения для этих многочленов при $n \leqslant 6$:

По критерию Эйзенштейна из (1) при простых $n$ многочлены ${{T}_{n}}(x)$ и ${{Q}_{n}}(x)$ неприводимы, причем при $n \geqslant 7$ степени многочленов ${{T}_{n}}(x)$ и ${{Q}_{n}}(x)$ больше 3, поэтому при простых $n$ многочлены ${{T}_{n}}(x)$ и ${{Q}_{n}}(x)$ корней в квадратичных полях не имеют. Обозначим множество различных корней многочленов ${{T}_{n}}(x)$ и ${{Q}_{n}}(x)$ при $n \leqslant 6$ через M. Имеем

Покажем, что других корней в квадратичных полях, кроме корней из множества $M$, многочлены ${{T}_{n}}(x)$ и ${{Q}_{n}}(x)$, $n \in \mathbb{N}$, не имеют.

Рассуждая по индукции по числу простых множителей числа n, с помощью формул (3) получаем следующее утверждение.

Предложение. При $n \in \mathbb{N}$ таких, что 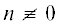(mod 2), 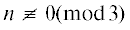, , многочлены ${{T}_{n}}(x)$ и ${{Q}_{n}}(x)$ в квадратичных полях корней не имеют.

Таким образом, корни многочленов ${{T}_{n}}(x)$ и ${{Q}_{n}}(x)$ из квадратичных полей могут быть только при $n$, кратных $2$, $3$ или $5$.

Теорема 1. Множество корней последовательностей многочленов ${{T}_{n}}(x)$ и ${{Q}_{n}}(x)$, принадлежащих квадратичным полям, исчерпывается множеством M, определенном в (4).

Доказательство. Пусть для некоторого $n \in \mathbb{N}$ имеем ${{T}_{n}}(a) = 0$, причем 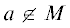– элемент некоторого квадратичного поля. Представим $n = {{n}_{1}} \cdot {{m}_{1}}$, где ${{n}_{1}}{{ = 2}^{\alpha }}{{3}^{\beta }}{{5}^{\gamma }}$, а число ${{m}_{1}}$ не имеет простых делителей меньше 7. Предположим, что ${{T}_{{{{n}_{1}}}}}(a) \ne 0$, тогда из (3) следует, что ${{T}_{{{{m}_{1}}}}}(b) = 0$, где b = $a{{({{Q}_{{{{n}_{1}}}}}(a){\text{/}}{{T}_{{{{n}_{1}}}}}(a))}^{2}}$. Но этого не может быть, так как b, как и a, принадлежит квадратичному полю. Значит, ${{T}_{{{{n}_{1}}}}}(a) = 0$ для .

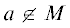Если ${{n}_{1}}$ четно, то представим ${{n}_{1}} = 2{{m}_{1}}$. Так как ${{T}_{2}}(a)\, \ne \,0$, ибо , то из (3) следует, что ${{T}_{{{{m}_{1}}}}}({{b}_{1}})$ = 0, где ${{b}_{1}} = a{{({{Q}_{2}}(a){\text{/}}{{T}_{2}}(a))}^{2}}$. Покажем, что из того, что следует, что 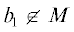. Предположим противное, т.е. ${{b}_{1}} \in M$. Перебрав все возможные значения для ${{b}_{1}} \in M$, видим, что значения a, удовлетворяющие уравнению b₁ = $a{{({{Q}_{2}}(a){\text{/}}{{T}_{2}}(a))}^{2}}$, либо принадлежат множеству M, либо не являются элементами квадратичных полей, что противоречит начальному предположению о корне a многочлена ${{T}_{n}}(x)$. Таким образом, 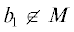и ${{T}_{{{{m}_{1}}}}}({{b}_{1}})$ = 0. Если ${{m}_{1}}$ четно, то снова представим ${{m}_{1}} = 2{{m}_{2}}$, и, рассуждая аналогично, придем к тому, что должно существовать число такое, что ${{T}_{{{{m}_{2}}}}}({{b}_{2}})$ = 0. Повторяя эти рассуждения необходимое количество раз, получаем, что должен существовать элемент 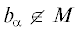некоторого квадратичного поля такой, что ${{T}_{{{{m}_{\alpha }}}}}({{b}_{\alpha }}) = 0$, причем ${{m}_{\alpha }}{{ = 3}^{\beta }}{{5}^{\gamma }}$. Далее, если $\beta > 0$, то представим ${{m}_{\alpha }} = 3k$. Так как ${{T}_{3}}({{b}_{\alpha }}) \ne 0$, ибо , то из (3) следует, что ${{T}_{k}}(c) = 0$, где $c = {{b}_{\alpha }}{{({{Q}_{3}}({{b}_{\alpha }}){\text{/}}{{T}_{3}}({{b}_{\alpha }}))}^{2}}$. Перебирая все возможные значения $c \in M$, приходим к выводу, что либо ${{b}_{\alpha }} \in M$, либо ${{b}_{\alpha }}$ не является элементом квадратичного поля, что противоречит нашему предположению об элементе ${{b}_{\alpha }}$. Значит, 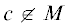– такой элемент квадратичного расширения, что ${{T}_{k}}(c) = 0$. При необходимости рассуждая аналогично, можно считать, что $k{{ = 5}^{\gamma }}$. Если $\gamma > 1$, то представим $k = 5{{k}_{1}}$. Так как ${{T}_{5}}(c) \ne 0$, ибо , то из (3) следует, что ${{T}_{{{{k}_{1}}}}}({{c}_{1}}) = 0$, где c₁ = $c{{({{Q}_{5}}(c){\text{/}}{{T}_{5}}(c))}^{2}}$. Перебирая все возможные значения ${{c}_{1}} \in M$, приходим к выводу, что либо $c \in M$, либо $c$ не является элементом квадратичного поля, что противоречит нашему предположению об элементе $c$. Значит, – такой элемент квадратичного расширения, что ${{T}_{{{{k}_{1}}}}}({{c}_{1}}) = 0$. При необходимости рассуждая аналогично, можно считать, что ${{k}_{1}} = 5$. Но все корни ${{T}_{5}}(x)$ лежат в M, что приводит нас к противоречию. Таким образом, у многочлена ${{T}_{n}}(x)$ не может быть других корней из квадратичного поля, кроме корней, указанных в множестве M.

Для многочлена ${{Q}_{n}}(x)$ рассуждения полностью аналогичны.

Теорема 1 доказана.

4. ОСНОВНЫЕ РЕЗУЛЬТАТЫ

Обозначим через ${{\mathcal{U}}_{0}}$ множество пар $[K,\;f(x)]$, состоящих из числового поля $K$ и свободного от квадратов многочлена $f \in K[x]$, $\deg f = 4$, имеющего периодическое разложение $\sqrt f $ в непрерывную дробь в поле $K((x))$. Множество пар $[K,\;f(x)]$ в ${{\mathcal{U}}_{0}}$ будем рассматривать с точностью до отношения эквивалентности, определенного допустимыми заменами многочлена f(x) на ${{a}^{2}}f(bx)$ для   a, $b \in K{\text{*}}$ и заменой $f(x)$ на ${{f}^{\sigma }}(x)$, где $\sigma \in {\text{Gal}}(K{\text{/}}\mathbb{Q})$.

Для $[K,\;f(x)] \in {{\mathcal{U}}_{0}}$ в силу критерия из [1] (теорема 1) эллиптическое поле $L = K(x)(\sqrt f )$ обладает фундаментальной S-единицей степени N, где множество $S = \{ v_{x}^{ - },\;v_{x}^{ + }\} $ состоит из двух сопряженных нормирований, являющихся продолжением нормирования ${{v}_{x}}$ поля $K(x)$. Отсюда следует, что класс дивизора $v_{x}^{ - }{\text{--}}v_{x}^{ + }$ имеет конечный порядок N в группе классов дивизоров Δ°(L), причем в случае $K = \mathbb{Q}$ из [10] следует, что $N \leqslant 12$, $N \ne 11$, а в случае $[K\;:\;\mathbb{Q}] = 2$ из [11] следует, что $N \leqslant 18$, $N \ne 17$.

Обозначим за $\mathcal{U}$ множество троек $[K,\;f(x),\;N]$, где $[K,\;f(x)] \in {{\mathcal{U}}_{0}}$ и $N$ – степень соответствующей фундаментальной S-единицы поля L = = $K(x)(\sqrt f )$.

Теорема 2. Пусть $[K:\mathbb{Q}] \leqslant 2$. Множество троек $[K,\;f(x),\;N]$, входящих в множество $\mathcal{U}$ и определяющих эллиптическое поле $L = K(x)(\sqrt f )$, содержащее фундаментальную S-единицу степени N, $4 \leqslant N \leqslant 12$, $N \ne 11$, описывается следующим образом

Обозначим через ${{X}_{1}}(N)$ модулярную кривую, чьи $K$-точки отвечают с точностью до изоморфизма парам $(E,{{P}_{N}})$, где $E$ – эллиптическая кривая, определенная над $K$, ${{P}_{N}}$ – $K$-точка порядка $N$ на $E$. Ограничение в теореме 2 на степень N фундаментальной $S$-единицы обусловлено тем фактом, что в случае $N \leqslant 12$, $N \ne 11$ кривые ${{X}_{1}}(N)$ рациональны, и дают так называемую рациональную параметризацию множества пар $(E,{{P}_{N}})$ в зависимости от единственного параметра t (явное представление см. в [12]). Для N = 11 и $N \geqslant 13$ кривые ${{X}_{1}}(N)$ перестают быть рациональными, и эти случаи являются темой для дальнейших исследований.

Доказательство теоремы 2 является обобщением доказательства основных результатов статьи [5], проведенных над полем $\mathbb{Q}$, на случай квадратичных полей констант. Отметим, что рассуждения нельзя назвать аналогичными, поскольку при расширениях поля $\mathbb{Q}$ существенным образом изменяется множество M корней многочленов ${{T}_{n}}(x)$ и ${{Q}_{n}}(x)$, определенных в (1). Для квадратичных расширений в теореме 1 явно найдены элементы множества M – их конечное число, что дает конечное число вариантов уравнений, связывающих параметры семейств эллиптических кривых, имеющих точку порядка $N$, $N \leqslant 12$, $N \ne 11$. Указанная связь возникает из условия периодичности разложения $\sqrt f $ в непрерывную дробь в поле $K((x))$, и явно представлена в теореме 4 [5].

Кроме того, ввиду необходимости объемных символьных компьютерных вычислений над квадратичными полями, была существенно изменена программная реализация используемых алгоритмов.

5. СХЕМА ДОКАЗАТЕЛЬСТВА

Пусть $K$ – числовое поле. Для каждого $4 \leqslant N \leqslant 12$, $N \ne 11$, в [13, 14] явно выписано полное параметрическое семейство приведенных многочленов $F = F(X,c) \in \mathbb{Q}[X]$ четвертой степени с параметром $c \in K$ таких, что класс дивизора – имеет порядок N в группе классов дивизоров степени ноль Δ°$(\mathcal{L})$ поля $\mathcal{L} = K(X)(\sqrt {F(X,c)} )$. Здесь приведенность многочлена F понимается в смысле дополнительных ограничений: коэффициент при X³ равен нулю, свободный член равен 1. При всевозможных значениях параметра $c \in K$, для которых дискриминант $F(X,c)$ не обращается в ноль, указанные параметрические семейства содержат все приведенные многочлены F четвертой степени над полем K, такие, что выполнены равносильные условия:

• непрерывная дробь элемента $\sqrt F $ в в поле $K((1{\text{/}}X))$ периодическая;

• норменное уравнение

Если пара многочленов ${{\Omega }_{1}},\;{{\Omega }_{2}}$ является решением норменного уравнения (6) с минимальной степенью $\deg {{\Omega }_{1}}$, причем ${{\Omega }_{2}} \ne 0$, то $\deg {{\Omega }_{1}} = N$ и ${{\Omega }_{1}} + {{\Omega }_{2}}\sqrt F $ является фундаментальной единицей поля $\mathcal{L} = K(X)(\sqrt F )$. По теореме 4 [5] периодичность непрерывной дроби элемента ${{X}^{s}}\sqrt F $ равносильна разрешимости норменного уравнения вида (6) с дополнительными условиями на значения ${{v}_{X}}({{\Omega }_{1}})$ и ${{v}_{X}}({{\Omega }_{2}})$, но теперь ${{\Omega }_{1}} + {{\Omega }_{2}}\sqrt F $ может не являться фундаментальной единицей, а может быть некоторой степенью k фундаментальной единицы, причем из теоремы 1 следует, что в случае $[K\;:\;\mathbb{Q}] \leqslant 2$ степень k ограничена числом 6 (см. [15]).

Обозначим через ${{p}_{j}}{\text{/}}{{q}_{j}}$, $j \in {{\mathbb{N}}_{0}}$, подходящие дроби к $\sqrt {F(X,c)} $, причем ${{p}_{j}} = {{p}_{j}}(X,c)$, q_j = q_j(X, $c) \in \mathbb{Q}(c)[X]$. Положим $K = \mathbb{Q}(c)$. Тогда фундаментальная единица поля $\mathcal{L} = K(X)(\sqrt F )$ имеет вид ${{p}_{n}}\, + \,{{q}_{n}}\sqrt F $ для некоторого минимального $n \in \mathbb{N}$ такого, что $p_{n}^{2} - q_{n}^{2}F \in K{\text{*}}$ (см. [2]). Обозначим $\Omega _{1}^{{(j)}} + \Omega _{2}^{{(j)}}\sqrt F = ({{p}_{n}} + {{q}_{n}}\sqrt F {{)}^{j}}$, где $\Omega _{1}^{{(j)}},\Omega _{2}^{{(j)}} \in K[X]$, $j \in \mathbb{N}$. Положим ${{r}_{j}} = {{v}_{X}}\left( {\Omega _{2}^{{(j)}}} \right)$, тогда согласно теореме 1 в силу (4) возможны только следующие 8 случаев: ${{r}_{n}} > 0$ при том, что ${{r}_{j}} = 0$, если $1 \leqslant j < n$, для каждого $n \in \Lambda = \{ 1,3,4,5,6,8,10,12\} $. Отметим, что, если для некоторого $n \in \mathbb{N}$ выполнено ${{r}_{n}} > 0$, то непрерывная дробь элемента $\sqrt F {\text{/}}{{X}^{{{{r}_{n}}}}}$, построенная в поле $K((1{\text{/}}X))$ периодическая.

Замена X на X + t соответствует изоморфизму кривых $C:{{Y}^{2}} = F(X)$ и ${{C}_{t}}:{{Y}^{2}} = F(X + t)$. Тем самым, с точностью до отношения эквивалентности, определяемого допустимыми заменами $F(X)$ на ${{a}^{2}}F(bX)$ для некоторых $a,b \in K{\kern 1pt} *$, имеем полное описание всех многочленов F = $F(c,t) \in \mathbb{Q}[X]$, $\deg F = 4$, для которых разложение $\sqrt F $ в непрерывную дробь в поле $\mathbb{Q}(c,t)((1{\text{/}}X))$ периодично. Наша задача сводится к поиску всех значений параметров $c,t \in K$ для каждого из случаев ${{v}_{X}}\left( {\Omega _{2}^{{(j)}}} \right)$ > 0, $n \in \Lambda $, причем мы ограничиваемся квадратичными расширениями, $K = \mathbb{Q}(c,t)$, $[K:\mathbb{Q}] \leqslant 2$.

Необходимым и достаточным условием периодичности непрерывной дроби $\sqrt {F(X + t,c)} {\text{/}}X$ в $K((1{\text{/}}X))$ является $\Omega _{2}^{{(n)}}(t) = 0$ хотя бы для одно из $n \in \Lambda $. Для того, чтобы непрерывная дробь $\sqrt {F(X + t,c)} {\text{/}}{{X}^{2}}$ была периодической, необходимо и достаточно, чтобы ${{r}_{n}} = {{v}_{X}}\left( {\Omega _{2}^{{(n)}}} \right) \geqslant 2$ для некоторого $j \in \Lambda $, т.е. $\Omega _{2}^{{(n)}}(t) = 0$ и $\frac{{\text{d}}}{{{\text{d}}t}}\Omega _{2}^{{(n)}}(t) = 0$, что  возможно только тогда, когда дискриминант d = ${{d}^{{(n)}}}(c)$ многочлена $\Omega _{2}^{{(n)}}(t) \in \mathbb{Q}(c)[t]$ равен нулю. То есть задача сводится к поиску корней c₀ дискриминанта ${{d}^{{(n)}}}(c)$ и соответствующих кратных корней t₀ многочлена $\Omega _{2}^{{(n)}}(t) \in \mathbb{Q}({{c}_{0}})[t]$ для каждого из $n \in \Lambda $, причем ограничиваемся значениями параметров ${{c}_{0}},\;{{t}_{0}}$ из квадратичных полей и таких, что дискриминант многочлена $F(X + {{t}_{0}},{{c}_{0}}) \in \mathbb{Q}({{c}_{0}},{{t}_{0}})[X]$ отличен от нуля. Если найдены все подходящие значения параметров ${{c}_{0}},\;{{t}_{0}}$, то для доказательства теоремы 2 достаточно положить f(x) = ${{x}^{4}}F(1{\text{/}}x + {{t}_{0}},{{c}_{0}}) \in K[x]$ и отобрать представителей с точностью до указанного в определении множества ${{\mathcal{U}}_{0}}$ отношения эквивалентности.

Изложенная схема доказательства существенным образом опирается на большие символьные компьютерные вычисления. Программный код реализовывался на языке программирования Python с использоваем библиотеки Sympy. Без подобных вычислений получить заявленные результаты не представляется возможным.

6. ЗАКЛЮЧЕНИЕ

Приведем новые примеры непрерывных дробей, которые определены над полями K, $[K:\mathbb{Q}]$ = 2.

Пример 1. Рассмотрим $K = \mathbb{Q}(\sqrt 3 )$ и

Непрерывная дробь $\sqrt f $ в поле $\mathbb{Q}(\sqrt 3 )((x))$ имеет вид

Длина квазипериода равна 5, коэффициент квазипериода равен –1/4, длина периода равна 10. Степень фундаментальной S-единицы равна 4.

Пример 2. Рассмотрим $K = \mathbb{Q}(\sqrt { - 7} )$ и

Непрерывная дробь $\sqrt f $ в поле $\mathbb{Q}(\sqrt { - 7} )((x))$ имеет вид

Длина квазипериода равна 5, коэффициент квазипериода равен –1/4, длина периода равна 10. Степень фундаментальной S-единицы равна 7.

Пример 3. Рассмотрим $K = \mathbb{Q}(\sqrt {21} )$ и

Непрерывная дробь $\sqrt f $ в поле $\mathbb{Q}(\sqrt {21} )((x))$ имеет вид

Длина квазипериода равна 5, коэффициент квазипериода равен –1/4, длина периода равна 10. Степень фундаментальной S-единицы равна 7.