Доклады Российской академии наук. Математика, информатика, процессы управления, 2022, T. 507, № 1, стр. 71-80
МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ РЫНКА ПОТРЕБИТЕЛЬСКОГО КРЕДИТА В РОССИИ В УСЛОВИЯХ САНКЦИЙ
Н. В. Трусов 1, 2, 3, 4, *, академик РАН А. А. Шананин 1, 2, 3, 4, 5, **
1 Федеральный исследовательский центр
“Информатика и управление” Российской академии наук
Москва, Россия
2 Московский физико-технический институт
Долгопрудный, Россия
3 Московский государственный университет
имени М.В. Ломоносова
Москва, Россия
4 Московский центр фундаментальной
и прикладной математики
Москва, Россия
5 Российский университет дружбы народов
Москва, Россия
* E-mail: trunick.10.96@gmail.com
** E-mail: alexshan@yandex.ru
Поступила в редакцию 18.10.2022
После доработки 22.10.2022
Принята к публикации 08.11.2022
- EDN: SVDFXQ
- DOI: 10.31857/S2686954322600525
Аннотация
В статье разработана и исследована новая модель формирования процентных ставок по потребительскому кредиту на основе анализа интересов и логики поведения коммерческих банков. В модели предполагается, что доходы заемщиков описываются геометрическим броуновским движением. Коммерческие банки оценивают риски дефолта заемщиков. По формуле Фейнмана–Каца оценка сводится к решению краевой задачи уравнений с частными производными, для которой построено аналитическое решение. Модель применена для анализа проблемы сохранения в сложившихся условиях потребительского кредита как механизма социальной адаптации домашних хозяйств.
1. ВВЕДЕНИЕ
За последние двадцать лет в России значительно вырос рынок потребительского кредита. Задолженность домашних хозяйств по потребительскому кредиту достигла 12.5 триллионов рублей, что составляет более 12% годового ВВП РФ и более 9% от активов консолидированного баланса коммерческих банков РФ. Поскольку отношение процентных ставок по потребительскому кредиту к депозитам изменялось в последнее десятилетие в диапазоне от 2.5 до 3.5, потребительский кредит являлся одним из самых привлекательных активов для коммерческих банков. Рост спроса на потребительский кредит, с одной стороны, отражает формирование в РФ “среднего слоя” в последние двадцать лет. Домашние хозяйства, относящиеся к “среднему слою”, управляют динамикой своих расходов, используя потребительский кредит, и соизмеряют свой спрос с величиной процентной ставки на кредит. С другой стороны, потребительский кредит в России выполнял функцию социальной адаптации и более половины по суммарному объему выданных кредитов составляют заимствования малообеспеченных домашних хозяйств, которые предъявляют спрос на кредит в сложных жизненных обстоятельствах в независимости от величины процентной ставки. Такая структура заемщиков повышает вероятность неисполнения обязательств по погашению кредита и порождает риски для банковской системы, которые вызывали озабоченность у руководства министерства экономического развития еще летом 2019 г. Пандемия COVID-19 оказала влияние на экономическое положение домашних хозяйств и осложнила состояние рынка потребительского кредита.
Наложенные в 2022 г. на Россию санкции были направлены на снижение уровня жизни домашних хозяйств за счет кризиса банковской системы и инфляции. Санкции ставят целью обострить социальную напряженность, снизить эффективность управления на федеральном уровне и вызвать дезинтеграцию власти. Ответные меры правительства предполагают компенсацию потерь домашних хозяйств в реальных располагаемых доходах. Имеются два канала поддержки и социальной адаптации домашних хозяйств: прямые трансферты из бюджета и потребительский кредит. Возникает вопрос: как изменится в сложившихся обстоятельствах рынок потребительского кредита и сможет ли он выполнять функцию социальной адаптации в сочетании с прямыми трансфертами из бюджета? В новых условиях изменились подходы коммерческих банков к выдаче потребительских кредитов. Поэтому для анализа возможных стратегий управляющих органов РФ и ответа на поставленный вопрос нужно использовать математические модели, в которых поведение на рынке потребительского кредита коммерческих банков, домашних хозяйств из различных социальных слоев описываются на основе исследования их интересов и логики поведения в изменяющихся условиях. Модели спроса на потребительский кредит домашних хозяйств из различных социальных слоев разрабатывались в [1, 2] и использовались для анализа состояния рынка потребительского кредита России в 2019–2021 гг. В этом анализе предполагалось, что коммерческие банки, имея большие запасы ликвидности, будут вести себя инерционно и их поведение можно моделировать эконометрическими моделями. В новых условиях дефицита ликвидности поведение ведущих коммерческих банков на рынке потребительского кредита изменилось и его нужно моделировать на основе анализа интересов и логики их поведения. Моделирование взаимодействия на рынке потребительского кредита коммерческих банков и домашних хозяйств основано на концепции равновесия по Штакельбергу. Предполагается, что коммерческие банки назначают ставку по потребительскому кредиту, исходя из своих интересов, оценивая ответное поведение домашних хозяйств.
В разделе 2 содержатся результаты работы [2] по моделированию спроса на потребительский кредит на основе концепции рационального репрезентативного домашнего хозяйства. В результате анализа задачи оптимального управления, моделирующей экономическое поведение рационального репрезентативного домашнего хозяйства, выделены четыре типа заемщиков, соответсвующие различным социальным слоям населения. В разделе 3 поставлена и исследована задача о формировании коммерческим банком процентной ставки по потребительскому кредиту. Модель предполагает, что доходы заемщиков описываются геометрическим броуновским движением, а коммерческие банки назначают процентную ставку, исходя из максимизации математического ожидания чистой приведенной прибыли, учитывая риски заемщиков. По формуле Фейнмана–Каца учет рисков невозврата потребительского кредита сводится к решению краевой задачи для уравнения с частными производными. Установив связь с уравнением Абеля, удается свести решение краевой задачи к задаче Коши для уравнения теплопроводности с внешним источником и получить оценку рисков в аналитической форме. В разделе 4 построенная модель идентифицирована по данным Росстата об обследовании бюджетов домашних хозяйств и проанализированы влияния шоков, вызванных санкциями, на состояние потребительского кредита в России.
2. МОДЕЛЬ ПОВЕДЕНИЯ ДОМАШНЕГО ХОЗЯЙСТВА
Для моделирования экономического поведения социального слоя домашних хозяйств будем опираться на концепцию рационального репрезентативного экономического агента, восходящую к работе Ф. Рамсея [3]. Будем использовать модель поведения репрезентативного домашнего хозяйства в форме задачи оптимального управления из работ [2, 4, 5]. В этой модели динамика ликвидных средств домашнего хозяйства ${{M}_{0}}(t)$ описывается уравнением
Здесь $S(t)$ доходы домашнего хозяйства в момент времени t, относительно которых предполагается рост с темпом $\gamma $, т.е. $S(t) = {{S}_{0}}{{e}^{{\gamma t}}}$; $C(t)$ потребление; $p(t)$ индекс потребительских цен, относительно которого предполагается рост с темпом $j$, т.е. $p(t) = {{p}_{0}}{{e}^{{jt}}}$; ${{H}_{L}}(t)$ заимствования по потребительскому кредиту; ${{H}_{D}}(t)$ сбережения в форме депозитов в коммерческом банке. При этом, если домашнее хозяйство осуществляет займ на величину ${{H}_{L}}$, то ${{H}_{L}} > 0$, если домашнее хозяйство осуществляет платеж по потребительскому кредиту, то ${{H}_{L}} < 0$. Аналогично, пополнение депозитарного счета на величину ${{H}_{D}}$ влечет к уменьшению запаса денег ${{M}_{0}}$, поэтому ${{H}_{D}} > 0$, ежели происходит снятие средств с депозитарного счета, то ${{H}_{D}} < 0$. Изменение задолженности $L(t) \geqslant 0$ по потребительскому кредиту описывается уравнением
где ${{r}_{L}}$ – процентная ставка по потребительскому кредиту. Уравнение изменения сбережений в форме депозитов $D(t) \geqslant 0$ под процентную ставку ${{r}_{D}}$:Отсутствие арбитража предполагает, что ставка по кредитам больше ставки по депозитам, т.е. ${{r}_{L}} > {{r}_{D}}$. Закон Фишера связывает между собой запас денег ${{M}_{0}}(t)$ и потребительские расходы домашнего хозяйства $C(t)$ через коэффициент θ > 0:
где $\frac{1}{\theta } > 0$ – скорость обращения денег.Для дальнейшего изложения удобно ввести переменную $X(t)$, определяющуюся как
и именуемую как финансовое состояние домашнего хозяйства. Из рационального поведения домашнего хозяйства следует, что оно не заимствует по потребительскому кредиту и не сберегает одновременно, поэтомуВ силу уравнений (1)–(3) получаем, что динамика финансового состояния описывается динамической системой
(4)
$\frac{{dX}}{{dt}} = S - \frac{1}{\theta }{{M}_{0}} - {{r}_{L}}{{\left( {{{M}_{0}} - X} \right)}_{ + }} + {{r}_{D}}{{\left( {X - {{M}_{0}}} \right)}_{ + }},$Домашнее хозяйство стремится максимизировать дисконтированное потребление с коэффициентом дисконтирования ${{\delta }_{0}} > 0$ и постоянным отвращением к риску $0 < 1 - \alpha < 1$ на временном интервале $[0,T]$, управляя запасом денег ${{M}_{0}} \geqslant 0$, т.е.
(6)
$\int\limits_0^T {{\left( {{{M}_{0}}(t)} \right)}^{\alpha }}{{e}^{{ - {{\delta }_{0}}t}}}dt \to \mathop {\max }\limits_{{{M}_{0}} \geqslant 0} .$Будем говорить, что финансовое состояние $X(t)$ является ликвидным, если существует управление ${{M}_{0}}(t)$, обеспечивающее выполнение условия $X(T) \geqslant 0$. Иными словами, к конечному моменту времени домашнее хозяйство должно расплатиться со своими кредитами. Пусть x(t) = $X(t){{e}^{{ - \gamma t}}}$, $M(t) = {{M}_{0}}(t){{e}^{{ - \gamma t}}}$, $\delta = {{\delta }_{0}} + \alpha j$, ${{\hat {H}}_{L}}(t) = {{H}_{L}}(t){{e}^{{ - \gamma t}}}$. Задача оптимального управления на конечном временном горизонте формулируется в следующем виде
(7)
$\int\limits_0^T {{M}^{\alpha }}{{e}^{{ - (\delta - \alpha \gamma )t}}}dt \to \mathop {\max }\limits_M ,$(8)
$\frac{{dx}}{{dt}} = S - \gamma x - \frac{1}{\theta }M - {{r}_{L}}{{\left( {M - x} \right)}_{ + }} + {{r}_{D}}{{\left( {x - M} \right)}_{ + }},$Чтобы обеспечить условие $x(T) \geqslant 0$, необходимо выполнение неравенства $X \geqslant - \frac{S}{{{{r}_{L}} - \gamma }}$ (если это неравенство нарушается, то домашнее хозяйство не имеет возможности расплатиться с кредитами при сохранении конъюнктуры и образуется финансовая пирамида). Если $T \to \infty $, то это условие является не только необходимым, но и достаточным.
Зная оптимальную траекторию $M(t)$, доставляющую максимум дисконтируемому потреблению (7), можно найти финансовое состояние $x(t)$ из задачи Коши (7)–(10), а также динамику задолженности по потребительским кредитам $L(t)$ и динамику сбережений в форме депозитов $D(t)$. В работе [2] показано, что оптимальная траектория $M(t)$ существует. В силу негладкости правой части дифференциального уравнения (8) применяется принцип максимума Понтрягина в форме Клакра, с помощью которого можно выделить 3 режима экономического поведения домашнего хозяйства: заимствования, не взаимодействия с банковской системой и сбережения в форме депозитов в зависимости от финансового состояния и параметров конъюнктуры (подробнее см. [2]).
Если устремить временной горизонт $T \to \infty $ в задаче оптимального управления (7)–(10), то можно построить синтез задачи оптимального управления практически в аналитическом виде (см. [2]). Синтез позволяет определить оптимальное управление в зависимости от текущего значения фазовой переменной $x$ и параметров экономической конъюнктуры. Он зависит от соотношения величин ${{r}_{L}}$, ${{r}_{D}}$, $\delta - \frac{{1 - \alpha }}{\theta }$, $\delta + (1 - \alpha )\gamma $ и определяет социальный слой, к которому относится домашнее хозяйство. Перебирая всевозможные допустимые сочетания величин ${{r}_{L}}$, ${{r}_{D}}$, $\delta - \frac{{1 - \alpha }}{\theta }$, $\delta + (1 - \alpha )\gamma $, можно получить различные типы социальных слоев, подробное описание которых представлено в [2]. Отметим, что в каждом социальном слое определяются режимы, в которых может находиться домашнее хозяйство.
Нас интересует проблема роста задолженности по потребительскому кредиту. Покажем, как с помощью представленной модели можно вычислить спрос на потребительский кредит ${{\hat {H}}_{L}}$. Тогда из уравнения баланса ликвидных средств заемщика (1) с учетом динамики финансового состояния домашнего хозяйства (4) и введенных перенормировок получаем, что спрос на потребительский кредит описывается уравнением
(11)
$\begin{gathered} {{{\hat {H}}}_{L}} = \left( {\frac{{dM(x)}}{{dx}}\left( {S - \gamma x - \frac{{M(x)}}{\theta } - {{r}_{L}}{{{(M(x) - x)}}_{ + }}} \right) - } \right. \\ \, - {{\left. {S + \gamma M(x) + \frac{{M(x)}}{\theta }} \right)}_{ + }}, \\ \end{gathered} $В зависимости от соотношения величин ${{r}_{L}}$, $\delta - \frac{{1 - \alpha }}{\theta }$, $\delta + (1 - \alpha )\gamma $ выделяются 4 типа поведения заемщиков, соответствующие различным социальным слоям.
Тип поведения 1. Если ${{r}_{L}} < \delta - \frac{{1 - \alpha }}{\theta }$, $1 + \gamma \theta \geqslant 0$, или ${{r}_{L}} < \delta + (1 - \alpha )\gamma $, $1 + \gamma \theta < 0$, то синтез оптимального управления задается функцией
Спрос на потребительский кредит определяется как
В данном типе поведения домашнее хозяйство осуществляет займы по потребительскому кредиту вне зависимости от своего финансового состояния.
Тип поведения 2. Если $\delta \, + \,(1\, - \,\alpha )\gamma \, < \,{{r}_{L}}$, $1\, + \,\theta \gamma $ < 0, то синтез оптимального управления задается функцией
Спрос на потребительский кредит определяется как
В данном типе поведения домашнее хозяйство также осуществляет займы по потребительскому кредиту вне зависимости от своего финансового состояния.
Тип поведения 3. Если δ – $\frac{{1 - \alpha }}{\theta } < {{r}_{L}}$ < δ + (1 – ‒ α)γ, а финансовое состояние домашнего хозяйства $x < \frac{{(\delta - \alpha {{r}_{L}})}}{{\left( {{{r}_{L}} - \delta + \frac{{1 - \alpha }}{\theta }} \right)}}\frac{S}{{\left( {{{r}_{L}} - \gamma } \right)}}$, то синтез оптимального управления и спрос на потреби-тельский кредит повторяют тип поведения 1. В противном случае, если $1\, + \,\theta \gamma \, \geqslant \,0$, $x \geqslant $ $ \geqslant \frac{{(\delta - \alpha {{r}_{L}})}}{{\left( {{{r}_{L}} - \delta + \frac{{1 - \alpha }}{\theta }} \right)}}\frac{S}{{\left( {{{r}_{L}} - \gamma } \right)}}$, то потребительский кредит не заимствуется.
Тип поведения 4. Если $\delta \, + \,(1\, - \,\alpha )\gamma \, < \,{{r}_{L}}$, $1\, + \,\theta \gamma \, \geqslant \,0$, а финансовое состояние $x < \frac{{S\theta }}{{1 + \gamma \theta }}$, то синтез определяется из решения уравнения
(12)
$\begin{gathered} x + \frac{S}{{{{r}_{L}} - \gamma }} = \frac{{S(1 + \theta {{r}_{L}})(\delta + (1 - \alpha )\gamma - {{r}_{L}})}}{{(\delta - \alpha {{r}_{L}})(1 + \gamma \theta )({{r}_{L}} - \gamma )}} \times \\ \, \times {{\left( {\frac{{{{M}_{2}}(1 + \gamma \theta )}}{{S\theta }}} \right)}^{{\frac{{(1 - \alpha )(\gamma - {{r}_{L}})}}{{(\delta + (1 - \alpha )\gamma - {{r}_{L}})}}}}}\, + \,\left( {\frac{{(1 - \alpha )(1 + \theta {{r}_{L}})}}{{\theta (\delta - \alpha {{r}_{L}})}}} \right){{M}_{2}}, \\ \end{gathered} $Спрос на потребительский кредит определяется как
В случае $x \geqslant \frac{{S\theta }}{{1 + \gamma \theta }}$ потребительский кредит не заимствуется.
Для использования модели необходимо задать поведенческие характеристики репрезентативного домашнего хозяйства, характерные для данного социального слоя: скорость обращения денег $\frac{1}{\theta }$, отвращение к риску 1 – α, коэффициент дисконтирования $\delta $ и показатели экономической конъюнктуры: процентную ставку по кредитам ${{r}_{L}}$, темп роста доходов $\gamma $ и инфляцию j. Для калибровки модели экономического поведения домашних хозяйств были использованы данные Росстата. Росстат предоставляет ежеквартальную статистику Обследования Бюджетов Домашних Хозяйств (ОБДХ) [6], проводя опрос среди 50 000 домашних хозяйтсв, проживающих в 82 регионах России. На основе данных по уровню потребления на душу населения эти регионы были разделены на 3 группы: богатую, среднюю и бедную. Основываясь на данных ОБДХ, мы обратили внимание, что примерно половина домашних хозяйств, относящихся к бедной группе регионов, проживает в городском типе населенного пункта, а вторая половина в селе. Поскольку стиль жизни в городе отличается от села, то кагорта домашних хозяйств из бедной группы регионов была разделена еще на две. В каждой группе регионов выделяются слои населения с разными уровнями доходов и расходов.
Мы разделили участников опроса ОБДХ на заемщиков и прочих домашних хозяйств, не выплачивающих кредит. Заемщики делятся на два типа: низкодоходные, имеющие высокий риск невозврата кредита, и высокодоходные. Анализируя статистику ОБДХ, можно видеть, что подушевые доходы у высокодоходных заемщиков примерно в 2 раза больше, чем подушевые доходы у низкодоходных заемщиков. Для идентификации поведенческих характеристик репрезентативных домашних хозяйств, относящихся к определенному слою, решаются обратные задачи. Для работы со статистикой ОБДХ, выделения социальных слоев домашних хозяйств в разных группах регионов, идентификации параметров модели, верификации полученных данных и построения прогнозов был разработан специальный программный комплекс в виде приложения MatLab AppDesigner [7].
3. МОДЕЛИРОВАНИЕ РЫНКА ПОТРЕБИТЕЛЬСКОГО КРЕДИТА
Рынок потребительского кредита является несовершенным рынком, на котором домашние хозяйства предъявляют спрос на кредит, а коммерческие банки предоставляют кредит. Формирование процентной ставки на рынке потребительского кредита моделируется с помощью равновесия по Штакельбергу. Коммерческие банки, оценив зависимость спроса на кредит в зависимости от процентной ставки, устанавливают процент по потребительскому кредиту на уровне, который максимизирует их прибыль.
Основной формой платежа по потребительскому кредиту является аннуитетный платеж. Пусть как и раньше ${{r}_{L}}$ – месячная ставка по вновь выдаваемому кредиту, $\hat {T}$ – срок кредита, исчисляемый в месяцах. Задолженность по кредиту равна ${{\hat {H}}_{L}}({{r}_{L}}){{e}^{{{{r}_{L}}\hat {T}}}}$, где ${{\hat {H}}_{L}}({{r}_{L}})$ – текущий спрос на кредит. Аннуитетный платеж A можно найти из уравнения
Коммерческие банки учитывают риск неплатежеспособности заемщика. Обозначим через $\tau $ момент времени, когда заемщик не сможет выполнять обязательства по аннуитетному платежу. С точки зрения коммерческих банков доходы заемщиков $S(t)$ не являются стабильными. Будем предполагать, что коммерческие банки моделируют доходы заемщика с помощью стохастического дифференциального уравнения геометрического броуновского движения
где $\gamma $ – темп роста доходов, ${{W}_{t}}$ – винеровский процесс, $\sigma > 0$ – параметр волатильности. Предположим, что заемщик объявляет дефолт по кредиту, если его доход не позволяет осуществлять аннуитетный платеж $A$ и потребительские расходы на минимальном уровне $\mu $, т.е.Поскольку доход заемщика является случайным процессом, величина $\tau \in (0,\hat {T})$ является случайным моментом остановки. Коммерческие банки устанавливают процентную ставку по потребительскому кредиту, максимизируя математическое ожидание чистой приведенной прибыли (NPV), т.е.
(13)
$\begin{gathered} NPV({{r}_{L}}) = {{\mathbb{E}}_{\tau }}\left( {A\int\limits_0^\tau {{e}^{{ - \lambda t}}}dt - {{{\hat {H}}}_{L}}({{r}_{L}})} \right) = \\ \, = {{\mathbb{E}}_{\tau }}\left( {\left( {\frac{{{{r}_{L}}(1 - {{e}^{{ - \lambda \tau }}})}}{{\lambda (1 - {{e}^{{ - {{r}_{L}}\hat {T}}}})}} - 1} \right){{{\hat {H}}}_{L}}({{r}_{L}})} \right) \to \mathop {\max }\limits_{{{r}_{L}}} , \\ \end{gathered} $Обозначим ${{\alpha }_{u}} = \frac{\sigma }{{\sqrt {2\gamma - {{\sigma }^{2}}} }}$.
Теорема. Если $\gamma > \frac{{{{\sigma }^{2}}}}{2}$, то
(14)
$\begin{gathered} {{\mathbb{E}}_{\tau }}{{e}^{{ - \lambda \tau }}} = {{e}^{{ - \lambda \hat {T}}}} + \\ \, + \frac{{{{\alpha }_{u}}}}{\pi }\int\limits_0^{\sqrt {\lambda \hat {T}} } {{e}^{{ - \left( {\frac{\lambda }{{4\alpha _{u}^{2}{{\tau }^{2}}}}{{{\left( {\ln \left( {\frac{{A + \mu }}{{{{S}_{0}}}}} \right)} \right)}}^{2}} + {{\tau }^{2}}} \right)}}}\left( {\int\limits_0^{\sqrt {\lambda \hat {T} - {{\tau }^{2}}} } {{e}^{{ - {{y}^{2}}}}}dy} \right)d\tau . \\ \end{gathered} $Доказательство. Стохастическое дифференциальное уравнение
имеет сильное решение (см. с. 364 в [8]):Откуда следует, что
(15)
$\tau = \min \left( {\hat {T},\mathop {\inf }\limits_{t \geqslant 0} \left\{ {{{W}_{t}} < \frac{1}{\sigma }\left( {\ln \frac{{A + \mu }}{{{{S}_{0}}}}} \right) - \left( {\frac{\gamma }{\sigma } - \frac{\sigma }{2}} \right)t} \right\}} \right).$Введем следующие обозначения:
Тогда ${{\mathbb{E}}_{\tau }}{{e}^{{ - \lambda \tau }}} = u(0,0)$. По формуле Фейнмана–Каца (см. теорема 21.14 на с. 378 в [8]) имеем, что $u(t,x)$ является решением следующей краевой задачи
(16)
$\left( {\gamma - \frac{{{{\sigma }^{2}}}}{2}} \right)\frac{{\partial u(t,x)}}{{\partial t}} + \frac{{{{\sigma }^{2}}}}{2}\frac{{{{\partial }^{2}}u(t,x)}}{{\partial {{x}^{2}}}} = 0,$(19)
$u\left( {t,\ln \left( {\frac{{A + \mu }}{{{{S}_{0}}}}} \right)} \right) = {{e}^{{ - \lambda t}}}.$Обозначим ${v}(t,x) = u(\hat {T} - t,x)$. Тогда
Эта задача эквивалентна задаче Коши для уравнения теплопроводности с внешним источником
Тогда, по формуле Пуассона, получаем
(20)
$\begin{gathered} {v}(t,x) = {{e}^{{ - \lambda \hat {T}}}} + \frac{{{{\alpha }_{u}}{{e}^{{ - \lambda \hat {T}}}}}}{{2\pi }} \times \\ \times \,\,\int\limits_0^t \sqrt {\frac{\lambda }{{t - z}}} {{e}^{{ - \frac{1}{{4\alpha _{u}^{2}(t - z)}}{{{\left( {x - \ln \left( {\frac{{A + \mu }}{{{{S}_{0}}}}} \right)} \right)}}^{2}}}}}{{e}^{{\lambda z}}}\left( {\int\limits_0^{\sqrt {\lambda z} } {{e}^{{ - {{y}^{2}}}}}dy} \right)dz. \\ \end{gathered} $С учетом введенной замены ${v}(t,x) = u(\hat {T} - t,x)$ из (20) получаем
(21)
$\begin{gathered} u(t,x) = {{e}^{{ - \lambda \hat {T}}}} + \\ \, + \frac{{{{\alpha }_{u}}{{e}^{{ - \lambda \hat {T}}}}}}{{2\pi }}\int\limits_0^{\hat {T} - t} \sqrt {\frac{\lambda }{{\hat {T} - t - z}}} {{e}^{{ - \frac{1}{{4\alpha _{u}^{2}(\hat {T} - t - z)}}{{{\left( {x - \ln \left( {\frac{{A + \mu }}{{{{S}_{0}}}}} \right)} \right)}}^{2}}}}} \times \\ \, \times {{e}^{{\lambda z}}}\left( {\int\limits_0^{\sqrt {\lambda z} } {{e}^{{ - {{y}^{2}}}}}dy} \right)dz. \\ \end{gathered} $Подставляя t = 0, x = 0 в формулу (21), получаем
Предложение. Если $\gamma - \frac{{{{\sigma }^{2}}}}{2} \leqslant 0$, то
Доказательство. Пусть $\gamma = \frac{{{{\sigma }^{2}}}}{2}$. Тогда уравнение (16) на множестве (17) с краевыми условиями (18)–(19) имеет вид
единственным решением которого является функция $u(t,x) = {{e}^{{ - \lambda t}}}$. Тогда $u(0,0) = 1$ и множительЕсли $\gamma < \frac{{{{\sigma }^{2}}}}{2}$, то вероятность неплатежеспособности домашнего хозяйства по займу вырастает, выход на граничное условие (15) происходит раньше. Значит, $u(0,0) > 1$ и множитель
Замечание. Если $\gamma - \frac{{{{\sigma }^{2}}}}{2} \leqslant 0$, то выдача потребительского кредита убыточна для коммерческого банка.
Мы используем средневзвешенную ставку по потребительскому кредиту в качестве параметра модели, поэтому считаем, что репрезентативное домашнее хозяйство осуществляет займ по потребительскому кредиту под процент ${{\tilde {r}}_{L}}$, где
(22)
$\frac{{d{{{\tilde {r}}}_{L}}}}{{dt}} = \left( {{{r}_{L}} - {{{\tilde {r}}}_{L}}} \right) \cdot \frac{{{{{\hat {H}}}_{L}}({{r}_{L}})}}{{M(x;{{r}_{L}},{{r}_{D}},\gamma ,\theta ,\alpha ,\delta )}},$4. РЕЗУЛЬТАТЫ РАСЧЕТОВ
Для построения прогнозов поведения заемщиков необходимо задать динамики доходов населения, ставок по кредитам и инфляции. Согласно данным Росстата месячная инфляция в марте 2022 г. составила 7.8%, после которой месячная инфляция резко сократилась. С учетом прогнозов Росстата мы предполагаем, что к концу 2022 г. ожидается годовая инфляция на уровне 15%.
В конце февраля 2022 г. ключевая ставка ЦБ была резко поднята до 20% годовых, количество отказов в выдаче потребительского кредита выросло до 75%. Несмотря на последующие снижения ключевой ставки ЦБ до 8%, процент, под который выдаются кредиты малоимущим домашним хозяйствам, остается запретительным и находится на уровне 40% годовых. Для моделирования процентной ставки высокодоходных заемщиков подходит модель рынка потребительского кредита, представленная в разделе 3. По результатам расчетов ожидается рост процентной ставки по потребительским кредитам до 25–30% для высокодоходных заемщиков к середине 2023 г.
В связи с уходом крупных фирм из России весной 2022 г., остановки заводов производства, немалая часть населения потеряла доходы. Основные потери доходов пришлись на малоимущие слои населения. Мы полагаем, что к концу 2023 г. номинальное падение доходов у малоимущих слоев населения составит 15% по отношению к началу 2022 г., в то время как динамика доходов у высокодоходных слоев населения будет сохраняться прежней.
4.1. Сценарий 1. Анализ финансового положения заемщиков
По результатам расчетов, весной 2022 г. разоряются как низкодоходные, так и высокодоходные заемщики во всех группах регионов (нарушается условие платежеспособности $x > - \frac{S}{{{{r}_{L}} - \gamma }}$). После весны 2022 г. платежеспособность заемщиков восстанавливается, но начиная с конца 2022 г. – начала 2023 г. низкодоходные заемщики вновь утрачивают свою платежеспособность, что приводит к ощутимому росту спроса на потребительский кредит среди малоимущих слоев населения. Как отмечалось ранее, с марта 2022 г. резко выросло количество отказов в выдаче потребительского кредита низкодоходным заемщикам. При подсчете суммарной задолженности по всем группам регионов мы учитываем эту тенденцию и считаем, что если малоимущее домашнее хозяйство находится в состоянии неплатежеспособности, то коммерческие банки не выдают ему потребительский кредит.
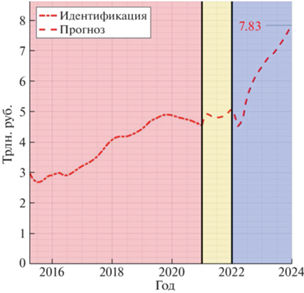
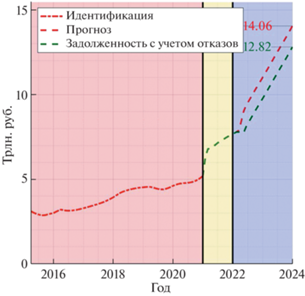
На рис. 1–2 представлены суммарные задолженности по всей стране с дифференциацией на низкодоходных и высокодохнодных заемщиков. Области описывают три этапа использования модели: идентификации с марта 2015 г. по декабрь 2020 г., верификации с января 2021 г. по декабрь 2021 г. и периода построения прогнозов с января 2022 г. по декабрь 2023 г.
Отметим, что если бы банки выдавали малоимущим домашним хозяйствам потребительские кредиты, то они бы поддерживали их уровень потребления на минимальном уровне, но это бы привело к ощутимому росту задолженности до 17.55 трлн руб. к концу 2023 г., а общая задолженность составила бы 25.38 трлн руб. Отказы в выдаче потребительского кредита малоимущим слоям населения приводят к социальной напряженности. На начало 2022 г. суммарная задолженность по потребительскому кредиту составляла 12.6 трлн руб. В данном сценарии с учетом отказов в выдаче кредитов к концу 2023 г. итоговая задолженность вырастет до 16.47 трлн руб., при этом объем отказов за прогнозный период составит 8.91 трлн руб. Потребительский кредит перестает выполнять роль социальной адаптации домашних хозяйств.
4.2. Сценарий 2. Субсидирование низкодоходных заемщиков
Главная проблема потребительского кредитования в России заключается в платежеспособности малоимущих заемщиков. Данный сценарий является ответом на вопрос: можно ли сохранить роль социальной адаптации у потребительского кредита за счет адресной финансовой поддержки малодоходных заемщиков? Предполагается рост доходов малоимущих заемщиков с августа 2022 г. до конца 2023 г. за счет осуществления их финансовой поддержки через государственные структуры. Было посчитано, что за этот период необходимо выделить 58.9 млрд руб. малоимущим заемщикам, проживающим в городском типе бедной группы регионов, 70.6 млрд руб. в сельском типе бедной группы регионов, 594.1 млрд руб. в средней группе регионов и 246 млрд руб. в богатой группе регионов. Данные величины были рассчитаны исходя из условия сохранении платежеспособности низкодоходных заемщиков после весны 2022 г. во всех группах регионов. Итоговая задолженность низкодоходных заемщиков во всех группах регионов представлена на рис. 3.
При выделении субсидий низкодоходным заемщикам в размере 969.6 млрд руб до конца 2023 г. их платежеспособность восстанавливается, а отказы в выдаче осуществлялись бы в весенний период 2022 г. Объем отказов в выдаче потребительского кредита составил бы 1.24 трлн руб, а итоговый рост задолженности за два года с учетом задолженности высокодоходных заемщиков вырос бы на 9.29 трлн руб.
5. ЗАКЛЮЧЕНИЕ
Экономическое поведение репрезентативного домашнего хозяйства описано в виде задачи оптимального управления рамсеевского типа. Используя данные ОБДХ Росстата, были выделены репрезентативные домашние хозяйства из различных групп регионов России. Модель идентифицирована по статистическим данным ОБДХ за март 2015 г. – декабрь 2020 г. и верифицирована по статистическим данным за 2021 г. С помощью модели проанализирована платежеспособность низкодоходных и высокодоходных домашних хозяйств до конца 2023 г. Назначение процентной ставки по кредитам для высокодоходных заемщиков моделируется исходя из максимизации приведенной чистой прибыли для коммерческих банков. Моделирование процентной ставки основывается на формуле Фейнмана–Каца.
Выяснилось, что основная проблема потребительского кредитования заключается в скорой неплатежеспособности малоимущих заемщиков, процентные ставки по кредитам для которых в настоящий момент являются запретительными. Отказы в выдаче потребительского кредита малоимущим домашним хозяйствам ведет к социальной напряженности. Расчеты по модели показывают, что целевое субсидирование малоимущих граждан может восстановить их платежеспособность, и, как следствие, снизить социальную напряженность в данных слоях населения. При этом объем выделенных средств к концу 2023 г. составляет менее 1 трлн руб. Программный комплекс [7] позволяет анализировать экономическое положение домашних хозяйств в России с учетом региональной специфики.
ИСТОЧНИК ФИНАНСИРОВАНИЯ
Работа выполнена при поддержке РФФИ (грант 20-07-00285).
Список литературы
Shananin A.A., Trusov N.V. The household behaviour modelling based on Mean Field Games approach // Lobachevskii Journal of Mathematics. 2021. V. 42. № 7. P. 1738–1752.
Тарасенко М.В., Трусов Н.В., Шананин А.А. Математическое моделирование экономического положения домашних хозяйств в России // ЖВМ и МФ. 2021. Т. 61. № 6. С. 1034–1056.
Ramsey F.P. A mathematical theory of savings // The Economic Journal. 1928. V. 152. № 38. P. 543–559.
Рудева А.В., Шананин А.А. Синтез управления в модифицированной модели Рамсея с учетом ограничения ликвидности // Дифференциальные уравнения. 2009. Т. 45. № 12. С. 1799–1803.
Shananin A.A., Tarasenko M.V., Trusov N.V. Consumer Loan Demand Modeling // Mathematical Optimization Theory and Operations Research: Recent Trends. 2021. CCIS. V. 1476. P. 417–428.
Обследование бюджетов домашних хозяйств [Электронный ресурс] / Федеральная служба государственной статистики. 2015–2020. https://obdx.gks.ru/ (дата обращения: 02.08.2022)
Свидетельство о государственной регистрации программы для ЭВМ No. 2022619524 “Анализ спроса на потребительский кредит в РФ”. Правообладатель: Трусов Николай Всеволодович. Заявка No. 2022618580. Дата государственной регистрации в Реестре программ для ЭВМ 23 мая 2022 г.
Коралов Л.Б., Синай Я.Г. Теория вероятностей и случайные процессы. М.: МЦНМО, 2013. 408 с.
Дополнительные материалы отсутствуют.
Инструменты
Доклады Российской академии наук. Математика, информатика, процессы управления