Доклады Российской академии наук. Математика, информатика, процессы управления, 2022, T. 507, № 1, стр. 66-70

СУБРИМАНОВА СФЕРА КАРТАНА

Ю. Л. Сачков^1, *

¹ Институт программных систем им. А.К. Айламазяна Российской академии наук
Переславль-Залесский, Россия

Поступила в редакцию 14.06.2022
После доработки 31.08.2022
Принята к публикации 13.09.2022

EDN: NSYAKS
DOI: 10.31857/S2686954322600434

Аннотация

Описана структура пересечения субримановой сферы на группе Картана с 3-мерным инвариантным многообразием основных симметрий.

Ключевые слова: группа Картана, субриманова геометрия, субриманова сфера

1. ГРУППА КАРТАНА

Алгебра Картана – это свободная нильпотентная алгебра $\mathfrak{g}$ с 2-мя образующими глубины 3. В ней существует базис ${{X}_{1}}, \ldots ,{{X}_{5}}$, в котором ненулевые скобки имеют вид

$[{{X}_{1}},{{X}_{2}}] = {{X}_{3}},\quad [{{X}_{1}},{{X}_{3}}] = {{X}_{4}},\quad [{{X}_{2}},{{X}_{3}}] = {{X}_{5}}.$

Алгебра Картана имеет градуировку

$\mathfrak{g} = {{\mathfrak{g}}^{{(1)}}} \oplus {{\mathfrak{g}}^{{(2)}}} \oplus {{\mathfrak{g}}^{{(3)}}},$

$\begin{gathered} {{\mathfrak{g}}^{{(1)}}} = {\text{span}}({{X}_{1}},{{X}_{2}}),\quad {{\mathfrak{g}}^{{(2)}}} = \mathbb{R}{{X}_{3}}, \\ {{\mathfrak{g}}^{{(3)}}} = {\text{span}}({{X}_{4}},{{X}_{5}}), \\ \end{gathered} $

$[{{\mathfrak{g}}^{{(1)}}},{{\mathfrak{g}}^{{(i)}}}] = {{\mathfrak{g}}^{{(i + 1)}}},\quad {{\mathfrak{g}}^{{(4)}}} = \{ 0\} ,$

поэтому она является алгеброй Карно. Соответствующая связная односвязная группа Ли $G$ называется группой Картана.

На пространстве $\mathbb{R}_{{x,y,z,{v},w}}^{5}$ можно ввести закон умножения, превращающий это пространство в группу Картана: $G \cong \mathbb{R}_{{x,y,z,{v},w}}^{5}$, см. [14] и статьи, цитированные в этой работе. В этой модели левоинвариантные поля, порождающие алгебру Картана, имеют вид

$\begin{gathered} {{X}_{1}} = \frac{\partial }{{\partial x}} - \frac{y}{2}\frac{\partial }{{\partial z}} - \frac{{{{x}^{2}} + {{y}^{2}}}}{2}\frac{\partial }{{\partial w}}, \\ {{X}_{2}} = \frac{\partial }{{\partial y}} + \frac{x}{2}\frac{\partial }{{\partial z}} + \frac{{{{x}^{2}} + {{y}^{2}}}}{2}\frac{\partial }{{\partial v}}. \\ \end{gathered} $

2. ПОСТАНОВКА СУБРИМАНОВОЙ ЗАДАЧИ НА ГРУППЕ КАРТАНА

2.1. Геометрическая постановка

Пусть на евклидовой плоскости заданы точки ${{a}_{0}},{{a}_{1}} \in {{\mathbb{R}}^{2}}$, соединенные кривой ${{\gamma }_{0}} \subset {{\mathbb{R}}^{2}}$. Пусть также заданы число $S \in \mathbb{R}$ и точка $c \in {{\mathbb{R}}^{2}}$. Требуется соединить точки ${{a}_{0}}$, ${{a}_{1}}$ кратчайшей кривой $\gamma \subset {{\mathbb{R}}^{2}}$ так, чтобы кривые ${{\gamma }_{0}}$ и $\gamma $ ограничивали на плоскости область алгебраической площади $S$, с центром масс c.

2.2. Задача оптимального управления

Эту геометрическую задачу можно переформулировать [13] как задачу оптимального управления

(1)

$\begin{gathered} \dot {q} = {{u}_{1}}{{X}_{1}}(q) + {{u}_{2}}{{X}_{2}}(q), \\ q = (x,y,z,v,w) \in G = {{\mathbb{R}}^{5}}, \\ \end{gathered} $

(2)

$q(0) = {{q}_{0}},\quad q({{t}_{1}}) = {{q}_{1}},$

(3)

$l = \int\limits_0^{{{t}_{1}}} {\sqrt {u_{1}^{2} + u_{2}^{2}} {\kern 1pt} dt \to \min .} $

Это субриманова задача для субримановой структуры на ${{\mathbb{R}}^{5}}$, заданной векторными полями ${{X}_{1}}$, ${{X}_{2}}$ как ортонормированным репером. Эта субриманова структура – единственная, с точностью до автоморфизма группы Картана, левоинвариантная субриманова структура с вектором роста $(2,3,5)$. Следовательно, можно считать, что q₀ = = Id = $(0, \ldots ,0)$.

3. ОСОБЕННОСТИ ЗАДАЧИ

Субриманова задача на группе Картана есть простейшая левоинвариантная задача со следующими свойствами:

• она имеет анормальные кратчайшие, касающиеся каждого вектора распределения,

• это следующая по сложности после задачи Дидоны задача на свободной группе Карно максимального роста (ее вектор роста равен (2, 3, 5)).

Эта задача – единственная свободная нильпотентная субриманова задача глубины 3 с интегрируемым по Лиувиллю нормальным гамильтоновым полем принципа максимума Понтрягина (неинтегрируемыми по Лиувиллю являются свободные нильпотентные задачи глубины 3, ранга более 2 [4], а также глубины более 3, ранга не менее 2 [1]).

Распределение $\Delta = {\text{span}}({{X}_{1}},{{X}_{2}})$ имеет 14-мерную алгебру инфинитезимальных симметрий – особую алгебру ${{\mathfrak{g}}_{2}}$, этот факт восходит к знаменитой “пятимерной” работе Эли Картана [5].

Наконец, субриманова задача на группе Картана доставляет нильпотентную аппроксимацию любой задачи с вектором роста (2, 3, 5), в частности:

• задачи о качении двух твердых тел друг по другу без прокручивания и проскальзывания [9, 10],

• машины с двумя прицепами [11],

• задачи о движении электрического заряда в плоскости под действием магнитного поля [12].

Любой из этих причин достаточно для детального исследования субримановой задачи на группе Картана.

4. РАНЕЕ ПОЛУЧЕННЫЕ РЕЗУЛЬТАТЫ

Напомним некоторые из результатов, полученных в предыдущих работах [13–16].

• Анормальные траектории (соответствующие анормальному случаю $\nu = 0$ принципа максимума Понтрягина [2, 3]):

– однопараметрические подгруппы ${{e}^{{ \pm t({{u}_{1}}{{X}_{1}} + {{u}_{2}}{{X}_{2}})}}}$, ${{u}_{i}} \equiv {\text{const}}$,

– проецируются на плоскость $(x,y)$ в прямые,

– поэтому оптимальны,

– нестрого анормальны, т.е. одновременно являются нормальными.

• Нормальные экстремали удовлетворяют гамильтоновой системе принципа максимума Понтрягина с гамильтонианом H(λ) = $({{\langle \lambda ,{{X}_{1}}\rangle }^{2}}\, + \,{{\langle \lambda ,{{X}_{2}}\rangle }^{2}}){\text{/}}2$:

(4)

$\begin{gathered} \dot {\theta } = c,\quad \dot {c} = - \alpha \sin (\theta + \beta ),\quad \dot {\alpha } = \dot {\beta } = 0, \\ \dot {q} = \cos \theta {\kern 1pt} {{X}_{1}} + \sin \theta {\kern 1pt} {{X}_{2}}. \\ \end{gathered} $

• В фазовом цилиндре уравнения маятника (4) введены координаты $(\varphi ,k)$, в которых это уравнение выпрямляется:

$\dot {\varphi } = \sqrt \alpha ,\quad \dot {k} = 0.$

• Получена параметризация геодезических экспоненциальным отображением:

$\begin{gathered} {\text{Exp}}{\kern 1pt} :\;C \times {{\mathbb{R}}_{ + }} \to G,\quad {\text{Exp}}(\lambda ,t) = \pi \circ {{e}^{{t\vec {H}}}}(\lambda ) = q(t), \\ C = \mathfrak{g}{\kern 1pt} *\; \cap {{H}^{{ - 1}}}(1{\text{/}}2). \\ \end{gathered} $

• Описана группа симметрий экспоненциального отображения

${\text{Sym}} = {\text{SO}}(2) \times {{\mathbb{Z}}_{2}} \times {{\mathbb{Z}}_{2}},$

$\begin{gathered} {\text{SO}}(2) = \{ {{e}^{{t{{X}_{0}}}}}\,{\text{|}}\,t \in \mathbb{R}\} , \\ {{X}_{0}} = - y\frac{{\partial {\kern 1pt} }}{{\partial {\kern 1pt} x}} + x\frac{{\partial {\kern 1pt} }}{{\partial {\kern 1pt} y}} - w\frac{{\partial {\kern 1pt} }}{{\partial {\kern 1pt} v}} + v\frac{{\partial {\kern 1pt} }}{{\partial {\kern 1pt} w}}, \\ \end{gathered} $

${{\mathbb{Z}}_{2}} \times {{\mathbb{Z}}_{2}} = \{ {{\varepsilon }^{i}}\,{\text{|}}\,i = 1, \ldots ,4\} ,$

дискретная подгруппа ${{\mathbb{Z}}_{2}} \times {{\mathbb{Z}}_{2}}$ порождена отражениями ${{\varepsilon }^{1}}$, ${{\varepsilon }^{2}}$ маятника в осях $\theta $, c:

${{\varepsilon }^{1}}{\kern 1pt} :\;(x,y,z,v,w) \mapsto (x,y, - z,v - xz,w - yz),$

${{\varepsilon }^{2}}{\kern 1pt} :\;(x,y,z,v,w) \mapsto (x, - y,z, - v + xz,w - yz).$

• Явно описано время разреза t_cut : $C \to (0, + \infty ]$.

5. СУБРИМАНОВЫ РАССТОЯНИЕ И СФЕРЫ

Напомним основные определения и свойства субримановой метрики и сфер.

Субриманово расстояние (метрика Карно-Каратеодори) определяется следующим образом:

$\begin{gathered} d({{q}_{0}},{{q}_{1}}) = \\ = \inf \left\{ {\int\limits_0^{{{t}_{1}}} {\sqrt {u_{1}^{2} + u_{2}^{2}} {\kern 1pt} dt\,{\text{|}}\,\,{\text{управление}}\;({{u}_{1}},{{u}_{2}})(t)} } \right. \\ \left. {_{{_{{_{{_{{_{{_{{_{{_{{_{{_{{_{{}}}}}}}}}}}}}}}}}}}}}}{\text{переводит}}\;{{q}_{0}}\;{\text{в}}\;{{q}_{1}}} \right\}. \\ \end{gathered} $

Субриманова сфера радиуса $R$ с центром ${{q}_{0}}$ есть

${{S}_{R}}({{q}_{0}}) = \{ q \in G\,{\text{|}}\,d({{q}_{0}},q) = R\} .$

В силу инвариантности метрики относительно левых сдвигов на группе Картана ${{L}_{q}}{\kern 1pt} :\;q{\kern 1pt} ' \mapsto qq{\kern 1pt} '$,

$d(q{{q}_{0}},q{{q}_{1}}) = d({{q}_{0}},{{q}_{1}}),$

${{L}_{q}}({{S}_{R}}({{q}_{0}})) = {{S}_{R}}(q{{q}_{0}}).$

В силу того, что группа Картана есть группа Карно, левоинвариантная субриманова структура согласована с дилатациями:

${{\delta }_{\beta }}{\kern 1pt} :\;(x,y,z,v,w) \mapsto (\beta x,\beta y,{{\beta }^{2}}z,{{\beta }^{3}}v,{{\beta }^{3}}w),\quad \beta > 0,$

$d({\text{Id}},{{\delta }_{\beta }}(q)) = \beta d({\text{Id}},q),$

${{\delta }_{\beta }}({{S}_{R}}({\text{Id}})) = {{S}_{{\beta R}}}({\text{Id}}).$

Поэтому достаточно исследовать единичную сферу

$S = {{S}_{1}}({\text{Id}}) = \{ q \in G\,{\text{|}}\,d(q,{\text{Id}}) = 1\} .$

Единичная сфера S параметризуется экспоненциальным отображением:

$S = \{ {\text{Exp}}(\lambda ,1)\,{\text{|}}\,\lambda \in C,{{t}_{{{\text{cut}}}}}(\lambda ) \geqslant 1\} .$

Субриманова структура и сфера инвариантны относительно группы симметрий Sym = = $SO(2) \times {{\mathbb{Z}}_{2}} \times {{\mathbb{Z}}_{2}}$:

$g(S) = S,\quad g \in {\text{Sym}}.$

Основной объект этой работы – сечение сферы трехмерным инвариантным многообразием основных симметрий ${{\varepsilon }^{1}}$, ${{\varepsilon }^{2}}$:

$\widetilde S = \{ q \in S\,{\text{|}}\,{{\varepsilon }^{1}}(q) = {{\varepsilon }^{2}}(q) = q\} = S \cap \{ z = V = 0\} ,$

$V(q) = xv + yw - z({{x}^{2}} + {{y}^{2}}){\text{/}}2,$

а также его фактор по группе вращений

$\widehat S = \widetilde S{\text{/}}SO(2).$

Мы ограничиваемся описанием лишь сечения $\widetilde S$, так как полная сфера S не допускает столь подробного исследования ввиду сложности ее параметризации: функция ${{t}_{{{\text{cut}}}}}(\lambda )$, задающая время разреза на группе Картана, в общем случае есть корень уравнения в эллиптических функциях, см. [14, 16].

6. СТРУКТУРА ФАКТОРА $\widehat S$

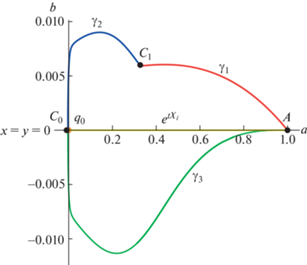
На рис. 1 изображен фактор сечения сферы $\widehat S$ на группе Картана в координатах

$a = \frac{{{{r}^{2}} - {{\sigma }^{2}}}}{{\sqrt {{{r}^{2}} + {{\sigma }^{2}}} }},\quad b = \frac{{2r\sigma }}{{\sqrt {{{r}^{2}} + {{\sigma }^{2}}} }},$

$r = \sqrt {{{x}^{2}} + {{y}^{2}}} ,\quad \sigma = \rho - \frac{{{{r}^{3}}}}{6},\quad \rho = \sqrt {{{v}^{2}} + {{w}^{2}}} .$

Рис. 1.

Фактор сечения сферы $\widehat S$ на группе Картана.

Кривая $\widehat S$ параметризуется параметром $k\, \in \,[0,1]$. Имеется стратификация

(5)

$\widehat S = \left( { \sqcup _{{i = 1}}^{3}{{\gamma }_{i}}} \right) \sqcup \{ A,{{C}_{0}},{{C}_{1}}\} ,$

$A = {{e}^{{\cos \theta {{X}_{1}} + \sin \theta {{X}_{2}}}}}$ есть точка на анормальной траектории, k = 0, C₀ есть точка на периодической эйлеровой эластике восьмерке (см. рис. 8 [13]),

(6)

$x = y = 0,\quad k = {{k}_{0}} \approx 0.9,$

${{C}_{1}}{\kern 1pt} :\;{{p}_{z}}(k) = {{p}_{V}}(k),\quad k = {{k}_{1}} \approx 0.8,$

(7)

$\begin{gathered} {{\gamma }_{1}}{\kern 1pt} :\;k \in (0,{{k}_{1}}), \\ {{\gamma }_{2}}{\kern 1pt} :\;k \in ({{k}_{1}},{{k}_{0}}), \\ \end{gathered} $

${{\gamma }_{3}}{\kern 1pt} :\;k \in ({{k}_{0}},1).$

Определение чисел ${{k}_{0}},{{k}_{1}} \in (0,1)$, а также функций ${{p}_{z}},{{p}_{V}}{\kern 1pt} :\;(0,1) \to \mathbb{R}$ приведено в работе [14].

На рис. 1:

• надпись ${{e}^{{t{{X}_{i}}}}}$ над горизонтальным отрезком, соединяющим точки ${{q}_{0}}$ и A, обозначает анормальные траектории, соединяющие начальную точку ${{q}_{0}}$ = Id с точками сферы, проецирующимися в точку A,

• надпись $x = y = 0$ справа от точки ${{C}_{0}}$ обозначает точки периодических эластик-восьмерок,

• точка ${{C}_{0}}$ имеет координаты $(a,b) = (0,{{b}_{0}})$, где ${{b}_{0}} \approx - 0.004$.

В последующих теоремах для краткости допускается некоторая вольность обозначений: точки множества $\widehat S$ рассматриваются иногда как окружности в $G$, а иногда как точки в $G$.

7. ХАРАКТЕРИЗАЦИЯ ТОЧЕК ФАКТОРА $\widehat S$

Напомним вкратце некоторые необходимые понятия субримановой геометрии, подробнее см. [2, 3].

В рассматриваемой задаче анормальные траектории, выходящие из точки ${{q}_{0}} = {\text{Id}}$, суть однопараметрические подгруппы, касающиеся распределения; при этом они являются субримановыми кратчайшими, т.е. реализуют минимум функционала длины (3) между любыми своими точками.

Первая сопряженная точка к ${{q}_{0}}$ на геодезической есть точка, в которой геодезическая теряет свою локальную оптимальность.

Точка Максвелла на геодезической есть точка, в которую приходят более одной геодезической одинаковой длины, начинающихся в ${{q}_{0}}$.

Точка разреза на геодезической есть точка, в которой геодезическая теряет свою (глобальную) оптимальность.

Теорема 1.

(1) A есть точка на анормальной кратчайшей,

(2) ${{C}_{i}}$ суть сопряженные точки к ${{q}_{0}}$, точки Максвелла, точки разреза,

(3) $q \in {{\gamma }_{i}}$ суть точки Максвелла, точки разреза, не сопряженные точки к ${{q}_{0}}$.

8. КРАТНОСТЬ ТОЧЕК ФАКТОРА $\widehat S$

Кратностью точки $q \in G$ называется мощность

$\mu (q) = {\text{card}}\{ {\text{кратчайшие,}}\;{\text{соединяющие}}\;{\text{Id}}\;{\text{и}}\;q\} .$

Теорема 2.

(1) $\mu (A) = 1$,

(2) $\mu ({{C}_{i}}) = \mathfrak{c}$ (континуум $ \cong {{S}^{1}}$),

(3) $q \in {{\gamma }_{i}} \Rightarrow \mu (q) = 2$.

9. РЕГУЛЯРНОСТЬ $\widehat S$ И $\widetilde S$

Теорема 3.

(1) кривые ${{\gamma }_{i}}$ аналитичны и регулярны,

(2) $A$, ${{C}_{i}}$ суть особые точки, в них $\widehat S$ негладкая, но липшицева,

(3) замыкания

(3.1) ${{\bar {\gamma }}_{1}} = {{\gamma }_{1}} \cup \{ A,{{C}_{0}}\} $,

(3.2) ${{\bar {\gamma }}_{2}} = {{\gamma }_{2}} \cup \{ {{C}_{0}},{{C}_{1}}\} $,

(3.3) ${{\bar {\gamma }}_{3}} = {{\gamma }_{1}} \cup \{ {{C}_{0}},A\} $,

суть гладкие кривые класса C^∞.

Теорема 4. $\widetilde S$ есть липшицево многообразие, аналитически диффеоморфное $\widehat S \times {{S}^{1}}$ и билипшицево эквивалентное (потому гомеоморфное) тору ${{\mathbb{T}}^{2}}$.

10. АНАЛИТИЧЕСКИЕ СВОЙСТВА ФАКТОРА $\widehat S$

Множество называется аналитическим , если в некоторой окрестности каждой своей точки оно задается конечной системой вещественно-аналитических уравнений. Множество называется полуаналитическим [6], если в некоторой окрестности каждой своей точки оно задается конечной системой вещественно-аналитических уравнений и неравенств. Множество называется субаналитическим [7], если его можно получить из полуаналитических множеств путем конечнократного применения операций объединения, пересечения и взятия образа собственного аналитического отображения. На двумерной плоскости понятия полуаналитических и субаналитических множеств совпадают.

Теорема 5.

• Множество $\widehat S{{\backslash }}\{ A\} $ полуаналитично, потому субаналитично.

• В окрестности точки A кривая ${{\gamma }_{3}}$ есть график гладкой неаналитической функции.

• Поэтому множество $\widehat S$ несубаналитично.

• Следовательно, сфера $S$ несубаналитична.

11. Exp–log КАТЕГОРИЯ

Функция $f{\kern 1pt} :\;{{\mathbb{R}}^{n}} \to \mathbb{R}$ принадлежит exp–log категории [18], если она представляется в виде конечной композиции субаналитических функций, экспонент и логарифмов. Множество принадлежит exp–log категории, если в некоторой окрестности любой своей точки оно является графиком отображения, компоненты которого – функции из exp–log категории.

Теорема 6. В окрестности точки $A$ кривая ${{\gamma }_{3}}$ есть график функции из exp–log категории. Поэтому множество $\widehat S$ принадлежит exp–log категории.

12. СТРАТИФИКАЦИЯ УИТНИ

Напомним следующие фундаментальные факты, относящиеся к стратификации Уитни [17]:

• если множество субаналитично, то оно является стратифицированным пространством Уитни [7],

• если множество принадлежит exp–log категории, то оно является стратифицированным пространством Уитни [8].

Теорема 7. Разбиение (5) есть стратификация Уитни.

Список литературы

Локуциевский Л.В., Сачков Ю.Л. Об интегрируемости по Лиувиллю субримановых задач на группах Карно глубины 4 и больше // Матем. сб. 2018. Т. 209. № 5. С. 74–119.
Agrachev A.A., Sachkov Yu.L. Control Theory from the Geometric Viewpoint. Springer-Verlag, Berlin. 2004.
Agrachev A., Barilari D., Boscain U. A Comprehensive Introduction to sub-Riemannian Geometry from Hamiltonian viewpoint. Cambridge Studies in Advanced Mathematics, Cambridge Univ. Press, 2019.
Bizyaev I.A., Borisov A.V., Kilin A.A., Mamaev I.S. Integrability and Nonintegrability of Sub-Riemannian Geodesic Flows on Carnot Groups, Regular and Chaotic Dynamics. 2016. V. 21. № 6. P. 759–774.
Cartan E. Lès systemes de Pfaff a cinque variables et lès equations aux derivees partielles du second ordre // Ann. Sci. Ècole Normale. 1910. V. 27. № 3. P. 109–192.
Łojasiewicz S. Ansembles semi-analitiques, Inst. Hautes Ètudes Sci., Bures-sur-Yvette, 1964.
Hironaka H. Subanalytic sets, Number Theory, Algebraic Geometry and Commutative Algebra, Tokyo, Kinokuniya, 1973. P. 453–493.
Ta Lê Loi. Verdier and strict Thom stratifications in o-minimal structures // Illinois J. Math. 1998. V. 42. Is. 2. P. 347–356.
Li Z., Canny J., Motion of two rigid bodies with rolling constraint // IEEE Trans. on Robotics and Automation. 1990. V. 1. № 6. P. 62–72.
Marigo A., Bicchi A. Rolling bodies with regular surface: the holonomic case, in book: “Differential geometry and control: Summer Research Institute on Differential Geometry and Control”, publ. Univ. Colorado, Boulder, G. Ferreyra et al. Eds., 1999. P. 241–256.
Laumond J.P. Nonholonomic motion planning for mobile robots // Preprint No. 98211. Toulouse, France: LAAS-CNRS, 1998.
Anzaldo-Menezes A., Monroy-Pérez F. Charges in magnetic fields and sub-Riemannian geodesics// Contemporary trends in nonlinear geometric control theory and its applications. Singapore: World Scientific, 2002. P. 183–202.
Сачков Ю.Л. Экспоненциальное отображение в обобщенной задаче Дидоны. Мат. Сборник. 2003. V. 194 (9). P. 63–90.
Сачков Ю.Л. Полное описание стратов Максвелла в обобщенной задаче Дидоны. Мат. Сборник. 2006. Т. 197. № 6. С. 111–160.
Sachkov Yu.L. Conjugate time in the sub-Riemannian problem on the Cartan group // Journal of Dynamical and Control Systems. 2021. V. 27. P. 709–751.
Ardentov A., Hakavuori E. Cut time in the sub-Riemannian problem on the Cartan group // ESAIM:COCV. 2022. V. 28. P. 12.
Горески М., Макферсон Р. Стратифицированная теория Морса, М.: Мир, 1991.
Van Den Dries L., Macintyre A., Marker D. The elementary theory of restricted analytic fields with exponentiation // Ann. of Math. 1994. V. 140. № 2. P. 183–205.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Доклады Российской академии наук. Математика, информатика, процессы управления

Архивы выпусков Информация о журнале Отправить рукопись в журнал