Доклады Российской академии наук. Математика, информатика, процессы управления, 2023, T. 509, № 1, стр. 36-45

Уточнение задачи оптимального управления для практической реализации ее решения

А. И. Дивеев^1, *

¹ Федеральный исследовательский центр “Информатика и управление” Российской академии наук
Москва, Россия

Поступила в редакцию 06.07.2022
После доработки 24.12.2022
Принята к публикации 26.12.2022

EDN: CPZONE
DOI: 10.31857/S2686954322600458

Аннотация

Решение задачи оптимального управления в классической постановке представляет собой управление в форме функции времени. Реализация такого решения приводит к разомкнутой системе управления и поэтому не может применяться непосредственно на практике. Считается, что решение классической задачи оптимального управления приводит к получению оптимальной программы управления и программной траектории в пространстве состояний. Для реализации движения объекта управления по программной траектории необходимо построение дополнительной системы стабилизации движения. Задача синтеза системы стабилизации движения по программной траектории и требования, которым должна удовлетворять эта система, не вытекают из классической постановки задачи оптимального управления. Приведена уточненная постановка задачи оптимального управления, которая включает дополнительное требование к оптимальной траектории, и решение которой может быть непосредственно применено на практике в реальном объекте управления.

Ключевые слова: оптимальное управление, синтез управления, сжимающее отображение

Рассмотрим классическую постановку задачи оптимального управления [1].

(1)

${\mathbf{\dot {x}}} = {\mathbf{f}}({\mathbf{x}},{\mathbf{u}}),$

(2)

${\mathbf{u}} \in \operatorname{U} \subseteq {{\mathbb{R}}^{m}},$

(3)

${\mathbf{x}}(0) = {{{\mathbf{x}}}^{0}},$

(4)

${\mathbf{x}}({{t}_{f}}) = {{{\mathbf{x}}}^{f}},$

(5)

$J = \int\limits_0^{{{t}_{f}}} {{{f}_{0}}({\mathbf{x}},{\mathbf{u}})dt} \to \mathop {\min }\limits_{{\mathbf{u}} \in \operatorname{U} } ,$

где ${\mathbf{x}}$ – вектор состояния, ${\mathbf{x}} \in {{\mathbb{R}}^{n}}$, ${\mathbf{u}}$ – вектор управления, $\operatorname{U} $ – компактное множество, ${{{\mathbf{x}}}^{0}}$ – заданный вектор начального состояния, ${{{\mathbf{x}}}^{f}}$ – заданный вектор терминального состояния, ${{t}_{f}}$ – время достижения терминального состояния, как правило, не задано, но ограничено, ${{t}_{f}} \leqslant {{t}^{ + }}$, ${{t}^{ + }}$ – заданная положительная величина, $J$ – значение критерия качества управления.

В классической постановке никаких дополнительных требований к управлению, кроме удовлетворения ограничению на управление (2), не предъявляется, поэтому управление ищется как функция времени

(6)

${\mathbf{u}} = {\mathbf{v}}(t) \in \operatorname{U} .$

Если подставить найденное управление (6) в правую часть модели объекта (1), то полученная система

(7)

${\mathbf{\dot {x}}} = {\mathbf{f}}({\mathbf{x}},{\mathbf{v}}(t))$

будет иметь частное решение ${\mathbf{x}}(t,{{{\mathbf{x}}}^{0}})$, которое из начального состояния (3) достигнет терминальное состояние (4)

(8)

${\mathbf{x}}({{t}_{f}},{{{\mathbf{x}}}^{0}}) = {{{\mathbf{x}}}^{f}},\quad {{t}_{f}} \leqslant {{t}^{ + }},$

с оптимальным значением критерия качества (5).

Математическая модель (7) описывает динамику разомкнутой системы управления, поскольку функция управления (6) не зависит от вектора состояния объекта управления. Математическая модель используется для оценки текущего состояния реального объекта управления. Любая математическая модель дает ошибку при оценке состояния реального объекта. Введем определения.

Определение 1. Математическая модель объекта является качественно подходящей, если в рассматриваемой области пространства состояний она описывает качественные свойства реального объекта.

Если объект устойчив относительно некоторой точки в пространстве состояний, то качественно подходящая математическая модель также устойчива.

Определение 2. Математическая модель объекта гарантированно реализуема, если на интервале $\Delta t > 0$ первоначальная ошибка не возрастает со временем

(9)

$\left\| {{\mathbf{\tilde {x}}}(\Delta t) - {\mathbf{x}}(\Delta t)} \right\| \leqslant \left\| {{\mathbf{\tilde {x}}}(0) - {\mathbf{x}}(0)} \right\|,$

где ${\mathbf{\tilde {x}}}(t)$ – вектор состояния реального объекта в момент $t$.

Теорема 1. Если качественно подходящая математическая модель реального объекта в области $\operatorname{X} \subseteq {{\mathbb{R}}^{n}}$ имеет свойство сжимающего отображения и ${\mathbf{x}}({{t}_{f}},{{{\mathbf{x}}}^{0}}) = {{{\mathbf{x}}}^{f}} \in \operatorname{X} $, является неподвижной точкой, то этого достаточно, чтобы она была реализуема в этой области.

Доказательство. Согласно определению 1, математическая модель и реальный объект обладают в области $\operatorname{X} \subseteq {{\mathbb{R}}^{n}}$ свойством сжимающего отображения.

Пусть

(10)

${\mathbf{\dot {x}}} = {\mathbf{f}}({\mathbf{x}}),$

модель объекта. Пусть в какой-то момент времени $t{\kern 1pt} '$ из-за неучтенных в модели возмущений реального объекта состояние реального объекта ${\mathbf{\tilde {x}}}(t{\kern 1pt} ')$ не совпадает с состоянием, вычисленным по модели

(11)

$\delta (t{\kern 1pt} ') = {\text{||}}{\mathbf{\tilde {x}}}(t{\kern 1pt} ') - {\mathbf{x}}(t{\kern 1pt} '){\text{||}},$

где $\delta $ – ошибка определения состояния объекта по его модели.

Согласно свойству сжимающего отображения $\forall \Delta t > 0$

(12)

$\begin{gathered} \delta (t{\kern 1pt} '\; + \Delta t) = {\text{||}}{\mathbf{\tilde {x}}}(t{\kern 1pt} '\; + \Delta t) - {\mathbf{x}}(t{\kern 1pt} '\; + \Delta t){\text{||}} \leqslant \\ \leqslant {\text{||}}{\mathbf{\tilde {x}}}(t{\kern 1pt} ') - {\mathbf{x}}(t{\kern 1pt} '){\text{||}} = \delta (t{\kern 1pt} '). \\ \end{gathered} $

Следовательно, ошибка не возрастает во времени. Так как ${{{\mathbf{x}}}^{f}} \in \operatorname{X} $ является неподвижной точкой сжимающего отображения, то

(13)

${\mathbf{\tilde {x}}}({{\tilde {t}}_{f}},{{{\mathbf{x}}}^{0}}) = {{{\mathbf{x}}}^{f}},$

где ${{\tilde {t}}_{f}}$ – время достижения неподвижной точки реальным объектом. Тогда в момент

(14)

${{t}_{1}} = \max \{ {{t}_{f}},{{\tilde {t}}_{f}}\} $

выполняются условия

(15)

$\delta ({{t}_{1}}) = {\text{||}}{\mathbf{\tilde {x}}}({{t}_{1}}) - {\mathbf{\tilde {x}}}({{t}_{1}}){\text{||}} = 0.$

Ошибка (11) не возрастает во времени и при $\Delta t \geqslant {{t}_{1}} - t{\kern 1pt} '$ равна нулю. Модель реализуема согласно определению 2.

Причиной нереализуемости решения задачи оптимального управления является то, что получаемая в результате решения модель разомкнутой системы управления описывает объект управления с ошибкой, которая может расти во времени из-за возмущений, например по начальным условиям. Для обеспечения реализуцемости решения задачи оптимального управления в классическую постановку задачи введены некоторые уточнения. Вместо соотношения (6) управление ищем в форме

(16)

${\mathbf{u}} = {\mathbf{g}}({\mathbf{x}},t) \in \operatorname{U} ,$

${\mathbf{g}}({\mathbf{x}},t):{{\mathbb{R}}^{n}} \times {{\mathbb{R}}_{ + }} \to {{\mathbb{R}}^{m}}.$

После подстановки функции управления (16) в правые части модели (1) получаем систему

(17)

${\mathbf{\dot {x}}} = {\mathbf{f}}({\mathbf{x}},{\mathbf{g}}({\mathbf{x}},t)).$

Частное решение системы (17) из начального состояния (3) достигает терминальное состояние (4) в момент ${{t}_{f}}$ (8) с оптимальным значением критерия качества (5).

Введем также дополнительные условия, которым должна удовлетворять оптимальная траектория, т.е. частное решения уравнения (17) из начального состояния (3). Для оптимального частного решения ${\mathbf{x}}{\kern 1pt} *{\kern 1pt} (t,{{{\mathbf{x}}}^{0}})$ должна существовать окрестность, определяемая параметром $\delta {\kern 1pt} *{\kern 1pt} (t) > 0$, $0 \leqslant t \leqslant {{t}^{ + }}$, такая, что, если для другого частного решения ${\mathbf{x}}(t,{\mathbf{y}})$ системы (17) из другого начального состояния

(18)

${\mathbf{x}}(0) = {\mathbf{y}} \ne {{{\mathbf{x}}}^{0}},$

в момент $t{\kern 1pt} '$, $0 \leqslant t{\kern 1pt} ' < {{t}^{ + }}$, выполняются условия

(19)

${\text{||}}{\mathbf{x}}(t{\kern 1pt} ',{{{\mathbf{x}}}^{0}}) - {\mathbf{x}}(t{\kern 1pt} ',{\mathbf{y}}){\text{||}} \leqslant \delta {\kern 1pt} *(t'),$

то $\exists \varepsilon {\kern 1pt} * > 0$ и $\exists t{\kern 1pt} '{\kern 1pt} ' > t{\kern 1pt} '$, $0 \leqslant t{\kern 1pt} '{\kern 1pt} ' \leqslant {{t}^{ + }} - t{\kern 1pt} '$ такие, что должно выполняться неравенство

(20)

${\text{||}}{\mathbf{x}}(t{\kern 1pt} '{\kern 1pt} ',{{{\mathbf{x}}}^{0}}) - {\mathbf{x}}(t{\kern 1pt} '{\kern 1pt} ',{\mathbf{y}}){\text{||}} < \varepsilon {\kern 1pt} *{\kern 1pt} .$

Тогда в области, определяемой параметром ε*, выполняются условия: $\forall \Delta t{\kern 1pt} '$, $\Delta t{\kern 1pt} '{\kern 1pt} '$, $0 \leqslant \Delta t{\kern 1pt} ' < \Delta t{\kern 1pt} '{\kern 1pt} '$

(21)

$\begin{gathered} {\text{||}}{\mathbf{x}}(t{\kern 1pt} '{\kern 1pt} '\; + \Delta t{\kern 1pt} '{\kern 1pt} ',{{{\mathbf{x}}}^{0}}) - {\mathbf{x}}(t{\kern 1pt} '{\kern 1pt} '\; + \Delta t{\kern 1pt} ',{\mathbf{y}}){\text{||}} < \\ < {\text{||}}{\mathbf{x}}(t{\kern 1pt} '{\kern 1pt} '\; + \Delta t{\kern 1pt} ',{{{\mathbf{x}}}^{0}}) - {\mathbf{x}}(t{\kern 1pt} '{\kern 1pt} '\; + \Delta t{\kern 1pt} ',{\mathbf{y}}){\text{||}} \leqslant \varepsilon {\kern 1pt} *{\kern 1pt} . \\ \end{gathered} $.

Определение 3. Задача (1)–(5), (16)–(21) называется расширенной задачей оптимального управления.

Цель формулировки расширенной постановки задачи оптимального управления состоит в обеспечение возможности непосредственного применения ее решения в реальном объекте управления. Параметр $\delta {\kern 1pt} *{\kern 1pt} (t) > 0$ определяет область в пространстве, из которой объект попадает в другую, возможно, большую область, определяемую параметром $\varepsilon {\kern 1pt} * > 0$, где выполняются условия сжимающего отображения. Величина $\delta {\kern 1pt} *{\kern 1pt} (t)$ указывает на сложность решения расширенной задачи оптимального управления. Если $\delta {\kern 1pt} *{\kern 1pt} (t) = 0$, то получаем задачу оптимального управления в классической постановке. Если $\delta {\kern 1pt} *{\kern 1pt} (t) = \infty $, то получаем самый сложный случай, когда необходимо решить задачу общего синтеза управления [2] для всего пространства состояний.

Теорема 2. Система дифференциальных уравнений, частные решения которой обладают свойством (16)–(21), при $\delta {\kern 1pt} *(0) > 0$ обладают свойством сжимающего отображения в области пространства состояний, определяемой параметром $\varepsilon {\kern 1pt} *$.

Доказательство. Пусть ${\mathbf{x}}(t,{{{\mathbf{x}}}^{{0,1}}})$ и ${\mathbf{x}}(t,{{{\mathbf{x}}}^{{0,2}}})$ – два частных решения дифференциального уравнения из двух разных начальных условий ${{{\mathbf{x}}}^{{0,1}}} \ne {{{\mathbf{x}}}^{{0,2}}} \ne {{{\mathbf{x}}}^{0}}$. Пусть в момент $t{\kern 1pt} ' = 0$ выполняются условия

(22)

${\text{||}}{\mathbf{x}}(0,{{{\mathbf{x}}}^{0}}) - {\mathbf{x}}(0,{{{\mathbf{x}}}^{{0,1}}}){\text{||}} \leqslant \delta {\kern 1pt} *{\kern 1pt} (0),$

(23)

${\text{||}}{\mathbf{x}}(0,{{{\mathbf{x}}}^{0}}) - {\mathbf{x}}(0,{{{\mathbf{x}}}^{{0,2}}}){\text{||}} \leqslant \delta {\kern 1pt} *{\kern 1pt} (0).$

Тогда в момент $t{\kern 1pt} '{\kern 1pt} ' > t{\kern 1pt} ' = 0$

(24)

${\text{||}}{\mathbf{x}}(t{\kern 1pt} '',{{{\mathbf{x}}}^{0}}) - {\mathbf{x}}(t{\kern 1pt} '',{{{\mathbf{x}}}^{{0,1}}}){\text{||}} \leqslant \varepsilon {\kern 1pt} *{\kern 1pt} ,$

(25)

${\text{||}}{\mathbf{x}}(t{\kern 1pt} '{\kern 1pt} ',{{{\mathbf{x}}}^{0}}) - {\mathbf{x}}(t{\kern 1pt} '{\kern 1pt} ',{{{\mathbf{x}}}^{{0,2}}}){\text{||}} \leqslant \varepsilon {\kern 1pt} *{\kern 1pt} .$

Согласно условию (21) $\exists \Delta t{\kern 1pt} '{\kern 1pt} ' > \Delta t{\kern 1pt} ' \geqslant 0$, что

(26)

$\begin{gathered} {\text{||}}{\mathbf{x}}(t{\kern 1pt} '{\kern 1pt} '\; + \Delta t{\kern 1pt} '{\kern 1pt} ',{{{\mathbf{x}}}^{0}}) - {\mathbf{x}}(t{\kern 1pt} '{\kern 1pt} '\; + \Delta t{\kern 1pt} '{\kern 1pt} ',{{{\mathbf{x}}}^{{0,1}}}){\text{||}} < \\ < {\text{||}}{\mathbf{x}}(t{\kern 1pt} '{\kern 1pt} '\; + \Delta t{\kern 1pt} ',{{{\mathbf{x}}}^{0}}) - {\mathbf{x}}(t{\kern 1pt} '{\kern 1pt} '\; + \Delta t{\kern 1pt} ',{{{\mathbf{x}}}^{{0,1}}}){\text{||}} \leqslant \varepsilon {\kern 1pt} *{\kern 1pt} , \\ \end{gathered} $

(27)

$\begin{gathered} {\text{||}}{\mathbf{x}}(t{\kern 1pt} '{\kern 1pt} '\; + \Delta t{\kern 1pt} '{\kern 1pt} ',{{{\mathbf{x}}}^{0}}) - {\mathbf{x}}(t{\kern 1pt} '{\kern 1pt} '\; + \Delta t{\kern 1pt} '{\kern 1pt} ',{{{\mathbf{x}}}^{{0,2}}}){\text{||}} < \\ < {\text{||}}{\mathbf{x}}(t{\kern 1pt} '{\kern 1pt} '\; + \Delta t{\kern 1pt} ',{{{\mathbf{x}}}^{0}}) - {\mathbf{x}}(t{\kern 1pt} '{\kern 1pt} '\; + \Delta t{\kern 1pt} ',{{{\mathbf{x}}}^{{0,2}}}){\text{||}} \leqslant \varepsilon {\kern 1pt} *{\kern 1pt} . \\ \end{gathered} $

Поэтому

(28)

$\begin{gathered} {\text{||}}{\mathbf{x}}(t{\kern 1pt} '{\kern 1pt} '\; + \Delta t{\kern 1pt} '{\kern 1pt} ',{{{\mathbf{x}}}^{{0,1}}}) - {\mathbf{x}}(t{\kern 1pt} '{\kern 1pt} '\; + \Delta t{\kern 1pt} '{\kern 1pt} ',{{{\mathbf{x}}}^{{0,2}}}){\text{||}} < \\ < {\text{||}}{\mathbf{x}}(t{\kern 1pt} '{\kern 1pt} '\; + \Delta t{\kern 1pt} ',{{{\mathbf{x}}}^{{0,1}}}) - {\mathbf{x}}(t{\kern 1pt} '{\kern 1pt} '\; + \Delta t{\kern 1pt} ',{{{\mathbf{x}}}^{{0,2}}}){\text{||}}. \\ \end{gathered} $

Система уравнений описывает сжимающее отображение в области, определяемой параметром $\varepsilon {\kern 1pt} * > 0$.

Рассмотрим методы решения расширенной задачи оптимального управления. Одним из подходов к решению расширенной задачи оптимального управления является решение задачи синтеза управления. В задаче синтеза управления задана модель объекта управления (1), ограничения на управления (2), начальные условия в виде области пространства состояний

(29)

${{\operatorname{X} }_{0}} \subseteq {{\mathbb{R}}^{n}}.$

Заданы терминальное состояние (4) и критерий качества управления (5). Необходимо найти управление в форме функции

(30)

${\mathbf{u}} = {\mathbf{h}}({{{\mathbf{x}}}^{f}} - {\mathbf{x}}) \in \operatorname{U} \subseteq {{\mathbb{R}}^{m}}.$

Если подставить найденную функцию управления (30) в модель объекта управления (1), то получим систему уравнений

(31)

${\mathbf{\dot {x}}} = {\mathbf{f}}({\mathbf{x}},{\mathbf{h}}({{{\mathbf{x}}}^{f}} - {\mathbf{x}})),$

любое частное решение которой из любого начального условия из заданной области (29)

(32)

${{{\mathbf{x}}}^{0}} \in {{\operatorname{X} }_{0}} \subseteq {{\mathbb{R}}^{n}}$

за конечное время ${{t}_{f}}({{{\mathbf{x}}}^{0}}) \leqslant {{t}^{ + }}$ попадет в терминальное состояние (4) с оптимальным значением критерия качества (5).

В данном случае после решения задачи синтеза управления получаем не одну оптимальную траекторию, а множество оптимальных траекторий из любого начального состояния из области (29). В этом случае область $\varepsilon {\kern 1pt} *$ со свойствами сжимающего отображения может оказаться малой окрестностью терминального состояния (4). Универсальных методов решения задачи синтеза управления нет. Аналитические методы решения задачи синтеза, метод бэкстеппинг [3] и аналитическое конструирование агрегированных регуляторов (АКАР) [4] привязаны к виду модели объекта управления и направлены на обеспечения его устойчивости по Ляпунову. В настоящее время для решения задачи синтеза управления используют машинное обучение численными методами символьной регрессии [5].

Методы символьной регрессии кодируют математическое выражение в форме специального кода и ищут оптимальное решение на пространстве кодов с помощью специального генетического алгоритма, в котором изменены основные операции скрещивания и мутации для работы с соответствующим кодом символьной регрессии. Для кодирования математического выражения первоначально устанавливается алфавит элементов кода. В алфавит входят элементарные функции и аргументы искомого математического выражения. Каждый элемент алфавита в общем случае кодирует элементарную функцию с помощью целочисленного вектора из двух компонент

(33)

${\mathbf{a}} = {{[\begin{array}{*{20}{c}} {{{a}_{1}}}&{{{a}_{2}}} \end{array}]}^{T}},$

где ${{a}_{1}}$ – количество аргументов элементарной функции, ${{a}_{2}}$ – номер функции. Если ${{a}_{1}} = 0$, то это код аргумента искомого математического выражения.

Код математического выражения любого метода символьной регрессии представляет собой упорядоченное множество упорядоченных множеств кодов элементов (33) алфавита

(34)

$\begin{gathered} \operatorname{G} = ({{\operatorname{G} }_{1}}, \ldots ,{{\operatorname{G} }_{L}}) = \\ = ({{\operatorname{G} }_{1}} = ({{{\mathbf{a}}}^{{1,1}}}, \ldots ,{{{\mathbf{a}}}^{{1,{{M}_{i}}}}}), \ldots ,{{\operatorname{G} }_{L}} = ({{{\mathbf{a}}}^{{L,1}}}, \ldots ,{{{\mathbf{a}}}^{{L,{{M}_{L}}}}})), \\ \end{gathered} $

где

(35)

${{{\mathbf{a}}}^{{i,j}}} = [\begin{array}{*{20}{c}} {a_{1}^{{i,j}}}&{a_{2}^{{i,j}}{{]}^{T}}} \end{array},\quad i = 1, \ldots ,{{M}_{j}},\quad j = 1, \ldots ,L.$

Операция скрещивания кодов математических выражений в форме (34), (35) выполняется в соответствии с правилами кодирования, чтобы полученные в результате скрещивания коды имели правильную запись и могли быть декодированы. Например, код генетического программирования [5] в общем случае представляет собой граф в форме дерева, на листьях которого расположены коды аргументов, которые можно в коде (33) рассматривать как функции без аргументов, ${{a}_{1}} = 0$. При скрещивании выполняется операция обмена ветвей двух отобранных деревьев. Скрещивание для кодов в форме (34) означает обмен двух подмножеств элементов кода. При этом необходимо найти по первому элементу обмениваемой ветви дерева конечный код подмножества, который соответствует последнему элементу этой ветви дерева, при этом длины кодов после операции скрещивания могут измениться.

Основным недостатком выполнения операции скрещивания для кодов в форме (34) является сильное изменение кодов полученных новых возможных решений. Коды “потомков” часто оказываются не похожими на коды их “родителей”. В результате операция скрещивания становится операцией генерации новых кодов, при этом не соблюдаются свойство наследования и принцип эволюционного поиска. Поиск решения в этом случае становится прямым случайным поиском, что не приемлемо для поиска на нечисловом пространстве.

Для эффективного поиска на пространстве кодов, сохранения свойства наследования и условий эволюции используется принцип малых вариаций базисного решения [5, 6], согласно которому множество возможных решений кодируется с помощью кода в форме (34) одного базисного возможного решения и упорядоченных множеств кодов малых вариаций этого базисного решения.

(36)

$\begin{gathered} \operatorname{W} = \{ {{\operatorname{W} }_{1}}, \ldots ,{{\operatorname{W} }_{H}}\} = \\ \, = \{ {{\operatorname{W} }_{1}} = ({{{\mathbf{w}}}^{{1,1}}}, \ldots ,{{{\mathbf{w}}}^{{1,d}}}), \ldots ,{{\operatorname{W} }_{H}} = ({{{\mathbf{w}}}^{{H,1}}}, \ldots ,{{{\mathbf{w}}}^{{H,d}}})\} , \\ \end{gathered} $

где

(37)

${{{\mathbf{w}}}^{{i,j}}} = {{[\begin{array}{*{20}{c}} {w_{1}^{{i,j}}}& \ldots &{w_{k}^{{i,j}}} \end{array}]}^{T}},\quad i = 1, \ldots ,H,\quad j = 1, \ldots ,d,$

вектор кода малой вариации, $H$ – количество возможных решений, $d$ – длина вариации.

Компоненты вектора кода малой вариации указывают тип и место изменения кода базисного решения. Например, ${{w}_{1}}$ – номер подмножества в коде (34), ${{w}_{2}}$ – номер элемента этого подмножества, ${{w}_{3}}$ – номер элемента в коде элементарной функции и ${{w}_{4}}$ – новое значение элемента,

(38)

$a_{{{{w}_{3}}}}^{{{{w}_{1}},{{w}_{2}}}} = {{w}_{4}}.$

Операция скрещивания в данном случае выполняется по правилам классического генетического алгоритма над упорядоченными множествами кодов малых вариаций. Отбираются два “родителя”

(39)

${{\operatorname{W} }_{\alpha }} = ({{{\mathbf{w}}}^{{\alpha ,1}}}, \ldots ,{{{\mathbf{w}}}^{{\alpha ,d}}}),\quad {{\operatorname{W} }_{\beta }} = ({{{\mathbf{w}}}^{{\beta ,1}}}, \ldots ,{{{\mathbf{w}}}^{{\beta ,d}}}),$

находится случайно точка скрещивания $k \in \{ 1$, ..., d} и обмениваются элементы после точки скрещивания. В результате получаем два новых возможных решения – “потомка”

(40)

$\begin{gathered} {{\operatorname{W} }_{{H + 1}}} = ({{{\mathbf{w}}}^{{\alpha ,1}}}, \ldots ,{{{\mathbf{w}}}^{{\alpha ,k}}},{{{\mathbf{w}}}^{{\beta ,k + 1}}}, \ldots ,{{{\mathbf{w}}}^{{\beta ,d}}}), \\ {{\operatorname{W} }_{{H + 2}}} = ({{{\mathbf{w}}}^{{\beta ,1}}}, \ldots ,{{{\mathbf{w}}}^{{\beta ,k}}},{{{\mathbf{w}}}^{{\alpha ,k + 1}}}, \ldots ,{{{\mathbf{w}}}^{{\alpha ,d}}}). \\ \end{gathered} $

Задача машинного обучения всегда связана с поиском неизвестной функции,

(41)

${\mathbf{y}} = {\mathbf{\alpha }}({\mathbf{x}},{\mathbf{q}}),$

где ${\mathbf{y}}$ – вектор значений функции, ${\mathbf{y}} \in \operatorname{Y} \subseteq {{\mathbb{R}}^{r}}$, ${\mathbf{x}}$ – вектор аргументов, ${\mathbf{x}} \in {{\mathbb{R}}^{n}}$, ${\mathbf{q}}$ – вектор постоянных параметров, ${\mathbf{q}} \in \operatorname{Q} \subseteq {{\mathbb{R}}^{p}}$, α(x, q) : ${{\mathbb{R}}^{n}} \times {{\mathbb{R}}^{p}} \to {{\mathbb{R}}^{r}}$, либо эта функция при обучении аппроксимирует некоторый набор данных, который называется обучающей выборкой,

(42)

$J = \sum\limits_{i = 1}^N {{\text{||}}{{{{\mathbf{\hat {y}}}}}^{i}} - {\mathbf{\alpha }}({{{\mathbf{x}}}^{i}},{\mathbf{q}}){\text{||}}} ,$

где $\hat {Y} = \{ {{{\mathbf{\hat {y}}}}^{1}}, \ldots ,{{{\mathbf{\hat {y}}}}^{N}}\} $ – обучающая выборка, либо она непосредственно используется для минимизации некоторого заданного функционала

(43)

$J = \int\limits_0^{{{t}_{f}}} {{{f}_{0}}({\mathbf{x}}(t),{\mathbf{\alpha }}({\mathbf{x}}(t),{\mathbf{q}}))dt} ,$

${{t}_{f}}$ – время достижения цели.

Особенность машинного обучения состоит в том, что при обучении не требуется точного достижения минимума критерия (42) или (43)

(44)

${{J}_{1}} \leqslant \min J + \Delta {\kern 1pt} *,$

где $\Delta {\kern 1pt} *$ – заданная положительная величина, которая определяет достижимое при обучении значение функционала.

Для критерия (42) минимальное значение равно нулю. Для критерия (43) оно может быть неизвестно, тогда вместо $\min J$ следует использовать предельное значение критерия ${{J}^{ - }}$

(45)

${{J}_{1}} \leqslant {{J}^{ - }} + \Delta {\kern 1pt} *,$

где ${{J}^{ - }} \leqslant \min J$.

Если в результате обучения найденная функция (41) должна приобрести некоторые свойства, то доказательство наличия этих свойств подтверждается моделированием

(46)

${{J}_{2}} = \sum\limits_{i = 1}^K {\vartheta (\varphi ({\mathbf{\alpha }}({{{\mathbf{x}}}^{i}},{\mathbf{q}})))} = 0,$

где $\vartheta (z)$ – функция Хэвисайда,

(47)

$\vartheta (z) = \left\{ {\begin{array}{*{20}{l}} {1,\quad {\text{если }}z > 0} \\ {0{\text{ }} - {\text{ иначе}}} \end{array}} \right.,$

$\varphi ({\mathbf{\alpha }}({\mathbf{x}},{\mathbf{q}}))$ – условие, которое определяет наличие свойства функции

(48)

$\varphi ({\mathbf{\alpha }}({\mathbf{x}},{\mathbf{q}})) \leqslant 0,$

$K$ – количество экспериментов с выполненным условием (48).

Переформулируем задачу синтеза управления так, чтобы при ее решении использовать машинное обучение методом символьной регрессии. Задана математическая модель объекта управления (1), ограничение на управление (2). Задано множество точек начальных состояний

(49)

${{\tilde {X}}_{0}} = \{ {{{\mathbf{x}}}^{{0,1}}}, \ldots ,{{{\mathbf{x}}}^{{0,K}}}\} .$

Задано терминальное состояние (4). Задан критерий качества управления

(50)

$\begin{gathered} {{J}_{3}} = \sum\limits_{i = 1}^K {\left( {{{p}_{1}}{\text{||}}{{{\mathbf{x}}}^{f}} - {\mathbf{x}}({{t}_{{f,i}}},{{{\mathbf{x}}}^{{0.i}}}){\text{||}} + \int\limits_0^{{{t}_{{f,i}}}} {{{f}_{0}}({\mathbf{x}},{\mathbf{u}})dt} } \right)} \to \\ \to \mathop {\min }\limits_{{\mathbf{u}} \in \operatorname{U} } , \\ \end{gathered} $

где ${{p}_{1}}$ – заданный весовой коэффициент,

(51)

${{t}_{{f,i}}} = \left\{ {\begin{array}{*{20}{l}} {t,\quad {\text{если }}t < {{t}^{ + }}\;\;{\text{и}}\;\;{\text{||}}{{{\mathbf{x}}}^{f}} - {\mathbf{x}}(t,{{{\mathbf{x}}}^{{0,i}}}){\text{||}} \leqslant \varepsilon } \\ {{{t}^{ + }},\quad {\text{иначе}}} \end{array}} \right.,$

${{t}^{ + }}$, $\varepsilon $ – заданные положительные величины. Необходимо найти управление в форме (30), чтобы минимизировать функционал (50) для любого количества $K$ начальных условий из заданной области (49). Постановка задачи включает функционал, который вместе с минимизацией заданного критерия (5) учитывает проверку свойства устойчивости терминального состояния. Решение задачи синтеза управления обеспечивает за счет свойства устойчивости терминального состояния свойство сжимающего отображения в окрестности этого терминального состояния.

Другим подходом к решению расширенной задачи оптимального управления является метод синтезированного управления [7]. Согласно этому методу, первоначально независимо от вида функционала (5) решается задача синтеза управления для обеспечения устойчивости относительно некоторой точки в пространстве состояний.

В задаче задана модель (1), множество точек начальных условий (49) в некоторой области (29) пространства состояний

(52)

${{\tilde {X}}_{0}} \subset {{\operatorname{X} }_{0}},$

задано терминальное состояние в той же области

(53)

${\mathbf{x}}{\kern 1pt} * \in {{\operatorname{X} }_{0}},\quad {\mathbf{x}}{\kern 1pt} * \notin {{\tilde {X}}_{0}},$

задан функционал качества

(54)

${{J}_{4}} = \sum\limits_{i = 1}^K {\left( {{{p}_{1}}{\text{||}}{{{\mathbf{x}}}^{f}} - {\mathbf{x}}({{t}_{{f,i}}},{{{\mathbf{x}}}^{{0.i}}}){\text{||}} + {{t}_{{f,i}}}} \right)} \to \mathop {\min }\limits_{{\mathbf{u}} \in \operatorname{U} } .$

Необходимо найти управление в форме

(55)

${\mathbf{u}} = {\mathbf{h}}({\mathbf{x}}{\kern 1pt} *\; - {\mathbf{x}}) \in \operatorname{U} ,$

чтобы минимизировать функционал (54).

На втором этапе рассматриваем модель замкнутой системы управления

(56)

${\mathbf{\dot {x}}} = {\mathbf{f}}({\mathbf{x}},{\mathbf{h}}({\mathbf{x}}{\kern 1pt} *\; - {\mathbf{x}})).$

Для этой системы решаем задачу оптимального управления с критерием качества (5).

(57)

${{J}_{5}} = \int\limits_0^{{{t}_{f}}} {{{f}_{0}}({\mathbf{x}},{\mathbf{h}}({\mathbf{x}}{\kern 1pt} * - {\mathbf{x}})} dt \to \mathop {\min }\limits_{{\mathbf{z}}{\kern 1pt} *} .$

В качестве управления используем вектор ${\mathbf{x}}{\kern 1pt} * = [\begin{array}{*{20}{c}} {x_{1}^{*}}& \ldots &{x_{n}^{*}{{]}^{T}}} \end{array}$, определяющий положение устойчивой точки равновесия в пространстве состояний с ограничением (55). В синтезированном управлении в окрестности оптимальной траектории всегда существует устойчивая точка равновесия, к которой стремится объект управления, поэтому траектория движения объекта всегда находится в области, где имеются свойства сжимающего отображения, т.е. выполняются требования расширенной задачи оптимального управления.

В качестве примера рассмотрим задачу оптимального управления группой из двух мобильных роботов с дифференциальном приводом [8]. Два одинаковых мобильных робота должны поменяться местами, не столкнувшись друг с другом в процессе движения за минимальное время. Математические модели роботов имеют следующий вид:

(58)

$\dot {x}_{1}^{j} = 0.5(u_{1}^{j} + u_{2}^{j})\cos (x_{3}^{j}),$

(59)

$\dot {x}_{2}^{j} = 0.5(u_{1}^{j} + u_{2}^{j})\sin (x_{3}^{j}),$

(60)

$\dot {x}_{3}^{j} = 0.5(u_{1}^{j} - u_{2}^{j}),$

(61)

$ - 10 = u_{i}^{ - } \leqslant u_{i}^{j} \leqslant u_{i}^{ + } = 10,\quad i = 1,2,$

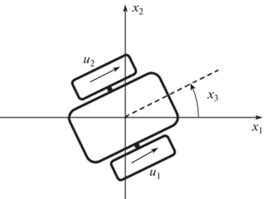
$j = 1,2.$

Схема мобильных роботов с дифференциальном приводом с указанием компонент вектора состояний приведена на рис. 1 [8].

Рис. 1.

Схема мобильного робота с дифференциальным приводом.

Для системы (58)–(61) заданы начальные условия

(62)

$\begin{gathered} {{{\mathbf{x}}}^{1}}(0) = {{{\mathbf{x}}}^{{1,0}}} = {{[\begin{array}{*{20}{c}} 0&0&0 \end{array}]}^{T}}, \\ {{{\mathbf{x}}}^{2}}(0) = {{{\mathbf{x}}}^{{2,0}}} = {{[\begin{array}{*{20}{c}} {10}&{10}&\pi \end{array}]}^{T}}. \\ \end{gathered} $

Заданы терминальные состояния

(63)

$\begin{gathered} {{{\mathbf{x}}}^{1}}({{t}_{f}}) = {{{\mathbf{x}}}^{{1,f}}} = {{[\begin{array}{*{20}{c}} {10}&{10}&0 \end{array}]}^{T}}, \\ {{{\mathbf{x}}}^{2}}({{t}_{f}}) = {{{\mathbf{x}}}^{{2,f}}} = {{[\begin{array}{*{20}{c}} 0&0&\pi \end{array}]}^{T}}, \\ \end{gathered} $

где ${{t}_{{j,f}}}$ – время достижения терминального состояния роботом j не задано, но ограничено и вычисляется из следующего соотношения

(64)

${{t}_{{j,f}}} = \left\{ {\begin{array}{*{20}{l}} {t{\text{,}}\quad {\text{если}}\;\;t < {{t}^{ + }}\;\;{\text{и}}\;\;{\text{||}}{{{\mathbf{x}}}^{{j,f}}} - {\mathbf{x}}(t){\text{||}} \leqslant {{\varepsilon }_{0}}} \\ {{{t}^{ + }}{\text{ }} - {\text{ иначе}}} \end{array}} \right.,$

${{t}^{ + }} = 2.8$, ${{\varepsilon }_{0}} = 0.01$, $j = 1,2$.

Задан критерий качества

${{J}_{6}} = {{p}_{1}}\sum\limits_{j = 1}^2 {{\text{||}}{{{\mathbf{x}}}^{{j,f}}} - {{{\mathbf{x}}}^{j}}({{t}_{{j,f}}}){\text{||}}} + {{t}_{f}} + $

(65)

$ + \;{{p}_{2}}\sum\limits_{j = 1}^2 {\int\limits_0^{{{t}_{f}}} {\sum\limits_{i = 1}^2 {\vartheta ({{\varphi }_{i}}({{{\mathbf{x}}}^{j}}))} dt} } + $

$ + \;{{p}_{3}}\int\limits_0^{{{t}_{f}}} {\theta (\chi ({{x}^{1}},{{x}^{2}}))dt} \to \mathop {\min }\limits_{{{{\mathbf{u}}}^{1}},{{{\mathbf{u}}}^{2}} \in \operatorname{U} } ,$

где ${{p}_{1}} = 1$, ${{p}_{2}} = 3$, ${{p}_{3}} = 3$, ${{t}_{f}} = \max \{ {{t}_{{1,f}}},{{t}_{{2,f}}}\} $,

(66)

${{\varphi }_{i}}({{{\mathbf{x}}}^{j}}) = {{r}_{i}} - \sqrt {{{{(x_{1}^{j} - {{x}_{{1,i}}})}}^{2}} + {{{(x_{2}^{j} - {{x}_{{2,i}}})}}^{2}}} ,\quad i = 1,2,$

${{r}_{1}} = 1$, ${{r}_{2}} = 1$, ${{x}_{{1,1}}} = 1$, ${{x}_{{1,2}}} = 2.5$, ${{x}_{{2,1}}} = 4$, ${{x}_{{2,2}}} = 2.5$, $j = 1,2$,

(67)

$\chi ({{{\mathbf{x}}}^{1}},{{{\mathbf{x}}}^{2}}) = {{r}_{0}} - \sqrt {{{{(x_{1}^{1} - x_{1}^{2})}}^{2}} + {{{(x_{2}^{1} - x_{2}^{2})}}^{2}}} ,$

${{r}_{0}} = 1$.

Первоначально была решена задача оптимального управления в классической постановке. Для решения задачи был использован прямой подход, в котором функция управления была аппроксимирована кусочно-линейной функцией времени

(68)

$u_{i}^{j} = \left\{ {\begin{array}{*{20}{l}} {u_{i}^{ + }{\text{,}}\quad {\text{если}}\;\;\tilde {u}_{i}^{j} \geqslant u_{i}^{ + }} \\ {u_{i}^{ - }{\text{,}}\quad {\text{если}}\;\;\tilde {u}_{i}^{j} \leqslant u_{i}^{ - }} \\ {\tilde {u}_{i}^{j}{\text{ }} - {\text{ иначе}}} \end{array}} \right.,\quad i = 1,2,\quad j = 1,2,$

где

(69)

$\begin{gathered} \tilde {u}_{i}^{j} = ({{q}_{{k + 1 + M(i - 1) + (j - 1)2(M + 1)}}} - {{q}_{{k + M(i - 1) + (j - 1)2(M + 1)}}}) \times \\ \, \times \frac{{t - k\Delta t}}{{\Delta t}} + {{q}_{{k + M(i - 1) + (j - 1)2(M + 1)}}}, \\ \end{gathered} $

$i = 1,2$, $j = 1,2$, $k = 1, \ldots ,M + 1$, $M$ – количество интервалов, $\Delta t$ – временной интервал, $\Delta t = 0.2$, M = $\left\lfloor {{{t}^{ + }}{\text{/}}\Delta t} \right\rfloor $ = $\left\lfloor {2.8{\text{/}}0.2} \right\rfloor $ = 14.

В каждом интервале необходимо найти по два значения на границах интервала для каждого управления. Итого необходимо найти (2 + 2) × (14 + + 1) = 4 × 15 = 60 значений параметров, q = = ${{[\begin{array}{*{20}{c}} {{{q}_{1}}}& \ldots &{{{q}_{{60}}}} \end{array}]}^{T}}$. Многочисленные исследования по сравнению градиентных алгоритмов с эволюционными для решения сложных задач оптимального управления с фазовыми оганичениями показали преимущество последних [9], так как фазовые ограничения рассматриваемого типа приводят к неунимодальности функционала. Для поиска решения был использован эволюционный гибридный алгоритм [10]. В результате были получены кусочно-линейные аппроксимации функций управления для каждого робота, определяемые значением вектора параметров. Найденное значение вектора параметров приведено в Приложении 1.

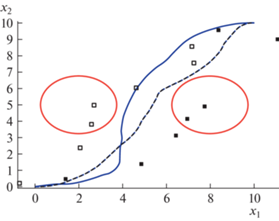
На рис. 2 представлены оптимальные траектории движения роботов на горизонтальной плоскости. На рисунке сплошная линия – траектория первого робота, пунктирная линия –траектория второго робота. Красные окружности обозначают фазовые ограничения. Как видно из рис. 2, оба робота достигают терминального состояния и не нарушают фазовых ограничений. Значение функционала (65) для найденного оптимального решения составило величину ${{J}_{6}} = 2.8101$.

Рис. 2.

Оптимальные траектории движения роботов по горизонтальной плоскости.

Далее данная задача была решена методом синтезированного управления. Первоначально решена задача синтеза управления для каждого объекта с целью обеспечения устойчивости относительно точки в пространстве состояний. Для этой цели сформируем множество из 27 начальных состояний

(70)

$\begin{gathered} {{{\hat {X}}}_{0}} = \{ {{{\mathbf{x}}}^{{0,i + (j - 1)3 + (k - 1)9}}} = \\ \, = {{[\begin{array}{*{20}{c}} {{{d}_{1}} + (i - 1){{\Delta }_{1}}}&{{{d}_{2}} + (j - 1){{\Delta }_{2}}}&{{{d}_{3}} + (k - 1){{\Delta }_{3}}} \end{array}]}^{T}}, \\ \end{gathered} $

где ${{d}_{1}} = - 2.5$, ${{d}_{2}} = - 2.5$, ${{d}_{3}} = - 5\pi {\text{/}}12$, ${{\Delta }_{1}} = 2.5$, ${{\Delta }_{2}} = 2.5$, ${{\Delta }_{3}} = 5\pi {\text{/}}12$, $i,j,k = 1,2,3$.

Задаем одно терминальное состояние

(71)

${\mathbf{x}}* = {{[\begin{array}{*{20}{c}} 0&0&0 \end{array}]}^{T}}.$

Необходимо найти функцию управления вида (55), обеспечивающую минимум следующего критерия

(72)

${{J}_{7}} = \sum\limits_{i = 1}^3 {\sum\limits_{j = 1}^3 {\sum\limits_{k = 1}^3 {\left( {{{p}_{1}}{\text{||}}{\mathbf{x}}{\kern 1pt} *\; - {\mathbf{x}}({{t}_{{f,r}}}){\text{||}} + {{t}_{{f,r}}}} \right)} } } \to \mathop {\min }\limits_{{\mathbf{u}} \in \operatorname{U} } ,$

где ${{t}_{{f,r}}}$ – время достижения терминального состояния (71) определяется из соотношения (51) с ${{t}^{ + }} = 2$, ${{\varepsilon }_{0}} = 0.01$, $r = i + (j - 1)3$ + $(k - 1)9$, $i,j,k = 1,2,3$.

Для решения задачи использован метод сетевого оператора [5], который нашел следующую функцию управления:

(73)

${{u}_{i}} = \left\{ {\begin{array}{*{20}{l}} {u_{i}^{ + }{\text{,}}\quad {\text{если}}\;\;{{{\hat {u}}}_{i}} \geqslant u_{i}^{ + }} \\ {u_{i}^{ - }{\text{,}}\quad {\text{если}}\;\;{{{\hat {u}}}_{i}} \leqslant u_{i}^{ - }} \\ {{{{\hat {u}}}_{i}}{\text{ }} - {\text{ иначе}}} \end{array}} \right.,\quad i = 1,2,$

где

(74)

$\begin{gathered} {{{\hat {u}}}_{1}} = {{A}^{{ - 1}}} + \sqrt[3]{A} + \operatorname{sgn} ({{q}_{3}}(x_{3}^{*} - {{x}_{3}})) \times \\ \, \times \exp ( - {\text{|}}{{q}_{3}}(x_{3}^{*} - {{x}_{3}}){\text{|}}) + \operatorname{sgn} (x_{3}^{*} - {{x}_{3}}) + \mu (B), \\ \end{gathered} $

(75)

${{\hat {u}}_{2}} = {{\hat {u}}_{1}} + \sin ({{\hat {u}}_{1}}) + \arctan (H) + \mu (B) + C - {{C}^{3}},$

$A = \tanh (D) + {{\left( {B + \sqrt[3]{{x_{1}^{*} - {{x}_{1}}}}} \right)}^{3}} + $

$ + \;C + \sin ({{q}_{3}}(x_{3}^{*} - {{x}_{3}})),$

$B = \operatorname{sgn} (\operatorname{sgn} (x_{1}^{*} - {{x}_{1}}){{q}_{2}}(x_{2}^{*} - {{x}_{2}})) \times $

$ \times \;\exp ( - {\text{|}}\operatorname{sgn} (x_{1}^{*} - {{x}_{1}}){{q}_{2}}(x_{2}^{*} - {{x}_{2}}){\text{|}}) + $

$ + \;G + \sin (x_{1}^{*} - {{x}_{1}}) + \tanh (G) + x_{1}^{*} - {{x}_{1}},$

$C = \operatorname{sgn} (\operatorname{sgn} (x_{1}^{*} - {{x}_{1}}){{q}_{2}}(x_{2}^{*} - {{x}_{2}})) \times $

$ \times \;\exp ( - {\text{|}}\operatorname{sgn} (x_{1}^{*} - {{x}_{1}}){{q}_{2}}(x_{2}^{*} - {{x}_{2}}){\text{|}}) + $

$ + \;\sin (x_{1}^{*} - {{x}_{1}}),$

$D = H + C - {{C}^{3}} + \operatorname{sgn} ({{q}_{1}}(x_{1}^{*} - {{x}_{1}})) + $

$\, + \arctan ({{q}_{1}}) + \vartheta (x_{3}^{*} - {{x}_{3}}),$

$G = \operatorname{sgn} (x_{1}^{*} - {{x}_{1}}){{q}_{2}}(x_{2}^{*} - {{x}_{2}}) + $

$ + \;{{q}_{3}}(x_{3}^{*} - {{x}_{3}}) + \tanh ({{q}_{1}}(x_{1}^{*} - {{x}_{1}})),$

$H = \arctan ({{q}_{1}}(x_{1}^{*} - {{x}_{1}})) + \operatorname{sgn} (W)\sqrt {{\text{|}}W{\text{|}}} + $

$ + \;W + V + 2\operatorname{sgn} (W + \tanh (V)) + $

$ + \;\sqrt[3]{{W + \tanh (V) + \sqrt[3]{{x_{1}^{*} - {{x}_{1}}}}}} + $

$ + \;\operatorname{sgn} (x_{1}^{*} - {{x}_{1}})\sqrt {{\text{|}}x_{1}^{*} - {{x}_{1}}{\text{|}}} + \sqrt[3]{{x_{1}^{*} - {{x}_{1}}}} + \tanh (V),$

$W = \operatorname{sgn} (x_{1}^{*} - {{x}_{1}}) + \operatorname{sgn} ({{q}_{2}}(x_{2}^{*} - {{x}_{2}})) \times $

$ \times \;\operatorname{sgn} (x_{1}^{*} - {{x}_{1}})\tanh (x_{1}^{*} - {{x}_{1}}),$

$V = {{q}_{3}}(x_{3}^{*} - {{x}_{3}}) + \operatorname{sgn} (x_{1}^{*} - {{x}_{1}}){{q}_{2}}(x_{2}^{*} - {{x}_{2}}) + $

$ + \;\tanh (x_{1}^{*} - {{x}_{1}}),$

$\mu (\alpha ) = \operatorname{sgn} (\alpha )\min \{ 1,{\text{|}}\alpha {\text{|}}\} ,\quad \tanh (\alpha ) = \frac{{1 - \exp ( - 2\alpha )}}{{1 + \exp ( - 2\alpha )}},$

${{q}_{1}} = 14.7288$, ${{q}_{2}} = 2.0271$, ${{q}_{3}} = 4.0222$.

На втором этапе решаем задачу оптимального управления, в которой необходимо найти кусочно-постоянную функцию времени

(76)

$x_{i}^{{j,*,k}} = {{q}_{{i + (k - 1)3 + (k - 1)M}}},\quad (k - 1)\Delta t \leqslant t < k\Delta t,$

где $j = 1,2$, $i = 1,2,3$, $k = 1, \ldots ,M$, $M$ – число интервалов времени, $\Delta t = 0.4$, M = $\left\lfloor {{{t}^{ + }}{\text{/}}\Delta t} \right\rfloor $ = = $\left\lfloor {2.8{\text{/}}0.4} \right\rfloor $ = 7. Всего необходимо найти вектор из $6 \times 7 = 42$ параметров для оптимизации функционала

${{J}_{8}} = {{p}_{1}}\sum\limits_{j = 1}^2 {{\text{||}}{{{\mathbf{x}}}^{{j,f}}} - {{{\mathbf{x}}}^{j}}({{t}_{{j,f}}}){\text{||}}} + {{t}_{f}} + $

(77)

$ + \;{{p}_{2}}\sum\limits_{j = 1}^2 {\int\limits_0^{{{t}_{f}}} {\sum\limits_{i = 1}^2 {\vartheta ({{\varphi }_{i}}({{{\mathbf{x}}}^{j}}))} dt} } + $

$ + \;{{p}_{3}}\int\limits_0^{{{t}_{f}}} {\theta (\chi ({{x}^{1}},{{x}^{2}}))dt} \to \mathop {\min }\limits_{{{{\mathbf{x}}}^{{1,*}}},{{{\mathbf{x}}}^{{2,*}}}} .$

Для решения задачи был использован тот же гибридный эволюционный алгоритм [10].

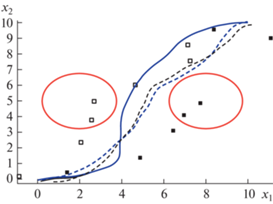
На рис. 3 приведены оптимальные траектории движения мобильных роботов на плоскости для найденного оптимального управления. Значение функционала для полученного решения равно ${{J}_{8}} = 2.9283$. Значения найденных оптимальных параметров приведены в приложении 2. На рис. 3 в виде малых квадратов приведены проекции на плоскость $\{ {{x}_{1}},{{x}_{2}}\} $ найденных оптимальных значений векторов управлений, черные квадраты – проекции точек стабилизации первого робота ${{{\mathbf{x}}}^{{1,*,k}}}$ = ${{[\begin{array}{*{20}{c}} {x_{1}^{{1,*,k}}}&{x_{2}^{{1,*,k}}}&{x_{3}^{{1,*,k}}} \end{array}]}^{T}}$, белые квадраты – проекции точек стабилизации второго робота ${{{\mathbf{x}}}^{{2,*,k}}}$ = ${{[\begin{array}{*{20}{c}} {x_{1}^{{2,*,k}}}&{x_{2}^{{2,*,k}}}&{x_{3}^{{2,*,k}}} \end{array}]}^{T}}$, $k = 1, \ldots ,7$.

Рис. 3.

Оптимальные траектории для синтезированного управления.

Для сравнения полученных результатов начальные состояния объектов управления были подвергнуты случайным возмущениям. Во всех испытаниях траектории, полученные синтезированным управлением, сохраняли характер движения. Значение функционала при возмущениях синтезированного управления не сильно отличалось от оптимального. Те же возмущения при прямом управлении существенно меняли характер движения и увеличивали значение функционала.

На рис. 4 и 5 приведены возмущенные траектории движения для прямого и синтезированного управлений для одних и тех же начальных условий

${{{\mathbf{x}}}^{{0,1}}} = {{[\begin{array}{*{20}{c}} {0.15}&{ - 0.1}&{0.15} \end{array}]}^{T}},\quad {{{\mathbf{x}}}^{{0,2}}} = {{[\begin{array}{*{20}{c}} {10.2}&{9.88}&{3.3} \end{array}]}^{T}}.$

Рис. 4.

Возмущенные и оптимальные траектории для прямого управления.

Рис. 5.

Возмущенные и оптимальные траектории для синтезированного управления.

На рис. 4, 5 приведены синим цветом для сравнения также оптимальные невозмущенные траектории. Как видно из результатов эксперимента, возмущенные траектории прямого управления имеют существенную ошибку достижения терминальных состояний. Значение функционала для возмущенного решения для прямого управления составило ${{J}_{6}} = 7.625$, т.е. увеличилось более, чем на 170%. Возмущенные траектории для синтезированного управления незначительно отличаются от оптимальных. Для первого робота возмущенная и оптимальная траектории практически совпали. Значение функционала для возмущенного решения для синтезированного управления составило ${{J}_{8}} = 4.11$, т.е. увеличилось на 40%, по-видимому, из-за нарушений динамических фазовых ограничений (67).

В результате решения расширенной задачи оптимального управления была найдена функция управления в форме (16), которая является кусочно-постоянной функцией времени и зависит от координат вектора пространства состояний. Найденная функция управления на каждом определенном временном интервале обеспечивает для модели замкнутой системы управления наличие устойчивой точки равновесия в пространстве состояний, что приводит к выполнению условий (20), (21), наличию окрестности у оптимального решения со свойствами сжимающего отображения. Экспериментально подтверждено, что найденное решение расширенной задачи оптимального управления существенно менее чувствительно к возмущениям модели, чем прямое решение классической задачи оптимального управления.

Список литературы

Понтрягин Л.С., Болтянский В.Г., Гамкрелидзе Р.В., Мищенко Е.Ф. Математическая теория оптимальных процессов. М. Наука. Главное издание физико-математической литературы. 1983. 392 с.

Болтянский В.Г. Математические методы оптимального управления. М.: Наука. Главное издание физико-математической литературы. 1969. 408 с.

Халил Х.К. Нелинейные системы. Ижевск.: Институт компьютерных исследований, 2009. 814 с.

Колесников А.А. Синергетические методы управления сложными системами. Теория системного анализа. М.: Книжный дом “ЛИБРОКОМ” 2012. 237 с.

Diveev A.I., Shmalko E.Yu. Machine learning Control by Symbolic Regression. Cham, Switzerland, Springer, 2021. 155 p. https://link.springer.com/book/10.1007/ 978-3-030-83213-1

Diveev A.I., Sofronova E.A. Universal Approach to Solution of Optimization Problems by Symbolic Regression// Applied Science. 2021. V. 11. P. 5081.

Diveev A., Shmalko E.Yu., Serebrenny V. Zentay P. Fundamentals of Synthesized Optimal Control // Mathematics. 2021. V. 9. P. 21.

Dhaouadi R., Abu Hatab A. Dynamic Modelling of Differential-Drive Mobile Robots using Lagrange and Newton-Euler Methodologies: A Unified Framework // Advances in Robotics A & Automation. 2013. V. 2. Issue 2. P. 1–7.

Дивеев А.И., Константинов С.В. Исследование практической сходимости эволюционных алгоритмов оптимального программного управления колесным роботом // Известия РАН. Теория и системы управления. 2018.Т. 57. № 4. С. 80–106.

Дивеев А.И. Гибридный эволюционный алгоритм для решения задачи оптимального управления// Вопросы теории безопасности и устойчивости систем. 2021. № 23. С. 3–12.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Доклады Российской академии наук. Математика, информатика, процессы управления

Архивы выпусков Информация о журнале Отправить рукопись в журнал