1. На главную
  2. Электронные версии
  3. Доклады Российской академии наук. Математика, информатика, процессы управления
  4. T. 509, № 1, 2023

Доклады Российской академии наук. Математика, информатика, процессы управления, 2023, T. 509, № 1, стр. 101-105

Математическое моделирование плавления вольфрама при воздействии лазерного импульса

Член-корреспондент РАН Г. Г. Лазарева 1, *, А. С. Аракчеев 2, **, В. А. Попов 2, ***

1 Российский университет дружбы народов
Москва, Россия

2 Федеральное государственное бюджетное учреждение науки Институт ядерной физики им. Г.И. Будкера Сибирского отделения Российской академии наук
Новосибирск, Россия

* E-mail: lazarevanovosibirsk@gmail.com
** E-mail: asarakcheev@gmail.com
*** E-mail: v.a.popov94@gmail.com

Поступила в редакцию 04.09.2022
После доработки 24.10.2022
Принята к публикации 26.12.2022

Полный текст (PDF)

Аннотация

Работа посвящена математическому моделированию процесса плавления в образце под воздействием импульсной тепловой нагрузки на основе решения двухфазной задачи Стефана. Численная модель основана на подходе Самарского, что позволяет не выделять свободную границу во время расчета. Учет аксиально-симметричной геометрии позволил показать, что на испарение расходуется около четверти падающей энергии в центре области расплава. Это в пять раз больше, чем дают оценки, основанные на решении одномерного уравнения теплопроводности. В случае учета испарения вещества получено хорошее соответствие расчетных и экспериментальных температуры остывающей поверхности и скорости сужения области расплава. Результаты математического моделирования подтвердили существование режима охлаждения испарением при нагреве вольфрама электронным пучком существенно выше порога плавления.

Ключевые слова: математическое моделирование, испарение вольфрама, задача Стефана

1. ВВЕДЕНИЕ

Современные системы магнитного удержания плазмы предполагают наличие контакта периферийной плазмы со стенкой. При этом в термоядерной плазме потоки мощности на поверхность оказываются достаточно велики [1], чтобы существенно влиять на материалы стенки. В случае же развития плазменных неустойчивостей находящиеся в контакте поверхности могут принимать значительную долю энергии удерживаемой плазмы, на несколько порядков превосходящую потоки энергии в стационарном режиме [2]. Это может приводить к разрушению первой стенки. При достаточном нагреве вольфрам разогревается до температуры вязко-хрупкого перехода и начинает деформироваться необратимо. При дальнейшем увеличении потока тепла вольфрам начинает очищаться от оксидов и захваченных газов. Известно, что при температуре плавления начинается быстрый рост интенсивности испарения. Наблюдается движение расплава вдоль поверхности под воздействием силы Ампера на токи, текущие сквозь расплав.

Существует три распространенных способа эмуляции теплового потока предполагаемого термоядерного реактора: лазером [3], плазмой [4] и электронным пучком [5]. Они не в полной мере соответствуют тем воздействиям, что будут происходить в термоядерных реакторах. Важно описание воздействия различных источников для их сравнения и понимания границ применимости обобщений экспериментальных результатов. Исследования вольфрама, как обращенного к плазме материала, проводятся в Курчатовском институте, МИФИ, МГУ, ФТИ им. А.Ф. Иоффе, Проектном центре ИТЭР, ГНЦ РФ ТРИНИТИ и др. Исследования, проводимые в ИЯФ СО РАН, сосредоточены на изучении эрозии поверхности вольфрамового образца при воздействии лазерного импульса или электронного пучка. Эксперименты проводятся на стенде Beam of Electrons for materials Test Applications (BETA), созданном в ИЯФ СО РАН [6]. Испарение вещества является одним из важнейших процессов, влияющих на импульсный тепловой нагрев выше температуры плавления, который ожидается в случае развития неустойчивостей плазмы на будущих термоядерных установках.

Модель нагрева и плавления вольфрама основана на решении в области образца двухфазной задачи Стефана для расчета температуры. Задача Стефана является классической задачей вычислительной математики, которая актуальна и сегодня [7]. Положение и скорость движения границы раздела фаз зависят от нелинейных коэффициентов. Условие на свободной границе расплав – твердое тело состоит в непрерывности температуры и разрывности теплового потока за счет поглощения или выделения известного количества тепла. Новизна и сложность решения задачи обусловлены необходимостью верного описания нелинейных граничных условий, описывающие нагрев и испарение материала на его поверхности.

2. ПОСТАНОВКА ЗАДАЧИ

В вакууме расположена пластинка вольфрама, которая нагревается мощным лазерным импульсом (рис. 1). Поскольку за такое короткое время образец нагревается на глубину нескольких сотен микрон, область моделирования представляла собой поперечное сечение образца 2 × 3 мм. Плотность мощности W(t, r) на нагреваемой поверхности по радиусу r имеет распределение, близкое к нормальному, что определяет выбор аксиально-симметричной постановки задачи:

(1)
$W(t,r)\, = \,{{W}_{{\max }}}(t) \cdot {\text{exp}}( - A \cdot {{r}^{2}}),\quad A\, = \,0.03088523.$
Рис. 1.

Схема эксперимента. Расчетная область в поперечном сечении образца (зеленый), область нагрева (желтый) и расплава (красный) со свободной границей Г, лазерный импульс (голубой).

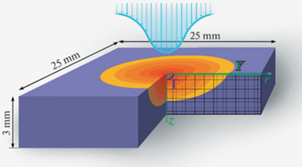
На каждом временном шаге численного моделирования ${{W}_{{\max }}}(t)$ берется из файла экспериментальных данных. Распределение плотности мощности нагрева по поверхности измерены с помощью рентгеновской визуализации [8]. Электроны с энергией 80–90 кэВ нагревают материал в тонком слое по сравнению с характерной глубиной нагрева материала. Для расчета поля температур в образце используется задача Стефана:

(2)
$\left\{ \begin{gathered} c\left( T \right)\rho \left( T \right)\frac{{\partial T}}{{\partial t}} = \frac{1}{r}\frac{\partial }{{\partial r}}r\lambda \left( T \right)\frac{{\partial T}}{{\partial r}} + \frac{\partial }{{\partial z}}\lambda \left( T \right)\frac{{\partial T}}{{\partial z}}, \hfill \\ {{\left. {\left( {n,\nabla T} \right)} \right|}_{\gamma }} = \frac{{W(t,r) - N(T)}}{{\lambda (T)}},\quad {{\left. {\left( {n,\nabla T} \right)} \right|}_{{\Omega - \gamma }}} = 0, \hfill \\ {{\left. {\left[ T \right]} \right|}_{\Gamma }} = 0,\quad {{\left. {\left[ {\lambda (T)\frac{{\partial T}}{{\partial t}}} \right]} \right|}_{\Gamma }} = {{L}_{m}}{{v}_{n}},\quad {{\left. T \right|}_{{t = 0}}} = {{T}_{0}}, \hfill \\ \end{gathered} \right.$
где $\Omega $ – вся поверхность образца, $\gamma $ – нагреваемая поверхность, $\Gamma $ – свободная поверхность раздела сред расплав-металл, $T(t,r,z)$ – температура, $c(T)$ – удельная теплоемкость, $\rho (T)$ – плотность, $\lambda (T)$ – теплопроводность, $W(t,r)$ – плотность мощности на поверхности $\gamma $, $N(T)$ – мощность испарения, $n$ – нормаль к поверхности, ${{T}_{0}}$ температура в начальный момент времени, ${{{v}}_{n}}$ – скорость границы фазового перехода. Во время нагревания вольфрам начинает испаряться, вследствие чего происходит уменьшение потока тепла на поверхность. Процесс испарения на границе учитывается с помощью заданного результирующего потока энергии ${{W}_{*}}(t,r)$ = $W\left( {t,r} \right)$ – $N\left( {{{{\left. T \right|}}_{\gamma }}} \right)$. Здесь плотность мощности $W(t,r)$ задается распределением (1), мощность испарения $N\left( {{{{\left. T \right|}}_{\gamma }}} \right)$ задается через потерю мощности ${{L}_{e}}$ с массовой скоростью испарения $\frac{1}{S}\frac{{dm}}{{dt}}$:

(3)
$N\left( {{{{\left. T \right|}}_{\gamma }}} \right) = {{L}_{e}} \cdot \frac{1}{S}\frac{{dm}}{{dt}},\quad \frac{1}{S}\frac{{dm}}{{dt}} = P\left( {{{{\left. T \right|}}_{\gamma }}} \right){\text{ }}\sqrt {\frac{M}{{2\pi R{{{\left. T \right|}}_{\gamma }}}}} .$

Здесь ${{L}_{e}} = 4.482 \times {{10}^{{12}}}$ , давление насыщенного пара:

$P\left( {{{{\left. T \right|}}_{\gamma }}} \right) = \exp \left( {26.19104{\text{ }} - \frac{{{\text{ }}83971.3\;{\text{K}}}}{{{{{\left. T \right|}}_{\gamma }}}}{\text{ }}} \right)\;\frac{{{\text{kg}}}}{{{\text{m}}{{{\text{m}}}^{2}}\;\mu {\text{s}}}}.$

Таким образом, потери мощности на испарение (рис. 2а), а значит и результирующий поток энергии на нагреваемой поверхности, можно определить через ее температуру. Потерю материала за счет испарения модель не учитывает. Время расчета определяется моментом, когда было произведено последнее измерение температуры поверхности.

Рис. 2.

Графики зависимости от температуры потери мощности на испарение (а), теплопроводности (б), удельной теплоемкости (в) и плотности (г).

3. МЕТОД РЕШЕНИЯ

Для учета процесса плавления в уравнение температуры была введена энтальпия фазового перехода ${{L}_{m}}$:

(5)
$\begin{gathered} \left( {c(T)\rho (T) + {{L}_{m}}\delta \left( {T,\varepsilon } \right)} \right)\frac{{\partial T}}{{\partial t}} = \operatorname{div} \left( {\lambda (T)\operatorname{grad} T} \right), \\ \delta \left( {T,\varepsilon } \right) = \left\{ \begin{gathered} \frac{1}{{2\varepsilon }},\quad \left| {T - {{T}_{m}}} \right| \leqslant \varepsilon , \hfill \\ 0,\quad \left| {T - {{T}_{m}}} \right| > \varepsilon , \hfill \\ \end{gathered} \right. \\ \end{gathered} $
где интервал сглаживания [−ε ε ], ε = 5 K, температура плавления Tm = 3695 K, энтальпия фазового перехода ${{L}_{m}} = 51.1 \times {{10}^{5}}$ $\frac{{{\text{W}}\;\mu {\text{s}}}}{{{\text{m}}{{{\text{m}}}^{{\text{3}}}}}}$. Вывод (5) и обоснование пренебрежения поверхностным температурным излучением в энергетическом балансе более подробно представлены в работе [9]. Численная реализация уравнения (5) основана на схеме стабилизирующей поправки [10].

Как показывают экспериментальные данные и аналитические оценки, разогрев поверхности не превышает 8000 K в исследуемых на BETA режимах. Это обусловлено экспоненциальным ростом потерь энергии на испарение с ростом температуры поверхности. Потери мощности, теплопроводность [11], удельная теплоемкость [11] и плотность (рис. 2) используются в виде зависимостей от температуры материала. Эти функции имеют разрывы производных при температуре плавления Tm. Оценки теплопроводности $\lambda (T)$ жидкого вольфрама взяты из [12, 13], при этом уточнена аппроксимация данных (рис. 2 б), что позволило проводить расчеты при значениях температуры более 6000 К.

4. РЕЗУЛЬТАТЫ МОДЕЛИРОВАНИЯ

Расчеты показали, что модель нагрева образца достаточно точно отражает характер решения (рис. 3а) с учетом особенностей диагностики. Учет охлаждения поверхности за счет испарения при достаточно высокой плотности мощности нагрева значительно уменьшает температуру, до которой нагревается материал. Энергия при этом уходит из вольфрама вместе с испаряющимся материалом. Как было показано в работе [14], потеря энергии S на испарение в центре пластинки составляет около 26% энергии импульсного нагрева:

(6)
${{S = \int\limits_0^\infty {\int\limits_0^\infty {N\left( {{{{\left. T \right|}}_{\gamma }}} \right)rdtdr} } } \mathord{\left/ {\vphantom {{S = \int\limits_0^\infty {\int\limits_0^\infty {N\left( {{{{\left. T \right|}}_{\gamma }}} \right)rdtdr} } } {\int\limits_0^\infty {\int\limits_0^\infty {W(t,r)rdtdr} } }}} \right. \kern-0em} {\int\limits_0^\infty {\int\limits_0^\infty {W(t,r)rdtdr} } }}.$
Рис. 3.

Распределение температуры на поверхности (а): расчет (красная линия) и экспериментальные данные (черная линия), температура плавления (черная черта), область, соответствующая расплаву (заштриховано красным). Зависимость радиуса расплавленной области от времени (б): экспериментальные данные (черные отрезки), результат расчета без учета испарения (красная линия), результат расчета с учетом охлаждения за счет испарения (синяя линия).

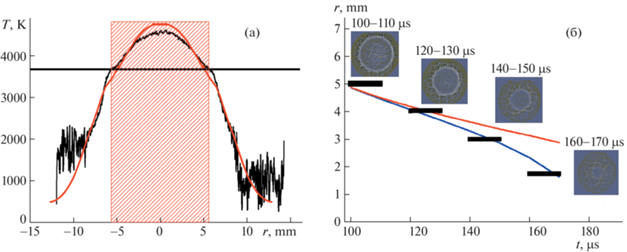
На установке BETA после импульсного нагрева во время остывания были сделаны последовательно четыре фотографии поверхности образца [6, 15]. Измерены значения радиуса расплавленной области в моменты времени, соответствующие времени экспозиции камеры от начала нагрева электронным пучком с длительностью выдержки 10 мкс. Результаты расчета совпадают с экспериментальными данными (рис. 3 б) в начале охлаждения, но на поздних стадиях остывания численный расчет давал радиус расплавленной области значительно больше наблюдаемого. Более того, в этом случае расчетная температура в центре нагреваемой области дает по формуле (3) невозможно большие значения потери мощности $N\left( {{{{\left. T \right|}}_{\gamma }}} \right)$, которые больше поверхностной плотности мощности нагрева $W(t,r)$. После того, как в численное моделирование был добавлен учет остывания поверхности за счет испарения, температура перестала превышать предельно допустимую, и рассчитанная зависимость радиуса расплавленной области совпала с экспериментальными данными.

5. ВЫВОДЫ

Математическое моделирование процесса плавления в образце под воздействием импульсной тепловой нагрузки подтвердило существование режима охлаждения испарением при нагреве вольфрама электронным пучком существенно выше порога плавления. Этот режим характеризуется тем, что мощность испарения становится сравнимой с поступающей мощностью, но толщина испаренного материала недостаточна для парового экранирования, в результате чего температура поверхности стабилизируется. Численное решение двухфазной задачи Стефана в аксиально-симметричной постановке показало, что на испарение расходуется около четверти падающей энергии в центре области расплава. Проведено сравнение расчетных и экспериментальных данных: температуры поверхности и радиуса области расплава. Получено хорошее соответствие в случае учета испарения вещества. Дальнейшее развитие модели предполагает решение уравнения для термотоков, определение граничных условий для паров вольфрама с использованием молекулярных моделей, и в итоге решение системы уравнений газовой динамики в самосогласованном электрическом поле. Это позволит описать движение расплава под воздействием термотоков, процесс ионизации паров, конденсацию газа в капли, а так же неустойчивости, при которых жидкость будет срываться с поверхности.

Список литературы

  1. Carpentier-Chouchana S., Hirai T., Escourbiac F., Durocher A., Fedosov A., Ferrand L., Firdaouss M., Kocan M., Kukushkin A.S., Jokinen T., Komarov V., Lehnen M., Merola M., Mitteau R., Pitts R.A., Stangeby P.C., Sugihara M., “Status of the ITER full-tungsten divertor shaping and heat load distribution analysis” Physica Scripta, T. 159, 014002, 2014.

  2. Shi Y., Miloshevsky G., Hassanein A., “Boiling induced macroscopic erosion of plasma facing components in fusion” Fusion Engineering and Design, Т. 86(2–3), p. 155–162, 2011.

  3. Huber A., Arakcheev A., Sergienko G., Steudel I., Wirtz M., Burdakov A.V., Coenen J.W., Kreter A., Linke J., Mertens Ph., Philipps V., Pintsuk G., Reinhart M., Samm U., Shoshin A., Schweer B., Unterberg B., Zlobinski M., “Investigation of the impact of transient heat loads applied by laser irradiation on ITER-grade tungsten” Physica Scripta, T. 159, 014005, 2014.

  4. Safronov V.M., Arkhipov N.I., Klimov N.S., Landman I.S., Petrov D.S., Podkovyrov V.L., Poznyak I.M., Toporkov D.A., Zhitlukhin A.M. , “Investigation of erosion mechanisms and erosion products in tungsten targets exposed to plasma heat loads relevant to ELMS and mitigated disruptions in ITER” Problems of Atomic Science and Technology. Series: Plasma Physics (14), pp. 52–54, 2008.

  5. Huber A., Burdakov A., Zlobinski M., Wirtz M., Coenen J. W., Linke J.,. Mertens Ph, Philipps V., Pintsuk G., Schweer B., Sergienko G., Shoshin A., Samm U., Unterberg B., “Investigation of the impact on tungsten of transient heat loads induced by laser irradiation, electron beams and plasma guns” Fusion Science and Technology, 63 (1T), pp. 197–200, 2013.

  6. Vyacheslavov L., Arakcheev A., Burdakov A., Kandaurov I., Kasatov A., Kurkuchekov V., Mekler K., Popov V., Shoshin A., Skovorodin D., Trunev Y., Vasilyev A. Novel electron beam based test facility for observation of dynamics of tungsten erosion under intense ELM-like heat loads, AIP Conference Proceedings, 1771, 060004 (2016).

  7. Apushkinskaya D. Free boundary problems: Regularity properties near the fixed boundary, Lecture Notes in Mathematics, 2218. Springer (2018).

  8. Trunev Yu.A., Arakcheev A.S., Burdakov A.V., Kandaurov I.V., Kasatov A.A., Kurkuchekov V.V., Mekler K.I., Popov V.A., Shoshin A.A., Skovorodin D.I., Vasilyev A.A., Vyacheslavov L.N., Heating of tungsten target by intense pulse electron beam, AIP Conference Proceedings 1771, 060016 (2016).

  9. Самарский А.А., Вабищевич П.Н. Вычислительная теплопередача // М.: Едиториал УРСС, 2003, 784 с.

  10. Яненко Н.Н., Метод дробных шагов решения многомерных задач математической физики // Новосибирск, 1967. 196 с.

  11. Davis J.W., Smith P.D., ITER material properties handbook, J. Nucl. Mater. 233 (1996) 1593–1596.

  12. Ho C.Y., Powell R.W., Liley P.E. Thermal conductivity of elements, Journal of Physical and Chemical Reference Data, 1, p. 279 (1972).

  13. Талуц С.Г. Экспериментальное исследование теплофизических свойств переходных металлов и сплавов на основе железа при высоких температурах: Автореф. дис. д-ра физ.-мат. наук: 01.04.14, Екатеринбург: 2001. 38 с.

  14. Arakcheev A.S., Apushkinskaya D.E., Kandaurov I.V., Kasatov A.A., Kurkuchekov V.V., Lazareva G.G., Maksimova A.G., Popov V.A., Snytnikov A.V., Trunev Yu.A., Vasilyev A.A., Vyacheslavov L.N. Two-dimensional numerical simulation of tungsten melting under pulsed electron beam, Fusion Engineering and Design, vol. 132, p. 13–17 (2018).

  15. Vasilyev A.A., Arakcheev A.S., Bataev I.A., Bataev V.A., Burdakov A.V., Kandaurov I.V., Kasatov A.A., Kurkuchekov V.V., Mekler K.I., Popov V.A., Shoshin A.A., Skovorodin D.I., Trunev Yu.A., Vyacheslavov L.N., In-situ imaging of tungsten surface modification under ITER-like transient heat loads, Nucl. Matter Energy 12 (2017) 553–558.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Доклады Российской академии наук. Математика, информатика, процессы управления

Архивы выпусков Информация о журнале Отправить рукопись в журнал