Доклады Российской академии наук. Математика, информатика, процессы управления, 2023, T. 509, № 1, стр. 17-22

1. Высокоскоростные течения вязкой сжимаемой жидкости характерны тем, что в них могут сосуществовать явления турбулентности и ударных волн (УВ). Численное моделирование таких течений сопряжено с определенной проблемой. С одной стороны, схема должна обладать как можно меньшей численной диссипацией (оптимально – нулевой), чтобы как можно качественнее воспроизводить динамику вихрей в турбулентном потоке. С другой стороны, схема должна обладать достаточно большой численной диссипацией, чтобы устойчиво и монотонно (без ложных осцилляций) разрешать фронты УВ. Очевидно, эти требования противоречат друг другу. Отыскание наилучшего баланса между ними является одной из важнейших задач при разработке новых или улучшении старых численных схем. В этом смысле, хорошими диссипативными (и дисперсионными) свойствами обладают компактные разностные схемы [1], схемы разрывного метода Галеркина (РМГ) [2], схема КАБАРЕ [3], балансно-характеристические разностные схемы [4].

В работах [5, 6] был предложен новый класс схем, называемых бикомпактными. Определяющим элементом этих схем является высокоточная компактная аппроксимация пространственных производных на шаблоне, который включает в себя не более двух целых узлов по каждому направлению (т.е., помещается в одну ячейку сетки). По сравнению с классическими компактными схемами, бикомпактные схемы имеют лучшее спектральное разрешение [7]. По сравнению со схемами РМГ, бикомпактные схемы обходятся меньшим числом степеней свободы на ячейку, а значит, экономичнее и по объему вычислений (элементарных арифметических операций), и по объему требуемой памяти. Таким образом, бикомпактные схемы сочетают и улучшают преимущества компактных схем и схем РМГ.

Бикомпактные схемы были плохо развиты для уравнений параболического типа, что являлось основным препятствием на пути к их практическому применению для численного моделирования течений вязкой жидкости. Данная проблема была решена лишь частично: в [8] для уравнений Навье–Стокса в случае несжимаемой жидкости, в [9] для квазилинейного уравнения теплопроводности.

Цель настоящей работы – построение бикомпактных схем для наиболее общих уравнений Навье–Стокса (в случае сжимаемой жидкости) на основе синтеза результатов из [8–10].

2. Нестационарные течения ньютоновской теплопроводной сжимаемой жидкости описываются уравнениями Навье–Стокса:

Поясним обозначения: ${{x}_{i}}$ – пространственные декартовы координаты ($i = \overline {1,3} $), $t$ – время, $\rho $ – плотность жидкости, ${\mathbf{v}}$ – скорость, $p$ – давление, $T$ – температура, $\varepsilon $ – удельная внутренняя энергия, $e$ – удельная полная энергия, ${{P}_{{ij}}}$ – компоненты тензора напряжений, $\mu $ – динамическая вязкость, ${{q}_{i}}$ – компоненты вектора потока тепла, $\varkappa $ – коэффициент теплопроводности. Искомой функцией в системе (1) является вектор консервативных переменных ${\mathbf{U}}({\mathbf{x}},t)$ (${\mathbf{x}} = ({{x}_{1}},{{x}_{2}},{{x}_{3}})$).

В качестве конкретной модели сжимаемой жидкости рассмотрим совершенный газ:

Число $\gamma $ – показатель адиабаты. Для динамической вязкости примем закон Сазерленда, а коэффициент теплопроводности зададим через критерий подобия Прандтля:

где ${\text{Re}}$ – число Рейнольдса, $C$ – параметр закона Сазерленда, ${\text{Pr}}$ – число Прандтля. Далее (в разд. 4) мы полагаем $\gamma = 1.4$, $C = 110.4{\text{/}}288$, ${\text{Pr}} = 0.72$ (число ${\text{Re}}$ варьируется).

Все уравнения записаны в безразмерной форме. Размерные масштабы ${{l}_{0}}$ и ${{\rho }_{0}}$ длины и плотности могут быть любыми; размерным масштабом скорости служит скорость звука ${{c}_{0}} = \sqrt {\gamma R{{T}_{0}}} $, где $R$ – это универсальная газовая постоянная, отнесенная к молярной массе газа, а ${{T}_{0}}$ – это параметр температуры в размерном законе Сазерленда. Размерными масштабами давления, температуры и вязкости являются соответственно $\rho _{0}^{{}}c_{0}^{2}$, ${{T}_{0}}$ и ${{\rho }_{0}}{{c}_{0}}{{l}_{0}}$.

3. Опишем методику построения бикомпактных схем для уравнений Навье–Стокса (1). Пусть система (1) решается в открытом прямоугольном параллелепипеде $\Pi $, ребра которого направлены параллельно осям координат. Введем в замкнутой области $\overline \Pi = \Pi \cup \partial \Pi $ декартову сетку ${{\overline \Omega }_{{\mathbf{h}}}}$, где ${\mathbf{h}} = ({{h}_{1}},{{h}_{2}},{{h}_{3}})$ – пространственные шаги.

Применим метод расщепления по физическим процессам Марчука–Стрэнга. Разобьем систему (1) на две подсистемы:

где ${{{\mathbf{G}}}_{i}} + {{{\mathbf{H}}}_{i}} = {{{\mathbf{F}}}_{i}}$. Векторы ${{{\mathbf{G}}}_{i}}$ включают в себя члены, отвечающие за конвективный перенос и силы давления, т.е. (2) представляет собой систему уравнений Эйлера. Векторы ${{{\mathbf{H}}}_{i}}$ включают в себя члены, отвечающие за диссипативные процессы – вязкость и теплопроводность.

Для аппроксимации системы (2) мы применяем метод локально-одномерного расщепления и метод глобального потокового расщепления Лакса–Фридрихса–Русанова. Разобьем систему (2) на шесть подсистем вида

где ${{{\mathbf{G}}}_{{i, \pm }}}({\mathbf{U}}) = 0.5{{{\mathbf{G}}}_{i}}({\mathbf{U}}) \pm s_{i}^{*}{\mathbf{U}}$. Постоянные коэффициенты $s_{i}^{*} > 0$ подбираются так, чтобы матрицы Якоби векторов ${{{\mathbf{G}}}_{{i, \pm }}}$ были определены положительно/отрицательно на некотором множестве значений ${\mathbf{U}}$. Для решения каждой одномерной системы (4) мы используем одномерные неявно-явные бикомпактные схемы из [10]. Решение осуществляется вдоль координатных линий ${{x}_{i}}$, проходящих через узлы сетки ${{\overline \Omega }_{{\mathbf{h}}}}$. Из всех схем, рассмотренных в [10], остановимся на схеме с погрешностью аппроксимации $O({{h}^{4}} + {{\tau }^{3}})$, где $h$ – максимальный пространственный шаг, $\tau $ – временной шаг. Обозначим оператор послойного перехода этой одномерной бикомпактной схемы как $S_{{i, \pm }}^{E}(\tau )$. Введем операторы $S_{i}^{E} = S_{{i, - }}^{E}{\kern 1pt} S_{{i, + }}^{E}$. Пользуясь конструкцией расщепления Марчука–Стрэнга, построим оператор послойного перехода локально-одномерной бикомпактной схемы для многомерной системы (2):

Для аппроксимации системы (3) мы применяем и, вместе с тем, обобщаем метод, впервые предложенный в [11] и развитый в [12, 13] (для скалярных параболических уравнений). Прибавим к обеим частям (3) члены с постоянными диссипативными коэффициентами ${{\nu }_{0}},{{\lambda }_{0}} > 0$:

где матрица ${{{\mathbf{D}}}_{0}} = {\text{diag}}(0,{{\nu }_{0}},{{\nu }_{0}},{{\nu }_{0}},{{\lambda }_{0}})$. Для решения системы (5) мы используем неявно-явные бикомпактные схемы из [9]: член ${{\mathcal{F}}_{1}}$ аппроксимируется явно, а член ${{\mathcal{F}}_{2}}$ – неявно. Разностные уравнения этих схем формально являются векторными, но решаются покомпонентно, так как матрица ${{{\mathbf{D}}}_{0}}$ диагональная. Отметим, что первое уравнение системы (5) имеет вид $\partial \rho {\text{/}}\partial t = 0$, следовательно, в рамках (5) плотность по сути не является искомой функцией. На разностном уровне это выражается в том, что сеточная функция плотности переносится со слоя на слой без изменений. Из всех бикомпактных схем, предложенных в [9], мы выбираем неявно-явную схему с погрешностью аппроксимации $O({{h}^{4}} + {{\tau }^{2}})$. Обозначим оператор послойного перехода этой схемы как ${{S}^{D}}(\tau )$.

Итак, расщепленная бикомпактная схема для исходной системы (1) имеет вид:

где ${{{\mathbf{U}}}^{n}}$ – численное решение на временном слое ${{t}_{n}}$. Уточним, что операторы ${{S}^{E}}$ и ${{S}^{D}}$ работают с двумя разными представлениями численного решения; переход между ними разобран в [8].

Схема (6) имеет аппроксимацию $O({{h}^{4}} + {{\tau }^{2}})$, устойчива при любом соотношении между ${\mathbf{h}}$ и $\tau $, консервативна. Эта схема реализуется без ньютоновских итераций и без обращений больших матриц (размера $\mathcal{N} \times \mathcal{N}$, где $\mathcal{N}$ – число узлов ${{\overline \Omega }_{{\mathbf{h}}}}$), несмотря на то, что формально она является неявной. Этого удается достичь за счет неявно-явной (линейно-неявной) аппроксимации по времени, а также локальной разрешимости уравнений бикомпактных схем.

Наконец, приведем формулы для вычисления коэффициентов (параметров) $s_{i}^{*},\;{{\nu }_{0}},\;{{\lambda }_{0}}$:

где $\delta > 0$ – задаваемый коэффициент запаса. Эти формулы применяются перед каждым переходом со слоя на слой. В пределах одного перехода со слоя на слой мы смотрим на коэффициенты $s_{i}^{*}$, ${{\nu }_{0}}$, ${{\lambda }_{0}}$ как на константы.

4. Испытаем бикомпактную схему (6) на ряде двумерных тестовых задач.

4.1. Прежде всего продемонстрируем сходимость схемы на сгущающихся сетках. Задача об изоэнтропическом вихре (см. [14]) представляется весьма подходящим тестом: в ней течение свободно от УВ и непостоянно по плотности, скорости и давлению. Расчетная область $\Pi = ( - {{5,5)}^{2}}$. Начальное распределение параметров газа (при $t = 0$):

Граничные условия периодические. Определим временной промежуток $\mathcal{T} = 10\sqrt \gamma $.

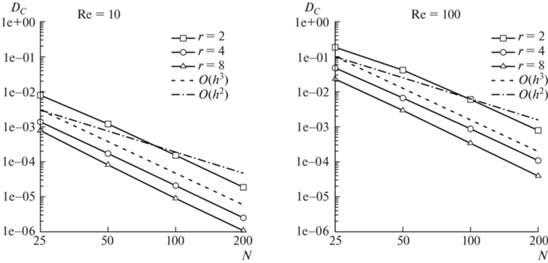
Расчеты проведем на сетках с шагами ${{h}_{1}} = {{h}_{2}} = 10{\text{/}}N$, $\tau = \mathcal{T}{\text{/}}(rN)$ при $N = 25$, 50, …, 400 и $r = 2$, 4, 8 (соответствующие числа Куранта $\kappa \approx 1.46$, 0.73, 0.37). Положим параметр $\delta = 0.5$. Рассмотрим два случая: ${\text{Re}} = 10$, 100. Небольшие значения числа Рейнольдса (особенно ${\text{Re}} = 10$) позволят проявиться погрешностям схемы расщепления, а также бикомпактной схемы для подсистемы (3). Поскольку точное решение данной задачи в случае неидеальной жидкости неизвестно, вместо ${{E}_{C}}$, нормы $C$ невязки, мы будем смотреть на ${{D}_{C}}$, норму $C$ разности между решениями на соседних сетках (по методу Рунге).

Полученные зависимости ${{D}_{C}}(N)$ при $t = \mathcal{T}$ приведены на рис. 1. Любопытно, что бикомпактная схема сходится с третьим порядком, несмотря на расщепление по физическим процессам. Похожий результат был получен в [8] для расщепленной бикомпактной схемы численного решения уравнений Навье–Стокса для несжимаемой жидкости.

4.2. Перейдем к задаче о вязком течении в ударной трубе (см. [15]). Динамическая вязкость в этом тесте полагается постоянной: $\mu = {\text{R}}{{{\text{e}}}^{{ - 1}}}$, ${\text{Re}} = 200$. Расчетная область $\Pi {{ = (0,1)}^{2}}$. В начальный момент времени газ покоится и разделен вертикально на две равные по объему части; в правой $\rho = 1.2$, $p = 1.2{\text{/}}\gamma $, в левой $\rho $ и $p$ в 100 раз больше. На $\partial \Pi $ ставятся условия прилипания и адиабатической стенки. Распад разрыва порождает УВ, бегущую направо; вдоль нижней и верхней стенок формируются погранслои. Эта УВ отражается от правой стенки и затем взаимодействует с погранслоями. Интерес в данной задаче представляет разрешение вихрей, возникающих в результате этого взаимодействия, и УВ-структур.

Вычисления выполним на сетке $500 \times 500$ ячеек при числе $\kappa = 0.6$ и параметре $\delta = 1$. Из-за больших амплитуд у начального разрыва и отраженной УВ, в операторе ${{S}^{E}}$ необходима монотонизация. Мы вводим ее по методу из [16]. Величина параметра монотонизации ${{C}_{1}} = 5$.

При дискретизации начальных или граничных условий, имеющих сильные разрывы, мы заменяем функцию Хэвисайда $\theta (x)$ (элементарный скачок) на гладкую функцию

Параметр $\sigma = 2h$, т.е. разрывы во входных данных размазываются на 4 ячейки.

Полученное поле плотности при $t = 1$ изображено на рис. 2. Сравним бикомпактную схему со схемой WENO5-MR из [17] по положению тройной точки и высоте/наклону крупнейшего вихря. Для бикомпактной схемы это (0.589, 0.138), 0.157, 75°. Для схемы WENO5-MR это (0.576, 0.113), 0.165, 55°. Эталонные данные из [18] – это (0.580, 0.138), 0.166, 74.5°. Очевидно, бикомпактная схема хуже предсказывает высоту вихря, но лучше – наклон вихря и положение тройной точки. Добавим, что бикомпактная схема значительно меньше “размазывает” меньший вихрь с центром в точке (0.68, 0.04) и фронты УВ.

4.3. Рассмотрим задачу о взаимодействии слоя смешения и косой УВ (см. [19]). Динамическая вязкость меняется по закону Сазерленда, как в тесте 4.1. Число ${\text{Re}} = 500$. Расчетная область $\Pi = (0,200)$ × (–20, 20). Начальное распределение параметров газа:

На нижней границе ставятся условия непротекания и адиабатической стенки. На левой границе задается периодическое во времени возмущение скорости:

В левом верхнем углу $\Pi $ (точечно) выставляются параметры газа за косой УВ:

На остальных границах ставятся условия свободного выхода. Течение газа развивается таким образом. Из левого верхнего угла $\Pi $ распространяется косая УВ. Она проходит (с преломлением) через слой сдвига и затем отражается от нижней границы. Отраженная УВ тоже проходит через слой сдвига. Вместе с тем возмущение вертикальной компоненты скорости в набегающем потоке нарушает устойчивость слоя сдвига и порождает вихревую дорожку, проходящую через систему УВ.

Расчет проведем на сетке $500 \times 100$ ячеек при числе $\kappa = 0.8$ и параметре $\delta = 1$.

На рис. 3 представлен график плотности при $t = 120$. Видно, что бикомпактная схема хорошо разрешает вихревую дорожку, несмотря на относительную грубость сетки. По сравнению со схемой WENO5-MR из [17], бикомпактная схема намного меньше “размазывает” спиралевидные уплотнения в центрах вихрей (см. последние четыре вихря). Отметим, что малость амплитуд УВ позволяет вести счет по бикомпактной схеме без монотонизации. Однако это не приводит к заполнению областей течения нефизическими осцилляциями.