Доклады Российской академии наук. Математика, информатика, процессы управления, 2023, T. 509, № 1, стр. 77-82
Идентификация узловых точек упругого включения в упругой плоскости
Е. И. Шифрин 1, *, А. В. Капцов 1, **
1 Институт проблем механики им. А.Ю. Ишлинского Российской академии наук
Москва, Россия
* E-mail: shifrin@ipmnet.ru
** E-mail: kaptsov@ipmnet.ru
Поступила в редакцию 16.11.2022
После доработки 20.12.2022
Принята к публикации 28.12.2022
- EDN: CTPNFY
- DOI: 10.31857/S268695432370011X
Аннотация
Рассматривается геометрическая обратная задача идентификации изотропного, линейно упругого включения в изотропной, линейно упругой плоскости. Предполагается, что на бесконечности заданы постоянные напряжения и на некоторой, охватывающей включение, замкнутой кривой известны перемещения и действующие усилия. В случае, когда включение представляет собой квадратурную область, разработан метод идентификации ее узловых точек. Рассмотрен численный пример.
1. ВВЕДЕНИЕ
В случае, когда переопределенные данные (данные Дирихле и Неймана) известны на замкнутой кривой (в пространственном случае поверхности), охватывающей неоднородность (включение, полость или трещину), весьма эффективным методом идентификации указанной неоднородности является метод, основанный на скачке в функционале взаимности [1]. В результате применения этого метода к обратным задачам теории упругости были решены задачи идентификации множественных прямолинейных трещин в упругой плоскости, а также плоской трещины, эллипсоидального включения и нескольких эллипсоидальных включений в упругом пространстве (см. [2–4] и имеющиеся там ссылки). В упомянутых публикациях, в основном, решались задачи для неоднородностей, имеющих каноническую форму. В данной работе рассматривается плоская задача обнаружения и идентификации неоднородностей, имеющих, в том числе, неканоническую форму.
Поскольку ниже рассматриваются включения, являющиеся квадратурными областями, коротко напомним определение и основные свойства квадратурных областей. Мы ограничимся рассмотрением односвязных областей $D \subset {{R}^{2}}$, ограниченных гладкой, замкнутой, жордановой кривой $\partial D$. Начало изучению квадратурных областей было положено в [5, 6]. Обозначим $A{{L}^{1}}\left( D \right)$ множество функций, голоморфных в $D$ и принадлежащих ${{L}_{1}}\left( D \right)$. Согласно [6] область $D$ называется квадратурной, если существуют точки ${{z}_{1}},{{z}_{2}}, \ldots ,{{z}_{m}}$, ${{z}_{i}} \in D$ такие, что $\forall $ $f\left( z \right) \in A{{L}^{1}}\left( D \right)$ справедливо равенство
(1)
$\int\limits_D {f\left( z \right)dS} = \sum\limits_{k = 1}^m {\sum\limits_{j = 0}^{{{n}_{k}} - 1} {{{a}_{{kj}}}{{f}^{{\left( j \right)}}}\left( {{{z}_{k}}} \right)} } .$Здесь $O{{x}_{1}}{{x}_{2}}$ – декартова система координат, $z = {{x}_{1}} + i{{x}_{2}}$, ${{a}_{{kj}}}$ – комплексные постоянные, не зависящие от функции $f\left( z \right)$. Точки ${{z}_{k}} = {{x}_{{k1}}} + i{{x}_{{k2}}}$ назовем узловыми точками. Величина $n$ = $\sum\limits_{k = 1}^m {{{n}_{k}}} $ называется порядком квадратурного тождества (1).
Другое, эквивалентное (1), определение квадратурной области дано в [5]. Согласно [5], область $D$ называется квадратурной, если существует функция $S\left( z \right)$, называемая функцией Шварца, которая удовлетворяет следующим условиям. Функция $S\left( z \right)$ мероморфна в $D$. Полюсы $S\left( z \right)$ совпадают с точками ${{z}_{k}}$ из (1), а порядок полюсов совпадает с соответствующими величинами ${{n}_{k}}$. Кроме того, на границе $\partial D$ справедливо равенство
Плотность квадратурных областей в классе односвязных областей, ограниченных простой, замкнутой, ${{C}^{\infty }}$ кривой, доказана в [7–9].
До настоящего времени открытой остается проблема единственности для квадратурных областей, т.е. вопрос о том, в какой степени равенство (1) определяет область $D$. Здесь известны лишь частные результаты. Например, доказано, что квадратурная область порядка 1 ($m = 1$, ${{n}_{1}} = 1$) является кругом. Другие результаты, касающиеся проблемы единственности для квадратурных областей, можно найти в [6, 10].
2. МАТЕМАТИЧЕСКАЯ ФОРМУЛИРОВКА ЗАДАЧИ
Пусть $D \subset {{R}^{2}}$ – односвязная область, ограниченная простой, замкнутой, ${{C}^{\infty }}$ кривой. Предположим, что область $D$ занята материалом с модулем сдвига ${{\mu }_{I}}$ и коэффициентом Пуассона ${{\nu }_{I}}$. Границу области $D$ обозначим $\partial D$. Предположим, что область $S = {{R}^{2}}{{\backslash }}D$ занята материалом с модулем сдвига ${{\mu }_{M}}$ и коэффициентом Пуассона ${{\nu }_{M}}$. Предполагается, что в заданной декартовой системе координат на бесконечности заданы постоянные напряжения $\sigma _{{11}}^{\infty }$, $\sigma _{{12}}^{\infty }$ и $\sigma _{{22}}^{\infty }$. Вектор перемещений, тензоры деформаций и напряжений в матрице $S$ будем помечать верхним индексом $M$: ${{{\mathbf{u}}}^{M}}\left( x \right)$ – вектор перемещений, $e_{{\alpha \beta }}^{M}\left( x \right)$ – тензор деформаций, $\sigma _{{\alpha \beta }}^{M}\left( x \right)$ – тензор напряжений, $x \in S$. Уравнения теории упругости в области $S$ имеют вид
(3)
$\sigma _{{\alpha \beta }}^{M}\left( x \right) = 2{{\mu }_{M}}\left( {\frac{{{{\nu }_{{M*}}}}}{{1 - 2{{\nu }_{{M*}}}}}{{\theta }^{M}}\left( x \right){{\delta }_{{\alpha \beta }}} + e_{{\alpha \beta }}^{M}\left( x \right)} \right),$Здесь ${{\delta }_{{\alpha \beta }}}$ – символ Кронекера, ${{\nu }_{{M*}}} = {{\nu }_{M}}$ в случае плоской деформации и ${{\nu }_{{M*}}}$ = ${{\nu }_{M}}{\text{/}}\left( {1 + {{\nu }_{M}}} \right)$ в случае плоского напряженного состояния.
Упругое поле во включении $D$ помечаем верхним индексом $I$: ${{{\mathbf{u}}}^{I}}\left( x \right)$ – вектор перемещений, $e_{{\alpha \beta }}^{I}\left( x \right)$ – тензор деформаций, $\sigma _{{\alpha \beta }}^{I}\left( x \right)$ – тензор напряжений, $x \in D$. Упругое поле во включении удовлетворяет уравнениям, аналогичным уравнениям (3), с заменой упругих постоянных ${{\mu }_{M}}$ и ${{\nu }_{M}}$ на упругие постоянные ${{\mu }_{I}}$ и ${{\nu }_{I}}$ соответственно.
Между матрицей и включением предполагаются выполненными условия полного сцепления
(4)
$\begin{gathered} {{{\mathbf{u}}}^{M}}\left( {x{\kern 1pt} *} \right) = {{{\mathbf{u}}}^{I}}\left( {x{\kern 1pt} *} \right), \\ \sigma _{{\alpha \beta }}^{M}\left( {x{\kern 1pt} *} \right){{N}_{\beta }}\left( {x{\kern 1pt} *} \right) = \sigma _{{\alpha \beta }}^{I}\left( {x{\kern 1pt} *} \right){{N}_{\beta }}\left( {x{\kern 1pt} *} \right),\quad x{\kern 1pt} * \in \partial D. \\ \end{gathered} $Здесь ${\mathbf{N}}\left( {x{\kern 1pt} *} \right) = \left( {{{N}_{1}}\left( {x{\kern 1pt} *} \right),{{N}_{2}}\left( {x{\kern 1pt} *} \right)} \right)$ – единичная нормаль к границе включения $\partial D$ в точке $x{\kern 1pt} *$.
Предполагается, что $D \subset \Omega $, где $\Omega $, односвязная, ограниченная область с кусочно-гладкой границей $\partial \Omega $. Предполагается также, что на границе $\partial \Omega $ известны приложенные усилия и перемещения:
(5)
$\sigma _{{\alpha \beta }}^{M}\left( {x{\kern 1pt} '} \right){{n}_{\beta }}\left( {x{\kern 1pt} '} \right) = t_{\alpha }^{0}\left( {x{\kern 1pt} '} \right),\quad x{\kern 1pt} ' \in \partial \Omega ,$(6)
${{{\mathbf{u}}}^{M}}\left( {x{\kern 1pt} '} \right) = {{{\mathbf{u}}}^{0}}\left( {x{\kern 1pt} '} \right),\quad x{\kern 1pt} ' \in \partial \Omega .$Здесь $n\left( {x{\kern 1pt} '} \right) = \left( {{{n}_{1}}\left( {x{\kern 1pt} '} \right),{{n}_{2}}\left( {x{\kern 1pt} '} \right)} \right)$ – единичная внешняя нормаль к $\partial \Omega $ в точке $x{\kern 1pt} '$.
В общем виде задача заключается в идентификации включения $D$ по имеющимся данным. В данной статье мы рассматриваем более скромную задачу идентификации узловых точек квадратурного включения $D$.
3. ФУНКЦИОНАЛ СКАЧКА В СООТНОШЕНИИ ВЗАИМНОСТИ И ЕГО СВОЙСТВА
Назовем регулярными упругие поля, удовлетворяющие уравнениям (3) во всей плоскости, и будем помечать их верхним индексом $r$. Рассмотрим функционал, зависящий от регулярных упругих полей
(7)
$\begin{gathered} RG({{{\mathbf{u}}}^{r}}) = \int\limits_{\partial \Omega } {\left( {t_{\alpha }^{0}\left( {x{\kern 1pt} '} \right)u_{\alpha }^{r}\left( {x{\kern 1pt} '} \right) - t_{\alpha }^{r}\left( {x{\kern 1pt} '} \right)u_{\alpha }^{0}\left( {x{\kern 1pt} '} \right)} \right)} dl, \\ t_{\alpha }^{r}\left( {x{\kern 1pt} '} \right) = \sigma _{{\alpha \beta }}^{r}\left( {x{\kern 1pt} '} \right){{n}_{\beta }}\left( {x{\kern 1pt} '} \right). \\ \end{gathered} $Из принципа взаимности следует, что в случае, когда внутри области $\Omega $ нет никаких дефектов, справедливо равенство $RG\left( {{{{\mathbf{u}}}^{r}}} \right) = 0$ для любого регулярного упругого поля ${{{\mathbf{u}}}^{r}}\left( x \right)$. Если внутри области $\Omega $ содержится включение $D$, то для некоторых регулярных упругих полей величина функционала $RG\left( {{{{\mathbf{u}}}^{r}}} \right)$ может отличаться от нуля, причем значения функционала несут информацию об области $D$. Заметим также, что из предположения о том, что функции $t_{\alpha }^{0}\left( {x{\kern 1pt} '} \right)$ и $u_{\alpha }^{0}\left( {x{\kern 1pt} '} \right)$ известны на всей границе $\partial \Omega $, следует, что величина $RG\left( {{{{\mathbf{u}}}^{r}}} \right)$ может быть вычислена для любого регулярного упругого поля. При наличии включения $D$ выражение (7) сводится к интегралу по области $D$.
(8)
$\begin{gathered} RG({{{\mathbf{u}}}^{r}}) = \\ = \int\limits_D {\left[ {\left( {{{\lambda }_{I}} - {{\lambda }_{M}}} \right){{\theta }^{I}}{{\theta }^{r}} + 2\left( {{{\mu }_{I}} - {{\mu }_{M}}} \right)e_{{\alpha \beta }}^{I}e_{{\alpha \beta }}^{r}} \right]dx} . \\ \end{gathered} $Здесь ${{\lambda }_{I}} = 2{{\mu }_{I}}{{\nu }_{{I*}}}{\text{/}}\left( {1 - 2{{\nu }_{{I*}}}} \right)$, ${{\lambda }_{M}} = 2{{\mu }_{M}}{{\nu }_{{M*}}}{\text{/}}(1$ – ‒ $2{{\nu }_{{M*}}})$ – постоянные Ламе, ${{\theta }^{r}}\left( x \right)$ = $\sum\limits_{k = 1}^2 {e_{{kk}}^{r}\left( x \right)} $.
Как известно [11], любое упругое поле в односвязной области может быть представлено с помощью двух голоморфных функций. В частности, регулярное упругое поле может быть представлено в виде
(9)
$2{{\mu }_{M}}\left( {u_{1}^{r} + iu_{2}^{r}} \right) = {{\kappa }_{M}}{{\varphi }_{r}}\left( z \right) - z\overline {\varphi _{r}^{'}\left( z \right)} - \overline {{{\psi }_{r}}\left( z \right)} $(10)
$\begin{gathered} \sigma _{{11}}^{r} + \sigma _{{22}}^{r} = 4\operatorname{Re} \left[ {{{\Phi }_{r}}\left( z \right)} \right], \\ \sigma _{{22}}^{r} - \sigma _{{11}}^{r} + 2i\sigma _{{12}}^{r} = 2\left[ {\bar {z}\Phi _{r}^{'}\left( z \right) + {{\Psi }_{r}}\left( z \right)} \right]. \\ \end{gathered} $Здесь ${{\kappa }_{M}} = 3 - 4{{\nu }_{M}}$ для плоско деформированного состояния и ${{\kappa }_{M}}$ = $\left( {3 - {{\nu }_{M}}} \right){\text{/}}\left( {1 + {{\nu }_{M}}} \right)$ для плоско напряженного состояния, ${{\Phi }_{r}}\left( z \right) = \varphi _{r}^{'}\left( z \right)$, ${{\Psi }_{r}}\left( z \right)$ = = $\psi _{r}^{'}\left( z \right)$ – голоморфные функции.
Пусть $H\left( z \right)$ – голоморфная функция во всей плоскости. Обозначим верхними индексами $r$ и $\rho $ регулярные упругие поля, построенные согласно формулам (9), (10) с помощью голоморфных функций ${{\Phi }_{r}}\left( z \right) = 0$, ${{\Psi }_{r}}\left( z \right)$ = ${{\mu }_{M}}H\left( z \right)$ и ${{\Phi }_{\rho }}\left( z \right) = 0$, ${{\Psi }_{\rho }}\left( z \right)$ = $i{{\mu }_{M}}H\left( z \right)$ соответственно.
Лемма 1. Нетрудно доказать следующее равенство
(11)
$\begin{gathered} RG\left( {{{{\mathbf{u}}}^{r}}} \right) - iRG\left( {{{{\mathbf{u}}}^{\rho }}} \right) = \\ = \frac{{\left( {{{\mu }_{I}} - {{\mu }_{M}}} \right)}}{{2{{\mu }_{I}}}}\int\limits_D {\left[ {\left( {\sigma _{{22}}^{I}\left( x \right) - \sigma _{{11}}^{I}\left( x \right)} \right) - 2i\sigma _{{12}}^{I}\left( x \right)} \right]H\left( z \right)dx} \\ \end{gathered} $Выражение в правой части (11) представляет собой функционал на пространстве голоморфных функций $H\left( z \right)$. Обозначим этот функционал $P\left( H \right)$.
Отметим, что упругое поле в односвязной области $D$ определяется двумя голоморфными функциями ${{\varphi }_{I}}\left( z \right)$ и ${{\psi }_{I}}\left( z \right)$ аналогично формулам (9) и (10) с заменой ${{\mu }_{M}}$ и ${{\kappa }_{M}}$ на ${{\mu }_{I}}$ и ${{\kappa }_{I}}$ соответственно.
Область $S$ не является односвязной, однако усилия, приложенные к границе $\partial D$, в силу условий сопряжения (4) самоуравновешены, поэтому напряженное состояние в области $S$ также представляется двумя голоморфными функциями ${{\varphi }_{M}}\left( z \right)$ и ${{\psi }_{M}}\left( z \right)$ согласно формулам (9) и (10). При этом, голоморфные функции удовлетворяют условиям [11]
(12)
$\begin{gathered} {{\varphi }_{M}}\left( z \right) = \Gamma z + \varphi _{M}^{0}\left( z \right),\quad {{\psi }_{M}}\left( z \right) = \Gamma {\kern 1pt} 'z + \psi _{M}^{0}\left( z \right), \\ \varphi _{M}^{0}\left( \infty \right) = \psi _{M}^{0}\left( \infty \right) = 0, \\ \end{gathered} $(13)
$\Gamma = \frac{1}{4}\left( {\sigma _{{11}}^{\infty } + \sigma _{{22}}^{\infty }} \right),\quad \Gamma {\kern 1pt} ' = \frac{1}{2}\left( {\sigma _{{22}}^{\infty } - \sigma _{{11}}^{\infty } + 2i\sigma _{{12}}^{\infty }} \right).$На границе $\left( {{{x}_{1}},{{x}_{2}}} \right) \in \partial D$ определим две функции
(14)
$\begin{gathered} {{f}_{I}}\left( {{{x}_{1}},{{x}_{2}}} \right) = {{\varphi }_{I}}\left( z \right) + z\overline {\varphi _{I}^{'}\left( z \right)} + \overline {{{\psi }_{I}}\left( z \right)} , \\ {{f}_{M}}\left( {{{x}_{1}},{{x}_{2}}} \right) = {{\varphi }_{M}}\left( z \right) + z\overline {\varphi _{M}^{'}\left( z \right)} + \overline {{{\psi }_{M}}\left( z \right)} . \\ \end{gathered} $Лемма 2. Выражение (11) для функционала $P\left( H \right)$ можно привести к следующему виду
(15)
$P\left( {H\left( z \right)} \right) = - \frac{{i\left( {{{\mu }_{I}} - {{\mu }_{M}}} \right)}}{{2{{\mu }_{I}}}}\int\limits_{\partial D} {H\left( z \right){{f}_{I}}\left( {{{x}_{1}},{{x}_{2}}} \right)dz} .$Условия сопряжения (4) в терминах введенных голоморфных функций имеют вид [11]
(16)
$\begin{gathered} \frac{1}{{2{{\mu }_{I}}}}\left[ {{{\kappa }_{I}}{{\varphi }_{I}}\left( z \right) - z\overline {\varphi _{I}^{'}\left( z \right)} - \overline {{{\psi }_{I}}\left( z \right)} } \right] = \\ = \frac{1}{{2{{\mu }_{M}}}}\left[ {{{\kappa }_{M}}{{\varphi }_{M}}\left( z \right) - z\overline {\varphi _{M}^{'}\left( z \right)} - \overline {{{\psi }_{M}}\left( z \right)} } \right], \\ \left( {{{x}_{1}},{{x}_{2}}} \right) \in \partial D, \\ \end{gathered} $(17)
${{f}_{I}}\left( {{{x}_{1}},{{x}_{2}}} \right) = {{f}_{M}}\left( {{{x}_{1}},{{x}_{2}}} \right).$Пусть область $D$ является квадратурной и $S\left( z \right)$ – мероморфная функция Шварца, определенная в $\bar {D}$. $\bar {D}$ – замыкание области $D$. Построим функции, определенные в $D \times \bar {D}$ и $D \times \left( {{{R}^{2}}{{\backslash }}D} \right)$ соответственно.
(18)
$\begin{gathered} {{Q}_{1}}\left( {z,\zeta } \right) = {{\varphi }_{I}}\left( z \right) + z{{{\bar {\Phi }}}_{I}}\left( \zeta \right) + {{{\bar {\psi }}}_{I}}\left( \zeta \right), \\ z \in D,\quad \zeta \in \bar {D}, \\ \end{gathered} $(19)
$\begin{gathered} {{Q}_{2}}\left( {z,\zeta } \right) = \frac{1}{{\gamma {{\kappa }_{M}} + 1}}\left[ {\left( {{{\kappa }_{I}} + 1} \right){{\varphi }_{I}}\left( z \right) + } \right. \\ + \;\left. {\gamma \left( {{{\kappa }_{M}} + 1} \right)\left( {z{{{\bar {\Phi }}}_{M}}\left( \zeta \right) + {{{\bar {\psi }}}_{M}}\left( \zeta \right)} \right)} \right], \\ z \in D,\quad \zeta \notin D. \\ \end{gathered} $Здесь $\gamma = \frac{{{{\mu }_{I}}}}{{{{\mu }_{M}}}}$.
Лемма 3. Из определения функции Шварца, определений (14) и условий сопряжения (16), (17) следует равенство
(20)
${{Q}_{1}}\left( {z,S\left( z \right)} \right) = {{Q}_{2}}\left( {z,S\left( z \right)} \right) = {{f}_{I}}\left( {{{x}_{1}},{{x}_{2}}} \right),\quad z\, \in \,\partial D.$Построим функцию, определенную в области $D$
(21)
$Q\left( z \right) = \left\{ \begin{gathered} {{Q}_{1}}\left( {z,S\left( z \right)} \right),\quad z \in D,\quad S\left( z \right) \in D, \hfill \\ {{Q}_{2}}\left( {z,S\left( z \right)} \right),\quad z \in D,\quad S\left( z \right) \notin \bar {D}. \hfill \\ \end{gathered} \right.$Теорема. Функция $Q\left( z \right)$ мероморфна в $D$, полюсами $Q\left( z \right)$ являются полюсы функции Шварца и справедливо равенство
(22)
$P\left( {H\left( z \right)} \right) = - \frac{{i\left( {{{\mu }_{I}} - {{\mu }_{M}}} \right)}}{{2{{\mu }_{I}}}}\int\limits_{\partial D} {H\left( z \right)Q\left( z \right)dz} .$Предположим для простоты, что функция $S\left( z \right)$ имеет простые полюсы в $D$. Обозначим их ${{z}_{1}},{{z}_{2}}, \ldots ,{{z}_{n}}$. Таким образом, в окрестности точки ${{z}_{k}}$ функция $S\left( z \right)$ имеет вид
где ${{g}_{k}}\left( z \right)$ – голоморфная в окрестности точки ${{z}_{k}}$ функция.Учитывая поведение упругого поля uM = = $\left( {u_{1}^{M},u_{2}^{M}} \right)$ на бесконечности (12), получим асимптотику ${{Q}_{2}}\left( {z,S\left( z \right)} \right)$ при $z \to {{z}_{k}}$
(24)
${{Q}_{2}}\left( {z,S\left( z \right)} \right) = \frac{{\gamma \left( {{{\kappa }_{M}} + 1} \right)\bar {\Gamma }{\kern 1pt} '{\kern 1pt} {{R}_{k}}}}{{\left( {\gamma {{\kappa }_{M}} + 1} \right)\left( {z - {{z}_{k}}} \right)}} + {{G}_{k}}\left( z \right).$Здесь ${{G}_{k}}\left( z \right)$ – голоморфная в окрестности точки ${{z}_{k}}$ функция.
Следствие. Из (22) и (24) следует
(25)
$P\left( {H\left( z \right)} \right) = \sum\limits_{k = 1}^n {{{A}_{k}}H\left( {{{z}_{k}}} \right)} ,$4. ОПРЕДЕЛЕНИЕ УЗЛОВЫХ ТОЧЕК КВАДРАТУРНОГО ВКЛЮЧЕНИЯ
Рассмотрим последовательность голоморфных функций ${{H}_{m}}\left( z \right) = {{\left( {\frac{z}{L}} \right)}^{m}}$, где $L$ – некоторый линейный размер, $m = 0,1,2, \ldots $. Обозначим
Из (25) и (26) получаем систему уравнений
(27)
$\sum\limits_{k = 1}^n {{{A}_{k}}w_{k}^{m}} = {{b}_{m}},\quad {{w}_{k}} = \frac{{{{z}_{k}}}}{L}.$Уравнения (27) содержат $2n$ неизвестных: ${{A}_{k}}$ и ${{w}_{k}}$, $k = 1, \ldots ,n$. Методы нахождения этих неизвестных по известным значениям ${{b}_{m}}$, $m = 0, \ldots ,2n - 1$ хорошо разработаны [12–14]. В этих методах предполагается, что число $n$ известно. В рассматриваемой задаче число узловых точек, отвечающих области $D$, заранее неизвестно. Поэтому нужно решать последовательность задач в предположении, что имеется $n = 1,2, \ldots $ узловых точек. В случае, когда предполагаемое количество узловых точек $n$ превосходит действительное количество узловых точек области $D$, некоторые получаемые значения ${{w}_{k}}$ окажутся паразитными. Для исключения паразитных решений используется следующий критерий.
Обозначим ${{A}_{{n\max }}} = \mathop {\max }\limits_{k = 1, \ldots ,n} \left| {{{A}_{k}}} \right|$. Узловые точки ${{z}_{k}}$, для которых соответствующие коэффициенты ${{A}_{k}}$ удовлетворяют неравенству $\left| {{{A}_{k}}} \right|{\text{/}}{{A}_{{n\max }}} < {{\varepsilon }_{{{\text{cr}}}}}$, где ${{\varepsilon }_{{{\text{cr}}}}}$ – некоторая малая величина, считаются паразитными и исключаются из рассмотрения. В численном примере, рассмотренном ниже, принято ${{\varepsilon }_{{{\text{cr}}}}} = 0.01$.
В представленных выше теоретических результатах упругое тело предполагалось безграничным. В рассмотренном ниже примере упругое тело конечно, но характерные размеры дефекта малы по сравнению с характерными размерами тела, что позволяет использовать полученные результаты.
Пример. Предположим, что упругое тело занимает квадратную область $\Omega $ = {x = $({{x}_{1}},{{x}_{2}})$ : $\left| {{{x}_{i}}} \right| \leqslant L$, $i = 1,2\} $, $L = 10$ см. Упругие постоянные материала предполагаются равными: модуль Юнга ${{E}_{M}} = 2{{\mu }_{M}}\left( {1 + {{\nu }_{M}}} \right)$ = 68.5 ГПа, коэффициент Пуассона ${{\nu }_{M}} = 0.36$. Предположим также, что приложенные к границе тела $\partial \Omega $ нагрузки представляют собой одноосное растяжение в направлении оси ${{x}_{2}}$.
(28)
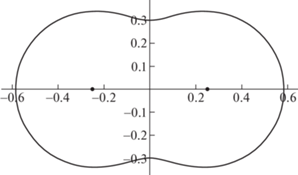
${{{\mathbf{t}}}^{0}}\left( {x{\kern 1pt} '} \right) = \left( {0,\sigma {{n}_{2}}\left( {x{\kern 1pt} '} \right)} \right),\quad x{\kern 1pt} ' \in \partial \Omega ,$Переопределенные данные (перемещения на внешней границе тела $\partial \Omega $) получены путем численного решения прямой задачи для тела с неоднородностью при заданных условиях (28) на границе тела $\partial \Omega $. Рассмотрим случай, когда дефектом является полость, имеющая форму овала Неймана, ограниченного контуром (см. рис. 1).
(29)
$\begin{gathered} {{x}_{1}}\left( t \right) = \sqrt {{{a}^{2}} + 4{{\varepsilon }^{2}}{{{\cos }}^{2}}\left( t \right)} \cos t, \\ {{x}_{2}}\left( t \right) = \sqrt {{{a}^{2}} + 4{{\varepsilon }^{2}}{{{\cos }}^{2}}\left( t \right)} \sin t,\quad 0 \leqslant t < 2\pi . \\ \end{gathered} $В примере приняты следующие значения постоянных: $a = 0.3$ и $\varepsilon = 0.25$.
Согласно [5], функция Шварца для овала Неймана, соответствующего уравнению (29), имеет вид
(30)
$S\left( z \right) = \frac{{z\left( {{{a}^{2}} + 2{{\varepsilon }^{2}}} \right) + z\sqrt {{{a}^{4}} + 4\left( {{{a}^{2}} + {{z}^{2}}} \right){{\varepsilon }^{2}}} }}{{2\left( {{{z}^{2}} - {{\varepsilon }^{2}}} \right)}}.$Как видно из (30), функция Шварца имеет два простых полюса в точках $z = \pm \varepsilon $. Таким образом, полость является квадратурной областью второго порядка. Проведенные численные расчеты показали, что, начиная с $n = 2$, после применения принятого выше критерия остаются ровно две узловые точки. Проиллюстрируем это результатом расчетов для предполагаемого количества узловых точек $n = 10$. В табл. 1 представлены все 10 узловых точек ${{z}_{k}}$, отвечающих $n = 10$, и соответствующие им нормированные коэффициенты ${{\alpha }_{k}} = \left| {{{A}_{k}}} \right|{\text{/}}{{A}_{{n\max }}}$.
Таблица 1.
Получаемые узловые точки в случае $n = 10$
| k | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| ${{\alpha }_{k}}$ | $5.54 \times {{10}^{{ - 8}}}$ | $4.60 \times {{10}^{{ - 10}}}$ | $1.40 \times {{10}^{{ - 7}}}$ | $9.61 \times {{10}^{{ - 5}}}$ | 1 |
| ${{z}_{k}}$ | $ - 9.55 - 9.63i$ | $ - 8.11 + 8.34i$ | $ - 7.56 - 7.98i$ | $ - 0.42 - 1.88i$ | $ - 0.226 - 0.003i$ |
| k | 6 | 7 | 8 | 9 | 10 |
| ${{\alpha }_{k}}$ | 0.997 | $5.36 \times {{10}^{{ - 8}}}$ | $1.04 \times {{10}^{{ - 7}}}$ | $1.88 \times {{10}^{{ - 10}}}$ | $4.14 \times {{10}^{{ - 8}}}$ |
| ${{z}_{k}}$ | $0.227 - 0.003i$ | $4.07 + 4.03i$ | $7.55 - 8.07i$ | $9.07 + 8.12i$ | $9.54 - 9.64i$ |
Из табл. 1 следует, что согласно принятому критерию остаются только две узловые точки под номерами $k = 5$ и $k = 6$. Полученные приближенно значения координат этих точек достаточно близки к точным.
Список литературы
Andrieux S., Ben Abda A. Identification of planar cracks by complete overdetermined data: inversion formulae // Inverse Problems. 1996. V. 12. P. 553–563.
Andrieux S., Ben Abda A., Bui H. Reciprocity principle and crack identification // Inverse Problems. 1999. V. 15. P. 59–65.
Shifrin E.I., Shushpannikov P.S. Identification of small well-separated defects in an isotropic elastic body using boundary measurements // International Journal of Solids and Structures. 2013. V. 50. P. 3707–3716.
Shifrin E.I., Kaptsov A.V. Identification of multiple cracks in 2D elasticity by means of the reciprocity principle and cluster analysis // Inverse Problems. 2018. V. 34. 015009.
Davis P.J. The Schwarz function and its applications. The Carus Mathematical Monographs 17. Mathematical Association of America. 1974. 228 p.
Aharonov D., Shapiro H.S. Domains on which analytic functions satisfy quadrature identities // Journal d’Analyse Mathematique. 1976. V. 30. P. 39–73.
Gustafsson B. Quadrature identities and the Schottky double // Acta Applicandae Mathematicae. 1983. V. 1. P. 209–240.
Bell S.R. Quadrature domains and kernel function zipping //Arkiv for matematik. 2005. V. 43. P. 271–287.
Bell S.R. Density of quadrature domains in one and several complex variables // Complex Variables and Elliptic Equations. 2009. V. 54. P. 165–171.
Ameur Y., Helmer M., Tellander F. On the uniqueness problem for quadrature domains // Computational Methods and Function Theory. 2021. V. 21. P. 473–504.
Мусхелишвили Н.И. Некоторые основные задачи математической теории упругости. М. Наука. 1966. 708 с.
Golub G.H., Milanfar P., Varah J. A stable numerical method for inverting shape from moments // SIAM J. Sci. Comput. 1999. V. 21. P. 1222–1243.
El Badia A., Ha-Duong T. An inverse source problem in potential analysis // Inverse Problems 2000. V. 16. P. 651–663.
Kang H., Lee H. Identification of simple poles via boundary measurements and an application of EIT // Inverse Problems. 2004. V. 20. P. 1853–1863.
Дополнительные материалы отсутствуют.
Инструменты
Доклады Российской академии наук. Математика, информатика, процессы управления