1. На главную
  2. Электронные версии
  3. Доклады Российской академии наук. Математика, информатика, процессы управления
  4. T. 510, № 1, 2023

Доклады Российской академии наук. Математика, информатика, процессы управления, 2023, T. 510, № 1, стр. 13-17

НЕСТАЦИОНАРНАЯ ЗАДАЧА ВЕНТЦЕЛЯ СО СТАРШИМИ КОЭФФИЦИЕНТАМИ ИЗ КЛАССА VMOx

Д. Е. Апушкинская 1, 2, *, А. И. Назаров 1, 3, **, Д. К. Палагачев 4, ***, Л. Г. Софтова 5, ****

1 Санкт-Петербургское отделение Математического института им. В.А. Стеклова Российской академии наук
Санкт-Петербург, Россия

2 Российский университет дружбы народов
Москва, Россия

3 Санкт-Петербургский государственный университет
Санкт-Петербург, Россия

4 Политехнический университет
Бари, Италия

5 Университет Салерно
Фишиано, Италия

* E-mail: apushkinskaya@gmail.com
** E-mail: al.il.nazarov@gmail.com
*** E-mail: dian.palagachev@poliba.it
**** E-mail: lsoftova@unisa.it

Поступила в редакцию 30.11.2022
После доработки 21.02.2023
Принята к публикации 24.02.2023

Полный текст (PDF)

Аннотация

Получены новые результаты о сильной разрешимости в пространствах Соболева линейной начально-краевой задачи Вентцеля для параболических уравнений с разрывными старшими коэффициентами.

Ключевые слова: линейные параболические уравнения второго порядка, задача Вентцеля, априорная оценка, класс VMOx, существование и единственность

Задача Вентцеля, впервые введенная в [1], представляет собой наиболее общую краевую задачу для эллиптического оператора второго порядка, которая порождает генератор марковского процесса. Эта задача, а также ее параболический аналог, возникают в различных приложениях (см. например, ссылки в [2] и [3]).

Практически все имеющиеся работы о разрешимости и регулярности решений задачи Вентцеля предполагают непрерывность старших коэффициентов как оператора в области, так и оператора в граничном условии. В недавней статье авторов [3] регулярность и сильная разрешимость в пространствах Соболева впервые были получены для стационарных задач Вентцеля в случае, когда и оператор в области, и граничный оператор имеют разрывные старшие коэффициенты из класса VMO. Отметим, что соответствующие результаты для краевых задач Дирихле, Неймана и Робена в эллиптическом и параболическом случаях были установлены ранее, см. [4–7].

Важно отметить, что в статье [3] ограничения на младшие коэффициенты операторов в области и на границе оптимальны в терминах пространств Лебега и Орлича. Вывод коэрцитивных оценок для решений линейной эллиптической задачи Вентцеля при этих ограничениях потребовал тонкой аналитической техники, включающей теоремы вложения для соболевских пространств, зависящие от соотношения показателей суммируемости в области и на границе, а также оценки норм специальных операторов продолжения.

В настоящей статье мы переносим результаты [3] на параболические задачи Вентцеля в композитных пространствах Соболева $W_{p}^{{2,1}}({{\mathcal{Q}}_{T}})\, \cap \,W_{q}^{{2,1}}({{\Gamma }_{T}})$. При этом предполагается, что старшие коэффициенты как в уравнении, так и в граничном условии, принадлежат пространству VMO по переменным $x$, но только измеримы относительно переменной $t$. Младшие же коэффициенты принадлежат пространствам Лебега или Орлича, причем ограничения на них оптимальны (неулучшаемы) в этих шкалах.

Для непрерывных старших коэффициентов аналогичные результаты были получены в [8], однако требования на младшие коэффициенты в этой статье далеки от оптимальных.

Наши результаты могут быть обобщены на случай анизотропных пространств Соболева $W_{{p,r}}^{{2,1}}$, но в этом сообщении мы ограничиваемся изотропным случаем.

В статье используются следующие обозначения:

$x = ({{x}_{1}}, \ldots ,{{x}_{n}}) \in {{\mathbb{R}}^{n}}$, $n \geqslant 2$; |x| – евклидова норма x; $(x;t) \in {{\mathbb{R}}^{{n + 1}}}$.

$\Omega $ – гладкая ограниченная область в ${{\mathbb{R}}^{n}}$; $\overline \Omega $ – ее замыкание, $\partial \Omega $ – граница.

${\mathbf{n}}(x) = ({{{\mathbf{n}}}_{1}}(x), \ldots ,{{{\mathbf{n}}}_{n}}(x))$ – единичный вектор внешней нормали к $\partial \Omega $ в точке x.

${{\mathcal{Q}}_{T}} = \Omega \times (0,T)$ – цилиндр в ${{\mathbb{R}}^{{n + 1}}}$; ΓT = = $\partial \Omega \times (0,T)$ – его боковая поверхность.

${{B}_{\rho }}({{x}^{0}})$ – открытый шар в ${{\mathbb{R}}^{n}}$ с центром в x0 и радиусом ρ, ${{Q}_{\rho }}({{x}^{0}};{{t}^{0}}) = {{B}_{\rho }}({{x}^{0}}) \times ({{t}^{0}} - {{\rho }^{2}},{{t}^{0}})$ – стандартный параболический цилиндр.

Для измеримого множества E обозначим через |E| меру Лебега соответствующей размерности, а через ${{L}^{p}}(E)$ – стандартное пространство Лебега с нормой ${\text{||}}\, \cdot \,{\text{|}}{{{\text{|}}}_{{p,E}}}$. Далее, ${{f}_{ + }} = \max \{ f;0\} $, а среднее значение функции f на E записывается как

$ - \int\limits_E f = \frac{1}{{{\text{|}}E{\text{|}}}}\int\limits_E f.$

Всюду в работе индексы i, j изменяются от 1 до n. По повторяющимся индексам предполагается суммирование.

Di, ${{\partial }_{t}}$ – операторы дифференцирования по переменным xi и t соответственно; Du = $({{D}_{1}}u, \ldots ,{{D}_{n}}u)$ – градиент функции u.

di – касательный дифференциальный оператор на $\partial \Omega $:

${{d}_{i}} = {{D}_{i}} - {{{\mathbf{n}}}_{i}}{{{\mathbf{n}}}_{j}}{{D}_{j}};$

$du = ({{d}_{1}}u, \ldots ,{{d}_{n}}u)$ – касательный градиент u на $\partial \Omega $.

$W_{p}^{{2,1}}({{\mathcal{Q}}_{T}})$ и $W_{q}^{{2,1}}({{\Gamma }_{T}})$ – параболические пространства Соболева с нормами

$\begin{gathered} {\text{||}}u{\text{|}}{{{\text{|}}}_{{W_{p}^{{2,1}}({{\mathcal{Q}}_{T}})}}} = {\text{||}}{{\partial }_{t}}u{\text{|}}{{{\text{|}}}_{{p,{{\mathcal{Q}}_{T}}}}} + \;{\text{||}}D(Du){\text{|}}{{{\text{|}}}_{{p,{{\mathcal{Q}}_{T}}}}} + \;{\text{||}}u{\text{|}}{{{\text{|}}}_{{p,{{\mathcal{Q}}_{T}}}}}, \\ {\text{||}}u{\text{|}}{{{\text{|}}}_{{W_{q}^{{2,1}}({{\Gamma }_{T}})}}} = {\text{||}}{{\partial }_{t}}u{\text{|}}{{{\text{|}}}_{{q,{{\Gamma }_{T}}}}} + \;{\text{||}}d(du){\text{|}}{{{\text{|}}}_{{q,{{\Gamma }_{T}}}}} + \;{\text{||}}u{\text{|}}{{{\text{|}}}_{{q,{{\Gamma }_{T}}}}}. \\ \end{gathered} $

Мы будем обозначать через ${{V}_{{p,q}}}({{\mathcal{Q}}_{T}})$ = = $W_{p}^{{2,1}}({{\mathcal{Q}}_{T}}) \cap W_{q}^{{2,1}}({{\Gamma }_{T}})$ пространство всех $W_{p}^{{2,1}}({{\mathcal{Q}}_{T}})$-функций, имеющих след из $W_{q}^{{2,1}}({{\Gamma }_{T}})$; норма в нем определяется формулой

${\text{||}}u{\text{|}}{{{\text{|}}}_{{{{V}_{{p,q}}}({{\mathcal{Q}}_{T}})}}} = {\text{||}}u{\text{|}}{{{\text{|}}}_{{W_{p}^{{2,1}}({{\mathcal{Q}}_{T}})}}} + \;{\text{||}}u{\text{|}}{{{\text{|}}}_{{W_{q}^{{2,1}}({{\Gamma }_{T}})}}}.$
${{\mathcal{C}}^{{1,1}}}$ – пространство функций, имеющих липшицевы первые производные. Далее, условие $\partial \Omega \in {{\mathcal{C}}^{{1,1}}}$ означает, что существует такой радиус ${{\Re }_{0}} > 0$, что для любой точки ${{x}^{0}} \in \partial \Omega $ множество $\partial \Omega \cap {{B}_{{{{\Re }_{0}}}}}({{x}^{0}})$ в подходящей декартовой системе координат есть график ${{y}_{n}} = f({{y}_{1}}, \ldots ,{{y}_{{n - 1}}})$ функции $f \in {{\mathcal{C}}^{{1,1}}}$. Выражение “константа зависит от свойств $\partial \Omega $” означает зависимость от ${{\Re }_{0}}$, от ${{\mathcal{C}}^{{1,1}}}$-норм диффеоморфизмов, используемых при локальном распрямлении $\partial \Omega $ и от площади $\partial \Omega $.

Различные положительные постоянные обозначаются через C и N с индексами или без них.

Следуя [6], для локально интегрируемой функции $a:\;{{\mathbb{R}}^{{n + 1}}} \to \mathbb{R}$ определим среднюю осцилляцию по пространственным переменным в цилиндре ${{Q}_{\rho }}(x;t)$ формулой:

(1)
$\begin{gathered} \,\,\,\,\,\,\,\,\,\,\,\,{\text{os}}{{{\text{c}}}_{x}}(a,{{Q}_{\rho }}(x;t)) = \\ - - - = \int\limits_{t - {{\rho }^{2}}}^t \int\limits_{{{B}_{\rho }}(x)} \int\limits_{{{B}_{\rho }}(x)\,} a(y;\tau ) - a(z,\tau ){\text{|}}{\kern 1pt} dydzd\tau \\ \end{gathered} $
и положим

$a_{R}^{{\# (x)}} = \mathop {\sup }\limits_{(x;t) \in {{\mathbb{R}}^{{n + 1}}}} \mathop {\sup }\limits_{\rho \leqslant R} {\text{os}}{{{\text{c}}}_{x}}(a,{{Q}_{\rho }}(x;t)).$

Говорят, что $a\, \in \,BM{{O}_{x}}$, если $a_{R}^{{\# (x)}}$ ограничена равномерно по R > 0, и $a\, \in \,VM{{O}_{x}}$, если ${{\lim }_{{R \to 0}}}a_{R}^{{\# (x)}}$ = 0 (при этом $a_{R}^{{\# (x)}}$ называется $VM{{O}_{x}}$-модулем непрерывности функции a).

Для цилиндра ${{\mathcal{Q}}_{T}}$ пространства $BM{{O}_{x}}({{Q}_{T}})$ и $VM{{O}_{x}}({{\mathcal{Q}}_{T}})$ вводятся аналогично, с заменой в (1) интегрирования по ${{B}_{\rho }}(x)$ на ${{B}_{\rho }}(x) \cap \Omega $ и $(t - {{\rho }^{2}},t)$ на $(t - {{\rho }^{2}},t) \cap (0,T)$. Пространства $BM{{O}_{x}}({{\Gamma }_{T}})$ и $VM{{O}_{x}}({{\Gamma }_{T}})$ (в случае гладкой поверхности $\partial \Omega $) определяются соответственно через поверхностные интегралы по ${{B}_{\rho }}(x) \cap \partial \Omega $ для $(x;t) \in {{\Gamma }_{T}}$.

В отличие от пространства Джона–Ниренберга BMO (см. [9]) и класса Сарасона VMO (см. [10]), которые требуют, соответственно, “ограниченности в среднем” и “непрерывности в среднем” по всем переменным $(x;t)$, пространства $BM{{O}_{x}}$ и $VM{{O}_{x}}$ требуют этих свойств лишь по пространственным переменным x, допуская функции, лишь измеримые по t. В частности, если $a(x;t)$ не зависит от x, то $a \in VM{{O}_{x}}$ автоматически, но вообще говоря, $a \notin VMO$.

Следующее утверждение является обобщением теоремы 6.1 [8].

Теорема 1. Пусть $\partial \Omega \in {{\mathcal{C}}^{{1,1}}}$ и пусть показатели p и q удовлетворяют условиям

$1 \leqslant p \leqslant q{\kern 1pt} \frac{{n + 2}}{{n + 1}},\quad q > 1.$

Тогда существует оператор продолжения

$\Pi :\;W_{q}^{{2,1}}({{\Gamma }_{T}}) \to W_{p}^{{2,1}}({{\mathcal{Q}}_{T}})$
такой, что
(2)
${\text{||}}\Pi u{\text{|}}{{{\text{|}}}_{{W_{p}^{{2,1}}({{\mathcal{Q}}_{T}})}}} \leqslant {{N}_{0}}{\text{||}}u{\text{|}}{{{\text{|}}}_{{W_{q}^{{2,1}}({{\Gamma }_{T}})}}},$
где N0зависит только от p, q и свойств $\partial \Omega $.

Доказательство базируется на применении теорем вложения [11, теорема 18.12] и продолжения [11, теорема 18.13] в пространствах Соболева и Бесова, а также на локальном распрямлении границы и склеивании полученных оценок с помощью подходящего разбиения единицы.

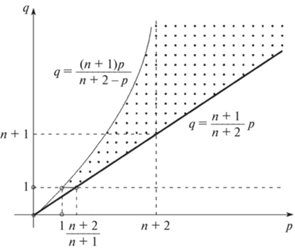
Пусть показатели q и p удовлетворяют условиям (см. рис. 1)

(3)
$1 < p \leqslant q{\kern 1pt} \frac{{n + 2}}{{n + 1}} < p{\kern 1pt} *: = \frac{{(n + 2)p}}{{{{{(n + 2 - p)}}_{ + }}}}\quad {\text{и}}\quad q > 1.$
Рис. 1.

Допустимые показатели p и q.

Рассмотрим линейный равномерно параболический оператор $\mathcal{L}$,

(4)
$\mathcal{L}: = {{\partial }_{t}} - {{a}^{{ij}}}(x;t){{D}_{i}}{{D}_{j}} + {{b}^{i}}(x;t){{D}_{i}} + c(x;t),$
(L1)
$\begin{gathered} {{a}^{{ij}}}(x;t) = {{a}^{{ji}}}(x;t)\quad (x;t) \in {{\mathcal{Q}}_{T}}, \\ {{a}^{{ij}}} \in VM{{O}_{x}}{\kern 1pt} ({{\mathcal{Q}}_{T}}), \\ \end{gathered} $
(L2)
$\begin{gathered} \nu {\text{|}}\xi {{{\text{|}}}^{2}} \leqslant {{a}^{{ij}}}{{\xi }_{i}}{{\xi }_{j}} \leqslant {{\nu }^{{ - 1}}}{\text{|}}\xi {{{\text{|}}}^{2}}\quad \forall \xi \in {{\mathbb{R}}^{n}}, \\ \nu = {\text{const}} > 0, \\ \end{gathered} $
и линейный равномерно параболический граничный оператор $\mathcal{B}$,

(5)
$\mathcal{B}: = {{\partial }_{t}} - {{\alpha }^{{ij}}}(x;t){{d}_{i}}{{d}_{j}} + {{\beta }^{i}}(x;t){{D}_{i}} + \gamma (x;t),$
(B1)
$\begin{gathered} {{\alpha }^{{ij}}}(x;t) = {{\alpha }^{{ji}}}(x;t)\quad (x;t) \in {{\Gamma }_{T}}, \\ {{\alpha }^{{ij}}} \in VM{{O}_{x}}{\kern 1pt} ({{\Gamma }_{T}}), \\ \end{gathered} $
(B2)
$\begin{gathered} \nu {\text{|}}\xi {\kern 1pt} *{{{\text{|}}}^{2}} \leqslant {{\alpha }^{{ij}}}\xi _{i}^{*}\xi _{j}^{*} \leqslant {{\nu }^{{ - 1}}}{\text{|}}\xi {\kern 1pt} *{{{\text{|}}}^{2}}, \\ \forall \xi {\kern 1pt} * \in {{\mathbb{R}}^{n}},\quad \xi {\kern 1pt} * \bot {\mathbf{n}}(x). \\ \end{gathered} $

Обозначим ${\mathbf{b}}(x;t) = ({{b}^{1}}(x;t), \ldots ,{{b}^{n}}(x;t))$ и предположим, что младшие коэффициенты оператора $\mathcal{L}$ удовлетворяют следующим условиям:

(L3)
$\begin{gathered} {\text{|}}{\mathbf{b}}{\text{|}} \in {{L}^{{\max \{ p,n + 2\} }}}({{\mathcal{Q}}_{T}}),\quad {\text{если}}\quad p \ne n + 2, \\ {\text{|}}{\mathbf{b}}{\text{|}}{{\left( {\log (1\; + \;{\text{|}}{\mathbf{b}}{\text{|}})} \right)}^{{\frac{{n + 1}}{{n + 2}}}}} \in {{L}^{{n + 2}}}({{\mathcal{Q}}_{T}}), \\ {\text{если}}\quad p = n + 2, \\ \end{gathered} $
и

(L4)
$\begin{gathered} c \in {{L}^{{\max \left\{ {p,\frac{{n + 2}}{2}} \right\}}}}({{\mathcal{Q}}_{T}}),\quad {\text{если}}\quad p \ne \frac{{n + 2}}{2}, \\ c{{\left( {\log (1\; + \;{\text{|}}c{\text{|}})} \right)}^{{\frac{n}{{n + 2}}}}} \in {{L}^{{\frac{{n + 2}}{2}}}}({{\mathcal{Q}}_{T}}), \\ {\text{если}}\quad p = \frac{{n + 2}}{2}. \\ \end{gathered} $

Далее, обозначим ${\mathbf{\beta }}(x;t) = ({{\beta }^{1}}(x;t), \ldots ,{{\beta }^{n}}(x;t))$, введем нормальную и касательную компоненты вектора ${\mathbf{\beta }}(x;t)$

$\begin{gathered} {{\beta }_{0}}(x;t): = {{\beta }^{i}}(x;t){{{\mathbf{n}}}_{i}}(x); \\ {\mathbf{\beta }}{\kern 1pt} *(x;t): = {\mathbf{\beta }}(x;t) - {{\beta }_{0}}(x;t){\mathbf{n}}(x) \\ \end{gathered} $
и предположим, что

(B3)
$\begin{gathered} {\text{|}}{\mathbf{\beta }}{\kern 1pt} *{\text{|}} \in {{L}^{{\max \{ q,n + 1\} }}}({{\Gamma }_{T}}),\quad {\text{если}}\quad q \ne n + 1, \\ {\text{|}}{\mathbf{\beta }}{\kern 1pt} *{\text{|}}{{\left( {\log (1\; + \;{\text{|}}{\mathbf{\beta }}{\kern 1pt} *{\text{|}})} \right)}^{{\frac{n}{{n + 1}}}}} \in {{L}^{{n + 1}}}({{\Gamma }_{T}}), \\ {\text{если}}\quad q = n + 1, \\ \end{gathered} $
(B4)
$\begin{gathered} {{\beta }_{0}} \in {{L}^{q}}({{\Gamma }_{T}}),\quad {\text{если}}\quad p > n + 2, \\ {{\beta }_{0}} \in {{L}^{{qp{\kern 1pt} */\left( {p{\kern 1pt} * - q\frac{{n + 2}}{{n + 1}}} \right)}}}({{\Gamma }_{T}}),\quad {\text{если}}\quad p < n + 2, \\ {{\beta }_{0}}{{(\log (1\, + \,{\text{|}}{{\beta }_{0}}{\text{|}}))}^{{\frac{{n + 1}}{{n + 2}}}}}\, \in \,{{L}^{q}}({{\Gamma }_{T}}),\quad {\text{если}}\quad p\, = \,n\, + \,2, \\ \end{gathered} $
(B5)
$\begin{gathered} \gamma \in {{L}^{{\max \left\{ {q,\frac{{n + 1}}{2}} \right\}}}}({{\Gamma }_{T}}),\quad {\text{если}}\quad q \ne \frac{{n + 1}}{2}, \\ \gamma {{(\log (1\; + \;{\text{|}}\gamma {\text{|}}))}^{{\frac{{n - 1}}{{n + 1}}}}}\, \in \,{{L}^{{\frac{{n + 1}}{2}}}}({{\Gamma }_{T}}),\quad {\text{если}}\quad q\, = \,\frac{{n + 1}}{2}. \\ \end{gathered} $

Теперь мы готовы сформулировать основной результат работы.

Теорема 2. Пусть $\partial \Omega \in {{\mathcal{C}}^{{1,1}}}$ и выполнены условия (3), (L1)–(L4) и (B1)–(B5).

Тогда для любых $f \in {{L}^{p}}({{\mathcal{Q}}_{T}})$ и $g \in {{L}^{q}}({{\Gamma }_{T}})$ начально-краевая задача

(6)
$\mathcal{L}u(x;t) = f(x;t)\quad {\text{в}}\quad {{\mathcal{Q}}_{T}},$
(7)
$\mathcal{B}u(x;t) = g(x;t)\quad {\text{на}}\quad {{\Gamma }_{T}}$
с начальным условием $u{{{\text{|}}}_{{t = 0}}} = 0$ в $\overline \Omega $ имеет единственное решение $u \in {{V}_{{p,q}}}({{\mathcal{Q}}_{T}})$, и справедлива оценка
(8)
${\text{||}}u{\text{|}}{{{\text{|}}}_{{{{V}_{{p,q}}}({{\mathcal{Q}}_{T}})}}} \leqslant C({\text{||}}f{\text{|}}{{{\text{|}}}_{{p,{{\mathcal{Q}}_{T}}}}} + \;{\text{||}}g{\text{|}}{{{\text{|}}}_{{q,{{\Gamma }_{T}}}}}),$
где C зависит только от $n$, $\nu $, p, q, ${\text{diam}}{\kern 1pt} \Omega $, T, свойств $\partial \Omega $ и от $VM{{O}_{x}}$-модулей непрерывности коэффициентов ${{a}^{{ij}}}(x;t)$ и ${{\alpha }^{{ij}}}(x;t)$, а также от модулей абсолютной непрерывности функций |b|, $c$, ${\text{|}}{\mathbf{\beta }}{\kern 1pt} *{\text{|}}$, ${{\beta }_{0}}$ и $\gamma $ в соответствующих функциональных пространствах, определенных условиями (L3)–(L4) и (B3)–(B5).

Набросок доказательства. Стандартное рассуждение, основанное на продолжении по параметру, сводит доказательство теоремы к выводу априорной оценки (8) для решений задачи (6)–(7) с однородным начальным условием.

Для получения этой оценки мы используем прием Мюнхаузена (ср. [3, теорема 3.1], см. также [8, теорема 2.2]). При введенных условиях на младшие коэффициенты, используя анизотропные теоремы вложения (см. [11, §§ 10.2–10.6]), мы получаем оценки на младшие члены в уравнениях (6) и (7), которые позволяют рассматривать их как компактные операторы из ${{V}_{{p,q}}}({{\mathcal{Q}}_{T}})$ в ${{L}^{p}}({{\mathcal{Q}}_{T}})$ и ${{L}^{q}}({{\Gamma }_{T}})$ соответственно. Вместе с теоремой 1 и теоремой о разрешимости задачи Дирихле для параболических уравнений со старшими коэффициентами из пространства VMOx [7, Theorem 6] это дает оценку

(9)
$\begin{gathered} {\text{||}}u{\text{|}}{{{\text{|}}}_{{{{V}_{{p,q}}}({{\mathcal{Q}}_{T}})}}} \leqslant {{C}_{1}}({\text{||}}f{\text{|}}{{{\text{|}}}_{{p,{{\mathcal{Q}}_{T}}}}} + \;{\text{||}}g{\text{|}}{{{\text{|}}}_{{q,{{\Gamma }_{T}}}}} + \\ + \;{\text{||}}u{\text{|}}{{{\text{|}}}_{{p,{{\mathcal{Q}}_{T}}}}} + \;{\text{||}}u{\text{|}}{{{\text{|}}}_{{q,{{\Gamma }_{T}}}}} + \;{\text{||}}{{\beta }_{0}}{{\partial }_{{\mathbf{n}}}}u{\text{|}}{{{\text{|}}}_{{q,{{\Gamma }_{T}}}}}), \\ \end{gathered} $
а затем позволяет оценить слагаемое ${{\beta }_{0}}{{\partial }_{{\mathbf{n}}}}u$ через само себя:
$\begin{gathered} {\text{||}}{{\beta }_{0}}{{\partial }_{{\mathbf{n}}}}u{\text{|}}{{{\text{|}}}_{{q,{{\Gamma }_{T}}}}} \leqslant \varepsilon {\text{||}}{{\beta }_{0}}{{\partial }_{{\mathbf{n}}}}u{\text{|}}{{{\text{|}}}_{{q,{{\Gamma }_{T}}}}} + \\ \, + \tilde {C}(\varepsilon )({\text{||}}f{\text{|}}{{{\text{|}}}_{{p,{{\mathcal{Q}}_{T}}}}} + \;{\text{||}}g{\text{|}}{{{\text{|}}}_{{q,{{\Gamma }_{T}}}}} + \;{\text{||}}u{\text{|}}{{{\text{|}}}_{{p,{{\mathcal{Q}}_{T}}}}} + \;{\text{||}}u{\text{|}}{{{\text{|}}}_{{q,{{\Gamma }_{T}}}}}) \\ \end{gathered} $
с произвольным $\varepsilon > 0$. Положим $\varepsilon = \frac{1}{2}$ и подставим в (9) очевидное неравенство ${\text{||}}u{\text{|}}{{{\text{|}}}_{{p,{{\mathcal{Q}}_{T}}}}}$ + ${\text{||}}u{\text{|}}{{{\text{|}}}_{{q,{{\Gamma }_{T}}}}}\, \leqslant \,T{\text{||}}u{\text{|}}{{{\text{|}}}_{{{{V}_{{p,q}}}({{\mathcal{Q}}_{T}})}}}$. При достаточно малом T это дает (8). В общем случае следует разбить ${{\mathcal{Q}}_{T}}$ на цилиндры малой высоты и получить в них оценки последова-тельно. 

Замечание 3. При $p < n + 2$ условие (L3) может быть ослаблено в терминах параболических пространств Морри с помощью теоремы 4.1 из [12] следующим образом:

$\begin{gathered} \mathop {\lim }\limits_{\rho \to 0} {{\rho }^{{1 - \frac{{n + 2}}{{{{p}_{1}}}}}}}\mathop {\sup }\limits_{(x;t) \in {{\mathcal{Q}}_{T}}} {\text{||}}{{b}^{i}}{\text{|}}{{{\text{|}}}_{{{{p}_{1}},{{Q}_{\rho }}(x;t) \cap {{\mathcal{Q}}_{T}}}}} = 0 \\ для\;некоторого\quad {{p}_{1}} \in (p,n + 2). \\ \end{gathered} $

Аналогичным образом можно ослабить условия (L4) (при $p\, < \,\frac{{n\, + \,2}}{2}$), (B3) (при $q < n + 1$) и (B5) (при $q\, < \,\frac{{n\, + \,1}}{2}$).

Отметим также, что условия ${{a}^{{ij}}} \in VM{{O}_{x}}{\kern 1pt} ({{\mathcal{Q}}_{T}})$ и ${{\alpha }^{{ij}}} \in VM{{O}_{x}}{\kern 1pt} ({{\Gamma }_{T}})$ можно заменить на условия достаточной малости величин $({{a}^{{ij}}})_{R}^{{\# (x)}}$ и $({{\alpha }^{{ij}}})_{R}^{{\# (x)}}$ при малых R, см. [7].

Список литературы

  1. Вентцель А.Д. О граничных условиях для многомерных диффузионных процессов // Теория вероятн. и ее примен. 1959. Т. 4. № 2. С. 172–185.

  2. Apushkinskaya D.E., Nazarov A.I. A survey of results on nonlinear Venttsel problems // Appl. Math. 2000. V. 45. № 1. P. 69–80.

  3. Apushkinskaya D.E., Nazarov A.I., Palagachev D.K., Softova L.G. Venttsel boundary value problems with discontinuous data // SIAM J. Math. Anal. 2021. V. 53. № 1. P. 221–252.

  4. Chiarenza F., Frasca M., Longo P. W2,p-solvability of the Dirichlet problem for nondivergence elliptic equations with VMO coefficients // Trans. Amer. Math. Soc. 1993. V. 336. № 2. P. 841–853.

  5. Maugeri A., Palagachev D.K., Softova L.G. Elliptic and parabolic equations with discontinuous coefficients, volume 109 of Mathematical Research. Wiley-VCH Verlag Berlin GmbH, Berlin, 2000.

  6. Krylov N.V. Lectures on elliptic and parabolic equations in Sobolev spaces, volume 96 of Graduate Studies in Mathematics. American Mathematical Society, Providence, RI, 2008.

  7. Dong H., Kim D. On the Lp-solvability of higher order parabolic and elliptic systems with BMO coefficients // Arch. Ration. Mech. Anal. 2011. V. 199. № 3. P. 889–941.

  8. Апушкинская Д.Е., Назаров А.И. Начально-краевая задача с граничным условием Вентцеля для недивергентных параболических уравнений // Алгебра и анализ. 1994. Т. 6. № 6. С. 1–29.

  9. John F., Nirenberg L. On functions of bounded mean oscillation // Comm. Pure Appl. Math. 1961. V. 14. P. 415–426.

  10. Sarason D. Functions of vanishing mean oscillation // Trans. Amer. Math. Soc. 1975. V. 207. P. 391–405.

  11. Бесов О.В., Ильин В.П., Никольский С.М. Интегральные представления функций и теоремы вложения. Наука, М., 1996. 2-е изд., перераб. и доп.

  12. Krylov N.V. On parabolic Adams’s, the Chiarenza-Frasca theorems, and some other results related to parabolic Morrey spaces // Math. Eng. 2023. V. 5. № 2. P. 1–20.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Доклады Российской академии наук. Математика, информатика, процессы управления

Архивы выпусков Информация о журнале Отправить рукопись в журнал