Доклады Российской академии наук. Математика, информатика, процессы управления, 2023, T. 510, № 1, стр. 52-56

1. Триангуляция используется для многих целей, включая геодезию, навигацию, метрологию, астрометрию, бинокулярное зрение и т.д. В геометрии триангуляция рассматривается как разбиение некоторой геометрической области n-мерного евклидова пространства на n-мерные симплексы. В настоящей работе рассматривается классическая триангуляция на плоскости. Одним из широко используемых методов является триангуляция Делоне, задача построения которой была впервые поставлена в 1934 г. в работе [1]. В вычислительном аспекте необходимость триангуляции обусловлена потребностью решения многих задач вычислительной математики и математической физики, сводящихся к решению дифференциальных уравнений в частных производных в нерегулярных областях и на нерегулярных сетках [2]. В частности, отметим разрывный метод Галеркина [3], для которого благодаря его универсальности и применимости к сложным геометрическим областям задача построения триангуляции является весьма актуальной. К настоящему времени в отечественных и зарубежных журналах и издательствах опубликовано большое число статей и монографий, посвященных методам построений триангуляций, включающих различные аспекты [4–11]. Обратим внимание, что точность вычислений может в значительной мере зависеть от того, насколько близки к вырождению присутствующие в триангуляции треугольные элементы. Поэтому помимо триангуляции, использующей заданные узлы [7–11], представляется актуальным построение некоторой модельной триангуляции с контролируемым качеством треугольных элементов, предназначенной для тестирования алгоритмов решения различных задач. В последнем случае узлы триангуляции могут не задаваться априори, а генерироваться по мере необходимости. Для генерации треугольных элементов заданного качества, например, имеющих углы в определенном диапазоне значений, может оказаться полезным вычисление некоторого скалярного показателя, характеризующего рассматриваемый элемент. В связи с этим в настоящей работе предлагается количественная оценка качества треугольного элемента − индекс вырождения треугольника. В процессе модельной триангуляции этот количественный показатель может быть использован таким образом, чтобы генерируемые треугольные элементы имели значение индекса вырождения не более некоторой заданной величины.

2. Для треугольника с углами α и β (α > 0, β > 0, α + β < π) рассмотрим функцию

где S и P − площадь и периметр этого треугольника соответственно. Нетрудно убедиться в справедливости неравенства и асимптотического неравенства при $\alpha \to 0$

Следовательно, согласно неравенству (3) значение функции $G(\alpha ,\beta )$, когда угол α предполагается достаточно малым и наименьшим в треугольнике, является оценкой порядка малости этого наименьшего угла.

В области определения ($\alpha > 0$, $\beta > 0$, $\alpha \, + \,\beta \, < \,\pi $) функция (1) является строго выпуклой вверх и достигает своего единственного максимума, равного $\sqrt 3 {\text{/}}18$, в точке $\alpha = \pi {\text{/}}3$, $\beta = \pi {\text{/}}3$. Таким образом, наибольшее значение функции (1) реализуется в случае правильного треугольника. Отмеченные выше свойства функции $G(\alpha ,\beta )$ позволяют ввести на ее основе характеристику вырожденности рассматриваемого треугольника

которую назовем индексом вырождения треугольника с углами α и β.

Замечание 1. Выбор основания логарифма 10 в (4) обусловлен тем удобством интерпретации, что при таком выборе значение индекса вырождения характеризует порядок малости по крайней мере одного угла треугольника. Например, значение индекса (4), равное 2, означает, что в рассматриваемом треугольнике есть острый угол с величиной порядка 10^–2 радиан.

Замечание 2. Вместо функции (1) можно было бы выбрать другую функцию, например,

где r и R есть радиусы вписанной и описанной окружности соответственно для рассматриваемого треугольника. Область определения функции (5) совпадает с областью определения функции (1). Хотя функция (5) также достигает максимума в той же самой точке $\alpha = \pi {\text{/}}3$, $\beta = \pi {\text{/}}3$, что и функция (1), она не сохраняет направление выпуклости в своей области определения. Поэтому топология линий уровня функций (1) и (4) является более простой по сравнению с функцией (5).

Замечание 3. В качестве естественной меры вырождения треугольной ячейки можно было бы рассмотреть число обусловленности $cond(A)\, = \,{\text{||}}{{A}^{{ - 1}}}{\text{||}}\, \cdot \,{\text{||}}A{\text{||}}$, где ||A|| − спектральная норма матрицы A перехода от локальных координат, связанных с треугольным элементом, к декартовым координатам. Однако выбор локального базиса в треугольной ячейке может быть выполнен тремя способами, что приводит к трем, вообще говоря, различным значениям этого числа. Разумеется, можно выбрать минимальное значение из трех для такой меры, но данная мера неудобна в использовании из-за недостаточной гладкости и своих экстремальных свойств. Тем не менее для малых углов α ${{[cond(A)]}^{{ - 1}}}$ имеет первый порядок малости по α, что согласуется с неравенством (3). Таким образом, меры вырождения, основанные на выражении (1) и обратной величине к числу обусловленности, характеризуются тем же самым порядком малости при $\alpha \to 0$ и в этом смысле эквивалентны.

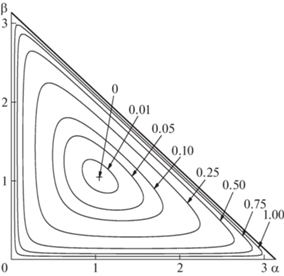
Согласно выражению (4) правильный треугольник среди всех треугольников является наименее вырожденным (что соответствует интуитивным представлениям) и имеет минимальный индекс вырождения, равный нулю. В частности, достаточно малые значения индекса вырождения гарантируют отсутствие в рассматриваемом треугольнике малых и тупых углов (см. рис. 1).

Так, неравенство $I(\alpha ,\beta ) \leqslant 0.0498$ обеспечивает принадлежность любого из углов треугольника интервалу $(\pi {\text{/}}5,\;\pi {\text{/}}2)$, т.е. все такие треугольники являются остроугольными. Как это видно из рис. 1, на котором изображены линии уровня индекса вырождения (4) треугольника $I(\alpha ,\beta ) = c$, с увеличением значений c соответствующая линия уровня стремится приблизиться изнутри к границе треугольника, задаваемого неравенствами $\alpha > 0$, $\beta > 0$ и $\alpha + \beta < \pi $.

Следовательно, соблюдение в алгоритмах триангуляции условия не превышения заданного верхнего порога c индекса вырождения обеспечит требуемое качество генерируемых треугольных элементов.

3. В тех случаях, когда необходимо протестировать какой-либо численный метод, предполагающий его применение в триангулированной области, естественно воспользоваться некоторым экономичным способом триангуляции, в котором контролируется качество производимых треугольников. С этой целью удобно воспользоваться регулярной сеткой на плоскости вида

где $h > 0$ − шаг сетки, $\varphi \in (0,\pi {\text{/}}2)$ − угловой параметр, Z – множество целых чисел.

Соединяя точки сетки (6), находящиеся на расстоянии h или $2h\cos \varphi $ друг от друга, отрезками прямых, получаем некоторую триангуляцию, состоящую из равнобедренных треугольников с боковыми сторонами h, основанием $2h\cos \varphi $ и углом φ между боковой стороной и основанием (см. рис. 2а). Точки, соединенные отрезками, назовем соседними точками. Далее, в положения узлов исходной сетки (6) внесем сдвиги и получим новую возмущенную, вообще говоря, нерегулярную сетку с узлами

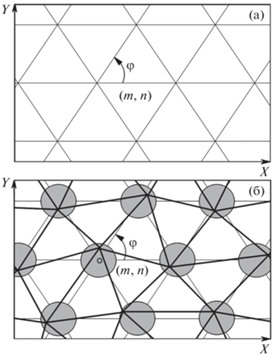
Сохраним в новой сетке (7) отношения соседства в том смысле, что если точки ${{{\mathbf{r}}}_{{mn}}}$ и ${{{\mathbf{r}}}_{{ij}}}$ являются соседями, то новые точки ${{{\mathbf{\tilde {r}}}}_{{mn}}}$ и ${{{\mathbf{\tilde {r}}}}_{{ij}}}$ также будут соседями, т.е. они по-прежнему считаются соединенными между собой отрезком прямой (см. рис. 2б). Нетрудно проверить, что при

построенные выше отрезки не будут иметь общих внутренних точек друг с другом и в совокупности образуют новую триангуляцию, состоящую, вообще говоря, из неправильных и не равных друг другу треугольников. Отметим, что максимально возможное значение правой части двойного неравенства (8) достигается при $\varphi = \pi {\text{/}}3$ и составляет $\sqrt 3 {\text{/}}4$. Триангуляцию, полученную на основе сетки (7), естественно назвать унаследованной от триангуляции порожденной сеткой (6) при указанном выше выборе соседних точек. В случае нарушения правого неравенства (8) возможно возникновение у различных отрезков общих внутренних точек, что, вообще говоря, допускает появление вырожденных треугольников.

Рассмотрим максимальное значение индекса вырождения треугольного элемента в унаследованной триангуляции

где максимум определяется на множестве всевозможных положений вершин рассматриваемого треугольника, определяемых правым неравенством (7). Очевидно, что величина (9) соответствует случаю максимально вырожденного треугольника в смысле критерия (4), допускаемого унаследованной триангуляцией. На рис. 3 показаны зависимости максимального индекса вырождения (9) от ε для различных значений углового параметра φ в (6). Каждая из представленных зависимостей определена в полуоткрытом интервале (8) и имеет вертикальную асимптоту

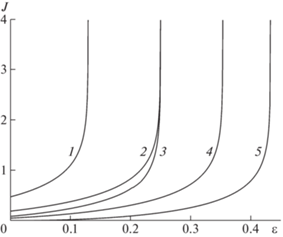
Обратим внимание, что для значений $\varphi = \pi {\text{/}}6$ и $\varphi = 5\pi {\text{/}}12$ (кривые 2 и 3 соответственно) вертикальные асимптоты совпадают и имеют уравнение $\varepsilon = 1{\text{/}}4$. Кривая 2 лежит выше кривой 3, что свидетельствует о большей вырожденности соответствующего треугольного элемента в случае $\varphi = \pi {\text{/}}6$ по сравнению со случаем $\varphi = 5\pi {\text{/}}12$. Отметим, что наименее вырожденными при одном и том же значении ε являются треугольные элементы при $\varphi = \pi {\text{/}}3$, когда исходная триангуляция, порождаемая сеткой (6), состоит из правильных треугольников.

4. Для оценки качества триангуляции, основанной на применении индекса вырождения (4), построим эмпирическую функцию распределения $F(I)$ значений (4) на треугольных элементах уже существующей триангуляции, сформированной тем или иным способом. Пусть некоторая триангуляция всего содержит N треугольников, N_I из которых имеют значение индекса (4), меньшее I. Тогда

Для иллюстрации предлагаемого подхода воспользуемся сеткой (7), выбрав значения параметров в (6) и (7) равными

Сдвиги в (7) $\Delta {{{\mathbf{r}}}_{{mn}}} = ({{\xi }_{{mn}}},\;{{\eta }_{{mn}}})$ будем считать случайными векторами, равномерно распределенными в круге, определяемом правым неравенством (7). Формирование соответствующей псевдослучайной последовательности координат $({{\xi }_{{mn}}},{{\eta }_{{mn}}})$ осуществляется методом, описанным в монографии [12], позволяющим генерировать псевдослучайные числа с произвольным распределением. Для вычисления эмпирической функции распределения $F(I)$ ограничимся рассмотрением только тех узлов сетки (7), которые располагаются в единичном круге ${{({{x}_{{mn}}} + {{\xi }_{{mn}}})}^{2}} + {{(\;{{y}_{n}} + {{\eta }_{{mn}}})}^{2}} \leqslant 1$. Указанный круг содержит N треугольных элементов, где $N > {\text{6}} \times {\text{1}}{{{\text{0}}}^{{\text{6}}}}$ для любой триангуляции, порожденной сетками (6) и (7) описанным выше способом со значениями параметров (12). Шаг дискретизации по I составляет ΔI = 0.01. Результат вычисления представлен на рис. 4.

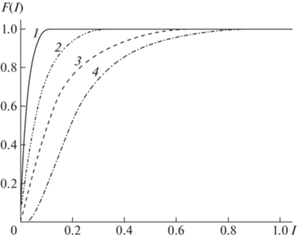
Наименее вырожденными являются треугольники для значения углового параметра $\varphi = \pi {\text{/}}3$. Соответствующая функция распределения имеет наиболее крутой фронт по сравнению со всеми другими представленными функциями. Второе место по качеству треугольников занимает триангуляция, отвечающая значению $\varphi = \pi {\text{/}}4$. Третье место соответствует случаю $\varphi = 5\pi {\text{/}}12$. И, наконец, последнее четвертое место относится к значению $\varphi = \pi {\text{/}}6$, что вполне понятно, так как соответствующие треугольные элементы являются преимущественно тупоугольными.

В заключение подчеркнем, что для любой иной триангуляции эмпирическая функция распределения (11) может быть легко построена, если известны узлы триангуляции. Таким образом, качество произвольной триангуляции допускает количественную оценку на основе индекса вырождения (4) с помощью вычисления соответствующей эмпирической функции распределения (11).

Авторы заявляют об отсутствии конфликта интересов.