Доклады Российской академии наук. Математика, информатика, процессы управления, 2023, T. 510, № 1, стр. 43-51
О ТОЧНОСТИ РАЗРЫВНОГО МЕТОДА ГАЛЕРКИНА ПРИ РАСЧЕТЕ ГАЗОДИНАМИЧЕСКИХ УДАРНЫХ ВОЛН
М. Е. Ладонкина 1, 2, *, О. А. Неклюдова 1, 2, В. В. Остапенко 2, член-корреспондент РАН В. Ф. Тишкин 1, 2
1 Институт прикладной математики
им. М.В. Келдыша Российской академии наук
Москва, Россия
2 Институт гидродинамики им. М.А. Лаврентьева Сибирского отделения Российской академии наук
Новосибирск, Россия
* E-mail: ladonkina@imamod.ru
Поступила в редакцию 15.02.2023
После доработки 27.03.2023
Принята к публикации 11.04.2023
- EDN: XITOZQ
- DOI: 10.31857/S268695432360009X
Аннотация
Приведены результаты расчета газодинамических ударных волн, возникающих при решении задачи Коши с гладкими периодическими начальными данными, по трем вариантам DG (Discontinuous Galerkin) метода, в котором решение ищется в виде кусочно-линейной разрывной функции. Показано, что DG методы, для монотонизации которых используется ограничитель Кокбурна, имеют приблизительно одинаковую точность в областях влияния ударных волн, в то время как немонотонный DG метод, в котором этот ограничитель не применяется, имеет в этих областях существенно более высокую точность, что позволяет использовать его в качестве базисного метода при построении комбинированной схемы, которая монотонно локализует фронты ударных волн и сохраняет повышенную точность в областях их влияния.
1. Поскольку в классической работе [1] было показано, что среди двухслойных по времени линейных численных схем нет монотонных схем повышенного порядка аппроксимации, то развитие теории схем сквозного счета для квазилинейных гиперболических систем законов сохранения в значительной степени было направлено на разработку численных схем, в которых повышенный порядок аппроксимации на гладких решениях и монотонность достигались за счет нелинейной коррекции потоков, приводящей к нелинейности этих схем при аппроксимации линейных гиперболических систем. Следующие работы лежат в основе целых классов NFC (Nonlinear Flux Correction) схем: MUSCL [2], TVD [3], WENO [4], DG [5], CABARET [6]. К NFC схемам относятся также гибридные схемы [7], в которых численное решение монотонизируется с помощью специального численного алгоритма в окрестностях больших градиентов точного решения. Различные методы построения NFC схем и результаты их применения при решении прикладных задач приводятся в [8–13]. Основное достоинство этих схем заключается в том, что они с высокой точностью локализуют ударные волны при отсутствии существенных нефизических осцилляций.
В [14] для исследования точности численных схем сквозного счета, аппроксимирующих систему законов сохранения теории мелкой воды [15], была предложена специальная задача Коши с гладкими периодическими начальными данными, в которых один инвариант аппроксимируемой системы является постоянным, а другой инвариант представляет собой синусоидальную функцию пространственной координаты; для этой задачи будем использовать аббревиатуру PCPW (Periodic Cauchy Problem for shallow Water). В точном решении задачи PCPW в некоторый момент времени формируется последовательность изолированных ударных волн, которые распространяются друг за другом с одинаковыми скоростями, в силу чего расстояние между соседними ударными волнами остается постоянным и равным длине периода. Выбор такой тестовой задачи был обусловлен тем, чтобы на первом этапе изучения сходимости схем сквозного счета избежать проблем, связанных с сохранением повышенной точности этих схем при взаимодействии ударных волн, а также при аппроксимации разрывных начальных и граничных условий.
В [14, 16–21] приводятся результаты численного решения задачи PCPW по различным схемам сквозного счета и изучается сходимость этих схем в негативной интегральной норме на интервалах, одна или обе границы которых находятся в областях влияния ударных волн; для такой сходимости будем использовать аббревиатуру NINSID (Negative Integral Norm Shock Influence Domain). Показано, что при расчете задачи PCPW по NFC схемам повышенной точности эти схемы, независимо от порядка аппроксимации на гладких решениях, имеют лишь первый порядок NINSID сходимости, что приводит к соответствующему снижению точности NFC схем в областях влияния ударных волн.
2. Схемы, которые не относятся к классу NFC и являются линейными при аппроксимации линейного приближения квазилинейной гиперболической системы, будем называть QL (Quasi-Linear) схемами. В [14, 17–19] показано, что некоторые QL схемы повышенного порядка аппроксимации, в частности, схемы Русанова из [22], CWA (Compact Weak Approximation) из [23] и DG1 из [5], при численном решении задачи PCPW имеют второй порядок NINSID сходимости, и, как следствие, в отличие от NFC схем, сохраняют повышенную точность в областях влияния ударных волн, несмотря на заметные схемные осцилляции на их фронтах. В обзорной работе [24] для таких QL схем введена специальная аббревиатура HASIA (High Accuracy Shock Influence Area) схемы. Обусловлено это тем, что при расчете задачи PCPW некоторые QL схемы повышенного порядка аппроксимации, в частности, схема Лакса-Вендроффа [25], а также QL схемы, получаемые при единичных весовых параметрах из схем WENO3 и WENO5 [4], подобно NFC схемам, имеют первый порядок NINSID сходимости, в силу чего теряют повышенную точность в областях влияния ударных волн.
Существование HASIA схем предопределило возможность построения для системы уравнений мелкой воды комбинированных схем сквозного счета [17–19, 24], которые монотонно локализуют фронты ударных волн и одновременно сохраняют повышенную точность в областях их влияния. В комбинированной схеме применяется базисная немонотонная HASIA схема, по которой разностное решение строится во всей расчетной области. В окрестностях больших градиентов, где это решение имеет нефизические осцилляции, оно корректируется путем численного решения внутренних начально-краевых задач по одной из NFC схем. Причем внутренняя NFC схема (в отличие от случая гибридных схем [7]) не влияет на решение, получаемое по базисной схеме, что позволяет комбинированной схеме сохранять повышенную точность в областях влияния ударных волн.
При построении первых комбинированных схем [17, 18] в качестве базисных HASIA схем применялись CWA схема [23] и схема Русанова [22], а в качестве внутренней NFC схемы – монотонная модификация схемы CABARET [6]. В дальнейшем были разработаны согласованные комбинированные схемы, в которых базисная HASIA схема и внутренняя NFC схема являются однотипными, в частности, DG схемами [5]. Предложенная в [19] комбинированная DG схема, для которой введена аббревиатура CDG (Combined Discontinuous Galerkin), построена на основе метода Галеркина, в котором численное решение ищется в виде кусочно-линейной разрывной функции; в качестве базисной схемы DG1 применяется алгоритм этого метода без ограничителя Кокбурна [5], а в качестве внутренней схемы DG1A1 используется алгоритм этого метода с ограничителем Кокбурна, в котором параметр монотонизации A = 1.
3. В настоящей работе изучается точность разрывного метода Галеркина при численном моделировании разрывных решений системы законов сохранения неизоэнтропической газовой динамики [8], которая, в отличие от системы уравнений теории мелкой воды, имеет вырожденное характеристическое поле, приводящее к формированию контактных разрывов, и в общем случае не допускает записи в форме инвариантов. Проведен сравнительный анализ точности HASIA схемы DG1 с двумя NFC схемами DG1A1 и DG1A2 (алгоритмы этих схем приведены в [19]) при расчете специальной задачи Коши с гладкими периодическими начальными данными. При решении этой задачи (так же, как при решении задачи PCPW) внутри расчетной области формируется последовательность изолированных ударных волн, распространяющихся с постоянными скоростями на одинаковом расстоянии друг от друга. Для такой газодинамической задачи Коши будем использовать аббревиатуру PCPG (Periodic Cauchy Problem for Gas dynamics).
Численные расчеты показали, что при расчете задачи PCPG в гладких частях точного решения вне областей влияния ударных волн схема DG1A1 (в которой схемная вязкость больше, чем в схеме DG1A2) является существенно менее точной, чем схемы DG1 и DG1A2. В то же время внутри областей влияния ударных волн точность NFC схем DG1A1 и DG1A2 становится сравнимой и существенно более низкой, чем точность HASIA схемы DG1, имеющей заметные нефизические осцилляции за фронтами ударных волн. Это служит основанием для эффективного применения при расчете задачи PCPG комбинированной схемы CDG.
4. Рассмотрим квазилинейную гиперболическую систему законов сохранения [8]
где ${\mathbf{u}}(x,t)$ – искомая, а f(u) – заданная гладкие вектор-функции. Поставим для системы (1) задачу Коши с гладкими периодическими начальными даннымиПредположим, что задача (1), (2) при t > 0 имеет единственное ограниченное обобщенное решение ${\mathbf{u}}(x,t)$, в котором с течением времени формируется последовательность изолированных ударных волн.
Численные схемы разрывного метода Галеркина, аппроксимирующие задачу (1), (2), будем строить на равномерной прямоугольной сетке
где $h = X{\text{/}}M$ – шаг сетки по пространству, $M$ – заданное целое положительное число,(4)
$\tau = zh{\text{/}}\mathop {\max }\limits_{k,j,n} {\text{|}}{{\lambda }_{k}}({{{\mathbf{v}}}_{h}}({{x}_{{j + 1/2}}},{{t}_{n}})){\text{|}}$Детальное описание схем DG1, DG1A1 и DG1A2, тестируемых в данной работе, приведено в [19]. Приводимые далее расчеты задачи PCPG на равномерной сетке (3) проводились при соотношении $\tau {\text{/}}h = 0.0012$, что гарантирует выполнение условия устойчивости (4).
5. Поскольку в рассматриваемой тестовой задаче Коши (1), (2) точное решение ${\mathbf{u}}(x,t)$ заранее неизвестно, то для приближенного вычисления ошибки численного решения ${{{\mathbf{v}}}_{h}}(x,{{t}_{n}})$ этой задачи мы применим метод Рунге [24]. Для этого зафиксируем на сетке (3) некоторый узел $({{x}_{{j + 1/2}}},{{t}_{n}})$, где $n \geqslant 1$, и введем для него обозначение $(\tilde {x},\tilde {t})$, где $\tilde {x} = (j + 1{\text{/}}2)h$ и $\tilde {t} = n\tau > 0$. Предположим, что на последовательности сгущающихся сеток
Вычитая из формулы (5) эту же формулу, в которой индекс i заменен на $i + 1$, получаем
(6)
$\begin{gathered} {{{\mathbf{v}}}_{{{{h}_{i}}}}} - {{{\mathbf{v}}}_{{{{h}_{{i + 1}}}}}} = {\mathbf{B}}(h_{i}^{r} - h_{{i + 1}}^{r}) \Rightarrow \\ \, \Rightarrow {\text{|}}{{{\mathbf{v}}}_{{{{h}_{i}}}}} - {{{\mathbf{v}}}_{{{{h}_{{i + 1}}}}}}{\text{|}} = {\text{|}}{\mathbf{B}}{\text{|}}h_{i}^{r}(1 - {{3}^{{ - r}}}). \\ \end{gathered} $Из отношения
(7)
$r = \mathop {\log }\nolimits_3 \frac{{{\text{|}}{{{\mathbf{v}}}_{{{{h}_{1}}}}} - {{{\mathbf{v}}}_{{{{h}_{2}}}}}{\text{|}}}}{{{\text{|}}{{{\mathbf{v}}}_{{{{h}_{2}}}}} - {{{\mathbf{v}}}_{{{{h}_{3}}}}}{\text{|}}}} = \mathop {\log }\nolimits_{1/3} \frac{{{\text{|}}{{{\mathbf{v}}}_{{{{h}_{2}}}}} - {{{\mathbf{v}}}_{{{{h}_{3}}}}}{\text{|}}}}{{{\text{|}}{{{\mathbf{v}}}_{{{{h}_{1}}}}} - {{{\mathbf{v}}}_{{{{h}_{2}}}}}{\text{|}}}},$Поскольку первое уравнение (6) при i = 1 записывается в виде
(8)
${\mathbf{B}} = \frac{{{{{\mathbf{v}}}_{{{{h}_{1}}}}} - {{{\mathbf{v}}}_{{{{h}_{2}}}}}}}{{h_{1}^{r}(1 - {{3}^{{ - r}}})}}.$Подставляя значение (8) в формулу (5), при $i = 1$ получаем
Отсюда с учетом (7) имеем приближенную оценку
(9)
$\Delta {{{\mathbf{v}}}_{h}} = \lg \frac{{{\text{|}}\delta {{{\mathbf{v}}}_{h}}{\text{|}}}}{{{\text{|}}{{{\mathbf{v}}}_{h}}{\text{|}}}} = \lg \frac{{{\text{|}}{{{\mathbf{v}}}_{h}} - {\mathbf{u}}{\text{|}}}}{{{\text{|}}{{{\mathbf{v}}}_{h}}{\text{|}}}}.$6. В качестве конкретной гиперболической системы (1) выберем систему законов сохранения неизэнтропической газовой динамики [8], для которой
(10)
${\mathbf{u}} = \left( {\begin{array}{*{20}{c}} \rho \\ {\rho u} \\ {\rho e} \end{array}} \right),\quad {\mathbf{f}}({\mathbf{u}}) = \left( {\begin{array}{*{20}{c}} {\rho u} \\ {\rho {{u}^{2}} + p} \\ {u(\rho e + p)} \end{array}} \right),$Рассмотрим для системы (1), (10) задачу Коши с гладкими периодическими начальными данными (задача PCPG)
(12)
$\begin{gathered} \rho (x,0) = {{\left( {\frac{{\gamma - 1}}{{2\sqrt \gamma }}\left( {u(x,0) + 10} \right)} \right)}^{{2/(\gamma - 1)}}}, \\ p(x,0) = {{\left( {\rho (x,0)} \right)}^{\gamma }}, \\ \end{gathered} $(15)
$\begin{gathered} {{w}_{1}}(x,0) = - 10,\quad s(x,0) = 0, \\ {{w}_{3}}(x,0) = 2\sin \left( {\frac{{2\pi x}}{X} + \frac{\pi }{4}} \right) + 10. \\ \end{gathered} $Рис. 1.
Плотность газа (а) и относительные локальные дисбалансы (б), получаемые в момент времени t = 1 при численном решении задачи PCPG.
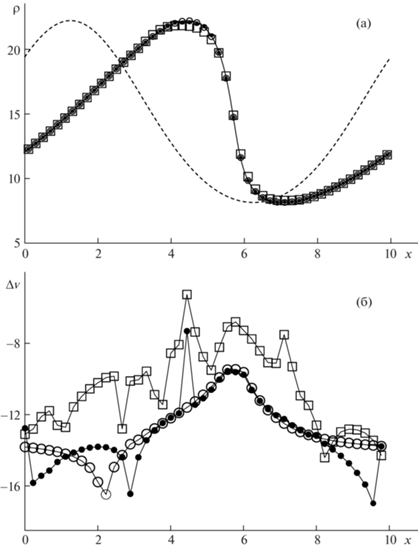
Поскольку в начальный момент времени энтропия газа постоянна, то во всех гладких частях точного решения, не входящих в области влияния ударных волн, течение газа является изоэнтропическим. Отметим, что с учетом формул (15) задача PCPG аналогична задаче PCPW, которая изучалась в [14, 16–21].
7. В точном решении задачи PCPG в момент времени ${{t}_{*}} \approx 1.35$ формируется последовательность изолированных ударных волн, которые распространяются друг за другом с одинаковыми скоростями в положительном направлении оси $x$. На рис. 1а, 2а, 3а и 4а в моменты времени $t = 1$, 2.5, 3.5, 5, сплошными линиями изображены квазиточные профили плотности, получаемые при расчете по схеме DG1A1 на мелкой сетке (3), в которой $h = 1{\text{/}}1215$. К моменту времени t = 1 в точном решении начинают формироваться области больших градиентов, но решение еще остается гладким (рис. 1а). В момент времени $t = 2.5$ ударные волны уже сформировались, но их области влияния еще не заполняют всю расчетную область (рис. 2а). К моменту времени $t = 3.5$ ударные волны проходят расстояние, большее длины периода $X = 10$, и вся расчетная область становится их областью влияния. С учетом этого сильные разрывы, расположенные на линиях, приведенных на рис. 3а и 4а, соответствуют ударной волне, которая сформировалась в момент времени ${{t}_{*}}$ внутри интервала $[ - X,0]$.
Рис. 2.
Плотность газа (а) и относительные локальные дисбалансы (б), получаемые в момент времени t = 2.5 при численном решении задачи PCPG.
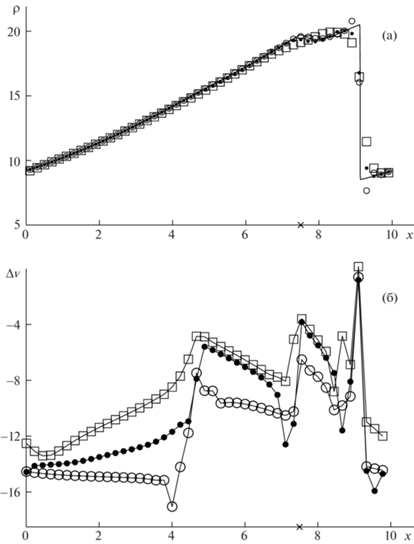
Рис. 3.
Плотность газа (а) и относительные локальные дисбалансы (б), получаемые в момент времени t = 3.5 при численном решении задачи PCPG.
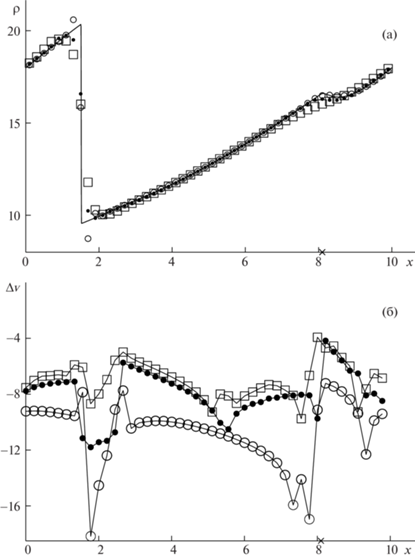
На рис. 1–4 приведены результаты расчетов задачи PCPG по схемам DG1 (кружки), DG1A1 (квадратики) и DG1A2 (точки) на равномерной сетке (3). На верхних рисунках с индексом (а) показаны значения плотности газа, получаемые при расчете, в котором $h = 0.2$. Из этих рисунков видно, что, в отличие от NFC схем DG1A1 и DG1A2, HASIA схема DG1 имеет заметные нефизические осцилляции в окрестностях ударных волн. На нижних рисунках с индексом (б) приведены относительные локальные дисбалансы (9), получаемые при расчете на базисной сетке (3), где h = = 1/135. Значения этих дисбалансов показаны для каждого 30-го полуцелого пространственного узла разностной сетки.
Рис. 4.
Плотность газа (а) и относительные локальные дисбалансы (б), получаемые в момент времени t = 5 при численном решении задачи PCPG.
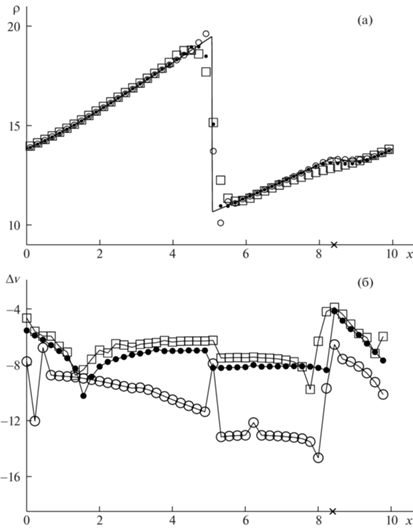
Из рис. 1б и 2б следует, что вне областей влияния ударных волн схема DG1A1 имеет существенно более низкую точность, чем схемы DG1 и DG1A2, точность которых в некоторых частях этих областей приблизительно одинаковая. Внутри областей влияния ударных волн точность схемы DG1A2 резко падает (рис. 2б, 3б и 4б), становится сравнимой с точностью схемы DG1A1 и существенно более низкой, чем точность схемы DG1. С течением времени преимущество в точности HASIA схемы DG1 по сравнению с NFC схемами DG1A1 и DG1A2 заметно возрастает, достигая к моменту времени $t = 5$ (рис. 4б) почти пяти порядков на интервале (5, 8) в области гладкости точного решения. В результате газодинамическая комбинированная схема CDG при расчете задачи PCPG монотонно (без заметных нефизических осцилляций) локализует фронты ударных волн и одновременно сохраняет повышенную точность в областях их влияния. При этом необходимо отметить, что точность всех схем (включая схему CDG) резко падает не только в окрестности фронта ударной волны, но и в окрестности слабого контактного разрыва, положение которого на рис. 2–4 отмечено крестиком на оси x.
Численные расчеты задачи PCPG так же показали, что схема DG1 (также как схемы DG1A1 и DG1A2) имеет лишь первый порядок NINSID сходимости, в чем заключается принципиальное отличие от аналогичной задачи PCPW, при расчете которой схема DG1 (в отличие от схем DG1A1 и DG1A2) сохраняет второй порядок NINSID сходимости [19]. Несмотря на это в областях влияния ударных волн преимущество в точности схемы DG1 по сравнению со схемами DG1A1 и DG1A2 при переходе от задачи PCPW к задаче PCPG не уменьшается (что можно было ожидать), а возрастает. При расчете задачи PCPW это преимущество составляет приблизительно три порядка, а при расчете задачи PCPG оно в некоторых подобластях возрастает до пяти порядков. В дальнейшем данные численные результаты требуют детального теоретического обоснования.
ИСТОЧНИК ФИНАНСИРОВАНИЯ
Исследование выполнено при финансовой поддержке РНФ, проект № 22-11-00060 (разделы 1–4) и проект № 21-11-00198 (разделы 5–7).
Список литературы
Годунов С.К. Разностный метод численного расчета разрывных решений уравнений гидродинамики // Мат. сб. 1959. Т. 47. № 3. С. 271–306.
Van Leer B. Toward the ultimate conservative difference scheme. V. A second-order sequel to Godunov’s method // J. Comput. Phys. 1979. V. 32. № 1. P. 101–136. https://doi.org/10.1016/0021-9991(79)90145-1
Harten A. High resolution schemes for hyperbolic conservation laws // J. Comput. Phys. 1983. V. 49. P. 357–393. https://doi.org/10.1016/0021-9991(83)90136-5
Jiang G.S., Shu C.W. Efficient implementation of weighted ENO schemes // J. Comput. Phys. 1996. V. 126. P. 202–228. https://doi.org/10.1006/jcph.1996.0130
Cockburn B. An introduction to the discontinuous Galerkin method for convection – dominated problems // Lect. Notes Math. 1998. V. 1697. P. 150–268. https://doi.org/10.1007/BFb0096353
Karabasov S.A., Goloviznin V.M. Compact accurately boundary-adjusting high-resolution technique for fluid dynamics // J. Comput. Phys. 2009. V. 228. P. 7426–7451. https://doi.org/10.1016/j.jcp.2009.06.037
Karni S., Kurganov A., Petrova, G. A smoothness indicator for adaptive algorithms for hyperbolic systems // J. Comput. Phys. 2002. V. 178. P. 323–341.
Куликовский А.Г., Погорелов Н.В., Семенов А.Ю. Математические вопросы численного решения гиперболических систем уравнений. М.: Физматлит, 2001.
Cockburn B., Shu C.-W. Runge-Kutta discontinuous Galerkin methods for convection-dominated problems // J. Sci. Comput. 2001. V. 16. № 3. P. 173–261.
LeVeque R.J. Finite volume methods for hyperbolic problems. Cambridge: Cambridge University Press, 2002.
Toro E.F. Riemann solvers and numerical methods for fluid dynamics: A practical introduction. Berlin: Springer-Verlag, 2009.
Головизнин В.М., Зайцев М.А., Карабасов С.А., Короткин И.А. Новые алгоритмы вычислительной гидродинамики для многопроцессорных вычислительных комплексов // М.: Изд. МГУ, 2013.
Shu C.-W. Essentially non-oscillatory and weighted essentially non-oscillatory schemes // Acta Numer. 2020. V. 29. P. 701–762.
Ковыркина О.А., Остапенко В.В. О реальной точности разностных схем сквозного счета // Матем. моделир. 2013. Т. 25. № 9. С. 63–74.
Стокер Дж.Дж. Волны на воде. Математическая теория и приложения. М.: Изд-во иностр. лит., 1959. Stoker J.J. Water Waves: The Mathematical Theory with Applications, Wiley-Interscience, 1957.
Михайлов Н.А. О порядке сходимости разностных схем WENO за фронтом ударной волны // Матем. моделир. 2015. Т. 27. № 2. С. 129–138.
Ковыркина О.А., Остапенко В.В. О построении комбинированных разностных схем повышенной точности // Докл. АН. 2018. Т. 478. № 5. С. 517–522.
Зюзина Н.А., Ковыркина О.А., Остапенко В.В. Монотонная разностная схема, сохраняющая повышенную точность в областях влияния ударных волн // Докл. АН. 2018. Т. 482. № 6. С. 639–643.
Ладонкина М.Е., Неклюдова О.А., Остапенко В.В., Тишкин В.Ф. Комбинированная схема разрывного метода Галеркина, сохраняющая повышенную точность в областях влияния ударных волн // Докл. АН. 2019. Т. 489. № 2. С. 119–124.
Ковыркина О.А., Остапенко В.В. О точности схем типа MUSCL при расчете ударных волн // Докл. РАН. Матем., информ., процессы управл. 2020. Т. 492. С. 43–48.
Брагин М.Д., Рогов Б.В. О точности бикомпактных схем при расчете нестационарных ударных волн // Ж. вычисл. матем. и матем. физ. 2020. Т. 60. № 5. С. 884–899.
Русанов В.В. Разностные схемы третьего порядка точности для сквозного счета разрывных решений // Докл. АН СССР. 1968. Т. 180. № 6. С. 1303–1305.
Остапенко В.В. О построении разностных схем повышенной точности для сквозного расчета нестационарных ударных волн // Ж. вычисл. матем. и матем. физ. 2000. Т. 40. № 12. С. 1857–1874.
Брагин М.Д., Ковыркина О.А., Ладонкина М.Е., Остапенко В.В., Тишкин В.Ф., Хандеева Н.А. Комбинированные численные схемы // Ж. вычисл. матем. и матем. физ. 2022. Т. 62. № 11. С. 1763–1803.
Lax P., Wendroff B. Systems of conservation laws // Commun. Pure Appl. Math. 1960. V. 13. P. 217–237. https://doi.org/10.1002/cpa.3160130205
Дополнительные материалы отсутствуют.
Инструменты
Доклады Российской академии наук. Математика, информатика, процессы управления


