Доклады Российской академии наук. Математика, информатика, процессы управления, 2023, T. 513, № 1, стр. 15-20
НАБЛЮДАТЕЛЬ, ДВИЖУЩИЙСЯ ПО КОНУСУ В ${{\mathbb{R}}^{3}}$ В УСЛОВИЯХ ПРОТИВОДЕЙСТВИЯ СО СТОРОНЫ ОБЪЕКТА
Академик РАН В. И. Бердышев 1, *
1 Институт математики и механики
им. Н.Н. Красовского Уральского отделения
Российской академии наук
Екатеринбург, Россия
* E-mail: bvi@imm.uran.ru
Поступила в редакцию 06.06.2023
После доработки 23.06.2023
Принята к публикации 07.08.2023
- EDN: CMCVBS
- DOI: 10.31857/S2686954323700261
Аннотация
В работе приведены две модели движения телесного наблюдателя по конической поверхности в ${{\mathbb{R}}^{3}}$, когда наблюдаемый движущийся объект обладает набором скоростных поражающих мини-объектов.
1. ВВЕДЕНИЕ
В пространстве ${{\mathbb{R}}^{3}}$ задана гладкая спрямляемая кривая $\mathcal{T}$. По $\mathcal{T}$ c постоянной по величине скоростью ${{v}_{t}}$ движется объект $t$ с мини-объектами m на борту, способными после запуска двигаться с большой постоянной по величине скоростью ${{v}_{m}}$. Мишенью для мини-объектов является наблюдатель. Слежение за объектом $t$ осуществляется с телесного вертикального конуса $S$ высоты $h$ с вершиной s и круговым основанием радиуса a с центром $A$, расположенным в горизонтальной плоскости Q, которая изображает поверхность Земли. Ось $\overline {s,A} $ конуса ортогональна плоскости Q. Наблюдатель является шаром ${{V}_{\varepsilon }}(f)$ малого радиуса $\varepsilon $, $0 < \varepsilon < a$, с локатором f в центре. Скорость ${{v}_{f}}$ наблюдателя ограничена $0\, < \,{\text{|}}{{v}_{f}}{\text{|}}\, < \,K\, \ll \,{\text{|}}{{{v}}_{m}}{\text{|}}$, где K – константа. Попадание мини-объекта в шар ${{V}_{\varepsilon }}(f)$ влечет гибель наблюдателя. Наблюдатель может двигаться по меридианам $L = L(b)$ (образующим) конуса и параллелям C = C(b) = = $\partial S \cap {{Q}_{b}}$, где $b \in \partial S$, ${{Q}_{b}}$ – плоскость, параллельная Q и содержащая точку $b$, а $\partial S$ – граница конуса.
Объект t, обнаружив наблюдателя, запускает в его сторону мини-объект. Наблюдатель, двигаясь от вершины s конуса по меридиану или параллели, следит за объектом, и за счет выбора траектории ${{\mathcal{T}}_{f}}$ и скорости движения ${{v}_{f}}$ должен за время движения мини-объекта к конусу уйти из его поля видимости. Следует отметить, что преимущество отдается траектории ${{\mathcal{T}}_{f}}$, содержащей высокие участки. Положение конуса $S$ выбирается так, чтобы с него была видна бóльшая часть траектории объекта, которую будем обозначать через $\mathcal{T} = \widehat {{{t}_{0}},{{t}^{0}}}$.
2. ПЕРВАЯ МОДЕЛЬ. ВСПОМОГАТЕЛЬНЫЕ ПРЕДЛОЖЕНИЯ
Пусть $\widetilde S$ – граница $\varepsilon $-расширения конуса S. Движение наблюдателя ${{V}_{\varepsilon }}(f)$ по меридиану (или параллели) осуществляется так, что $f \in \widetilde S$ и точка $q(f)\;\mathop = \limits^{{\text{def}}} \;{{V}_{\varepsilon }}(f) \cap S$ (она в пересечении единственная) движется по указанным линиям.
Пусть (см. рис. 1) $t \in \mathcal{T}$, $T$ – проекция точки $t$ на плоскость Q, прямая $\overline {s,t} $ пересекает Q, B = = $\overline {s,t} \cap Q$, $\alpha $ – угол между отрезками $[B,s]$ и $[B,A]$, $R(t)$ – плоскость, содержащая точки $s,\;A,\;t$; нам понадобятся точки $c = T + \lambda (A - T)$, где $\lambda > 0$, ${\text{||}}c - A{\text{||}} = a$, $\tilde {c} = 2A - c$ и угол $\beta $ между отрезками $[s,B]$, $[s,c]$. Имеем $\alpha + \beta + \xi = 90^\circ $, где $\xi $ – угол между осью $[s,A]$ и меридианом конуса $S$. Пусть $X$ – двугранный угол минимального раствора, содержащий конус S, с ребром $\overline {s,t} $, $\gamma $ – раствор этого двугранного угла. Угол X своими гранями пересекается с границей $\partial S$ по двум меридианам $L(D) = [s,D]$, $L(D{\kern 1pt} ') = [s,D{\kern 1pt} ']$. Отрезок $[D,D{\kern 1pt} ']$ разделяет точки $B$ и $A$, а углы $\angle BDs$, $\angle BD{\kern 1pt} 's$ прямые. Возможны случаи:
Рис. 1.
На рисунке изображены конус S с высотой $[s,A]$ и меридианами $L(D)$, $L(D{\kern 1pt} ')$, ограничивающими невидимую из точки $t$ часть границы $\partial S$; отрезок $[B,t]$ принадлежит ребру двугранного угла X, опорного для S; шар ${{V}_{\varepsilon }}(f{\kern 1pt} *)$ радиуса $\varepsilon $ с центром $f{\kern 1pt} *$, касающийся конуса в точке $q{\kern 1pt} *$.
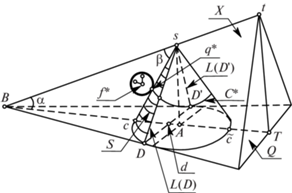
Меридианы $L(D)$, $L(D{\kern 1pt} ')$ разграничивают поверхность $\partial S$ на видимую с позиции $t$ и невидимую (теневую) части.
Случай а) Теневой участок пространства над плоскостью Q, обозначаемый через $\mathcal{M} = \mathcal{M}(t)$ есть “тетраэдр” с плоскими треугольными гранями $\overline {BDD{\kern 1pt} '} $, $\overline {BDs} $, $\overline {BD{\kern 1pt} 's} $ и конической гранью $\widehat {sDD{\kern 1pt} '}\, \subset \,\partial S$. Пусть число $\varepsilon $ настолько мало, что существует ${{V}_{\varepsilon }}(f) \subset \mathcal{M}$. Для построения траектории движения наблюдателя от вершины $s$ “вниз” важно знать, на каком расстоянии от $s$ наблюдатель ${{V}_{\varepsilon }}(f)$ имеет возможность укрыться внутри множества $\mathcal{M}$. Это множество симметрично относительно плоскости $R(t)$.
Искомая точка $f = f{\kern 1pt} *$ является ближайшей к $s$, она равноудалена от граней $\overline {BDs} $, $\overline {BD{\kern 1pt} 's} $, $\overline {sDD{\kern 1pt} '} $ на расстояние $\varepsilon $. При этом
Имеет место
Лемма 1. Пусть $\rho (t,Q) > h$. Шар ${{V}_{\varepsilon }}(f{\kern 1pt} *) \subset \mathcal{M}$, ближайший к вершине s, единственный, он удовлетворяет условию
Любой шар ${{V}_{\varepsilon }}(f)$, касающийся конуса S и удовлетворяющий неравенству
Случай б) При $\rho (t,Q)\;\leqslant \;h$ множество $\mathcal{M}$ невидимых из t (теневых) точек является усеченной пирамидой
Лемма 2. Пусть $\rho (t,Q)\;\leqslant \;h$. Шар ${{V}_{\varepsilon }}(f{\kern 1pt} *) \subset \mathcal{M}$, ближайший к вершине s, единственный. Для него выполняется равенство
Любой шар ${{V}_{\varepsilon }}(f)$, касающийся конуса S и удовлетворяющий неравенству ${\text{||}}s - f{\kern 1pt} *{\text{||}}\;\leqslant \;{\text{||}}s - f{\text{||}}$, может переместиться внутрь множества $\mathcal{M}$ с меридиана $L(q(f))$ на меридиан $L(c)$ так, что в каждый момент времени $\tau $ выполняется условие $q({{f}_{\tau }})\, \in \,C(q(f))$.
3. ТРАЕКТОРИЯ НАБЛЮДАТЕЛЯ
Конус S выбран так, что расстояние ${\text{||}}s - {{t}_{0}}{\text{||}}$ настолько велико, что за время $\tau < {\text{||}}s - {{t}_{0}}{\text{||/}}{{v}_{m}}$ наблюдатель успевает из точки s перейти внутрь множества $\mathcal{M}({{t}_{0}})$. Процесс наблюдения за движущимся объектом осуществляется по шагам.
Шаг № 0. Участники $t,\;m,\;f$ начинают движение одновременно: объект $t$, определив положение наблюдателя f, и мини-объект ${{m}_{0}}$ – с позиции ${{t}_{0}}$; наблюдатель f, определив направление вектора ${{v}_{{{{t}_{0}}}}}$ и вычислив расстояния ${\text{||}}s - f{\kern 1pt} *{\text{||}}$, ${\text{||}}s - q{\kern 1pt} *{\text{||}}$ – “вниз” по одному из меридианов $L = L(D)$, или $L = L(D{\kern 1pt} ')$ из положения, при котором $q(f) = s$. Выбор меридиана определяется по положению вектора скорости ${{v}_{{{{t}_{0}}}}}$ объекта: нужный меридиан принадлежит тому полупространству, образованному плоскостью $R({{t}_{0}})$, в котором содержится вектор ${{v}_{{{{t}_{0}}}}}$. Если ${{v}_{{{{t}_{0}}}}} \in R({{t}_{0}})$, то можно брать любой из указанных меридианов.
Мини-объект нацелен на наблюдателя, двигающегося по видимой из точки ${{t}_{0}}$ части поверхности $\partial S$, которая заключена между $L(D)$ и $L(D')$ и содержит точку $\tilde {c}$. При исчезновении наблюдателя из этой части $\partial S$ мини-объект прекращает преследование. Начиная движение “вниз” из точки $s$, наблюдатель включает локатор. При движении наблюдателя ${{V}_{\varepsilon }}(f)$ точка касания $q(f) = {{V}_{\varepsilon }} \cap \partial S$ скользит по $L$ от $s$ до параллели $C{\kern 1pt} * = C(q(f{\kern 1pt} *))$ (см. леммы 1, 2). Если время, назначенное наблюдателю, истекает, он переходит с $L$ на меридиан $L(c)$, скрываясь от мини-объекта. Последний сходит с дистанции. При наличии времени наблюдатель движется по видимой из точки ${{t}_{0}}$ части $\partial S$, отслеживая объект и по мере приближения мини-объекта возвращается на меридиан L, чтобы пойти в обратный путь: в нужный момент скрыться в $\mathcal{M}$ от мини-объекта и далее двигаться к точке $s$.
Покажем, что двигаясь на прямом пути (даже по $L$), наблюдатель видит точку ${{t}_{0}}$ и ее окрестность. В самом деле, с любой позиции $g \in L$ точка ${{t}_{0}}$ видна, а если $g = q(f)$, то отрезок $[f,g]$ ортогонален грани двугранного угла $X$ и ${\text{||}}f - g{\text{||}} = \varepsilon $. Поэтому существует и плоскость, содержащая точку f и строго отделяющая конус от точки ${{t}_{0}}$. Из таких выберем максимально удаленную от точки ${{t}_{0}}$ плоскость ${{Q}_{q}}$, она будет опорной к конусу $S$. Расстояние $\rho ({{t}_{0}},{{Q}_{q}})$ будет увеличиваться при росте $\rho ({{t}_{0}},S)$. Наблюдателю f видна вся окрестность, поэтому он может отследить движение объекта и на дуге $\widehat {{{t}_{0}},{{p}_{0}}}$, длина которой не менее, чем $\rho ({{t}_{0}},{{Q}_{q}})$. Обозначим $\rho ({{t}_{0}},{{Q}_{L}})\, = \,{{\max }_{{q \in L}}}\rho ({{t}_{0}},{{Q}_{q}})$. Для дуги $\widehat {{{t}_{0}},{{p}_{0}}}$ движения под наблюдением имеем ${\text{|}}\widehat {{{t}_{0}},{{p}_{0}}}{\text{|}}\; \geqslant \;\rho ({{t}_{0}},{{Q}_{L}})$. Отметим, что кругозор наблюдателя увеличится, если он будет двигаться по близкому к $L$ меридиану, сдвинутому по видимой из ${{t}_{0}}$ части границы $\partial S$ в сторону точки ${{t}_{0}}$.
Наблюдателю целесообразно пройти прямой путь от $s$ до $\mathcal{M}$ с возможно минимальной скоростью за отведенное ему время, тем самым увеличивая длину дуги $\widehat {{{t}_{0}},{{p}_{0}}}$. Обратный путь до точки $s$ он проходит на максимальной скорости $K$ с выключенным локатором. На вершине $s$ наблюдатель демаскирует себя, определяя положение двигающегося объекта ${{t}_{1}} \in \mathcal{T}$, и приступает к выполнению шага № 1. За счет выбора скорости наблюдателя очевидно выполняются неравенства ${\text{|}}\widehat {{{t}_{0}},{{p}_{0}}}{\text{|}} > {\text{|}}\widehat {{{p}_{0}},{{t}_{1}}}{\text{|}}$, ${\text{|}}\widehat {{{t}_{1}},{{p}_{1}}}{\text{|}} > {\text{|}}\widehat {{{p}_{1}},{{t}_{2}}}{\text{|}}$ и т.д. Если с увеличением количества шагов расстояние ${\text{||}}s - {{t}_{i}}{\text{||}}$ уменьшается, то уменьшается и участок прямого пути, с которого наблюдатель следит за движением объекта по траектории ${{\mathcal{T}}_{t}}$. Наблюдатель решает, с какого номера $i = n$ выгоднее прекратить наблюдение и возобновить его, когда величина ${\text{|}}s - {{t}_{i}}{\text{|}}$ станет достаточно большой.
Справедлива
Теорема 1. Предложенный способ движения наблюдателя по конусу $S$ позволяет построить на траектории $\mathcal{T}$ сетку узлов
4. ВТОРАЯ МОДЕЛЬ
В первой модели предполагалось, что наблюдатель ${{V}_{\varepsilon }}(f)$ не может быть поврежден мини-объектом, если он содержится в теневом множестве $\mathcal{M}$. Во второй модели предполагается, что наблюдатель ${{V}_{\varepsilon }}(f)$ $(f \in \widetilde S)$ с выключенным локатором, касающийся конуса $S$ и плоскости $Q$, недоступен для мини-объекта, а локатор способен сформировать как обычную осесимметричную, так и плоскую диаграмму направленности.
Пусть ${{Z}_{t}} = [s,g]$ – меридиан конуса $S$, ${{Z}_{t}} \subset R(t) \cap \partial S$, из пары меридианов, ближайший к $t$. Через ${{f}_{t}}$ обозначим точку такую, что ${\text{||}}s - {{f}_{t}}{\text{||}}$ = ε, а меридиан ${{Z}_{t}}$ является касательным к шару ${{V}_{\varepsilon }}({{f}_{t}})$ в точке $s$. Для обозначения параллели, содержащей все точки $f$, для которых ${{V}_{\varepsilon }}(f)$ касается одновременно плоскости $Q$ и конуса $S$, используется обозначение ${{C}^{b}} = C(f)$. Позицию участников движения будем обозначать через $\{ f,t,m\} $, а условие присутствия мини-объекта на движущемся объекте $t$ – в виде $m \in t$. Процедура слежения наблюдателем за объектом выполняется по шагам.
Шаг № 1 (см. рис. 2). Из исходной позиции $\{ {{f}_{0}},{{t}_{0}},{{m}_{0}} \in {{t}_{0}}\} $ объект, обнаружив наблюдателя ${{f}_{0}}$, где ${{f}_{0}} = {{f}_{{{{t}_{0}}}}}$, с включенным локатором, направляет мини-объект ${{m}_{0}}$ в сторону конуса $S$, а сам движется по $\mathcal{T}$ со скоростью ${{v}_{t}}$. Мини-объект преследует движущегося наблюдателя. Ради простоты предполагается, что выбранное положение конуса $S$ позволяет наблюдателю, стартующему из начальной позиции ${{f}_{0}}$, установить скорость ${{v}_{f}}$, $0 < {\text{|}}{{v}_{f}}{\text{|}} < K$ такую, что время ${{\tau }_{0}}$ его движения с включенным локатором по меридиану ${{Z}_{t}}$ от точки ${{f}_{{{{t}_{0}}}}}$ до точки ${{f}^{b}} = f_{{{{t}_{0}}}}^{b} = R({{t}_{0}}) \cap {{C}^{b}}$ меньше времени движения мини-объекта от ${{t}_{0}}$ до ${{f}^{b}}$:
Рис. 2.
Жирной линией изображена траектория $\mathcal{T}$ движения объекта t с точками ${{t}_{i}}$, начальными на i-м шаге, с граничными точками дуги $\widehat {t{\kern 1pt} ',t{\kern 1pt} '{\kern 1pt} '}$, близкой к конусу $\widetilde S$. На конусе изображены боковые меридианы $[{{f}_{{{{t}_{i}}}}},f_{{{{t}_{i}}}}^{b}]$ и окружность ${{C}^{b}}$, по которым движется наблюдатель.
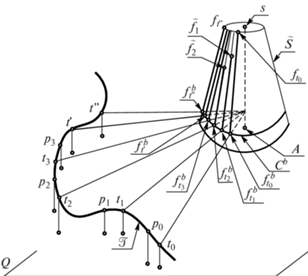
За это время наблюдатель достигает недосягаемой для мини-объекта ${{m}_{0}}$ точки ${{f}^{b}}$ (для нее шар ${{V}_{\varepsilon }}({{f}^{b}})$ касается конуса $S$ и плоскости $Q$) и выключает локатор, а объект $t$, двигаясь по $\mathcal{T}$ со скоростью ${{v}_{t}}$, приходит в точку ${{p}_{0}} \in \mathcal{T}$ такую, что
В итоге мини-объект не достигает цели, наблюдатель отследил движение объекта на дуге $\widehat {{{t}_{0}},{{p}_{0}}} \subset \mathcal{T}$, и реализуется позиция
Сформируем позицию $\{ {{f}_{{{{t}_{1}}}}},{{t}_{1}},{{m}_{1}}\} $. С позиции $f_{{{{t}_{0}}}}^{b}$ наблюдатель ${{V}_{\varepsilon }}(f_{{{{t}_{0}}}}^{b})$ начинает движение на максимальной скорости ${\text{|}}{{{v}}_{f}}{\text{|}} = K$ по окружности ${{C}^{b}}$ (вдогонку за объектом), используя локатор с плоской диаграммой направленности, определяемой плоскостью $R({{f}^{b}})$, натянутой на $s,\;A,\;{{f}^{b}}$. Скорость движения точки $r = R({{f}^{b}}) \cap \mathcal{T}$ не менее, чем $V\;\mathop = \limits^{{\text{def}}} \;(\rho (A,\mathcal{T}) \cdot K){\text{/}}a$. Точка r, стартующая с позиции ${{t}_{0}}$, догоняет объект $t = {{t}_{1}} \in \mathcal{T}$, стартующий с точки p0 в момент времени τ* = ${\text{|}}\widehat {{{p}_{0}},{{t}_{0}}}{\text{|/}}V\, - \,{{v}_{t}}$, поэтому ${\text{|}}\widehat {{{p}_{0}},{{t}_{1}}}{\text{|}}\, \leqslant \,{\text{|}}\widehat {{{p}_{0}},{{t}_{0}}}{\text{|}}({{{v}}_{t}}{\text{/}}(V\, - \,{{{v}}_{t}}))$. Участок $\widehat {{{p}_{0}},{{t}_{1}}}\, \subset \,\mathcal{T}$ объект проходит вне наблюдения. Пусть $f_{{{{t}_{1}}}}^{b} \in {{C}^{b}}$ – позиция наблюдателя в момент, когда случилось равенство $R({{f}^{b}}) \cap \mathcal{T} = {{t}_{1}}$. В этот момент объект ${{t}_{1}}$ обнаруживает наблюдателя и посылает в его сторону мини-объект ${{m}_{1}}$. Сформирована позиция
На шаге № 1 наблюдатель, отслеживая объект, со скоростью движения ${{v}_{f}}$, ${\text{|}}{{v}_{f}}{\text{|}} < K$, движется “вверх” по меридиану ${{Z}_{{{{t}_{1}}}}}$ так, что центр f шара ${{V}_{\varepsilon }}(f)$ преодолевает расстояние от $f_{{{{t}_{1}}}}^{b}$ до некоторой точки ${{\widetilde f}_{1}} \in {{Z}_{{{{t}_{1}}}}}$ и затем обратно по ${{Z}_{{{{t}_{1}}}}}$ от точки ${{\widetilde f}_{1}}$ до $f_{{{{t}_{1}}}}^{b}$, также отслеживая объект $t$. После этого он выключает локатор. За потраченное наблюдателем время объект приходит в некоторую точку ${{p}_{1}} \in \widehat {{{t}_{1}},{{t}^{0}}}$. Точка ${{\widetilde f}_{1}}$ выбирается в виде
(1)
$\frac{{2{\text{||}}f_{{{{t}_{1}}}}^{b} - {{{\widetilde f}}_{1}}{\text{||}}}}{{{\text{|}}{{v}_{f}}{\text{|}}}} < \frac{{{\text{||}}f_{{{{t}_{1}}}}^{b} - {{t}_{1}}{\text{||}}}}{{{\text{|}}{{v}_{m}}{\text{|}}}},$(2)
$\mathop {\min }\limits_{{\text{|}}{{{v}}_{f}}{\text{|}}} \max \left\{ {\lambda :\frac{{{\text{||}}f_{{{{t}_{1}}}}^{b} - {{{\widetilde f}}_{1}}{\text{||}}}}{{{\text{||}}f_{{{{t}_{1}}}}^{b} - {{t}_{1}}{\text{||}}}}\;\leqslant \;\frac{{{\text{|}}{{{v}}_{f}}{\text{|}}}}{{{\text{|}}{{{v}}_{m}}{\text{|}}}},\;0 < \lambda \;\leqslant \;1} \right\}.$В момент возвращения наблюдателя в точку $f_{{{{t}_{1}}}}^{b}$ образуется позиция $\{ f_{{{{t}_{1}}}}^{b},{{p}_{1}},{{m}_{1}} \in {{V}_{\delta }}(f_{{{{t}_{1}}}}^{b}){{\backslash }}f_{{{{t}_{1}}}}^{b}\} $. Далее наблюдатель, включив локатор с плоской диаграммой направленности, определяемой плоскостью $R({{f}^{b}})$, на максимальной скорости $K$ движется по окружности ${{C}^{b}}$, догоняя движущийся по $\mathcal{T}$ объект. Пусть в момент “захвата” плоскостью $R({{f}^{b}})$ объект находился в позиции ${{t}_{2}}$, а наблюдатель – в позиции $f_{{{{t}_{2}}}}^{b}$. В итоге наблюдатель демаскирован, а объект направляет в сторону наблюдателя $f_{{{{t}_{2}}}}^{b}$ очередной мини-объект ${{m}_{2}}$. Сформирована позиция
Следующий шаг 2 выполняется по аналогии с шагом 1 и т.д.
Процесс формирования позиций приостанавливается с точки tn, когда, по мнению наблюдателя, величина ${\text{||}}{{\widetilde f}_{n}} - f_{{{{t}_{n}}}}^{b}{\text{||}}$ становится малой и нецелесообразно решать задачу (2) для номера $n + 1$. Начиная с точки ${{t}_{n}}\;\mathop = \limits^{{\text{def}}} \;t_{n}^{'}$ он отключает локатор и возобновляет слежение за объектом, когда точка $t \in \mathcal{T}$, $t\;\mathop = \limits^{{\text{def}}} \;t_{n}^{{''}}$, отстоит достаточно далеко от конуса S, точнее, когда
Обозначим $V = (1{\text{/}}a)(\rho (A,\mathcal{T}) \cdot K)$. Справедлива
Теорема 2. Предложенный способ движения наблюдателя по конусу S позволяет построить на траектории $\mathcal{T}$ сетку узлов
Список литературы
Бердышев В.И. Оптимальная траектория наблюдателя, отслеживающего движение объекта с поражающим устройством // Докл. АН. Математика, информатика, процессы управления. 2021. Т. 499. С. 73–76.
Лю В. Методы планирования пути в среде с препятствиями (обзор) // Математика и мат. моделирование. 2018. № 1. С. 15–58.
Дополнительные материалы отсутствуют.
Инструменты
Доклады Российской академии наук. Математика, информатика, процессы управления


