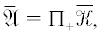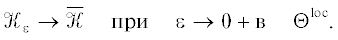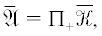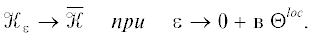1. На главную
  2. Электронные версии
  3. Доклады Российской академии наук. Математика, информатика, процессы управления
  4. T. 513, № 1, 2023

Доклады Российской академии наук. Математика, информатика, процессы управления, 2023, T. 513, № 1, стр. 9-14

ОБ АТТРАКТОРАХ УРАВНЕНИЙ ГИНЗБУРГА–ЛАНДАУ В ОБЛАСТИ С ЛОКАЛЬНО ПЕРИОДИЧЕСКОЙ МИКРОСТРУКТУРОЙ. СУБКРИТИЧЕСКИЙ, КРИТИЧЕСКИЙ И СУПЕРКРИТИЧЕСКИЙ СЛУЧАИ

К. А. Бекмаганбетов 1, 2, *, А. А. Толемис 3, 2, **, В. В. Чепыжов 4, ***, Г. А. Чечкин 6, 5, 2, ****

1 Московский государственный университет имени М.В. Ломоносова, Казахстанский филиал
Астана, Казахстан

2 Институт математики и математического моделирования
Алматы, Казахстан

3 Евразийский национальный университет имени Л.Н. Гумилева
Астана, Казахстан

4 Институт проблем передачи информации имени А.А. Харкевича Российской академии наук
Москва, Россия

5 Институт математики с компьютерным центром – подразделение Уфимского федерального исследовательского центра Российской академии наук
Уфа, Россия

6 Московский государственный университетимени М.В. Ломоносова
Москва, Россия

* E-mail: bekmaganbetov-ka@yandex.kz
** E-mail: abylaikhan9407@gmail.com
*** E-mail: chep@iitp.ru
**** E-mail: chechkin@mech.math.msu.su

Поступила в редакцию 30.03.2023
После доработки 02.07.2023
Принята к публикации 17.08.2023

Полный текст (PDF)

Аннотация

В работе рассматривается задача для комплексных уравнений Гинзбурга–Ландау в среде с локально периодическими мелкими препятствиями. При этом предполагается, что поверхность препятствий может иметь разные коэффициенты проводимости. Доказано, что траекторные аттракторы этой системы стремятся в определенной слабой топологии к траекторным аттракторам задачи для усредненных уравнений Гинзбурга–Ландау с дополнительным потенциалом (в критическом случае), без дополнительного потенциала (в субкритическом случае) в среде без препятствий или просто исчезают (в суперкритическом случае).

Ключевые слова: аттракторы, усреднение, уравнения Гинзбурга–Ландау, нелинейные уравнения, слабая сходимость, перфорированная область, быстро осциллирующие члены

1. ВВЕДЕНИЕ

В этой работе изучается поведение аттракторов начально-краевой задачи для комплексного уравнения Гинзбурга–Ландау в области с локально периодическими мелкими препятствиями, расстояние между которыми и их диаметры зависят от малого параметра, при стремлении этого малого параметра к нулю. Отметим некоторые результаты по усреднению аттракторов, которые появились в последнее время (см. [1–5]). В работах [2] и [5] изучалось усреднение аттракторов эволюционных уравнений и систем с диссипацией в периодически перфорированной области. Результаты по усреднению аттракторов системы уравнений Навье–Стокса в периодической изотропной среде см. в [3]. В работе [4] рассмотрена задача усреднения для уравнения Гинзбурга–Ландау в стохастической постановке. Методы, которые использовались при исследовании таких задач, были разработаны в [6–10].

2. ОБОЗНАЧЕНИЯ И ПОСТАНОВКА ЗАДАЧИ

Сначала мы определим перфорированную область. Пусть $\Omega $ – гладкая ограниченная область в ${{\mathbb{R}}^{d}}$, $d \geqslant 2$. Введем обозначения

$\begin{gathered} {{\Upsilon }_{\varepsilon }} = \left\{ {r \in {{\mathbb{Z}}^{d}}:{\text{dist}}\left( {\varepsilon r,\partial \Omega } \right) \geqslant \sqrt d \varepsilon } \right\}, \\ \square \; \equiv \left\{ {\xi : - \frac{1}{2} < {{\xi }_{i}} < \frac{1}{2},i = 1, \ldots ,d} \right\}. \\ \end{gathered} $

Пусть $F(x,\xi )$ – гладкая, 1-периодическая по переменной $\xi $ функция и такая, что $F(x,\xi ){{{\text{|}}}_{{\xi \in \partial \square }}} \geqslant $ ≥ const > 0, $F(x,0) = - 1$, ${{\nabla }_{\xi }}F \ne 0$ при $\xi \in \;\square \backslash \{ 0\} $. Определим множества

$G_{\varepsilon }^{r} = \left\{ {x \in \varepsilon \left( {\square \; + r} \right)\,{\text{|}}\,F\left( {x,\frac{x}{\varepsilon }} \right) \leqslant 0} \right\},\quad {{G}_{\varepsilon }} = \bigcup\limits_{r \in {{\Upsilon }_{\varepsilon }}} G_{\varepsilon }^{r}$
и вводим перфорированную область следующим образом

${{\Omega }_{\varepsilon }} = \Omega {{\backslash }}{{G}_{\varepsilon }}.$

Обозначим через G(x) множество $\{ \xi \in {{\mathbb{R}}^{d}}\,{\text{|}}\,F(x,\xi )$ < < 0}, и через S(x) множество $\{ \xi \in {{\mathbb{R}}^{d}}\,{\text{|}}\,F(x,\xi ) = 0\} $.

В соответствии с вышеприведенной конструкцией граница $\partial {{\Omega }_{\varepsilon }}$ состоит из $\partial \Omega $ и границы включений ${{S}_{\varepsilon }} \subset \Omega $, ${{S}_{\varepsilon }}: = \partial {{\Omega }_{\varepsilon }} \cap \Omega $.

Мы будем изучать асимптотическое поведение траекторных аттракторов следующей начально-краевой задачи для комплексных уравнений Гинзбурга–Ландау

(1)
$\left\{ \begin{gathered} \frac{{\partial {{u}_{\varepsilon }}}}{{\partial t}} = (1 + \alpha {\text{i}})\Delta {{u}_{\varepsilon }} + R\left( {x,\frac{x}{\varepsilon }} \right){\kern 1pt} {{u}_{\varepsilon }} - \hfill \\ - \left( {1 + \beta \left( {x,\frac{x}{\varepsilon }} \right){\text{i}}} \right){\text{|}}{{u}_{\varepsilon }}{{{\text{|}}}^{2}}{{u}_{\varepsilon }} + f(x),\quad x \in {{\Omega }_{\varepsilon }}, \hfill \\ (1 + \alpha {\text{i}})\frac{{\partial {{u}_{\varepsilon }}}}{{\partial \nu }} + {{\varepsilon }^{\theta }}q\left( {x,\frac{x}{\varepsilon }} \right){{u}_{\varepsilon }} = 0, \hfill \\ x \in {{S}_{\varepsilon }},\quad t \in (0, + \infty ), \hfill \\ {{u}_{\varepsilon }} = 0,\quad x \in \partial \Omega , \hfill \\ {{u}_{\varepsilon }} = U(x),\quad x \in {{\Omega }_{\varepsilon }},\quad t = 0. \hfill \\ \end{gathered} \right.$

Здесь $\alpha $ – вещественная константа, $\nu $ – единичный вектор внешней нормали к границе области, $u\, = \,{{u}_{1}}\, + \,{\text{i}}{{u}_{2}}\, \in \,\mathbb{C}$, $R(x,\xi ) \in C(\Omega \times {{\mathbb{R}}^{d}})$, $f(x) \in {{C}^{1}}(\Omega ;\mathbb{C})$, $q(x,\xi ) \in {{C}^{1}}(\Omega \times {{\mathbb{R}}^{d}})$ и $q(x,\xi )$ – неотрицательная 1‑периодическая по $\xi $ функция. Предполагается, что

(2)
$ - {{R}_{1}} \leqslant R(x,\xi ) \leqslant {{R}_{2}},\quad 0 < {{\beta }_{1}} \leqslant \beta (x,\xi ) \leqslant {{\beta }_{2}}$
для $x \in \Omega $, $\xi \in {{\mathbb{R}}^{d}}$ и функции $R\left( {x,\frac{x}{\varepsilon }} \right)$ и $\beta \left( {x,\frac{x}{\varepsilon }} \right)$ имеют средние $\bar {R}(x)$ и $\bar {\beta }(x)$ в смысле пространства ${{L}_{{\infty ,*w}}}(\Omega )$ соответственно, т.е.,
(3)
$\begin{gathered} \int\limits_\Omega R\left( {x,\frac{x}{\varepsilon }} \right)\varphi (x)dx \to \int\limits_\Omega \bar {R}(x)\varphi (x)dx, \\ \int\limits_\Omega \beta \left( {x,\frac{x}{\varepsilon }} \right)\varphi (x)dx \to \int\limits_\Omega \bar {\beta }(x)\varphi (x)dx \\ \end{gathered} $
при $\varepsilon \to 0 + $ для любой функции $\varphi (x) \in {{L}_{1}}(\Omega )$.

Введем следующие обозначения для пространств ${\mathbf{H}}\,: = \,{{L}_{2}}(\Omega ;\mathbb{C})$, ${{{\mathbf{H}}}_{\varepsilon }}\,: = \,{{L}_{2}}({{\Omega }_{\varepsilon }};\mathbb{C})$, ${\mathbf{V}}\,: = \,H_{0}^{1}(\Omega ;\mathbb{C})$, ${{{\mathbf{V}}}_{\varepsilon }}\,: = \,{{H}^{1}}({{\Omega }_{\varepsilon }},\partial \Omega ;\mathbb{C})$ – множество функций из ${{H}^{1}}({{\Omega }_{\varepsilon }};\mathbb{C})$ с нулевым следом на $\partial \Omega $ и Lp := ${{L}_{p}}(\Omega ;\mathbb{C})$, ${{{\mathbf{L}}}_{{p,\varepsilon }}}: = {{L}_{p}}({{\Omega }_{\varepsilon }};\mathbb{C})$. Нормы в этих пространствах определяются, соответственно, следующим образом

${\text{||}}v{\text{||}}_{0}^{2}: = \int\limits_\Omega {\text{|}}{v}(x){{{\text{|}}}^{2}}dx,\quad {\text{||}}v{\text{||}}_{{0,\varepsilon }}^{2}: = \int\limits_{{{\Omega }_{\varepsilon }}} {\text{|}}{v}(x){{{\text{|}}}^{2}}dx,$
${\text{||}}v{\text{||}}_{1}^{2}: = \int\limits_\Omega {\text{|}}\nabla {v}(x){{{\text{|}}}^{2}}dx,\quad {\text{||}}v{\text{||}}_{{1,\varepsilon }}^{2}: = \int\limits_{{{\Omega }_{\varepsilon }}} {\text{|}}\nabla {v}(x){{{\text{|}}}^{2}}dx,$
${\text{||}}v{\text{||}}_{{{{{\mathbf{L}}}_{p}}}}^{p}: = \int\limits_\Omega {\text{|}}{v}(x){{{\text{|}}}^{p}}dx,\quad {\text{||}}v{\text{||}}_{{{{{\mathbf{L}}}_{{p,\varepsilon }}}}}^{p}: = \int\limits_{{{\Omega }_{\varepsilon }}} {\text{|}}{v}(x){{{\text{|}}}^{p}}dx.$

Напомним, что Lq и ${{{\mathbf{L}}}_{{q,\varepsilon }}}$ являются сопряженными пространствами к Lp и ${{{\mathbf{L}}}_{{p,\varepsilon }}}$, где q = $p{\text{/}}(p - 1)$. Обозначим через ${\mathbf{V}}{\kern 1pt} ': = {{H}^{{ - 1}}}(\Omega ;\mathbb{C})$ и ${\mathbf{V}}_{\varepsilon }^{'}\,: = \,{{H}^{{ - 1}}}({{\Omega }_{\varepsilon }};\mathbb{C})$ пространства, сопряженные, соответственно, к V и ${{{\mathbf{V}}}_{\varepsilon }}$.

Предполагается, что параметр θ принимает положительные значения. В зависимости от этого параметра будут получаться различные предельные (усредненные) задачи.

Рассматриваются (см. [7]) обобщенные решения задачи (1), т.е. функции ${{u}_{\varepsilon }} = {{u}_{\varepsilon }}(x,t)$, $x \in {{\Omega }_{\varepsilon }}$, $t \geqslant 0$,

${{u}_{\varepsilon }} \in L_{\infty }^{{{\text{loc}}}}({{\mathbb{R}}_{ + }};{{{\mathbf{H}}}_{\varepsilon }}) \cap L_{2}^{{{\text{loc}}}}({{\mathbb{R}}_{ + }};{{{\mathbf{V}}}_{\varepsilon }}) \cap L_{4}^{{{\text{loc}}}}\left( {{{\mathbb{R}}_{ + }};{{{\mathbf{L}}}_{{4,\varepsilon }}}} \right),$
удовлетворяющие интегральному тождеству
$ - \int\limits_0^\infty \int\limits_{{{\Omega }_{\varepsilon }}} {{u}_{\varepsilon }}\frac{{\partial \psi }}{{\partial t}}\;dxdt + (1 + \alpha {\text{i}})\int\limits_0^\infty \int\limits_{{{\Omega }_{\varepsilon }}} \nabla {{u}_{\varepsilon }}\nabla \psi \;dxdt - $
(4)
$\, - \int\limits_0^\infty \int\limits_{{{\Omega }_{\varepsilon }}} \left( {\left( {R\left( {x,\frac{x}{\varepsilon }} \right){{u}_{\varepsilon }} - \left( {1 + \beta \left( {x,\frac{x}{\varepsilon }} \right){\text{i}}} \right){\text{|}}{{u}_{\varepsilon }}{{{\text{|}}}^{2}}{{u}_{\varepsilon }}} \right)} \right)\psi \,dxdt + $
$\, + {{\varepsilon }^{\theta }}\int\limits_0^{ + \infty } \int\limits_{{{S}_{\varepsilon }}} q\left( {x,\frac{x}{\varepsilon }} \right){{u}_{\varepsilon }}\psi \,d\sigma dt = \int\limits_0^\infty \int\limits_{{{\Omega }_{\varepsilon }}} f(x)\psi \,dxdt$
для любой функции $\psi \in C_{0}^{\infty }({{\mathbb{R}}_{ + }};{{{\mathbf{V}}}_{\varepsilon }} \cap {{{\mathbf{L}}}_{{4,\varepsilon }}})$.

Если ${{u}_{\varepsilon }} \in {{L}_{4}}(0,M;{{{\mathbf{L}}}_{{4,\varepsilon }}})$, то

$\begin{gathered} R\left( {x,\frac{x}{\varepsilon }} \right){{u}_{\varepsilon }}(x,t) - \left( {1 + \beta \left( {x,\frac{x}{\varepsilon }} \right){\text{i}}} \right){\text{|}}{{u}_{\varepsilon }}(x,t){{{\text{|}}}^{2}}{{u}_{\varepsilon }}(x,t) \in \\ \, \in {{L}_{{4/3}}}(0,M;{{{\mathbf{L}}}_{{4/3,\varepsilon }}}), \\ \end{gathered} $
если ${{u}_{\varepsilon }} \in {{L}_{2}}(0,M;{{{\mathbf{V}}}_{\varepsilon }}),$ то (1 + αi)Δuε(x, t) + + $f(x)\, \in \,{{L}_{2}}(0,M;{\mathbf{V}}_{\varepsilon }^{'}),$ поэтому для любого решения uε задачи (1) имеем

$\frac{{\partial {{u}_{\varepsilon }}}}{{\partial t}} \in {{L}_{{4/3}}}(0,M;{{{\mathbf{L}}}_{{4/3,\varepsilon }}}) + {{L}_{2}}(0,M;{\mathbf{V}}_{\varepsilon }^{'}).$

По теореме вложения Соболева

${{L}_{{4/3}}}(0,M;{{{\mathbf{L}}}_{{4/3,\varepsilon }}}) + {{L}_{2}}(0,M;{\mathbf{V}}_{\varepsilon }^{'}) \subset {{L}_{{4/3}}}\left( {0,M;{\mathbf{H}}_{\varepsilon }^{{ - r}}} \right),$
где ${\mathbf{H}}_{\varepsilon }^{{ - r}}: = {{H}^{{ - r}}}({{\Omega }_{\varepsilon }})$ и $r = \max \left\{ {1,d{\text{/}}4} \right\}$. Следовательно, для любого обобщенного решения uε задачи (1) имеем $\frac{{\partial {{u}_{\varepsilon }}}}{{\partial t}} \in {{L}_{{4/3}}}(0,M;{\mathbf{H}}_{\varepsilon }^{{ - r}})$.

Замечание 2.1. Существование обобщенного решения ${{u}_{\varepsilon }}(x,t)$ задачи (1) для любой $U \in {{{\mathbf{H}}}_{\varepsilon }}$ и фиксированного $\varepsilon $, так, что ${{u}_{\varepsilon }}(x,0) = U(x)$ доказывается стандартным методом (см., например, [6, 7, 11]).

Имеет место следующая лемма (ее доказательство проводится аналогично доказательству утверждения XV.3.1 из [7]).

Лемма 2.1. Пусть ${{u}_{\varepsilon }}(x,t)$ — обобщенное решение задачи (1). Тогда

(i) $u \in C({{\mathbb{R}}_{ + }};{{{\mathbf{H}}}_{\varepsilon }});$

(ii) функция ${\text{||}}{{u}_{\varepsilon }}( \cdot ,t){\text{||}}_{{0,\varepsilon }}^{2}$ является абсолютно непрерывной на ${{\mathbb{R}}_{ + }}$ и более того

$\frac{1}{2}\frac{d}{{dt}}{\text{||}}{{u}_{\varepsilon }}( \cdot ,t){\text{||}}_{{0,\varepsilon }}^{2}\; + \;{\text{||}}\nabla {{u}_{\varepsilon }}( \cdot ,t){\text{||}}_{{0,\varepsilon }}^{2}\; + \;{\text{||}}{{u}_{\varepsilon }}( \cdot ,t){\text{||}}_{{{{{\mathbf{L}}}_{{4,\varepsilon }}}}}^{4} - $
$\, - \int\limits_{{{\Omega }_{\varepsilon }}} R\left( {x,\frac{x}{\varepsilon }} \right){\text{|}}{{u}_{\varepsilon }}(x,t){{{\text{|}}}^{2}}{\kern 1pt} dx + $
$\, + {{\varepsilon }^{\theta }}\int\limits_{{{S}_{\varepsilon }}} q\left( {x,\frac{x}{\varepsilon }} \right){\text{|}}{{u}_{\varepsilon }}(x,t){{{\text{|}}}^{2}}d\sigma = \int\limits_{{{\Omega }_{\varepsilon }}} \mathbb{R}\,f(x){{\overline u }_{\varepsilon }}(x,t)dx,$
для почти всех $t \in {{\mathbb{R}}_{ + }}$.

При описании пространства траекторий $\mathcal{K}_{\varepsilon }^{ + }$ для задачи (1), будем следовать общей схеме (см., например, [1, 2]) и определим для каждого отрезка $[{{t}_{1}},{{t}_{2}}] \in \mathbb{R}$ банаховы пространства

(5)
$\begin{gathered} {{\mathcal{F}}_{{{{t}_{1}},{{t}_{2}}}}}:{{L}_{4}}({{t}_{1}},{{t}_{2}};{{{\mathbf{L}}}_{4}}) \cap {{L}_{2}}({{t}_{1}},{{t}_{2}};{\mathbf{V}}) \cap {{L}_{\infty }}({{t}_{1}},{{t}_{2}};{\mathbf{H}}) \cap \\ \, \cap \left\{ {v\,{\text{|}}\,\frac{{\partial v}}{{\partial t}} \in {{L}_{{4/3}}}({{t}_{1}},{{t}_{2}};{{{\mathbf{H}}}^{{ - r}}})} \right\} \\ \end{gathered} $
с нормой

(6)
$\begin{gathered} {\text{||}}v{\text{|}}{{{\text{|}}}_{{{{\mathcal{F}}_{{{{t}_{1}},{{t}_{2}}}}}}}}: = {\text{||}}v{\text{|}}{{{\text{|}}}_{{{{L}_{4}}({{t}_{1}},{{t}_{2}};{{{\mathbf{L}}}_{4}})}}}\; + \;{\text{||}}v{\text{|}}{{{\text{|}}}_{{{{L}_{2}}({{t}_{1}},{{t}_{2}};{\mathbf{V}})}}}\; + \\ + \;{\text{||}}v{\text{|}}{{{\text{|}}}_{{{{L}_{\infty }}(0,M;{\mathbf{H}})}}} + {{\left\| {\frac{{\partial v}}{{\partial t}}} \right\|}_{{{{L}_{{4/3}}}({{t}_{1}},{{t}_{2}};{{{\mathbf{H}}}^{{ - r}}})}}}. \\ \end{gathered} $

Положив ${{\mathcal{D}}_{{{{t}_{1}},{{t}_{2}}}}} = {{{\mathbf{L}}}_{2}}\left( {{{t}_{1}},{{t}_{2}};{\mathbf{V}}} \right)$, получаем, что ${{\mathcal{F}}_{{{{t}_{1}},{{t}_{2}}}}} \subseteq {{\mathcal{D}}_{{{{t}_{1}},{{t}_{2}}}}}$, и если $u \in {{\mathcal{F}}_{{{{t}_{1}},{{t}_{2}}}}}$, тогда $A(u) \in {{\mathcal{D}}_{{{{t}_{1}},{{t}_{2}}}}}$, где $A(u) = (1 + \alpha {\text{i}})\Delta u + R( \cdot , \cdot ){\kern 1pt} u$ – $\left( {1 + \beta ( \cdot , \cdot ){\text{i}}} \right){\text{|}}u{{{\text{|}}}^{2}}u + f( \cdot )$ (см. [1, 2]). Будем рассматривать обобщенные решения задачи (1).

Определим пространства

$\begin{gathered} \mathcal{F}_{ + }^{{{\text{loc}}}} = L_{4}^{{{\text{loc}}}}({{\mathbb{R}}_{ + }};{{{\mathbf{L}}}_{4}}) \cap L_{2}^{{{\text{loc}}}}({{\mathbb{R}}_{ + }};{\mathbf{V}}) \cap L_{\infty }^{{{\text{loc}}}}({{\mathbb{R}}_{ + }};{\mathbf{H}}) \cap \\ \, \cap \left\{ {v\,{\text{|}}\,\frac{{\partial v}}{{\partial t}} \in L_{{4/3}}^{{{\text{loc}}}}({{\mathbb{R}}_{ + }};{{{\mathbf{H}}}^{{ - r}}})} \right\}, \\ \end{gathered} $
$\begin{gathered} \mathcal{F}_{{ + ,\varepsilon }}^{{{\text{loc}}}} = L_{4}^{{{\text{loc}}}}({{\mathbb{R}}_{ + }};{{{\mathbf{L}}}_{{4,\varepsilon }}}) \cap L_{2}^{{{\text{loc}}}}({{\mathbb{R}}_{ + }};{{{\mathbf{V}}}_{\varepsilon }}) \cap L_{\infty }^{{{\text{loc}}}}({{\mathbb{R}}_{ + }};{{{\mathbf{H}}}_{\varepsilon }}) \cap \\ \, \cap \left\{ {v\,{\text{|}}\,\frac{{\partial v}}{{\partial t}} \in L_{{4/3}}^{{{\text{loc}}}}({{\mathbb{R}}_{ + }};{\mathbf{H}}_{\varepsilon }^{{ - r}})} \right\}. \\ \end{gathered} $

Обозначим через $\mathcal{K}_{\varepsilon }^{ + }$ множество всех обобщенных решений задачи (1). Напомним, что для любой функции $U \in {\mathbf{H}}$ существует хотя бы одна траектория $u( \cdot ) \in \mathcal{K}_{\varepsilon }^{ + }$ такая, что $u(0) = U(x)$ (см., например, [6, 7, 11]). Следовательно, пространство траекторий $\mathcal{K}_{\varepsilon }^{ + }$ задачи (1) не пусто и достаточно велико. Заметим, что теорема единственности для обобщенного решения задачи (1) доказана не для всех возможных диапазонов изменения дисперсионных параметров $\alpha $ и $\beta $ (см., [11]).

Ясно, что $\mathcal{K}_{\varepsilon }^{ + } \subset \mathcal{F}_{{ + ,\varepsilon }}^{{loc}}$ и пространство траекторий $\mathcal{K}_{\varepsilon }^{ + }$ является трансляционно-инвариантным, то есть, если $u( \cdot )\, \in \,\mathcal{K}_{\varepsilon }^{ + }$, тогда и T(h)u(·) = $u(h + \cdot )\, \in \,\mathcal{K}_{\varepsilon }^{ + }$ для любых $h \geqslant 0$. Операторы трансляций $\{ T(h),h \geqslant 0\} $ образуют полугруппу, действующую в фазовом пространстве траекторий:

$T(h):\mathcal{K}_{\varepsilon }^{ + } \to \mathcal{K}_{\varepsilon }^{ + },\quad h \geqslant 0.$

Определим метрики ${{\rho }_{{{{t}_{1}},{{t}_{2}}}}}( \cdot , \cdot )$ в пространствах ${{\mathcal{F}}_{{{{t}_{1}},{{t}_{2}}}}}$ следующим образом:

$\begin{gathered} {{\rho }_{{{{t}_{1}},{{t}_{2}}}}}(u,v) = {{\left( {\int\limits_{{{t}_{1}}}^{{{t}_{2}}} {\text{||}}u(s) - v(s){\text{||}}_{0}^{2}ds} \right)}^{{1/2}}}, \\ \forall \;u,{v} \in {{\mathcal{F}}_{{{{t}_{1}},{{t}_{2}}}}}. \\ \end{gathered} $

Эти метрики порождают топологию $\Theta _{ + }^{{{\text{loc}}}}$ в пространстве $\mathcal{F}_{ + }^{{{\text{loc}}}}$. По определению последовательность $\{ {{v}_{k}}\} \subset \mathcal{F}_{ + }^{{{\text{loc}}}}$ сходится к функции $v \in \mathcal{F}_{ + }^{{{\text{loc}}}}$ при $k \to \infty $ в $\Theta _{ + }^{{{\text{loc}}}}$, если ${\text{||}}{{v}_{k}}( \cdot ) - v( \cdot ){\text{|}}{{{\text{|}}}_{{{{{\mathbf{L}}}_{2}}({{t}_{1}},{{t}_{2}};{\mathbf{H}})}}} \to 0$ $(k \to \infty )$ для любых ${{t}_{1}},{{t}_{2}} \geqslant 0$. Аналогично определяется топология $\Theta _{{ + ,\varepsilon }}^{{{\text{loc}}}}$ в пространстве $\mathcal{F}_{{ + ,\varepsilon }}^{{{\text{loc}}}}$ для перфорированной области. Топологии $\Theta _{ + }^{{{\text{loc}}}}$ и $\Theta _{{ + ,\varepsilon }}^{{{\text{loc}}}}$ метризуемы и соответствующие метрические пространства являются полными. Мы рассматриваем топологию $\Theta _{{ + ,\varepsilon }}^{{{\text{loc}}}}$ в пространстве траекторий $\mathcal{K}_{\varepsilon }^{ + }$ задачи (1).

Напомним, что норма в пространстве $L_{p}^{b}({{\mathbb{R}}_{ + }};E)$, где E – некоторое банахово пространство, определяется по формуле

${\text{||}}f{\text{|}}{{{\text{|}}}_{{L_{p}^{b}({{\mathbb{R}}_{ + }};E)}}} = {{\left( {\mathop {\sup }\limits_{h \geqslant 0} \int\limits_h^{h + 1} {\text{||}}f(s){\text{||}}_{E}^{p}ds} \right)}^{{1/p}}}.$

Для определения ограниченных множеств в пространстве траекторий $\mathcal{K}_{\varepsilon }^{ + }$ введем банахово пространство

(7)
$\begin{gathered} \mathcal{F}_{{ + ,\varepsilon }}^{b} = L_{4}^{b}({{\mathbb{R}}_{ + }};{{{\mathbf{L}}}_{{4,\varepsilon }}}) \cap L_{2}^{b}({{\mathbb{R}}_{ + }};{{{\mathbf{V}}}_{\varepsilon }}) \cap {{L}_{\infty }}({{\mathbb{R}}_{ + }};{{{\mathbf{H}}}_{\varepsilon }}) \cap \\ \, \cap \left\{ {v\,{\text{|}}\,\frac{{\partial v}}{{\partial t}} \in L_{{4/3}}^{b}({{\mathbb{R}}_{ + }};{\mathbf{H}}_{\varepsilon }^{{ - r}})} \right\}. \\ \end{gathered} $

Аналогично вводим пространство

$\begin{gathered} \mathcal{F}_{ + }^{b} = L_{4}^{b}({{\mathbb{R}}_{ + }};{{{\mathbf{L}}}_{4}}) \cap L_{2}^{b}({{\mathbb{R}}_{ + }};{\mathbf{V}}) \cap {{L}_{\infty }}({{\mathbb{R}}_{ + }};{\mathbf{H}}) \cap \\ \, \cap \left\{ {v\,{\text{|}}\,\frac{{\partial v}}{{\partial t}} \in L_{{4/3}}^{b}({{\mathbb{R}}_{ + }};{{{\mathbf{H}}}^{{ - r}}})} \right\}. \\ \end{gathered} $

Пространства $\mathcal{F}_{ + }^{b}$ и $\mathcal{F}_{{ + ,\varepsilon }}^{b}$ являются подпространствами пространств $\mathcal{F}_{ + }^{{{\text{loc}}}}$ и $\mathcal{F}_{{ + ,\varepsilon }}^{{{\text{loc}}}}$ соответственно.

Напомним, что траекторным аттрактором трансляционной полугруппы $\{ T(h)\} $ в пространстве $\mathcal{K}_{\varepsilon }^{ + }$ называется множество ${{A}_{\varepsilon }} \subset \mathcal{K}_{\varepsilon }^{ + }$, которое ограничено в $F_{{ + ,\varepsilon }}^{b}$, компактно в $\Theta _{{ + ,\varepsilon }}^{{{\text{loc}}}}$, строго инвариантно, т.е., $T(h){{A}_{\varepsilon }} = {{A}_{\varepsilon }}$ при всех $h \geqslant 0$, и которое притягивает ограниченные в $F_{{ + ,\varepsilon }}^{b}$ множества из $\mathcal{K}_{\varepsilon }^{ + }$ в топологии $\Theta _{{ + ,\varepsilon }}^{{{\text{loc}}}}$ при $h \to + \infty $ (см. [6, 7, 9]).

Пусть ${{\mathcal{K}}_{\varepsilon }}$ означает ядро задачи (1), которое состоит из всех обобщенных решений ${{u}_{\varepsilon }}(x,t)$, т.е. функций, удовлетворяющих интегральному тождеству

$ - \int\limits_{ - \infty }^\infty \int\limits_{{{\Omega }_{\varepsilon }}} {{u}_{\varepsilon }}\frac{{\partial \psi }}{{\partial t}}\,dxdt + (1 + \alpha {\text{i}})\int\limits_{ - \infty }^\infty \int\limits_{{{\Omega }_{\varepsilon }}} \nabla {{u}_{\varepsilon }}\nabla \psi \,dxdt - $
$\, - \int\limits_{ - \infty }^\infty \int\limits_{{{\Omega }_{\varepsilon }}} \left( {\left( {R\left( {x,\frac{x}{\varepsilon }} \right){{u}_{\varepsilon }} - \left( {1 + \beta \left( {x,\frac{x}{\varepsilon }} \right){\text{i}}} \right){\text{|}}{{u}_{\varepsilon }}{{{\text{|}}}^{2}}{{u}_{\varepsilon }}} \right)} \right)\psi \,dxdt + $
(8)
$\, + {{\varepsilon }^{\theta }}\int\limits_{ - \infty }^{ + \infty } \int\limits_{{{S}_{\varepsilon }}} q\left( {x,\frac{x}{\varepsilon }} \right){{u}_{\varepsilon }}\psi \,d\sigma dt = \int\limits_{ - \infty }^\infty \int\limits_{{{\Omega }_{\varepsilon }}} f(x)\psi \,dxdt$
для любой функции $\psi \in C_{0}^{\infty }(\mathbb{R};{{{\mathbf{V}}}_{\varepsilon }} \cap {{{\mathbf{L}}}_{{4,\varepsilon }}})$ и ограниченных в пространстве

$\begin{gathered} \mathcal{F}_{\varepsilon }^{b} = L_{4}^{b}(\mathbb{R};{{{\mathbf{L}}}_{{4,\varepsilon }}}) \cap L_{2}^{b}(\mathbb{R};{{{\mathbf{V}}}_{\varepsilon }}) \cap {{L}_{\infty }}(\mathbb{R};{{{\mathbf{H}}}_{\varepsilon }}) \cap \\ \, \cap \left\{ {v\,{\text{|}}\,\frac{{\partial v}}{{\partial t}} \in L_{{4/3}}^{b}(\mathbb{R};{\mathbf{H}}_{\varepsilon }^{{ - r}})} \right\}. \\ \end{gathered} $

Аналогично определяется ${{\mathcal{F}}^{b}}$ для области без перфорации.

Имеет место утверждение, доказательство которого практически полностью совпадает с доказательством, приведенным в [7] для более частного случая, с использованием вывода диссипативного неравенства для перфорированных областей (см. [5]). Обозначим через ${{\Pi }_{ + }}$ — оператор сужения на полуось ${{\mathbb{R}}_{ + }}.$

Утверждение 2.1. Задача (1) имеет траекторные аттракторы ${{\mathfrak{A}}_{\varepsilon }}$ в топологическом пространстве $\Theta _{{ + ,\varepsilon }}^{{{\text{loc}}}}$. Множество ${{\mathfrak{A}}_{\varepsilon }}$ равномерно (по $\varepsilon \in (0,1)$) ограничено в $\mathcal{F}_{{ + ,\varepsilon }}^{b}$ и компактно в $\Theta _{{ + ,\varepsilon }}^{{{\text{loc}}}}$. Более того,

${{\mathfrak{A}}_{\varepsilon }} = {{\Pi }_{ + }}{{\mathcal{K}}_{\varepsilon }},$
причем ядро ${{\mathcal{K}}_{\varepsilon }}$ непусто и равномерно (по $\varepsilon \in (0,1)$) ограничено в $\mathcal{F}_{\varepsilon }^{b}$.

3. ОСНОВНЫЕ УТВЕРЖДЕНИЯ

В этом разделе изучаются предельное поведение траекторных аттракторов ${{\mathfrak{A}}_{\varepsilon }}$ для уравнений Гинзбурга–Ландау (1) при $\varepsilon \to 0 + $ и их сходимость к траекторному аттрактору соответствующего усредненного уравнения для различных значений параметра $\theta > 0$.

3.1. Критический случай $\theta = 1$

Усредненная (предельная) задача имеет следующий вид:

(9)
$\left\{ \begin{gathered} \frac{{\partial {{u}_{0}}}}{{\partial t}} - \left( {1 + \alpha {\text{i}}} \right)\sum\limits_{i,j = 1}^d \frac{\partial }{{\partial {{x}_{i}}}}\left( {{{{\hat {a}}}_{{ij}}}(x)\frac{{\partial {{u}_{0}}}}{{\partial {{x}_{j}}}}} \right) - \hfill \\ \, - \bar {R}(x){{u}_{0}} + (1 + \bar {\beta }(x){\text{i}}){{\left| {{{u}_{0}}} \right|}^{2}}{{u}_{0}} + Q(x){{u}_{0}} = \hfill \\ \, = \left| {\square \backslash G(x)} \right|f(x),\quad x \in \Omega , \hfill \\ {{u}_{0}} = 0,\quad x \in \partial \Omega , \hfill \\ {{u}_{0}} = U(x),\quad x \in \Omega ,\quad t = 0, \hfill \\ \end{gathered} \right.$
где

$\begin{gathered} {{{\hat {a}}}_{{ij}}}(x) = \int\limits_{\square \backslash G(x)} \sum\limits_{l = 1}^d \left( {\frac{{\partial {{M}_{i}}(x,\xi )}}{{\partial {{\xi }_{l}}}} + {{\delta }_{{ij}}}} \right)d\xi , \\ Q(x) = \int\limits_{S(x)} q(x,\xi ){\kern 1pt} d{{\sigma }_{\xi }}. \\ \end{gathered} $

Здесь ${{M}_{i}}(x,\xi )$ – 1-периодические функции по $\xi $, удовлетворяющие задачам

$\begin{gathered} {{\Delta }_{\xi }}\left( {{{M}_{i}} + {{\xi }_{i}}} \right) = 0\quad {\text{в}}\quad \square \backslash G(x), \\ \frac{{\partial {{M}_{i}}}}{{\partial {{\nu }_{\xi }}}} = {{\nu }_{i}}\quad {\text{на}}\quad S(x), \\ \end{gathered} $
и имеющие нулевые средние по ячейке периодичности, $G(x) = \left\{ {\xi \in \,\square :F(x,\xi ) \leqslant 0} \right\}$ – локальное включение, а $S(x) = \left\{ {\xi \in \,\square :F(x,\xi ) = 0} \right\}$ – граница включения $G(x)$ в растянутом пространстве $\xi $, ${{\nu }_{\xi }}$ – вектор единичной внешней нормали к S(x).

Рассматриваются обобщенные решения задачи (9), т.е. функции ${{u}_{0}} = {{u}_{0}}(x,t)$, $x \in \Omega $, $t \geqslant 0$,

$\begin{gathered} {{u}_{0}} \in L_{4}^{{{\text{loc}}}}({{\mathbb{R}}_{ + }};{{{\mathbf{L}}}_{4}}) \cap L_{2}^{{{\text{loc}}}}({{\mathbb{R}}_{ + }};{\mathbf{V}}) \cap L_{\infty }^{{{\text{loc}}}}({{\mathbb{R}}_{ + }};{\mathbf{H}}) \cap \\ \, \cap \left\{ {v\,{\text{|}}\,\frac{{\partial v}}{{\partial t}} \in L_{{4/3}}^{{{\text{loc}}}}({{\mathbb{R}}_{ + }};{{{\mathbf{H}}}^{{ - r}}})} \right\}, \\ \end{gathered} $
удовлетворяющие интегральному тождеству
$ - \int\limits_0^\infty \int\limits_\Omega {{u}_{0}}\frac{{\partial v}}{{\partial t}}dtdx + \left( {1 + \alpha {\text{i}}} \right)\int\limits_0^\infty \int\limits_\Omega \sum\limits_{i,j = 1}^d {{\hat {a}}_{{ij}}}(x){\kern 1pt} \frac{{\partial {{u}_{0}}}}{{\partial {{x}_{i}}}}\frac{{\partial v}}{{\partial {{x}_{j}}}}dtdx - $
(10)
$\, - \int\limits_0^\infty \int\limits_\Omega (\bar {R}(x){{u}_{0}} - (1 + \bar {\beta }(x){\text{i}}){{\left| {{{u}_{0}}} \right|}^{2}}{{u}_{0}} - Q(x){{u}_{0}})vdtdx = $
$\, = \int\limits_0^\infty \int\limits_\Omega {\text{|}}{\kern 1pt} \square \backslash G(x){\text{|}}{\kern 1pt} f(x){\kern 1pt} v{\kern 1pt} dtdx$
для любой функции $v \in C_{0}^{\infty }({{\mathbb{R}}_{ + }};{\mathbf{V}} \cap {{{\mathbf{L}}}_{4}}).$

Задача (9) имеет траекторный аттрактор $\bar {\mathfrak{A}}$ в соответствующем пространстве траекторий 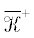, причем

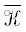где – ядро задачи (9) в ${{\mathcal{F}}^{b}}$, которое определяется по аналогии с 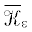, но для области без перфорации.

Сформулируем основную теорему об усреднении аттракторов уравнений Гинзбурга–Ландау в этом случае.

Теорема 3.1. В топологическом пространстве $\Theta _{ + }^{{{\text{loc}}}}$ справедливо предельное соотношение

(11)
${{\mathfrak{A}}_{\varepsilon }} \to \bar {\mathfrak{A}}\quad {\text{при}}\quad \varepsilon \to 0 + .$

Кроме того

(12)

Замечание 3.1. Заметим, что все функции, определенные в перфорированной области и удовлетворяющие граничным условиям, могут быть продолжены внутрь отверстий с сохранением соответствующих норм (см. [12, 13] и [14]). Отметим, что оператор продолжения строится аналогично работе [14]. Он действует только по переменной x и не зависит от t. Соотношения (11) и (12) надо понимать с учетом оператора продолжения и они выполняются для любого такого продолжения.

3.2. Субкритический случай $\theta > 1$

Усредненная (предельная) задача имеет следующий вид:

(13)
$\left\{ \begin{gathered} \frac{{\partial {{u}_{0}}}}{{\partial t}} - \left( {1 + \alpha {\text{i}}} \right)\sum\limits_{i,j = 1}^d \frac{\partial }{{\partial {{x}_{i}}}}\left( {{{{\hat {a}}}_{{ij}}}(x)\frac{{\partial {{u}_{0}}}}{{\partial {{x}_{j}}}}} \right) - \bar {R}(x){{u}_{0}} + \hfill \\ + (1 + \bar {\beta }(x){\text{i}}){{\left| {{{u}_{0}}} \right|}^{2}}{{u}_{0}} = \left| {\square \backslash G(x)} \right|f(x),\quad x \in \Omega , \hfill \\ {{u}_{0}} = 0,\quad x \in \partial \Omega , \hfill \\ {{u}_{0}} = U(x),\quad x \in \Omega ,\quad t = 0, \hfill \\ \end{gathered} \right.$
здесь ${{\hat {a}}_{{ij}}}(x)$ – определены также как и в подразделе 2.1 ($i,j = 1, \ldots ,d$).

Рассматриваются обобщенные решения задачи (13), т.е. функции ${{u}_{0}} = {{u}_{0}}(x,t)$, $x \in \Omega $, $t \geqslant 0$,

$\begin{gathered} {{u}_{0}} \in L_{4}^{{{\text{loc}}}}({{\mathbb{R}}_{ + }};{{{\mathbf{L}}}_{4}}) \cap L_{2}^{{{\text{loc}}}}({{\mathbb{R}}_{ + }};{\mathbf{V}}) \cap L_{\infty }^{{{\text{loc}}}}({{\mathbb{R}}_{ + }};{\mathbf{H}}) \cap \\ \, \cap \left\{ {v\,{\text{|}}\,\frac{{\partial v}}{{\partial t}} \in L_{{4/3}}^{{{\text{loc}}}}({{\mathbb{R}}_{ + }};{{{\mathbf{H}}}^{{ - r}}})} \right\}, \\ \end{gathered} $
удовлетворяющие интегральному тождеству
$ - \int\limits_0^\infty \int\limits_\Omega {{u}_{0}}\frac{{\partial v}}{{\partial t}}dtdx + \left( {1 + \alpha {\text{i}}} \right)\int\limits_0^\infty \int\limits_\Omega \sum\limits_{i,j = 1}^d {{\hat {a}}_{{ij}}}(x){\kern 1pt} \frac{{\partial {{u}_{0}}}}{{\partial {{x}_{i}}}}\frac{{\partial v}}{{\partial {{x}_{j}}}}dtdx - $
(14)
$\, - \int\limits_0^\infty \int\limits_\Omega (\bar {R}(x){{u}_{0}} - (1 + \bar {\beta }(x){\text{i}}){{\left| {{{u}_{0}}} \right|}^{2}}{{u}_{0}})vdtdx = $
$\, = \int\limits_0^\infty \int\limits_\Omega {\text{|}}{\kern 1pt} \square \backslash G(x){\text{|}}{\kern 1pt} f(x){\kern 1pt} v{\kern 1pt} dtdx$
для любой функции $v \in C_{0}^{\infty }({{\mathbb{R}}_{ + }};{\mathbf{V}} \cap {{{\mathbf{L}}}_{4}})$.

Задача (13) имеет траекторный аттрактор $\bar {\mathfrak{A}}$ в соответствующем пространстве траекторий 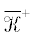, причем

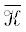где – ядро задачи (13) в ${{\mathcal{F}}^{b}}$.

Сформулируем основную теорему об усреднении аттракторов уравнений Гинзбурга–Ландау в этом случае.

Теорема 3.2. В топологическом пространстве $\Theta _{ + }^{{{\text{loc}}}}$ справедливо предельное соотношение

(15)
${{\mathfrak{A}}_{\varepsilon }} \to \bar {\mathfrak{A}}\quad при\quad \varepsilon \to 0 + .$

Кроме того

(16)

3.3. Суперкритический случай $\theta < 1$

Решения исходной задачи в этом случае стремятся к нулю при $\varepsilon \to 0 + $.

Сформулируем основную теорему об усреднении аттракторов уравнений Гинзбурга–Ландау в этом случае.

Теорема 3.3. В топологическом пространстве $\Theta _{ + }^{{{\text{loc}}}}$ справедливо предельное соотношение

(17)
${{\mathfrak{A}}_{\varepsilon }} \to 0\quad при\quad \varepsilon \to 0 + .$

Кроме того

(18)
${{\mathcal{K}}_{\varepsilon }} \to 0\quad при\quad \varepsilon \to 0 + \quad в\quad {{\Theta }^{{{\text{loc}}}}}.$

4. КОММЕНТАРИИ

Доказательство основных утверждений проводится на основе асимптотического анализа. Решения ищутся в виде асимптотического ряда

(19)
$\begin{gathered} {{u}_{\varepsilon }}(t,x) = {{u}_{0}}(t,x) + \\ \, + \varepsilon {{u}_{1}}\left( {t,x,\frac{x}{\varepsilon }} \right) + {{\varepsilon }^{2}}{{u}_{2}}\left( {t,x,\frac{x}{\varepsilon }} \right) + {{\varepsilon }^{3}}{{u}_{3}}\left( {t,x,\frac{x}{\varepsilon }} \right) + \ldots , \\ \end{gathered} $
после подстановки которого в задачу приравниваются слагаемые с соответствующими степенями $\varepsilon $ (см., например, [15]).

Используя равномерные оценки по малому параметру, которые доказываются с помощью леммы 2.1, получаем утверждения о сходимости решений, а затем и аттракторов.

Список литературы

  1. Bekmaganbetov K.A., Chechkin G.A., Chepyzhov V.V. Strong Convergence of Trajectory Attractors for Reaction–Diffusion Systems with Random Rapidly Oscillating Terms // Communications on Pure and Applied Analysis (CPAA). 2020. V. 19. № 5. P. 2419–2443.

  2. Bekmaganbetov K.A., Chechkin G.A., Chepyzhov V.V. “Strange Term” in Homogenization of Attractors of Reaction–Diffusion Equation in Perforated Domain // Chaos, Solitons & Fractals. 2020. V. 140. Art. No 110208.

  3. Бекмаганбетов К.А., Толеубай А.М., Чечкин Г.А. Об аттракторах системы уравнений Навье–Стокса в двумерной пористой среде // Проблемы математического анализа. 2022. Т. 115. С. 15–28.

  4. Chechkin G.A., Chepyzhov V.V., Pankratov L.S. Homogenization of Trajectory Attractors of Ginzburg–Landau equations with Randomly Oscillating Terms // Discrete and Continuous Dynamical Systems. Series B (DCDS-B). 2018. V. 23. № 3. P. 1133–1154.

  5. Бекмаганбетов К.А., Чепыжов В.В., Чечкин Г.А. Сильная сходимость аттракторов системы реакции–диффузии с быстро осциллирующими членами в ортотропной пористой среде // Известия РАН. Серия математическая. 2022. Т. 86. № 6. С. 47–78.

  6. Бабин А.В., Вишик М.И. Аттракторы эволюционных уравнений. М.: Наука, 1989.

  7. Chepyzhov V.V., Vishik M.I. Attractors for equations of mathematical physics. Providence (RI): Amer. Math. Soc., 2002.

  8. Lions J.-L. Quelques méthodes de résolutions des problèmes aux limites non linкires. Paris: Dunod, Gauthier-Villars, 1969.

  9. Temam R. Infinite-dimensional dynamical systems in mechanics and physics. Applied Mathematics Series. V. 68. New York (NY): Springer-Verlag, 1988.

  10. Chepyzhov V.V., Vishik M.I. Evolution equations and their trajectory attractors // J. Math. Pures Appl. 1997. V. 76. № 10. P. 913–964.

  11. Mielke A. The complex Ginzburg–Landau equation on large and unbounded domains: sharper bounds and attractors // Nonlinearity. 1997. V. 10. P. 199–222.

  12. Лионс Ж.-Л., Мадженес Е. Неоднородные граничные задачи и их приложения. М.: Мир, 1971.

  13. Жиков В.В. Об усреднении в перфорированных случайных областях общего вида // Матем. заметки. 1993. Т. 53. № 1. С. 41–58.

  14. Conca C. On the application of the homogenization theory to a class of problems arising in fluid mechanics. // J. Math. Pures Appl. 1985. (9) 64. № 1. P. 31–75.

  15. Беляев А.Г., Пятницкий А.Л., Чечкин Г.А. Асимптотическое поведение решения краевой задачи в перфорированной области с осциллирующей границей // Сиб. матем. журн. 1998. Т. 39. № 4. С. 730–754.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Доклады Российской академии наук. Математика, информатика, процессы управления

Архивы выпусков Информация о журнале Отправить рукопись в журнал