Доклады Российской академии наук. Науки о Земле, 2021, T. 496, № 2, стр. 176-180

Остывание жидкого проводящего ядра Земли приводит к появлению конвекции и генерации переменного во времени магнитного поля, наблюдаемого на поверхности планеты [1]. Согласно сейсмическим наблюдениям, достоверно известно, что внутри жидкого ядра существует твердое ядро [2]. Далее, по степени надежности, следует информация о свойствах вещества в жидком ядре [3, 4], величине теплового потока на границе ядро–мантия и состоянии ядра после завершения процесса аккреции [5, 6]. На основе этих данных удается построить модель остывания ядра, позволяющую наблюдать зарождение твердого ядра и областей устойчивой стратификации. Появление твердого ядра приводит к переходу от режима чистой тепловой конвекции к режиму тепловой и композиционной конвекции [7], и может сопровождаться значительным резким увеличением энергии, доступной для генерации магнитного поля [8]. Более того, возможны сценарии эволюции, когда до появления твердого ядра тепловой энергии недостаточно для генерации магнитного поля. В то же время палеомагнитологи не только наблюдают древнее магнитное поле в те времена, когда твердого ядра, вероятно, еще не было [9], но и не видят значительных изменений в его напряженности на протяжении большей части эволюции нашей планеты.

Ниже мы рассмотрим модель остывания ядра Земли [8, 10] и решим обратную задачу, выяснив, при каких значениях параметров появление твердого ядра не будет приводить к существенным изменениям напряженности поля.

В модели предполагается существование трех областей в ядре [6, 10, 11]: твердого ядра $0 \leqslant r \leqslant c$ (I), области, где существует развитая конвекция, приводящая к появлению адиабатического состояния $c \leqslant r \leqslant {{r}_{1}}$ (II), и области субадиабатического градиента температуры ${{r}_{1}} \leqslant r \leqslant {{r}_{{\text{b}}}}$ (III), где r – сферический радиус, r_b – радиус жидкого ядра, не зависящий от времени. В начальный момент времени после формирования жидкого ядра, t = 0, существовала только адиабатическая область (II), c = 0, r₁ = r_b, с температурой в центре T₀. На границе r_b задается тепловой поток с плотностью q_b(t). Задача состоит в том, чтобы описать остывание ядра Земли, в процессе которого может появиться как твердое ядро (область I), так и область субадиабатического градиента III.

Распределения плотности $\rho (r)$, давления P(r) и гравитационного ускорения g(r) удовлетворяют гидростатическому балансу, задаваемому соотношениями:

где G – гравитационная постоянная.

Замыкает систему уравнений для трех переменных ($P$, $\rho $, $g$) логарифмическое уравнение состояния [12]:

где K₀ – модуль объемной упругости, ${{\rho }_{0}}$ – плотность при нулевом давлении.

Для учета скачка на границе ядро–мантия вводится поправка:

Зная распределения ($P$, $\rho $, $g$), найдем адиабатическое распределение температуры:

где T_c(c) – температура на границе r = c. Коэффициент объемного расширения $\alpha $ задан соотношением: где C_p – удельная теплоемкость при постоянном давлении, $\gamma $ – параметр Грюнайзена.

До появления твердого ядра, c = 0, T_c(c) = T_c(0) = = T₀, где T₀ – температура в центре Земли. Значение T₀ находится из уравнения теплового баланса:

где q₁ – плотность теплового потока на r₁ и

Рост твердого ядра начинается, когда температура станет меньше температуры кристаллизации:

где $T_{{\text{s}}}^{{\text{0}}}$ – температура кристаллизации в центре ядра Земли. Кристаллизация начинается в центре ядра. Появление твердого ядра сводится к выполнению условия T_c = T₀ = T_s(r) в центре r = c = 0. Далее, при росте твердого ядра, c > 0, температура кристаллизации дает значение для адиабаты на границе твердого ядра: T_ad(c) = T_c(c) = T_s(c).

Положение границы твердого ядра c может быть найдено из баланса энергии:

где ${{Q}_{{\text{L}}}}$, ${{Q}_{{\text{G}}}}$, ${{Q}_{{\text{C}}}}$ – латентная теплота, изменение энергии, связанное с дифференциацией вещества и адиабатическое охлаждение соответственно. С левой стороны в (10) стоит разность тепловых потоков ${{Q}_{{{\text{CMB}}}}} = 4\pi r_{1}^{2}{{q}_{{\text{b}}}}$, ${{Q}_{{{\text{ICB}}}}} = 4\pi c_{{}}^{2}{{q}_{c}}$ за единицу времени, входящих в адиабатическую область II, справа – скорость изменения энергий и теплот. Далее мы полагаем, что ${{Q}_{{{\text{CMB}}}}} = Q_{{_{{{\text{CMB}}}}}}^{0} - \lambda t.$ Коэффициент $\lambda $ выбран так, чтобы обеспечить уменьшение потока на 20% за 4.5 млрд лет. Для дальнейшего изложения удобно ввести переменные ${{P}_{{\text{i}}}}$:

Источник, связанный с латентной теплотой, равен

где $\delta S$ – удельная энтропия кристаллизации.

Оценка изменения гравитационной энергии при росте твердого ядра [13] имеет вид:

где ${{M}_{0}} = \frac{4}{3}\pi \int_0^{{{r}_{{\text{b}}}}} {\rho {{r}^{2}}dr} $ – масса ядра, величина постоянная в модели. Дифференцируя (13) по времени, получаем

Изменение теплоты, связанное с адиабатическим охлаждением, дает следующий вклад в (10):

Уравнения (10)–(15) могут быть разрешены относительно производной по времени $\dot {c}$ и проинтегрированы по времени¹¹.

Считая температуру непрерывной на границе c, получаем, что значение температуры T_s(c) является граничным условием на границе c для задачи теплопроводности внутри твердого ядра 0 < r < c (I) с движущейся границей c(t):

где $k$ – коэффициент температуропроводности. В центре r = 0 имеем второе граничное условие $\frac{{\partial T}}{{\partial r}} = 0$. Совместное решение уравнений (1)–(16) дает распределение физических полей в областях I, II²², см. значения параметров в табл. 1 и в работах [9, 10].

Течения жидкости в области II могут генерировать магнитное поле. На больших временах примем, что вся энергия магнитного поля превратится в тепло ${{Q}_{{\text{J}}}}$,составив некоторую долю от полного потока ${{Q}_{{{\text{CMB}}}}}$. Оценить ${{Q}_{{\text{J}}}}$ из баланса энергий (10) нельзя, поскольку это уравнение не включает промежуточные формы энергии: т.е. не описывает появление конвекции в явном виде, возникновение магнитного поля с последующим превращением его в тепло. Для того, чтобы оценить ${{Q}_{{\text{J}}}}$, кроме уравнения баланса энергии (10) используется дополнительное уравнение для энтропии [7, 8, 14], в которое ${{Q}_{{\text{J}}}}$ входит в явном виде:

где до появления твердого ядра ${{Q}_{{\text{L}}}} = {{Q}_{G}} = {{Q}_{{{\text{ICB}}}}}$ = = 0. Вклад генерации энтропии адиабатой равен $\Sigma = \int \kappa {{\left( {\frac{{\alpha g}}{{{{C}_{{\text{P}}}}}}} \right)}^{2}}d{{V}_{{{\text{II}}}}}$,$\kappa $ – коэффициент теплопроводности, ${{V}_{{{\text{II}}}}}$ – объем области II. $\bar {T}$ = $V_{{{\text{II}}}}^{{ - 1}}\int {{{T}_{{{\text{ad}}}}}} d{{V}_{{{\text{II}}}}}$ – средняя по объему температура. Обратим внимание, что ${{Q}_{{\text{G}}}}$, напрямую не связанный с энтропией, не входит в (17). Величина температуры области диссипации магнитного поля ${{T}_{{\text{D}}}}$: ${{T}_{{{\text{ICB}}}}} < {{T}_{{\text{D}}}} < {{T}_{{{\text{CMB}}}}}$, выбрана по порядку величины, равной $\bar {T}$, до появления ядра и $\frac{{\bar {T} + {{T}_{{{\text{ICB}}}}}}}{2}$ – после его появления. Последнее отражает тот факт, что магнитное поле сконцентрировано вблизи твердого ядра. Все величины в (10), (17), кроме ${{Q}_{{\text{J}}}}$, известны после решения (1)–(16).

Выражение для ${{Q}_{{\text{J}}}}$, с учетом (10), (17), удобно записать в следующем виде:

Как и прежде, второй член, содержащий ${{Q}_{{\text{L}}}}$ и ${{Q}_{{{\text{ICB}}}}}$, равен нулю при c = 0. За меру эффективности динамо-механизма примем отношение $\eta = {{Q}_{{\text{J}}}}{\text{/}}{{Q}_{{{\text{CMB}}}}}.$ Обсуждение сходства и различия (18) с аналогичным выражением для цикла Карно можно найти в [7].

Решим обратную задачу для модели (1)–(18) методом Монте-Карло [9] на интервале времени 6 млрд лет и найдем такие $Q_{{{\text{CMB}}}}^{0}$, ${{T}_{{\text{0}}}}$ и $T_{{\text{s}}}^{{\text{0}}}$, лежащие в допустимых интервалах 7.6–30 ТВт, 5800–7000 K, 5100–5700 K соответственно, чтобы: 1) радиус твердого ядра при t = 4.6 млрд лет был максимально близок к современному значению c_m = 1220 км; 2) средняя по времени омическая диссипация до и после появления твердого ядра $Q_{{\text{J}}}^{{\text{a}}}$, $Q_{{\text{J}}}^{{\text{b}}}$, соответственно, была больше некоторого заданного значения $Q_{{\text{J}}}^{0}$; 3) отношение минимального значения диссипации $Q_{{\text{J}}}^{{\text{a}}}$, $Q_{{\text{J}}}^{{\text{b}}}$ к максимальному было в интервале $({{R}_{{{\text{min}}}}}{\kern 1pt} - {\kern 1pt} 1)$. Для этого введем штрафную функцию $\Psi $ = 1 – ${{e}^{{\frac{1}{3}\left( {{{R}_{1}} + {{R}_{2}} + {{R}_{3}}} \right)}}}$, где R_i определены следующим образом: ${{R}_{1}} = \frac{{\left| {c - {{c}_{{\text{m}}}}} \right|}}{{{{c}_{{\text{m}}}}}}$. ${{R}_{2}} = 1$, если $Q_{{\text{J}}}^{{\text{a}}} < Q_{{\text{J}}}^{{\text{0}}}$, или $Q_{{\text{J}}}^{{\text{b}}} < Q_{{\text{J}}}^{{\text{0}}}$, в противном случае – ${{R}_{2}} = 0$. ${{R}_{3}} = 1$, ${\text{если}}$ $\min (Q_{{\text{J}}}^{{\text{a}}},Q_{{\text{J}}}^{{\text{b}}}){\text{/}}\max (Q_{{\text{J}}}^{{\text{a}}},Q_{{\text{J}}}^{{\text{b}}})$ < < ${{R}_{{\min }}}$, в противном случае – ${{R}_{3}} = 0$. Минимум функции $\Psi $ будет соответствовать искомому решению.

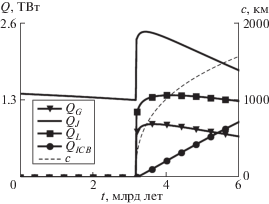
Решение обратной задачи для $Q_{{\text{J}}}^{0} = 0.5$ ТВт, ${{R}_{{\min }}} = 0.6$ методом Монте-Карло [9] дает Ψ = = $1.6 \times {{10}^{{ - 4}}}$, $Q_{{_{{{\text{CMB}}}}}}^{0} = 18.9$ ТВт, ${{T}_{{\text{0}}}} = 6681$ K, $T_{s}^{0}$ = = 5396 K, и современный радиус ядра c = 1223 км. Выбор $Q_{{\text{J}}}^{0}$ основан на современных оценках энергии, требующейся для генерации магнитного поля [8]. Эволюция радиуса твердого ядра c и ${{Q}_{{\text{i}}}}$ на интервале времени от появления жидкого ядра, t = 0, и до 6 млрд лет представлена на рис. 1. Настоящий момент времени соответствует t = 4.6 млрд лет. Модель позволяет сделать экстраполяцию на 1.4 млрд лет в будущее. Данный сценарий соответствует достаточно молодому твердому ядру, начавшемуся образовываться 1.4 млрд лет назад. В момент появления твердого ядра (t = 3.17 млрд лет) эффективность динамо $\eta $ возрастает от 0.078 до 0.135, что связано с увеличением ${{Q}_{{\text{J}}}}$. Увеличение энергии ${{Q}_{{\text{J}}}}$, доступной для генерации магнитного поля, происходит всего в 1.7 раза, что соответствует увеличению напряженности поля на 30%. Такое увеличение, если и является значимым с точки зрения палеомагнитных методов, то все же не является катастрофичным. Следует также отметить, что появление источников энергии вблизи границы твердого ядра ${{Q}_{{\text{L}}}}$, ${{Q}_{{\text{G}}}}$ приводит к изменению генерации магнитного поля, и требует решения уравнений динамо для более точной оценки напряженности магнитного поля на поверхности Земли. Выше мы лишь показали, что появление твердого ядра не обязательно приводит к существенному изменению напряженности магнитного поля. При имеющейся точности входных данных модели такой сценарий эволюции ядра вполне вероятен.