Доклады Российской академии наук. Науки о Земле, 2021, T. 501, № 1, стр. 73-77

Источниками внутренних гравитационных волн (ВГВ) в океане могут быть любые возмущения стратифицированной среды [13, 15, 16]. Однако наиболее сильные “генераторы” внутренних волн – это прилив и ветер. Приливные течения набегают на подводный склон и генерируют ВГВ приливного периода, которые затем распространяются как свободные волны. Вблизи источника поля ВГВ описываются лучами или множеством мод, при этом высокие моды быстро затухают и далее распространяются волны низших мод [13, 16]. При ветровом воздействии на поверхность океана прямой генерации ВГВ практически не происходит: ветровое воздействие генерирует инерционные колебания, которые, разрушаясь, генерируют волновые пакеты широкого диапазона частот [15, 18]. Генерация ВГВ метеорологическими возмущениями рассматривалась в [9, 10, 18]. Сильнейшим генератором инерционных колебаний являются тайфуны и ураганы: тайфун может перемещаться по поверхности океана со скоростью несколько метров в секунду, что, как правило, больше фазовых скоростей ВГВ в океане [2, 7, 9, 15, 18]. За тайфуном образуется волновой след, напоминающий конус Маха, в котором возбуждаются сначала инерционные колебания, а потом широкий спектр внутренних волн [9, 10, 18]. Практически в океане такие возбуждаемые волны имеют период порядка одного часа в зависимости от глубины океана [2, 6, 7, 15]. Внутренние волны могут генерироваться также другими сильными возмущениями в океане, например, неустойчивыми струями течений, фронтами, вихрями [2–4, 8, 20]. Возбуждаемые с помощью этого механизма генерации волновые поля могут генерироваться также другими сильными возмущениями, которые играют значительную роль в различных механизмах переноса энергии в толще океана [13, 15, 16]. Распространение диспергирующих ВГВ в океане имеет особенности, связанные с зависимостью скорости распространения от длины волны. Структура волновых картин на больших расстояниях от движущегося источника практически не зависит от его формы и определяется в основном законом дисперсии и скоростью источника. Современные подходы к описанию линейных ВГВ основаны на представлении волновых полей интегралами Фурье, анализе их асимптотик и на построении фазовых структур в рамках кинематической теории диспергирующих волн [3, 7, 11].

В работе рассматриваются особенности фазовой и амплитудной структур дальних полей ВГВ, используя распределения частоты плавучести, характерные для акватории Северной Атлантики [5, 12, 17, 19]. Учет реальной стратификации температуры и солености позволяет учитывать особенности волновой динамики с учетом изменчивости плотности морской среды, наблюдаемой при натурных измерениях ВГВ в Мировом океане. Район Северной Атлантики был выбран, поскольку в этой части океана часто наблюдаются достаточно сильные ветры. Также был рассмотрен район западной тропической Атлантики, где в осенний сезон проходят траектории ураганов. Аналогичная ситуация наблюдается в северной части Тихого океана и в других районах океана с сильными ветрами, поэтому принципиального различия в физических особенностях волновых процессов нет, однако возможны определенные отличия в численных значениях решений.

Ниже приводится табл. 1 частоты Вяйсяля-Брента на характерных глубинах сезонного термоклина 100 м и главного термоклина 1000 м для рассмотренных районов Северной Атлантики, где проводились отечественные измерения [5, 6, 12, 17, 18].

В движущейся вместе с источником системе координат установившееся поле возвышения $\eta (\xi ,y,z,{{z}_{0}})$ линейных ВГВ, возбуждаемых в невязкой, несжимаемой, стратифицированной по вертикали среде конечной глубины $H$ при $t \to \infty $ определяется из задачи [3, 11]

где $V$ – скорость движения источника, $\xi = x + Vt$, ${{z}_{0}}$ – глубина погружения источника, $\eta = 0$, $z = 0$, $ - H$, ${{N}^{2}}(z)$ = $ - \frac{g}{{\mathop \rho \nolimits_0 (z)}}\frac{{d\mathop \rho \nolimits_0 (z)}}{{dz}}$ – частота Вяйсяля–Брента, ${{\rho }_{0}}(z)$ – невозмущенная плотность среды, функция $Q\left( {\xi ,y,z,{{z}_{0}}} \right)$ описывает плотность распределения источников в движущейся системе координат. На больших расстояниях реальные источники возмущений ВГВ допускают физически обоснованную аппроксимацию некоторой системой точечных локализованных источников, взятых с определенными весами [3, 4, 7, 20]. Решение задачи (1) описывает установившийся волновой режим в движущейся со скоростью $V$ вместе с источником возмущений системе координат, и имеет вид суммы волновых мод [3, 11] где подынтегральная функция ${{D}_{n}}(z,{{z}_{0}},\nu )$ зависит от собственных функций и собственных значений ${{\mu }_{n}}(\nu )$, являющихся решением уравнения: $\omega _{n}^{2}(k)$ = ${{V}^{2}}\mu _{n}^{2}(\nu )$, ${{k}^{2}}$ = $\mu _{n}^{2}(\nu ) + {{\nu }^{2}}$, $\omega _{n}^{{}}(k)$ – собственное число основной вертикальной спектральной задачи ВГВ [3, 15]. В [3] показано, что при $t \to \infty $ и фиксированных значениях $\xi = x + Vt$ вклад слагаемых, описывающих переходной режим и явно зависящих от времени, экспоненциально мал.

Асимптотики интегралов (2), описывающие поле отдельной моды ВГВ вдали от источников возмущений, можно вычислить методом стационарной фазы, стационарные точки фазовой функции определяются из решения уравнения: $\mu {\kern 1pt} '(\nu ) = y{\text{/}}\xi $. Асимптотики стационарной фазы перестают работать в окрестности волновых фронтов, т.е. в случае, когда стационарные точки стремятся друг к другу и $\mu {\kern 1pt} ''(\nu ) \to 0$. Волновые фронты определяются такими значениями $\nu {\kern 1pt} *$, при которых $\mu {\kern 1pt} ''(\nu {\kern 1pt} *) = 0$, асимптотики волнового поля вблизи каждого из волновых фронтов могут выражаться через функции Эйри и ее производные [3, 11]. Вблизи волновых фронтов стационарные точки стремятся к нулю, т.е. к краю области интегрирования и одновременно к особенности подынтегрального выражения ${{D}_{n}}(z,{{z}_{0}},\nu )$. В этом случае метод стационарной фазы неприменим, и для построения локальных асимптотик с помощью подходящей замены следует свести исходный интеграл к более сложному эталонному интегралу. Выбор эталонного интеграла определяется распределением стационарных точек фазовой функции и особых точек подынтегральной функции ${{D}_{n}}(z,{{z}_{0}},\nu )$ [14].

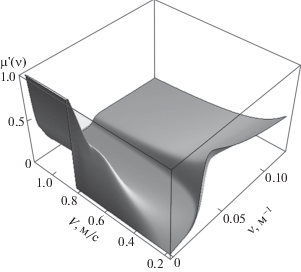
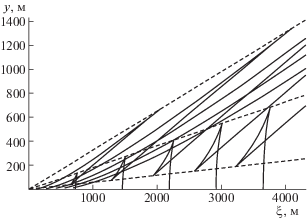
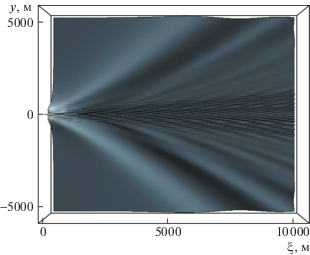
Вдали от источников возмущений качественное поведение волнового поля определяется наличием или отсутствием на интервалах интегрирования в (2) экстремумов функции $\mu {\kern 1pt} '(\nu )$, отвечающих соответствующим стационарным точкам фазовых функций в (2) [3, 11]. Особенности распределения частоты плавучести в различных акваториях Мирового океана приводят к тому, что дисперсионные зависимости и соответствующие им фазовые функции могут иметь несколько стационарных точек. Далее, без ограничения общности, все численные результаты приведены для второй волновой моды. На рис. 1 представлены результаты расчетов дисперсионных поверхностей $\mu {\kern 1pt} '(\nu ,V)$. На рис. 2 представлены результаты расчетов линий равной фазы (сплошные линии), штриховые линии – соответствующие волновые фронты. На рис. 3 представлены результаты расчетов возвышения. Численные расчеты для различных волновых мод показывают, что для различных распределений частоты плавучести может наблюдаться (в зависимости от скорости движения источника возмущений) дисперсионная картина, при которой имеются от одного до нескольких экстремумов функции $\mu {\kern 1pt} '(\nu )$. С увеличением номера волновой моды число экстремумов $\mu {\kern 1pt} '(\nu )$ функции, как правило, возрастает, это означает, что вклад в дальнее поле ВГВ вносят несколько волновых цугов.

Результаты численных расчетов показывают, что топология дисперсионных поверхностей $\mu {\kern 1pt} '(\nu ,V)$ может иметь достаточно сложную структуру, зависящую как от стратификации среды, так и от параметров волновой генерации. Кроме того, численные расчеты показывают, что при изменении параметров волновой генерации (увеличение скорости движения источника возмущений) происходит заметная перестройка фазовых картин возбуждаемых волновых полей. В частности, может наблюдаться характерная фазовая картина типа “ласточкин хвост” (рис. 2) [1]. В этом случае в фиксированной точке наблюдения происходит качественная перестройка одновременно приходящих волновых фронтов. Тогда полное поле ВГВ представляет собой сложную картину волновых биений, когда в фиксированную точку пространства одновременно приходит несколько волновых цугов с различными амплитудами и фазами.

Сложность топологии рассчитанных дисперсионных зависимостей требует для корректного асимптотического исследования дальних полей ВГВ применения специального математического аппарата. Особые точки фазовых функций в интегралах (2) могут сближаться с другими особыми точками или с какой-либо особенностью (полюсом, точкой ветвления) подынтегральной функции ${{D}_{n}}(z,{{z}_{0}},\nu )$. В этом случае стандартные методы исследования асимптотик полей ВГВ становятся неприменимы. Важно отметить, что наиболее интересными с практической точки зрения являются локальные экстремумы дисперсионных поверхностей $\mu {\kern 1pt} '(\nu ,V)$, так как асимптотику поля ВГВ в окрестности соответствующих волновых фронтов и каустик, отвечающих этим экстремумам, можно описать с помощью метода эталонных интегралов. Например, при слиянии двух стационарных точек асимптотика интегралов (2) выражается через функцию Эйри, при слиянии стационарных точек и полюса – через интеграл Френеля. Случай слияния трех стационарных точек может описываться функцией Пирси, часто применяемой в теории особенностей и катастроф [14]. Если две из трех сливающихся стационарных точек находятся строго симметрично относительно третьей, то асимптотика соответствующего интеграла может выражаться через функцию Ханкеля. Если подынтегральная функция ${{D}_{n}}(z,{{z}_{0}},\nu )$ имеет корневую особенность вблизи края области интегрирования, то асимптотики решений описываются с помощью квадрата функции Эйри [3].

Численные расчеты дисперсионных зависимостей, фазовых поверхностей и амплитудно-фазовых характеристик полей ВГВ показывают, что для реально наблюдаемых вертикальных стратификаций Мирового океана могут возникать физически интересные случаи генерации волновых структур, которые не описываются известными эталонными интегралами [1, 3, 14].