Доклады Российской академии наук. Науки о Земле, 2022, T. 504, № 1, стр. 60-64

ИЗГИБ ТОНКОЙ УПРУГОЙ ДВУМЕРНОЙ ПЛИТЫ

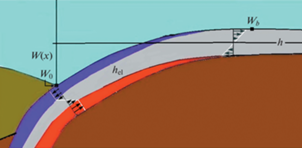
На рис. 1 представлен профиль океанической плиты толщиной h и длиной L. Стрелками показано распределение по высоте для напряжения σ_xx . Серым цветом показана область упругих деформаций переменной толщиной h_el. Фиолетовым – зона растяжений с хрупкой пластичностью, красным – зона сжатия с пластическим течением.

Величину вертикального смещения срединной линии плиты, называемую функцией изгиба, обозначим через W(x). Ось z направим вниз и x – вправо. На концах плиты x = 0 и x = L примем заданными вертикальное смещение W и его производную dW/dx

Верхнюю и нижнюю поверхности плиты примем скользкими, с нулевыми касательными напряжениями

При нагрузках q₁ на верхнюю и q₂ – на нижнюю поверхности плиты граничное условие для нормальных напряжений имеет вид (положительными считаются растягивающие напряжения):

Поскольку решения уравнений для изгиба и для горизонтального растяжения/сжатия аддитивны, то в дальнейшем будем рассматривать только изгибные деформации плиты.

Плиту примем тонкой и изгиб малым. Обычно тонкой считается плита при h/L < 1/6. Рассматриваемая двумерная модель является частным случаем трехмерной модели, когда все свойства плиты, нагрузки и граничные условия не зависят от третьей координаты.

Поскольку для большинства океанических плит h/L < 1/10, то формально условие тонкости плиты h/L < 1/6 выполняется с большим запасом и вопрос о поправках ранее не возникал. Однако для океанических плит вертикальной нагрузкой служит выталкивающая сила мантии, которая не задается заранее, а сама зависит от изгиба. Она создает специфический выгиб (внешнее поднятие W_b). В результате деформации изгиба оказываются распределенными по длине не равномерно, а сосредоточены вблизи зоны субдукции. При этом эффективная длина плиты (область основной деформации) может быть существенно меньшей, порядка L_eff ≈ 200 км. При толщине плиты h = 50 км получим h/L_eff ≈ 1/4, что несколько не соответствует критерию тонкости плит. В настоящей работе находятся поправки к теории тонких плит Кирхгофа для деформаций и на примере изгиба Тихоокеанской плиты у Японского желоба оценивается их величина.

Напряженное состояние упругого тела в трехмерной модели описывается 15 функциями: тремя компонентами вектора смещения U_i, шестью компонентами тензора напряжения σ_ik и шестью компонентами тензора деформаций e_ik. Для них имеется 15 взаимосвязанных уравнений: три соотношения Коши, связывающие смещения U_i, и деформации e_ik, шесть соотношений закона Гука, связывающие деформации e_ik и напряжения σ_ik, и три уравнения равновесия для напряжений. Они приведены, например, в [1]. В рассматриваемой двумерной модели остаются восемь уравнений для восьми функций переменных x и z.

Математически задачу об изгибе тонких плит сформулируем следующим образом. Учитывая, что h < L, нужно упростить все соотношения между напряжениями и деформациями и общие уравнения равновесия. Для этого их зависимость от координаты z представим в виде ряда Тейлора, ограничиваясь первыми по порядку малости ненулевыми членами, в частности для U_x(x, z) = = z∂U_x/∂z. При этом коэффициенты разложения будем искать методом итераций. Пробное решение первого приближения будем искать в форме, при которой x-компонента вектора смещений имеет вид

и компоненты деформаций e_xz и тензора напряжений σ_zz являются малыми по сравнению с соответствующими другими компонентами.

Наводящим указанием на выбор такого пробного решения является следующее. Если плита тонкая, то в соответствии с постулатом Кирхгофа угол изгиба ее срединной линии и угол поворота поперечного сечения плиты в первом приближении равны, т.е. равны их тангенсы или производные, с учетом направления поворота ∂U_x/∂z ≈ –dW/dx. Отметим, что в предлагаемой в настоящей работе постановке задачи этот выбор рассматривается как пробный и относится только к первому приближению. Решение будет искомым только, если итерации сойдутся, и после подстановки конечных выражений в исходные уравнения равновесия они удовлетворяются.

Подставляя пробное соотношение U_x(x, z) = = –zdW/dx в определение xx-компоненты тензора деформаций, найдем

В выражении для zz-компоненты тензора напряжений теории упругости [1]

можно в первом приближении пренебречь компонентой σ_zz, поскольку мы ищем решение в виде, при котором она принята величиной следующего порядка малости по сравнению с σ_xx и σ_xz. Подставив затем в него (5), найдем

В результате получены выражения для компонент тензора деформаций e_xx и напряжений σ_xx первого приближения, выраженные через одну функцию изгиба одной переменной W(x). Поскольку z меняется от –h/2 до h/2, то эти компоненты имеют первый порядок малости.

Далее выражения (5), (7) можно подставить в уравнение равновесия с учетом граничных условий (2), (3) и найти компоненты тензора напряжений σ_zz и σ_xz, а также уравнение для нахождения функции изгиба W(x), полученное С. Жермен еще в 1816 г. В классической теории Кирхгофа полученными так выражениями для напряжений и деформаций и ограничиваются. Однако при этом формально оказывается, что общим уравнениям равновесия удовлетворяют только уравнение Жермен и выражения для напряжений, а выражения для деформаций оказываются не согласованными с напряжениями, так как не удовлетворяют соотношениям Гука и уравнениям равновесия для деформаций. Поэтому до настоящего времени во многих монографиях и пособиях по теории упругости и сопромату, например [3–5], говорится, что гипотезы Кирхгофа, используемые в теории тонких пластин, приводят к неустранимым противоречиям, с которыми, однако, приходится мириться, так как формулы для изгибов и напряжений достаточны для практических приложений. Такие комментарии можно объяснить, по-видимому, нечеткой формулировкой проблемы, в которой формулы Кирхгофа рассматриваются как окончательный результат. Однако, как подчеркнуто в настоящей работе, они являются лишь первым приближением.

Для нахождения деформаций следующего приближения e_xz нужно в выражения (6) подставить теперь уже не нулевое значение σ_zz, а новое найденное значение первого приближения. Также находятся и остальные компоненты тензора деформаций. В результате этой итерации, уточняющей деформации, вся система уравнений для напряжений и деформаций примет нижеследующий вид, где ζ = z/h. Тензор напряжений:

тензор деформаций: и уравнение равновесия Жермен: где D = Eh³/12(1 – ν²) – изгибная жесткость плиты.

Таким образом, чтобы найти все характеристики упругого состояния двумерных тонких плит как функции двух переменных x и z, достаточно решить одно обыкновенное дифференциальное уравнение для функции изгиба одного переменного x (10) и подставить его в (8), (9). Проверка полученных выражений (8)–(10) подстановкой в исходные общие уравнения упругого равновесия показывает, что теперь они удовлетворяются не только для напряжений (как было ранее), но и для деформаций. Однако, чтобы удовлетворить еще и условиям совместности Сен-Венана и получить поправки не только к деформациям, но и к напряжениям и уравнению Жермен, итерации нужно продолжить. Ввиду громоздкости получаемых выражений в настоящей работе они не приводятся.

Полученные после указанной итерации выражения (8) для компонент тензора деформаций e_xx и e_zz отличаются от классической теории изгиба Кирхгофа дополнительными членами соответственно –νσ_zz/E и σ_zz/E, которые учитывают эффект “сплющивания” плиты под действием вертикальной нагрузки. Хотя эти члены и являются малыми поправками, но только при их учете в первом приближении удовлетворяются и законы Гука, и уравнения равновесия в деформациях.

Далее, как видно по (8), система формул изгиба обязательно должна включать компоненту e_yy. Даже в двумерной модели она не может быть равной нулю, так как при отличном от нуля коэффициенте Пуассона вертикальное сжатие всегда вызывает вытеснение вещества не только по оси x, но и по оси y.

МОДЕЛЬ УПРУГОЙ ОКЕАНИЧЕСКОЙ ПЛИТЫ

На океаническую плиту без учета осадков сверху действует давление воды q₁, снизу – давление мантии q₂. Мы рассматриваем изменения всех величин при изгибе плиты W, отсчитывая их от ранее уравновешенной плавающей плиты. Без учета осадков эти силы будут иметь вид

Поэтому уравнение равновесия Жермен (10) для изгиба океанических плит примет вид [2]

где δρ = ρ_m – ρ_w. Простой подстановкой можно убедиться, что для случая бесконечно длинной плиты уравнение (12) с граничными условиями (1) имеет аналитическое решение, соответствующее форме изгиба с поднятием перед желобом, как на рис. 1: где W₀ – глубина желоба, tgφ₀ = $W_{0}^{'}$ – тангенс угла погружения плиты и

Обычно в литературе используется не (13), а другое аналитическое решение, а именно полученное в [2], для которого на левой границе плиты в зоне субдукции задаются заранее неизвестные и неизмеряемые перерезывающая сила и закручивающий момент. Однако более естественно использовать измеряемые величины – глубину желоба и угол наклона плиты.

Найдя производные от функции W(x) по (13) и подставив их в (9), (10), найдем распределения упругих напряжений и деформаций внутри всей плиты. При этом для океанических плит компонента напряжений σ_zz будет иметь вид

Отсюда, в частности, можно найти распределения напряжений и деформаций по глубине при x = 0 на левом конце плиты, погружающейся в мантию.

В качестве примера рассмотрим область Японского желоба. Для нее, согласно [2, 6–9], средняя эффективная толщина плиты h_ef = 40 км, упругие параметры E = 70 ГПа, ν = 0.25, угол субдукции φ₀ = 2.8 град или tg φ₀ = –0.05, глубина желоба W₀ = 2.4 км, ρ_w = 1000 кг/м³, ρ_m = 3300 кг/м³. При этих значениях получим D = Eh³/12(1 – ${{{v}}^{2}}$) = 4 × × 10²³ н м, α = (4D/δρg)^1/4 = 90 км и производные от функции изгиба на левом конце плиты dW/dx = = –0.05, d²W/dx² = 5.2 × 10^–7 м^–1, d³W/dx³ = 0.82 × × 10^–12 м^–2.

Подставляя эти значения в (8), найдем распределения напряжений в поперечном сечении в месте погружения плиты в мантию. В соответствии с общими формулами (8) нормальное напряжение σ_xx линейно зависит от z в пределах ±780 МПа, обращаясь в нуль в срединной плоскости. Напряжение σ_xz параболически меняется по глубине от нуля на верхней и нижней границах до –12 МПа в срединной плоскости. Вертикально сжимающее напряжение σ_zz нарастает сверху вниз по закону кубической параболы от –24 МПа наверху плиты (давление вышележащего слоя воды в желобе) до –79 МПа на нижней границе литосферы, что в среднем составляет около 10% от значения для σ_xx.

Вычисленные по теории Кирхгофа деформации e_xx линейно меняются с глубиной в пределах ±10.4 × 10^–3, а e_zz в пределах ±3.5 × 10^–3, но с обратным знаком. Дополнительные поправки δe_xx и δe_zz увеличиваются с глубиной соответственно от 0.08 × 10^–3 до 0.28 × 10^–3 и от –0.35 × 10^–3 до –1.13 × × 10^–3. Угловая деформация e_xz поправку не содержит и имеет максимум –0.22 × 10^–3 в срединной плоскости.

Относительные поправки к деформациям δe_xx/e_xx и δe_zz/e_zz в среднем составляют порядка 10%, что соответствует квадрату (h/L_eff)². Повышенная величина поправки к e_zz по сравнению с e_xx обусловлена меньшим исходным значением e_zz и отсутствием множителя ν = 0.25. Кроме того, надо учитывать, что исходные деформации и поправки к ним по-разному зависят от z. Предварительная оценка показывает, что при проведении последующих более громоздких итераций суммарные поправки также могут быть порядка 10%.

ЗАКЛЮЧЕНИЕ

При расчетах напряжений и деформаций изгиба океанических плит используется теория тонких пластин Кирхгофа. Критерием ее применимости является малость отношения толщины к длине, а вероятные поправки могут быть порядка (h/L)². Поскольку для океанических плит h ≈ 50 км и L ≈ 1000 км, то было общепринятым, что поправки пренебрежимо малы и поэтому вопрос об их учете ранее не ставился.

В настоящей работе указано, что в критерий тонкости плиты должна входить не ее реальная длина, а эффективная длина ее изгибающейся части L_eff. Для плавающих океанических плит внешней нагрузкой является выталкивающая сила мантии, которая пропорциональна величине изгиба. Упругий выгиб плиты образуется не на середине плиты, а вблизи зоны субдукции в виде внешнего поднятия. При этом основные деформации распределены не равномерно вдоль плиты, а сосредотачиваются в области вблизи зоны субдукции. Для типичных океанических плит ее размер L_eff < 200 км. Поэтому в расчеты напряжений и деформаций океанических плит нужно вносить поправки порядка (h/L_eff)² ~ 10%.

В настоящей работе выражения для деформаций теории Кирхгофа дополняются малыми поправками, возникающими при одной следующей итерации. Конкретный пример расчета для Японского желоба показывает, что эти поправки имеют порядок около 10% и не являются (как ранее полагалось) пренебрежимо малыми. Помимо этого, в расчете использовано аналитическое решение уравнения изгиба с граничными условиями в виде измеряемых глубины желоба и угла погружения плиты, а не в виде заранее неизвестных сил и моментов, как обычно принято в литературе.

Однако отметим, что во многих реальных плитах вблизи зоны субдукции упругие напряжения у верхней и нижней поверхностей плит превышают предел прочности и возникают зоны пластичности. Поэтому полученные выше соотношения (8)–(10) для упругих деформаций усложняются. Приближенно эффект зон пластичности можно учесть, просто заменяя реальную толщину плиты h на эффективную меньшую толщину h_el, соответствующую упругой части плиты [9]. Ввиду ограниченности объема статьи эффекты неупругости в данной работе не рассматриваются.