Электрохимия, 2020, T. 56, № 3, стр. 282-288
ВЯЗКИЙ ПОДСЛОЙ
Джон Ньюман *
Отделение химической и биомолекулярной технологии, Калифорнийский университет
94720-1462 Калифорния, Беркли, США
* E-mail: newman@newman.cchem.berkeley.edu
Поступила в редакцию 17.06.2019
После доработки 16.07.2019
Принята к публикации 05.09.2019
Аннотация
Вихревая вязкость и вихревая диффузия рассчитаны для вязкого подслоя в турбулентном потоке вблизи твердой поверхности с использованием преобразований Фурье спектрального элемента профилей скорости, давления и концентрации. Предполагается, что различные спектральные элементы ведут себя независимо друг от друга в этой области, а величины изображены как функции расстояния от стены. Профили тангенциальной скорости показывают наклон, равный 1 на диаграммах log–log относительно расстояния y от стены, в то время как нормальный компонент показывает наклон, равный 2. Профили концентрации обычно показывают наклон, равный 1, за исключением области вблизи внешнего предела вязкого подслоя. Существует также зависимость от значения числа Шмидта, а также от предположения, что флуктуация концентрации преобладает на расстоянии δ0 на внешней границе вязкого подслоя. Когда нормальная флуктуация скорости коррелируется либо с флуктуацией скорости потока, либо с флуктуацией концентрации, можно получить наклон для вихревой вязкости или вихревой диффузии, равный 3. Вихревая диффузия имеет большую структуру, чем вихревая вязкость, и может существенно отличаться от последней в глубине вязкого подслоя.
ВВЕДЕНИЕ
С 1932 г. является очевидным, что в вязком подслое присутствуют турбулентные колебания [1, 2]. Они просто распадаются при приближении к твердой поверхности. Левич [3, раздел 4, с. 29] предполагает, что в этом регионе разные вихри ведут себя независимо, так что их поведение определяется их индивидуальными величинами на внешнем пределе δ0 вязкого подслоя.
Левич [3, раздел 4, с. 29] утверждает: “В вязком подслое Re меньше единицы, а члены второго порядка в уравнениях Навье–Стокса малы по сравнению с членами первого порядка. Следовательно, распределение скорости в вязком подслое может быть определено только линейными уравнениями. Если определенный спектр вихрей проникает в вязкий подслой, взаимодействие между отдельными вихрями прекращается. Затем поток становится суммой независимых периодических движений, период Т которых остается постоянным во всем вязком подслое”.
Воротынцев и соавторы [4] рассматривают подслой и приходят к выводу, что вихревая вязкость пропорциональна y3, но вихревая диффузия начинает отклоняться от вихревой кинематической вязкости внутри вязкого подслоя, показывая зависимость y4 только внутри подслоя, имеющую зависимость y3 глубоко в слое, коэффициент которого зависит от коэффициента диффузии D. В своей статистической обработке этой ситуации Мартемьянов [5] приходит к аналогичным выводам, но определяет, что в области y3 вихревая диффузия вихрей пропорциональна квадратному корню из D.
АНАЛИЗ
Разделим скорость на устойчивый компонент и колеблющийся компонент:
Подставим в уравнение непрерывности и исключим член для устойчивого компонента:
Подставим в уравнение импульса.
(3)
$\begin{gathered} \frac{{\partial {\mathbf{\bar {v}}} + {\mathbf{v}}{\kern 1pt} '}}{{\partial t}} + \nabla \cdot [({\mathbf{\bar {v}}} + {\mathbf{v}}{\kern 1pt} ')({\mathbf{\bar {v}}} + {\mathbf{v}}{\kern 1pt} ')] = {\nu }\nabla \cdot \nabla ({\mathbf{\bar {v}}} + {\mathbf{v}}{\kern 1pt} ') - \\ - \,\,\frac{1}{{\rho }}\nabla (\mathcal{P} + \mathcal{P}{\kern 1pt} '{\text{)}}. \\ \end{gathered} $Когда 𝒫 принято как динамическое давление, гравитационное ускорение не требуется. Возьмем среднее значение этого уравнения:
(4)
$\frac{{\partial {\mathbf{\bar {v}}}}}{{\partial t}} + \nabla \cdot ({\mathbf{\bar {v}\bar {v}}} + \left\langle {{\mathbf{v}}{\kern 1pt} '{\mathbf{v}}{\kern 1pt} '} \right\rangle ) = {\nu }\nabla \cdot \nabla {\mathbf{\bar {v}}} - \frac{1}{\rho }\nabla \bar {\mathcal{P}},$(5)
$\begin{gathered} \frac{{\partial {\mathbf{v}}{\kern 1pt} '}}{{\partial t}} + \nabla \cdot {\mathbf{\bar {v}v}}{\kern 1pt} ' + \nabla \cdot {\mathbf{v}}{\kern 1pt} '{\mathbf{\bar {v}}} + \nabla \cdot {\mathbf{v}}{\kern 1pt} '{\mathbf{v}}{\kern 1pt} ' - \nabla \cdot \left\langle {{\mathbf{v}}{\kern 1pt} '{\mathbf{v}}{\kern 1pt} '} \right\rangle = \\ = {\nu }\nabla \cdot \nabla {\mathbf{v}}{\kern 1pt} ' - \frac{1}{{\rho }}\nabla \mathcal{P}{\kern 1pt} '. \\ \end{gathered} $В пределах вязкого подслоя v' должно быть небольшим по сравнению с усредненной величиной, а квадрат должен быть незначительным. Хотя это может быть неверно на внешнем пределе вязкого подслоя, оно становится действительным глубже в вязком подслое, и, таким образом, уравнения (2) и (5) могут описывать изменения флуктуирующих величин в пределах вязкого подслоя. Для массопереноса внутри этого слоя при средних и высоких числах Шмидта аналогичное приближение следует применять к флуктуациям концентрации. Этому выводу уравнений, управляющих флуктуациями, способствовали Воротынцев и соавторы [4].
Таким образом, мы имеем линейную задачу для изменения флуктуаций в пределах вязкого подслоя. Кроме того, вязкий подслой очень тонкий, и средние скорости зависят только от y и фактически ${{{\bar {v}}}_{x}}$ = βy, где β – постоянная величина. Таким образом, ${{{\bar {v}}}_{y}}$ = ${{{\bar {v}}}_{z}}$ = 0. В конце концов, мы можем пожелать ослабления строгой линейности ${{{\bar {v}}}_{x}},$ в этом случае ${{{\bar {v}}}_{y}}$ больше не будет нулевым. (Сравним с универсальным профилем скорости.) Управляющие дифференциальные уравнения для флуктуирующих составляющих скорости принимают следующий вид:
(6)
$\frac{{\partial {\text{v}}_{x}^{'}}}{{\partial x}} + \frac{{\partial {\text{v}}_{y}^{'}}}{{\partial y}} + \frac{{\partial {\text{v}}_{z}^{'}}}{{\partial z}} = 0,$(7)
$\begin{gathered} \frac{{\partial {{{{\text{v'}}}}_{x}}}}{{\partial t}} + \beta y\frac{{\partial {\text{v}}_{x}^{'}}}{{\partial x}} + \beta {\text{v}}_{y}^{'} = \\ = {\nu }\left( {\frac{{{{\partial }^{2}}{\text{v}}_{x}^{'}}}{{\partial {{x}^{2}}}} + \frac{{{{\partial }^{2}}{\text{v}}_{x}^{'}}}{{\partial {{y}^{2}}}} + \frac{{{{\partial }^{2}}{\text{v}}_{x}^{'}}}{{\partial {{z}^{2}}}}} \right) - \frac{1}{\rho }\frac{{\partial{ \mathcal{P}}{\kern 1pt} '}}{{\partial x}}, \\ \end{gathered} $(8)
$\frac{{\partial {\text{v}}_{y}^{'}}}{{\partial t}} + {\beta }y\frac{{\partial {\text{v}}_{y}^{'}}}{{\partial x}} = {\nu }\left( {\frac{{{{\partial }^{2}}{\text{v}}_{y}^{'}}}{{\partial {{x}^{2}}}} + \frac{{{{\partial }^{2}}{\text{v}}_{y}^{'}}}{{\partial {{y}^{2}}}} + \frac{{{{\partial }^{2}}{\text{v}}_{y}^{'}}}{{\partial {{z}^{2}}}}} \right) - \frac{1}{{\rho }}\frac{{\partial{ \mathcal{P}}{\kern 1pt} {\text{'}}}}{{\partial y}},$(9)
$\frac{{\partial {\text{v}}_{z}^{'}}}{{\partial t}} + {\beta }y\frac{{\partial {\text{v}}_{z}^{'}}}{{\partial x}} = {\nu }\left( {\frac{{{{\partial }^{2}}{\text{v}}_{z}^{'}}}{{\partial {{x}^{2}}}} + \frac{{{{\partial }^{2}}{\text{v}}_{z}^{'}}}{{\partial {{y}^{2}}}} + \frac{{{{\partial }^{2}}{\text{v}}_{z}^{'}}}{{\partial {{z}^{2}}}}} \right) - \frac{1}{{\rho }}\frac{{\partial{ \mathcal{P}}{\kern 1pt} {\text{'}}}}{{\partial z}}.$Обращаем внимание на то, что мы можем устранить колебания давления, взяв ротор уравнения движения. Отметим также, что на основе уравнения (6) мы можем выразить флуктуирующие компоненты скорости как ротор функции векторного потока. Однако при таких преобразованиях можно легко допустить ошибку.
Для граничных условий мы ожидаем, что флуктуирующие компоненты скорости исчезнут при y = 0 и примут значения на внешней границе вязкого подслоя, которые отражают турбулентные флуктуации во внешнем потоке.
Поскольку уравнения являются линейными в вязком подслое, вихри не взаимодействуют, и мы можем выразить флуктуирующие компоненты в рядах Фурье, которые отражают периодическое поведение во времени, а также вдоль потока x и в поперечном направлении z. Таким образом, мы пишем
(10)
${\text{v}}_{x}^{'} = \operatorname{Re} \{ {{V}_{x}}(y)\exp (i{{k}_{x}}x + i{{k}_{z}}z + i\omega t)\} ,$(11)
${\text{v}}_{y}^{'} = \operatorname{Re} \{ {{V}_{y}}(y)\exp (i{{k}_{x}}x + i{{k}_{z}}z + i\omega t)\} ,$(12)
${\text{v}}_{z}^{'} = \operatorname{Re} \{ {{V}_{z}}(y)\exp (i{{k}_{x}}x + i{{k}_{z}}z + i\omega t)\} ,$(13)
$\mathcal{P}{\kern 1pt} {\text{'}} = \operatorname{Re} \{ P(y)\exp (i{{k}_{x}}x + i{{k}_{z}}z + i\omega t)\} .$Каждый спектральный компонент может быть идентифицирован значениями kx, kz и ω, и каждый спектральный компонент может обрабатываться отдельно от всех остальных. Если бы мы знали спектр внешней турбулентности, скажем вне расстояния y = δ0, это было бы граничным условием для вязкого подслоя на этом расстоянии. Затем мы хотим решить для изменения Vx, Vy, Vz и P как функции y от y = 0 до y = δ0. Поскольку мы не знаем внешний спектр, мы должны угадать значения для Vx, Vy, Vz и P при y = δ0, возможно, пытаясь сопоставить ожидаемое значение вихревой кинематической вязкости при δ0.
Теперь подставим компоненты Фурье (10)–(13) в уравнения (6)–(9).
(15)
$\begin{gathered} i\omega {{V}_{x}} + \beta yi{{k}_{x}}{{V}_{x}} + \beta {{V}_{{\text{y}}}} = \\ = \nu \left( { - k_{x}^{2}{{V}_{x}} + \frac{{{{d}^{2}}{{V}_{x}}}}{{d{{y}^{2}}}} - k_{z}^{2}{{V}_{x}}} \right) - \frac{{i{{k}_{x}}P}}{\rho }, \\ \end{gathered} $(16)
$\begin{gathered} i\omega {{V}_{y}} + \beta yi{{k}_{x}}{{V}_{y}} = \\ = \nu \left( { - k_{x}^{2}{{V}_{y}} + \frac{{{{d}^{2}}{{V}_{y}}}}{{d{{y}^{2}}}} - k_{z}^{2}{{V}_{y}}} \right) - \frac{1}{\rho }\frac{{dP}}{{dy}}, \\ \end{gathered} $(17)
$i\omega {{V}_{z}} + \beta yi{{k}_{x}}{{V}_{z}} = \nu \left( { - k_{x}^{2}{{V}_{z}} + \frac{{{{d}^{2}}{{V}_{z}}}}{{d{{y}^{2}}}} - k_{z}^{2}{{V}_{z}}} \right) - \frac{{i{{k}_{z}}P}}{\rho }.$Мы могли бы исключить P из двух из этих уравнений, но это привело бы к ненужному усложнению выражений.
Затем сделаем задачу безразмерной, введя y+ = = (y/ν)(τ0/ρ)0.5 и безразмерные коэффициенты Фурье и безразмерное давление. Под функциями скорости Vx, Vy и Vz можно понимать деление на значение Vx при y = δ0. Параметры и зависимые переменные определяются в соответствии со следующими выражениями:
(18)
${{K}_{x}} = {{k}_{x}}\frac{\nu }{{{\text{v*}}}},\,\,\,\,{{K}_{z}} = {{k}_{z}}\frac{\nu }{{{\text{v*}}}}{\text{,}}\,\,\,\,{\text{где}}\,\,\,\,{\text{v}}* = \sqrt {\frac{{{{\tau }_{0}}}}{\rho }} ,$(19)
$\Omega = \omega {\text{ }}\frac{\nu }{{{{{\left( {{\text{v*}}} \right)}}^{2}}}}{\text{,}}\,\,\,\,B = \beta {\text{ }}\frac{\nu }{{{{{\left( {{\text{v*}}} \right)}}^{2}}}}{\text{,}}\,\,\,\,{\text{и}}\,\,\,\,p = \frac{P}{{\rho {\text{v*}}}}.$Уравнения (14)–(17) принимают следующий вид:
(15′)
$\begin{gathered} i\Omega {{V}_{x}} + B{{y}^{ + }}i{{K}_{x}}{{V}_{x}} + B{{V}_{y}} = \\ = - K_{x}^{2}{{V}_{x}} + \frac{{{{d}^{2}}{{V}_{x}}}}{{d{{y}^{ + }}^{2}}} - K_{z}^{2}{{V}_{x}} - i{{K}_{x}}p, \\ \end{gathered} $(16′)
$\begin{gathered} i\Omega {{V}_{y}} + B{{y}^{ + }}i{{K}_{x}}{{V}_{y}} = \\ = - K_{x}^{2}{{V}_{y}} + \frac{{{{d}^{2}}{{V}_{y}}}}{{d{{y}^{ + }}^{2}}} - K_{z}^{2}{{V}_{y}} - \frac{{dp}}{{d{{y}^{ + }}}}, \\ \end{gathered} $(17′)
$i\Omega {{V}_{z}} + B{{y}^{ + }}i{{K}_{x}}{{V}_{z}} = - K_{x}^{2}{{V}_{z}} + \frac{{{{d}^{2}}{{V}_{z}}}}{{d{{y}^{ + }}^{2}}} - K_{z}^{2}{{V}_{z}} - i{{K}_{z}}p.$Таким образом, кинематическая вязкость ν, плотность ρ и напряжение на стенке τ0 исключаются, и формулировка предназначена для учета всех таких значений, которые могут возникнуть в турбулентных потоках. (Давление должно быть совместимым с безразмерными скоростями. Поскольку мы не используем p непосредственно, это может не иметь значения.) Значение B можно сделать равным 1, поскольку очень близко к стенке vx пропорционально y, и это обычно выражается как ${\text{v}}_{x}^{ + }$ = y+ на графиках скорости ниже по потоку в зависимости от расстояния от стенки в турбулентном потоке.
Для численного решения уравнения (15') и (17) вторые производные следует аппроксимировать “центральными разностями”. Уравнение (14') первого порядка следует аппроксимировать “обратными разностями”; по существу интегрируется уравнение неразрывности с известными профилями тангенциальных компонент скорости vx и vz, чтобы получить нормальную компоненту скорости vy. Уравнение (16') следует рассматривать как уравнение первого порядка для флуктуаций давления p с известными профилями составляющих скорости. Вторая производная Vy может быть заменена первыми производными Vx и Vz путем подстановки уравнения (14'). Учет граничных условий является сложной задачей, когда существует градиентный член, в данном случае градиент р, в общем случае может входить градиент электрического потенциала. Сравним обработку преобразования Кармана для ламинарного потока с вращающимся диском, где три уравнения (уравнение непрерывности и радиальная и угловая составляющие уравнения импульса) определяют три составляющие скорости, а затем определяется распределение давления (при необходимости) от осевой составляющей уравнения импульса. (Сравним раздел 15.4 в работе [6].) Если градиент переменной известен по всему полю, значение переменной достаточно указать только в одной точке поля. То же самое относится и к функциям состояния в термодинамике. В данном случае в принципе можно устранить давление из уравнений (15') и (17') с помощью уравнения (16'). Это равносильно устранению давления из полного уравнения движения путем взятия ротора уравнения, но при этом удается избежать введения дополнительных констант интегрирования. Таким образом, граничные условия фактически не включают значение Vy при y = δ0, и флуктуации давления не стремятся к нулю на стенке.
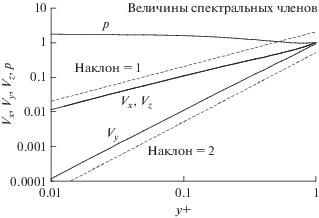
На рис. 1 представлены результаты, полученные путем численного решения разработанных здесь уравнений. Требуется много дальнейшей работы, чтобы рассмотреть спектр турбулентности при y = δ0, при разработке вихревой вязкости по результатам Фурье и при разработке вихревой диффузии.
Рис. 1.
Расчетные профили флуктуирующих составляющих скорости и давления для одной компоненты спектра Фурье (для Kx = Kz = Ω = 1). Здесь B принимается равным 1. Vx, Vy и Vz принимаются равными нулю на стенке. Vx и Vz и p принимаются равными 1 при y+ = 1. В то время как флуктуации сравнимы в трех направлениях координат во внешнем турбулентном потоке, нормальная составляющая уменьшается с наклоном 2 (на билогарифмическом графике) во внутренней части вязкого подслоя, в то время как тангенциальные компоненты почти равны друг другу и принимают наклон 1. Колебания давления сохраняются с небольшими изменениями вплоть до поверхности.
ФЛУКТУАЦИИ КОНЦЕНТРАЦИИ
Моделирование массопереноса позволяет рассчитать профиль вихревой диффузии. Профиль концентрации подчиняется уравнению конвективной диффузии
(20)
$\frac{{\partial {{c}_{i}}}}{{\partial t}} + \nabla \cdot ({\mathbf{v}}{{c}_{i}}) = \mathcal{D}\nabla \cdot \nabla {{c}_{i}}.$С граничными условиями
(21)
$\begin{gathered} {{c}_{i}} = {{c}_{0}}\,\,\,\,{\text{при}}\,\,\,\,y = 0\,\,\,\,{\text{и}}\,\,\,\,{{c}_{i}} \to {{c}_{\infty }}\,\,\,\, \\ {\text{когда}}\,\,\,\,y \to \infty , \\ \end{gathered} $В терминах постоянных и колеблющихся величин уравнение (20) принимает вид
(23)
$\frac{{\partial{ \bar {\theta }} + \theta {\kern 1pt} '}}{{\partial t}} + \nabla \cdot \left[ {({\mathbf{\bar {v}}} + {\mathbf{v}}{\kern 1pt} ')(\bar {\theta } + \theta {\kern 1pt} ')} \right] = \mathcal{D}\nabla \cdot \nabla (\bar {\theta } + \theta {\kern 1pt} '),$(24)
$\frac{{\partial{ \bar {\theta }}}}{{\partial t}} + \nabla \cdot \left[ {{\mathbf{\bar {v}}}\bar {\theta } + \left\langle {{\mathbf{v'}}\theta {\kern 1pt} '} \right\rangle } \right] = \mathcal{D}\nabla \cdot \nabla \bar {\theta }.$Это похоже на исходное уравнение, но для усредненной величины и с появлением дополнительного турбулентного транспортного члена. Вычитание из предыдущего уравнения дает уравнение, управляющее колебаниями концентрации
(25)
$\frac{{\partial \theta {\kern 1pt} '}}{{\partial t}} + \nabla \cdot \left[ {{\mathbf{\bar {v}}}\theta {\kern 1pt} ' + {\mathbf{v}}{\kern 1pt} '\bar {\theta } + {\mathbf{v}}{\kern 1pt} '\theta {\kern 1pt} ' - \left\langle {{\mathbf{v'}}\theta {\kern 1pt} '} \right\rangle } \right] = \mathcal{D}\nabla \cdot \nabla \theta {\kern 1pt} ',$Мы отбрасываем два квадратичных члена, исходя из того, что они глубоко, пренебрежимо глубоко в вязком подслое. Мы делаем те же предположения относительно средней скорости, а именно, что x-компонента может быть аппроксимирована βy, а y- и z-компоненты равны нулю. Средняя концентрация зависит также только от y. Уравнение (25) затем упрощается до
(26)
$\frac{{\partial \theta {\kern 1pt} '}}{{\partial t}} + \beta y\frac{{\partial \theta {\kern 1pt} '}}{{\partial x}} + {\text{v}}_{y}^{'}\frac{{\partial{ \bar {\theta }}}}{{\partial y}} = \mathcal{D}\left( {\frac{{{{\partial }^{2}}\theta {\kern 1pt} '}}{{\partial {{x}^{2}}}} + \frac{{{{\partial }^{2}}\theta {\kern 1pt} '}}{{\partial {{y}^{2}}}} + \frac{{{{\partial }^{2}}\theta {\kern 1pt} '}}{{\partial {{z}^{2}}}}} \right),$(27)
$\theta {\kern 1pt} ' = \operatorname{Re} \{ C(y)\exp (i{{k}_{x}}x + i{{k}_{z}}z + i\omega t)\} ,$(28)
$i\omega C + \beta yi{{k}_{x}}C + {{V}_{y}}\frac{{\partial{ \bar {\theta }}}}{{\partial y}} = \mathcal{D}\left( { - k_{x}^{2}C + \frac{{{{d}^{2}}C}}{{d{{y}^{2}}}} - k_{z}^{2}C} \right).$Сходство с уравнением (15) является очевидным. Существенными отличиями являются замена кинематической вязкости коэффициентом диффузии, отсутствие члена давления и замена β производной от среднего профиля концентрации. Для безразмерной формы определения (18) и (19) дают
(29)
$\begin{gathered} i\Omega C + B{{y}^{ + }}i{{K}_{x}}C + {{{\text{V}}}_{y}}\frac{{\partial{ \bar {\theta }}}}{{\partial {{y}^{ + }}}} = \\ = \,\frac{\mathcal{D}}{\nu }\left( { - K_{x}^{2}C + \frac{{{{d}^{2}}C}}{{d{{y}^{ + }}^{2}}} - K_{z}^{2}C} \right). \\ \end{gathered} $Для граничных условий можно ожидать
(30)
$\begin{gathered} C = 0\,\,\,\,{\text{при}}\,\,\,\,{{y}^{ + }} = 0\,\,\,\,{\text{и}}\,\,\,\,C \to {\text{0,}}\,\, \\ {\text{когда}}\,\,\,\,{{y}^{ + }} \to \delta _{0}^{ + }, \\ \end{gathered} $Некоторые результаты расчетов показаны на рис. 2.
Рис. 2.
Величины флуктуаций концентрации для четырех различных чисел Шмидта Sc в диапазоне от 1 до 1000. Сплошные кривые используют нулевое граничное условие для θ' при y+ = $\delta _{0}^{ + }$ = 1. Тогда флуктуации концентрации полностью обусловлены скоростью колебания в пределах вязкого подслоя. Кривые с короткими штрихами устанавливают θ' = 1 при y+ = δ0, что может быть более подходящим для Sc = 1, поскольку диффузионный слой может несколько выходить за пределы вязкого подслоя. Для Sc = 1000 две кривые почти совпадают, за исключением значений y+, очень близких к $\delta _{0}^{ + }.$ Пунктирные линии показывают для сравнения наклоны 1 и 2.

При Sc = 1 может иметь место аналогия Рейнольдса (где профили vx и ci могут быть очень похожими, потому что управляющие уравнения похожи, и, следовательно, число Стентона может быть близко к половине коэффициента трения). При более высоких числах Шмидта обнаруживаются существенные различия, и StSc2/3 становится пропорциональным квадратному корню из коэффициента трения. Некоторые особенности на кривых на рис. 2 могут возникнуть из граничного условия при y+ = $\delta _{0}^{ + }.$ Для Sc = 1 существенные флуктуации концентрации могут исходить от внешнего потока, но для более высоких Sc диффузионный слой находится в пределах вязкого подслоя, и условие нулевой границы может быть более подходящим.
Можно ожидать, что для турбулентного потока производная от средней концентрации будет следовать уравнению [7]
(31)
$\frac{{d\bar {\theta }}}{{d{{y}^{ + }}}} = \frac{{\gamma {\text{ S}}{{{\text{c}}}^{{{\text{1/3}}}}}}}{{1.2092}}\frac{1}{{1 + {{\xi }^{3}}}},\,\,\,\,{\text{где}}\,\,\,\,\xi = \gamma {\text{ S}}{{{\text{c}}}^{{1/3}}}{{y}^{ + }}{\text{,}}$Рис. 3.
Профиль средней концентрации для турбулентного сдвигового потока и для ламинарного пограничного слоя, такого, который обнаружен на вращающемся диске. Безразмерное расстояние ξ в диффузионном слое определяется соответствующим образом для двух разных систем.

Возможно, что предположение о зависимости от y3 коэффициента вихревой диффузии влияет на результат наклонов на рис. 2, что, в свою очередь, может повлиять на выводы, полученные для самой коэффициента вихревой диффузии. По этой причине вычисления были переделаны с показателем 1/4 для Sc в уравнении (31) и показателем 4 на ξ в знаменателе. Результаты показаны на рис. 4. Разница невелика; в частности, наклоны не изменяются.
Рис. 4.
Флуктуации концентрации пересчитаны с изменениями, упомянутыми в тексте, чтобы гарантировать, что форма уравнения (31) не влияет на наклоны на рис. 2 и 4.

ВИХРЕВАЯ ДИФФУЗИЯ И ВИХРЕВАЯ КИНЕМАТИЧЕСКАЯ ВЯЗКОСТЬ
Процедура для расчета профилей коэффициентов турбулентного переноса будет состоять в том, чтобы выбрать несколько спектральных точек где-то между 1 и 100, выбранных для представления точек, характерных для фактической турбулентности. Для каждой спектральной точки можно рассчитать средние значения 〈VyC〉 для массопереноса и 〈VyVx〉 для напряжения Рейнольдса. Различные спектральные точки не ожидали бы корреляции друг с другом. Следовательно, можно взять среднее для каждой спектральной точки. Это означает, что нужно взять величину объединенной действительной и мнимой частей, предполагая, что среднее значение различных углов даст число порядка 1 и примерно одинаковое для всех спектральных точек. Нужно делить на плотность потока или напряжение на поверхности. Это должно быть автоматическим для безразмерных формулировок.
Результат такой попытки представлен на рис. 5.
Рис. 5.
Профили относительной величины вихревой диффузии D(t) и вихревой кинематической вязкости ν(t). Число Шмидта является параметром для коэффициентов диффузии, и снова граничное условие было взято как C = 1 для коротких пунктирных линий и C = 0 для сплошных линий, причем оба граничных условия применяются при at y+ = $\delta _{0}^{ + }$ = 1. Граничные условия обеспечивают некоторое искажение вблизи максимального значения. Вихревая кинематическая вязкость расположена чуть выше короткой пунктирной линии для Sc = 1. Штрихпунктирные линии представляют сравнение для наклонов 3 и 4.

Предполагается, что линии для всех спектральных точек, как правило, будут иметь одинаковый наклон, так что при усреднении по спектру можно получить одинаковые наклоны, очевидные для отдельных спектральных точек.
ОБСУЖДЕНИЕ
Воротынцев и соавторы [4, 5] развивают прогнозы вихревой диффузии в вязком подслое более сложным методом, но все еще используя ту же базовую концепцию обработки колебаний скорости и концентрации. Они заключают, что вихревая диффузия изменяется как y4, по-видимому, в области вблизи внешнего предела вязкого подслоя. Можно вывести такую зависимость y4 из рис. 5 (видно для Sc = 100 и 1000) и соответствующую зависимость y2 для флуктуации концентрации из рис. 2 или 4. Они также заключают зависимость y3 глубже в вязком подслое, но с коэффициентом, пропорциональным корню квадратному из коэффициента диффузии. Здесь мы проверяем зависимость y3, но не обязательно зависимость от коэффициента диффузии. На рис. 2 и 4 показана зависимость от числа Шмидта. Следует иметь в виду, что диффузионный слой все глубже проникает в вязкий подслой с увеличением Sc [9]. Например, внешний предел диффузионного слоя при Sc = 1000 должен быть приблизительно при y+ = 0.08, хотя этот переход должен быть гораздо менее резким для турбулентного потока, чем для ламинарного потока, как упомянуто в связи с рис. 3. [11–13] дают дополнительную перспективу по этим вопросам, включая поведение при меньших числах Шмидта, которые также рассматриваются здесь на рис. 2, 3 и 5.
НЕОПРЕДЕЛЕННОСТИ
Поведение турбулентного массопереноса в вязком подслое не полностью разрешено. Уравнение (29) требует производной от средней концентрации, чтобы вычислить колебания. Однако для расчета средней концентрации требуется профиль вихревой диффузии, которая исходит от колебаний. Развитие рис. 4 показывает, что можно угадать профиль средней концентрации и что сделанный выбор оказывает лишь слабое влияние на результат. Можно сделать лучше, перебирая между ними. На самом деле, можно сделать еще лучше, сделав это со всем профилем. На рис. 5 представлен полный профиль вихревой диффузии в вязком подслое, намекающий на наклоны как 3, так и 4. Он может использовать этот профиль в уравнении (29) для расчета нового профиля флуктуирующей концентрации и в конечном итоге прийти к согласованному профилю для средней концентрации и для вихревой диффузии. Следует отметить, что эта процедура не предполагает или требует использования аналогий между передачей тепла, массы и импульса.
Эта проблема также присутствует при обработке профилей скорости. Профиль средней скорости был использован для выбора значения β. К счастью, ясно, что B = 1 в большей части вязкого подслоя, и аналогичный итерационный процесс может быть реализован, если не выходить слишком далеко за пределы вязкого подслоя.
ВЫВОДЫ
Поведение вихревой вязкости и вихревой диффузии в вязком подслое можно исследовать путем обработки отдельных компонентов Фурье, поскольку в этой области вихри ведут себя независимо друг от друга. Воротынцев и соавторы [4] вдохновили нас на вывод основных уравнений для флуктуаций (уравнения с (6) по (9) и (25)). Внутри вязкого подслоя флуктуации нормальной составляющей скорости пропорциональны y2, тогда как колебания тангенциальной составляющей и концентрации пропорциональны y. Следовательно, вихревая вязкость и вихревая диффузия должны быть пропорциональны y3. Последние два не равны друг другу, и вихревая диффузия показывает некоторую зависимость от числа Шмидта. Флуктуации концентрации производятся постоянным градиентом концентрации, взаимодействующим с флуктуирующей нормальной составляющей скорости. Следовательно, они должны отсутствовать в объемном турбулентном потоке при больших числах Шмидта, потому что тогда он находится вне диффузионного слоя. С другой стороны, при Sc = 1 флуктуации концентрации должны доходить до центральной линии трубы и напоминать флуктуацию нормальной компоненты скорости [10]. Таким образом, существует сомнение относительно надлежащего граничного условия для флуктуаций концентрации на внешнем пределе вязкого подслоя в зависимости от числа Шмидта. Было бы желательно обрабатывать больше спектральных компонентов одновременно, чтобы быть более количественными относительно величин турбулентных величин и того, как они эволюционируют в области y+ от 1 до 30.
Список литературы
Murphree, E.V., Relation between Heat Transfer and Fluid Friction, Industrial and Engineering Chemistry, 1932, vol. 24, p. 726. https://doi.org/10.1021/ie50271a004
Levich, B., The Theory of Concentration Polarization, I, Acta Physicochimica U.R.S.S., 1942, vol. 17, p. 257.
Levich, V.G., Physicochemical Hydronamics, Englewood Cliffs, N.J.: Prentice-Hall, Inc., 1962.
Воротынцев, М.А., Мартемьянов, С.А., Графов, Б.М. Замкнутое уравнение турбулентного тепломассопереноса. Журн. эксп. теор. физ. 1980. Т. 52. С. 909. [Vorotyntsev, M.A., Martem’yanov, S.A., and Grafov, B.M., Closed equation of turbulent heat and mass transport, J. Exp. Theor. Phys., 1980, vol. 52, p. 909.]
Мартемьянов, С.А. Статистическая теория турбулентного массопереноса в электрохимических системах. Электрохимия. 2017. Т. 53. С. 1212. [Martemianov, S.A., Statistical Theory of Turbulent Mass Transfer in Electrochemical Systems, Russ. J. Electrochem., 2017, vol. 53, p. 1076.]
Newman, J. and Thomas-Alyea, K.E., Electrochemical Systems, Hoboken, N.J., 2004.
Newman, J., Theoretical Analysis of Turbulent Mass Transfer with Rotating Cylinders, J. Electrochem. Soc, 2016, vol. 163, p. E191.
Ньюман, Дж. Применение диссипационной теоремы к турбулентному течению и массопереносу в канале. Электрохимия. 2017. Т. 53. С. 1195. [Newman, J., Application of the Dissipation Theorem to Turbulent Flow and Mass Transfer in a Pipe, Russ. J. Electrochem., 2017, vol. 53, p. 1061.]
Ньюман, Дж. Вихревая диффузия в вязком подслое. Электрохимия. 2019. Т. 55. С. 1272. [Newman, J., Eddy Diffusivity in the Viscous Sublayer, Russ. J. Elecrochem., 2019, vol. 55, p. 1031.]
Ньюман, Дж. Развитие представлений о турбулентном течении в трубе. Электрохимия. 2019. Т. 55. С. 39. doi . [Newman, J., Further Thoughts on Turbulent Flow in a Pipe, Russ. J. of Elecrochem., 2019, vol. 55, p. 34. https://doi.org/10.1134/S1023193519010105.]10.1134/S1023193519010105
Мартемьянов, С.А., Воротынцев, М.А., Графов, Б.М. Вывод уравнения нелокального переноса вещества в турбулентном диффузионном слое. Электрохимия. 1979. Т. 15. С. 913. [Martem’yanov, S.A., Vorotyntsev, M.A., and Grafov, B.M., Derivation of the nonlocal transport equation of matter in the turbulent diffusion layer, Sov. Electrochem., 1979, vol. 15, .787.]
Мартемьянов, С.А., Воротынцев, М.А., Графов, Б.М. О функциональном виде коэффициента турбулентной диффузии в приэлектродном слое. Электрохимия. 1979. Т. 15. С. 916. [Martem’yanov, S.A., Vorotyntsev, M.A., and Grafov, B.M., Functional Form of the Turbulent Diffusion Coefficient in the Layer Next to the Electrode, Sov. Electrochem., 1979, vol. 15, p.790.]
Мартемьянов, С.А., Воротынцев, М.А., Графов, Б.М. О турбулентном тепло- и массопереносе вблизи плоской поверхности при умеренных и малых числах Прандтля–Шмидта. Электрохимия. 1980. Т. 16. С. 919. [Martem’yanov, S.A., Vorotyntsev, M.A., and Grafov, B.M., Turbulent Heat and Mass Transfer near Flat Surfaces at Moderate and Small Prandtl–Schmidt Numbers, Sov. Electrochem., 1980, vol. 16, p. 783.]
Дополнительные материалы отсутствуют.
Инструменты
Электрохимия


