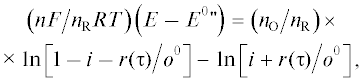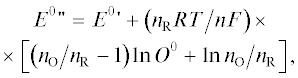Электрохимия, 2022, T. 58, № 11, стр. 802-818
Моделирование медиаторно-каталитического процесса внутри проточной редокс-батареи
М. А. Воротынцев a, *, П. А. Задер a, **
a Институт физической химии и электрохимии им. А.Н. Фрумкина РАН
Москва, Россия
* E-mail: mivo2010@yandex.com
** E-mail: paul.zadyor@gmail.com
Поступила в редакцию 17.03.2022
После доработки 19.05.2022
Принята к публикации 03.06.2022
- EDN: OKWKSB
- DOI: 10.31857/S0424857022110111
Аннотация
Восстановление хлоратов щелочных или щелочноземельных металлов до их хлоридов представляет большой интерес в качестве процесса на положительном электроде проточной редокс-батареи ввиду очень больших теоретических оценок его удельного заряда на единицу массы или объема раствора благодаря высоким растворимостям реагента и продукта, а также переносу 6 электронов на один хлорат-анион. Для такого использования этого окислителя необходимо преодолеть фундаментальную трудность – неэлектроактивность хлорат-аниона на электродах в нужном интервале потенциалов. Перспективный подход к реализации данного процесса состоит в использовании медиаторного катализа на основе редокс-пары Ox/Red, которая имеет высокий положительный потенциал и достаточно большой ток обмена, а Red-форма которой способна реагировать химически в растворе с хлорат-анионом, восстанавливая его до хлорид-аниона – с регенерацией Ох-формы. Подобный медиаторный цикл может быть реализован в положительной части проточной батареи на основе многократной прокачки раствора из резервуара через разрядное устройство для электрохимического превращения Ох-формы редокс-пары в Red-форму с генерацией электричества, тогда как химическая стадия – реакция хлорат-аниона с Red-формой – происходит внутри резервуара. В данной работе выполнен теоретический анализ функционирования подобной системы при гальваностатическом режиме. Предсказаны зависимости от времени концентраций компонентов системы и потенциала электрода. Обнаружено существование двух различных сценариев эволюции системы в зависимости от соотношения между проходящим током и его критическим значением. Предложены способы установления величин параметров системы – включая величины критического значения тока и константы скорости химической стадии процесса – на основе экспериментальных данных для эволюции потенциала катода и/или концентрации компонента Ох или Red редокс-пары.
ВВЕДЕНИЕ
Проточные редокс-батареи позволяют независимым образом варьировать мощность и емкость энергоустановки, а также осуществлять быструю механическую перезарядку путем перезаполнения резервуаров хранения энергозапаса. В качестве окислителей для таких систем рассматривались многочисленные реагенты, в частности галогены [1–5], перекись водорода [6–10], перманганат [11–13], хромат [14–16], соли катионов металлов переменной валентности [17–24], а также органические соединения [25–27]. В большинстве случаев восстановителем для вышеперечисленных систем служат металл (например, цинк или литий) или водород, которые имеют, как правило, гораздо более высокую удельную емкость в расчете на 1 л или 1 кг вещества. Поэтому плотность редокс-заряда, а следовательно, и удельная энергия таких систем в основном лимитируются катодным процессом на положительном электроде источника тока, а именно растворимостью реагирующей редокс-пары и числом переносимых электронов на 1 моль окислителя. Ввиду важности этих параметров для мобильных и транспортных приложений продолжается поиск эффективных катодных полуреакций [28–30].
Другим важным параметром при выборе катодной реакции является интенсивность кроссовера ее компонентов в анодное пространство. При использовании кислотных сред и катион-обменных мембран для ее снижения является желательной анионная природа этих компонентов.
По этим причинам большое внимание привлекают системы на основе галогенатов легких металлов [31], обладающие как высокими растворимостями, так и многоэлектронным характером процесса их восстановления до соответствующих галоидных ионов. Наибольшее развитие получила разработка источников тока на основе процесса восстановления бромата:
(1)
${\text{BrO}}_{3}^{ - } + 6{{{\text{H}}}^{ + }} + 6{\text{e}} = {\text{B}}{{{\text{r}}}^{ - }} + 3{{{\text{H}}}_{{\text{2}}}}{\text{O}},$Фундаментальной проблемой всех многоэлектронных окислителей в водных растворах [31] является практическое отсутствие реакции их прямого восстановления в нужном для источников тока интервале потенциалов – даже на каталитически модифицированных электродах. Для процесса (1) ее удалось преодолеть благодаря редокс-медиаторному автокатализу (ЕС-механизм [33]) на основе пары Br2/Br– [31–33]:
(2)
$\begin{gathered} {\text{BrO}}_{3}^{ - } + 5{\text{B}}{{{\text{r}}}^{ - }} + 6{{{\text{H}}}^{ + }} = 3{\text{B}}{{{\text{r}}}_{2}} + 3{{{\text{H}}}_{{\text{2}}}}{\text{O}}~~~{\text{в растворе}}; \\ {\text{B}}{{{\text{r}}}_{2}} + 2{\text{e}} = 2{\text{B}}{{{\text{r}}}^{ - }}\,\,{\text{на электроде}}. \\ \end{gathered} $Теоретические представления о прохождении этого процесса в кислых средах [33–36] показали, что благодаря этому механизму бромат-анион может реагировать в растворе около поверхности электрода настолько быстро, что реализуется режим диффузионного контроля для бромат-аниона, т.е. скорость процесса лимитируется его транспортом из объема раствора (а не каталитического компонента редокс-пары Br2, концентрация которого в объеме раствора может быть очень низкой) внутрь реакционного слоя около поверхности электрода. Эти предсказания теории были позднее подтверждены экспериментальными данными для этого процесса на вращающемся дисковом электроде [37], на микроэлектродах [38] и внутри проточного пористого электрода [39]. Были созданы и источники тока с использованием этого процесса как катодного в сочетании с водородным [39, 40] или цинковым [41] анодом.
Использование хлоратов в качестве окислителя в источниках тока представляется еще более перспективным, поскольку они и продукты их восстановления – хлориды, имеют еще более высокие растворимости и редокс-потенциал [31], а также настолько доступны и дешевы, что регенерация этих реагентов из хлоридов, видимо, менее оправдана, чем замена батареи новой порцией реагента.
Как и в случае броматов, из-за отсутствия редокс-активности хлорат-аниона на электроде процесс их восстановления, видимо, должен проводиться с помощью подходящей медиаторной редокс-пары, которая будет реагировать обратимо даже на дешевых немодифицированных электродах и иметь достаточно положительный стандартный потенциал.
По аналогии со случаем броматного процесса очевидным кандидатом выступает пара Cl2/Cl–, которая при этом обладает существенно более высоким стандартным потенциалом: 1.396 В с.в.э. [42, 43], что дает надежду на более высокую величину рабочего напряжения источника тока, например водородно-хлоратного. Однако анализ литературных данных показывает, что хлорат-анион является гораздо менее химически активным реагентом, чем бромат-анион. Химическая стадия цикла (2) с использованием пары Br2/Br– проходит с очень большой скоростью уже при концентрациях сильной кислоты на уровне 1 М [33], благодаря чему происходит накапливание больших количеств компонентов этой пары внутри диффузионного слоя за счет автокаталитического эффекта – с параллельным увеличением проходящего тока. Напротив, экспериментальные данные для аналогичной реакции конпропорционирования хлората и хлорида [44]:
(3)
${\text{ClO}}_{3}^{ - } + 5{\text{C}}{{{\text{l}}}^{ - }} + 6{{{\text{H}}}^{ + }} = 3{\text{C}}{{{\text{l}}}_{2}} + 3{{{\text{H}}}_{{\text{2}}}}{\text{O}}~~~{\text{в растворе}},$Поэтому возникает необходимость исследования альтернативного подхода к ускорению процесса восстановления хлората посредством редокс-медиаторного каталитического цикла, основанного на участии “посторонней” (т.е., использующей другой редокс-активный химический элемент вместо хлора) редокс-пары Ox/Red, который под названием “EC-механизм” активно исследуется для всевозможных экспериментальных электрохимических методов [50–67]:
(4a)
$\begin{gathered} {\text{A}} + {\text{R }} = {\text{P}} + {\text{O}}~{\text{\;в}}\,\,{\text{растворе}},~~~~{\text{A}} = {\text{ClO}}_{3}^{ - } + 6{{{\text{H}}}^{ + }}, \\ {\text{P}} = {\text{C}}{{{\text{l}}}^{ - }} + 3{{{\text{H}}}_{{\text{2}}}}{\text{O}},~\,\,{\text{R}} = {\text{Red}},\,\,{\text{O}} = {\text{Ox}}, \\ \end{gathered} $Принципиальными различиями редокс-медиаторных циклов (4а)–(4б) и (2) являются их следующие черты:
– продукт Р химической стадии (4а) предполагается инертным как химически, так и электрохимически, тогда как продуктом аналогичной стадии (2) является Br2, т.е. компонент каталитически редокс-пары, который способен реагировать на электроде;
– компоненты редокс-пары R и O (Red и Ох) взаимно превращаются в ходе стадий (4а) и (4б), однако суммарное количество этих двух компонентов не изменяется; напротив, при прохождении цикла (2) атомы брома прореагировавшего бромата превращаются в каталитические компоненты Br2 и Br–, так что их суммарное количество возрастает по мере восстановления бромата, что и приводит к автокаталитическому характеру цикла (2) – в отличие от обычного каталитического поведения цикла (4а)–(4б);
– брутто-реакция имеет вид:
т.е. в нее не входят компоненты редокс-пары, так что они удовлетворяют фундаментальному определению термина “катализатор”: вещество, которое принимает участие в ходе процесса, но не расходуется и не увеличивается в количестве в результате процесса.Целью данной работы является теоретический анализ прохождения такого процесса (4а)–(4б) в катодной части источника тока, которая включает резервуар большого объема со смешанным раствором хлората и Ох-компонента редокс-пары (которые будут ниже обозначаться соответственно как компоненты А и Ох), откуда этот раствор прокачивается через разрядное устройство – с прохождением тока через внешнюю цепь за счет электрохимической реакции (4б) с превращением части компонента Ох в Red. После выхода из него раствор изменившегося состава возвращается в резервуар, внутри которого происходит химическая стадия (4а) каталитического цикла, в результате которого регенерируется компонент редокс-пары Ох за счет расходования основного окислителя А $\left( {{\text{ClO}}_{3}^{ - }} \right).$
В результате такого анализа будут установлены закономерности проходящего процесса, т.е. эволюция во времени концентраций компонентов раствора А, Ох и Red, а также потенциала катода разрядного устройства в зависимости от задаваемых параметров системы: начальных концентраций компонентов, проходящего тока, интенсивности прокачки раствора через разрядное устройство, константы скорости химической стадии (4a) и др.
ОПИСАНИЕ СИСТЕМЫ
В резервуаре первоначально (t = 0) находится раствор смеси хлората (концентрация А0) и Ох-компонента редокс-пары (4a) (концентрация O0), причем O0много меньше (на несколько десятичных порядков), чем А0. Имеется также кислота, концентрация которой считается постоянной. В последующий период времени (t > 0) производится прокачка раствора из резервуара через разрядное устройство, через которое проходит катодный ток I постоянной интенсивности, связанный с превращением (восстановлением) компонента Оx в компонент Red. Предполагается, что раствор прокачивается с такой скоростью, что за время его пребывания внутри реактора реакция между компонентами раствора А $\left( {{\text{ClO}}_{3}^{ - }} \right)$ и R (Red) практически не происходит из-за ее сравнительно малой скорости (“медленный редокс-медиаторный катализ”).
Прошедший через реактор раствор возвращается в резервуар. В результате в нем образуется смешанный раствор с концентрациями компонентов A $\left( {{\text{ClO}}_{3}^{ - }} \right),$ R (Red) и O (Ox), которые изменяются во времени как из-за реакции конпропорционирования между А и R внутри резервуара, так и из-за электрохимической реакции внутри реактора.
Так как среди возможных кандидатов на роль медиаторной редокс-пары имеется и система с неединичной стехиометрией Br2/Br–, которая не подчиняется схеме (4б), будет рассматриваться более общий вариант редокс-медиаторного катализа, который описывается схемой (5а)–(5б):
(5a)
$\begin{gathered} {\text{A}} + {{n}_{{\text{R}}}}{\text{R}} = {\text{P}} + {{n}_{{\text{O}}}}{\text{O}}\,\,{\text{в}}\,\,{\text{растворе}},{\text{ }} \\ {\text{A}} = {\text{ClO}}_{3}^{ - } + 6{{{\text{H}}}^{ + }}, \\ {\text{P}} = {\text{C}}{{{\text{l}}}^{ - }} + 3{{{\text{H}}}_{{\text{2}}}}{\text{O}},{\text{ R}} = {\text{Red}},{\text{ O}} = {\text{Ox}}; \\ \end{gathered} $(5б)
${{n}_{{\text{O}}}}{\text{O}} + n{\text{e}} = {{n}_{{\text{R}}}}{\text{R}}\,\,\,{\text{на электроде}}.$Очевидно, что для этой схемы сохраняются те же принципиальные черты, что и у схемы (4а)–(4б) – включая ту же брутто-реакцию (4в).
Кинетика этого процесса описывается уравнениями:
(6a)
$\begin{gathered} --{\text{d}}A{\text{/}}dt = {\text{d}}P{\text{/d}}t = {{v}_{{{\text{chem}}}}};{\text{ }} \\ --{{({{n}_{{\text{R}}}})}^{{--1}}}{\text{d}}R{\text{/d}}t = {{({{n}_{{\text{O}}}})}^{{--1}}}{\text{d}}O{\text{/d}}t = {{v}_{{{\text{chem}}}}}--{{v}_{{{\text{elchem}}}}}. \\ \end{gathered} $Предполагается, что скорость химической стадии (5а) – первого порядка по каждому из реагентов А и В, т.е. пропорциональна произведению их мгновенных концентраций A(t) и R(t), k – константа скорости этой реакции. Cкорость электрохимической стадии прямо связана с проходящим током I, который, в свою очередь, выражается через разность концентраций Ох-формы на входе в разрядное устройство О(t) и на выходе из него О'(t):
(6б)
$\begin{gathered} {{v}_{{{\text{chem}}}}} = kAR,\, \\ {{v}_{{{\text{elchem}}}}} = I{\text{/}}\left( {nFV} \right) = \left( {O--O{\text{'}}} \right)u{\text{/}}\left( {{{n}_{O}}V} \right), \\ \end{gathered} $(7)
$\begin{gathered} {\text{d}}A{\text{/d}}t = --kAR,{\text{ }}\,\,\,{{\left( {{{n}_{{\text{R}}}}} \right)}^{{--1}}}{\text{d}}R{\text{/d}}t = --{{\left( {{{n}_{{\text{O}}}}} \right)}^{{--1}}}{\text{d}}O{\text{/d}}t = \\ = --kAR + I{\text{/}}\left( {nFV} \right). \\ \end{gathered} $Начальные условия имеют вид:
После исключения члена со скоростью химической стадии можно получить соотношения между величинами концентраций в любой момент времени:
(9)
$\begin{gathered} A\left( t \right)--{{A}^{0}} + {{It} \mathord{\left/ {\vphantom {{It} {\left( {nFV} \right)}}} \right. \kern-0em} {\left( {nFV} \right)}} = {{R\left( t \right)} \mathord{\left/ {\vphantom {{R\left( t \right)} {{{n}_{{\text{R}}}}}}} \right. \kern-0em} {{{n}_{{\text{R}}}}}} = \\ = {{\left[ {{{O}^{0}}--O\left( t \right)} \right]} \mathord{\left/ {\vphantom {{\left[ {{{O}^{0}}--O\left( t \right)} \right]} {{{n}_{{\text{O}}}}}}} \right. \kern-0em} {{{n}_{{\text{O}}}}}}. \\ \end{gathered} $C учетом соотношения между начальными концентрациями: А0$ \gg $ О0 рассмотрим начальный этап эволюции, когда концентрация основного реагента А $\left( {{\text{ClО}}_{3}^{ - }} \right)$ пока мало изменилась по сравнению с его начальным значением: А ≅ А0. Тогда получается линейное дифференциальное уравнение для компонента R(t):
(10)
$\begin{gathered} {\text{d}}R{\text{/d}}t \cong --{{n}_{{\text{R}}}}k{{A}^{0}}R + {{{{n}_{{\text{R}}}}I} \mathord{\left/ {\vphantom {{{{n}_{{\text{R}}}}I} {(nFV) \equiv }}} \right. \kern-0em} {(nFV) \equiv }} \\ \equiv --{{n}_{{\text{R}}}}k{{A}^{0}}(R--R*), \\ \end{gathered} $(11)
$R{\kern 1pt} {\text{* }} = {I \mathord{\left/ {\vphantom {I {(nFVk{{A}^{0}})}}} \right. \kern-0em} {(nFVk{{A}^{0}})}}.$Начальное условие для этого уравнения: R = 0 при t = 0.
Таким образом, приближенное решение имеет вид:
(12)
$R\left( t \right) \cong R{\text{*}}\left[ {1{\text{ }}--{\text{exp}}\left( {--{{n}_{{\text{R}}}}k{{A}^{0}}t} \right)} \right],$Отсюда из точных соотношений (9) и (6б) можно найти зависимости A(t), О(t) и О'(t). В частности, имеем для зависимости концентрации O от времени:
(13)
$O(t) = {{O}^{0}}--({{{{n}_{{\text{O}}}}} \mathord{\left/ {\vphantom {{{{n}_{{\text{O}}}}} {{{n}_{{\text{R}}}}}}} \right. \kern-0em} {{{n}_{{\text{R}}}}}})R{\text{* }}[1{\text{ }}--{\text{exp}}(--{{n}_{{\text{R}}}}k{{A}^{0}}t)],$(14)
$О* = {{O}^{0}}--{\text{ }}({{{{n}_{{\text{O}}}}} \mathord{\left/ {\vphantom {{{{n}_{{\text{O}}}}} {{{n}_{{\text{R}}}}}}} \right. \kern-0em} {{{n}_{{\text{R}}}}}})R{\text{*}}.$Концентрация компонента Оx на выходе из разрядного устройства O' изменяется параллельно с концентрацией O(t) на входе в него:
(15)
$\begin{gathered} О{\text{'*}} = {{O}^{0}}--\left( {{{{{n}_{{\text{O}}}}} \mathord{\left/ {\vphantom {{{{n}_{{\text{O}}}}} {{{n}_{{\text{R}}}}}}} \right. \kern-0em} {{{n}_{{\text{R}}}}}}} \right)R{\text{*}}\left[ {1{\text{ }} + {{{{n}_{{\text{R}}}}Vk{{A}^{0}}} \mathord{\left/ {\vphantom {{{{n}_{{\text{R}}}}Vk{{A}^{0}}} u}} \right. \kern-0em} u}} \right] \equiv \\ \equiv {{O}^{0}}--\left[ {u{{{\left( {{{n}_{{\text{R}}}}Vk{{A}^{0}}} \right)}}^{{--1}}} + {\text{ }}1} \right]{{{{n}_{{\text{O}}}}I} \mathord{\left/ {\vphantom {{{{n}_{{\text{O}}}}I} {\left( {nFu} \right)}}} \right. \kern-0em} {\left( {nFu} \right)}}, \\ \end{gathered} $Ввиду неотрицательности величины концентрации O' во втором случае эволюция должна окончиться при приближении к нулевому значению этой концентрации: O′(tfin) = 0 (случай А ниже). Соответственно, в зависимости от величины тока и других параметров системы эволюция происходит совершенно по-разному в зависимости от знака этого предела.
A: режим запредельного тока
Он реализуется при условии:
(16)
$\begin{gathered} I > {{I}_{{{\text{crit}}}}},\,\,\,{\text{где}}\,\,{{I}_{{{\text{crit}}}}} = \\ = nF{{O}^{0}}{{\left( {{{n}_{{\text{O}}}}} \right)}^{{ - 1}}}{{\left[ {{{{\left( {{{n}_{{\text{R}}}}Vk{{A}^{0}}} \right)}}^{{ - 1}}} + {{u}^{{ - 1}}}} \right]}^{{ - 1}}}. \\ \end{gathered} $Тогда внутри периода релаксации имеется момент времени tfin, когда концентрация Оx на выходе из разрядного устройства обращается в нуль: O'(tfin) = 0. Если разность I – Icritне очень мала, то этот момент окончания эволюции лежит в области tfin ~ trelax ~ (nRkA0)–1. За это время успевает преобразоваться лишь очень малая часть основного реагента А (${\text{ClO}}_{3}^{ - }$).
В: режим допредельного тока
(17)
$R{\text{*}} < {{R}_{{{\text{crit}}}}},{\text{ }}\,{\text{т}}{\text{.е}}{\text{.}}\,\,\,I < {{I}_{{{\text{crit}}}}}.$Тогда во время быстрой релаксации, т.е. при t ~ trelax = (kA0)–1, концентрации R(t), O(t) и O'(t) претерпевают экспоненциальную эволюцию, после которой они приближаются к положительным значениям, зависящим от тока I, причем R → R*, О → О*, О′ → О′*, определенные формулами (11), (14) и (15).
Заметим, что ограничение выше на величину тока приводит к неравенству:
(18)
$R{\text{*}} < {{O}^{0}}\left( {{{{{n}_{{\text{R}}}}} \mathord{\left/ {\vphantom {{{{n}_{{\text{R}}}}} {{{n}_{{\text{O}}}}}}} \right. \kern-0em} {{{n}_{{\text{O}}}}}}} \right) \ll ~{{A}^{0}}.$Это означает, что указанная эволюция концентраций R(t), O(t) и O'(t) во время периода релаксации trelax ~ (nRkA0)–1 сопровождается прохождением через цепь заряда порядка nF VR*/nR, т.е. меньше, чем начальный заряд Ох-компонента nFVO0/nО, который не может существенно изменить концентрацию основного реагента А $\left( {{\text{ClO}}_{3}^{ - }} \right)$ из-за ее очень большой величины по сравнению с О0, тогда как существенное изменение этой концентрации А(t) имеет место в течение гораздо большего промежутка времени по сравнению с переходом между компонентами редокс-пары Оx и Red для приближения их концентраций к квазистационарным значениям R* и О*.
Эта последующая эволюция системы с большим изменением концентрации основного реагента А(t) требует вывода более точных выражений для концентраций компонентов системы. Такое выражение для концентрации компонента Red дается ниже в виде формулы (31б), которая в размерных переменных имеет вид:
(19)
$\begin{gathered} R\left( t \right) \cong R{\text{*}}\left[ {1--{\text{exp}}\left( {--{{n}_{{\text{R}}}}k{{A}^{0}}t} \right)} \right]{{(1{\text{ }}--{{tI} \mathord{\left/ {\vphantom {{tI} {nFV{{А}^{0}}}}} \right. \kern-0em} {nFV{{А}^{0}}}})}^{{--1}}},\,\, \\ R{\text{*}} = {I \mathord{\left/ {\vphantom {I {nFVk{{A}^{0}}}}} \right. \kern-0em} {nFVk{{A}^{0}}}}, \\ \end{gathered} $Формула (19) предсказывает два резко различающихся масштаба изменений во времени:
1) период релаксации концентраций R(t) и О(t) (t ~ trelax ~ (nRkA0)–1) к своим квазистационарным значениям R* и О*, который уже обсуждался выше, причем ввиду условия (17) концентрация Ох-компонента на выходе из разрядной ячейки О'(t) остается положительной, включая конец периода релаксации;
2) дальнейшая эволюция происходит на гораздо более длительном интервале по времени:
когда происходит постепенное расходование основного реагента А, на что расходуется основная часть проходящего тока I. Большая продолжительность этого этапа эволюции при допредельном режиме обусловлена большой величиной его начальной концентрации A0.Во время этапа (20) происходит постепенное уменьшение A(t) по формуле (9): A(t) ≅ A0 – It/nFV + + R(t)/nR, где последнее слагаемое играет малую роль ввиду ограничения его величины сверху величиной O0/nO. Одновременно происходит рост R(t) по формуле (19) за счет уменьшения знаменателя 1 – tI/nFVА0, что приводит ввиду соотношения (9) к монотонному уменьшению концентраций О(t). В результате понижается и концентрация О'(t) на выходе из разрядного устройства вплоть до момента ее приближения к нулю при t = tfin, где концентрации компонентов редокс-пары и реагента А в резервуаре приближаются к значениям:
(21а)
$А\left( {{{t}_{{{\text{fin}}}}}} \right) \cong {{A}^{0}}--{{I{{t}_{{{\text{fin}}}}}} \mathord{\left/ {\vphantom {{I{{t}_{{{\text{fin}}}}}} {nFV}}} \right. \kern-0em} {nFV}} + {{{{R}_{{{\text{fin}}}}}} \mathord{\left/ {\vphantom {{{{R}_{{{\text{fin}}}}}} {{{n}_{{\text{R}}}}}}} \right. \kern-0em} {{{n}_{{\text{R}}}}}}.$Из формул (19) и (21а) следует выражение для полного времени эволюции в допредельном режиме в предположении, что оно намного больше времени релаксации:
(21б)
$\begin{gathered} {{t}_{{{\text{fin}}}}} \cong nFV{{А}^{0}}{{I}^{{--1}}} \times \\ \times \,\,[1{\text{ }}--\left( {{{{{n}_{{\text{O}}}}I} \mathord{\left/ {\vphantom {{{{n}_{{\text{O}}}}I} {nF{{O}^{0}}k{{n}_{R}}{{А}^{0}}V}}} \right. \kern-0em} {nF{{O}^{0}}k{{n}_{R}}{{А}^{0}}V}}} \right){{(1--{{{{n}_{{\text{O}}}}I} \mathord{\left/ {\vphantom {{{{n}_{{\text{O}}}}I} {nFu{{O}^{0}}}}} \right. \kern-0em} {nFu{{O}^{0}}}})}^{{--1}}}], \\ \end{gathered} $ИЗМЕНЕНИЕ ПОТЕНЦИАЛА ЭЛЕКТРОДА
При экспериментальной реализации рассматриваемого процесса можно следить за его эволюцией как измерениями концентрации Ох- или Red-компонентов раствора в резервуаре, так и потенциала Е катода ячейки, в которой проходит превращение Ох- в Red-форму.
Будем предполагать, что электрохимическая стадия процесса (5б) происходит внутри проточного пористого электрода, через который проходит указанный в соотношениях (6б) поток раствора из резервуара с расходом u, причем для описания его транспорта сквозь электрод и изменения его состава можно использовать принципы подхода работы [34], за исключением иного механизма процесса. А именно, будет считаться, что ввиду малого размера сечения пор (микрометрического масштаба) поперечная диффузия эффективно выравнивает градиенты концентраций внутри каждого сечения поры – несмотря на проходящую электрохимическую реакцию (5б) на стенках пор, а интенсивность проходящего тока сравнительно невелика, так что можно пренебречь перепадом потенциала поперек течения раствора как внутри электрода, так и внутри порового пространства. Тогда все концентрации внутри электродного пространства зависят только от одной пространственной координаты y вдоль оси течения раствора. Хотя рассматривается нестационарный процесс (поскольку в электрод поступает раствор из резервуара, состав которого изменяется во времени), однако время нахождения каждой частицы раствора внутри электрода очень мало по сравнению с временем изменения концентраций внутри резервуара, ввиду его большого объема. Поэтому распределения концентраций внутри разрядной ячейки можно рассчитывать приближенно на основе стационарных уравнений (без временной производной), решение которых зависит от времени только из-за постепенного изменения состава поступающего из резервуара потока раствора. Как уже указывалось при обсуждении схемы (5а), предполагается, что химическая стадия, т.е. реакция между основным окислителем А $\left( {{\text{ClO}}_{3}^{ - }} \right)$ и Red компонентом редокс-пары является сравнительно медленной, так что можно пренебречь ее прохождением внутри катода (в отличие от случая броматного процесса, рассмотренного в работе [34]).
В результате этих приближений следует проанализировать эволюцию состава раствора, который переносится конвективно внутри пористого электрода с постоянной скоростью U = u/(S0ε) [34] (S0 – площадь поперечного сечения электрода, ε – его пористость, т.е. доля его объема, занятого порами), тогда как на стенках пор происходит электрохимическая стадия (5б) – превращение Ох-компонента в Red-компонент.
Так как данная редокс-пара имеет, согласно схеме (5а), (5б), в общем случае неединичную стехиометрию, т.е. коэффициенты nO и nRмогут различаться (например, для пары Br2/Br–), то для скорости электрохимической стадии (5б) неприменимы общие соотношения типа уравнения Батлера–Фольмера. Тем не менее можно получить выражение для потенциала электрода в предположении о том, что эта стадия является достаточно быстрой, чтобы за время прохождения раствора сквозь пористый электрод концентрации компонентов редокс-пары успели стать приближенно равными их равновесным значениям для потенциала электрода Е, т.е. удовлетворяющим уравнению Нернста
(22)
$\begin{gathered} ({{nF} \mathord{\left/ {\vphantom {{nF} {RT}}} \right. \kern-0em} {RT}}){\text{ }}(E--{{E}^{0}}{\kern 1pt} {\text{')}} = {{n}_{{\text{O}}}}{\text{ln}}O{\text{'}}--{{n}_{{\text{R}}}}{\text{ln}}R',{\text{ }} \\ {\text{где}}\,\,\,{{R{\text{'}}} \mathord{\left/ {\vphantom {{R{\text{'}}} {{{n}_{{\text{R}}}}}}} \right. \kern-0em} {{{n}_{{\text{R}}}}}} = {{({{O}^{0}}--O{\text{'}})} \mathord{\left/ {\vphantom {{({{O}^{0}}--O{\text{'}})} {{{n}_{{\text{O}}}}}}} \right. \kern-0em} {{{n}_{{\text{O}}}}}}. \\ \end{gathered} $Для стехиометрий 1 : 1, 1 : 2 и 2 : 1 реакции (5б) можно получить аналитические решения для концентраций O' и R' на выходе раствора из электрода как функций его потенциала Е.
Входящую в формулу (22) концентрацию О' можно выразить через концентрацию этого компонента в резервуаре О (или через концентрацию R компонента Red в резервуаре) и проходящий ток I, используя общие соотношения (6б) и (9):
(23)
$\begin{gathered} O{\text{'}} = O--{{{{n}_{{\text{O}}}}I} \mathord{\left/ {\vphantom {{{{n}_{{\text{O}}}}I} {nFu}}} \right. \kern-0em} {nFu}} = {{O}^{0}}--{{{{n}_{{\text{O}}}}I} \mathord{\left/ {\vphantom {{{{n}_{{\text{O}}}}I} {nFu}}} \right. \kern-0em} {nFu}}--{{R{{n}_{{\text{O}}}}} \mathord{\left/ {\vphantom {{R{{n}_{{\text{O}}}}} {{{n}_{{\text{R}}}}}}} \right. \kern-0em} {{{n}_{{\text{R}}}}}}, \\ {{R{\text{'}}} \mathord{\left/ {\vphantom {{R{\text{'}}} {{{n}_{{\text{R}}}}}}} \right. \kern-0em} {{{n}_{{\text{R}}}}}} = {I \mathord{\left/ {\vphantom {I {nFu}}} \right. \kern-0em} {nFu}} + {R \mathord{\left/ {\vphantom {R {{{n}_{{\text{R}}}}}}} \right. \kern-0em} {{{n}_{{\text{R}}}}}}. \\ \end{gathered} $Комбинация соотношений (22) и (23) дает зависимость потенциала электрода Е от тока и концентрации компонента O в резервуаре. Напомним, что при фиксированной величине проходящего тока все концентрации в этих формулах, в частности компонента Red, зависят от времени, т.е. R(t), вид которой задается формулой (12) внутри периода релаксации или более общей формулой (19) для режима допредельного тока (17), что приводит к изменению потенциала со временем.
БЕЗРАЗМЕРНЫЕ ПЕРЕМЕННЫЕ. ГРАФИЧЕСКИЕ ИЛЛЮСТРАЦИИ
Ввиду большого числа независимых параметров системы: nR, nO, n, A0, O0, V, u, k и I, целесообразно использовать в графических иллюстрациях безразмерные величины, чтобы резко уменьшить (до 3) число независимых безразмерных параметров:
(24)
$\begin{gathered} {{о}^{0}} = {{{{O}^{0}}} \mathord{\left/ {\vphantom {{{{O}^{0}}} {{{n}_{{\text{O}}}}{{А}^{0}}~ \ll 1}}} \right. \kern-0em} {{{n}_{{\text{O}}}}{{А}^{0}}~ \ll 1}},\,\,\,K = {{{{n}_{{\text{R}}}}k{{А}^{0}}V} \mathord{\left/ {\vphantom {{{{n}_{{\text{R}}}}k{{А}^{0}}V} u}} \right. \kern-0em} u},\,\, \\ i = {{{{n}_{{\text{O}}}}I} \mathord{\left/ {\vphantom {{{{n}_{{\text{O}}}}I} {nFu{{O}^{0}}}}} \right. \kern-0em} {nFu{{O}^{0}}}} < {\text{ }}1,\,\,{\text{т}}{\text{.е}}.\,\,\,i{{o}^{0}} = {I \mathord{\left/ {\vphantom {I {nFu{{A}^{0}}}}} \right. \kern-0em} {nFu{{A}^{0}}}}. \\ \end{gathered} $Параметр о0 характеризует отношение начальных концентраций основного реагента А и Ох-компонента редокс-пары, которое предполагается очень малой величиной. Второй параметр K представляет отношение характерных времен прокачки всего раствора резервуара через разрядное устройство V/u и релаксации концентраций компонентов редокс-пары к их квазистационарным значениям (nRkА0)–1, которое может быть и большим, и малым числом по сравнению с 1. Третий параметр i сравнивает проходящий ток I с потоком редокс-заряда за счет компонента Ох через разрядную ячейку nFuO0/nO, где второй должен, очевидно, быть больше первого. Дополнительное (более жесткое) ограничение сверху на параметр i дано ниже.
Система уравнений (7) и начальные условия (8) принимают вид:
(25)
$\begin{gathered} {{{\text{d}}a} \mathord{\left/ {\vphantom {{{\text{d}}a} {{\text{d}}\tau }}} \right. \kern-0em} {{\text{d}}\tau }} = --Kar,\,\,{\text{ }}{{{\text{d}}r} \mathord{\left/ {\vphantom {{{\text{d}}r} {{\text{d}}\tau }}} \right. \kern-0em} {{\text{d}}\tau }} = {\text{ }}{{--{\text{d}}o} \mathord{\left/ {\vphantom {{--{\text{d}}o} {{\text{d}}\tau }}} \right. \kern-0em} {{\text{d}}\tau }} = --Kar + i{{o}^{0}}; \\ a = 1,\,\,\,\,r = {\text{ }}0,\,\,\,o = {{o}^{0}}\,\,\,{\text{при}}\,\,\,\tau = 0. \\ \end{gathered} $Соотношения между всеми концентрациями (9), вытекающие из уравнений (25), принимают вид:
(26)
$\begin{gathered} a(\tau )--1 + i{{o}^{0}}\tau = r(\tau ) = {{о}^{0}}--o(\tau );\,\, \\ i{{o}^{0}} = o(\tau )--o{\text{'}}(\tau ). \\ \end{gathered} $Дополнительные условия следуют из неотрицательности концентрации Ох-компонента (o'(τ) > > 0) на выходе из разрядной ячейки, в частности:
(27)
$o'(\tau ) > 0,\,\,\,\,o(\tau ) > i{{o}^{0}},{\text{ т}}{\text{.е}}{\text{.}}\,\,\,r(\tau ) < \left( {1--i} \right){{o}^{0}}.$Из соотношений (25) и (26) можно получить дифференциальное уравнение первого порядка относительно одной из концентраций, например:
(28)
$\begin{gathered} {{{\text{d}}a} \mathord{\left/ {\vphantom {{{\text{d}}a} {{\text{d}}\tau }}} \right. \kern-0em} {{\text{d}}\tau }} = --Ka(\tau )\left[ {a(\tau ) - 1 + i{{o}^{0}}\tau } \right]\,\,\,\, \\ {\text{или}}\,\,\,{{{\text{d}}r} \mathord{\left/ {\vphantom {{{\text{d}}r} {{\text{d}}\tau }}} \right. \kern-0em} {{\text{d}}\tau }} = --K\left[ {r(\tau ) + 1 - i{{o}^{0}}\tau } \right]r(\tau ) + i{{o}^{0}}, \\ \end{gathered} $Полученные выше приближенные аналитические решения можно переписать в безразмерных переменных.
При выполнении ограничений на величины параметров (24) эволюция системы всегда начинается с периода релаксации, где величина a(τ) близка к 1. Тогда, согласно формулам (12) и (11), концентрация r(τ) растет по закону:
(29)
$r(\tau ) \cong r{\text{*}}[1--{\text{exp}}(--K\tau )],{\text{ }}\,\,{\text{где}}\,\,\,r{\text{*}} = {{i{{o}^{0}}} \mathord{\left/ {\vphantom {{i{{o}^{0}}} K}} \right. \kern-0em} K},$Основное условие, приводящее к двум принципиально различающимся режимам эволюции приобретает вид:
(30а)
$\begin{gathered} {\text{A: режим запредельного тока}}\,\, \\ i > {{i}_{{{\text{crit}}}}} = K{{(1{\text{ }} + K)}^{{--1}}}, \\ \end{gathered} $(30б)
$\begin{gathered} {\text{Б: режим критического тока}}\,\, \\ i = {{i}_{{{\text{crit}}}}} = K{{(1{\text{ }} + K)}^{{--1}}}, \\ \end{gathered} $(30в)
$\begin{gathered} {\text{В: режим допредельного тока}}\,\, \\ i < {{i}_{{{\text{crit}}}}} = K{{(1{\text{ }} + K)}^{{--1}}}. \\ \end{gathered} $При выполнении условия (30а) для запредельного режима вся эволюция проходит по закону (29), т.е. в интервале относительно малых времен, когда exp(–Kτ) еще не успевает стать очень малой, так что ограничение (27) нарушается еще до выхода r(τ) на его стационарное значение r* = io0/K.
Вид зависимостей концентраций от времени для этого режима показан на рис. 1 для различных значений безразмерных параметров K (которое определяет, в частности, критическое значение безразмерного тока icrit в формуле (30а)) и тока i.
Рис. 1.
Зависимость концентраций от времени в безразмерных переменных для режима запредельного тока: a(τ) (а), o(τ), r(τ) и o′(τ) (б, в, г) на основе приближенной формулы (29). Величины параметров: о0 = 0.01; K = 0.1 (а, б), 1 (а, в) или 3 (а, г); величины параметра i указаны около каждой линии. Эволюция заканчивается при обращении в нуль концентрации o'(τ). Для сравнения приведены также эволюции концентраций для двух критических величин тока, отвечающих условию (30б): K = 1, i = icrit = 0.5 (а, в) и K = 3, i = icrit = 0.75 (а, г), для интервала времени внутри периода релаксации (дальнейшая эволюция для случая K = 1, i = icrit = 0.5 дана на рис. 2а и 2г).

Рисунок 1а представляет иллюстрации для концентрации основного окислителя А (хлората) а = A/A0. Эта концентрация начинается от ее начального значения: а = 1 при начале эволюции, и монотонно убывает с ростом времени по параболическому закону за счет прохождения восстановительного тока через разрядное устройство. Понижение концентрации а до окончания эволюции усиливается с ростом параметра К, например, за счет увеличения константы скорости химической стадии k в формуле (24) – при одном и том же значении i. Следует, однако, учитывать, что увеличение параметра К приводит к росту величины критического тока icrit, а следовательно, и токов, относящихся к запредельному режиму. В любом случае рисунок 1а наглядно показывает, что практически для всех эволюций при этом режиме (за исключением случаев, когда ток i очень близок к критическому значению icrit) расходуется лишь очень малая доля основного реагента А, т.е. его концентрация остается близкой к ее начальному значению.
На рис. 1б–1г показаны эволюции безразмерных концентраций компонентов медиаторной редокс-пары Red (r) и Ox (o) внутри резервуара, а также компонента Ох на выходе из разрядного устройства (o') для тех же значений параметров K и i.
Функция r(τ) начинается от своего начального значения, равного нулю, и изменяется затем вдоль кривой (29), которая при условии K τ $ \gg $ 1 приближается к стационарному значению r*, которое растет с увеличением тока i. Однако на самом деле эволюция прекращается до приближения к значению r* из-за нарушения условия (27), которое становится все более ограничительным при увеличении тока i, из-за чего продолжительность эволюции по времени очень мала для значений тока, равных 0.75 и тем более 0.9 (в пределах 1 для безразмерного времени), но существенно удлиняется при i = 0.5 и, особенно, 0.3.
Так как при всех моментах времени, согласно соотношению (26): r(τ) + o(τ) = о0, при любых значениях параметров системы кривая о(τ) для безразмерной концентрации Ох формы внутри резервуара (рис. 1б–1г) получается из кривой r(τ) ее инверсией относительно горизонтальной линии на высоте o0/2 = 0.005, т.е. имеет ту же форму, но монотонно убывает от своего начального значения, равного o0 = 0.01.
Другое соотношение (26): o'(τ) = o(τ) – io0, показывает, что безразмерная концентрация Ох-формы на выходе из разрядной ячейки o'(τ) в каждый момент времени меньше, чем o(τ), на постоянную величину, так что ее график получается из графика для o(τ) сдвигом вниз на io0. Для любого тока i, удовлетворяющего неравенству (30а), существует момент времени окончания эволюции, когда концентрация o' обращается в нуль при расчете концентраций на основе формулы (29), т.е. внутри интервала сравнительно малых времен τ.
Увеличение параметра K при фиксированном значении тока i приводит к уменьшению r*, т.е. амплитуды изменения всех трех функций o(τ), r(τ) и o'(τ) внутри периода релаксации. В то же время продолжительность эволюции увеличивается.
Для иллюстрации на рис. 1а–1г приведены – помимо концентраций для наборов параметров, отвечающих запредельному режиму (30а) – также результаты для промежуточного критического режима, когда безразмерный ток i равен своему критическому значению icrit, а именно, для K = 1, i = icrit = 0.5 и K = 3, i = icrit = 0.75. Как видно из рис. 1в и 1г, в этом случае эволюция происходит на основе той же формулы (29), однако кривая o'(τ) не обращается в нуль внутри рассматриваемого интервала, а приближается асимптотически сверху к нулевому значению. Это означает, что приближенная формула (29) не позволяет описать эволюцию системы полностью – как будет видно из более точного анализа ниже на рис. 2г.
Рис. 2.
Зависимость концентраций от времени в безразмерных переменных на основе приближенной формулы (31б): (а, б, в) для режима допредельного тока: a(τ) (а); o(τ), r(τ) и o'(τ) (б, в) при i = 0.25 и 0.1 для К = 1 (а, б); i = 0.45 для K = 1 или 3 (а, в); (а, г) для критической величины тока (30б): K = 0.3, i = icrit = 0.231, K = 1, i = icrit = 0.5, K = 3, i = icrit = 0.75. Везде о0 = 0.01.

Более сложное изменение концентраций имеет место при выполнении условия докритического режима (30в), когда пропускается безразмерный ток i ниже его критического значения icrit = = K (1 + K)–1. Период релаксации, где по-прежнему остается применимой приближенная формула (29), продолжается вплоть до достаточно больших значений безразмерного времени: K τ $ \gg $ 1, когда концентрации обоих компонентов редокс-пары приближаются к их квазистационарным значениям: r(τ) ≅ r* = io0/K, o(τ) ≅ о0 – r*, o'(τ) ≅ о0 – r* – – io0 = о0 (1 – i/icrit), причем эти значения для всех концентраций, включая o', положительны.
Скорость изменения этих концентраций после окончания периода релаксации становится очень малой, так что основная часть проходящего через цепь заряда расходуется на восстановление реагента А $\left( {{\text{ClO}}_{3}^{ - }} \right).$ Из-за его большой концентрации А0 по сравнению с концентрациями компонентов редокс-пары изменение концентрации А происходит на очень большом интервале по сравнению с периодом релаксации (порядка K–1).
Для описания этого “интервала больших времен эволюции” можно использовать другое приближенное решение нелинейного уравнения (28) для концентрации r(τ). Для его вывода пренебрежем слагаемым r(τ) в квадратной скобке по сравнению с комбинацией двух других слагаемых 1 – io0τ:
Ввиду ограничения сверху на величину r(τ) неравенством (27) использованное приближение заведомо справедливо при выполнении условия: 1 – io0τ $ \gg $ (1 – i)o0. Это приближенное линейное дифференциальное уравнение имеет точное решение:
Подынтегральная функция монотонно убывает с ростом t, т.е. она максимальна при t = 0. Если K τ порядка или меньше 1, то 0.5io0K t2 < 0.5io0Kτ2 $ \ll $ 1, т.е. квадратичным членом в показателе экспоненты можно пренебречь внутри всего интервала интегрирования. Если время намного больше, но множитель 1 – io0τ еще не очень мал, то K τ (1 – io0τ) $ \gg $ 1, тогда как при t ~ K–1 (1 – io0τ)–1 квадратичный член в показателе не превышает 0.5io0K–1 (1 – io0τ)–2, т.е. им можно пренебречь при условии:
При выполнении условия (31) и пренебрежении квадратичным членом получается приближенное выражение (32) для r(τ):
(31б)
$\begin{gathered} r(\tau ) \cong r{\text{*}}{{(1--i{{o}^{0}}\tau )}^{{--1}}}[1--{\text{exp}}(--K\tau )],\,\, \\ {\text{где}}\,\,r{\text{*}} = {{i{{o}^{0}}} \mathord{\left/ {\vphantom {{i{{o}^{0}}} K}} \right. \kern-0em} K}, \\ \end{gathered} $Сравнение с выражением (29) показывает, что они различаются только множителем (1 – io0τ)–1 в формуле (31б), который отличается от 1 только при большом значении безразмерного времени τ, когда уже можно пренебречь членом exp (–Kτ), а концентрация а(τ) уже становится заметно меньше 1.
Другие концентрации могут быть затем найдены по формулам:
(32)
$\begin{gathered} o(\tau ){\text{ }} = {{о}^{0}}--r(\tau ),\,\,\,o'(\tau ) \cong o(\tau )--i{{o}^{0}},\,\,\, \\ a(\tau ) = 1--i{{o}^{0}}\tau + r(\tau ). \\ \end{gathered} $Согласно этим формулам, концентрация a(τ) монотонно спадает от 1 до величины, близкой к нулю, а концентрация r(τ) возрастает до очень больших величин. На самом деле это изменение прерывается – и эволюция заканчивается – в момент времени τfin, когда начинает нарушаться условие (27), т.е.
(33)
$\begin{gathered} a({{\tau }_{{{\text{fin}}}}}) = 1--i{{o}^{0}}{{\tau }_{{{\text{fin}}}}} + r({{\tau }_{{{\text{fin}}}}}) \cong {{K}^{{--1}}}i{{(1--i)}^{{--1}}} < 1,\,\, \\ {\text{поскольку}}\,\,i < {{i}_{{{\text{crit}}}}},\,\,\,a(\tau ) \cong 1--i{{o}^{0}}\tau . \\ \end{gathered} $Рисунки 2а–2в дают иллюстрации поведения концентраций в зависимости от времени на основе формул (31б) и (32) при K = 1 и различных значениях безразмерного тока i, которые отвечают допредельному режиму: i < icrit = 0.5, а также при K = 3, i = 0.45 < icrit = 0.75. Для всех этих функций эволюция начинается с периода релаксации в интервале времен τ ~ K–1 = 1, в котором происходит быстрый переход значений концентраций r(τ), о(τ) и о'(τ) от их начальных значений к квазистационарным. После окончания периода релаксации скорость их изменения резко снижается, и их дальнейшие изменения (рост r(τ) и убывание о(τ) и о'(τ)) происходят на гораздо большем масштабе. Сначала эти функции меняются по линейному закону (когда величина концентрации основного реагента а(τ) остается близкой к своему начальному значению), а потом графики этих функций искривляются в соответствии с гиперболическим законом их изменения (31б) на масштабе (io0)–1. Напротив, эволюция а(τ) во всем очень продолжительном интервале времени после окончания периода релаксации, внутри которого эта функция изменяется лишь на малую величину – порядка o0 (вставка на рис. 2а), происходит приблизительно по линейному закону: a(τ) ≅ 1 – io0τ без существенной зависимости от величины K (рис. 2а). Следует отметить, что, как видно из рис. 2а, эволюция прекращается задолго до приближения функции a(τ) к нулю, т.е. значительная часть начального вещества А $\left( {{\text{ClO}}_{3}^{ - }} \right)$ остается непрореагировавшей, причем эта доля уменьшается при понижении пропускаемого тока i.
Условием применимости приближенных формул (33) является большая продолжительность эволюции τfin по сравнению с длительностью периода релаксации K–1, т.е. K τfin$ \gg $ 1, которое выполняется для допредельного режима (30в), если величина безразмерного тока i не очень близка к ее критическому значению icrit = K (1 + K)–1. Например, при K = 1, когда критическое значение тока равно 0.5, формула (33) дает для времени эволюции τfin величину 889 при i = 0.1, 267 при i = = 0.25, 40.4 при i = 0.45 – в соответствии с рис. 2а–2в.
Как видно из выражений (31б) и (32), величина параметра К определяет эволюцию концентраций o(τ), r(τ) и o'(τ) как внутри периода релаксации (при τ ~ K–1), так и после его окончания (через величину параметра r*). Зависимость концентраций от величины K иллюстрирует рис. 2в, где сравниваются случаи K = 1 и K = 3 при i = 0.45. Видно, что увеличение этого параметра замедляет эволюцию концентраций o(τ), r(τ) и o'(τ). В то же время величины всех этих функций в момент окончания эволюции не зависят от величины K – в соответствии с общими формулами (33).
Приближенная формула (31б) может быть использована и для проведения расчета эволюции концентраций для критического режима (30б), когда ток совпадает со своим критическим значением (рис. 2г). В то же время точность формулы (33) для τfin недостаточна (она дает τfin = 0), и следует исходить из полного выражения (31б), которое дает значение τfin около 1.75 при K = 3, около 4 при K = 1 и около 12 при K = 0.3.
Для анализа точности приближенной формулы (31б) было проведено также численное интегрирование уравнения (28) для r(τ) с начальным условием (25) и ограничением (27) с использованием стандартного метода Рунге–Кутты 4-го порядка [68]:
(34)
$\begin{gathered} r(\tau ) = {{r}_{{n{\text{ }} + {\text{ }}1}}} = {{r}_{n}} + \\ + \,\,\left[ {{{F}^{{(1)}}} + 2{{F}^{{(2)}}} + 2{{F}^{{(3)}}} + {{F}^{{(4)}}}} \right]{{\Delta \tau } \mathord{\left/ {\vphantom {{\Delta \tau } 6}} \right. \kern-0em} 6}, \\ \end{gathered} $(35)
${{b}_{n}} = 1--i{{o}^{0}}{{\tau }_{{n\,\, + \,\,1}}} + {{2{{K}^{{--1}}}} \mathord{\left/ {\vphantom {{2{{K}^{{--1}}}} {\Delta \tau }}} \right. \kern-0em} {\Delta \tau }}.$В течение периода релаксации (при Kτ меньше или порядка 1) величина концентрации а близка к 1. Предсказания приближенных формул (29) и (31б) практически совпадают, и их хорошая точность не вызывает сомнений. Поэтому сопоставление с результатами численных расчетов (рис. 3) проводилось для значений тока, отвечающих докритическому режиму, когда величина концентрации а за время эволюции существенно уменьшается по сравнению с 1.
Рис. 3.
Сопоставление предсказаний для изменения концентрации r(τ) по приближенной формуле (31б) (линии 4) и с помощью численного интегрирования по методу Рунге–Кутты (34) для двух значений шага по времени: Δτ = 0.01 (линии 1) и Δτ = 0.1 (линии 2) или по неявной схеме (35) для шага по времени: Δτ = 0.01 (линии 3). Основной рисунок: i = 0.45, вставка: i = 0.1. Остальные параметры: o0 = 0.01, K = 1.

Поэтому на рис. 3 показаны результаты для этого режима при K = 1 и величинах безразмерного тока i < 0.5, а именно при i = 0.45 на основном рисунке (линии 1, 2, 3 и 4) и при i = 0.1 для вставки (линии 1', 2 ', 3 ' и 4 '). Помимо линий 4 и 4 ', найденных на основе приближенной формулы (31б), были проведены расчеты посредством численного интегрирования уравнения (28):
– по стандартному методу Рунге–Кутты 4-го порядка для двух величин шага по времени: Δτ = = 0.01 (линии 1 и 1') и Δτ = 0.1 (линии 2 и 2') для проверки, достаточно ли мала выбранная величина шага;
– по неявной схеме 1 -го порядка при Δτ = 0.01 (линии 3 и 3 ').
Все три линии, полученные численным интегрированием, полностью накладываются на рисунке. Анализ их табличных данных показывает, что при всех моментах времени для величин r, найденных для трех расчетов, совпадают все первые четыре значащие цифры. Расчет по неявной схеме при Δτ = 0.1 (не приведен на рис. 3) показывает отличие от трех предыдущих величин r в четвертой значащей цифре. Такая погрешность, конечно, достаточно мала для использования такого шага, например, для сравнения с экспериментальными данными. В то же время можно сделать вывод о том, что неявная схема 1 -го порядка дает меньшую точность при той же величине шага по времени, чем стандартный метод Рунге–Кутты, т.е. при заданной величине допустимой погрешности вычислений последний позволяет проводить расчеты при большей величине шага, что согласуется с общим выводом о его точности 4‑го порядка.
Что касается линий 4 и 4 ', полученных с помощью приближенной формулы (31б), то для рассмотренных на рис. 3 случаев докритического режима с продолжительной эволюцией во времени эти кривые слегка отличаются от линий, полученных численным интегрированием. Однако очевидно, что их различие весьма мало: даже в конце эволюции сдвиг по времени, в частности различие величин τfin, не превышает 1–2%. Таким образом, можно сделать вывод, что формула (31б) позволяет получать достоверную информацию как об общей форме соответствующей кривой, так и о величине всех концентраций в любой момент времени, см. результаты на ее основе на рис. 1, 2 и 4.
Рис. 4.
Зависимость потенциала (nF/RT) (E – E0") от времени τ в безразмерных переменных: (а, б) при nO = nR для набора значений тока i (указаны около каждой линии) при K = 1, icrit = 0.5 (сплошные линии), K = 0.3, icrit = 0.231 (пунктирные линии) и K = 3, icrit = 0.75 (точечные линии) для интервалов малых (а) и больших (б) времен; (в, г) те же зависимости при nO = 0.5nR; о0 = 0.01.

Формулы (22) и (23) для связи между мгновенными значениями потенциала и концентрации Ох- или Red-компонентов могут быть представлены в безразмерном виде:
где а зависимость потенциала Е от времени определяется функцией r(τ) по формуле (12) для запредельного режима (30а) или по формуле (31б) для критического (30б) или допредельного (30в) режима.Иллюстрация зависимостей потенциала от времени в безразмерном виде представлена на рис. 4.
ОБСУЖДЕНИЕ РЕЗУЛЬТАТОВ ДЛЯ РАЗМЕРНЫХ ПЕРЕМЕННЫХ
Проведенный в предыдущих разделах анализ показал, что существует критическая величина проходящего тока Icrit, определяемая выражением (16), которая разделяет два интервала токов: I > Icrit и I < Icrit, в которых временная эволюция состава раствора в резервуаре происходит по существенно различающимся сценариям.
В первом случае (I > Icrit) реализуется “режим запредельного тока” (рис. 1), при котором концентрации компонентов редокс-пары R(t) и O(t) быстро меняются в противоположных направлениях – при сохранении их суммы: (nО/nR) R(t) + + O(t) = O0 (рис. 1). Внутри этого периода релаксации убывающая концентрация O(t) и растущая концентрация R(t) приближаются к своим конечным значениям Оfin = O(tfin) = I/(nFu) и Rfin = R(tfin) = = O0 – (nR/nO) Ofin, при которых концентрация компонента Ох на выходе из разрядного устройства обратилась бы в нуль: O'(tfin) = 0, что потребовало бы наложения бесконечно большого катодного потенциала на электрод, преобразующий Oх в Red. На практике это означает начало резкого роста этого потенциала при приближении к этому моменту времени tfin.
Отметим, что конечные значения концентраций компонентов редокс-пары Оfin и Rfin определяются величинами тока I, скоростью прокачки раствора u, начальной концентрацией Ох-формы в растворе O0 и стехиометрическими коэффициентами nR, nO и n, т.е. не зависят от константы скорости химической стадии k. В то же время продолжительность эволюции tfin для “режима запредельного тока” (30а) входит в соотношение (38), которое является следствием формул (11) и (12):
(38)
$\begin{gathered} {{R}_{{{\text{fin}}}}} = {{O}^{0}}--{{\left( {{{{{n}_{{\text{R}}}}} \mathord{\left/ {\vphantom {{{{n}_{{\text{R}}}}} {{{n}_{{\text{O}}}}}}} \right. \kern-0em} {{{n}_{{\text{O}}}}}}} \right)I} \mathord{\left/ {\vphantom {{\left( {{{{{n}_{{\text{R}}}}} \mathord{\left/ {\vphantom {{{{n}_{{\text{R}}}}} {{{n}_{{\text{O}}}}}}} \right. \kern-0em} {{{n}_{{\text{O}}}}}}} \right)I} {\left( {nFu} \right)}}} \right. \kern-0em} {\left( {nFu} \right)}}{\text{ }} = \\ = \left( {{I \mathord{\left/ {\vphantom {I {nFVk{{A}^{0}}}}} \right. \kern-0em} {nFVk{{A}^{0}}}}} \right)\left[ {1--{\text{exp}}\left( {--{{n}_{{\text{R}}}}k{{A}^{0}}{{t}_{{{\text{fin}}}}}} \right)} \right]. \\ \end{gathered} $Если величину концентрации компонента Red или компонента Оx можно контролировать в ходе эксперимента, например по эволюции спектра раствора в резервуаре, то можно измерить величину Rfin, а из нее по известным значениям стехиометрических параметров nR и nO, объема раствора V, скорости прокачки раствора через реактор u и начальных концентрациях основного окислителя A0 и Ох-компоненты редокс-пары О0 можно найти величину константы k скорости химической реакции (5а) с использованием соотношения (38).
Константу скорости химической стадии k можно найти также из данных для эволюции R(t) во времени по формуле (12) – как показателя экспоненты nRkA0, так и из величины R* по формуле (11).
Заметим, что концентрация основного окислителя А за время этой эволюции практически не успевает измениться по сравнению с ее начальным значением А0.
Константу скорости k можно находить и из данных для величин концентрации Rcrit или Оcrit и тока Icrit при критическом режиме эволюции согласно формулам (16). Для экспериментального определения этих параметров нужно рассмотреть зависимость характера эволюции от величины пропускаемого тока, чтобы установить его критическое значение, при котором продолжительность эволюции начнет резко увеличиваться при снижении величины тока.
Во втором случае (I < Icrit) реализуется “режим допредельного тока” (рис. 2), при котором на первом этапе эволюции происходит относительно быстрая “релаксация системы”, аналогичная процессу для запредельного тока: концентрации компонентов редокс-пары R(t) и O(t) быстро меняются в противоположных направлениях – при сохранении их суммы: (nО/nR)R(t) + O(t) = O0. Однако в отличие от первого случая в результате этих изменений концентраций компонентов редокс-пары в резервуаре в конце периода релаксации они приближаются к своим квазистационарным положительным значениям R*, O* и O′*, заданным выражениями (11), (14) и (15).
После этой стабилизации значений концентраций их дальнейшее изменение происходит на гораздо большем интервале времени (рис. 2). Согласно формуле (21а), основная часть проходящего через цепь заряда расходуется на понижение концентрации основного реагента А $({\text{ClO}}_{3}^{ - }),$ тогда как концентрации компонентов редокс-пары R(t) и O(t) подстраиваются под это изменение, как это видно из сравнения соотношений (19) и (21а). Происходящее при этом уменьшение концентраций Ох-компонента в резервуаре O(t) и на выходе из разрядного устройства O′(t) заканчивает эволюцию в момент t = tfin, заданного формулой (21б), когда O'(t) приближается к нулю – с резким ростом катодного потенциала. Концентрации компонентов в этот момент заданы формулами (21а).
Как и при “режиме запредельного тока” константу скорости химической стадии k можно найти из данных для эволюции R(t) во времени по формуле (12) – как показателя экспоненты nRkA0, так и из величины R* по формуле (11). Эволюция концентраций на более продолжительном этапе практически не зависит от величины константы скорости химической реакции. С другой стороны, полная продолжительность эволюции для “режима допредельного тока” tfin по формуле (21б) существенно зависит от величины константы скорости химической реакции в резервуаре.
ЗАКЛЮЧЕНИЕ
При изучении функционирования проточной ячейки в режиме “медленного медиаторного катализа” было установлено, что эволюция системы при пропускании постоянного тока I кардинально различается в зависимости от того, будет ли величина этого тока больше или меньше его критического значения Icrit, которое, согласно выражению (16), определяется комбинацией параметров системы: начальных концентраций Ох-формы O0 и основного окислителя А0 (хлората), константы скорости химической стадии редокс-медиаторного цикла k и его стехиометрических чисел nR, nО, n, объема резервуара V и скорости прокачки раствора через разрядное устройство u.
При выполнении условия: I > Icrit реализуется “запредельный режим” эволюции системы, при котором через сравнительно короткое время – внутри “периода релаксации” системы – концентрация Ох-компонента редокс-пары на выходе из разрядного устройства О' приближается к нулю, а потенциал катода разрядного устройства начинает неограниченно возрастать, что делает невозможным дальнейшее пропускания тока этой амплитуды за счет превращения Ох-компонента раствора в Red-форму.
Существенно иной характер эволюции системы имеет место для тока ниже критического значения: I < Icrit, когда реализуется “допредельный режим” эволюции. В этом случае система за короткое время переходит в квазистационарное состояние, при котором концентрации обоих компонентов редокс-пары Ох и Red (О* и R*) определяются балансом скоростей переходов между ними за счет электрохимического процесса внутри разрядного устройства (4б) и химической стадии (4а) внутри резервуара. Дальнейшая эволюция происходит на гораздо более длительном интервале времени, когда концентрация основного окислителя А (хлората) в резервуаре медленно понижается за счет тока I, проходящего через разрядное устройство, что приводит к постепенному смещению квазистационарных концентраций компонентов редокс-пары в стороны Red-формы. В результате этого понижения концентрации компонента Ох в резервуаре она приближается в определенным момент времени к своему минимальному значению, при котором ее концентрация на выходе из разрядного устройства становится близкой к нулю, что прекращает эволюцию.
Наличие выведенных выше аналитических выражений для эволюции концентраций компонентов и потенциала электрода позволяет провести обработку экспериментальных данных для таких систем (например, катализа хлоратного процесса “посторонними” медиаторами на основе брома или ванадия) с целью измерения их характеристических параметров.
Список литературы
Huskinson, B., Rugolo, J., Mondal, S.K., and Aziz, M.J., A high power density, high efficiency hydrogen-chlorine regenerative fuel cell with a low precious metal content catalyst, Energy and Environmental Sci., 2012, vol. 5, no. 9, p. 8690. https://doi.org/10.1039/C2EE22274D
Kreutzer, H., Yarlagadda, V., and Nguyen, T.V., Performance evaluation of a regenerative hydrogen-bromine fuel cell, J. Electrochem. Soc., 2012, vol. 159, no. 7, p. F331. https://doi.org/10.1149/2.086207jes
Tolmachev, Y.V., Hydrogen-halogen electrochemical cells: A review of applications and technologies, Russ. J. Electrochem., 2014, vol. 50, p. 301. https://doi.org/10.1134/S1023193513120069
Jameson, A. and Gyenge, E., Halogens as positive electrode active species for flow batteries and regenerative fuel cells, Electrochem. Energy Rev., 2020, vol. 3, no. 3, p. 431. https://doi.org/10.1007/s41918-020-00067-2
Li, X., Xie, C., Li, T., Zhang, Y., and Li, X., Low-Cost Titanium–Bromine Flow Battery with Ultrahigh Cycle Stability for Grid-Scale Energy Storage, Advanced Mater., 2020, vol. 32, no. 49, p. 2005036. https://doi.org/10.1002/adma.202005036
Pan, Z., Bi, Y., and An, L., Performance characteristics of a passive direct ethylene glycol fuel cell with hydrogen peroxide as oxidant, Appl. Energy, 2019, vol. 250, p. 846. https://doi.org/10.1016/j.apenergy.2019.05.072
Oh, T.H., Gold-based bimetallic electrocatalysts supported on multiwalled carbon nanotubes for direct borohydride–hydrogen peroxide fuel cell, Renewable Energy, 2021, vol. 163, p. 930. https://doi.org/10.1016/j.renene.2020.09.028
Li, B., Song, C., Huang, X., Ye, K., Cheng, K., Zhu, K., and Wang, G., A novel anode for direct borohydride-hydrogen peroxide fuel cell: Au nanoparticles decorated 3D self-supported reduced graphene oxide foam, ACS Sustainable Chemistry & Engineering, 2019, vol. 7, no. 13, p. 11129. https://doi.org/10.1021/acssuschemeng.9b00192
Lu, B., Yuan, W., Su, X., Zhuang, Z., Ke, Y., and Tang, Y., Passive Direct Methanol–Hydrogen Peroxide Fuel Cell with Reduced Graphene Oxide–Supported Prussian Blue as Catalyst, Energy Technol., 2020, vol. 8, no. 3, p. 1901360. https://doi.org/10.1002/ente.201901360
Zhang, H., Yang, Y., Liu, T., and Chang, H., Boosting the power-generation performance of micro-sized Al–H2O2 fuel cells by using silver nanowires as the cathode, Energies, 2018, vol. 11, no. 9, p. 2316. https://doi.org/10.3390/en11092316
Yang, Z., Gerhardt, M. R., Fortin, M., Shovlin, C., Weber, A.Z., Perry, M.L., and Saraidaridis, J.D., Polysulfide-permanganate flow battery using abundant active materials, J. Electrochem. Soc., 2021, vol. 168, no. 7, p. 070516. https://doi.org/10.1149/1945-7111/ac1036
Liu, C., Liu, H., and Liu, L., Potassium permanganate as an oxidant for a microfluidic direct formate fuel cell, Int. J. Electrochem. Sci., 2019, vol. 14, p. 4557. https://doi.org/10.20964/2019.05.01
Licht, S., A novel aqueous aluminum| permanganate fuel cell, Electrochem. Commun., 1999, vol. 1, p. 33. https://doi.org/10.1016/S1388-2481(98)00010-1
Kim, C., Lee, C.R., Song, Y.E., Heo, J., Choi, S.M., Lim, D.H., and Kim, J.R., Hexavalent chromium as a cathodic electron acceptor in a bipolar membrane microbial fuel cell with the simultaneous treatment of electroplating wastewater, Chem. Engineering J., 2017, vol. 328, p. 703. https://doi.org/10.1016/j.cej.2017.07.077
Shimin, Z., Sulin, C., Debi, Z., Wei, Q., Yu, H., and Xiang, C., Pilot study of an aqueous zinc–bichromate battery, Energy & fuels, 2009, vol. 23, no. 3, p. 1668. https://doi.org/10.1021/ef800848p
Hsu, L., Masuda, S.A., Nealson, K.H., and Pirbazari, M., Evaluation of microbial fuel cell Shewanella biocathodes for treatment of chromate contamination, RSC Advances, 2012, vol. 2, p. 5844. https://doi.org/10.1039/C2RA20478A
Leung, P.K., Ponce-de-León, C., Low, C.T.J., Shah, A.A., and Walsh, F.C., Characterization of a zinc–cerium flow battery, J. Power Sources, 2011, vol. 196, no. 11, p. 5174. https://doi.org/10.1016/j.jpowsour.2011.01.095
Leung, P.K., Mohamed, M.R., Shah, A.A., Xu, Q., and Conde-Duran, M.B., A mixed acid based vanadium–cerium redox flow battery with a zero-gap serpentine architecture, J. Power Sources, 2015, vol. 274, p. 651. https://doi.org/10.1016/j.jpowsour.2014.10.034
Sankarasubramanian, S., Zhang, Y., and Ramani, V., Methanesulfonic acid-based electrode-decoupled vanadium–cerium redox flow battery exhibits significantly improved capacity and cycle life, Sustainable Energy & Fuels, 2019, vol. 3, no. 9, p. 2417. https://doi.org/10.1039/C9SE00286C
Amini, K. and Pritzker, M.D., In situ polarization study of zinc–cerium redox flow batteries, J. Power Sources, 2020, vol. 471, p. 228463. https://doi.org/10.1016/j.jpowsour.2020.228463
Li, Y., Geysens, P., Zhang, X., Sniekers, J., Fransaer, J., Binnemans, K., and Vankelecom, I. F., Cerium-containing complexes for low-cost, non-aqueous redox flow batteries (RFBs), J. Power Sources, 2020, vol. 450, p. 227634. https://doi.org/10.1016/j.jpowsour.2019.227634
Chakrabarti, B., Yufit, V., Kavei, A., Xia, Y., Stevenson, G., Kalamaras, E., and Brandon, N., Charge/discharge and cycling performance of flexible carbon paper electrodes in a regenerative hydrogen/vanadium fuel cell, Intern. J. Hydrogen Energy, 2019, vol. 44, no. 57, p. 30093. https://doi.org/10.1016/j.ijhydene.2019.09.151
Dewage, H.H., Yufit, V., and Brandon, N.P., Study of loss mechanisms using half-cell measurements in a regenerative hydrogen vanadium fuel cell, J. Electrochem. Soc., 2015, vol. 163, no. 1, p. A5236. https://doi.org/10.1149/2.0301601jes
Pasala, V. and Ramanujam, K., Paper-Based Disposable Zinc–Vanadium Fuel Cell for Micropower Applications, Chem. Select, 2019, vol. 4, no. 29, p. 8398. https://doi.org/10.1002/slct.201802624
Rubio-Garcia, J., Kucernak, A., Parra-Puerto, A., Liu, R., and Chakrabarti, B., Hydrogen/functionalized benzoquinone for a high-performance regenerative fuel cell as a potential large-scale energy storage platform, J. Mater. Chem. A, 2020, vol. 8, no. 7, p. 3933. https://doi.org/10.1039/C9TA12396B
Han, S.B., Kwak, D.H., Park, H.S., Park, J.Y., Ma, K.B., Won, J.E., and Park, K.W., A chemically regenerative redox fuel cell using (2,2,6,6-tetramethylpiperidin-1-yl)oxyl redox reaction in acid medium, J. Power Sources, 2018, vol. 393, p. 32. https://doi.org/10.1016/j.jpowsour.2018.05.009
Li, G., Wang, Y., Yu, F., Lei, Y., and Hu, Z., Deep oxidization of glucose driven by 4-acetamido-TEMPO for a glucose fuel cell at room temperature, Chem. Commun., 2021, vol. 57, no. 33, p. 4051. https://doi.org/10.1039/D0CC08381J
Ovsyannikov, N.A., Romadina, E.I., Akhmetov, N.O., Gvozdik, N.A., Akkuratov, A.V., Pogosova, M.A., and Stevenson, K.J., All-organic non-aqueous redox flow batteries with advanced composite polymer-ceramic Li-conductive membrane, J. Energy Storage, 2022, vol. 46, p. 103810. https://doi.org/10.1016/j.est.2021.103810
Петров, М.М., Модестов, А.Д., Конев, Д.В., Антипов, А.E., Локтионов, П.А., Пичугов, Р.Д., Карташова, Н.В., Глазков, А.Т., Абунаева Л.З., Андреев, В.Н., Воротынцев, М.А. Проточные редокс-батареи: место в современной структуре электроэнергетики и сравнительные характеристики основных типов. Успехи химии. 2021. Т. 90. С. 677. [Petrov, M.M., Modestov, A.D., Konev, D.V., Antipov, A.E., Loktionov, P.A., Pichugov, R.D., Kartashova, N.V., Glazkov, A.T., Abunaeva, L.Z., Andreev, V.N., and Vorotyntsev, M.A., Redox flow batteries: importance in modern electrical energy industry and comparative characteristics of the main types, Russ. Chem. Rev., 2021, vol. 90, p. 677.]
Fang, X., Li, Z., Zhao, Y., Yue, D., Zhang, L., and Wei, X., Multielectron organic redoxmers for energy-dense redox flow batteries, ACS Mater. Lett., 2022, vol. 4, p. 277. https://doi.org/10.1021/acsmaterialslett.1c00668
Tolmachev, Y.V., Piatkivskyi, A., Ryzhov, V.V., Konev, D.V., and Vorotyntsev, M.A., Energy cycle based on a high specific energy aqueous flow battery and its potential use for fully electric vehicles and for direct solar-to-chemical energy conversion, J. Solid State Electrochem., 2015, vol. 19, no. 9, p. 2711. https://doi.org/10.1007/s10008-015-2805-z
Vorotyntsev, M.A., Antipov, A.E., and Konev, D.V., Bromate anion reduction: novel autocatalytic (EC") mechanism of electrochemical processes. Its implication for redox flow batteries of high energy and power densities, Pure and Appl. Chem., 2017, vol. 89, no. 10, p. 1429. https://doi.org/10.1515/pac-2017-0306
Vorotyntsev, M.A., Konev, D.V., and Tolmachev, Y.V., Electroreduction of halogen oxoanions via autocatalytic redox mediation by halide anions: novel EC" mechanism. Theory for stationary 1D regime, Electrochim. Acta, 2015, vol. 173, p. 779. https://doi.org/10.1016/j.electacta.2015.05.099
Vorotyntsev, M.A. and Antipov, A.E., Bromate electroreduction in acidic solution inside rectangular channel under flow-through porous electrode conditions, Electrochim. Acta, 2019, vol. 323, p. 134799. https://doi.org/10.1016/j.electacta.2019.134799
Vorotyntsev, M.A. and Konev, D.V., Halate electroreduction via autocatalytic mechanism for rotating disk electrode configuration evolution of concentrations and current after large-amplitude potential step, Electrochim. Acta, 2021, vol. 391, p. 138914. https://doi.org/10.1016/j.electacta.2021.138914
Vorotyntsev, M.A., Volgin, V.M., and Davydov, A.D., Halate electroreduction from acidic solution at rotating disc electrode. Theoretical study of the steady-state convective-migration-diffusion transport for comparable concentrations of halate ions and protons, Electrochim. Acta, 2022, vol. 409, p. 139961. https://doi.org/10.1016/j.electacta.2022.139961
Modestov, A.D., Konev, D.V., Antipov, A.E., Petrov, M.M., Pichugov, R.D., and Vorotyntsev, M.A., Bromate electroreduction from sulfuric acid solution at rotating disk electrode: experimental study, Electrochim. Acta, 2018, vol. 259, p. 655. https://doi.org/10.1016/j.electacta.2017.10.199
Konev, D.V., Antipov, A.E., Petrov, M.M., Shamraeva, M.A., and Vorotyntsev, M.A., Surprising dependence of the current density of bromate electroreduction on the microelectrode radius as manifestation of the autocatalytic redox-cycle (EC") reaction mechanism, Electrochem. Commun., 2018, vol. 86, p. 76. https://doi.org/10.1016/j.elecom.2017.11.006
Modestov, A.D., Konev, D.V., Tripachev, O.V., Antipov, A.E., Tolmachev, Y.V., and Vorotyntsev, M.A., A Hydrogen–Bromate Flow Battery for Air-Deficient Environments, Energy Technol., 2018, vol. 6, p. 242. https://doi.org/10.1002/ente.201700447
Modestov, A.D., Konev, D.V., Antipov, A.E., and Vorotyntsev, M.A., Hydrogen-bromate flow battery: can one reach both high bromate utilization and specific power? J. Solid State Electrochem., 2019, vol. 23, no. 11, p. 3075. https://doi.org/10.1007/s10008-019-04371-w
Modestov, A.D., Andreev, V.N., Antipov, A.E., and Petrov, M.M., Novel aqueous zinc–halogenate flow batteries as an offspring of zinc–air fuel cells for use in oxygen-deficient environment, Energy Technol., 2021, vol. 9, p. 2100233. https://doi.org/10.1002/ente.202100233
Mussini, T. and Longhi, P., The Halogens. Bromine, in Standard potentials in aqueous solutions, Bard, A.J., Parsons, R., and Jordan J., Eds., N.Y.: Marcel Dekker Inc., 1985, p. 78. https://books.google.ru/books?id=fuJV1H18KtEC&pg=PA67&hl=ru&source=gbs_toc_r&cad=4#v=onepage&q&f=false
Задер, П.А., Конев, Д.В., Гун, Дж., Лев, О., Воротынцев, М.А. Теоретический анализ изменения состава системы при окислительном электролизе кислого водного раствора хлорида. Электрохимия. 2022. Т. 58. № 10. в печати. [Zader, P.A., Konev, D.V., Gun, J., Lev, O., and Vorotyntsev, M.A., Theoretical analysis of system’s composition changes in the course of electrolysis of acidic aqueous chloride solution, Russ. J. Electrochem., 2022, vol. 58, no. 10, in press.]
Skrabal, A. and Schreiner, H., Die Reduktionsgeschwindigkeit der Chlorsäure und Bromsäure, Monatshefte für Chemie und verwandte Teile anderer Wissenschaften, 1934, Bd. 65, Nr. 1, S. 213. https://doi.org/10.1007/bf01522061
Taube, H. and Dodgen H., Applications of radioactive chlorine to the study of the mechanisms of reactions involving changes in the oxidation state of chlorine, J. Amer. Chem. Soc., 1949, vol. 71, no. 10, p. 3330. https://doi.org/10.1021/ja01178a016
Lenzi, F. and Rapson, W.H., Effets ioniques spécifiques sur le taux de formation du ClO2 par la réaction chlorure–chlorate, Canad. J. Chem., 1968, vol. 46, no. 6, p. 979. https://doi.org/10.1139/v68-160
Schmitz, G., Kinetics and mechanism of the iodate–iodide reaction and other related reactions, Phys. Chem. Chem. Phys., 1999, vol. 1, no. 8, p. 1909. https://doi.org/10.1039/a809291e
Vogt, H., Balej, J., Bennett, J.E., Wintzer, P., Sheikh, S.A., Gallone, P., Vasudevan, S., and Pelin, K., Chlorine Oxides and Chlorine Oxygen Acids, in Ullmann’s Encyclopedia of Industrial Chemistry, Ullmann, F., Ed, Berlin: Wiley Online Library, 2010, p. 622. https://doi.org/10.1002/14356007.a06_483.pub2
Sant’Anna, R.T.P., Santos, C.M.P., Silva, G.P., Ferreira, R.J.R., Oliveira, A.P., Côrtes, C.E.S., and Faria, R.B., Kinetics and mechanism of chlorate-chloride reaction, J. Brazil. Chem. Soc., 2012, vol. 23, no. 8, p. 1543. https://doi.org/10.1590/S0103-50532012005000017
Fleischmann, M., Lasserre, F., Robinson, J., and Swan, D., The application of microelectrodes to the study of homogeneous processes coupled to electrode reactions: Part I. EC0 and CE reactions, J. Electroanal. Chem. Interfacial Electrochem., 1984, vol. 177, p. 97. https://doi.org/10.1016/0022-0728(84)80215-6
Compton, R.G., Day, M.J., Laing, M.E., Northing, R.J., Penman, J.I., and Waller, A.M., Rotating-disc electrode voltammetry. The catalytic mechanism (EC') and its nuances, J. Chem. Soc., Faraday Trans. I, 1988, vol. 8, p. 2013. https://doi.org/10.1039/F19888402013
Denuault, G., Fleischmann, M., Pletcher, D., and Tutty, O.R., Development of the theory for the interpretation of steady state limiting currents at a microelectrode: EC’ processes: first and second order reactions, J. Electroanal. Chem. Interfacial Electrochem., 1990, vol. 280, p. 243. https://doi.org/10.1016/0022-0728(90)87001-Z
Denuault, G. and Pletcher, D., Improvement to the equation for the steady state limiting currents at a microelectrode: EC’ processes (1st and 2nd order reactions), J. Electroanal. Chem. Interfacial Electrochem., 1991, vol. 305, no. 1, p. 131.
Lavagnini, I., Pastore, P., and Magno, F., Digital simulation of steady state and non-steady state voltammetric responses for electrochemical reactions occurring at an inlaid microdisk electrode: Application to ECirr, EC' and CE first-order reactions, J. Electroanal. Chem., 1993, vol. 358, p. 193. https://doi.org/10.1016/0022-0728(93)80438-N
Tutty, O.R., Second-order kinetics for steady state EC' reactions at a disc microelectrode, J. Electroanal. Chem., 1994, vol. 377, p. 39. https://doi.org/10.1016/0022-0728(94)03447-8
Molina, A., Analytical solution corresponding to the i/t response to a multipotential step for a catalytic mechanism, J. Electroanal. Chem., 1998, vol. 443, no. 2, p. 163. https://doi.org/10.1016/S0022-0728(97)00566-4
Molina, A., Serna, C., and Martinez-Ortiz, F., Square wave voltammetry for a pseudo-first-order catalytic process at spherical electrodes, J. Electroanal. Chem., 2000, vol. 486, no. 1, p. 9. https://doi.org/10.1016/S0022-0728(00)00115-7
Mirceski, V. and Gulaboski, R., Surface catalytic mechanism in square-wave voltammetry, Electroanalysis, 2001, vol. 13, p. 1326. https://doi.org/10.1002/1521-4109(200111)13:16<1326:: AID-ELAN1326>3.0.CO;2-S
Mirceski, V. and Gulaboski, R., The surface catalytic mechanism: a comparative study with square-wave and staircase cyclic voltammetry, J. Solid State Electrochem., 2003, vol. 7, p. 157. https://doi.org/10.1007/s10008-002-0290-7
Compton, R.G. and Banks, C.E., Understanding voltammetry, London: Imperial College Press, 2011, 429 p.
Molina, A., Gonzalez, J., Laborda, E., Wang, Y., and Compton, R.G., Analytical theory of the catalytic mechanism in square wave voltammetry at disc electrodes, Phys. Chem. Chem. Phys., 2011, vol. 13, p. 16748. https://doi.org/10.1039/C1CP22032B
Ward, K.R., Lawrence, N.S., Hartshorne, R.S., and Compton, R.G., Cyclic voltammetry of the EC' mechanism at hemispherical particles and their arrays: the split wave, J. Phys. Chem., 2011, vol. 115, no. 22, p. 11204. https://doi.org/10.1021/jp2023204
Calhoun, R.L. and Bard, A.J., Study of the EC' mechanism by scanning electrochemical microscopy (SECM), ECS Transactions, 2011, vol. 35, no. 29, p. 39. https://doi.org/10.1149/1.3645611
Gulaboski, R. and Mihajlov, L., Catalytic mechanism in successive two-step protein-film voltammetry – Theoretical study in square-wave voltammetry, Biophys. Chem., 2011, vol. 155, no. 1, p. 1. https://doi.org/10.1016/j.bpc.2011.01.010
Gulaboski, R., Mirceski, V., Bogeski, I., and Hoth, M., Protein film voltammetry: electrochemical enzymatic spectroscopy: A review on recent progress, J. Solid State Electrochem., 2012, vol. 16, p. 2315. https://doi.org/10.1007/s10008-011-1397-5
Yue, D., Jia, Y., Yao, Y., Sun, J., and Jing, Y., Structure and electrochemical behavior of ionic liquid analogue based on choline chloride and urea, Electrochim. Acta, 2012, vol. 65, p. 30. https://doi.org/10.1016/j.electacta.2012.01.003
Gulaboski, R. and Mirceski, V., New aspects of the electrochemical-catalytic (EC') mechanism in square-wave voltammetry, Electrochim. Acta, 2015, vol. 167, p. 219. https://doi.org/10.1016/j.electacta.2015.03.175
Метод Кунге–Кутта. [Электронный ресурс]. URL: https://en.wikipedia.org/wiki/Runge–Kutta_methods
Дополнительные материалы отсутствуют.
Инструменты
Электрохимия