Электрохимия, 2022, T. 58, № 12, стр. 821-837
Зависимость дифференциальной проводимости электрохимического транзистора от перенапряжения в полностью неадиабатическом режиме
И. Г. Медведев *
Институт физической химии и электрохимии им. А.Н. Фрумкина РАН
119071 Москва, Ленинский просп., 31, Россия
* E-mail: theor@elchem.ac.ru
Поступила в редакцию 25.02.2022
После доработки 25.05.2022
Принята к публикации 01.06.2022
- EDN: ALOYZO
- DOI: 10.31857/S0424857022120040
Аннотация
Проведено теоретическое исследование зависимости дифференциальной проводимости электрохимического транзистора от перенапряжения при фиксированном напряжении смещения в рамках полностью неадиабатического (диабатического) режима работы транзистора. Электрохимический транзистор включает редокс-группу с одним вырожденным по спину электронным уровнем, для которого учитывается кулоновское отталкивание между электронами с противоположной проекцией спина. Электроды рассматриваются в модели с широкой зоной проводимости. На основании численных расчетов выявлены области максимальных значений дифференциальной проводимости, которые существенно зависят от параметров системы. Использование приближенных аналитических методов позволяет выяснить физический смысл этих областей. Знание указанных областей имеет важное практическое значение, так как именно в этих областях происходит резкое изменение туннельного тока с изменением напряжения на электродах.
ВВЕДЕНИЕ
Исследование электронного переноса на границе раздела двух фаз является одной из основных задач электрохимии. В настоящее время эта задача приобрела новый характер как задача об электронном переносе в мостиковых электрохимических туннельных наноконтактах. Практическое значение изучения электрохимических туннельных контактов связано с тем, что они представляют собой наиболее интересные системы для использования в элементах молекулярной электроники, поскольку, в отличие от вакуумных систем, могут функционировать при комнатных температурах и демонстрируют эффекты выпрямления и усиления туннельного тока (см. обзоры [1–6]). Наиболее простым, эффективным и перспективным способом контроля туннельного тока является использование электрохимического управления положением электронного уровня εb редокс-группы (РГ) в электрохимических мостиковых туннельных контактах посредством изменения потенциала одного из рабочих электродов относительно третьего электрода сравнения или, на электрохимическом языке, изменением перенапряжения η [1, 7–17]. Этот способ управления туннельным током посредством изменения перенапряжения был впервые предложен в работе [7], а возникающая в результате система может рассматриваться как электрохимический транзистор [18–20].
Вычислению туннельного тока j в мостиковых туннельных контактах (как вакуумных, так и электрохимических) посвящено обширное количество исследований, базирующихся на разных методах расчета и учитывающих как электрон-фононное взаимодействие, так и кулоновское отталкивание U между двумя электронами с противоположной проекцией спина на электронном уровне мостиковой молекулы (см., например, статьи, цитированные в [21]). В этих работах рассматривались различные возможные режимы работы мостикового туннельного контакта, в каждом из которых применяются различные алгоритмы вычисления туннельного тока. Наибольшую связь с классической электрохимией имеет метод расчета туннельного тока в полностью неадиабатическом (диабатическом) режиме электронного переноса на рабочих электродах (предел слабого взаимодействия РГ с электродами) [22–25]. В этом режиме процесс состоит из двух последовательных диабатических реакций электронного переноса и в результате полный электронный перенос между рабочими электродами имеет последовательный характер [23]. Сначала, вследствие флуктуации поляризации растворителя, происходит восстановление РГ путем переноса электрона из левого электрода (при Vb > 0) на валентный уровень РГ. Затем, после релаксации полярного растворителя и последующей его активации происходит окисление РГ в результате переноса электрона с валентного уровня РГ на правый электрод. Таким образом, в диабатическом режиме имеет место кратковременная локализация электрона на РГ, что соответствует прыжковому механизму электронного транспорта, который имеет активационный характер. Напротив, в механизме суперобмена происходит виртуальный перенос электрона через валентный уровень РГ, и медленные степени свободы растворителя не успевают отреагировать на этот процесс.
Диабатический предел важен тем, что в его рамках можно аналитически получить важные корреляции для ряда характеристик туннельного контакта, которые позволяют на качественном уровне понять экспериментальные результаты. Тем не менее, этот предел дает заниженные значения туннельного тока, которые много меньше значений, наблюдаемых в эксперименте.
Помимо вычислений и экспериментальных измерений туннельного тока в мостиковых контактах большое значение имеет исследование дифференциальной проводимости (ДП) G = dj/dVb, которая является одной из важнейших характеристик туннельного контакта и позволяет обнаружить более тонкие черты поведения туннельного тока с изменением напряжения смещения. Эти черты, связанные с существенными изменениями туннельного тока в разных областях значений Vb, часто бывает трудно увидеть на кривых j(Vb), полученных теоретически или экспериментально. В то же время, указанные черты находят свое отражения на соответствующих пиках ДП и их ширине.
Вычисления зависимости ДП от Vb выполнялись, главным образом, при низких температурах для случая взаимодействия электронов, заполняющих электронный уровень мостиковой молекулы, с квантовыми фононами, обусловленными колебаниями самой мостиковой молекулы. Вычисления функции G(Vb) в полностью неадиабатическом режиме были проведены в [25] для симметричного взаимодействия РГ с электродами с учетом кулоновского отталкивания и для случая классических фононов, который является характерным именно для электрохимических туннельных контактов. Были обнаружены новые интересные черты в поведении функций G(Vb), относящиеся к высоте пиков, их ширине и обусловленные эффектом реорганизации растворителя. Учет несимметричного взаимодействия РГ с электродами рассмотрен в [26]. Показано, что эффект асимметрии существенно влияет на вид кривых G(Vb).
В цитированных выше работах [25, 26] ДП G(Vb) вычислялась как функция напряжения смещения. При этом ДП характеризует скорость изменения тока с изменением Vb при данном перенапряжении η в разных областях значений Vb. Однако не меньший интерес представляет изучение зависимости ДП от перенапряжения (т.е., функции G(η)), которая характеризует скорость изменения тока с изменением Vb при данном значении напряжения смещения, но различных значениях перенапряжения. Для электрохимического транзистора линейная проводимость (ДП при Vb = 0) как функция перенапряжения исследовалась в [27] для полностью неадиабатического режима. В [27] также рассматривалась ДП G(η) при произвольных Vb с целью проверки точных соотношений для ДП, которые были получены в [27].
Цель настоящей работы состоит в более детальном изучении зависимости ДП электрохимического транзистора от перенапряжения η при данных фиксированных значениях Vb. Учитывается влияние энергии реорганизации растворителя Er, энергии кулоновского отталкивания U и асимметрии взаимодействия электронов РГ с электродами. В частности, в полностью неадиабатическом пределе получено выражение, устанавливающее связь между величинами и положениями максимумов ДП G(η) с плотностью электронных состояний на валентном уровне РГ, а также с числами заполнения электронами этого уровня. Анализируется физический смысл того или иного положения максимумов ДП в зависимости от величины энергии реорганизации растворителя, напряжения смещения и энергии кулоновского отталкивания электронов.
Статья построена следующим образом. В следующем разделе сформулирована модель и приводятся основные соотношения, которые используются в статье. Затем рассмотрены два предельных случая: слабо полярные растворители (Er ≈ 0) и предел больших значений Er. В основном разделе рассчитывается и обсуждается ДП при произвольных значениях энергии реорганизации растворителя и напряжения смещения. Статья завершается выводами и заключительными замечаниями.
МОДЕЛЬ И ОСНОВНЫЕ СООТНОШЕНИЯ
Модель аналогична модели, которая принята в работах [24, 25]. Электрохимический транзистор состоит из двух рабочих электродов, которые будем условно называть левым (L) и правым (R). Мостиковая молекула, содержащая РГ, погружена в раствор электролита и расположена между рабочими электродами. Потенциал левого рабочего электрода может изменяться относительно третьего электрода сравнения. При этом перенапряжение η определяется как “катодное” перенапряжение левого электрода $\eta = \varphi _{{\text{L}}}^{{\text{0}}} - {{\varphi }_{{\text{L}}}}$, где $\varphi _{{\text{L}}}^{{\text{0}}}$ и φL являются равновесным потенциалом этого электрода и его потенциалом [24]. Рабочие электроды рассматриваются как макроскопические резервуары невзаимодействующих электронов. В ситуации, когда только небольшое количество электронов вовлечено в процесс туннелирования, рабочие электроды находятся в состоянии равновесия и их электронные подсистемы характеризуются электрохимическими потенциалами μα и функциями Ферми fα = f(ε − μα) (α = L или R). Принимается, что рабочие электроды имеют одинаковую комнатную температуру T, совпадающую с температурой электролита. Если напряжение смещения Vb, где eVb определяется как разность электрохимических потенциалов левого и правого рабочих электродов (eVb = μL – μR, e – абсолютное значение заряда электрона, см. рис. 1), не равно нулю, через электрохимический транзистор протекает ток, обусловленный электронными переходами между рабочими электродами и РГ. Прямое туннелирование электронов между рабочими электродами не учитывается. Принимается также, что РГ содержит только один активный электронный уровень, который может быть заполнен двумя электронами с противоположной проекцией спина. Взаимодействие электронов друг с другом характеризуется энергией кулоновского отталкивания U. Эти электроны взаимодействуют также с фононами раствора электролита, характеризующими флуктуации поляризации растворителя, и фононами, возникающими вследствие колебаний мостиковой молекулы. В дальнейшем рассматриваются только классические фононы, так что средняя частота колебаний $\hbar {{\omega }_{{{\text{av}}}}} \ll kT$, где k – постоянная Больцмана.
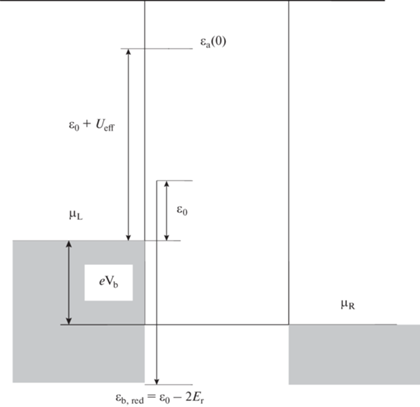
Рис. 1.
Энергетическая диаграмма электрохимического транзистора. μL и μR – электрохимические потенциалы левого и правого электродов, Vb = (μL – μR)/e – напряжение смещения, ε0 и εb, red – энергии электронного уровня РГ в окисленном и восстановленном состояниях, εа(0) – уровень сродства РГ к электрону, Ueff = U – 2Er – эффективная энергия кулоновского отталкивания, Er – энергия реорганизации растворителя. Энергии одночастичных состояний отсчитываются от μL.
Энергия электронного уровня РГ ${{\varepsilon }_{{\text{b}}}}$ (qk) в случае, когда взаимодействие с рабочими электродами отсутствует, дается выражением [25]
(1)
${{\varepsilon }_{{\text{b}}}}({{q}_{k}}) = {{\varepsilon }_{{\text{0}}}} - \sum\limits_k {{{\gamma }_{k}}{{q}_{k}}} .$(2)
${{\varepsilon }_{{\text{0}}}} = - e\xi \eta - e\gamma {{V}_{{\text{b}}}} + {{E}_{{\text{r}}}} + kT\ln (2),$Обозначим через Vpα электронный матричный элемент, описывающий взаимодействие электронного уровня РГ с электронным состоянием |pα❭ электрода α, имеющим энергию ${{\varepsilon }_{{p\alpha }}}$. Тогда энергия ${{\Gamma }_{\alpha }} = 2\pi {{\sum\nolimits_p {\left| {{{V}_{{p\alpha }}}} \right|} }^{2}}\delta (\varepsilon - {{\varepsilon }_{{p\alpha }}})$ представляет собой эффективный электронный матричный элемент, соответствующий взаимодействию электронного уровня РГ с электродом α. Энергия Γα имеет также физический смысл ширины электронного уровня РГ, возникающей вследствие взаимодействия РГ с электродом α. Полная ширина Γ электронного уровня РГ равна ΓL + ΓR. Для простоты электронный спектр рабочих электродов рассматривается в приближении широких зон проводимости. В этом случае эффективные матричные элементы Γ и Γα не зависят от энергии ε. В принципе Γ и Γα могут зависеть от напряжения смещения и перенапряжения, но эта зависимость ниже не рассматривается. Тогда условием применимости полностью неадиабатического приближения является условие ${{\Gamma }_{\alpha }} \ll \hbar {{\omega }_{{{\text{av}}}}}$. В стационарном режиме работы электрохимического транзистора фононная подсистема находится в равновесии при любом заполнении n электронного уровня РГ. В этом случае состояния РГ могут быть охарактеризованы только числом заполнения n и вероятностями Pn обнаружить эти состояния. Для определения вероятностей Pn можно использовать кинетические уравнения [23]. Стационарные решения этих уравнений имеют вид [25]:
(3)
${{P}_{0}} = {{k}_{{10}}}{{k}_{{21}}}/Z,\,\,\,{{P}_{1}} = 2{{k}_{{01}}}{{k}_{{21}}}/Z,\,\,\,{{P}_{2}} = {{k}_{{01}}}{{k}_{{12}}}/Z,$(4)
$j = 2e\left[ {{{k}_{{21}}}\left( {k_{{01}}^{{\text{L}}}k_{{10}}^{{\text{R}}} - k_{{10}}^{{\text{L}}}k_{{01}}^{{\text{R}}}} \right)\, + \,{{k}_{{01}}}\left( {k_{{12}}^{{\text{L}}}k_{{21}}^{{\text{R}}} - k_{{21}}^{{\text{L}}}k_{{12}}^{{\text{R}}}} \right)} \right]/Z.$Ряд других важных для дальнейшего изложения выражений для туннельного тока помещен в Приложение.
Первое последовательное квантовомеханическое вычисление константы скорости неадиабатического электронного переноса между электродом и ионом с использованием явного выражения для предэкспоненциального множителя в константе скорости было проведено в работах [28, 29]. В этих работах полный электронный перенос рассматривался в рамках теории возмущений как результат совокупности независимых электронных переносов с уровня $\left| p \right\rangle $ электрода на электронный уровень иона и обратно. Более последовательное выражение, включающее функцию фермиевского распределения электронов в электроде, получено в работе [30]. Используемое в настоящей работе выражение для константы скорости неадиабатического электронного переноса с учетом кулоновского отталкивания электронов на электронном уровне РГ имеет вид:
(5)
$\begin{gathered} k_{{ij}}^{\alpha } = \frac{{{{\Gamma }_{\alpha }}}}{\hbar }{{\left( {\frac{{kT}}{{\pi {{E}_{{\text{r}}}}}}} \right)}^{{1/2}}} \times \\ \times \,\,\int {\frac{{{\text{d}}\varepsilon }}{{2kT}}f(\varepsilon )\exp } \left[ { - {{{{{\left( {{{E}_{{\text{r}}}} - \Delta F_{{ji}}^{\alpha } - \varepsilon } \right)}}^{2}}} \mathord{\left/ {\vphantom {{{{{\left( {{{E}_{{\text{r}}}} - \Delta F_{{ji}}^{\alpha } - \varepsilon } \right)}}^{2}}} {4{{E}_{{\text{r}}}}kT}}} \right. \kern-0em} {4{{E}_{{\text{r}}}}kT}}} \right] \\ \end{gathered} $(6)
$k_{{ij}}^{\alpha } = k_{{ji}}^{\alpha }\exp \left( {{{ - \Delta F_{{ij}}^{\alpha }} \mathord{\left/ {\vphantom {{ - \Delta F_{{ij}}^{\alpha }} {kT}}} \right. \kern-0em} {kT}}} \right)$Из формул (4) и (5) следует, что при прыжковом механизме электронного транспорта ток в целом пропорционален квадрату электронного матричного элемента, тогда как при суперобменном механизме он пропорционален его четвертой степени, поэтому в диабатическом режиме вкладом в ток от суперобменного механизма можно пренебречь.
На рисунках, приведенных в этой статье, графики ДП G(eξη) вычисляются на компьютере с использованием формулы (4) для тока и точных констант скорости (5)–(6). Но для интерпретации и выяснения физического смысла полученных результатов необходимо проведение аналитических оценок, полученных для ряда предельных случаев. Все расчеты проводятся при комнатной температуре и принимается, что kT = = 0.025 эВ.
ДИФФЕРЕНЦИАЛЬНАЯ ПРОВОДИМОСТЬ ДЛЯ ПРЕДЕЛЬНЫХ ЗНАЧЕНИЙ ЭНЕРГИИ РЕОРГАНИЗАЦИИ
В этом разделе рассмотрено вычисление ДП для двух предельных случаев: Er ≈ 0 (вакуумные туннельные контакты или слабо полярные растворители) и предел больших Er → ∞. В обоих случаях можно получить приближенные аналитические выражения для ДП. Существенно, что в каждом из этих случаев пики ДП имеют разную физическую интерпретацию. Реальное значение Er в электрохимическом транзисторе находится между указанными предельными случаями.
Случай, когда Er ≈ 0
Значения констант скоростей для этого случая хорошо известны и могут быть получены, например, из формул (5)–(6) в пределе Er → 0 [26]:
(7)
$\begin{gathered} {\kern 1pt} {\kern 1pt} k_{{01}}^{\alpha } = {{\Gamma }_{\alpha }}{{f}_{\alpha }}({{\varepsilon }_{{\text{b}}}}),\,\,\,\,{\kern 1pt} k_{{10}}^{\alpha } = {{\Gamma }_{\alpha }}[1 - {{f}_{\alpha }}({{\varepsilon }_{{\text{b}}}})], \\ k_{{12}}^{\alpha } = {{\Gamma }_{\alpha }}{{f}_{\alpha }}({{\varepsilon }_{{\text{a}}}}),\,\,\,\,{\kern 1pt} k_{{21}}^{\alpha } = {{\Gamma }_{\alpha }}[1 - {{f}_{\alpha }}({{\varepsilon }_{{\text{a}}}})]. \\ \end{gathered} $Отметим, что при Er → 0 значение Ueff совпадает с U. Тогда из уравнений (3)–(4) находим, что
(8)
$\begin{gathered} P_{0}^{0} = \frac{{[1 - \tilde {f}({{\varepsilon }_{{\text{b}}}})][1 - \tilde {f}({{\varepsilon }_{{\text{b}}}} + U)]}}{{1 + \tilde {f}({{\varepsilon }_{{\text{b}}}}) - \tilde {f}({{\varepsilon }_{{\text{b}}}} + U)}}, \\ P_{1}^{0} = \frac{{2\tilde {f}({{\varepsilon }_{{\text{b}}}})[1 - \tilde {f}({{\varepsilon }_{{\text{b}}}} + U)]}}{{1 + \tilde {f}({{\varepsilon }_{{\text{b}}}}) - \tilde {f}({{\varepsilon }_{{\text{b}}}} + U)}}, \\ \end{gathered} $$P_{2}^{0} = 1 - P_{0}^{0} - P_{1}^{0},$
(9)
${{j}^{0}} = \frac{{2e{{\Gamma }_{{\text{L}}}}{{\Gamma }_{{\text{R}}}}\left\{ {\left[ {1 - \tilde {f}({{\varepsilon }_{{\text{b}}}} + U)} \right]\left[ {{{f}_{{\text{L}}}}({{\varepsilon }_{{\text{b}}}}) - {{f}_{{\text{R}}}}({{\varepsilon }_{{\text{b}}}})} \right] + \tilde {f}({{\varepsilon }_{{\text{b}}}})\left[ {{{f}_{{\text{L}}}}({{\varepsilon }_{{\text{b}}}} + U) - {{f}_{{\text{R}}}}({{\varepsilon }_{{\text{b}}}} + U)} \right]} \right\}}}{{\hbar \Gamma \left[ {1 + \tilde {f}({{\varepsilon }_{{\text{b}}}}) - \tilde {f}({{\varepsilon }_{{\text{b}}}} + U)} \right]}},$(10)
${{j}_{{\max }}} = \frac{{2e{{\Gamma }_{{\text{L}}}}{{\Gamma }_{{\text{R}}}}}}{{\hbar \Gamma }} = \frac{{2e{{\Gamma }_{{\text{L}}}}d}}{{\hbar (1 + d)}}.$При выводе формулы (10) использовалось, что при указанных выше условиях и, например, Vb > 0, имеем fL(εb) = fL(εb + U) ≈ 1, fR(εb) = fR(εb + U) ≈ 0, а вероятности $P_{n}^{0}$ (и, следовательно, Pn при больших Vb) даются равенствами P0 = d2/(1 + d)2, P1 = 2d/(1 + d)2, P2 = 1/(1 + d)2. В частности, P0 = 1/4, P1 = 1/2, P2 = = 1/4 при d = 1 [25] и P0 = 1, P1 = P2 = 0 при d $ \gg $ 1. Последний результат имеет простой физический смысл, так как электронный уровень РГ является практически пустым при Vb > 0 и d $ \gg $ 1. Очевидно также, что P2 = 1 при Vb > 0 и d $ \ll $ 1. Если Vb < 0, то вероятности Pn получаются из приведенных выше результатов с помощью формулы (П6) (в этом случае d → 1/d). Можно также показать, что в пределе больших значений $\left| {e\xi \eta } \right|$ и произвольных Er, Vb, Ueff имеем P0 = 0, P1 = 0, P2 = 1 для положительных η, P0 = 1, P1 = 0, P2 = 0 для отрицательных η.
Физический смысл появления пиков у ДП легко понять, если изучить функцию G(Vb). Для получения аналитических выражений рассмотрим сначала случаи, когда $\left| {e\xi \eta } \right|$ $ \gg $ kT, U $ \gg $ kT. Ниже в статье ДП будет измеряться в единицах ${{G}_{{{\text{scale}}}}} = {{{{G}_{0}}\pi {{\Gamma }_{{\text{L}}}}} \mathord{\left/ {\vphantom {{{{G}_{0}}\pi {{\Gamma }_{{\text{L}}}}} {(2kT)}}} \right. \kern-0em} {(2kT)}}$, где ${{G}_{0}} = {{{{e}^{2}}} \mathord{\left/ {\vphantom {{{{e}^{2}}} {(\pi \hbar )}}} \right. \kern-0em} {(\pi \hbar )}}$. При этом возможны четыре сценария изменения энергий εb и εа = εb + U при изменении Vb. Частично эти сценарии были рассмотрены в работах [31–33, 25]. В первом сценарии при Vb = 0 уровни εb и εа лежат выше уровня Ферми левого электрода, что возможно только при отрицательных η. Этот сценарий представляет практический интерес, так как для РГ при Vb = 0 в окисленном состоянии уровень ${{\varepsilon }_{{\text{b}}}} > \varepsilon _{{\text{F}}}^{{\text{L}}}$. С увеличением напряжения смещения в положительную сторону уровень εb пересекает уровень $\varepsilon _{{\text{F}}}^{{\text{L}}}$. В момент пересечения, с точностью до слагаемого порядка kT, имеем равенство $ - \xi \eta - \gamma {{V}_{{\text{b}}}} = 0$. Соответствующее значение Vb обозначим через V0γ, где V0γ = −ξη/γ. Как следует из формулы (8), в окрестности точки V0γ в интервале значений eγVb порядка kT вероятность $P_{0}^{0}$ резко падает от 1 до $P_{0}^{0}$ ≈ d/(2 + d) ($P_{0}^{0}$ ≈ 1/3 при d = 1, но по-прежнему $P_{0}^{0}$ ≈ 1 при d $ \gg $ 1), а вероятность $P_{1}^{0}$ возрастает от 0 до $P_{1}^{0}$ ≈ ≈ 2/(2 + d) ($P_{1}^{0}$ ≈ 2/3 при d = 1, но по-прежнему $P_{1}^{0}$ ≈ 0 при d $ \gg $ 1). Значения $\tilde {f}({{\varepsilon }_{{\text{a}}}})$ и fR(εb) примерно равны нулю, а значение fL(εb) возрастает от 0 до 1. При этом ток изменяется от 0 до (1 + d)jmax/(2 + d), что равно 2jmax /3 для d = 1 [33, 25] (это обусловлено спиновыми эффектами) и от 0 до jmax при d $ \gg $ 1 [33], так как в этом случае вероятность $P_{1}^{0}$ остается равной нулю, т.е. электрон сразу переходит на правый электрод. Высоту пика Gmax и его ширину в половине максимума можно оценить, исходя их простых соображений [25]. Так как изменение тока происходит в интервале значений eγVb порядка kT, то Gmax имеет порядок ejmaxγ/kT, а ширина пропорциональна kT/γ. Более точный анализ дает ${{G}_{{\max 0\gamma }}} \approx {{d\gamma } \mathord{\left/ {\vphantom {{d\gamma } {(2 + d)}}} \right. \kern-0em} {(2 + d)}}$ (в единицах Gscale), $e{{V}_{{\max }}} \approx {{ - e\xi \eta } \mathord{\left/ {\vphantom {{ - e\xi \eta } \gamma }} \right. \kern-0em} \gamma } - $ ${{kT\ln \{ {{(2 + d)} \mathord{\left/ {\vphantom {{(2 + d)} {[2(1 + d)]}}} \right. \kern-0em} {[2(1 + d)]}}\} } \mathord{\left/ {\vphantom {{kT\ln \{ {{(2 + d)} \mathord{\left/ {\vphantom {{(2 + d)} {[2(1 + d)]}}} \right. \kern-0em} {[2(1 + d)]}}\} } \gamma }} \right. \kern-0em} \gamma }$ и ширина пика W = 3.5kT/γ. Таким образом, Gmax = γ/3 при d = 1 и Gmax = γ при d $ \gg $ 1.
При дальнейшем увеличении Vb уже уровень εа пересекает уровень Ферми левого электрода при значении напряжения смещения, которое обозначим через Vaγ = (U − eξη)/eγ. В результате анализа находим, что в окрестности точки Vaγ${{G}_{{\max a\gamma }}} \approx {{d\gamma } \mathord{\left/ {\vphantom {{d\gamma } {[(1 + d)(2 + d)]}}} \right. \kern-0em} {[(1 + d)(2 + d)]}}$ при той же ширине W = = 3.5kT/γ, так что Gmax = γ/6 при d = 1 и Gmax = 0 при d $ \gg $ 1, так как в последнем случае вероятность $P_{1}^{0}$ остается равной нулю и при V ≥ Vaγ. Поэтому пик ДП в точке Vaγ при d $ \gg $ 1 отсутствует.
При уменьшении Vb от нуля уровень Ферми правого электрода пересечет последовательно уровни εb и εа. В соответствующих точках, которые обозначим через V0 = ξη/(1 – γ) и Va = (eξη – U)/e(1 – γ), находим, что ${{G}_{{\max 0}}} \approx d(1 - \gamma )/(1 + 2d)$ (что равно (1 – γ)/3 при d = 1 и (1 – γ)/2 при d $ \gg $ 1) и ${{G}_{{\max 0}}} \approx {{d}^{2}}(1 - \gamma )/[(1 + d)(1 + 2d)]$ (что равно (1 – γ)/6 при d = 1 и (1 – γ)/2 при d $ \gg $ 1). Ширина обоих пиков W равна 3.5kT/(1 – γ).
На рис. 2а показана зависимость ДП от напряжения смещения при eξη = –0.2 эВ, U = 0.3 эВ, γ = 0.2 для двух значений d: d = 1 и d = 100 (такое значение d, моделирующее случай d $ \gg $ 1, выбрано не очень большим, чтобы на правом электроде сохранялся неадиабатический режим электронного переноса). Вычисления проводились с использованием формулы (9). Положения максимумов слева направо соответствуют точкам Va, V0, V0γ и Vаγ. Из рисунка следует, что высоты максимумов и их ширина находятся в согласии с приведенными выше выражениями. Как уже отмечалось, вклад в ДП в окрестности точки Vaγ при d $ \gg $ 1 отсутствует.
Рис. 2.
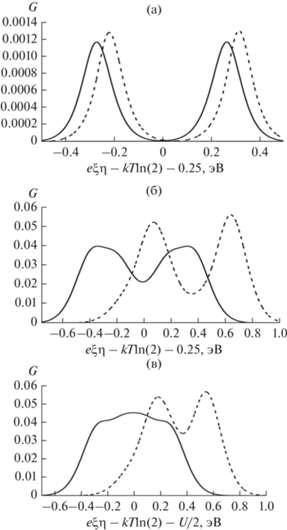
Безразмерная дифференциальная проводимость G электрохимического транзистора в случае слабо полярного растворителя (Er ≈ 0) и параметров U = 0.3 эВ, γ = 0.2, kT = 0.025 эВ. Зависимость дифференциальной проводимости от напряжения смещения Vb при eξη = −0.2 эВ (а); от разности eξη − kTln(2) − U/2 при Vb = 1 В (б). Сплошная линия: ΓR = ΓL; пунктирная линия: ΓR = 100ΓL. Дифференциальная проводимость измеряется в единицах ${{{{G}_{0}}\pi {{\Gamma }_{{\text{L}}}}} \mathord{\left/ {\vphantom {{{{G}_{0}}\pi {{\Gamma }_{{\text{L}}}}} {(2kT)}}} \right. \kern-0em} {(2kT)}}$ (${{G}_{0}} = {{{{e}^{2}}} \mathord{\left/ {\vphantom {{{{e}^{2}}} {(\pi \hbar )}}} \right. \kern-0em} {(\pi \hbar )}}$).

Если U = 0, то точка V0 совпадает с точкой Vа, а точка V0γ совпадает с точкой Vаγ. При этом соответствующие значения Gmax складываются. Если дополнительно eξη = kTln(2), то ДП имеет единственный максимум, расположенный в точке Vb = 0. Высота максимума равна d/(1 + d) и стремится к 1 при d $ \gg $ 1. В последнем случае размерная ДП равна Gscale, откуда и следует физический смысл выбранного нами масштаба для ДП.
Во втором сценарии уровни εb и εа при Vb = 0 находятся ниже уровня Ферми левого электрода, что возможно при положительном перенапряжении. График зависимости G(Vb) для этого сценария можно получить из соответствующего графика для первого сценария, если воспользоваться формулой (П7). Для рис. 2а значение Δ(eξη) = eξη − − kTln(2) − U/2 равно −0.367 эВ. Тогда значение −Δ(eξη) отвечает значению eξη, равному приблизительно 0.5 эВ. Тогда зависимость ДП от Vb для eξη = 0.5 эВ, U = 0.3 эВ, γ = 0.2, kT = 0.025 эВ может быть получена из рис. 2а его зеркальным отражением относительно оси G. Однако при этом точки положения максимумов слева направо будут соответствовать точкам V0γ, Vаγ, Va и V0, так что, например, значение Gmax в точке V0γ для варианта 1 не будет совпадать со значением Gmax в точке V0γ для варианта 2.
В вариантах 3 и 4 при Vb = 0 уровень εb меньше уровня Ферми левого электрода (т.е., η > 0), но уровень εа лежит выше. В сценарии 3 при увеличении Vb сначала εb = $\varepsilon _{{\text{F}}}^{{\text{R}}}$, а затем εa = $\varepsilon _{{\text{F}}}^{{\text{L}}}$. При этом V0 < Vаγ (или Ueff > eξη/(1 – γ)). В сценарии 4 при увеличении Vb сначала εa = $\varepsilon _{{\text{F}}}^{{\text{L}}}$, а затем уже εb доходит до $\varepsilon _{{\text{F}}}^{{\text{R}}}$, т.е. V0 > Vаγ (или Ueff < eξη/(1 – γ)).
При изучении функции G(η) возможны только два сценария. В обоих сценариях при данном Vb и увеличении перенапряжения от больших отрицательных значений уровни εb и εa опускаются вниз. Далее, в сценарии 1, сначала εb = $\varepsilon _{{\text{F}}}^{{\text{L}}}$, затем εa = $\varepsilon _{{\text{F}}}^{{\text{L}}}$. Потом εb = $\varepsilon _{{\text{F}}}^{{\text{R}}}$, а затем εa = $\varepsilon _{{\text{F}}}^{{\text{R}}}$. В сценарии 2 сначала εb = $\varepsilon _{{\text{F}}}^{{\text{L}}}$, затем εb = $\varepsilon _{{\text{F}}}^{{\text{R}}}$ и только потом εa = $\varepsilon _{{\text{F}}}^{{\text{L}}}$. Аналогично введенным выше характерным значениям напряжения смещения имеем точки $e\xi {{\tilde {\eta }}_{{0\gamma }}} = - e\gamma {{V}_{{\text{b}}}}$, $e\xi {{\tilde {\eta }}_{{{\text{a}}\gamma }}} = - e\gamma {{V}_{{\text{b}}}} + U$, $e\xi {{\tilde {\eta }}_{0}} = e(1 - \gamma ){{V}_{{\text{b}}}}$ и $e\xi {{\tilde {\eta }}_{{\text{a}}}} = e(1 - \gamma ){{V}_{{\text{b}}}} + U$, где $e\xi \tilde {\eta } = e\xi \eta - kT\ln (2)$. В результате для сценария 1 ${{\tilde {\eta }}_{{{\text{a}}\gamma }}} < {{\tilde {\eta }}_{0}}$ (или eVb > U), а для сценария 2 ${{\tilde {\eta }}_{{0\gamma }}} < {{\tilde {\eta }}_{0}}$ (или eVb < U).
На рис. 2б приведена зависимость G(Δ(eξη)). Как и для случая, представленного на рис. 2а, U = = 0.3 эВ, γ = 0.2, d = 1 и d = 100. Значение Vb = 1 В выбрано таким образом, чтобы пик в точке V0γ ≈ 1 В на рис. 2а соответствовал левому пику в точке ${{\tilde {\eta }}_{{0\gamma }}} \approx - 0.2$ В (или Δ(eξη) ≈ –0.35 В) на рис. 2б. Максимумы ДП, расположенные слева направо, находятся в точках ${{\tilde {\eta }}_{{0\gamma }}}$, ${{\tilde {\eta }}_{{{\text{a}}\gamma }}}$, ${{\tilde {\eta }}_{0}}$ и ${{\tilde {\eta }}_{{\text{a}}}}$. Высоты максимумов в первых двух точках равны ${{G}_{{\max 0\gamma }}}$ и ${{G}_{{\max {\text{a}}\gamma }}}$. Но для точек ${{\tilde {\eta }}_{0}}$ и ${{\tilde {\eta }}_{{\text{a}}}}$ высоты максимумов равны ${{G}_{{\max {\text{a}}}}}$ и ${{G}_{{\max 0}}}$. Ширина всех пиков равна приблизительно 3.5 kT, а например, положение максимума в окрестности точки ${{\tilde {\eta }}_{{0\gamma }}}$ дается выражением ${{\tilde {\eta }}_{{\max 0\gamma }}} \approx {{\tilde {\eta }}_{{0\gamma }}} - kT\ln [{{(2 + d)} \mathord{\left/ {\vphantom {{(2 + d)} {(1 + d)}}} \right. \kern-0em} {(1 + d)}}]$. В результате ${{\tilde {\eta }}_{{\max 0\gamma }}} \approx {{\tilde {\eta }}_{{0\gamma }}}$ при d $ \gg $ 1. В соответствии с формулой (П7), график функции G(Δ(eξη)) при Vb = –1 В получается зеркальным отражением относительно прямой Δ(eξη) = 0.
Таким образом, при Er ≈ 0 положения максимумов функций G(Vb) и G(η) соответствуют пересечению уровнями энергии εb и εa уровней Ферми левого и правого электродов. В связи с этим представляет интерес сравнение поведения функций G(η) и j0(η) при d = 1. График зависимости функции j0(η) симметричен относительно точки eξηsymm = = $e\xi {{\eta }_{{{\text{symm}}}}} = (0.5 - \gamma )e{{V}_{{\text{b}}}} + U/2 + kT\ln (2)$ [27]. Ток j0(η) также можно приблизительно представить как сумму токов $j_{\infty }^{0}(\eta )$ и $j_{a}^{0}(\eta )$ при U $ \gg $ kT и небольших значениях Vb (см. формулы (П1), (П2) и рис. 1а в работе [25]). Эти токи даются, например, формулой (35) работы [26] и имеют максимальные значения в точках $e\xi \eta _{{{\text{max}}\infty }}^{0} = (0.5 - \gamma )e{{V}_{{\text{b}}}} + kT\ln (2)$ и $e\xi \eta _{{{\text{max,a}}}}^{0} = (0.5 - \gamma )e{{V}_{{\text{b}}}} + U + 1.5kT\ln (2)$. Эти точки, физический смысл которых обсуждается в Приложении, не совпадают с точками максимумов функции G(η), которые имеют абсолютно другой физический смысл. Но, используя формулу (35) работы [26], можно показать, что положения максимумов производных по Vb от функций $j_{\infty }^{0}$ и $j_{a}^{0}$ при $\left| {e{{V}_{b}}} \right| \gg kT$ дают именно точки максимумов функции G(η), как и должно быть. С увеличением напряжения смещения кривые, соответствующие $j_{\infty }^{0}(\eta )$ и $j_{a}^{0}(\eta )$, начинают перекрываться (см. рис. 1б в [25]), так как ширина каждой из кривых при положительном Vb равна eVb и при U ≈ eVb уже имеет место почти полное перекрывание. Перекрывание заведомо происходит в случае параметров, использованных при построении рис. 2б настоящей работы, так как при этом полный ток имеет единственный максимум, расположенный в точке $e\xi {{\eta }_{{{\text{symm}}}}}$. Однако по-прежнему этот ток приблизительно равен сумме токов $j_{\infty }^{0}(\eta )$ и $j_{a}^{0}(\eta )$. Точка $e\xi {{\eta }_{{{\text{symm}}}}}$ также не совпадает с точками максимумов функции G(η), которые, тем не менее, получаются при вычислении производной ${{\partial {{j}^{0}}} \mathord{\left/ {\vphantom {{\partial {{j}^{0}}} {\partial {{V}_{{\text{b}}}}}}} \right. \kern-0em} {\partial {{V}_{{\text{b}}}}}} \approx {{\partial (j_{\infty }^{0} + j_{{\text{a}}}^{{\text{0}}})} \mathord{\left/ {\vphantom {{\partial (j_{\infty }^{0} + j_{{\text{a}}}^{{\text{0}}})} {\partial V}}} \right. \kern-0em} {\partial V}}$.
Предел большой энергии реорганизации
Этот предел часто используется для интерпретации экспериментальных данных. В этом случае в показателе экспоненты формуле (5) для константы скорости удерживается только линейный по $\Delta F_{{ji}}^{a}$ член [24]. Выражение для тока jlarge в этом пределе при произвольных d и Ueff дается формулой (41) работы [26]. При Ueff > Ueff* = 2kTln(2) [25] и умеренных значениях Vb, при которых нет перекрывания пиков, jlarge(η) также можно приближенно представить в виде суммы $j_{\infty }^{{{\text{large}}}}(\eta )$ и $j_{{\text{a}}}^{{{\text{large}}}}(\eta )$ (см. Приложение). Выражения для токов $j_{\infty }^{{{\text{large}}}}$ (при условии Er $ \gg $ $\left| {\Delta F_{{01}}^{\alpha }} \right|$, $\left| {\Delta F_{{10}}^{\alpha }} \right|$) и $j_{{\text{a}}}^{{{\text{large}}}}$ (при условии Er$ \gg $ $\left| {\Delta F_{{12}}^{\alpha }} \right|$, $\left| {\Delta F_{{21}}^{\alpha }} \right|$) при любых d даются формулой (46) работы [26]. Ниже для определенности рассматриваются только случаи d = 1 и d $ \gg $ exp(eVb/2kT). Для этих случаев формула для $j_{{\infty {\text{(a)}}}}^{{{\text{large}}}}$ имеет простой вид и является обобщением формулы (43) работы [25]:
(11)
$\begin{gathered} j_{{\infty {\text{(a)}}}}^{{{\text{large}}}} = \\ = \frac{{e{{\Gamma }^{{\text{L}}}}{{{({{\pi kT} \mathord{\left/ {\vphantom {{\pi kT} {{{E}_{{\text{r}}}}}}} \right. \kern-0em} {{{E}_{{\text{r}}}}}})}}^{{1/2}}}\exp ({{ - {{E}_{{\text{r}}}}} \mathord{\left/ {\vphantom {{ - {{E}_{{\text{r}}}}} {4kT}}} \right. \kern-0em} {4kT}}){\text{sh}}({{e{{V}_{{\text{b}}}}c} \mathord{\left/ {\vphantom {{e{{V}_{{\text{b}}}}c} {2kT}}} \right. \kern-0em} {2kT}})}}{{{{2}^{{1/2}}}\hbar {\text{ch}}\{ {{[e\xi (\eta - \eta _{{\max \infty ({\text{a}})}}^{{{\text{large}}}})]} \mathord{\left/ {\vphantom {{[e\xi (\eta - \eta _{{\max \infty ({\text{a}})}}^{{{\text{large}}}})]} {2kT}}} \right. \kern-0em} {2kT}}\} }}, \\ \end{gathered} $(12)
$\begin{gathered} e\xi \eta _{{\max \infty }}^{{{\text{large}}}}({{V}_{{\text{b}}}}) = (c - \gamma )e{{V}_{{\text{b}}}}, \\ e\xi \eta _{{\max ,{\text{a}}}}^{{{\text{large}}}}({{V}_{{\text{b}}}}) = (c - \gamma )e{{V}_{{\text{b}}}} + {{U}_{{{\text{eff}}}}} + 2kT\ln (2). \\ \end{gathered} $Физический смысл формул (11) и (12) для общего случая обсуждается в Приложении. Ширина пиков токов $j_{\infty }^{{{\text{large}}}}(\eta )$ и $j_{{\text{a}}}^{{{\text{large}}}}(\eta )$ одинакова, не зависит от d [26] и приблизительно равна 0.13 эВ/eξ [25].
Если Ueff = 0 (или U = 2Er), то выражение для тока в пределе больших Er также имеет вид, который дается формулой (11), но с дополнительным множителем 21/2 в числителе и заменой $e\xi \eta _{{\max \infty ({\text{a}})}}^{{{\text{large}}}}$ на $e\xi \eta _{{\max \infty }}^{{{\text{large}}}} + kT\ln (2)$. Формулу (11) можно также получить из формулы (П3). Например, учитывая только линейные по ε члены в экспонентах в формуле (П5), находим, что в пределе больших Ueff и Er
(13)
$A_{\infty }^{{{\text{large}}}}(\varepsilon ) = \frac{{{{{\text{2}}}^{{{\text{1/2}}}}}\exp ({{ - {{E}_{{\text{r}}}}} \mathord{\left/ {\vphantom {{ - {{E}_{{\text{r}}}}} {4kT}}} \right. \kern-0em} {4kT}}){\text{ch}}[{{(\varepsilon + ceV)} \mathord{\left/ {\vphantom {{(\varepsilon + ceV)} {2kT}}} \right. \kern-0em} {2kT}}]}}{{{{{(4\pi {{E}_{{\text{r}}}}kT)}}^{{1/2}}}{\text{ch}}[{{e\xi (\eta - \eta _{{{\text{max}}\infty }}^{{{\text{large}}}})} \mathord{\left/ {\vphantom {{e\xi (\eta - \eta _{{{\text{max}}\infty }}^{{{\text{large}}}})} {2kT}}} \right. \kern-0em} {2kT}}]}}.$Из формулы (13) следует, что функция $A_{\infty }^{{{\text{large}}}}(\varepsilon )$ резко убывает, когда абсолютная величина разности $e\xi (\eta - \eta _{{{\text{max}}\infty }}^{{{\text{large}}}})$ становится больше kT. Этот факт объясняет малую ширину пиков тока jlarge(η), имеющую порядок kT, по сравнению со случаем Er = 0.
Используя формулы (47)–(48) работы [26], запишем выражения для вероятностей Pn в пределе больших Er в виде, который позволяет выявить ряд важных предельных случаев:
(14)
$\begin{gathered} {{P}_{0}} = {1 \mathord{\left/ {\vphantom {1 {\tilde {Z}}}} \right. \kern-0em} {\tilde {Z}}};\,\,\,\,{{P}_{1}} = {{2\exp \{ {{[e\xi \tilde {\eta } - (c - \gamma )eV]} \mathord{\left/ {\vphantom {{[e\xi \tilde {\eta } - (c - \gamma )eV]} {kT}}} \right. \kern-0em} {kT}}\} } \mathord{\left/ {\vphantom {{2\exp \{ {{[e\xi \tilde {\eta } - (c - \gamma )eV]} \mathord{\left/ {\vphantom {{[e\xi \tilde {\eta } - (c - \gamma )eV]} {kT}}} \right. \kern-0em} {kT}}\} } {\tilde {Z}}}} \right. \kern-0em} {\tilde {Z}}}; \\ {{P}_{2}} = 1 - {{P}_{0}} - {{P}_{1}}, \\ \tilde {Z} = 1 + 2\exp \{ {{[e\xi \tilde {\eta } - (c - \gamma )eV]} \mathord{\left/ {\vphantom {{[e\xi \tilde {\eta } - (c - \gamma )eV]} {kT}}} \right. \kern-0em} {kT}}\} + \\ + \,\,\exp \{ 2{{[e\xi \tilde {\eta } - (c - \gamma )eV - {{{{U}_{{{\text{eff}}}}}} \mathord{\left/ {\vphantom {{{{U}_{{{\text{eff}}}}}} 2}} \right. \kern-0em} 2}]} \mathord{\left/ {\vphantom {{[e\xi \tilde {\eta } - (c - \gamma )eV - {{{{U}_{{{\text{eff}}}}}} \mathord{\left/ {\vphantom {{{{U}_{{{\text{eff}}}}}} 2}} \right. \kern-0em} 2}]} {kT}}} \right. \kern-0em} {kT}}\} . \\ \end{gathered} $Формула (14) интересна тем, что она дает не только вероятности в пределе больших Er для параметров c, определенных выше, но и равновесные вероятности, которые не зависят от конкретных выражений для констант скоростей и поэтому справедливы для любых значений Er. Так, при Vb = 0 получаем равновесные вероятности Гиббса. При d $ \ll $ 1 (c = 0) и d $ \gg $ exp(eVb/2kT (c = 1) формула (14) дает равновесные вероятности для случаев, когда РГ находится как бы в равновесии с левым и правым электродами (реально равновесие отсутствует, так как туннельный ток не равен нулю). Отметим, что при вычислении равновесных вероятностей по формуле (14) учитывается электростатическое взаимодействие электронов РГ с растворителем. Но так как в формуле (2) для εb в качестве слагаемого входит Er, то в формулы (14) энергия реорганизации не входит. Случай, когда c = 1, будем далее условно называть случаем равновесия РГ с правым электродом. Из формулы (14) следует, что при ${{U}_{{{\text{eff}}}}} \gg kT$ и возрастании η вероятность P0 экспоненциально уменьшается от 1 до 0, а вероятность P1 экспоненциально увеличивается от 0 до 1 в окрестности точки eξη = (c – γ)eVb + $ + \,\,kT\ln (2)$ в интервале порядка kT. Например, из формулы (14) находим, что в пределе Ueff → ∞ ${{P}_{{0\infty }}}\, = \,{1 \mathord{\left/ {\vphantom {1 {\{ 1\, + \,\exp [{{(e\xi \eta - (c - \gamma )e{{V}_{{\text{b}}}})} \mathord{\left/ {\vphantom {{(e\xi \eta - (c - \gamma )e{{V}_{{\text{b}}}})} {kT}}} \right. \kern-0em} {kT}}]\} }}} \right. \kern-0em} {\{ 1\, + \,\exp [{{(e\xi \eta - (c - \gamma )e{{V}_{{\text{b}}}})} \mathord{\left/ {\vphantom {{(e\xi \eta - (c - \gamma )e{{V}_{{\text{b}}}})} {kT}}} \right. \kern-0em} {kT}}]\} }}$, ${{P}_{{1\infty }}} = 1 - {{P}_{{0\infty }}}$. В то же время вероятность P1 экспоненциально уменьшается от 1 до 0, а вероятность P2 экспоненциально возрастает от 0 до 1 в окрестности точки $e\xi \eta = (c - \gamma )e{{V}_{{\text{b}}}} + {{U}_{{{\text{eff}}}}} + kT\ln (2)$ также в интервале порядка kT. При этом абсолютные значения производных ${{\partial {{P}_{n}}} \mathord{\left/ {\vphantom {{\partial {{P}_{n}}} {\partial (e\xi \eta )}}} \right. \kern-0em} {\partial (e\xi \eta )}}$ равны 1/(4kT) и очень велики. Отметим, что ${{\partial {{P}_{n}}} \mathord{\left/ {\vphantom {{\partial {{P}_{n}}} {\partial (e{{V}_{{\text{b}}}})}}} \right. \kern-0em} {\partial (e{{V}_{{\text{b}}}})}} = $ ${{ - (c - \gamma )\partial {{P}_{n}}} \mathord{\left/ {\vphantom {{ - (c - \gamma )\partial {{P}_{n}}} {\partial (e\xi \eta )}}} \right. \kern-0em} {\partial (e\xi \eta )}}$.
Выражения для ДП получаются непосредственно из формулы (11). Например, в окрестности точки $e\xi \eta _{{\max \infty }}^{{{\text{large}}}}$ ДП $G_{\infty }^{{{\text{large}}}} = {{\partial j_{\infty }^{{{\text{large}}}}} \mathord{\left/ {\vphantom {{\partial j_{\infty }^{{{\text{large}}}}} {\partial {{V}_{{\text{b}}}}}}} \right. \kern-0em} {\partial {{V}_{{\text{b}}}}}}$ в безразмерной форме имеет вид:
(15)
$\begin{gathered} G_{\infty }^{{{\text{large}}}} = {{2}^{{ - 1/2}}}{{({{\pi kT} \mathord{\left/ {\vphantom {{\pi kT} {{{E}_{{\text{r}}}}}}} \right. \kern-0em} {{{E}_{{\text{r}}}}}})}^{{1/2}}}\exp ({{ - {{E}_{{\text{r}}}}} \mathord{\left/ {\vphantom {{ - {{E}_{{\text{r}}}}} {4kT}}} \right. \kern-0em} {4kT}}) \times \\ \times \,\,\left\{ {\frac{{c{\text{ch(}}ce{{{{V}_{{\text{b}}}}} \mathord{\left/ {\vphantom {{{{V}_{{\text{b}}}}} {2kT}}} \right. \kern-0em} {2kT}})}}{{{\text{ch\{ }}{{{\text{[}}e\xi \eta + (\gamma - c)e{{V}_{{\text{b}}}}]} \mathord{\left/ {\vphantom {{{\text{[}}e\xi \eta + (\gamma - c)e{{V}_{{\text{b}}}}]} {2kT}}} \right. \kern-0em} {2kT}}\} }} + } \right. \\ + \,\,\left. {\frac{{\left. {(c - \gamma ){\text{sh(}}{{ce{{V}_{{\text{b}}}}} \mathord{\left/ {\vphantom {{ce{{V}_{{\text{b}}}}} {2kT}}} \right. \kern-0em} {2kT}}){\text{sh\{ }}{{{\text{[}}e\xi \eta + (\gamma - c)e{{V}_{{\text{b}}}}]} \mathord{\left/ {\vphantom {{{\text{[}}e\xi \eta + (\gamma - c)e{{V}_{{\text{b}}}}]} {2kT}}} \right. \kern-0em} {2kT}}\} } \right\}}}{{{\text{c}}{{{\text{h}}}^{{\text{2}}}}{\text{\{ }}{{{\text{[}}e\xi \eta + (\gamma - c)e{{V}_{{\text{b}}}}]} \mathord{\left/ {\vphantom {{{\text{[}}e\xi \eta + (\gamma - c)e{{V}_{{\text{b}}}}]} {2kT}}} \right. \kern-0em} {2kT}}\} }}} \right\}. \\ \end{gathered} $Из формулы (15) следует, что, в отличие от случая Er ≈ 0, ДП $G_{\infty }^{{{\text{large}}}}$ при c = γ в точности пропорциональна току $j_{\infty }^{{{\text{large}}}}$, поэтому ДП максимальна в точке $e\xi \eta _{{\max \infty }}^{{{\text{large}}}}$. Аналогично вклад в G, равный ${{\partial j_{{\text{a}}}^{{{\text{large}}}}} \mathord{\left/ {\vphantom {{\partial j_{{\text{a}}}^{{{\text{large}}}}} {\partial {{V}_{{\text{b}}}}}}} \right. \kern-0em} {\partial {{V}_{{\text{b}}}}}}$, максимален в точке $e\xi \eta _{{\max ,{\text{a}}}}^{{{\text{large}}}}$. Таким образом, ДП максимальна когда средние значения флуктуирующих уровней εb и εа лежат в центре энергетического окна электрохимического транзистора. Из формулы (15) следует, что поправка первого порядка по c – γ к значению ДП в точках $e\xi \eta _{{\max \infty }}^{{{\text{large}}}}$ и $e\xi \eta _{{\max ,{\text{a}}}}^{{{\text{large}}}}$ отсутствует. Однако поправка первого порядка по c – γ к положению максимумов ДП отлична от нуля и равна 2kTarcsh[(c – γ) × × th(ceVb/2kT)/c] ≈ 2kT(c – γ)th(ceVb/2kT)/c при малых значениях (c – γ)/c. При eVb$ \gg $ kT поправка равна 2kT(c – γ)/c = 1.2kT ≈ 0.039 эВ при d = 1, γ = = 0.2, что много меньше, чем $e\xi \eta _{{\max \infty }}^{{{\text{large}}}}$ и $e\xi \eta _{{\max ,{\text{a}}}}^{{{\text{large}}}}$. Максимальное значение ДП с учетом этой поправки получается из максимального значения ДП без учета этой поправки умножением на множитель 1 + [(c – γ)th(ceVb/2kT)/c]2/2.
В электрохимическом транзисторе энергия реорганизации может изменяться в пределах от 0.1 до 0.5 эВ [23]. Ниже для определенности рассматриваются варианты, когда Er = 0.25 эВ и Er = 0.5 эВ. Область, в которой применимо приближение больших Er, можно оценить, используя рис. 1а работы [26]. На этом рисунке точная константа скорости как функция ΔF/Er приблизительно совпадает с константой скорости, вычисленной в приближении больших Er, при значениях ΔF/Er , меньших или порядка 0.1 для Er = 0.5 эВ, что в точке максимумов ДП соответствует Vb ≤ 0.1 В. ДП как функция перенапряжения для Vb = 0.1 В, Ueff = 0.5 эВ, d = 1 и Er = 0.5 эВ, вычисленная с использованием точной формулы (4) для тока, представлена на рис. 3а при γ = 0.5 и γ = 0.2. При этом точные значения ДП в полностью неадиабатическом пределе и значения ДП, полученные в приближении большой энергии реорганизации, практически совпадают. Из рис. 3а видно, что для обоих значений γ ДП состоит из двух ярко выраженных пиков. При тех же параметрах, но d = 100 ДП в точке максимума больше, чем ДП при d = 1, приблизительно на 2ch(2)/ch(1) ≈ 5. Максимальное значение ДП при d = 1 и γ = 0.2 больше, чем при γ = 0.5, и может быть получено с использованием приведенной выше оценки.
РЕЗУЛЬТАТЫ РАСЧЕТА ДИФФЕРЕНЦИАЛЬНОЙ ПРОВОДИМОСТИ ДЛЯ ПРОИЗВОЛЬНЫХ ЗНАЧЕНИЙ ПАРАМЕТРОВ ЭЛЕКТРОХИМИЧЕСКОГО ТРАНЗИСТОРА И ИХ ОБСУЖДЕНИЕ
Структура ДП, характерная для предела больших Er и включающая два пика от ${{G}_{\infty }}$ и ${{G}_{{\text{a}}}}$ (или один пик в случае перекрывания ${{G}_{\infty }}$ и ${{G}_{{\text{a}}}}$), сохраняется в практически важной области, в которой значения $\left| {\Delta F_{{ji}}^{a}} \right|$ в окрестности точек максимумов ДП меньше энергии реорганизации (или eVb/2 < Er). Это хорошо видно из рис. 3б, где представлена ДП как функция перенапряжения при Vb = 0.9 В и прочих параметрах, использованных при построении рис. 3а. Указанный эффект связан с тем, что при $\left| {\Delta F_{{ji}}^{a}} \right|$ < Er электронный перенос имеет активационный характер [34] и близок по физическому механизму к случаю, соответствующему пределу больших Er. Например, используя формулы (9) и (10) работы [34], можно показать, что точка ΔF = Er является точкой перегиба точной константы скорости k(ΔF) полностью неадиабатического электронного переноса. Поэтому при ΔF < Er точная константа скорости достаточно сильно возрастает с ростом ΔF (хотя и в меньшей степени, чем в пределе больших Er, см. рис. 1а работы [26]). Но при ΔF > Er возрастание становится достаточно слабым с последующим выходом на асимптотическое значение.
Однако максимальная величина ДП вне предела больших Er (но при $\left| {\Delta F_{{ji}}^{a}} \right|$ < Er) значительно отличается от соответствующих значений, которые можно получить с использованием формулы (15). Например для случая, представленного на рис. 3б, максимальное значение ДП составляет примерно 0.04, тогда как по формуле (15) получается сильно завышенное значение, примерно равное 3.9 и отличающееся от точного на два порядка. Получить более точную оценку максимального значения ДП ${{G}_{\infty }}$ можно, используя формулу (39) работы [26], которая, в пределе больших Ueff, справедлива для любых Er. При d = 1 в точке максимума тока j∞ с точностью до членов порядка kT имеем $\Delta F_{{10}}^{{\text{L}}}$ ≈ eVb/2 и $\Delta F_{{10}}^{{\text{R}}}$ ≈ −eVb /2. Тогда
(16)
${{j}_{{\infty \max }}}\, \approx \,j_{{\infty {\text{max}}}}^{{{\text{large}}}}\exp [{{ - {{{({{e{{V}_{{\text{b}}}}} \mathord{\left/ {\vphantom {{e{{V}_{{\text{b}}}}} 2}} \right. \kern-0em} 2})}}^{2}}} \mathord{\left/ {\vphantom {{ - {{{({{e{{V}_{{\text{b}}}}} \mathord{\left/ {\vphantom {{e{{V}_{{\text{b}}}}} 2}} \right. \kern-0em} 2})}}^{2}}} {4{{E}_{{\text{r}}}}kT}}} \right. \kern-0em} {4{{E}_{{\text{r}}}}kT}}]2I{{({{e{{V}_{{\text{b}}}}} \mathord{\left/ {\vphantom {{e{{V}_{{\text{b}}}}} 2}} \right. \kern-0em} 2})} \mathord{\left/ {\vphantom {{({{e{{V}_{{\text{b}}}}} \mathord{\left/ {\vphantom {{e{{V}_{{\text{b}}}}} 2}} \right. \kern-0em} 2})} \pi }} \right. \kern-0em} \pi },$(17)
$\begin{gathered} {{G}_{{\infty \max }}} \approx G_{{\infty \max }}^{{{\text{large}}}}\left\{ {\frac{{2I({{e{{V}_{{\text{b}}}}} \mathord{\left/ {\vphantom {{e{{V}_{{\text{b}}}}} 2}} \right. \kern-0em} 2})}}{\pi } - \frac{{e{{V}_{{\text{b}}}}}}{{2{{E}_{{\text{r}}}}}}{\text{th}}\left( {\frac{{e{{V}_{{\text{b}}}}}}{{4kT}}} \right)} \right. \times \\ \times \,\,\left. {\left[ {\frac{{2I({{e{{V}_{{\text{b}}}}} \mathord{\left/ {\vphantom {{e{{V}_{{\text{b}}}}} 2}} \right. \kern-0em} 2})}}{\pi } - \frac{{{{\pi }^{2}}kT}}{{2{{E}_{{\text{r}}}}}}} \right]\exp \left( { - \frac{{{{{(e{{V}_{{\text{b}}}})}}^{2}}}}{{16{{E}_{{\text{r}}}}kT}}} \right)} \right\}. \\ \end{gathered} $Используя формулу (17), получаем, что для сплошной кривой на рис. 3б Gmax∞ ≈ 0.03. Если учесть, что для этого случая имеет место довольно сильное перекрывание двух пиков, то существует некоторый вклад от Ga в Gmax∞, поэтому полученная оценка находится в хорошем согласии со значением Gmax∞ ≈ 0.04. Если d $ \gg $ 1, то ввиду того, что в формулах для $\Delta F_{{ji}}^{a}$ следует положить с = 1, имеем eVb > Er, что выходит за пределы рассматриваемой области.
Для параметров, использованных при построении рис. 3б, основной пик и пик кулоновской блокады не перекрываются полностью. Как указывалось выше, значение Vb, при котором происходит практически полное перекрывание пиков, можно оценить из условия eξW(Vb) ≈ Ueff. В работе [26] показано, что при малых Er$ \ll $ eVb ширина кривых токов j∞(η) и ja(η) равна приблизительно eVb – 2Er. Поэтому при eVb = 1.5 эВ, Er = 0.5 эВ ширину можно оценить как eξW ≈ eVb/3. Действительно, численные расчеты показывают, что при Ueff = 0.5 эВ практически полное перекрывание происходит именно при eVb = 1.5 эВ. Так как в пределе больших Er ширина имеет порядок kT, а при Er ≈ 0 имеем eξW ≈ eVb, то для промежуточных значений Er вблизи eVb ≈ 1 эВ можно приблизительно принять ширину равной eVb/3. Тогда для случая, когда Ueff = 0.3 эВ и γ = 0.5, практически полное перекрывание двух ветвей ДП происходит при eVb ≈ 0.9 эВ < 2Er. Этот случай, когда ДП имеет только один максимум в точке eξηsymm при γ = 0.5, представлен на рис. 3в. С другой стороны, этот случай интересен тем, что при γ = 0.2 имеет место лишь частичное перекрывание, поскольку оценка eξW ≈ eVb/3 является приближенной. Отметим, что функции G(Δ(eξη)), приведенные на рис. 3а–3в для γ = 0.5, симметричны относительно оси Δ(eξη) = 0, что следует из формулы (П8). Отметим также, что графики, аналогичные представленным на рис. 3а–3в, можно получить и при Er = 0.25 эВ, но при этом напряжение Vb для каждого из рисунков следует уменьшить в 2 раза.
Если Ueff = 0, то при eVb < 2Er кривые зависимости ДП от перенапряжения также имеют единственный максимум в точке eξηsymm.
Таким образом, в отличие от предела Er ≈ 0, в котором пики ДП были обусловлены пересечением уровней εb и εa с $\varepsilon _{{\text{F}}}^{{\text{L}}}$ или $\varepsilon _{{\text{F}}}^{{\text{R}}}$, в случае $\left| {\Delta F_{{ji}}^{a}} \right|$ < Er и в отсутствие перекрывания пики ДП, указывающие на область наибольшего изменения туннельного тока с изменением напряжения смещения, находятся вблизи точек $e\xi \eta _{{\max \infty }}^{{{\text{large}}}}$ и $e\xi \eta _{{\max ,{\text{a}}}}^{{{\text{large}}}}$ (физический смысл точекξηmax∞ и ξηmax,a обсуждается в Приложении). Если же пики G∞ и Ga перекрываются или существует единственный максимум (при Ueff < Ueff*), то ДП принимает максимальные значения в окрестности точки eξηsymm.
Область $\left| {\Delta F_{{ji}}^{a}} \right|$ > Er является областью перехода от предела больших Er к случаю Er ≈ 0. В этой промежуточной области для получения аналитических оценок для ДП необходимо непосредственно использовать формулу (П3) для тока и найти производные по Vb от вероятностей Pn и спектральных функций Aν(ε). Анализ упрощается, если ширина спектральных функций много больше kT (для этого достаточно рассмотреть случай Er > kT). В этом случае спектральная функция “не чувствует” структуру фермиевских функций вблизи ферми-уровней рабочих электродов, поэтому интегрирование от –∞ до ∞ в формуле (П3) можно заменить интегрированием от – eVb до 0. Используя формулу (53) работы [25], находим, что безразмерную ДП можно представить в виде
(18)
$\begin{gathered} G = \frac{{4kTd}}{{(1 + d)}}\sum\limits_\nu {\left\{ {\frac{{{{P}_{\nu }}(\eta ,{{V}_{{\text{b}}}})}}{{{{{(4\pi {{E}_{{\text{r}}}}kT)}}^{{1/2}}}}} \times } \right.} \\ \times \,\,\left[ {(1 - \gamma )\exp \left[ { - \frac{{{{{(e{{V}_{{\text{b}}}}\, + \,{{E}_{\nu }})}}^{2}}}}{{4{{E}_{{\text{r}}}}kT}}} \right] + \gamma \exp \left[ { - \frac{{E_{\nu }^{2}}}{{4{{E}_{{\text{r}}}}kT}}} \right]} \right] + \\ + \,\,\frac{{\partial {{P}_{\nu }}(\eta ,{{V}_{{\text{b}}}})}}{{\partial (e{{V}_{{\text{b}}}})}}\left. {\int\limits_{ - e{{V}_{{\text{b}}}}}^0 {{{A}_{\nu }}(\varepsilon ){\text{d}}\varepsilon } } \right\}, \\ \end{gathered} $(19)
$e\xi {{\tilde {\eta }}_{{{\text{ox}}}}} = {{E}_{{\text{r}}}} + (1 - \gamma )e{{V}_{{\text{b}}}},\,\,\,\,e\xi {{\tilde {\eta }}_{{{\text{ox,}}\gamma }}} = {{E}_{{\text{r}}}} - \gamma e{{V}_{{\text{b}}}},$(20)
$\begin{gathered} e\xi {{{\tilde {\eta }}}_{{{\text{red}}}}} = - {{E}_{{\text{r}}}} + (1 - \gamma )e{{V}_{{\text{b}}}}, \\ e\xi {{{\tilde {\eta }}}_{{{\text{red,}}\gamma }}} = - ({{E}_{{\text{r}}}} + \gamma e{{V}_{{\text{b}}}}), \\ \end{gathered} $(21)
$\begin{gathered} e\xi {{{\tilde {\eta }}}_{{{\text{ox,a}}}}} = {{E}_{{\text{r}}}} + (1 - \gamma )e{{V}_{{\text{b}}}} + {{U}_{{{\text{eff}}}}}, \\ e\xi {{{\tilde {\eta }}}_{{{\text{ox,a}}\gamma }}} = {{E}_{{\text{r}}}} - \gamma e{{V}_{{\text{b}}}} + {{U}_{{{\text{eff}}}}}, \\ \end{gathered} $(22)
$\begin{gathered} e\xi {{{\tilde {\eta }}}_{{{\text{red,a}}}}} = - {{E}_{{\text{r}}}} + (1 - \gamma )e{{V}_{{\text{b}}}} + {{U}_{{{\text{eff}}}}}, \\ e\xi {{{\tilde {\eta }}}_{{{\text{red,a}}\gamma }}} = - ({{E}_{{\text{r}}}} + \gamma e{{V}_{{\text{b}}}}) + {{U}_{{{\text{eff}}}}}, \\ \end{gathered} $Хотя при Er ≈ 0 формула (18) неприменима, точки максимумов ДП, определяемые формулами (19)–(22) имеют физический смысл, схожий с физическим смыслом точек $e\xi {{\tilde {\eta }}_{{0\gamma }}}$, $e\xi {{\tilde {\eta }}_{{{\text{a}}\gamma }}}$, $e\xi {{\tilde {\eta }}_{0}}$ и $e\xi {{\tilde {\eta }}_{{\text{a}}}}$, рассмотренных для случая Er ≈ 0. В частности, при Er = 0, получаем равенства $e\xi {{\tilde {\eta }}_{{0\gamma }}} = e\xi {{\tilde {\eta }}_{{{\text{ox,}}\gamma }}} = e\xi {{\tilde {\eta }}_{{{\text{red}},\gamma }}}$, $e\xi {{\tilde {\eta }}_{{{\text{a}}\gamma }}} = e\xi {{\tilde {\eta }}_{{{\text{ox,a}}\gamma }}} = e\xi {{\tilde {\eta }}_{{{\text{red,a}}\gamma }}}$, $e\xi {{\tilde {\eta }}_{0}} = e\xi {{\tilde {\eta }}_{{{\text{ox}}}}} = e\xi {{\tilde {\eta }}_{{{\text{red}}}}}$ и $e\xi {{\tilde {\eta }}_{{\text{a}}}} = e\xi {{\tilde {\eta }}_{{{\text{ox,a}}}}} = e\xi {{\tilde {\eta }}_{{{\text{red,a}}}}}$. Отличие заключается в том, что при Er > 0 появляются вклады в ДП от точек, связанных с пересечением уровней εb,red и εa,red с уровнями Ферми левого и правого электродов.
Из формулы (18) также находим, что ширина всех пиков ДП G(eξη) одинакова и также равна WА, где ширина WА определена в Приложении и равна примерно 0.37 эВ для Er = 0.5 эВ и 0.26 эВ для Er = 0.25 эВ. Очевидно, что ДП имеет максимумы в точках $e\xi {{\tilde {\eta }}_{\nu }}$ и $e\xi {{\tilde {\eta }}_{{\nu ,\gamma }}}$только в случаях, если соответствующие вероятности Pν в этих точках отличны от нуля, слабо изменяются при изменении перенапряжения и если пики не перекрываются.
Отметим, что вероятности Pν практически равны нулю в приближении большой энергии реорганизации, так как в этом случае абсолютные значения $e\xi {{\tilde {\eta }}_{\nu }}$ и $e\xi {{\tilde {\eta }}_{{\nu ,\gamma }}}$ имеют порядок Er. Поэтому главный вклад в ДП (формула (18)) дают окрестности точек $e\xi \eta _{{\max \infty }}^{{{\text{large}}}}$ и $e\xi \eta _{{\max ,{\text{a}}}}^{{{\text{large}}}}$. В результате пик ДП определяется формулой (15). Это же имеет место при eVb/2 < Er, поскольку при увеличении Vb и выходе из предела большой энергии реорганизации вероятности Pν остаются малыми, а производные ${{\partial {{P}_{\nu }}} \mathord{\left/ {\vphantom {{\partial {{P}_{\nu }}} {\partial (e\xi \eta )}}} \right. \kern-0em} {\partial (e\xi \eta )}}$ по-прежнему велики в окрестности точек $e\xi \eta _{{\max \infty }}^{{{\text{large}}}}$ и $e\xi \eta _{{\max ,{\text{a}}}}^{{{\text{large}}}}$. Это показано на рис. 4а, где зависимости Pn от $e\xi \eta $ приведены для случая Vb = 0.5 В, где eVb/2 < Er. К тому же соответствующие максимумы в точках $e\xi {{\tilde {\eta }}_{\nu }}$ и $e\xi {{\tilde {\eta }}_{{\nu ,\gamma }}}$ перекрываются. Тем не менее, на левой и правой ветвях кривой на рис. 3б, отвечающей значению γ = 0.5, видны “плечи”, обусловленные, например, точками $e\xi {{\tilde {\eta }}_{{{\text{ox,}}\gamma }}} = 0.05\;{\text{эВ}}$ и $e\xi {{\tilde {\eta }}_{{{\text{red}}}}} = - 0.05\;{\text{эВ}}$. При дальнейшем росте eVb производные $\left| {{{\partial {{P}_{\nu }}} \mathord{\left/ {\vphantom {{\partial {{P}_{\nu }}} {\partial (e\xi \eta )}}} \right. \kern-0em} {\partial (e\xi \eta )}}} \right|$ уменьшаются, становятся более гладкими (что видно из сравнения рис. 4а и рис. 4б), и, окончательно, при Er ≈ 0, максимальные значения $\left| {{{\partial {{P}_{\nu }}} \mathord{\left/ {\vphantom {{\partial {{P}_{\nu }}} {\partial (e\xi \eta )}}} \right. \kern-0em} {\partial (e\xi \eta )}}} \right|$ имеют место уже в точках $e\xi {{\tilde {\eta }}_{\nu }}$ и $e\xi {{\tilde {\eta }}_{{\nu ,\gamma }}}$.
Рис. 4.
Зависимость вероятностей Pn заполнения электронного уровня редокс-группы от Δ(eξη) = = eξη − kTln(2) − Ueff/2 для параметров Er = 0.5 эВ, Ueff = 0.5 эВ, γ = 0.5 и kT = 0.025 эВ. (а) Vb = 0.5 В, ΓR = ΓL; (б) Vb = 1.5 В, ΓR = ΓL; (в) Vb = 1.5 В, ΓR = = 100ΓL. Сплошная линия: P1; пунктирная линия: P0; линия из точек: P2.

Рисунки 4а и 4б соответствуют случаю γ = 0.5 и d = 1. Для этого случая, в соответствии с формулами (13)–(14) работы [27], функции P0(Δ(eξη)) симметричны относительно оси Δ(eξη) = 0, а функции P1(Δ(eξη)) и P2(Δ(eξη)) переходят друг в друга при зеркальном отражении относительно оси Δ(eξη) = 0. На рис. 4в представлены зависимости Pn от $e\xi \eta $ также для γ = 0.5, но d = 100. Из рис. 4в видно, что указанные выше свойства симметрии при γ = 0.5 и d = 100 отсутствуют. Кроме того, несмотря на то, что соответствующее значение Vb достаточно велико, нет эффекта сглаживания, как на рис. 4б. Вместо этого, как и на рис. 4а, имеет место резкое изменение функций Pn(Δ(eξη) в окрестности точек $e\xi \eta _{{\max \infty ({\text{a}})}}^{{{\text{large}}}}$ (формула (12)). Выше отмечалось, что в пределе больших Er для равновесия РГ с правым электродом необходимо выполнение не только условия d $ \gg $ 1, но и условия d $ \gg $ exp(eVb/2kT). Это условие выполняется, например, при Vb ≤ 0.1 В. С другой стороны, можно показать, что для равновесия РГ с правым электродом при Er ≈ 0 достаточно только условия d $ \gg $ 1 независимо от Vb. Поэтому для промежуточных значений Er, Vb и d = 100 имеет место только приближение к равновесию, а рис. 4в качественно описывает такое приближение. Например, максимальная величина безразмерной производной ${{4kT\partial {{P}_{1}}} \mathord{\left/ {\vphantom {{4kT\partial {{P}_{1}}} {\partial (e\xi \eta )}}} \right. \kern-0em} {\partial (e\xi \eta )}}$, равная 1 в случае полного равновесия, при d = 100 начинает зависеть от Er и Vb. Так, для параметров, использованных при построении рис. 4в, эта максимальная величина равна ≈0.38 < 1, но все еще достаточно велика.
Так как вероятности Pn зависят от eξη через комбинацию eξη + γeVb (формула (2)), то графики функций Pn(Δ(eξη) для любого значения γ можно получить из графиков, представленных на рис. 4а–4в, сдвигом на (0.5 – γ)eVb вдоль оси Δ(eξη).
Таким образом, представляет интерес исследование ДП в областях 1 В ≤ Vb ≤ 1.5 В для Er = 0.5 эВ и 0.5 В ≤ Vb ≤ 1. В для Er = 0.25 эВ. На рис. 5а показана зависимость ДП от Δ(eξη) при Er = 0.5 эВ, γ = 0.5, d = 1, Ueff = 0.5 эВ, Vb = 1 и 1.5 эВ. При Vb = = 1 эВ ДП все еще демонстрирует две ветви, связанные с G∞ и Ga. Однако на левой и правой ветвях ДП появляются по два новых максимума, смещенные от центра каждой ветви влево и вправо. Если же использовать формулы (19)–(22), то для каждой ветви имеется только один максимум (для выбранных параметров формально совпадающий с точкой максимума в пределе больших Er), так как $e\xi {{\tilde {\eta }}_{{{\text{red}}}}} - {{{{U}_{{{\text{eff}}}}}} \mathord{\left/ {\vphantom {{{{U}_{{{\text{eff}}}}}} 2}} \right. \kern-0em} 2} = $ $e\xi {{\tilde {\eta }}_{{{\text{ox,}}\gamma }}} - {{{{U}_{{{\text{eff}}}}}} \mathord{\left/ {\vphantom {{{{U}_{{{\text{eff}}}}}} 2}} \right. \kern-0em} 2} = - 0.25\;{\text{эВ}}$ и $e\xi {{\tilde {\eta }}_{{{\text{red,a}}}}} - {{{{U}_{{{\text{eff}}}}}} \mathord{\left/ {\vphantom {{{{U}_{{{\text{eff}}}}}} 2}} \right. \kern-0em} 2} = $ $e\xi {{\tilde {\eta }}_{{{\text{ox,a}}\gamma }}} - {{{{U}_{{{\text{eff}}}}}} \mathord{\left/ {\vphantom {{{{U}_{{{\text{eff}}}}}} 2}} \right. \kern-0em} 2} = 0.25\;{\text{эВ}}$ (для других характерных точек $e\xi {{\tilde {\eta }}_{\nu }}$ и $e\xi {{\tilde {\eta }}_{{\nu ,\gamma }}}$ значения Δ(eξη) лежат в областях, где соответствующие вероятности Pν ≈ 0).
Рис. 5.
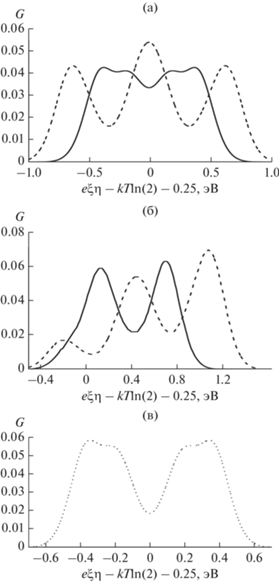
Зависимость безразмерной дифференциальной проводимости от Δ(eξη) = eξη − kTln(2) − Ueff/2 для параметров ΓR = ΓL, Ueff = 0.5 эВ и kT = 0.025 эВ. (а) Er = 0.5 эВ, γ = 0.5; (б) Er = 0.5 эВ, γ = 0.2; (в) Er = = 0.25 эВ, γ = 0.5. Сплошная линия: Vb = 1 В; пунктирная линия: Vb = 1.5 В; линия из точек: Vb = 0.5 В.
Поскольку в этом случае зависимости Pn от $e\xi \eta $ являются достаточно гладкими (см. рис. 4б), то производные ∂Pν/∂(eVb), ∂Pν/∂(eξη) достаточно малы. Тогда из формулы (18) для вероятностей Pν, отличных от нуля, находим поправки к точкам максимумов ДП:
(23)
$\begin{gathered} \delta e\xi {{{\tilde {\eta }}}_{\nu }} = \\ = \frac{{2{{E}_{r}}kT}}{{{{P}_{\nu }}({{{\tilde {\eta }}}_{\nu }},{{V}_{{\text{b}}}})}}\left[ {\frac{{\partial {{P}_{\nu }}({{{\tilde {\eta }}}_{\nu }},{{V}_{{\text{b}}}})}}{{\partial (e\xi \eta )}} - \frac{1}{{1 - \gamma }}\frac{{\partial {{P}_{\nu }}({{{\tilde {\eta }}}_{\nu }},{{V}_{{\text{b}}}})}}{{\partial (e{{V}_{{\text{b}}}})}}} \right], \\ \end{gathered} $(24)
$\begin{gathered} \delta e\xi {{{\tilde {\eta }}}_{{\nu ,\gamma }}} = \\ = \frac{{2{{E}_{r}}kT}}{{{{P}_{\nu }}({{{\tilde {\eta }}}_{{\nu ,\gamma }}},{{V}_{{\text{b}}}})}}\left[ {\frac{{\partial {{P}_{\nu }}({{{\tilde {\eta }}}_{{\nu ,\gamma }}},{{V}_{{\text{b}}}})}}{{\partial (e\xi \eta )}} + \frac{1}{\gamma }\frac{{\partial {{P}_{\nu }}({{{\tilde {\eta }}}_{{\nu ,\gamma }}},{{V}_{{\text{b}}}})}}{{\partial (e{{V}_{{\text{b}}}})}}} \right]. \\ \end{gathered} $При выводе формул (23)–(24) принималось, что производная второго порядка ∂2Pν/∂(eξη)∂(eV) ≈ 0.
С учетом этих поправок к положениям максимумов, полученным выше (±0.25 эВ), максимумы расщепляются. Например, для левой ветви ДП поправки равны ≈–0.16 и 0.08 эВ, что находится в хорошем согласии с графиком, приведенным на рис. 5а.
Для Vb = 1.5 эВ для точек, дающих вклад в ДП, имеем $e\xi {{\tilde {\eta }}_{{{\text{ox,}}\gamma }}} - {{{{U}_{{{\text{eff}}}}}} \mathord{\left/ {\vphantom {{{{U}_{{{\text{eff}}}}}} 2}} \right. \kern-0em} 2} = - 0.5\;{\text{эВ}}$, $e\xi {{\tilde {\eta }}_{{{\text{red}}}}} - {{{{U}_{{{\text{eff}}}}}} \mathord{\left/ {\vphantom {{{{U}_{{{\text{eff}}}}}} 2}} \right. \kern-0em} 2} = $ $ = e\xi {{\tilde {\eta }}_{{{\text{ox,a}}\gamma }}} - {{{{U}_{{{\text{eff}}}}}} \mathord{\left/ {\vphantom {{{{U}_{{{\text{eff}}}}}} 2}} \right. \kern-0em} 2} = 0$ и $e\xi {{\tilde {\eta }}_{{{\text{red,a}}}}} - {{{{U}_{{{\text{eff}}}}}} \mathord{\left/ {\vphantom {{{{U}_{{{\text{eff}}}}}} 2}} \right. \kern-0em} 2} = 0.5\;{\text{эВ}}$. Учет поправок к положениям максимумов левого и правого пиков ДП дает сдвиги на ≈±0.12 эВ, что находится в согласии с соответствующей кривой ДП на рис. 5а. Максимум в точке Δ(eξη) = 0 также расщепляется, но очень незначительно (±0.04 эВ), поэтому имеет место очень сильное перекрывание расщепленных пиков, что в результате дает только один центральный максимум на пунктирной кривой на рис. 5а. Максимальные значения ДП в точках максимумов пиков, которые можно оценить по формуле (18), имеют порядок соответствующих вероятностей (см. рис. 4б). Отметим, что высота центрального пика на пунктирной линии на рис. 5а больше высоты левого и правого пиков, поскольку центральный пик содержит вклад от двух перекрывающихся пиков.
Рисунок 5б построен для тех же параметров, что рис. 5а, но для γ = 0.2. Это приводит к тому, что (1) все линии, показанные на рис. 5а, в целом сдвигаются вправо на (0.5 – γ) eVb, (2) максимумы левой и правой ветвей сплошной кривой, пропорциональные γ, практически не видны на рис. 5б и дают малозаметные левое и правое плечи у каждой ветви, (3) если на рис. 5а высоты левого и правого пиков пунктирной линии одинаковы, то на рис. 5б высоты этих пиков пропорциональны γ и 1 – γ.
На рис. 5в проиллюстрирована зависимость ДП от Er на примере, когда Er = 0.25 эВ. Так как в этом случае eVb/2 = Er при Vb = 0.5 В, то кривая для Vb = 0.5 В на рис. 5в аналогична кривой на рис. 5а, построенной для Vb = 1 В.
На рис. 6а приведены графики функций G(eξη) для тех же параметров, что на рис. 5а, но для сильно асимметричного взаимодействия РГ с рабочими электродами (d = 100). При этом значения характерных точек $e\xi {{\tilde {\eta }}_{\nu }}$ и $e\xi {{\tilde {\eta }}_{{\nu ,\gamma }}}$ являются теми же, что и для случая, представленного на рис. 5а. Вероятности P0 в точках $e\xi {{\tilde {\eta }}_{{{\text{ox}},\gamma }}}$ примерно равны 1 как для Vb = 1 В, так и для Vb = 1.5 В (см. рис. 4с, где представлены кривые вероятностей для Vb = 1.5 В), производные ∂Pn/∂(eVb) в этих точках пренебрежимо малы. Поэтому, в соответствии с формулой (18), высоты пиков в точках $e\xi {{\tilde {\eta }}_{{{\text{ox}},\gamma }}}$ также одинаковы и равны приблизительно 4kTP0γ/(4πErkT) ≈ ≈ 0.12. С другой стороны, из рис. 4с следует, что при Vb = 1.5 В вероятности P1 примерно равны нулю в точках $e\xi {{\tilde {\eta }}_{{{\text{red}}}}}$, $e\xi {{\tilde {\eta }}_{{{\text{ox,a}}\gamma }}}$ и P2 ≈ 0 в точке $e\xi {{\tilde {\eta }}_{{{\text{red,a}}}}}$, так что максимумы в этих точках отсутствуют. Поэтому центральный и правый пики пунктирной линии на рис. 6а появляются вследствие больших значений соответствующих производных ∂Pn/∂(eVb) в точках $e\xi {{\tilde {\eta }}_{{\text{1}}}} \approx 0.62$эВ (≈(1 – γ) eVb) и $e\xi {{\tilde {\eta }}_{{\text{2}}}} \approx 1.2$ эВ (≈(1 – γ) eVb + Ueff) (см. рис. 4с). Так, например, в точке $e\xi {{\tilde {\eta }}_{{\text{1}}}}$ ∂P0/∂(eVb) ≈ 1.88 эВ–1 = = −∂P1/∂(eVb). Для очень больших значений d, когда достигается точное равновесие РГ с правым электродом, имеем ∂P0/∂(eVb) = 1/(4kT) = 5 эВ–1. Тем не менее, уже при d = 100 вероятности Pn (рис. 4с) близки к равновесным по отношению к правому электроду, а абсолютные значения производных ∂Pn/∂(eVb) в точках $e\xi {{\tilde {\eta }}_{{\text{1}}}}$ и $e\xi {{\tilde {\eta }}_{{\text{2}}}}$ достаточно велики. Высоту соответствующих пиков можно оценить, используя формулу (18). Так как в этом случае вклад первых слагаемых в формуле (18) пренебрежимо мал, то высоты пиков определяются последним слагаемым в формуле (18). Например, высота центрального пика на пунктирной кривой на рис. 6а приблизительно равна ${{{\text{4}}{{k}_{{\text{B}}}}T\partial {{P}_{{\text{0}}}}} \mathord{\left/ {\vphantom {{{\text{4}}{{k}_{{\text{B}}}}T\partial {{P}_{{\text{0}}}}} {\partial (e{{V}_{{\text{b}}}})}}} \right. \kern-0em} {\partial (e{{V}_{{\text{b}}}})}}\int_{ - eV}^0 {[{{A}_{{{\text{ox}}}}}(\varepsilon ) - 0.5{{A}_{{{\text{ox}}{\text{.a}}}}}(\varepsilon )]{\text{d}}\varepsilon } $, так как соответствующий интеграл от ${{A}_{{{\text{red}}}}}(\varepsilon )$ пренебрежимо мал. С другой стороны, интегралы от ${{A}_{{{\text{ox}}}}}(\varepsilon )$ и ${{A}_{{{\text{ox}}{\text{.a}}}}}(\varepsilon )$ примерно равны единице, так что высоту центрального пика можно оценить как ${{2{{k}_{{\text{B}}}}T\partial {{P}_{{\text{0}}}}} \mathord{\left/ {\vphantom {{2{{k}_{{\text{B}}}}T\partial {{P}_{{\text{0}}}}} {\partial (e{{V}_{{\text{b}}}})}}} \right. \kern-0em} {\partial (e{{V}_{{\text{b}}}})}}$ ≈ 0.094, что находится в хорошем согласии с рис. 6а. Таким образом, полученный вклад в ДП обусловлен увеличением тока с ростом Vb, поскольку одновременное резкое увеличение P0 и уменьшение P1 означает, что электроны уходят с электронного уровня РГ на правый электрод, увеличивая тем самым ток. Отметим также, что при Vb = 1 В правый пик находится в точке $e\xi {{\tilde {\eta }}_{{\text{2}}}}$ ≈ 0.96 эВ, а центральный пик является суммой двух вкладов, соответствующих точкам $e\xi {{\tilde {\eta }}_{{{\text{ox,a}}\gamma }}}$ и $e\xi {{\tilde {\eta }}_{{\text{1}}}}$ ≈ 0.38 эВ.
Рис. 6.
Зависимость безразмерной дифференциальной проводимости электрохимического транзистора с сильно несимметричным взаимодействием редокс-группы с электродами (ΓR = 100ΓL) от Δ(eξη) = = eξη − kTln(2) − Ueff/2 для параметров Er = 0.5 эВ, Ueff = 0.5 эВ и kT = 0.025 эВ. (а), γ = 0.5; (б) γ = 0.2. Сплошная линия: Vb = 1 В; пунктирная линия: Vb = = 1.5 В.

На рис. 6б представлен тот же случай, что на рис. 6а, но для γ = 0.2 и Vb = 1 В. Соотношение между рис. 6а и рис. 6б в целом то же самое, что между рис. 5а и рис. 5б. Именно, кривая рис. 6б сдвинута примерно на (0.5 – γ)eVb по отношению к сплошной кривой рис. 6а, высота левого пика для кривой на рис. 6б пропорциональна γ. Важное отличие заключается в роли величины производных ∂Pn/∂(eVb) в высоте центрального и правого пиков. Выше отмечалось, что кривые Pn/(eξη) для γ = 0.2 получаются из кривых Pn/(eξη) для случая, когда γ = 0.5, сдвигом на (0.5 − γ) eVb по оси eξη. При этом производные вероятностей по eξη в соответствующих точках совпадают, но для производных ∂Pn/∂(eVb) такое совпадение не имеет места. Здесь играет приблизительную роль фактор (1 − γ), который связывал производные по eξη и eVb в пределе больших энергий реорганизации, рассмотренном выше. Например, для центрального пика на рис. 6б производная ∂P0/∂(eVb) действительно примерно в 1.6 раз больше (вместо 1.5 раз, как это было бы в пределе больших Er), чем для аналогичного пика на рис. 6а, что находит отражение в разной высоте этих пиков.
В заключение коротко остановимся на случае, когда Ueff = 0. В этом случае можно использовать только уравнения (19)–(20). Кроме того, упрощается формула (П4) для Aσ(ε), так как при Ueff = 0 плотность состояний Aσ(ε) = PoxAox(ε) + PredAred(ε), где Pox = P0 + P1/2 и Pred = 1 − Pox. Используя уравнение (14), легко показать, что в пределе больших Er выражение для ${{P}_{{{\text{ox}}}}}$ имеет тот же вид, что и для ${{P}_{{{\text{0}}\infty }}}$, но с заменой eξη на $e\xi \tilde {\eta }$. Поведение ДП аналогично рассмотренному выше для Ueff > 0 с тем лишь отличием, что, например, при Vb = 1 В и Er = 0.5 эВ изменение структуры ДП происходит на основе кривой с одним максимумом. Именно при Vb = 1 В первоначальный единственный максимум расщепляется на два максимума, аналогично тому, как это имело место для каждого из пиков на рис. 5а. Точно также при d $ \gg $ 1 появляются новые максимумы, обусловленные большими значениями производных ∂Pn/∂(eVb).
ЗАКЛЮЧЕНИЕ
В настоящей статье, в отличие от других работ, исследована зависимость дифференциальной проводимости (ДП) электрохимического транзистора от перенапряжения в режиме полностью неадиабатического (диабатического) приближения для электронного переноса, что позволило определить области значения перенапряжения, в которых происходит сильное изменение туннельного тока с ростом напряжения смещения. Показано:
1. В случае слабополярного растворителя (Er ≈ 0) пики функции G(η) непосредственно связаны с прохождением электронного уровня РГ и уровня сродства к электрону через уровни Ферми рабочих электродов.
2. В приближении большой энергии реорганизации максимумы ДП обусловлены максимумами основного пика и пика кулоновской блокады в зависимости туннельного тока от перенапряжения j(η) и соответствуют значениям перенапряжения, при которых средние значение флуктуирующего электронного уровня РГ или уровня сродства к электрону совпадают с центром энергетического окна электрохимического транзистора.
3. Структура функции G(η), состоящая из двух максимумов, характерных для приближения больших Er, сохраняется вплоть до значений eVb < 2Er. Максимумы ДП имеют тот же физический смысл, как и в приближении больших Er, что обусловлено активационным режимом электронного переноса в этой области значений Vb.
4. В области eVb > 2Er поведение ДП имеет тесную связь со структурой плотности электронных состояний A(ε) на электронном уровне РГ и с поведением вероятностей заполнения Pn электронного уровня как функций перенапряжения и напряжения смещения. При гладком изменении функций Pn(η,Vb) максимумы ДП G(η) возможны в точках, в которых отдельные функции Aν(ε), описывающие плотность состояний на пустом электронном уровне, электронном уровне восстановленной РГ, пустом уровне сродства к электрону (при этом электронный уровень РГ однократно заполнен) и электронном уровне полностью восстановленной РГ (при n = 2) принимают максимальные значения при соблюдении условия, что в этих точках соответствующие вероятности отличны от нуля.
5. При сильно асимметричном взаимодействии РГ с электродами происходит резкое изменение вероятностей Pn(η) в точках, отвечающих совпадению средних значений флуктуирующего электронного уровня РГ и уровня сродства к электрону с уровнем Ферми левого (d $ \ll $ 1) или правого (d $ \gg $ 1) электродов, что приводит к существованию максимумов ДП в этих точках.
ПРИЛОЖЕНИЕ
При изучении зависимости туннельного тока от перенапряжения при постоянном Vb можно применить следующий подход. Рассмотрим случай, когда для произвольного значения энергии реорганизации Er выполняются неравенства eξη < Ueff/2, Ueff > 2kT и Ueff не мало по сравнению с eVb. Тогда, используя уравнение (5), можно показать, что k12 имеет порядок exp(−Ueff/2kT) и по этой причине много меньше других констант скорости. В результате электронный перенос типа 1 → 2 пренебрежимо мал, поэтому из уравнения (4) следует, что
(П1)
$j \approx {{j}_{\infty }} = 2e{{\left( {k_{{{\text{01}}}}^{{\text{L}}}k_{{{\text{10}}}}^{{\text{R}}} - k_{{{\text{10}}}}^{{\text{L}}}k_{{{\text{01}}}}^{{\text{R}}}} \right)} \mathord{\left/ {\vphantom {{\left( {k_{{{\text{01}}}}^{{\text{L}}}k_{{{\text{10}}}}^{{\text{R}}} - k_{{{\text{10}}}}^{{\text{L}}}k_{{{\text{01}}}}^{{\text{R}}}} \right)} {(2{{k}_{{01}}} + {{k}_{{10}}})}}} \right. \kern-0em} {(2{{k}_{{01}}} + {{k}_{{10}}})}}.$(П2)
$j \approx {{j}_{{\text{a}}}} = 2e{{\left( {k_{{{\text{12}}}}^{{\text{L}}}k_{{{\text{21}}}}^{{\text{R}}} - k_{{{\text{21}}}}^{{\text{L}}}k_{{{\text{12}}}}^{{\text{R}}}} \right)} \mathord{\left/ {\vphantom {{\left( {k_{{{\text{12}}}}^{{\text{L}}}k_{{{\text{21}}}}^{{\text{R}}} - k_{{{\text{21}}}}^{{\text{L}}}k_{{{\text{12}}}}^{{\text{R}}}} \right)} {({{k}_{{12}}} + 2{{k}_{{21}}})}}} \right. \kern-0em} {({{k}_{{12}}} + 2{{k}_{{21}}})}}.$Поэтому, если Ueff не мало по сравнению с eVb и Ueff$ \gg $ 2kT, то, для всех ξη, j ≈ j∞ + ja. Это разбиение полного туннельного тока на отдельные слагаемые j∞ и ja имеет ясный физический смысл и довольно удобно, поскольку токи j∞ и ja достаточно просто зависят от напряжения смещения и перенапряжения по сравнению с полным туннельным током.
В работе [26] было показано, что токи j∞ и ja, рассматриваемые как функции перенапряжения, имеют максимальные значения в точках ξηmax,∞ и ξηmax,a ≈ ξηmax,∞ + Ueff, так что полный ток j(η) демонстрирует два пика. При d = 1 и произвольной энергии Er положения первого (левого) и второго (правого) пиков соответствуют случаям, когда энергии εb av или εa av = εb av + Ueff флуктуирующих уровней РГ попадают приблизительно в центр энергетического окна туннельного контакта, который расположен в точке −eVb/2. При этом выполняется приближенное равенство j∞(ηmax,∞) ≈ ja(ηmax,a). По определению туннельного тока ja, правый пик может наблюдаться при больших значениях перенапряжения eξη ~ Ueff, которое является достаточным для преодоления кулоновского отталкивания. Поэтому второй максимум полного туннельного тока называется пиком кулоновской блокады. Очевидно, что второй максимум отсутствует при U = 0 и появляется с увеличением Ueff, когда Ueff становится больше некоторого значения Ueff* [25].
Наряду с формулой (4), полученной для полностью неадиабатического режима, туннельный ток для любого режима можно вычислить по формуле работы [31]:
(П3)
$j = \frac{{e{{\Gamma }_{{\text{L}}}}{{\Gamma }_{{\text{R}}}}}}{{\hbar \Gamma }}\int\limits_{ - \infty }^\infty {\left[ {{{f}_{{\text{L}}}}(\varepsilon ) - {{f}_{{\text{R}}}}(\varepsilon )} \right]A(\varepsilon ){\text{d}}\varepsilon } ,$(П4)
$\begin{gathered} {{A}_{\sigma }}(\varepsilon ) = {{P}_{0}}{{A}_{{{\text{ox}}}}}(\varepsilon ) + {{{{P}_{1}}{{A}_{{{\text{red}}}}}(\varepsilon )} \mathord{\left/ {\vphantom {{{{P}_{1}}{{A}_{{{\text{red}}}}}(\varepsilon )} 2}} \right. \kern-0em} 2} + \\ + \,\,{{{{P}_{1}}{{A}_{{{\text{ox,a}}}}}(\varepsilon )} \mathord{\left/ {\vphantom {{{{P}_{1}}{{A}_{{{\text{ox,a}}}}}(\varepsilon )} 2}} \right. \kern-0em} 2} + {{P}_{2}}{{A}_{{{\text{red,a}}}}}(\varepsilon ), \\ \end{gathered} $(П5)
$\begin{gathered} {{A}_{\nu }}(\varepsilon ) = {{(4\pi {{E}_{{\text{r}}}}kT)}^{{ - 1/2}}} \times \\ \times \,\,\exp \{ - {{{{{[\varepsilon - {{E}_{\nu }}({{E}_{{\text{r}}}},{{\varepsilon }_{{\text{0}}}},{{U}_{{{\text{eff}}}}})]}}^{2}}} \mathord{\left/ {\vphantom {{{{{[\varepsilon - {{E}_{\nu }}({{E}_{{\text{r}}}},{{\varepsilon }_{{\text{0}}}},{{U}_{{{\text{eff}}}}})]}}^{2}}} {4{{E}_{{\text{r}}}}kT}}} \right. \kern-0em} {4{{E}_{{\text{r}}}}kT}}\} . \\ \end{gathered} $Ширина WА в половине максимума одинакова для этих функций, не зависит от ν и равна 4[ErkTln(2)]1/2. Энергии Eν положений максимумов спектральных функций Aν(ε) определяются выражениями Eox = ε0 = −eξη − γeV + kTln(2) + Er, Ered = εb(qkα) = = ε0 − 2Er, Eox,a = ε0 + Ueff и Ered,a = ε0 + = Ueff − 2Er. Эти энергии имеют следующий физический смысл. Eox и Eox,aa являются энергиями пустых уровней εb и εa. Вследствие флуктуаций поляризации растворителя и соответствующих флуктуаций уровней εb и εa эти уровни оказываются заполненными. После релаксации среды к новым значениям чисел заполнения РГ энергии этих уровней сдвигаются на −2Er к Ered или Ered,a. Вероятности P0, P1, P2 определяются формулами (3) и в полностью адиабатическом режиме не зависят от Γ, но зависят от параметра d.
Для произвольного режима эти вероятности удовлетворяют точному соотношению, полученному в [27]:
(П6)
$\begin{gathered} {{P}_{n}}({{V}_{{\text{b}}}},e\xi \eta ,{{U}_{{{\text{eff}}}}},\gamma ,{{\Gamma }_{{\text{L}}}},{{\Gamma }_{{\text{R}}}}) = \\ = {{P}_{n}}( - {{V}_{{\text{b}}}},e\xi \eta ,{{U}_{{{\text{eff}}}}},1 - \gamma ,{{\Gamma }_{{\text{R}}}},{{\Gamma }_{{\text{L}}}}). \\ \end{gathered} $Для ДП в [27] были получены следующие два точных соотношения, справедливые для произвольного режима работы электрохимического транзистора:
(П7)
$\begin{gathered} G({{V}_{{\text{b}}}},\Delta (e\xi \eta ),{{U}_{{{\text{eff}}}}},\gamma ,{{\Gamma }_{{\text{L}}}},{{\Gamma }_{{\text{R}}}}) = \\ = G( - {{V}_{{\text{b}}}}, - \Delta (e\xi \eta ),{{U}_{{{\text{eff}}}}},\gamma ,{{\Gamma }_{{\text{L}}}},{{\Gamma }_{{\text{R}}}}), \\ \end{gathered} $(П8)
$\begin{gathered} G({{V}_{{\text{b}}}},\Delta (e\xi \eta ),{{U}_{{{\text{eff}}}}},\gamma ,{{\Gamma }_{{\text{L}}}},{{\Gamma }_{{\text{R}}}}) = \\ = G({{V}_{{\text{b}}}}, - \Delta (e\xi \eta ),{{U}_{{{\text{eff}}}}},1 - \gamma ,{{\Gamma }_{{\text{R}}}},{{\Gamma }_{{\text{L}}}}), \\ \end{gathered} $Список литературы
Tao, N.G., Electron transport in molecular junctions, Nature Nanotechnol., 2006, vol. 1, p. 173.
Lindsay, S.M. and Ratner, M.A., Molecular junctions: clearing mists, Adv. Mater., 2007, vol. 19, p. 23.
Zhang, J., Kuznetsov, A.M., Medvedev, I.G., Chi, Q., Albrecht, T., Jensen, P.S., and Ulstrup, J., Single-molecule electron transfer in electrochemical environments, Chem. Rev., 2008, vol. 108, p. 2737.
Bergfield, J.P. and Ratner, M.A., Forty years of molecular electronics: Non-equilibrium heat and charge transport at the nanoscale, Phys. Status Solidi B, 2013, vol. 250, p. 2239.
Nichols, R.J. and Higgins, S.J., Single molecule nanoelectrochemistry in electrical junctions, Acc. Chem. Res., 2016, vol. 49, p. 2640.
Nichols, R.J., Moleculat electronics at electrode-electrolyte interfaces, Curr. Opin. Electrochem., 2021, vol. 25, p. 100650.
Tao, N.J., Probing potential-tuned resonant tunneling through redox molecules with scanning tunneling microscopy, Phys. Rev. Lett., 1996, vol. 76, p. 4066.
Gittins, D.I., Berthell, D., Schiffrin, D.J., and Nichols, R.J., A nanometer-scale electronic switch consisting of a metal cluster and redox-addressable grous, Nature, 2000, vol. 408, p. 67.
Haiss, W., van Zalinge, H., Higgins, S.J., Bethell, D., Höbenreich, H., Schiffrin, D.J., and Nichols, R.J., Redox state dependence of single molecule conductivity, J. Amer. Chem. Soc., 2003, vol. 125, p. 15294.
Xu, B., Xiao, X., Yang, X., Zang, L., and Tao, N., Large gate modulation in the current of at room temperature single molecule transistor, J. Amer. Chem. Soc., 2005, vol. 127, p. 2386.
Albrecht, T., Guckian, A., Ulstrup, J., and Vos, J.G., Transistor-like behavior of transition metal complexes, Nano Lett., 2005, vol. 5, p. 1451.
Chen, F., He, J., Nuckolls, C., Roberts, T., Klare, J.E., and Lindsay, S., A molecular switch based on potential-induced changes of oxidation state, Nano Lett., 2005, vol. 5, p. 503.
Xiao, X., Nagahara, L.A., Rawlett, A.M., and Tao, N., Electrochemical gate-controlled conductance of single oligo(phenylene ethynglene)s, J. Amer. Chem. Soc., 2005, vol. 127, p. 9235.
Li, X., Xu, B., Xiao, X., Yang, X., Zang, L., and Tao, N., Controlling charge transport in single molecules using electrochemical gate, 2006, Faraday Discuss., 2006, vol. 131, p. 111.
Li, Z., Han, B., Meszaros, G., Pobelov, I., Wandlowski, Th., Blaszczyk, A., and Mayor, M., Two-dimensional assembly and local redox-activity of molecular hybrid structure in an electrochemical environment, Faraday Discuss., 2006, vol. 131, p. 121.
Kay, N.J., Higgins, S.J., Jepsen, J.O., Leary, E., Lycoops, J., Ulstrup, J., and Nichols, R.J., Single-molecule electrochemical gating in ionic liquids, J. Amer. Chem. Soc., 2012, vol. 134, p. 16817.
Darwish, N., Diez-Perez, I., Guo, S., Tao, N., Gooding, J.J., and Paddon-Row, M.N., Single molecule switches: electrochemical gating of a single anthraquinone-based norbornylogous bridge molecule, J. Phys. Chem. C, 2012, vol. 116, p. 21093.
Kuznetsov, A.M. and Ulstrup, J., Mechanisms of molecular electronic rectification through electronic levels with strong vibrational coupling, J. Chem. Phys., 2002, vol. 116, p. 2149.
Schmickler, W., A model for bridge-assisted electron exchange between two electrodes, Chem. Phys., 2003, vol. 289, p. 349.
Kuznetsov, A.M. and Ulstrup, J., Single-molecule electron tunneling through multiple redox levels with environmental relaxation, J. Electroanal. Chem., 2004, vol. 564, p. 209.
Medvedev, I.G., Classical master equations and broadened classical master equations: Some analytical results, J. Chem. Phys., 2021, vol. 155, p. 114 116.
Sumi, H., V-I-characteristics of STM processes as a probe detecting vibronic interactions at a redox state in large molecular adsorbates such as electron-transfer metalloproteins, J. Phys.Chem. B, 1998, vol. 102, p. 1833.
Kuznetsov, A.M. and Ulstrup, J., Mechanisms of in situ scanning tunneling microscopic of organized redox molecular assemblies, J. Phys. Chem. A, 2000, vol. 104, p. 11 531.
Kuznetsov, A.M., Medvedev, I.G., and Ulstrup, J., Electric double layer effect on observable characteristics of the tunnel current through a bridged electrochemical contact, J. Chem. Phys., 2007, vol. 127, p. 104708.
Kuznetsov, A.M., Medvedev, I.G., and Ulstrup, J., Coulomb repulsion effect in two-electron non-adiabatic tunneling through a one-level redox molecule, J. Chem. Phys., 2009, vol. 131, p. 164703.
Medvedev, I.G., Effect of the asymmetry of the coupling of the redox molecule to the electrodes in the one-level electrochemical bridged tunneling contact on the Coulomb blockade and the operation of molecular transistor, J. Chem. Phys., 2014, vol. 141, p. 124 706.
Medvedev, I.G., Exact relations for the differential conductance and rectification ratio of the tunnel current in the redox-mediated tunneling junctions and demonstration within the fully diabatic approximation for electron transitions, J. Electroanal. Chem., 2020, vol. 856, p. 113 640.
Догонадзе, Р.Р., Чизмаджев, Ю.А. Вычисление вероятности элементарного акта некоторых гетерогенных окислительно-восстановительных реакций. Докл. АН СССР. 1962. Т. 144. С. 1077. [Dogonadze, R.R. and Chizmadzhev, Yu.A., Calculation of the elementary act probability of some heterogeneous oxidation-reduction reactions, Proc. Acad. Sci. USSR, Phys. Chem. Sect., 1962, vol. 144, p. 463.]
Догонадзе, Р.Р., Чизмаджев, Ю.А. Кинетика некоторых электрохимических окислительно-восстановительных реакций на металлах. Докл. АН СССР. 1962. Т. 145. С. 849. [Dogonadze, R.R. and Chizmadzhev, Yu.A., Kinetics of some electrochemical oxidation-reduction reactions on metals, Proc. Acad. Sci. USSR, Phys. Chem. Sect., 1962, vol. 145, p. 563.]
Догонадзе, Р.Р., Кузнецов, А.М., Чизмаджев, Ю.А. Кинетика некоторых гетерогенных реакций на границе полупроводник–электролит. Журн. физ. химии. 1964. Т. 38. С. 1195. [Dogonadze, R.R., Kuznetsov, A.M., and Chizmadzhev, Yu.A., Kinetics of some heterogeneous reactions on the semiconductor-electrolyte interface, Zh. Fiz. Khim. (in Russian), 1964, vol. 38, p.1202.]
Meir, Y. and Wingreen, N.S., Landauer formula for the current through an interacting electron region, Phys. Rev. Lett, 1992, vol. 68, p. 2512.
Глазман, Л.И., Матвеев, К.А. Кулоновские корреляции при туннелировании через резонансные центры. Письма ЖЭТФ. 1988. Т. 48. С. 403. [Glazman, L.I. and Matveev, K.A., Coulomb correlations in the tunneling through resonance centers, JETP Lett., 1988, vol. 48, p. 445.]
Muralidharan, B., Ghosh, A.W., and Datta, S., Probing electron excitations in molecular conduction, Phys. Rev. B, 2006, vol. 73, p. 155410.
Medvedev, I.G., On the evaluation of the rate constant of the heterogeneous non-adiabatic electron transfer reaction, J. Electroanal. Chem., 2016, vol. 761, p. 46.
Дополнительные материалы отсутствуют.
Инструменты
Электрохимия