Электрохимия, 2022, T. 58, № 5, стр. 242-250

Погрешность приближенных расчетов степени диссоциации слабых бинарных электролитов

А. В. Гребенник^a, *, О. А. Райтман^a, b, **

^a Российский химико-технологический университет им. Д.И. Менделеева
Москва, Россия

^b Институт физической химии и электрохимии им. А.Н. Фрумкина РАН
Москва, Россия

^* E-mail: physchem@muctr.ru
^** E-mail: rightman@muctr.ru

Поступила в редакцию 30.06.2021
После доработки 22.09.2021
Принята к публикации 18.10.2021

EDN: VZIIVS
DOI: 10.31857/S0424857022040065

Полный текст (PDF)

Аннотация

Выполнен анализ погрешности расчета степени диссоциации слабых бинарных электролитов по приближенной формуле $\alpha = \sqrt {{{{{K}_{c}}} \mathord{\left/ {\vphantom {{{{K}_{c}}} c}} \right. \kern-0em} c}} $ и по закону разведения Оствальда. Даны выражения для относительной ошибки и пределы применимости названных приближений, в том числе при необходимости учета собственной диссоциации растворителя.

Ключевые слова: закон разведения Оствальда, константа диссоциации, бинарный электролит

ВВЕДЕНИЕ

При анализе процессов в растворах слабых электролитов существенной является информация о равновесных концентрациях ионов, которые связаны с равновесной степенью диссоциации электролита. Расчет равновесных концентраций ионов в растворах слабых электролитов выполняется на основе материального и электрического балансов и выражения для константы диссоциации по закону действующих масс. Задачи такого рода являются типовыми во всех вузовских курсах общей и физической химии. Чаще всего они рассматриваются на примерах слабых бинарных электролитов валентного типа 1-1 и решаются на основе допущения о том, что степень диссоциации слабого электролита априори мала.

Для решения подобных задач применительно к разбавленным растворам слабого электролита без добавок сильных электролитов используют практическую константу диссоциации ${{K}_{c}},$ выражаемую через равновесные концентрации (моль/дм³) сольватированных ионов (${{c}_{ + }},$ ${{c}_{ - }}$) и нераспавшихся молекул электролита AB (${{c}_{{{\text{AB}}}}}$):

(1)

${{K}_{c}} = \frac{{{{c}_{ + }}{{c}_{ - }}}}{{{{c}_{{{\text{AB}}}}}}}.$

Если равновесные концентрации ионов (${{c}_{ + }},$ ${{c}_{ - }}$) при диссоциации электролита существенно выше концентраций ионов при собственной диссоциации растворителя, последние можно не учитывать в электрическом балансе раствора: ${{c}_{ + }} = {{c}_{ - }}.$ В соответствии с материальным и электрическим балансами диссоциации бинарного электролита AB концентрации ионов ${{c}_{ + }},$ ${{c}_{ - }}$ и нераспавшихся молекул ${{c}_{{{\text{AB}}}}}$ связаны с начальной концентрацией электролита c и его степенью диссоциации α:

${{c}_{ + }} = {{c}_{ - }} = \alpha c,\,\,\,\,{{c}_{{{\text{AB}}}}} = c - \alpha c = (1 - \alpha )c.$

Подставляя эти выражения в (1), получаем уравнение, называемое законом разведения Оствальда:

(2)

${{K}_{c}} = \frac{{\alpha c\alpha c}}{{c - \alpha c}} = \frac{{{{\alpha }^{2}}c}}{{1 - \alpha }}.$

В курсах общей и физической химии всегда демонстрируется типовая задача расчета степени диссоциации α слабого электролита в водном растворе с концентрацией c. При этом без подробного анализа ошибки в выражении (2) обычно рекомендуют пренебречь α в знаменателе (см., например, [1, c. 292], а также [2, с. 410] и [3, с. 8]) и решать упрощенное уравнение относительно α:

(3)

${{K}_{c}} = {{\alpha }^{2}}c,\,\,\,\,\alpha = \sqrt {\frac{{{{K}_{c}}}}{c}} .$

В соответствии с уравнением (3) степень диссоциации электролита при уменьшении концентрации неограниченно возрастает и формально может превысить 1, что в реальности, конечно, невозможно.

Точное решение (2) относительно α есть положительный корень квадратного уравнения

${{\alpha }^{2}}c + \alpha {{K}_{c}} - {{K}_{c}} = 0,$

который можно найти по общеизвестной формуле [4]:

(4)

$\alpha = \frac{{ - {{K}_{c}} + \sqrt {K_{c}^{2} + 4c{{K}_{c}}} }}{{2c}}.$

В соответствии с уравнением (4) степень диссоциации слабых бинарных электролитов с уменьшением концентрации стремится к 1. Следовательно, должно существовать ограничение применимости приближенного выражения (3) применительно к растворам малых концентраций. Однако строгие критерии применимости (3) в учебных изданиях отсутствуют. В учебнике по электрохимии [4] без подробного анализа ошибки указано, что формула (3) – она же (1.2.4) в [4, с. 21] – может применяться “при малых константах диссоциации и при не очень низких концентрациях, когда ${{K}_{c}} \ll 4c$“. Но, как будет показано ниже, практическое применение условия ${{K}_{c}} \ll 4c$ по тексту учебника затруднительно, поскольку неясен смысл знака “много меньше” в этом неравенстве, т.е. неясно, насколько произведение 4c должно численно превышать константу диссоциации для достижения приемлемой точности расчета степени диссоциации α.

С целью получения упрощенных приближенных формул выражение (4) может быть преобразовано с последующим разложением в степенной ряд. Если в (4) вынести за скобки множитель $\sqrt {{{{{K}_{c}}} \mathord{\left/ {\vphantom {{{{K}_{c}}} c}} \right. \kern-0em} c}} ,$ то получим уравнение

$\alpha = \sqrt {\frac{{{{K}_{c}}}}{c}} \left( {\sqrt {\frac{{{{K}_{c}}}}{{4c}} + 1} - \sqrt {\frac{{{{K}_{c}}}}{{4c}}} } \right).$

Умножая и деля записанную в скобках разность радикалов на сумму тех же радикалов, придем к выражению

(5)

$\alpha = \frac{{\sqrt {\frac{{{{K}_{c}}}}{c}} }}{{\sqrt {\frac{{{{K}_{c}}}}{{4c}} + 1} + \sqrt {\frac{{{{K}_{c}}}}{{4c}}} }},$

в котором первое слагаемое в знаменателе разложим в степенной ряд Маклорена относительно $\tfrac{{{{K}_{c}}}}{{4c}}{\text{:}}$

$\sqrt {\frac{{{{K}_{c}}}}{{4c}} + 1} \approx 1 + \frac{1}{2} \cdot \frac{{{{K}_{c}}}}{{4c}} - \frac{1}{8} \cdot {{\left( {\frac{{{{K}_{c}}}}{{4c}}} \right)}^{2}} + ....$

Подстановка этого разложения в знаменатель (5) приводит к приближенному равенству

(6)

$\alpha \approx \sqrt {\frac{{{{K}_{c}}}}{c}} \cdot {{\left[ {1 + \sqrt {\frac{{{{K}_{c}}}}{{4c}}} + \frac{1}{2} \cdot \frac{{{{K}_{c}}}}{{4c}} - \frac{1}{8} \cdot {{{\left( {\frac{{{{K}_{c}}}}{{4c}}} \right)}}^{2}}} \right]}^{{ - 1}}}.$

Выражение (6) позволяет пояснить смысл упомянутого выше условия ${{K}_{c}} \ll 4c$ из [4, с. 21], при котором справедливо уравнение (3). Видно, что это условие по существу является предельным, и знак “много меньше” без дополнительных уточнений надо понимать как “бесконечно меньше”. Если $4c \gg {{K}_{c}},$ то значение ${{{{K}_{c}}} \mathord{\left/ {\vphantom {{{{K}_{c}}} {(4c)}}} \right. \kern-0em} {(4c)}}$ мало, с увеличением концентрации c оно стремится к нулю. При этом выражение в квадратных скобках в (6) стремится к единице и в пределе (6) переходит в уравнение (3).

В данной работе поставлена задача анализа погрешности выражения (3) и точного решения (2) – уравнения (4), а также выяснения пределов их применимости, в том числе с учетом влияния ион-ионного взаимодействия и диссоциации молекул растворителя.

РЕЗУЛЬТАТЫ И ОБСУЖДЕНИЕ

Слабый бинарный электролит в разбавленном растворе

Простейший случай применения уравнения (2) соответствует ситуации, когда единственным источником ионов в разбавленном растворе является слабый бинарный электролит и взаимодействием между ионами можно пренебречь.

Приближенное значение степени диссоциации ${{\alpha }_{{{\text{пр}}}}},$ найденное по уравнению (3), всегда завышено по сравнению с результатом (4). Найдем относительную ошибку выражения (3) по сравнению с более точным решением (4). Обозначим ее буквой δ и выразим в долях:

(7)

$\delta = \frac{{{{\alpha }_{{{\text{пр}}}}} - \alpha }}{\alpha } = \frac{{{{\alpha }_{{{\text{пр}}}}}}}{\alpha } - 1.$

Подставим (3) и (4) в (7) и после преобразований получим выражение, однозначно определяющее искомую ошибку относительно соотношения $\tfrac{c}{{{{K}_{c}}}}{\text{:}}$

(8)

$\delta = \frac{2}{{\sqrt {\frac{1}{{\left( {\frac{c}{{{{K}_{c}}}}} \right)}} + 4} - \sqrt {\frac{1}{{\left( {\frac{c}{{{{K}_{c}}}}} \right)}}} }} - 1.$

Из выражения (6) можно получить более простое приближенное уравнение, ограничившись первыми двумя членами в квадратных скобках:

(9)

$\alpha \approx \sqrt {\frac{{{{K}_{c}}}}{c}} \cdot {{\left[ {1 + \sqrt {\frac{{{{K}_{c}}}}{{4c}}} } \right]}^{{ - 1}}} = \frac{{\sqrt {\frac{{{{K}_{c}}}}{c}} }}{{\frac{1}{2}\sqrt {\frac{{{{K}_{c}}}}{c}} + 1}} = \frac{1}{{\frac{1}{2} + \sqrt {\frac{c}{{{{K}_{c}}}}} }}.$

Если при выводе формулы для ошибки δ в уравнение (7) мы подставим приближенное выражение степени диссоциации α по (9), то в результате получим

(10)

${{\delta }_{{{\text{пр}}}}} \approx \sqrt {\frac{{{{K}_{c}}}}{{4c}}} = \frac{1}{2}{{\left( {\frac{c}{{{{K}_{c}}}}} \right)}^{{ - \tfrac{1}{2}}}}.$

Результаты расчета по уравнениям (8) и (10) представлены на рис. 1, ошибка в процентах дана как функция от $z = \tfrac{c}{{{{K}_{c}}}}.$ Данный расчет и все последующие расчеты выполнены в среде Mathcad 2000, с ее помощью построены графики на рис. 1–3 .

Рис. 1.

Относительная ошибка (100% · δ) расчета степени диссоциации по уравнению (3) как функция от $z = \tfrac{c}{{{{K}_{c}}}}$ в соответствии с уравнениями (8) – сплошная линия и (10) – пунктир. Вертикальными пунктирными линиями отмечены значения z = 0.25 и z = 100.

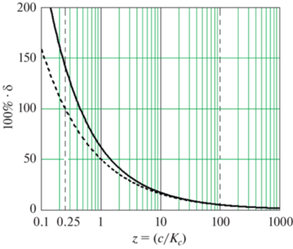
Рис. 2.

Зависимость равновесной степени диссоциации слабых одноосновных кислот от концентрации при 298 К, рассчитано по (19). Варианты значений ${{K}_{c}}{\text{:}}$ (1) ${{K}_{c}} = 1.7 \times {{10}^{{ - 5}}},$ ${{\alpha }_{\infty }} = 0.994$ (CH₃COOH); (2) ${{K}_{c}} = 2.0 \times {{10}^{{ - 6}}},$ ${{\alpha }_{\infty }} = 0.952;$ (3) ${{K}_{c}} = 4.0 \times {{10}^{{ - 7}}},$ ${{\alpha }_{\infty }} = 0.800;$ (4) ${{K}_{c}} = 1.0 \times {{10}^{{ - 7}}},$ ${{\alpha }_{\infty }} = 0.500;$ (5) ${{K}_{c}} = 2.0 \times {{10}^{{ - 8}}},$ ${{\alpha }_{\infty }} = 0.167.$

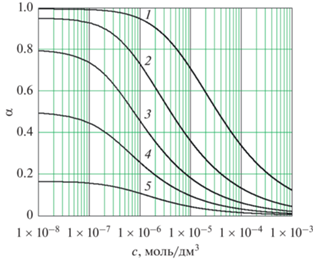
Рис. 3.

Относительная погрешность (%) расчета степени диссоциации ${{\alpha }_{4}}$ по уравнению (4) по сравнению с результатом ${{\alpha }_{{19}}}$ выражения (19) для слабых одноосновных кислот в водных растворах при 298 К: (1) ${{K}_{c}} = 1.7 \times {{10}^{{ - 5}}},$ ${{\alpha }_{\infty }} = 0.994$ (CH₃COOH); (2) ${{K}_{c}} = 2.0 \times {{10}^{{ - 6}}},$ ${{\alpha }_{\infty }} = 0.952;$ (3) ${{K}_{c}} = 4.0 \times {{10}^{{ - 7}}},$ ${{\alpha }_{\infty }} = 0.800;$ (4) ${{K}_{c}} = 1.0 \times {{10}^{{ - 7}}},$ ${{\alpha }_{\infty }} = 0.500;$ (5) ${{K}_{c}} = 2.0 \times {{10}^{{ - 8}}},$ ${{\alpha }_{\infty }} = 0.167.$

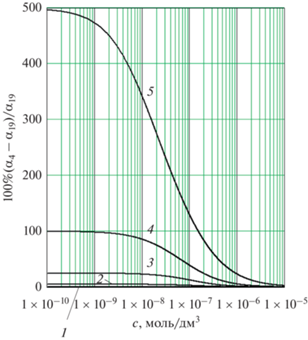
Видно, что при $\tfrac{c}{{{{K}_{c}}}} < 100$ ошибка расчета степени диссоциации электролита по уравнению (3) превышает 5% и резко возрастает с уменьшением соотношения $\tfrac{c}{{{{K}_{c}}}}.$

Видно также, что критерий применимости уравнения (3), приведенный в [4] ($4c \gg {{K}_{c}},$ т.е. $\tfrac{c}{{{{K}_{c}}}} \gg \tfrac{1}{4}$), не позволяет оценить погрешность расчета по (3), так как предельному значению $\tfrac{c}{{{{K}_{c}}}} = \tfrac{1}{4}$ соответствует ошибка уравнения (3), равная 141%, и большая часть диапазона значений абсциссы на рис. 1 соответствует условию $\tfrac{c}{{{{K}_{c}}}} > \tfrac{1}{4}.$

Для решения обратной задачи – нахождения соотношения $\tfrac{c}{{{{K}_{c}}}},$ отвечающего заданной относительной погрешности δ, уравнение (8) надо решить относительно $\tfrac{c}{{{{K}_{c}}}}.$ Соответствующее точное выражение, получающееся в результате ряда последовательных преобразований уравнения (8), имеет следующий вид:

(11)

$\frac{c}{{{{K}_{c}}}} = {{\left( {\frac{{1 + \delta }}{{1 - {{{(1 + \delta )}}^{2}}}}} \right)}^{2}}.$

Подобное выражение можно получить и с использованием приближения (10):

(12)

$\frac{c}{{{{K}_{c}}}} \approx \frac{1}{{4\delta _{{{\text{пр}}}}^{{\text{2}}}}}.$

Результаты расчета по уравнениям (8) и (10)–(12) приведены в табл. 1.

Таблица 1.

Относительная ошибка $100\% \cdot \delta $ приближенного расчета α по уравнению (3)

$\frac{c}{{{{K}_{c}}}}$	$100\% \cdot \delta $ по (8)	$100\% \cdot \delta $ по (10)	$100\% \cdot \delta $	$\frac{c}{{{{K}_{c}}}}$ по (11)	$\frac{c}{{{{K}_{c}}}}$ по (12)
1000	1.6	1.6	1	2525	2500
500	2.2	2.2	3	286	278
100	5.1	5.0	5	105	100
50	7.3	7.1	10	27.4	25
10	17.0	15.8	50	1.44	1
1	61.8	50.0	100	0.444	0.25
0.1	245	158	200	0.141	0.0625

Проведенные расчеты показывают, что для конкретного слабого бинарного электролита погрешность приближенной формулы (3) растет с уменьшением начальной концентрации c. В качестве нижней границы применимости выражения (3) можно рекомендовать такую концентрацию c, при которой соотношение $\tfrac{c}{{{{K}_{c}}}}$ превышает 100. Ошибка уравнения (3) при этом будет не более 5%. К примеру, для уксусной кислоты при температуре 298 К в водном растворе (${{K}_{c}} = 1.7 \times {{10}^{{ - 5}}}$) нижняя граница применимости выражения (3) соответствует $c = 1.7 \times {{10}^{{ - 3}}}$ моль/дм³ ($c = 100{{K}_{c}}$). При тех же условиях для хлорноватистой (гипохлорной) кислоты HClO с константой диссоциации $3.0 \times {{10}^{{ - 8}}}$ нижний предел применимости (3) снизится до $3.0 \times {{10}^{{ - 6}}}$ моль/дм³.

Для расчета погрешности уравнения (3) можно также использовать приближенную формулу (10), которая правильно характеризует ошибку формулы (3) при не очень малых значениях отношения $\tfrac{c}{{{{K}_{c}}}}.$ При $\tfrac{c}{{{{K}_{c}}}} \geqslant 10$ разность значений δ, полученных по (8) и по (10), не превышает 0.02 (т.е., 2%). Это хорошо заметно на рис. 1, где в указанной области сплошная и пунктирная кривые практически совпадают. Но на рис. 1 видно также, что при $\tfrac{c}{{{{K}_{c}}}} < 10$ расхождение точного значения δ, полученного по (8), и приближенного по (10) быстро увеличивается, при $\tfrac{c}{{{{K}_{c}}}} = 0.25$ разность этих значений составляет 0.41 (т.е., 41%).

Стоит заметить также, что относительная ошибка уравнения (3), приближенно представленная уравнением (10), равна половине приближенного значения степени диссоциации по (3):

${{\delta }_{{{\text{пр}}}}} \approx \sqrt {\frac{{{{K}_{c}}}}{{4c}}} = \frac{1}{2}\sqrt {\frac{{{{K}_{c}}}}{c}} = \frac{1}{2}{{\alpha }_{{{\text{пр}}}}}.$

Это простое соотношение легко запомнить, оно применимо при том же условии $\tfrac{c}{{{{K}_{c}}}} \geqslant 10,$ что и уравнение (10). Связанное с ним приближенное уравнение (9) можно рассматривать как второе приближение степени диссоциации α, не требующее решения квадратного уравнения. Анализ погрешности показывает, что уравнение (9) применимо при $\tfrac{c}{{{{K}_{c}}}} \geqslant 1$ с относительной ошибкой не более 8% по сравнению с результатом (4).

Учет ион-ионного взаимодействия

При малых концентрациях электролита в водном растворе количество ионов невелико, ион-ионным взаимодействием можно пренебречь. В этих условиях практическая константа диссоциации ${{K}_{c}}$ не зависит от концентрации электролита c и численно равна термодинамической константе диссоциации электролита ${{K}_{a}}.$ С повышением исходной концентрации электролита c концентрации ионов (${{c}_{ + }},$ ${{c}_{ - }}$) в растворе возрастают. При этом может быть достигнут такой уровень концентрации ионов, при котором ион-ионным взаимодействием в растворе пренебречь уже нельзя. Вследствие этого константа диссоциации ${{K}_{c}}$ начинает заметно изменяться с ростом концентрации. Максимальную концентрацию однозарядных ионов (${{c}_{ + }},$ ${{c}_{ - }}$) в водном растворе, при которой допущение ${{K}_{c}} \approx {{K}_{a}}$ не приводит к большой ошибке, можно принять равной 0.001 моль/дм³ (при 298 К для этой концентрации ионов средний ионный коэффициент активности по теории Дебая–Хюккеля ${{\gamma }_{ \pm }} = 0.96,$ и ошибка расчета α при допущении ${{\gamma }_{ \pm }} = 1$ составит около 4%). По этой предельной концентрации ионов можно оценить максимальную концентрацию водного раствора электролита (${{c}_{{\max }}},$ моль/дм³), при которой еще могут быть применимы выражение (4), а также приближенные формулы (3) и (9), с константой диссоциации ${{K}_{c}}.$ Для концентрации ионов (${{c}_{ + }} = {{c}_{ - }}$) с подстановкой α в соответствии с (4) запишем:

$\begin{gathered} {{c}_{ + }} = {{c}_{ - }} = \alpha {{c}_{{\max }}} = \frac{{ - {{K}_{c}} + \sqrt {K_{c}^{2} + 4{{c}_{{\max }}}{{K}_{c}}} }}{2} = \\ = 0.001\,\,\frac{{{\text{моль}}}}{{{\text{д}}{{{\text{м}}}^{{\text{3}}}}}}. \\ \end{gathered} $

Далее из последнего равенства получим выражение для ${{c}_{{\max }}}{\text{:}}$

(13)

$\begin{gathered} {{c}_{{\max }}} = \frac{{4 \times {{{10}}^{{ - 6}}} + 0.004{{K}_{c}}}}{{4{{K}_{c}}}} = \\ = \frac{{1 \times {{{10}}^{{ - 6}}}}}{{{{K}_{c}}}} + 0.001\,\,\frac{{{\text{моль}}}}{{{\text{д}}{{{\text{м}}}^{{\text{3}}}}}}. \\ \end{gathered} $

Видно, что максимальная концентрация электролита ${{c}_{{\max }}}$ зависит от значения константы диссоциации ${{K}_{c}}.$ Результаты расчетов ${{c}_{{\max }}}$ по уравнению (13) для бинарных электролитов в зависимости от константы диссоциации ${{K}_{c}}$ приведены в табл. 2.

Таблица 2.

Верхний предел применимости (4) в зависимости от значения ${{K}_{c}}$ (водные растворы, 298 К)

${{K}_{c}}$	${{c}_{{\max }}}$, моль/дм³	${{K}_{c}}$	${{c}_{{\max }}}$, моль/дм³
5 × 10^–7	2	5 × 10^–5	0.021
1 × 10^–6	1	1 × 10^–4	0.011
5 × 10^–6	0.201	5 × 10^–4	0.003
1 × 10^–5	0.101	1 × 10^–3	0.002

По данным табл. 2 можно отметить, что при 298 К для водных растворов бинарных электролитов с константами диссоциации ниже 1 × 10^–4 хорошим приближением для верхнего предела применимости уравнения (4) будет выражение

${{c}_{{\max }}} = \frac{{1 \times {{{10}}^{{ - 6}}}}}{{{{K}_{c}}}}.$

Для описания диссоциации слабых бинарных электролитов при концентрациях, больших ${{c}_{{\max }}},$ или в присутствии избытка сильного фонового электролита, ионные компоненты которого отличаются от ионов слабого электролита, используют термодинамическую константу диссоциации электролита ${{K}_{a}}{\text{:}}$

${{K}_{a}} = \frac{{{{a}_{ + }}{{a}_{ - }}}}{{{{a}_{{{\text{AB}}}}}}} = \frac{{{{\gamma }_{ + }}{{\gamma }_{ - }}}}{{{{\gamma }_{{{\text{AB}}}}}}}\frac{{{{c}_{ + }}{{c}_{ - }}}}{{{{c}_{{{\text{AB}}}}}}} = {{K}_{\gamma }}\frac{{{{c}_{ + }}{{c}_{ - }}}}{{{{c}_{{{\text{AB}}}}}}} = {{K}_{\gamma }}\frac{{{{\alpha }^{2}}c}}{{1 - \alpha }}.$

В этих случаях задача расчета степени диссоциации также может быть сведена к приближенному решению уравнения вида (2), если для электролита известно значение ${{K}_{a}},$ а также если есть возможность оценить значение ${{K}_{\gamma }}$ и считать его постоянным:

$\frac{{{{K}_{a}}}}{{{{K}_{\gamma }}}} = \frac{{{{\alpha }^{2}}c}}{{1 - \alpha }}.$

Постоянство значения ${{K}_{\gamma }}$ для слабого электролита достигается в присутствии большого избытка сильного фонового электролита (метод постоянной ионной среды). При этом в уравнениях (3), (4) и (9) вместо ${{K}_{c}}$ следует использовать отношение $\tfrac{{{{K}_{a}}}}{{{{K}_{\gamma }}}} = {\text{const}},$ ограничение применимости данных уравнений при концентрациях, больших ${{c}_{{\max }}},$ при этом снимается (но сохраняются нижние пределы применимости (3) и (9), указанные выше).

Используя выражение (13), можно найти значение константы диссоциации ${{K}_{c}},$ при котором концентрационная область применения уравнения (3) стягивается в точку. Это значение легко получить из сочетания условий $c \leqslant {{c}_{{\max }}}$ и $c \geqslant 100{{K}_{c}},$ которое дает единственную точку при ${{c}_{{\max }}} = 100{{K}_{c}}{\text{:}}$

$\frac{{1 \times {{{10}}^{{ - 6}}}}}{{{{K}_{c}}}} + 0.001 = 100{{K}_{c}},$

откуда наибольшее значение ${{K}_{c}},$ при котором возможно применение (3) для бинарных электролитов при 298 К в водных растворах, $1.051 \times {{10}^{{ - 4}}} \approx 1 \times {{10}^{{ - 4}}}.$ Для бинарных электролитов, константы диссоциации ${{K}_{c}}$ которых больше указанного значения, использование уравнений (3), (4), (9) при концентрациях, больших ${{c}_{{\max }}},$ предполагает замену ${{K}_{c}}$ отношением ${{{{K}_{a}}} \mathord{\left/ {\vphantom {{{{K}_{a}}} {{{K}_{\gamma }}}}} \right. \kern-0em} {{{K}_{\gamma }}}}.$

Учет диссоциации растворителя

Выражения (2), (4), а также их приближения (3), (6) и (9), имеют ограничения применимости для разбавленных растворов слабых кислот или слабых оснований в условиях, когда концентрации ионов, полученных при диссоциации растворенного электролита, соизмеримы с концентрациями ионов при собственной диссоциации чистого растворителя. В учебной литературе эти ограничения и возможности уточнения расчета в большинстве случаев не рассмотрены. В частности, в учебном пособии [5], целиком посвященном анализу ионных равновесий в растворах, указано лишь, что в сильно разбавленных водных растворах кислот и оснований уравнение (4) может приводить к некорректным значениям pH, но описание уточненного расчета отсутствует.

Рассмотрим расчет концентраций ионов в разбавленном водном растворе слабой одноосновной кислоты HA с учетом собственной диссоциации воды. В данном случае в растворе имеют место равновесия

HA ⇄ H⁺ + A^–	${{K}_{c}} = \frac{{{{c}_{{{{{\text{H}}}^{ + }}}}}{{c}_{{{{{\text{A}}}^{ - }}}}}}}{{{{c}_{{{\text{HA}}}}}}} = {{c}_{{{{{\text{H}}}^{ + }}}}}\frac{{\alpha c}}{{c - \alpha c}} = {{c}_{{{{{\text{H}}}^{ + }}}}}\frac{\alpha }{{1 - \alpha }}$
H₂O ⇄ H⁺ + OH^–	${{K}_{W}} = {{c}_{{{{{\text{H}}}^{ + }}}}}{{c}_{{{\text{O}}{{{\text{H}}}^{ - }}}}}$

Выражение баланса электрических зарядов в растворе включает концентрации ионов всех видов:

${{c}_{{{{{\text{H}}}^{ + }}}}} = {{c}_{{{{{\text{A}}}^{ - }}}}} + {{c}_{{{\text{O}}{{{\text{H}}}^{ - }}}}} = {{c}_{{{{{\text{A}}}^{ - }}}}} + \frac{{{{K}_{W}}}}{{{{c}_{{{{{\text{H}}}^{ + }}}}}}} = \alpha c + \frac{{{{K}_{W}}}}{{{{c}_{{{{{\text{H}}}^{ + }}}}}}}.$

Подставляя ${{c}_{{{{{\text{H}}}^{ + }}}}}$ в соответствии с выражением

${{c}_{{{{{\text{H}}}^{ + }}}}} = {{K}_{c}}\frac{{1 - \alpha }}{\alpha }$

после несложных преобразований получим уравнение, которое можно назвать расширенным законом разведения Оствальда, учитывающим диссоциацию растворителя:

${{K}_{c}} = \frac{{{{\alpha }^{2}}c}}{{1 - \alpha }} + \frac{{{{K}_{W}}}}{{{{K}_{c}}}}\frac{{{{\alpha }^{2}}}}{{{{{(1 - \alpha )}}^{2}}}}.$

В случаях, когда концентрация ${{c}_{{{{{\text{H}}}^{ + }}}}},$ предполагаемая по значению степени диссоциации α из (4), оказывается меньше наблюдаемой при собственной диссоциации воды ($\sqrt {{{K}_{W}}} $), именно диссоциация воды создает буферное равновесие, поддерживающее ${{c}_{{{{{\text{H}}}^{ + }}}}}$ на более высоком уровне. В этих условиях в уравнении (14) преобладает второе слагаемое. При бесконечном разведении раствора первое слагаемое в (14) стремится к нулю, а по значению второго слагаемого можно найти предельную степень диссоциации электролита ${{\alpha }_{\infty }}{\text{:}}$

(15)

${{K}_{c}} = \frac{{{{K}_{W}}}}{{{{K}_{c}}}}\frac{{\alpha _{\infty }^{2}}}{{{{{(1 - {{\alpha }_{\infty }})}}^{2}}}},\,\,\,\,\frac{{{{\alpha }_{\infty }}}}{{1 - {{\alpha }_{\infty }}}} = \frac{{{{K}_{c}}}}{{\sqrt {{{K}_{W}}} }},$

(16)

${{\alpha }_{\infty }} = \frac{1}{{\frac{{\sqrt {{{K}_{W}}} }}{{{{K}_{c}}}} + 1}}.$

Уравнение (14) может быть получено и для слабого бинарного основания.

Для аналитического решения уравнение (14) можно свести к кубическому относительно α. Введем обозначения: $z = \tfrac{c}{{{{K}_{c}}}},$ $y = \tfrac{{\sqrt {{{K}_{W}}} }}{{{{K}_{c}}}}$ и разделим почленно (14) на ${{K}_{c}}{\text{:}}$

(17)

$1 = \frac{{{{\alpha }^{2}}z}}{{1 - \alpha }} + \frac{{{{\alpha }^{2}}{{y}^{2}}}}{{{{{(1 - \alpha )}}^{2}}}}.$

Полученное уравнение (17) несложно преобразуется в кубическое:

(18)

${{\alpha }^{3}} + r{{\alpha }^{2}} + s\alpha + t = 0,$

где

$r = {{(1 - z - {{y}^{2}})} \mathord{\left/ {\vphantom {{(1 - z - {{y}^{2}})} z}} \right. \kern-0em} z},\,\,\,\,s = - {2 \mathord{\left/ {\vphantom {2 z}} \right. \kern-0em} z},\,\,\,\,t = {1 \mathord{\left/ {\vphantom {1 z}} \right. \kern-0em} z}.$

Уравнение (18) в данном случае имеет три различных действительных корня, методы расчета которых известны. Первый его корень всегда больше единицы, второй – всегда меньше нуля. Третий корень имеет значения в интервале (0, ${{\alpha }_{\infty }}$), и, следовательно, только он имеет физический смысл. Для упрощения вида математических выражений расчет корня α кубического уравнения (18) целесообразно разделить на несколько шагов.

Введем дополнительные обозначения:

$\begin{gathered} p = \frac{{3s - {{r}^{2}}}}{3},\,\,\,\,q = \frac{{2{{r}^{3}}}}{{27}} - \frac{{rs}}{3} + t,\,\,\,\,\rho = \sqrt { - \frac{{{{p}^{3}}}}{{27}}} , \\ \varphi = \arccos \left( { - \frac{q}{{2\rho }}} \right). \\ \end{gathered} $

Выполнив расчеты p, q, ρ, $\varphi $ (определяется в радианах), можем вычислить интересующий нас корень кубического уравнения:

(19)

$\alpha = \left[ {2\sqrt[3]{\rho }\cos \left( {\frac{\varphi }{3} + \frac{{4\pi }}{3}} \right)} \right] - \frac{r}{3}.$

Результаты расчета по уравнению (19) степени диссоциации α для слабых одноосновных кислот с различными значениями ${{K}_{c}}$ в водных растворах в зависимости от концентрации при температуре 298 К представлены на рис. 2.

Относительная ошибка расчета степени диссоциации ${{\alpha }_{4}}$ по уравнению (4) по сравнению с результатом ${{\alpha }_{{19}}}$ наиболее точного выражения (19) возрастает с уменьшением концентрации раствора (рис. 3).

Наибольшая относительная ошибка значения ${{\alpha }_{4}}$ по сравнению с ${{\alpha }_{{19}}}$ будет наблюдаться при бесконечном разведении и составит

$\left( {\frac{1}{{{{\alpha }_{\infty }}}} - 1} \right) \times 100\% = \frac{{\sqrt {{{K}_{W}}} }}{{{{K}_{c}}}} \times 100\% .$

К примеру, для уксусной кислоты при 298 К в водном растворе ${{\alpha }_{\infty }} = 0.994$ и во всем интервале концентраций ошибка уравнения (4) не превышает 1% (линия 1 на рис. 3). При концентрации кислоты 0.01 М первое слагаемое в уравнении (14) составляет 99.5%, второе слагаемое – только 0.5%, ошибка уравнения (4) около 0.3%.

При тех же условиях для хлорноватистой (гипохлорной) кислоты HClO с константой диссоциации $3.0 \times {{10}^{{ - 8}}}$ предельная степень диссоциации составит 0.23, ошибка уравнения (4) достигает 5% при концентрации $3.4 \times {{10}^{{ - 6}}}$ моль/дм³. При этой концентрации степень диссоциации, рассчитанная по уравнению (19), равна 0.085 (8.5%), первое слагаемое в (14) составляет 90%, а второе слагаемое – около 10%. При концентрациях раствора HClO, бóльших указанной, для расчета степени диссоциации можно применять как уравнение (4), так и уравнение (3), поскольку в этом случае $c > 100{{K}_{c}}.$

Погрешность уравнения (4) в области разбавленных растворов не превысит 1% для слабых кислот или оснований, константа диссоциации которых ${{K}_{c}} \geqslant 100\sqrt {{{K}_{W}}} .$ При 298 К это условие соответствует ${{K}_{c}} \geqslant 1 \times {{10}^{{ - 5}}}.$

Погрешность уравнения (4) будет не более 5% для слабых кислот или оснований с константой диссоциации ${{K}_{c}} \geqslant 20\sqrt {{{K}_{W}}} .$ При 298 К это условие дает ${{K}_{c}} \geqslant 2 \times {{10}^{{ - 6}}}.$ Электролит, для которого ${{K}_{c}} = 2 \times {{10}^{{ - 6}}},$ представляют линии 2 на рис. 2 и на рис. 3.

Для слабой кислоты, у которой в данных условиях ${{K}_{c}} = 1 \times {{10}^{{ - 6}}},$ ошибка расчета по уравнению (4) более 5% наблюдается при концентрациях, меньших $1.2 \times {{10}^{{ - 7}}}$ моль/дм³, при бесконечном разведении эта ошибка составит 10%.

Если при тех же условиях ${{K}_{c}} = 1 \times {{10}^{{ - 7}}},$ т.е. ${{K}_{c}} = \sqrt {{{K}_{W}}} $ (линии 4 на рис. 2 и на рис. 3), предельная степень диссоциации при бесконечном разведении ${{\alpha }_{\infty }} = 0.5,$ и 5-процентная ошибка уравнения (4) достигается уже при концентрации $1.2 \times {{10}^{{ - 6}}}$ моль/дм³, а предельная ошибка при бесконечном разведении составляет 100%.

Для слабой кислоты с константой диссоциации $6 \times {{10}^{{ - 10}}}$ (HCN) в работе [6] уравнение (4) считается в принципе не применимым. Ошибка расчета степени диссоциации по (4) по сравнению с (19) более 5% в этом случае наблюдается при концентрациях, меньших $1.6 \times {{10}^{{ - 4}}}$ моль/дм³. При концентрациях, бóльших указанной, отношение ${c \mathord{\left/ {\vphantom {c {{{K}_{c}}}}} \right. \kern-0em} {{{K}_{c}}}}$ значительно более 100, и вместо (4) можно использовать уравнение (3).

Для слабой кислоты или слабого основания в водном растворе с помощью уравнения (19) можно найти нижний предел концентрации (${{c}_{{\min }}},$ моль/дм³) при 298 К, при котором ошибка уравнения (4) по сравнению с (19) достигает 5% (табл. 3). Логарифм ${{c}_{{\min }}}$ линейно зависит от логарифма константы диссоциации, уравнение этой зависимости для электролитов с константой диссоциации ${{K}_{c}} < 2 \times {{10}^{{ - 6}}}$ найдено в виде

$\lg {{c}_{{\min }}} = - 12.6 - 0.954\lg {{K}_{c}}.$

Таблица 3.

Нижний предел ${{c}_{{\min }}}$ применимости (4) для слабых бинарных кислот или оснований в зависимости от значения ${{K}_{c}}$ (водные растворы, 298 К)

${{K}_{c}}$	${{c}_{{\min }}}$, моль/дм³	${c \mathord{\left/ {\vphantom {c {{{K}_{c}}}}} \right. \kern-0em} {{{K}_{c}}}}$	${{K}_{c}}$	${{c}_{{\min }}}$, моль/дм³	${c \mathord{\left/ {\vphantom {c {{{K}_{c}}}}} \right. \kern-0em} {{{K}_{c}}}}$
1 × 10^–6	1.2 × 10^–7	0.123	5 × 10^–8	2.1 × 10^–6	42.0
8 × 10^–7	1.7 × 10^–7	0.207	2 × 10^–8	5.1 × 10^–6	253
5 × 10^–7	2.7 × 10^–7	0.540	1 × 10^–8	1.0 × 10^–5	996
2 × 10^–7	6.0 × 10^–7	3.01	5 × 10^–9	2.0 × 10^–5	3960
1 × 10^–7	1.1 × 10^–6	11.1	6 × 10^–10	1.6 × 10^–4	2.73 × 10⁵

Ограничения применимости уравнения (2) в области малых концентраций могут объяснить дополнительную ошибку при определении предельной электропроводности растворов слабых кислот или оснований по методу Брея–Крауса (примеры использования данного метода в учебной лаборатории приведены в [7]).

ЗАКЛЮЧЕНИЕ

Таким образом, сформулированы критерии применимости уравнений (3) и (4), полученных по закону разведения Оствальда (2) для расчета степени диссоциации слабых бинарных электролитов в разбавленных растворах. Получено выражение второго приближения для степени диссоциации слабых бинарных электролитов (9), применимое при $\tfrac{c}{{{{K}_{c}}}} \geqslant 1.$ Для слабых кислот и оснований рассмотрены выражение расширенного закона разведения Оствальда (14) с учетом собственной диссоциации растворителя и его точное решение (19) относительно степени диссоциации электролита.

1. Получено выражение (8) для относительной ошибки приближенного расчета степени диссоциации электролита по уравнению (3) по сравнению с (4). Уравнение (3) является приближением уравнения (4) с ошибкой не более 5.1% при условии $\tfrac{c}{{{{K}_{c}}}} > 100$ или $c > 100{{K}_{c}}.$ В области концентраций $c < 100{{K}_{c}}$ ошибка приближенного расчета степени диссоциации по уравнению (3) будет больше 5% и быстро увеличивается с уменьшением концентрации электролита.

2. Для расчета погрешности уравнения (3) возможно использование приближенной формулы (10), которая правильно характеризует ошибку формулы (3) при не очень малых значениях отношения $\tfrac{c}{{{{K}_{c}}}}.$ При $\tfrac{c}{{{{K}_{c}}}} \geqslant 10$ разность значений, полученных по (8) и (10), не превышает 0.02 (т.е., 2%).

3. Для практических расчетов удобно простое следствие уравнения (10): относительная ошибка уравнения (3) равна половине приближенного значения степени диссоциации по (3). Связанное с ним уравнение (9) можно рассматривать как второе приближение для степени диссоциации слабых бинарных электролитов, которое применимо при $\tfrac{c}{{{{K}_{c}}}} \geqslant 1$ с ошибкой, не превышающей 8% по сравнению с результатом (4).

4. Для водных растворов слабых бинарных электролитов при температуре 298 К верхний предел области концентраций (${{c}_{{\max }}},$ моль/дм³), в которой могут быть применимы уравнения (3), (4) и (9) в приближении ${{K}_{c}} = {\text{const}},$ определяется выражением (13). При ${{K}_{c}} < 1 \times {{10}^{{ - 4}}}$ значение ${{c}_{{\max }}}$ с достаточной точностью равно ${{1 \times {{{10}}^{{ - 6}}}} \mathord{\left/ {\vphantom {{1 \times {{{10}}^{{ - 6}}}} {{{K}_{c}}}}} \right. \kern-0em} {{{K}_{c}}}}.$ При концентрациях, больших ${{c}_{{\max }}},$ использование уравнений (3), (4) и (9) возможно после замены ${{K}_{c}}$ отношением ${{{{K}_{a}}} \mathord{\left/ {\vphantom {{{{K}_{a}}} {{{K}_{\gamma }}}}} \right. \kern-0em} {{{K}_{\gamma }}}}$ с учетом ограничений применимости (3), (9) и зависимости ${{K}_{\gamma }}$ от концентрации. В присутствии избытка сильного фонового электролита ${{K}_{\gamma }} = {\text{const}}$ и, следовательно, ${{{{K}_{a}}} \mathord{\left/ {\vphantom {{{{K}_{a}}} {{{K}_{\gamma }}}}} \right. \kern-0em} {{{K}_{\gamma }}}} = {\text{const}}.$

5. Для слабых кислот или слабых оснований применимость уравнения (4), а также его приближений (3), (6), (9), в области разбавленных растворов ограничена необходимостью учета собственной диссоциации растворителя. В случае водных растворов учет диссоциации воды – расчет по уравнению (19) – необходим для бинарных электролитов с константой диссоциации ${{K}_{c}} < 20\sqrt {{{K}_{W}}} $ (что соответствует ${{K}_{c}} < 2 \times {{10}^{{ - 6}}}$ при 298 К). Максимальная ошибка значения степени диссоциации, найденного по уравнению (4), по сравнению с результатом более точного расчета по (19) наблюдается при бесконечном разведении, при ${{K}_{c}} = 20\sqrt {{{K}_{W}}} $ она составляет 5%.

6. Для слабых кислот или слабых оснований с константой диссоциации ${{K}_{c}} < 20\sqrt {{{K}_{W}}} $ в водных растворах интервал применимости уравнения (4) ограничен нижним пределом концентрации (${{c}_{{\min }}},$ моль/дм³), при котором ошибка (4) по сравнению с (19) достигает 5%. Логарифм ${{c}_{{\min }}}$ в зависимости от логарифма константы диссоциации при 298 К с достаточной точностью описывается уравнением