1. На главную
  2. Электронные версии
  3. Электрохимия
  4. T. 58, № 9, 2022

Электрохимия, 2022, T. 58, № 9, стр. 491-495

Применение флуктуационно-диссипационной концепции Эйнштейна к анализу электрохимического шумового сопротивления

Б. М. Графов a, *, А. Л. Клюев a, А. Д. Давыдов a

a Институт физической химии и электрохимии им. А.Н. Фрумкина РАН
119071 Москва, Ленинский просп., 31, корп. 4, Россия

* E-mail: boris.grafov@yandex.ru

Поступила в редакцию 28.12.2021
После доработки 04.03.2022
Принята к публикации 09.03.2022

Полный текст (PDF)

Аннотация

В рамках флуктуационно-диссипационной концепции Эйнштейна проведен теоретический анализ шумового сопротивления для двух классических электрохимических цепей переменного тока: Эршлера–Рэндлса и Фрумкина–Мелик-Гайказяна. Показано, что при увеличении периода считывания шумового сигнала шумовое сопротивление цепи Эршлера–Рэндлса стремится к предельному значению, которое совпадает с сопротивлением замедленного разряда. Асимптотическое поведение цепи Фрумкина–Мелик-Гайказяна имеет другой характер. При увеличении периода считывания шумового сигнала кривая шумового сопротивления цепи Фрумкина–Мелик-Гайказяна переходит в прямую, наклон которой обратно пропорционален термодинамической емкости электрода. Флуктуационно-диссипационная концепция Эйнштейна может быть применена к теоретическому анализу шумового сопротивления и других электрохимических цепей переменного тока.

Ключевые слова: электрохимический шум, флуктуационно-диссипационная концепция Эйнштейна, шумовое сопротивление, цепь Эршлера–Рэндлса, цепь Фрумкина–Мелик-Гайказяна

ВВЕДЕНИЕ

Понятие шумового сопротивления (${{R}_{{{\text{noise}}}}}$) широко используется в шумовом анализе электрохимических систем [1–12]. Стандартным определением шумового сопротивления (${{R}_{{{\text{noise}}}}}$) служит уравнение (1):

(1)
${{R}_{{{\text{noise}}}}} = \frac{{\sqrt {\left\langle {{{\varepsilon }^{2}}} \right\rangle } }}{{\sqrt {\left\langle {{{i}^{2}}} \right\rangle } }}~~.$

В уравнении (1) $\left( {\left\langle {{{\varepsilon }^{2}}} \right\rangle } \right)$ представляет собой дисперсию случайного напряжения ($\varepsilon $) в разомкнутой цепи, а $\left( {\left\langle {{{i}^{2}}} \right\rangle } \right)$ – дисперсию случайного электрического тока (i) в режиме короткого замыкания. Угловые скобки обозначают статистическое усреднение. Согласно (1), шумовое сопротивление равно отношению стандартного отклонения потенциального шума к стандартному отклонению токового шума.

В основе уравнения (1) лежат два флуктуационно-диссипационных соотношения Найквиста [13–17] для резистора c сопротивлением ($R$):

(2)
$\left\langle {{{i}^{2}}} \right\rangle = 4kT{{R}^{{ - 1}}}B,$
(3)
$\left\langle {{{\varepsilon }^{2}}} \right\rangle = 4kTRB,$
где ($kT$) – произведение постоянной Больцмана ($k$) и температуры ($T$), ($B$) – частотная полоса пропускания измерительной аппаратуры. Из (2) и (3) находим:

(4)
$\frac{{\sqrt {\left\langle {{{\varepsilon }^{2}}} \right\rangle } }}{{\sqrt {\left\langle {{{i}^{2}}} \right\rangle } }} = R.$

Сопоставление уравнений (1) и (4) показывает, что согласно флуктуационно-диссипационным соотношениям Найквиста шумовое сопротивление резистора (${{R}_{{{\text{noise}}}}}$) совпадает с его электрическим сопротивлением ($R$). Если исследуемая цепь является более сложной, чем простой резистор, то уравнение (1) определяет некоторое эффективное шумовое сопротивление изучаемой электрохимической цепи.

Первые работы по теории броуновского движения были выполнены в рамках флуктуационно-диссипационной концепции Эйнштейна [18‒20]. Флуктуационно-диссипационная концепция Эйнштейна будет применена в настоящей работе. В случае резистора пара флуктуационно-диссипационных соотношений Эйнштейна включает уравнение (5) для дисперсии $\left( {\left\langle {{{q}^{2}}} \right\rangle } \right)$ случайного количества электричества ($q$), измеряемого в режиме короткого замыкания резистора, и уравнение (6) для дисперсии $\left( {\left\langle {{{\psi }^{2}}} \right\rangle } \right)$ потенциальной броуновской координаты ($\psi $), измеряемой в режиме разомкнутой цепи.

(5)
$\left\langle {{{q}^{2}}} \right\rangle = 2kT{{R}^{{ - 1}}}\tau ,$
(6)
$\left\langle {{{\psi }^{2}}} \right\rangle = 2kTR\tau .$

Время ($\tau $) представляет собой верхний предел интегрирования как в интеграле, определяющем токовую броуновскую координату ($q$), так и в интеграле, определяющем потенциальную броуновскую координату ($\psi $).

(7)
$q = \int\limits_0^\tau {i\left( {t{\kern 1pt} '} \right)dt{\kern 1pt} '} ,\,\,\,\,\psi = \int\limits_0^\tau {\varepsilon \left( {t{\kern 1pt} '} \right)dt{\kern 1pt} '} .$

Одновременно, время ($\tau $) является периодом считывания как броуновской координаты ($q$), так и броуновской координаты ($\psi $).

Из уравнений (5) и (6) находим

(8)
$\frac{{\sqrt {\left\langle {{{\psi }^{2}}} \right\rangle } }}{{\sqrt {\left\langle {{{q}^{2}}} \right\rangle } }} = R.$

Уравнение (8) показывает, что в рамках флуктуационно-диссипационной концепции Эйнштейна шумовое сопротивление электрохимической цепи целесообразно определить в соответствии с уравнением

(9)
${{R}_{{{\text{noise}}}}} = \frac{{\sqrt {\left\langle {{{\psi }^{2}}} \right\rangle } }}{{\sqrt {\left\langle {{{q}^{2}}} \right\rangle } }}.$

Уравнение (9) существенно отличается от уравнения (1). Видно, что вместо дисперсии $\left( {\left\langle {{{\varepsilon }^{2}}} \right\rangle } \right)$ потенциального электрохимического шума стоит дисперсия $\left( {\left\langle {{{\psi }^{2}}} \right\rangle } \right)$ потенциальной броуновской координаты, а вместо дисперсии $\left( {\left\langle {{{i}^{2}}} \right\rangle } \right)$ токового электрохимического шума стоит дисперсия $\left( {\left\langle {{{q}^{2}}} \right\rangle } \right)$ токовой броуновской координаты. Согласно уравнению (9) шумовое сопротивление в концепции Эйнштейна равно отношению стандартного отклонения потенциального броуновской координаты к стандартному отклонению токовой броуновской координаты.

Если электрохимическая цепь состоит не из одного резистора и является более сложной, то формулу (9) можно использовать для нахождения некоторого эффективного шумового сопротивления в концепции Эйнштейна.

Цель настоящей работы – применить флуктуационно-диссипационную концепцию Эйнштейна для анализа шумового сопротивления двух классических электрохимических цепей переменного тока: Эршлера–Рэндлса [21, 22] и Фрумкина–Мелик-Гайказяна [23].

Ранее флуктуационно-диссипационная концепция Эйнштейна к анализу электрохимического шумового сопротивления не применялась.

ФЛУКТУАЦИОННО-ДИССИПАЦИОННАЯ КОНЦЕПЦИЯ ЭЙНШТЕЙНА

Формулы Эйнштейна (5) и (6) для резистора имеют обобщение на произвольные равновесные системы [24–26] в виде уравнений (10) и (11).

(10)
$\left\langle {{{q}^{2}}} \right\rangle = 2kT{{Q}_{E}}\left( \tau \right),$
(11)
$\left\langle {{{\psi }^{2}}} \right\rangle = 2kT{{{{\Psi }}}_{I}}\left( \tau \right).$

Величина (${{Q}_{E}}$) есть макроскопический линейный отклик в момент времени ($\tau $) в виде количества электричества, прошедшего через изучаемую систему после наложения единичной ступеньки напряжения (${{E}_{1}}\left( \tau \right)$). Определение (${{E}_{1}}\left( \tau \right)$) записывается в следующем виде:

$\left( {{{E}_{1}}\left( \tau \right) = 0\,\,~\left( {{\text{при}}\,\,\tau < 0} \right),\,\,\,\,{{E}_{1}}\left( \tau \right) = 1\,\,({\text{при}}\,\,\tau > 0)} \right).$

Аналогичный смысл имеет макроскопическая величина (${{\Psi }_{I}}$). Она представляет собой макроскопический линейный отклик в момент времени ($\tau $) потенциальной броуновской координаты на единичную ступеньку электрического тока (${{I}_{1}}\left( \tau \right)$):

$\left( {{{I}_{1}}\left( \tau \right) = 0\,\,\left( {{\text{при}}\,\,\tau < 0} \right),\,\,\,\,{{I}_{1}}\left( \tau \right) = 1\,\,({\text{при}}\,\,\tau > 0)} \right).$

Из уравнений (10) и (11) находим общее выражение (12) для шумового сопротивления в концепции Эйнштейна:

(12)
${{R}_{{{\text{noise}}}}} = \frac{{\sqrt {{{{{\Psi }}}_{I}}\left( \tau \right)} }}{{\sqrt {{{Q}_{E}}\left( \tau \right)} }}.$

Уравнение (12) применимо для любой равновесной электрохимической цепи переменного тока. Уравнение (12) позволяет рассчитать шумовое сопротивление любой равновесной системы, исходя из свойств макроскопического линейного отклика. В следующем разделе статьи уравнение (12) применено для расчета шумового сопротивления двух классических электрохимических цепей переменного тока.

ШУМОВОЕ СОПРОТИВЛЕНИЕ ЭЛЕКТРОХИМИЧЕСКОЙ ЦЕПИ ЭРШЛЕРА–РЭНДЛСА В КОНЦЕПЦИИ ЭЙНШТЕЙНА

Модельная цепь Эршлера–Рэндлса (рис. 1) содержит емкость двойного электрического слоя ($C$) и фарадеевское сопротивление (${{R}_{{\text{F}}}}$).

Рис. 1.

Электрохимическая цепь Эршлера–Рэндлса.

Вычисление макрокопического линейного отклика (${{Q}_{E}}$) токовой броуновской координаты ($q$) для цепи Эршлера–Рэндлса приводит к результату:

(13)
${{Q}_{E}}\left( \tau \right) = {{\left[ {\tau + {{R}_{{\text{F}}}}C} \right]} \mathord{\left/ {\vphantom {{\left[ {\tau + {{R}_{{\text{F}}}}C} \right]} {{{R}_{{\text{F}}}}}}} \right. \kern-0em} {{{R}_{{\text{F}}}}}}~.$

Макроскопический линейный отклик (${{{{\Psi }}}_{I}}$) потенциальной броуновской координаты ($\psi $) для цепи Эршлера–Рэндлса имеет следующий вид:

(14)
${{{{\Psi }}}_{I}}\left( \tau \right) = {{R}_{{\text{F}}}}\left[ {\tau - {{R}_{{\text{F}}}}C + {{R}_{{\text{F}}}}C{\text{exp}}\left( { - \frac{\tau }{{{{R}_{{\text{F}}}}C}}} \right)} \right].$

Подставив (13) и (14) в (12), приходим к теоретическому выражению (15) для нормированного шумового сопротивления (${{{{R}_{{{\text{noise}}}}}} \mathord{\left/ {\vphantom {{{{R}_{{{\text{noise}}}}}} {{{R}_{{\text{F}}}}}}} \right. \kern-0em} {{{R}_{{\text{F}}}}}}$) цепи Эршлера–Рэндлса.

(15)
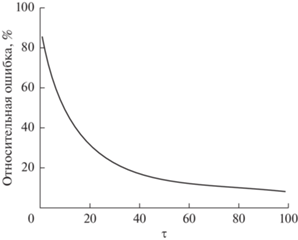
$\frac{{{{R}_{{{\text{noise}}}}}}}{{{{R}_{{\text{F}}}}}} = \sqrt {{{{\left[ {\frac{{\frac{\tau }{{{{R}_{{\text{F}}}}C}} - 1 + {\text{exp}}\left( { - \frac{\tau }{{{{R}_{{\text{F}}}}C}}} \right)}}{{\frac{\tau }{{{{R}_{{\text{F}}}}C}} + 1}}} \right]}}^{{~~}}}} .$

Графическое представление уравнения (15) дано на рис. 2. Видно, что в области малых периодов считывания ($\tau \ll {{R}_{{\text{F}}}}C$) шумовое сопротивление (${{R}_{{{\text{noise}}}}}$) линейно растет с увеличением периода считывания ($\tau $). В области больших периодов считывания ($\tau \gg {{R}_{{\text{F}}}}C$) шумовое сопротивление (${{R}_{{{\text{noise}}~}}}$) асимптотически приближается к сопротивлению электрохимического разряда (${{R}_{{\text{F}}}}$).

Рис. 2.

Зависимость нормированного шумового сопротивления (${{{{R}_{{{\text{noise}}}}}} \mathord{\left/ {\vphantom {{{{R}_{{{\text{noise}}}}}} {{{R}_{{\text{F}}}}}}} \right. \kern-0em} {{{R}_{{\text{F}}}}}}$) для электрохимической цепи Эршлера–Рэндлса от нормированного периода считывания (${\tau \mathord{\left/ {\vphantom {\tau {{{R}_{{\text{F}}}}C}}} \right. \kern-0em} {{{R}_{{\text{F}}}}C}}$) электрохимической броуновской координаты. Кривая 1 соответствует уравнению (15). Прямая 2 является асимптотой для кривой 1.

ШУМОВОЕ СОПРОТИВЛЕНИЕ ЭЛЕКТРОХИМИЧЕСКОЙ ЦЕПИ ФРУМКИНА–МЕЛИК-ГАЙКАЗЯНА В КОНЦЕПЦИИ ЭЙНШТЕЙНА

Модельная цепь Фрумкина–Мелик-Гайказяна (рис. 3) содержит высокочастотную емкость электрода ($C$), адсорбционную емкость (${{C}_{A}}$) и сопротивление замедленной адсорбции (${{R}_{A}}$).

Рис. 3.

Электрохимическая цепь Фрумкина–Мелик-Гайказяна.

Макроскопический линейный отклик потенциальной броуновской координаты цепи Фрумкина–Мелик-Гайказяна записывается в виде уравнения (16):

(16)
$\begin{gathered} {{{{\Psi }}}_{I}}\left( \tau \right) = \frac{{C_{A}^{2}{{R}_{A}}\tau }}{{{{{\left( {{{C}_{A}} + C} \right)}}^{2}}}} + \frac{{{{\tau }^{2}}}}{{2\left( {{{C}_{A}} + C} \right)}} - \\ - \,\,\frac{{R_{A}^{2}CC_{A}^{3}}}{{{{{\left( {{{C}_{A}} + C} \right)}}^{3}}}}\left( {1 - \exp \left( { - \frac{{\left( {{{C}_{A}} + C} \right)\tau }}{{C{{R}_{A}}{{C}_{A}}}}} \right)} \right). \\ \end{gathered} $

Макроскопический линейный отклик токовой броуновской координаты цепи Фрумкина–Мелик-Гайказяна дается уравнением

(17)
${{Q}_{E}}\left( \tau \right) = \left( {C + {{C}_{A}}_{~} - {{C}_{A}}\exp \left( { - \frac{\tau }{{{{R}_{A}}{{C}_{A}}}}} \right)} \right).$

Отсюда находим для шумового сопротивления цепи Фрумкина–Мелик-Гайказяна, нормированного на сопротивление замедленной адсорбции (${{R}_{A}}$):

(18)
$\frac{{{{R}_{{{\text{noise}}}}}}}{{{{R}_{A}}}} = \sqrt {\frac{{\frac{{C_{A}^{2}{{R}_{A}}\tau }}{{{{{\left( {{{C}_{A}} + C} \right)}}^{2}}}} + \frac{{{{\tau }^{2}}}}{{2\left( {{{C}_{A}} + C} \right)}} - \,\,\frac{{R_{A}^{2}CC_{A}^{3}}}{{{{{\left( {{{C}_{A}} + C} \right)}}^{3}}}}\left( {1 - \exp \left( { - \frac{{\left( {{{C}_{A}} + C} \right)\tau }}{{C{{R}_{A}}{{C}_{A}}}}} \right)} \right)}}{{R_{A}^{2}\left( {C + {{C}_{A}}_{~} - {{C}_{A}}\exp \left( { - \frac{\tau }{{{{R}_{A}}{{C}_{A}}}}} \right)} \right)}}} .$

Из уравнения (18) следует, что при больших временах наблюдения ($\tau $) шумовое сопротивление (${{R}_{{{\text{noise}}}}}$) цепи Фрумкина–Мелик-Гайказяна имеет асимптоту

(19)
${{R}_{{{\text{noise}}}}} = \frac{\tau }{{\sqrt 2 \left( {{{C}_{A}} + C} \right)}}.$

Сумма емкостей (${{C}_{A}} + C$), стоящая в знаменателе уравнения (19), представляет собой термодинамическую емкость электрода.

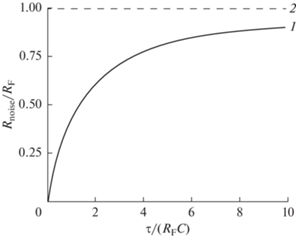
Графическая иллюстрация выражения (18) для шумового сопротивления электрохимической цепи Эршлера–Рэндлса приведена на рис. 4.

Рис. 4.

Зависимость нормированного (${{{{R}_{{{\text{noise}}}}}} \mathord{\left/ {\vphantom {{{{R}_{{{\text{noise}}}}}} {{{R}_{A}}}}} \right. \kern-0em} {{{R}_{A}}}}$) шумового сопротивления для электрохимической цепи Фрумкина–Мелик-Гайказяна от периода считывания ($\tau $) при соблюдении условия (20). Кривая 1 рассчитана по уравнению (18). Прямая 2 рассчитана по уравнению (19).

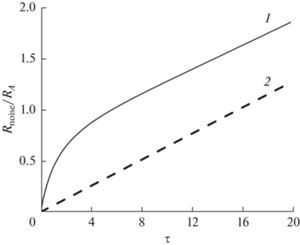
Для графического представления уравнения (18) было принято, что

(20)
${{R}_{A}}C = 1,\,\,\,\,{{{{C}_{A}}} \mathord{\left/ {\vphantom {{{{C}_{A}}} C}} \right. \kern-0em} C} = 10.$

Видно, что кривая шумового сопротивления цепи Фрумкина–Мелик-Гайказяна, начиная с времени наблюдения ($\tau $), равного 10, идет с наклоном, который весьма слабо отличается от наклона асимптоты (19). Количественное расхождение кривой шумового сопротивления и ее асимптоты представлено на рис. 5. Видно, что при $\tau ,$ равном 100 ($\tau = 100{{R}_{A}}C$), относительное расхождение составляет менее 10%.

Рис. 5.

Относительное расхождение между кривой шумового сопротивления и ее асимптотой для электрохимической цепи Фрумкина–Мелик-Гайказяна.

ЗАКЛЮЧЕНИЕ

Флуктуационно-диссипационная концепция Эйнштейна применена для анализа шумового сопротивления двух классических электрохимических цепей переменного тока: Эршлера–Рэндлса и Фрумкина–Мелик-Гайказяна. Применение концепции Эйнштейна в данном случае имеет ряд преимуществ. Во-первых, флуктуационно-диссипационная концепция Эйнштейна не требует знания такого трудноопределяемого параметра обработки электрохимического шума, как частотная полоса пропускания измерительной аппаратуры. Во-вторых, концепция Эйнштейна имеет дело с электрохимической броуновской координатой, которая может быть измерена аналого-цифровыми преобразователями с сигма-дельта архитектурой, например сигма-дельта преобразователем AD7176-2 компании Analog Device. В-третьих, флуктуационно-диссипационная концепция Эйнштейна допускает как непрерывное, так и дискретное описание электрохимического шума.

Установлено, что шумовые сопротивления рассмотренных цепей переменного тока при низких скоростях считывания выходного сигнала обладают принципиально разной асимптотикой. Шумовое сопротивление в концепции Эйнштейна для цепи Фрумкина–Мелик-Гайказяна асимптотически растет пропорционально периоду считывания. При этом наклон асимптотической прямой обратно пропорционален термодинамической емкости электрода. Шумовое сопротивление в концепции Эйнштейна для цепи Эршлера–Рэндлса асимптотически (при больших периодах считывания) выходит на постоянное значение, равное сопротивлению замедленного разряда.

На примере двух классических цепей переменного тока, Эршлера–Рэндлса и Фрумкина–Мелик-Гайказяна, показано, что флуктуационно-диссипационная концепция Эйнштейна является мощным инструментом, позволяющим проводить теоретический анализ шумового сопротивления равновесных электрохимических систем.

Список литературы

  1. Bierwagen, G.P., Calculation of noise resistance from simultaneous electrochemical voltage and current noise data, J. Electrochem. Soc., 1994, vol. 141, p. L155.

  2. Chen, J.F. and Bogaerts, W.F., The physical meaning of noise resistance, Corros. Sci., 1995, vol. 37, p.1839.

  3. Bertocci, U., Gabrielli, C., Huet, F., and Keddam, M., Noise resistance applied to corrosion measurements: I. Theoretical analysis, J. Electrochem. Soc., 1997, vol. 144, p. 31.

  4. Bautista, A., Bertocci, U., and Huet, F., Noise resistance applied to corrosion measurements: V. Influence of electrode asymmetry, J. Electrochem. Soc., 2001, vol. 148, p. B412.

  5. Cottis, R.A., Interpretation of electrochemical noise data, Corrosion, 2001, vol. 57, p. 265.

  6. Lowe, A.M., Eren, H., and Bailey, S.I., Electrochemical noise analysis: detection of electrode asymmetry, Corros. Sci., 2003, vol. 45, p. 941.

  7. Rivera, A.L. and Castaño, V.M., Corrosion analysis by electrochemical noise: A teaching approach, J. Mater. Educ., 2012, vol. 34, p. 5.

  8. Jamali, S.S. and Mills, D.J., A critical review of electrochemical noise measurement as a tool for evaluation of organic coatings, Prog.Org. Coat., 2016, vol. 95, p. 26.

  9. Tang, Y., Dai, N., Wu, J., Jiang, Y., and Li, J., Effect of surface roughness on pitting corrosion of 2205 duplex stainless steel investigated by electrochemical noise measurements, Materials, 2019, vol. 12, p. 738.

  10. Obot, I.B., Onyeachu, I.B., Zeino, A., and Umoren, S.A., Electrochemical noise (EN) technique: review of recent practical applications to corrosion electrochemistry research, J. Adhes. Sci. Technol., 2019, vol. 33, p. 1453.

  11. Xia, D.H., Song, S., Behnamian, Y., Hu, W., Cheng, Y.F., Luo, J.L., and Huet, F., Review-Electrochemical noise applied in corrosion science: theoretical and mathematical models towards quantitative analysis, J. Electrochem. Soc., 2020, vol. 167, p. 081507.

  12. Тимашев, С.Ф. Обобщение флуктуационно-диссипационных соотношений. Журн. физ. химии. 2005. Т. 79. № 11. С. 1938.

  13. Nyquist, H., Thermal agitation of electric charge in conductors, Phys. Rev., 1928, vol. 32, p. 110.

  14. Johnson, J.B., Thermal agitation of electricity in conductors, Phys. Rev., 1928, vol. 32, p. 97.

  15. Callen, H.B. and Welton, T.A., Irreversibility and generalized noise, Phys. Rev., 1951, vol. 83, p. 34.

  16. Johnson, P.J., Clark, C.D., and Artus, R.G., The determination of electrical conductivity by thermal noise measurements, J. Phys. D: Appl. Phys., 1986, vol. 19, p. 835.

  17. Gomila, G., Pennetta, C., Reggiani, L., Sampietro, M., Ferrari, G., and Bertuccio, G., Shot noise in linear macroscopic resistors, Phys. Rev. Lett., 2004, vol. 92, p. 226601.

  18. Einstein, A., On the movement of small particles suspended in a stationary liquid demanded by the molecular-kinetic theory of heat, Ann. Phys., 1905, vol. 17, p. 549.

  19. Einstein, A., Elementare theorie der brownschen bewegung, Z. Elektrochem. Angew. Phys. Chem., 1908 Apr 24; 14(17):235-9.

  20. Coffey, W. and Kalmykov, Y.P., The Langevin Equation: with Applications to Stochastic Problems in Physics, Chemistry and Electrical Engineering, in World Scientific Series in Contemporary Chemical Physics, World Scientific, 2012, vol. 27.

  21. Ershler, B.V., Investigation of electrode reactions by the method of charging-curves and with the aid of alternating currents, Disc. Faraday Soc., 1947, vol. 1, p. 269.

  22. Randles, J.E.B., Kinetics of rapid electrode reactions, Disc. Farad. Soc., 1947, vol. 1, p. 11.

  23. Фрумкин, А.Н., Мелик-Гайказян, В.И. Определение кинетики адсорбции органических веществ по измерениям емкости и проводимости границы электрод/раствор переменным током. Докл. АН СССР. 1951. Т. 77. С. 855.

  24. Bouchaud, J.P. and Georges, A., Anomalous diffusion in disordered media: statistical mechanisms, models and physical applications, Phys. Rep., 1990, vol. 195, p. 127.

  25. Barkai, E. and Fleurov, V.N., Generalized Einstein relation: A stochastic modeling approach, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, 1998, vol. 58, p. 1296.

  26. Gradenigo, G., Sarracino, A., Villamaina, D., and Vulpiani, A., Einstein relation in superdiffusive systems, J. Stat. Mech.: Theory Exp., 2012, p. L06001.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска содержание выпуска

Электрохимия

Архивы выпусков Информация о журнале Отправить рукопись в журнал