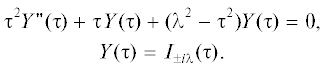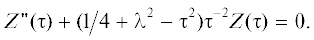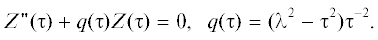Известия РАН. Физика атмосферы и океана, 2020, T. 56, № 1, стр. 104-111
Внутренние гравитационые волны в океане с разнонаправленными сдвиговыми течениями
В. В. Булатов a, *, Ю. В. Владимиров a, **
a Институт проблем механики им. А.Ю. Ишлинского РАН
119526 Москва, просп. Вернадского 101, к. 1, Россия
* E-mail: internalwave@mail.ru
** E-mail: vladimyura@yandex.ru
Поступила в редакцию 24.07.2019
После доработки 03.09.2019
Принята к публикации 25.09.2019
Аннотация
Рассмотрена задача о построении решений, описывающих внутренние гравитационных волны в стратифицированной среде конечной глубины с разнонаправленными сдвиговыми течениями. Рассмотрено модельное постоянное распределение частоты Брента–Вяйсля и линейная зависимость сдвигового течения по глубине и получено аналитическое решение задачи, которое выражается через модифицированные функции Бесселя мнимого индекса. С помощью дебаевских асимптотик модифицированной функции Бесселя получены аналитические выражения для дисперсионных соотношений, исследованы фазовые характеристики волновых полей. Исследованы зависимости волновых характеристик возбуждаемых полей от основных параметров использованных моделей стратификации, течений и режимов генерации.
Среди большого многообразия наблюдаемых волновых процессов различной физической природы в океане и атмосфере Земли особый интерес вызывает взаимодействие возбуждаемых волн с гидродинамическими потоками [1–6]. Движение стратифицированной среды является одним из основных факторов, влияющих на динамику внутренних гравитационных волн (ВГВ) как в естественных условиях, так и в технических устройствах. В современных научных исследованиях при анализе динамики ВГВ в природных стратифицированных средах с учетом наличия течений применяются асимптотические методы исследования аналитических моделей волновой генерации. В линейном приближении существующие подходы к описанию волновой картины возбуждаемых полей ВГВ основаны на представлении волновых полей интегралами Фурье и их асимптотическом анализе [7]. В реальных океанических условиях необходимо рассматривать ВГВ, распространяющиеся на фоне средних течений с вертикальным сдвигом скорости, причем вариация скорости по вертикали составляют десятки см/с и м/с, то есть имеет тот же порядок, что и максимальные скорости ВГВ. Такие течения должны существенно сказываться на распространении ВГВ [8–16]. Если масштаб изменения течений по горизонтали много больше длин ВГВ, а масштаб временной изменчивости много больше периодов внутренних волн, то естественной математической моделью является случай стационарных и горизонтальных однородных сдвиговых течений [2–4, 10]. Целью настоящей работы является построение аналитических решений, описывающих поля ВГВ в стратифицированной среде конечной глубины с учетом разнонаправленных сдвиговых течений.
Рассматривается вертикально стратифицированная среда конечной глубины $H$. Пусть $(U(z),V(z))$ – вектор сдвигового течения на горизонте $z$. Исходной для дальнейшего анализа является линеаризованная система уравнений гидродинамики относительно невозмущенного состояния, которая имеет вид [2–4, 10]
(1)
$\begin{gathered} \frac{{{{D}^{2}}}}{{Dt{}^{2}}}\Delta W - \frac{D}{{Dt}}\left( {\frac{{{{d}^{2}}U}}{{dz{}^{2}}}\frac{{\partial W}}{{\partial x}} + \frac{{{{d}^{2}}V}}{{dz{}^{2}}}\frac{{\partial W}}{{\partial y}}} \right) + \\ + \,\,{{N}^{2}}(z){{\Delta }_{2}}W = 0,\,\,\,\,\Delta = {{\Delta }_{2}} + \frac{{{{\partial }^{2}}}}{{\partial {{z}^{2}}}}, \\ {{\Delta }_{2}} = \frac{{{{\partial }^{2}}}}{{\partial x{}^{2}}} + \frac{{{{\partial }^{2}}}}{{\partial {{y}^{2}}}},\,\,\,\,{{N}^{2}}(z) = - \frac{g}{{{{\rho }_{0}}(z)}}\frac{{d{{\rho }_{0}}(z)}}{{dz}}, \\ \end{gathered} $Далее используются следующие предположения. Частота Брента–Вяйсяля предполагается постоянной: $N(z) = N = {\text{const}}.$ Сдвиговое течение предполагается одномерным: $V(z) \equiv 0.$ Функция $U(z)$ – линейная функция глубины: $U(z) = {{U}_{0}}$ + $ + \,\,{{({{U}_{0}} - {{U}_{H}})z} \mathord{\left/ {\vphantom {{({{U}_{0}} - {{U}_{H}})z} H}} \right. \kern-0em} H},$ ${{U}_{0}} = U(0) > 0,$ ${{U}_{H}} = U( - H) < 0.$ Использование данной модельной гидрологии (постоянное распределение частоты плавучести, разнонаправленные сдвиговые течения) широко применяется в реальных океанологических расчетах и позволяет учитывать основные особенности волновой динамики с учетом реальной изменчивости плотности морской среды, наблюдаемой при натурных измерениях ВГВ в океане, а также исследовать задачу аналитически [10–19]. В [9] в том числе с использованием данной модели анализировались результаты многочисленных исследований по натурным измерениям внутренних волн, течений, а также их взаимодействию в различных областях Мирового океана. В [11, 12] рассмотрена генерация ВГВ волн сдвиговым течением в проливе Карские Ворота, причем течение меняется с приливной частотой, и пакеты ВГВ появляются с периодичностью, определяемой сдвиговой неустойчивости течений. Аналогичные результаты получены в [9, 10] на примере Гибралтарского пролива, где рассмотрены измерения течений и ВГВ, амплитуда которых может составлять десятки метров. Многочисленные измерения придонных потоков в глубоководных акваториях Северной Атлантики показывают, что на больших глубинах градиенты сдвиговых скоростей и значения частоты плавучести малы, основные изменения этих гидрофизических параметров наблюдаются в верхних слоях океана на глубинах порядка 100–200 метров, что позволяет использовать предложенную модельную гидрологию и линейную зависимость сдвиговых течений от глубины [8–10, 13, 14]. Также предполагается, что выполнено условие устойчивости Майлса для числа Ричардсона: $Ri = {{N}^{2}}{{\left( {\frac{{dU}}{{dz}}} \right)}^{{ - 2}}} > {1 \mathord{\left/ {\vphantom {1 4}} \right. \kern-0em} 4}$ [1–4]. Характерные значения чисел Ричардсона в акваториях Мирового океана (Атлантический океан, моря Арктического бассейна) при отсутствии динамической неустойчивости течений могут находиться в интервалах от 2 до 20 [8, 9, 13, 14]. Тогда в безразмерных координатах и переменных
(3)
$\begin{gathered} {{\left( {\frac{\partial }{{\partial t}} + M(z)\frac{\partial }{{\partial x}}} \right)}^{2}}\Delta W + {{N}^{2}}(z){{\Delta }_{2}}W = 0, \\ W = 0\,\,\,\,{\text{при}}\,\,\,\,z = 0, - \pi . \\ \end{gathered} $Введенный выше параметр $b$ есть величина обратная квадратному корню из числа Ричардсона: $b = {1 \mathord{\left/ {\vphantom {1 {\sqrt {{\text{Ri}}} }}} \right. \kern-0em} {\sqrt {{\text{Ri}}} }},$ параметр $a$ – отношение амплитуды приповерхностного течения ${{U}_{0}}$ к максимальной групповой скорости распространения ВГВ в океане, равной ${{NH} \mathord{\left/ {\vphantom {{NH} \pi }} \right. \kern-0em} \pi }$ [2, 3, 7]. Решение задачи (3) ищется виде свободных гармонических волн: $W\left( {t,x,y,z} \right)$ = $\varphi (z)exp(i(\omega t - \mu x - \nu y).$ Тогда для определения функции $\varphi (z)$ имеем
(4)
$\begin{gathered} \frac{{{{\partial }^{2}}\varphi }}{{\partial {{z}^{2}}}} + {{k}^{2}}({{(\omega - \mu M(z))}^{{ - 2}}} - 1)\varphi = 0, \\ \varphi = 0\,\,\,\,{\text{при}}\,\,\,\,z = 0, - \pi ,\,\,\,\,{{k}^{2}} = {{\mu }^{2}} + {{\nu }^{2}}. \\ \end{gathered} $В качестве двух линейно независимых решений задачи (4) возьмем
где ${{I}_{{ \pm i\lambda }}}$ – модифицированная функция Бесселя мнимого индекса $i\lambda $, $r(z) = \omega - \mu M(z),$ $\lambda = \sqrt {{{\beta }^{2}} - {1 \mathord{\left/ {\vphantom {1 4}} \right. \kern-0em} 4}} ,$ $\beta = {k \mathord{\left/ {\vphantom {k {b\mu }}} \right. \kern-0em} {b\mu }}.$ Решение, удовлетворяющее граничному условию при $z = 0$ имеет вид: $\varphi (z) = i({{f}_{ + }}(0){{f}_{ - }}(z)$ – $ - \,\,{{f}_{ - }}(0){{f}_{ + }}(z)).$ Функции ${{f}_{ \pm }}(z)$ – комплексно сопряжены, поэтому решение $\varphi (z)$ является действительным. Так как предполагается, что выполнено условие устойчивости Майлса для числа Ричардсона, то ${{b}^{2}} < 4.$ Отсюда в частности следует, что ${{\beta }^{2}} > {1 \mathord{\left/ {\vphantom {1 4}} \right. \kern-0em} 4}$ и значения $\lambda $ действительны. Требование удовлетворения граничному условию при $z = - \pi .$ определяет дисперсионное соотношение(5)
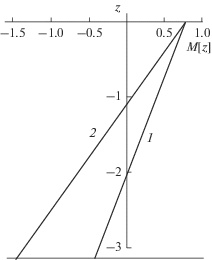
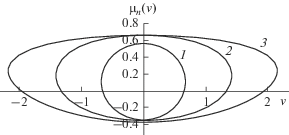
${{I}_{{i\lambda }}}(\beta r(0)){{I}_{{ - i\lambda }}}(\beta r( - \pi )) - {{I}_{{ - i\lambda }}}(\beta r(0)){{I}_{{i\lambda }}}(\beta r( - \pi )) = 0.$В [16] для аналогичной модельной гидрологии (постоянная частота плавучести, линейный профиль сдвигового течения, конечная толщина стратифицированного слоя) получено дисперсионное соотношение в виде, аналогичном (5), и было отмечено, что решение этого уравнения представляет большую математическую трудность. Более сложной задачей является исследование аналитических свойств полученного дисперсионного уравнения, так как это дает возможность получить асимптотические выражения для полей ВГВ при различных режимах волновой генерации. Далее будут изучены основные особенности решений дисперсионного уравнения (5) и построены асимптотические представления решения этого уравнения. Решения дисперсионного уравнения (5) можно представить в виде ${{\omega }_{n}}(\mu ,\nu )$ или ${{\mu }_{n}}(\nu ,\omega ).$ В настоящей работе будет использоваться дисперсионная зависимость виде ${{\mu }_{n}}(\nu ),$ считая $\omega $ фиксированным параметром. Рассматривается гидрологическая модель линейного разнонаправленного сдвигового течения – течение изменяет свое направление с увеличением глубины, то есть придонные и приповерхностные течения разнонаправлены (рис. 1). Далее будут использоваться два модельных распределения сдвигового течения по глубине, обозначаемые на рис. 1 индексами 1 (первая модель) и 2 (вторая модель). В первом случае значения всех параметров следующие: $a = 0.8,$ $b = 0.39,$ $\omega = 0.54,$ ${\text{Ri}} = 6.5$, во втором случае: $a = 0.8,$ $b = 0.72,$ $\omega = 0.54,$ ${\text{Ri}} = 1.9$. В первом случае приповерхностное течение быстрее придонного, во втором случае придонное течение больше по амплитуде приповерхностного. В использованных моделях $a < 1$ это означает, что амплитуды сдвиговых течений не превышают максимальной групповой скорости распространения ВГВ, что наблюдаемо в условиях Мирового океана. Параметр $\omega < 1$ определяет отношение частоты свободной волны к максимальному значению частоты плавучести, данные модельные параметры описывают распространение ВГВ с частотой почти в два раза меньше частоты плавучести, что также наблюдаемо в реальных океанических условиях [8–10, 14]. В использованной модели гидрологии разнонаправленных сдвиговых течений дисперсионные кривые представляют собой замкнутые линии. На рис. 2 изображены дисперсионные кривые первых трех мод для первой модели, на рис. 3 – дисперсионные кривые первых трех мод для второй модели. Каждая дисперсионная кривая пересекает ось $O\nu $ в точках ${{\nu }_{n}}$, значения которых определяются из решения краевой задачи (4) при $\mu = 0$: ${{\nu }_{n}} = \pm \omega n{{(1 - {{\omega }^{2}})}^{{{{ - 1} \mathord{\left/ {\vphantom {{ - 1} 2}} \right. \kern-0em} 2}}}},$ $n = 1,2, \ldots $.
Рис. 2.
Дисперсионные кривые первых трех мод (первая модель), 1 – первая мода, 2 – вторая мода, 3 – третья мода.
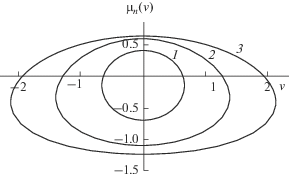
Рис. 3.
Дисперсионные кривые первых трех мод (вторая модель), 1 – первая мода, 2 – вторая мода, 3 – третья мода.
Рассмотрим асимптотические решения дисперсионного уравнения (5), считая большим параметром $\beta $, тогда $\lambda $ можно заменить на $\left| \beta \right|.$ Воспользуемся дебаевской асимптотикой $(\lambda \gg 1)$ модифицированной функции Бесселя мнимого индекса ${{I}_{{ \pm i\lambda }}}(\tau ),$ которая, в отличие от классической асимптотики при $\tau \to \infty ,$ определяет поведение функции ${{I}_{{ \pm i\lambda }}}(\tau )$ при больших значениях как индекса $\lambda $, так и аргумента $\tau .$ Модифицированная функция Бесселя ${{I}_{{ \pm i\lambda }}}(\tau )$ удовлетворяет уравнению [21–23]
С помощью замены $Y(\tau ) = {{Z(\tau )} \mathord{\left/ {\vphantom {{Z(\tau )} {\sqrt \tau }}} \right. \kern-0em} {\sqrt \tau }}$ переменной это уравнение можно представить в виде
При $\lambda \gg {1 \mathord{\left/ {\vphantom {1 4}} \right. \kern-0em} 4}$ уравнение (6) упрощается
Тогда ВКБ асимптотика уравнения (7) в случае $\tau < \lambda ,$ описывающая осциллирующие решения, имеет вид
Для экспоненциально растущих или убывающих решений ВКБ асимптотика уравнения (7) при $\tau > \lambda $ имеет вид
Далее будут рассматриваться только функции ${{I}_{{ - i\lambda }}}(\tau )$ (функция ${{I}_{{ - i\lambda }}}(\tau )$ комплексно сопряжена с ${{I}_{{i\lambda }}}(\tau )$ и ${{I}_{{i\lambda }}}( - \tau ) = \exp ( - \pi \lambda ){{I}_{{i\lambda }}}(\tau )$). Для нахождения множителей ${{D}_{ \pm }}$ необходимо сравнить ВКБ асимптотику с классической асимптотикой ${{I}_{{ - i\lambda }}}(\tau )$ при $\tau \to \infty $
Выражение для ВКБ асимптотики функции ${{I}_{{ - i\lambda }}}(\tau )$ при $\tau > \lambda $ имеет вид
(8)
$\begin{gathered} \operatorname{Re} {{I}_{{ - i\lambda }}}(\tau ) \approx {{({{\tau }^{2}} - {{\lambda }^{2}})}^{{ - 1/4}}}\exp {{({{\Lambda }_{ + }})} \mathord{\left/ {\vphantom {{({{\Lambda }_{ + }})} {\sqrt {2\pi } }}} \right. \kern-0em} {\sqrt {2\pi } }}, \\ \operatorname{Im} {{I}_{{ - i\lambda }}}(\tau ) \approx {{({{\tau }^{2}} - {{\lambda }^{2}})}^{{ - 1/4}}}\exp {{({{\Lambda }_{ - }})} \mathord{\left/ {\vphantom {{({{\Lambda }_{ - }})} 2}} \right. \kern-0em} 2}\sqrt {2\pi } , \\ {{\Lambda }_{ \pm }} = \pm \sqrt {{{\tau }^{2}} - {{\lambda }^{2}}} \mp \lambda arctg({{\sqrt {{{\tau }^{2}} - {{\lambda }^{2}}} } \mathord{\left/ {\vphantom {{\sqrt {{{\tau }^{2}} - {{\lambda }^{2}}} } \lambda }} \right. \kern-0em} \lambda }) + \pi {\lambda \mathord{\left/ {\vphantom {\lambda 2}} \right. \kern-0em} 2}. \\ \end{gathered} $Продолжим аналитически первую из формул (8) из области $\tau > \lambda $ в область $\tau < \lambda $ через верхнюю полуплоскость комплексной переменной τ, в результате получим
(9)
$\begin{gathered} {{I}_{{ - i\lambda }}}(\tau ) \approx {{({{\tau }^{2}} - {{\lambda }^{2}})}^{{ - 1/4}}}\exp {{(\alpha )} \mathord{\left/ {\vphantom {{(\alpha )} {\sqrt {2\pi } }}} \right. \kern-0em} {\sqrt {2\pi } }}, \\ \alpha = - i\left( {\sqrt {{{\lambda }^{2}} - {{\tau }^{2}}} - \frac{\lambda }{2}\ln \frac{{\lambda + \sqrt {{{\lambda }^{2}} - {{\tau }^{2}}} }}{{\lambda - \sqrt {{{\lambda }^{2}} - {{\tau }^{2}}} }} - {\pi \mathord{\left/ {\vphantom {\pi 4}} \right. \kern-0em} 4}} \right) + \\ + \,\,{{\pi \lambda } \mathord{\left/ {\vphantom {{\pi \lambda } 2}} \right. \kern-0em} 2}. \\ \end{gathered} $Тогда дебаевская асимптотика модифицированной функции Бесселя ${{I}_{{ - i\lambda }}}(\tau )$ мнимого индекса (при больших значениях как индекса $\lambda $, так и аргумента $\tau $) получается подстановкой в (8), (9) вместо $\tau $ значения $\lambda r$ [21–23]
(10)
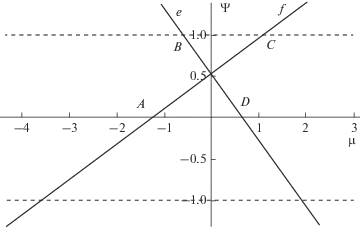
$\begin{gathered} {{I}_{{ - i\lambda }}}(\lambda r) \approx {{({{r}^{2}} - 1)}^{{ - 1/4}}}\exp ( \pm i(\lambda \Theta - {\pi \mathord{\left/ {\vphantom {\pi 4}} \right. \kern-0em} 4}) \times \\ \times \,\,\exp {{(\pi {\lambda \mathord{\left/ {\vphantom {\lambda 2}} \right. \kern-0em} 2})} \mathord{\left/ {\vphantom {{(\pi {\lambda \mathord{\left/ {\vphantom {\lambda 2}} \right. \kern-0em} 2})} {\sqrt {2\pi \lambda } }}} \right. \kern-0em} {\sqrt {2\pi \lambda } }}, \\ \Theta = \sqrt {1 - {{r}^{2}}} - \frac{1}{2}\ln \frac{{1 + \sqrt {1 - {{r}^{2}}} }}{{1 - \sqrt {1 - {{r}^{2}}} }}),\,\,\,\,0 < r < 1, \\ \operatorname{Re} {{I}_{{ \pm i\lambda }}}(\lambda r) \approx {{({{r}^{2}} - 1)}^{{ - 1/4}}} \times \\ \times \,\,\exp (\lambda (\Phi (r) + {{{\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0em} 2}))} \mathord{\left/ {\vphantom {{{\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0em} 2}))} {\sqrt {2\pi \lambda } }}} \right. \kern-0em} {\sqrt {2\pi \lambda } }}, \\ \operatorname{Im} {{I}_{{ \pm i\lambda }}}(\lambda r) \approx \mp {{({{r}^{2}} - 1)}^{{ - 1/4}}} \times \\ \times \,\,\exp ( - \lambda (\Phi (r) - {{{\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0em} 2}))} \mathord{\left/ {\vphantom {{{\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0em} 2}))} 2}} \right. \kern-0em} 2}\sqrt {2\pi \lambda } , \\ \Phi (r) = \sqrt {{{r}^{2}} - 1} - arctg(\sqrt {{{r}^{2}} - 1} ),\,\,\,\,r > 1. \\ \end{gathered} $Значение $r = 0$ – точка ветвления, значение $r = 1$ – точка поворота, где асимптотики (10) не работают. Если $r < 0,$ то имеем: ${{I}_{{i\lambda }}}(\lambda r)$ = $ = \exp ( - \pi \lambda ){{I}_{{i\lambda }}}( - \lambda r),$ ${{I}_{{ - i\lambda }}}(\lambda r) = \exp (\pi \lambda ){{I}_{{ - i\lambda }}}( - \lambda r).$ Для дальнейших расчетов параметр $\beta = 6.57,$ все численные результаты приведены для первой модели. На рис. 4 приведена геометрия расположения особых точек, определяющих основные качественные особенности поведения дисперсионных кривых в плоскости переменных ($\Psi ,\mu $), где $\Psi = \omega - \mu M(z).$ На рис. 4 показаны зависимости $r(0)$ (линия e) и $r( - \pi )$ (линия f) как функции $\mu $. Точки A, D являются точками ветвления, они отвечают тем значения $\mu $, при которых $r(0) = r( - H) = 0.$ Разрез в комплексной плоскости $\mu $ проведен от $ - \infty $до A и от D до $ + \infty $. Точки поворота, отделяющие значения переменной μ, при которых существуют волновые решения – это точки B, C на рис. 4. При $\mu > {{\mu }_{C}}$ и при $\mu < {{\mu }_{B}}$ волновые возмущения отсутствуют.
Cоответствующие численные значения равны: ${{\mu }_{A}} = - 1.67,$ ${{\mu }_{D}} = 0.675,$ ${{\mu }_{B}} = - 0.575,$ ${{\mu }_{C}} = 1.08.$ Из рис. 4 видно, что действительные решения дисперсионного уравнения существуют в интервале ${{\mu }_{A}} < \mu < {{\mu }_{D}}.$ В интервале ${{\mu }_{B}} < \mu < {{\mu }_{D}}$ дисперсионное уравнение (5), используя асимптотики (10), можно представить в виде
Откуда можно получить
(11)
${{\nu }_{n}}(\mu ) = \pm \left| \mu \right|{{({{(\pi nb)}^{2}}{{(\Theta (r( - \pi )) - \Theta (r(0)))}^{{ - 2}}} - 1)}^{{1/2}}}.$В интервале ${{\mu }_{A}} < \mu < {{\mu }_{B}}$ решение дисперсионного уравнения (5) имеет вид
(12)
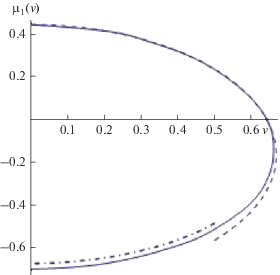
${{\nu }_{n}}(\mu ) = \pm \left| \mu \right|{{({{((\pi n - {\pi \mathord{\left/ {\vphantom {\pi 4}} \right. \kern-0em} 4})b)}^{2}}{{(\Theta (r( - \pi )))}^{{ - 2}}} - 1)}^{{1/2}}}.$Получить зависимости ${{\mu }_{n}}(\nu )$ из выражений (11), (12) возможно, используя стандартные вычислительные системы типа “Математика”. На рис. 5 изображена дисперсионная кривая ${{\mu }_{1}}(\nu ),$ рассчитанная численно (сплошная линия), и ее приближения, рассчитанные с использования формулы (11) (штриховая линия) и формулы (12) (штрих-пунктирная линия).
Для исследования вынужденных ВГВ в стратифицированном океане со сдвиговыми течениями
необходимо решать задачу (3) с ненулевой правой частью $Q\left( {t,x,y,z,{{z}_{0}}} \right),$ конкретный вид которой определяется видом источника возмущений. Если рассматривать
в качестве источника направленную по вертикали силу, то имеем: $Q\left( {t,x,y,z,{{z}_{0}}} \right)$ = 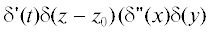 + +
+ + 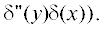 В случае точечного источника массы: $Q\left( {t,x,y,z,{{z}_{0}}} \right)$ =
В случае точечного источника массы: $Q\left( {t,x,y,z,{{z}_{0}}} \right)$ = 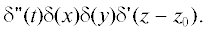 Если эта функция имеет вид: $Q\left( {t,x,y,z,{{z}_{0}}} \right)$ $ = \delta (x)\delta (y)\delta (z - {{z}_{0}}) \times $ × $exp(i\omega t),$ то рассматривается функция Грина задачи (3) для осциллирующего точечного источника
возмущений, расположенного на глубине ${{z}_{0}}$. Очевидно, что в силу линейности рассматриваемой задачи, используя полученные асимптотические
решения для функции Грина, в дальнейшем можно получить представления для полей ВГВ,
генерируемых произвольными нелокальными и нестационарными источниками в стратифицированном
океане со сдвиговыми течениями [7, 17–19]. Одним из основных источников генерации ВГВ в океане могут являться движущиеся атмосферные
циклоны. Возбуждаемые с помощью этого механизма генерации волновые поля играют значительную
роль в различных механизмах переноса энергии в толще океана. Экспериментальное обнаружение
следа ВГВ от движущегося урагана явилось одним из впечатляющих достижений современной
океанологии [17, 20]. На больших расстояниях реальные источники возмущений (тайфун, возмущения атмосферного
давления, циклон) допускают физически обоснованную аппроксимацию некоторой системой
точечных локализованных источников, взятых с определенными весами. Точечным нестационарным
источником генерации ВГВ в реальном океане также можно считать крутой склон поперечного
хребта в проливах, который обтекается сдвиговым течением и периодическим приливным
течением [9, 11–14]. Такой подход является физически обоснованным для решения многих задач моделирования
генерации линейных ВГВ в океане с учетом сдвиговых течений [2–4, 10]. На больших расстояниях от источников возмущений точная форма источника практически
не влияет на волновые характеристики ВГВ, которые определяются параметрами стратифицированной
среды и соответствующими законами дисперсии [7, 18, 19]. В общем случае решение представляет собой сумму вертикальных волновых мод: $W = \sum\limits_n {{{W}_{n}}} ,$ где каждая мода является суперпозицией плоских волн вида
Если эта функция имеет вид: $Q\left( {t,x,y,z,{{z}_{0}}} \right)$ $ = \delta (x)\delta (y)\delta (z - {{z}_{0}}) \times $ × $exp(i\omega t),$ то рассматривается функция Грина задачи (3) для осциллирующего точечного источника
возмущений, расположенного на глубине ${{z}_{0}}$. Очевидно, что в силу линейности рассматриваемой задачи, используя полученные асимптотические
решения для функции Грина, в дальнейшем можно получить представления для полей ВГВ,
генерируемых произвольными нелокальными и нестационарными источниками в стратифицированном
океане со сдвиговыми течениями [7, 17–19]. Одним из основных источников генерации ВГВ в океане могут являться движущиеся атмосферные
циклоны. Возбуждаемые с помощью этого механизма генерации волновые поля играют значительную
роль в различных механизмах переноса энергии в толще океана. Экспериментальное обнаружение
следа ВГВ от движущегося урагана явилось одним из впечатляющих достижений современной
океанологии [17, 20]. На больших расстояниях реальные источники возмущений (тайфун, возмущения атмосферного
давления, циклон) допускают физически обоснованную аппроксимацию некоторой системой
точечных локализованных источников, взятых с определенными весами. Точечным нестационарным
источником генерации ВГВ в реальном океане также можно считать крутой склон поперечного
хребта в проливах, который обтекается сдвиговым течением и периодическим приливным
течением [9, 11–14]. Такой подход является физически обоснованным для решения многих задач моделирования
генерации линейных ВГВ в океане с учетом сдвиговых течений [2–4, 10]. На больших расстояниях от источников возмущений точная форма источника практически
не влияет на волновые характеристики ВГВ, которые определяются параметрами стратифицированной
среды и соответствующими законами дисперсии [7, 18, 19]. В общем случае решение представляет собой сумму вертикальных волновых мод: $W = \sum\limits_n {{{W}_{n}}} ,$ где каждая мода является суперпозицией плоских волн вида
(13)
${{W}_{n}} = \int\limits_{ - \infty }^\infty {{{F}_{n}}(z,\nu )\exp ( - i({{\mu }_{n}}(\nu )x + \nu y - \omega t))d\nu } ,$где собственные функции спектральной задачи (3) входят в амплитуду ${{F}_{n}}(z,\nu ),$ которая является медленно меняющейся функцией переменной $\nu $. Интегралы типа (9) на больших расстояниях от источников возмущений ВГВ можно вычислить методом стационарной фазы [7, 18, 19]. Каждую дисперсионную кривую ${{\mu }_{n}}(\nu )$ можно представить в виде двух ветвей: верхней, обозначаемой через $\mu _{n}^{1}(\nu )$ и нижней, обозначаемой через $\mu _{n}^{2}(\nu ).$ Рассмотрим сначала случай верхней ветви дисперсионной кривой. Введем обозначения для фазы: $\Omega = \mu _{n}^{1}(\nu ) + \nu y - \omega t.$ Используя условие стационарности фазы $\frac{{\partial \Omega }}{{\partial \nu }} = 0$, получим семейство линий постоянной фазы с параметром ν
Полученные выражения описывают волновую картину возбуждаемых полей ВГВ при $x > 0.$ При $x < 0$ аналогичное семейство линий постоянной фазы описываются этими выражениями, где в уравнении для фазы Ω вместо $\mu _{n}^{1}(\nu )$ необходимо использовать $\mu _{n}^{2}(\nu ).$ На рис. 6 показаны линии постоянной фазы при $t = 4,$ $\Omega = 2\pi k,$ $k = 1,2, \ldots ,6,$ рассчитанные для первой волновой моды. Эти результаты показывают значительную зависимость фазовой структуры возбуждаемых полей ВГВ от соотношения амплитуд придонного и приповерхностного сдвиговых течений. В частности, если амплитуды придонного и приповерхностного течений равны, то соответствующая фазовая картина волнового поля – симметрична. Если амплитуды придонного и приповерхностного течений различны, то фазовая картина возбуждаемых полей ВГВ становится ассиметричной. Поэтому ассиметричность фазовых картин волновых полей может являться одним из признаков заметной перестройки в распределении по глубине сдвиговых океанических течений.
Таким образом, решена задача о поле внутренних гравитационных волн в стратифицированной среде конечной глубины с разнонаправленными сдвиговыми течениями. Для аналитического решения задачи использовано постоянное распределение частоты плавучести и линейная зависимость сдвигового течения от глубины. Используя модельную гидрологию, получены аналитические выражения, описывающие дисперсионные зависимости, которые выражаются через модифицированную функцию Бесселя мнимого индекса. При выполнении условия устойчивости Майлса и больших числах Ричардсона для построения аналитических решений были использованы дебаевские асимптотики модифицированной функции Бесселя мнимого индекса. Изучены свойства дисперсионного уравнения и исследованы основные аналитические свойства дисперсионных кривых. Численно рассчитаны фазовые картины возбуждаемых полей ВГВ для данной модели волновой генерации.
Работа выполнена по теме государственного задания № АААА-А17-117021310375-7.
Список литературы
Miles J.W. On the stability of heterogeneous shear flow // J. Fluid Mech. 1961. V. 10(4). P. 495–509.
Миропольский Ю.З. Динамика внутренних гравитационных волн в океане. Л.: Гидрометеоиздат, 1981. 302 с.
Филлипс О. Динамика верхнего слоя океана. Л.: Гидрометеоиздат, 1980. 320 с.
Fabrikant A.L., Stepanyants Yu.A. Propagation of waves in shear flows. World Scientific Publishing, 1998. 304 p.
Pedlosky J. Waves in the ocean and atmosphere: introduction to wave dynamics. Berlin-Heildelberg: Springer, 2010. 260 p.
Sutherland B.R. Internal gravity waves. Cambridge: Cambridge University Press, 2010. 394 p.
Булатов В.В., Владимиров Ю.В. Волны в стратифицированных средах. М.: Наука, 2015. 735 с.
Vlasenko V., Stashchuk N., Hutter K. Baroclinic tides. N.Y.: Cambridge University Press, 2005. 372 p.
Morozov E.G. Oceanic internal tides. Observations, analysis and modeling. Berlin: Springer, 2018. 317 p.
Velarde M.G., Tarakanov R.Yu., Marchenko A.V. (Eds.). The ocean in motion. Springer Oceanography. Springer International Publishing AG, 2018. 625 p.
Morozov E.G., Paka V.T., Bakhanov V.V. Strong internal tides in the Kara Gates Strait // Geoph. Res. Letters. 2008. V. 35. L16603.
Morozov E.G., Parrilla-Barrera G., Velarde M.G., Scherbinin A.D., The Straits of Gibraltar and Kara Gates: a comparison of internal tides // Oceanologica Acta. 2003. V. 26(3). P. 231–241.
Morozov E.G., Tarakanov R.Yu., Frey D.I., Demidova T.A., Makarenko N.I. Bottom water flows in the tropical fractures of the Northern Mid-Atlantic Ridge // J. Oceanography. 2018. V. 74(2). P. 147–167.
Frey D.I., Novigatsky A.N., Kravchishina M.D., Morozov E.G. Water structure and currents in the Bear Island Trough in July–August 2017 // Russian J. Earth Sciences. 2017. V. 17. ES3003.
Fraternale F., Domenicale L, Staffilan G.,Tordella D. Internal waves in sheared flows: lower bound of the vorticity growth and propagation discontinuities in the parameter space // Phys. Rev. 2018.V. 97. № 6. P. 063102.
Гаврильева А.А., Губарев Ю.Г., Лебедев М.П. Теорема Майлса и новые частные решения уравнения Тейлора–Гольдстейна // Ученые Записки Казанского университета. Серия физ.-мат. науки. 2016. Т. 158. Кн. 2. С. 156–171.
Свиркунов П.Н., Калашник М.В. Фазовые картины диспергирующих волн от движущихся локализованных источников // Успехи физических наук. 2014. Т. 184. № 1. С. 89–100.
Булатов В.В., Владимиров Ю.В. Дальние поля внутренних гравитационных волн при произвольных скоростях движения источника возмущений // Изв. РАН. Физика атмосферы и океана. 2015. Т. 51. № 6. С. 684–689.
Bulatov V.V., Vladimirov Yu.V. Unsteady regimes of internal gravity wave generation in the ocean // Russ. J. Earth Sciences. 2018. V. 18. ES2004.
Voelker G.S., Myers P.G., Walter M., Sutherland B.R. Generation of oceanic internal gravity waves by a cyclonic surface stress disturbance // Dynamics Atm. Oceans. 2019. V. 86. P. 16–133.
Никифоров А.Ф, Уваров В.В. Специальные функции математической физики. М.: ИД Интеллект, 2008. 344 с.
Олвер Ф. Асимптотика и специальные функции. М.: Физматлит, 1990. 528 с.
Watson G.N. A treatise on the theory of Bessel functions (2nd edn). Cambridge: Cambridge University Press, 1995.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Физика атмосферы и океана