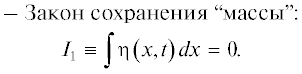1. На главную
  2. Электронные версии
  3. Известия РАН. Физика атмосферы и океана
  4. T. 56, № 1, 2020

Известия РАН. Физика атмосферы и океана, 2020, T. 56, № 1, стр. 20-42

Нелинейные волны во вращающемся океане (уравнение Островского, его обобщения и приложения)

Ю. А. Степанянц a, b, *

a Университет Южного Квинсленда
4350 Тувумба, Вест стрит, Австралия

b Нижегородский государственный технический университет им. Р.Е. Алексеева
603950 Нижний, Новгород, ул. Минина, 24, Россия

* E-mail: Yury.Stepanyants@usq.edu.au

Поступила в редакцию 11.09.2019
После доработки 25.09.2019
Принята к публикации 25.09.2019

Полный текст (PDF)

Аннотация

В обзоре представлены теретические, численные и экспериментальные результаты исследования структуры и динамики слабонелинейных внутренних волн во вращающемся океане, накопленные за последние 40 лет с тех пор, как в 1978 г. было выведено приближенное уравнение, получившее название уравнения Островского. Обсуждается связь данного уравнения с другими известными волновыми уравнениями, интегрируемость уравнения Островского, условие существования уединенных стационарных волн и уединенных волн огибающей. Описана адиабатическая динамика солитонов Кортевега–де Вриза при наличии вращения жидкости, а также взаимное влияние неоднородности океана и эффектов вращения не динамику уединенных волн. Отмечается универсальность уравнения Островского в приложении к волнам в других средах (твердых телах, плазме, кварк-глюонной плазме, оптике).

Ключевые слова: поверхностные и внутренние волны, вращающаяся жидкость, уединенные волны, солитоны, интегрируемые уравнения

ВВЕДЕНИЕ

Хорошо известна роль уравнения Кортевега–де Вриза (КдВ) в описании нелинейных волновых явлений в слабодиспергирующих средах. Это уравнение удачно сочетает конкуренцию основных эффектов в физике нелинейных волн, дисперсии и нелинейности. После многочисленных работ в 50-х–60-х годах 20-го столетия, главным образом в физике плазмы, приведшим к выводу уравнения КдВ в этих средах, была осознана универсальная роль данного уравнения и путем численного моделирования открыто явление образования уединенных волн, названных солитонами, из произвольных начальных возмущений [1, 2]. Дальнейший интерес к этому уравнению привел к открытию метода решения широкого класса нелинейных уравнений – методу обратной задачи рассеяния и его обобщениям [3–5].

Вскоре в теории нелинейных волн стали появляться родственные уравнения такие как модифицированное уравнение КдВ (мКдВ) для описания волн в средах с кубичной нелинейностью, уравнение Гарднера, содержащее комбинированную квадратичную и кубичную нелинейность, ставшее особенно популярным в теории внутренних волн в океане, уравнения Бенджамина–Оно (БО) и Джозефа–Куботы–Ко–Доббса для описания внутренних волн в глубоком океане [5], уравнение Кадомцева–Петвиашвили (КП) [6, 7], описывающее неодномерные эффекты, связанные с поперечной дифракцией волновых пучков и др. В этом же ряду можно назвать и уравнение Островского, опубликованное в 1978 г. [8] и описывающее слабонелинейные волновые процессы в океане при учете вращения Земли. Данное уравнение обобщает уравнение КдВ путем включения дополнительного дисперсионного члена и имеет следующий вид:

(1)
$\frac{\partial }{{\partial x}}\left( {\frac{{\partial \eta }}{{\partial t}} + c\frac{{\partial \eta }}{{\partial x}} + \alpha \eta \frac{{\partial \eta }}{{\partial x}} + \beta \frac{{{{\partial }^{3}}\eta }}{{\partial {{x}^{3}}}}} \right) = \gamma \eta .$

Здесь через η обозначено смещение свободной поверхности в случае поверхностных волн или возмущение пикноклина в случае внутренних волн. Коэффиценты уравнения выражаются следующим образом через гидрологические параметры задачи:

– для поверхностных волн:

(2)
$c = \sqrt {gh} ,\,\,\,\,\alpha = \frac{{3c}}{{2h}},\,\,\,\beta = \frac{{c{{h}^{2}}}}{6},\,\,\,\,\gamma = \frac{{{{f}^{2}}}}{{2c}},$
где h – глубина водоема, g – ускорение свободного падения, f = 2Ω sinφ – параметр Кориолиса, включающий в себя частоту вращения Земли Ω и географическую широту места φ.

– для внутренних волн в двухслойной жидкости в приближении Буссинеска:

(3)
$\begin{gathered} c = \sqrt {g\frac{{\delta \rho }}{\rho }\frac{{{{h}_{1}}{{h}_{2}}}}{{{{h}_{1}} + {{h}_{2}}}}} ,\,\,\,\,\alpha = \frac{{3c}}{2}\frac{{{{h}_{1}} - {{h}_{2}}}}{{{{h}_{1}}{{h}_{2}}}}, \\ \beta = \frac{{c{{h}_{1}}{{h}_{2}}}}{6},\,\,\,\gamma = \frac{{{{f}^{2}}}}{{2c}}, \\ \end{gathered} $
где h1,2 – толщины верхнего и нижнего слоев соответственно, δρ – скачок плотности на пикноклине, а ρ – среднее значение плотности слоев.

В общем случае внутренних волн в непрерывно стратифицированной жидкости с учетом сдвиговых течений коэффициенты уравнения (1) выводились во многих работах, упомянем здесь лишь некоторые: [9, 10].

За прошедшие 40 лет уравнение Островского стало весьма популярным не только в океанологии, но также и в других областях физики. Оно вместе с его укороченной версией, в которой отсутствует член с третьей производной (“редуцированное уравнение Островского”) описывает, в частности, волновые процессы в релаксирущих средах [11], в плазме [12], включая даже кварк-глюонную плазму [13], в диэлектриках [14]. Оно описывает также звуковые волны в жидкости с пузырьками газа [15], упругие волны в нелинейных цепочках [16], сверхкороткие импульсы лазерного излучения [17], волны любой природы в случайно-неоднородных средах [18] (см. также обзоры [19–21]). Известны также обобщенные уравнения Островского:

– уравнение Гарднера–Островского, содержащее комбинированную квадратичную и кубичную нелинейность и описывающие внутренние волны в океане [22]:

(4)
$\frac{\partial }{{\partial x}}\left( {\frac{{\partial \eta }}{{\partial t}} + c\frac{{\partial \eta }}{{\partial x}} + \alpha \eta \frac{{\partial \eta }}{{\partial x}} + {{\alpha }_{1}}{{\eta }^{2}}\frac{{\partial \eta }}{{\partial x}} + \beta \frac{{{{\partial }^{3}}\eta }}{{\partial {{x}^{3}}}}} \right) = \gamma \eta .$

Укороченный вариант этого уравнения с α = β = 0 используется для описания ультракоротких волн в волоконной оптике [17, 23], интенсивных акустических волн в фокальной области [24], волн на струне, закрепленной на упруго-инерционной подложке [25].

– уравнение Кадомцева–Петвиашвили–Островского, содержащее дополнительный член, описывающий медленную диффузию волнового поля в поперечном к распространению волн направлении (подобное уравнение упоминалось без вывода еще в оригинальной работе Островского [8], но потом было выведено в работах [26, 27]):

(5)
$\frac{\partial }{{\partial x}}\left( {\frac{{\partial \eta }}{{\partial t}} + c\frac{{\partial \eta }}{{\partial x}} + \alpha \eta \frac{{\partial \eta }}{{\partial x}} + \beta \frac{{{{\partial }^{3}}\eta }}{{\partial {{x}^{3}}}}} \right) = \gamma \eta - \frac{c}{2}\frac{{{{\partial }^{2}}\eta }}{{\partial {{y}^{2}}}}.$
– аналогичное уравнение может быть выведено для описания внутренних волн в глубоком океане с учетом вращения Земли (двумерное уравнение Бенджамина–Оно с вращением) [28]:

(6)
$\begin{gathered} \frac{\partial }{{\partial x}}\left( {\frac{{\partial \eta }}{{\partial t}} + c\frac{{\partial \eta }}{{\partial x}} + \alpha \eta \frac{{\partial \eta }}{{\partial x}} + \frac{\beta }{\pi }\frac{{{{\partial }^{2}}}}{{\partial {{x}^{2}}}}\int\limits_{ - \infty }^{ + \infty } {\frac{{\eta \left( {x{\kern 1pt} ',t} \right)dx{\kern 1pt} '}}{{x - x{\kern 1pt} '}}} } \right) = \\ = \gamma \eta - \frac{c}{2}\frac{{{{\partial }^{2}}\eta }}{{\partial {{y}^{2}}}}. \\ \end{gathered} $

В следующем разделе будут приведены основные свойства уравнения Островского.

1. ОСНОВНЫЕ СВОЙСТВА УРАВНЕНИЯ ОСТРОВСКОГО

Дисперсионные зависимости

При рассмотрении волн бесконечно малой амплитуды нелинейным членом в уравнении (1) можно пренебречь и рассматривать простейшие решения вида η ~ ei(ωt–kx), где ω частота гармонической волны, а k – волновое число. Подставляя это решение в уравнении Островского (1) с α = 0, находим связь между частотой волны и волновым числом (дисперсионное соотношение):

(7)
$\omega = ck - \beta {{k}^{3}} + \frac{\gamma }{k}.$

Отсюда вытекают выражения для фазовой и групповой скоростей:

(8)
$\begin{gathered} {{V}_{{ph}}} \equiv \frac{\omega }{k} = c - \beta {{k}^{2}} + \frac{\gamma }{{{{k}^{2}}}}; \\ {{V}_{g}} \equiv \frac{{d\omega }}{{dk}} = c - 3\beta {{k}^{2}} - \frac{\gamma }{{{{k}^{2}}}}. \\ \end{gathered} $

График дисперсионного соотношения показан на рис. 1, а графики фазовой и групповой скоростей приведены на рис. 2.

Рис. 1.

Дисперсионная зависимость частоты волны от волнового числа для длинных волн (kh $ \ll $ 1) во вращающейся жидкости. Кривая 1 соответствует полным уравнениям гидродинамики вращающейся жидкости [29] при различных знаках дисперсионного коэффициента β; пунктирная кривая 2, переходящая в кривую 1 при увеличении волнового числа, соответсвует уравнению Островского (1).

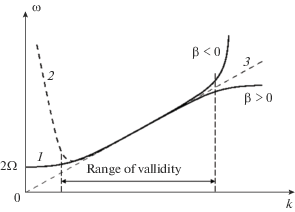
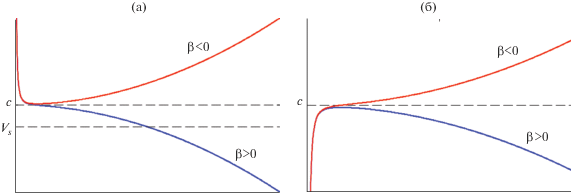
Рис. 2.

Качественные зависимости фазовой (левая панель) и групповой (правая панель) скоростей от волнового числа при различных знаках мелкомасштабной дисперсии β. При β > 0 и любой скорости Vs воображаемого источника всегда найдется синхронно движущаяся с той же скоростью линейная волна.

Как видно из рис. 1, уравнение Островского применимо к волновым процессам средних масштабов (но все же в длинноволновой области там, где kh $ \ll $ 1), для которых дисперсионные поправки в области малых и больших волновых чисел, относительно невелики (т.е., там, где отклонение дисперсионной зависимости от прямой линии 3, мало). Таким образом, условие применимости уравнения Островского сводится к двойному неравенству:

(9)
$\sqrt {{{\left| \gamma \right|} \mathord{\left/ {\vphantom {{\left| \gamma \right|} c}} \right. \kern-0em} c}} \ll k \ll \sqrt {{c \mathord{\left/ {\vphantom {c {\left| \beta \right|}}} \right. \kern-0em} {\left| \beta \right|}}} .$

При этом условие применимости длинноволнового приближения требует дополнительно выполнения неравенства $h\sqrt {{c \mathord{\left/ {\vphantom {c {\left| \beta \right|}}} \right. \kern-0em} {\left| \beta \right|}}} < 1,$ где h есть глубина водоема.

Как видно из рис. 2а, в случае β > 0 фазовая скорость линейных возмущений не ограничена и может быть любой, тогда как групповая скорость не может превышать c (см. рис. 2б). При этом максимальная групповая скорость достигается при ${{k}_{c}} = \sqrt[4]{{{\gamma \mathord{\left/ {\vphantom {\gamma {3\left| \beta \right|}}} \right. \kern-0em} {3\left| \beta \right|}}}}.$

В случае β < 0 групповая скорость не ограничена, тогда как фазовая скорость линейных возмущений ограничена снизу:

(10)
${{V}_{{ph}}} \geqslant {{\left( {{{V}_{{ph}}}} \right)}_{{\min }}} \equiv c + 2\sqrt {\left| \beta \right|\gamma } ,$
и минимум достигается при ${{k}_{m}} = \sqrt[4]{{{\gamma \mathord{\left/ {\vphantom {\gamma {\left| \beta \right|}}} \right. \kern-0em} {\left| \beta \right|}}}}$ (см. рис. 2а).

Такая зависимость фазовой скорости от волнового числа приводит к важному физическому выводу: источник возмущения, движущийся с определенной скоростью Vs при β > 0, всегда находится в резонансе с соответствуюшей линейной волной, имеющей ту же фазовую скорость (см. пересечение пунктирной прямой с дисперсионной кривой на рис. 2а). В результате этого источник может эффективно возбуждать такую волну, затрачивая на это часть своей кинетической энергии и, таким образом, испытывая радиационное торможение. (Отметим однако, что существуют примеры волновых систем, когда по каким-то причинам генерация линейных возмущений не происходит. В этих случаях возможно даже существование стационарных солитонов, погруженных в сплошной спектр линейных волн. Интересно, что такого рода солитоны могут быть как устойчивыми, так и неустойчивыми по отношению к малым возмущениям; подробнее об этом см. в [30, 31]). При β < 0 и скорости источника меньше минимальной, резонанс с линейными возмущениями вовсе отсутствует, поэтому такой источник с Vs < (Vph)min может двигаться стационарно, без потерь энергии.

Модуляционная неустойчивость квазимонохроматических волновых пакетов

При изучении устойчивости квазимонохроматических волновых пакетов по отношению к автомодуляции обычно пользуются критерием Лайтхилла, который вытекает из анализа устойчивости однородных решений нелинейного уравнения Шредингера (НУШ) [32, 33]. Применительно к волнам на воде было установлено, что в отсутствие поверхностного натяжения модуляционная неустойчивость проявляется только в достаточно глубоких водоемах при условии kh > 1.363 (см. об этом, например, в [5]). Отсюда, в частности, следует, что в длинноволновом приближении, когда kh $ \ll $ 1, модуляционная неустойчивость отсутствует, что согласуется с анализом устойчивости в рамках уравнения КдВ, которое применимо именно в этой области длин волн.

Тем неожиданней выглядит результат, полученный впервые в работе [34] в рамках уравнения Островского. Согласно данной работе, при учете вращения модуляционная неустойчивость проявляется в относительно “коротковолновой” области kch < kh $ \ll $ 1, тогда как для более длинных волн при kh < kch она отсутствует. Этот вывод впоследствии был подтвержден и в рамках более общих моделей с учетом кубичной нелинейности (уравнение Гарднера–Островского (8) [35, 36] и уравнения Шриры [37]). Схематически области модуляционной устойчивости и неустойчивости показаны на рис. 3.

Рис. 3.

Интервалы модуляционной устойчивости при 0 < k < kc и неустойчивости при kc < k < (c /|β|)1/2.

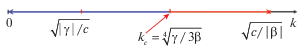
Кажущаяся парадоксальность этого результата связана с тем, что вращение сказывается на дисперсионной зависимости только в области малых волновых чисел, а с ростом волнового числа ее влияние ослабевает, как это видно из рис. 1. Поэтому интуитивно можно было бы ожидать, что какие-либо изменения в модуляционной неустойчивости длинных волн (kh $ \ll $ 1) могли бы проявляться именно при k → 0. Объяснение этому явлению заключается в том, что, во-первых, модифицируется нелинейный коэффициент в уравнении НУШ, т.к. вращение жидкости подавляет генерацию нулевой гармоники (“среднего течения”). Поэтому вклад в нелинейный коэффициент вносит только вторая гармоника квазимонохроматической волны. Во-вторых, становится знакопеременным дисперсионный коэффициент НУШ, равный половине производной групповой скорости по волновому числу (при k = kc он обращается в нуль – см. рис. 2). Явление модуляционной неустойчивости, согласно критерию Лайтхилла [32, 33], определяется произведением нелинейного и дисперсионного коэффициентов НУШ.

Законы сохранения и интегрируемость уравнения Островского

Уравнение Островского обладает несколькими законами сохранения.

(11)
(12)
(13)
$\begin{gathered} - {\text{ Гамильтониан}}{\kern 1pt} : \\ {{I}_{3}} \equiv \frac{1}{2}\int {\left[ {\beta {{{\left( {{{\eta }_{x}}} \right)}}^{2}} - \frac{\alpha }{3}{{\eta }^{3}} - \gamma {{\upsilon }^{2}}} \right]dx = {\text{const}}} , \\ \eta = {{\upsilon }_{x}}. \\ \end{gathered} $

В этих формулах интегрирование подразумевается по всей оси x для локализованных возмущений или по периоду периодического возмущения. В формулах (12) и (13) константы определяются начальными условиями, а закон сохранения “массы” представляет собой, по существу, ограничение на класс допустимых возмущений, требующее, чтобы среднее значение возмущения за период или же полная масса локализованного возмущения была нулевой. Это ограничение естественно вытекает из условия применимости самого уравнения Островского (9).

Интересный вопрос о том, как из начальных возмущений с ненулевой массой в рамках исходных уравнений гидродинамики вращающейся жидкости постепенно выделяется та часть волны, которую можно описывать упрощенным уравнением Островского, изучался в работах [38, 39].

В дополнение к трем указанным выше законам сохранения в работе Бенилова [40] были найдены еще и другие сохраняющиеся величины “моментного” типа; простейшие из них имеют вид:

(14)
$\begin{gathered} {{J}_{1}} \equiv \int {x\eta \left( {x,t} \right)dx = 0} , \\ {{J}_{2}} \equiv \int {\left[ {{{x}^{2}}\eta \left( {x,t} \right) + \frac{{{{\eta }^{2}}\left( {x,t} \right)}}{2}} \right]dx = 0} . \\ \end{gathered} $

Этих интегралов движения заведомо недостаточно, чтобы считать уравнение Островского интегрируемым. Более того, до сих пор не известно ни одного точного решения этого уравнения. Вместе с тем, в предельных случаях, когда крупномасштабная (Кориолисова) дисперсия отсутствует (γ = 0 в уравнении (1)) или когда мелкомасштабная дисперсия Буссинеска отсутствует (β = 0 в уравнении (1)), данное уравнение сводится к полностью интегрируемым моделям. В первом случае – это хорошо известное уравнение КдВ, во втором случае интегрируемость редуцированного уравнения Островского была показана в работе [41].

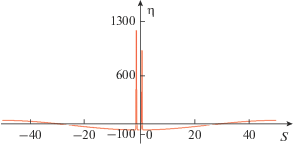
Редуцированное уравнение Островского (иногда называемое уравнением Вахненко или уравнением Хантера–Островского) представляет собой самостоятельную ценность и используется в различных областях физики (см., например, [15, 42] и имеющиеся там ссылки). Данное уравнение рассматривалось еще в оригинальной работе Островского в качестве модели длинных поверхностных и внутренних волн во вращающемся океане, когда дисперсия Буссинеска становится пренебрежимо малой [8]. В этой же работе были найдены стацонарные решения редуцированного уравнения, представляющие собой семейство периодических волн (см. рис. 4), форма которых в зависимости от амплитуды изменяется от квазисинусоидальной до параболической (в последнем случае периодическая волна – это последовательность параболических сегментов). Подробное описание стационарных решений редуцированного уравнения Островского содержится в работе [42] (см. также [21]).

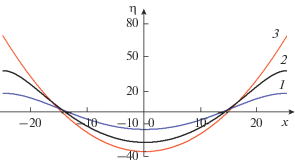
Рис. 4.

Форма периодических стационарных решений уравнения (1) с β  = 0 при различных амплитудах: 1 – квазисинусоидальная волна малой амплитуды; 2 – нелинейная волна умеренной амплитуды; 3 – предельная волна параболической формы.

Редуцированное уравнение Островского содержит как гладкие решения, регулярные при всех x и t, так и сингулярные решения, которые описывают формирование разрывов или обрушение волн. Эти вопросы подробно обсуждаются в работе [34], в которой установлен критерий обрушения волн в зависимости от их начальной крутизны. В частности, было установлено, что если начальное условие η(x) таково, что вторая производная η"(x) > γ/3α в какой-либо точке профиля, то неизбежно возникает обрушение волны. В противном случае решение остается гладким на всех временах, а редуцированное уравнение Островского в этом случае может быть сведено к полностью интегрируемому уравнению Цицейки, известному также как уравнение Додда–Булафа–Михайлова. Здесь же уместно отметить, что в работе [43] была показана полная интегрируемость родственного редуцированного уравнения Островского с кубичной нелинейностью. Данное уравнение, как уже отмечалось, тоже находит применение в различных областях физики (см., например, [14, 17, 23–25]).

Стационарные решения уравнения Островского, “антисолитонная теорема” и существование уединенных волн

Как уже отмечалось выше, стацонарных аналитических решений уравнения Островского до сих пор получить не удалось даже в виде уединенных волн. В работах [44, 45] было показано, что стационарных уединенных решений данного уравнения в случае βγ > 0 не существует. Этот случай наиболее типичен для поверхностных и внутренних волн в океане. При исследовании стационарных решений уравнения Островского (1) его удобно привести к безразмерной форме вида:

(15)
$\frac{{{{d}^{2}}}}{{d{{\xi }^{2}}}}\left( {\frac{1}{{{\text{Ur}}}}\frac{{{{d}^{2}}u}}{{d{{\xi }^{2}}}} - u + \frac{1}{2}{{u}^{2}}} \right) = \frac{u}{{{\text{So}}}},$
где ξ = (x – V t)/(V – c), u = αη/(V – c), Ur = (V – c)3/β, So = 1/γ(V – c).

Здесь Ur и So представляют собой безразмерные параметры, определяющие структуру периодических решений, а V – есть скорость стационарных волн. Попытка построения первой карты решений уравнения (15) на плоскости (Ur, So) была предпринята в работе [46] численными методами. При этом было обнаружено существование определенного класса решений, представляющих собой комбинацию длинных периодических волн с короткими одиночными волнами, похожими на солитоны КдВ (см. рис. 5).

Рис. 5.

Форма периодических стационарных решений уравнения (15) при определенных значениях параметров Ur и So.

Впоследствии такие решения в аналитической форме были построены в рамках приближенной асимптотической теории [47] путем сшивки точных периодических решений редуцированного уравнения Островского (см. линию 3 на рис. 4) и солитонов КдВ. Такие же и более сложные стацонарные перидические решения были построены также в работах [48, 49] численными методами.

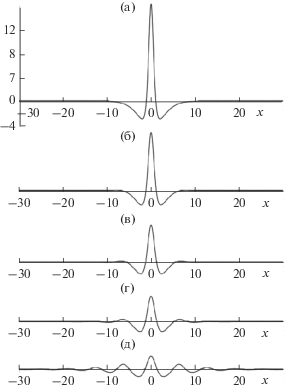
В случае “аномальной дисперсии” βγ < 0 “антисолитонная теорема” не работает и запрета на существование уединенных волн нет. Это согласуется с тем, что изложено после рис. 2 и изображено на рис. 2а. “Аномальная дисперсия” имеет место для волн в замагниченной вращающейся плазме [12], а также, вероятно, для внутренних волн на сдвиговых течениях [10]. Решения уравнения Островского в виде уединенных волн были численно построены в работе [12], в которой было показано, что их структура зависит от амплитуды. Типичные профили изображены на рис. 6; у всех решений полная масса равна нулю. Решения с малой амплитудой, например, такие, как на рис. 6д можно описать с помощью нелинейного уравнения Шредингера (НУШ).

Рис. 6.

Изменение формы уединенных волн при увеличении амплитуды в уравнении Островского с аномальной дисперсией при βγ < 0.

Немонотонный характер профиля уединенной волны приводит к тому, что волны могут образовывать стационарные связанные состояния, би-солитоны, три-солитоны и т.д.; примеры таких стационарных решений показаны на рис. 7. Подобные же решения были численно построены в работах [58, 90].

Рис. 7.

Примеры связанных стационарных состояний из двух уединенных волн в случае аномальной дисперсии βγ < 0. На рис. 7а показана одиночная волна с немонотонным профилем.

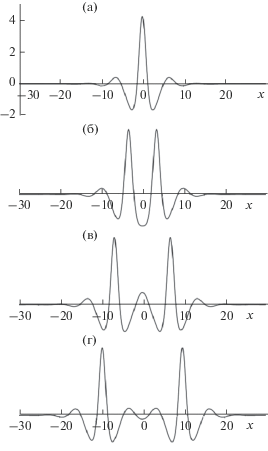
Связанные состояния могут быть устойчивые, когда пик каждой из уединенных волн находится в одном из минимумов соседней волны (см. рис. 7б и 7г), или неустойчивые, когда пики волн приходятся на локальные максимумы соседней волны (см. рис. 7в). Из подобного рода мультисолитонов можно составить бесконечную стационарную волну со случайным чередованием максимумов.

При возмущении связанных уединенных волн в окрестности устойчивых состояний могут возникать осциллирующие пары – бризеры, подобные тем, что наблюдались в экспериментах с электромагнитными линиями передачи – MLC-цепочках [50]. Волновые процессы в таких цепочках описываются уравнением КдВ с пятой производной (КдВ5), в котором также существуют солитоны с немонотонными профилями (“осциллирующими хвостами”). В системах из трех и более связанных уединенных волн могут возникать и значительно более сложные режимы, по-видимому, даже стохастические (см., например, [51]).

2. АДИАБАТИЧЕСКАЯ ЭВОЛЮЦИЯ СОЛИТОНОВ ВО ВРАЩАЮЩЕЙСЯ ЖИДКОСТИ И ОБРАЗОВАНИЕ НЕЛИНЕЙНЫХ ВОЛНОВЫХ ПАКЕТОВ

Как было отмечено выше, стационарных уединенных решений в уравнении Островского с “нормальной” океанской дисперсией не существует. Однако, если эффект вращения мал, то правую часть уравнения (1) можно рассматривать как малое возмущение в уравнении КдВ. Тогда для начального возмущения в виде солитона КдВ можно построить приближенное решение, описывающее медленную (адиабатическую) эволюцию параметров солитона (амплитуды, полуширины, скорости) при сохранении его формы. Асимптотическое описание этого процесса было выполнено в работе [52]. В этой же работе было показано, что солитон КдВ в процессе распостранения излучает длинную волну и вследствие этого постепенно затухает. Его амплитуда формально обращается в ноль за конечное время Tex:

(16)
$A(t) = {{A}_{0}}{{\left( {1 - \frac{t}{{{{T}_{{{\text{ex}}}}}}}} \right)}^{2}};\,\,\,\,{{T}_{{{\text{ex}}}}} = \frac{1}{\gamma }\sqrt {\frac{{\alpha {{A}_{0}}}}{{12\beta }}} .$

График зависимости нормированной амплитуды солитона от времени показан на рис. 8. На этом же рисунке показаны результаты численных расчетов, выполненных в рамках уравнения Островского с “нормальной” океанской дисперсией (βγ > 0) и “аномальной” дисперсией (βγ < 0) [53, 54]. В последнем случае первоначально заданный солитон КдВ не затухает, а в зависимости от его амплитуды быстро трансформируется в один из “солитонов Островского” с нулевой массой и немонотонным профилем (см. рис. 6).

Рис. 8.

Зависимость нормированной амплитуды солитона КдВ от времени. Сплошная кривая 1 – теоретическая зависимость (16), точки 2 – численный расчет для случая “нормальной” океанской дисперсии (βγ > 0), ромбики 3 – численный расчет для случая “аномальной” дисперсии (βγ < 0).

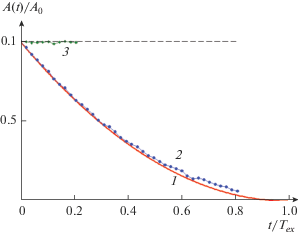
В процессе затухания солитона КдВ вследствие радиационных потерь при βγ > 0 за ним возникает поле излучения, структура которого была вычислена в работе [52]. В ближнем поле излученной волны постепенно формируется уединенная волна, похожая по структуре на исходный солитон КдВ (см. рис. 9), но несколько меньшей амплитуды (см. импульсы максимальной амплитуды на кривых 6, 8, 10), а исходный солитон постепенно затухает. После этого вторичный солитон испытывает ту же судьбу, что и первоначальный, и тоже постепенно затухает, тогда как за ним формируется третичный солитон еще меньшей амплитуды и т.д. [46, 52, 54].

Рис. 9.

Эволюция солитона КдВ в рамках уравнения Островского (1) с периодическими граничными условиями. Кривая 0 – начальное условие (солитон КдВ на небольшом отрицательном пъедестале, чтобы обеспечить нулевую полную массу возмущения (11)), остальные кривые 2, 4, …, 10 иллюстрируют форму возмущения в последующие моменты времени.

После долговременной эволюции в конце концов из начального КдВ солитона формируется волновой пакет в виде солитона огибающей, который при малых амплитудах хорошо описывается нелинейным уравнением Шредингера, что было подтверждено как численными расчетами [34–36, 55], так и лабораторным экспериментом [56].

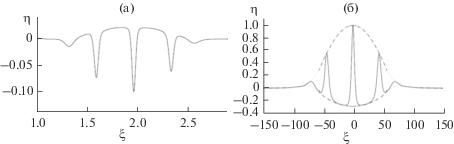
Если же амплитуда образующегося волнового пакета не мала, то в этом случае несущая волна внутри волнового пакета становится заметно несинусоидальной и содержит малое число длин волн. Это явление было обнаружено в численных расчетах на основе модели Мияты–Чоя–Камассы с учетом вращения [57], а также в рамках уравнения Гарднера–Островского, содержащего кубичную нелинейность [58]. Типичные профили волновых пакетов показаны на рис. 10. Следует отметить, что эти волновые образования нестационарны, скорости огибающих и несущих волн у них различны. Интересно также, что импульсы внутри пакетов весьма похожи на солитоны КдВ, а основания волн имеют параболические профили.

Рис. 10.

Примеры сильнонелинейных волновых пакетов образующихся при эволюции солитонов КдВ в рамках системы уравнений Мияты–Чоя–Камассы с учетом вращения (a) [57] и в рамках модельного уравнения Гарднера–Островского (4) (б) [58]. В первом случае полярность внутренних волн в океане с более тонким верхним слоем отрицательная.

Подобным образом расчет адиабатического затухания алгебраических солитонов на пикноклине в глубоком океане был выполнен в работе [59] в рамках уравнения БО с вращением (6). В этой работе было показано, что вследствие радиационных потерь, обусловленных влиянием кориолисовой дисперсии (βγ > 0), амплитуда солитона затухает по линейному закону:

(17)
$A(t) = {{A}_{0}}\left( {1 - \frac{t}{{{{T}_{{{\text{ex}}}}}}}} \right);\,\,\,\,{{T}_{{{\text{ex}}}}} = \frac{{\alpha {{A}_{0}}}}{{8\pi \beta \gamma }}.$

При этом за солитоном образуется квазисинусоидальный волновой след, как показано на рис. 11.

Рис. 11.

Алгебраический солитон уравнения Бенджамина–Оно, излучающий квазисинусоидальный волновой пакет в процессе затухания в рамках уравнения (6) с “нормальной” океанской дисперсией (βγ > 0).

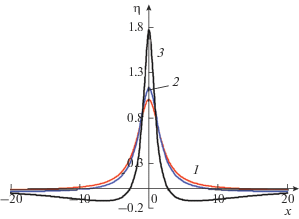
В случае аномальной дисперсии (βγ < 0) алгебраический солитон не затухает а трансформируется в солитон с немонотонным профилем, амплитуда которого зависит от параметра γ (см. рис. 12). Как видно из этого рисунка, при увеличении |γ | солитон становится ỳже и выше по сравнению с алгебраическим солитоном Бенджамина–Оно (БО).

Рис. 12.

Алгебраический солитон уравнения Бенджамина–Оно (линия 1) в сравнении со стационарным решением уравнения (6) с “аномальной” дисперсией (βγ < 0), построенным численно для различных значений параметра γ и фиксированных значениях α = 2, β = 1. Линия 2 – γ = –10–4; линия 3 – γ = –10–2.

Расчет адиабатического затухания солитонов Гарднера в рамках уравнения Гарднера–Островского (4) приводит к более сложным зависимостям параметров солитона от времени; этот вопрос был подробно исследован в работе [60]. Структура солитонов Гарднера существенно зависит от знака кубичной нелинейности в уравнении (4), хотя при этом их форма описывается единой формулой (см., например, [21]):

(18)
$\begin{gathered} u(x,t) = \frac{A}{{1 + B{\text{cosh}}\left[ {{{\left( {x - Vt} \right)} \mathord{\left/ {\vphantom {{\left( {x - Vt} \right)} \Delta }} \right. \kern-0em} \Delta }} \right]}},\,\,\,\,A = \frac{{6\beta }}{{\alpha {{\Delta }^{2}}}}, \\ {{B}^{2}} = 1 + \frac{{6{{\alpha }_{1}}\beta }}{{{{\alpha }^{2}}{{\Delta }^{2}}}},\,\,\,\,V = \frac{\beta }{{{{\Delta }^{2}}}},\,\,\,\,{{U}_{0}} = \frac{A}{{1 + B}}, \\ \end{gathered} $
где V есть скорость солитона, Δ – его характерная ширина, U0 – амплитуда. Безразмерный параметр B определяет структуру солитона, так при α1 < 0 он может изменяться в интервале 0 < B < 1, а при α1 > 0 он должен быть больше единицы по модулю, |B| > 1.

При α1 < 0 (что является наиболее типичным случаем для океанских внутренних волн) семейство солитонов имеет вид, показанный на рис. 13a). В этом случае могут существовать лишь солитоны одной полярности, которая зависит от знака коэффициента α. При α > 0 солитоны имеют положительную полярность, как изображено на рис. 13a), а при α < 0 – отрицательную.

Рис. 13.

Формы солитонов Гарднера в уравнении (4) при α = β = 1 и различных знаках α1. На левой панеле a) показан случай α1 = –1 для различных амплитуд солитонов: линия 1 соответствует солитону малой амплитуды КдВ типа, линия 2 – “толстому солитону”, линия 3 – солитону с плоской вершиной. На правой панеле б) показан случай α1 = 1. В верхней полуплоскости изображены солитоны колоколообразной формы различной амплитуды положительной полярности; в нижней полуплоскости изображен один из семейства солитонов отрицательной полярности (линия 4) и алгебраический солитон предельной амплитуды (линия 5).

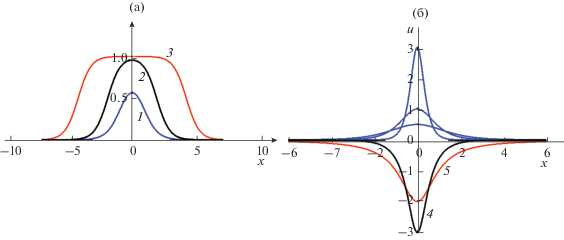
При α1 > 0 (менее типичный, но тоже возможный случай для океанских внутренних волн [20]) семейство солитонов может иметь различную полярность при любом знаке коэффициента α; типичные формы солитонов показаны на рис. 13б). При указанных под рисунком коэффициентах уравнения Гарднера–Островского (4) α = α1 = 1 солитоны отрицательной полярности могут существовать лишь, когда их амплитуда больше некоторой критической (при этом параметр B в формуле (18) отрицательный, B < –1). При уменьшении амплитуды до критической (когда B → –1 слева) солитон с экспоненциальной асимптотикой вырождается в алгебраический солитон (с B = –1), асимптотически убывающий с расстоянием от центра степенным образом ~x–2 (подробности можно найти в обзоре [21], где указаны дальнейшие ссылки).

Исследование влияния вращения Земли на затухание солитонов Гарднера приводит к тому, что динамика солитонов колоколообразной формы независимо от их полярности и параметра α1 довольно хорошо описывается адиабатической теорией, предполагающей, что форма солитонов в процессе эволюции не изменяется. При α1 < 0 солитоны малой и умеренной амплитуды затухают по закону, близкому к закону затухания КдВ солитонов (см. рис. 8). Однако же солитоны с плоскими вершинами (см. линию 3 на рис. 13a) затухают иначе, чем предсказывает адиабатическая теория. Это связано с тем, что, как показывают прямые численные расчеты [60], их форма в процессе эволюции не сохраняется, это иллюстрирует рис. 14.

Рис. 14.

Начальная стадия эволюции солитона с плоской вершиной (линия 1) в два последующих момента времени (линии 2 и 3). Графики представлены в безразмерных переменных, детали можно найти в работе [60].

При α1 > 0 форма солитонов любой полярности, как видно из рис. 13б), является колоколообразной. Поэтому их затухание хорошо описывается адиабатической теорией. На рис. 15 из работы [60] представлено сравнение результатов асимптотической теории и прямых численных расчетов, выполненных в рамках уравнения Гарднера–Островского (4).

Рис. 15.

Зависимость нормированных амплитуд солитонов от времени в процессе их затухания. Кривая 1 относится к солитону КдВ положительной полярности малой амплитуды (то же, что и на рис. 8). Кривая 2 относится к солитону относительно большой амплитуды положительной полярности, а кривая 3 – к солитону той же амплитуды, но отрицательной полярности. С ростом амплитуды кривые 2 и 3 приближаются к пунктироной линии 4. Линия 3 обрывается при некотором значении амплитуды солитона, когда он трансформируется в алгебраический солитон. Символами показаны численные данные.

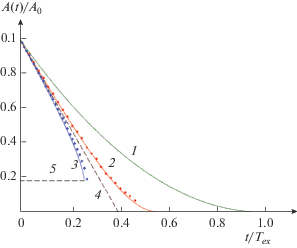
Отдельно следует отметить затухание солитонов отрицательной полярности, амплитуда которых не может быть меньше некоторого порогового значения. При пороговом значении (см. пунктир 5 на рис. 15) образуется алгебраический солитон, затухание которого приводит к его сложной трансформации, по-видимому, в бризер – пульсирующую уединенную волну; этот процесс еще требует подробного исследования.

Время жизни солитонов зависит от их формы и полярности; по существу, оно определяется начальным значением параметра B. Как показано в работе [60], наибольшим времени жизни обладают “толстые солитоны” при α1 < 0 и любом знаке α, а наименьшим временем жизни обладают солитоны отрицательной полярности при α1 > 0, в особенности солитоны, близкие к алгебраическому. Рисунок 16 иллюстрирует время жизни различных солитонов в зависимости от начального значения параметра B.

Рис. 16.

Зависимость времени жизни солитонов Гарднера в безразмерных единицах от начального значения параметра B0, определяющего форму солитнов. В этой нормировке время жизни солитона КдВ с B0 = 1 равно 1 (показано черной точкой на рисунке). Кривая 1 относится к случаю солитонов, изображенных на рис. 13а) для α1 < 0. Кривая 2 относится к солитонам положительной полярности, изображенных на рис. 13б) для α1 > 0, а кривая 3 – к солитонам отрицательной полярности, изображенных на том же рис. 13б). В промежутке значений –1 < B0 < 0 солитоны Гарднера не существуют.

В размерных переменных характерная оценка времени жизни солитонов при B0 → ±∞ (см. пунктирную горизонтальную прямую на рис. 16), вычисляется по формуле Tlim = (4/π2γ)(αU0/12β)1/2 [60]. Принимая для оценок следующие значения параметров двухслойной модели океана δρ/ρ = 5 × 10–4, f = 10–4 с–1, h1 = 24 м, h2 = 26 м и используя формулы (3), получаем Tlim ≈ 15.65 ч. При этом время жизни солитона КдВ с амплитудой 2 м и длительностью 0.8 ч составляет 38.6 ч.

3. ВЗАИМОДЕЙСТВИЕ СОЛИТОНОВ КДВ С ДЛИННЫМИ ПЕРИОДИЧЕСКИМИ ВОЛНАМИ

При построении стационарных решений, показанных на рис. 5, необходимо подбирать скорость и амплитуду уединенных волн так, чтобы они двигались синхронно с периодической несущей волной. Если же скорость уединенной волны не согласована с несущей волной, то уединенная волна начинет дрейфовать по несущей волне. Такой процесс наблюдался в численных расчетах работы [61]. Подробное теоретическое исследование этого процесса в рамках уравнения Островского было проведено впоследствии в работе [62]. В качестве несущей периодической волны рассматривались длинная синусоидальная волна и периодическая волна, состоящая из последовательности параболических арок. Приближенное асимптотическое решение взаимодействия солитона КдВ и длинной несущей волны можно построить, предполагая, что характерная ширина солитона Δ много меньше длины несущей волны Λ, т.е. Δ/Λ $ \ll $ 1. В этом случае солитон можно рассматривать как точечный объект, а несущую волну – как внешнее поле. Теоретическая основа описания солитонов как классических частиц была разработана в работах [50, 63, 64].

В рамках такого асимптотического подхода основными переменными являются положение солитона на длинной несущей волне S, амплитуда солитона A и амплитуда несущей волны U. В случае синусоидальной несущей волны система уравнений для этих переменных имеет вид:

(19)
$\frac{{dS}}{{dt}} = \frac{A}{3} - UcoskS - \frac{1}{{{{k}^{2}}}},$
(20)
$\frac{{dA}}{{dt}} = - 2AUk\sin kS - 4\sqrt {3A} ,$
(21)
$\frac{{dU}}{{dt}} = \frac{{4\sqrt 3 }}{\pi }{{A}^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}}{{k}^{2}}\sin kS.$

Здесь k = 2π/Λ – волновое число несущей волны, а исходное уравнение Островского (1) обезразмерено так, что все его коэффициенты равны единице.

Первое из этих уравнений (19) – это кинематическое соотношение, варажающее разность скоростей солитона и длиной синусоидальной волны малой амплитуды c = 1/k2. В скорость солитона входит поправка, обусловленная его положением в определенной фазе несущей волны (своеобразный пъедестал).

Второе уравнение (20) есть следствие баланса энергии выражающее тот факт, что энергия солитона убывает (а вместе с ней и амплитуда солитона) вследствие радиационных потерь на излучение (последнее слагаемое в правой части), но может возрастать или убывать в зависмости от положения солитона на несущей волне из-за обмена энергией с этой волной (первое слагаемое в правой части (20)). На отрицательном склоне несущей волны происходит подкачка энергии в солитон (он как бы скатывается с горки), а на положительном склоне он отдает энергию несущей волне взбираясь на потенциальную горку.

Наконец, третье уравнение (21) показывает, что вследствие обмена энергией с солитоном амплитуда несущей волны может либо возрастать, либо убывать. В отсутствие радиационных потерь полная энергия солитона и несущей волны сохранялась бы, но потери энергии солитона на излучение приводят к убыванию полной энергии системы, которое описывается следующим уравнением, непосредственно вытекающим из уравнений (20) и (21):

(22)
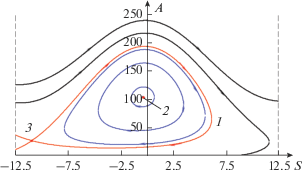
$\frac{d}{{dt}}\left( {\frac{{8\sqrt 3 }}{3}{{A}^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}} + \frac{{{{U}^{2}}\Lambda }}{2}} \right) = - 48A.$

Если не учитывать обратного влияния солитона на длинную несущую волну, то уравнение (21) можно отбросить и найти стационарное состояние оставшейся динамической системы уравнений (19) и (20). В стационарном режиме солитон может формально находиться в двух положениях, либо вблизи подошвы несушей волны (см. импульс 1 на рис. 17), либо вблизи вершины (см. импульсы 2 на рис. 17); без учета радиационных потерь стационарным состояниям отвечают положения минимума и максимума несущей волны, обозначенной символом 0 на рис. 17.

Рис. 17.

Состояния равновесия для солитонов на синусоидальной несущей волне заданной амплитуды (кривая 0). Положения солитонов 1 и 2 соответствуют случаю, когда радиационные потери не учитываются, а положения 3 и 4 – когда учитываются.

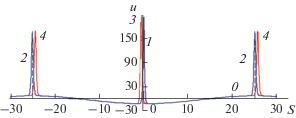
Однако дальнейший анализ показывает, что состояния равновесия вблизи вершин неустойчивы по отношению к малым возмущениям, тогда как вблизи впадин – устойчивы. Малые радиационные потери энергии в стационарном режиме для солитонов, находящихся вблизи впадины несущей волны, компенсируются подкачкой энергии на отрицательном склоне несущей волны. Поэтому в стационарном состоянии солитон в системе с потерями смещается влево от центра, причем тем дальше, чем больше потери.

Без учета потерь на излучение солитон выведенный из состояния равновесия в минимуме синусоидальной волны испытывает малые колебания вокруг равновесного положения с периодом T = (Λ/U)(2 + Λ2/2π2U)–1/2.

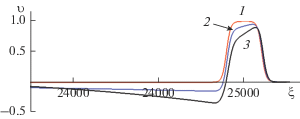
Подробное исследование возможных режимов движения, задаваемых системой уравнений (19)–(21), представлено в работе [62]. На рис. 18 показан один из типичных режимов затухающих колебаний солитона вблизи впадины несущей волны.

Рис. 18.

Зависимисть амплитуд солитона (кривая 1) и синусоидальной волны (кривая 2) от времени. Пунктирная горизонтальная прямая 3 показывает амплитуду стационарного солитона, когда амплитуда несущей волны задана и не меняется во времени. Пунктирная кривая 4 показывает зависимость солитона от времени (16) под действием только радиационных потерь при отсутствии несущей волны.

Как видно из этого рисунка, постепенное излучение энергии приводит к тому, что амплитуды солитона и несушей волны уменьшаются настолько, что несущая волна становится неспособной удерживать солитон. После этого он затухает в основном вследствие радиационных потерь и блуждает по несущей волне, получая определенную порцию энергии в нужной фазе волны, но недостаточную, чтобы скомпенсировать его потери на излучение. Поэтому его амплитуда колеблется вокруг кривой 4 на рис. 18, которая показывает затухание солитона согласно формуле (16) без учета несущей волны. Прямой численный расчет динамики солитона в поле несущей синусоидальной волны, выполненый в рамках уравнения (1) [62], подтвердил основные выводы теории. На рис. 19 показана ранняя стадия затухания амплитуды солитона со временем при его колебаниях вблизи впадины несущей волны.

Рис. 19.

Зависимисть нормированной амплитуды солитона от времени при его колебаниях вблизи впадины несущей синусоидальной волны. Кривая 1 – теория, кривая 2 с точками – данные численного расчета.

Некоторое расхождение между теорией и численными данными может быть связано с тем, что в теории не учитывается влияние излученной солитоном волны на несущую. Это должно приводить к искажению профиля несущей волны и менять амплитудно-фазовые характеристики динамической системы.

В работе [62] исследовалось также взаимодействие солитона КдВ с длинной несущей волной, представляющей собой последовательность параболических арок; при этом качественные выводы остаются такими же, как и в случае синусоидальной несущей волны.

В недавней работе [65] подобный подход был использован для анализа взаимодействия солитона Бенджамина–Оно с несущей синусоидальной волной в рамках уравнения БО с вращением (6). В этом случае основная динамическая система похожа на приведенную выше систему (19)–(21) и имеет следующий вид:

(23)
$\frac{{dS}}{{dt}} = \frac{A}{4} - UcoskS - \frac{1}{{{{k}^{2}}}},$
(24)
$\frac{{dA}}{{dt}} = - AUk\sin kS - 8\pi ,$
(25)
$\frac{{dU}}{{dt}} = A{{k}^{2}}\sin kS.$

Особенность этой системы уравнений в том, что при заданной амплитуде несущей волны (после отбрасывания уравнения (25)) система уравнений (23), (24) является квази-гамильтоновой, несмотря на то, что она диссипативна; при этом она обладает первым интегралом:

(26)
${{H}_{{rl}}}\left( {A,S} \right) = \frac{{{{A}^{2}}}}{8} - AU\cos kS - \frac{A}{{{{k}^{2}}}} - 8\pi S.$

Фазовый портрет системы (23), (24), т.е. зависимость амплитуды солитона от его положения на синусоидальной волне длины Λ = 25 изображен на рис. 20. Точка 2 изображает положение устойчивого равновесия, несколько смещенного влево от минимума несущей волны, расположенного в точке S = 0. Точка 3 изображает положение неустойчивого равновесия седлового типа. Кривая 1 изображает сепаратрису, т.е. кривую, отделяющую замкнутые траектории, соответствующие периодическим решениям, от незамкнутых траекторий, соответствующих непериодическим затухающим в конечном счете решениям.

Рис. 20.

Фазовый портрет системы уравнений (23), (24).

При учете влияния солитона на несущую волну ее амплитуда тоже постепенно уменьшается подобно тому, как показано на рис. 18 кривой 2. Интересно, что в этом случае уравнение баланса энергии, подобное уравнению (22), интегрируемо и выглядит так:

(27)
$2\pi \left( {A - {{A}_{0}}} \right) + \frac{1}{2}\left( {{{U}^{2}} - U_{0}^{2}} \right)\Lambda = - 16{{\pi }^{2}}t.$

Используемый асимптотический подход можно обобщить и включить в рассмотрение несколько солитонов, захваченных длинной несущей волной и взаимодействующих с ней и друг с другом. В качестве примера в работе [66] рассматривалась динамика двух солитонов заключенных внутри синусоидальной волны в рамках отнормированного уравнения Островского (1), в котором все коэффициенты равны единице. Соответствующая система уравнений принимает следующий вид:

(28)
$\begin{gathered} \frac{{d{{S}_{1}}}}{{dt}} = \frac{{{{A}_{1}}}}{3} - U\cos k{{S}_{1}} + \\ + \,\,4{{A}_{2}}\exp \left( { - \sqrt {\frac{{{{A}_{2}}}}{3}} \left| {{{S}_{2}} - {{S}_{1}}} \right|} \right) - \frac{1}{{{{k}^{2}}}}, \\ \end{gathered} $
(29)
$\begin{gathered} \frac{{d{{S}_{2}}}}{{dt}} = \frac{{{{A}_{2}}}}{3} - U\cos k{{S}_{2}} + \\ + \,\,4{{A}_{1}}\exp \left( { - \sqrt {\frac{{{{A}_{1}}}}{3}} \left| {{{S}_{2}} - {{S}_{1}}} \right|} \right) - \frac{1}{{{{k}^{2}}}}, \\ \end{gathered} $
(30)
$\begin{gathered} \frac{{d{{A}_{1}}}}{{dt}} = - \frac{8}{3}{{A}_{1}}\left[ {Uk\sin k{{S}_{1}} - \frac{{2\sqrt 3 }}{3}A_{2}^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}} \right. \times \\ \times \,\,\left. {\exp \left( { - \sqrt {\frac{{{{A}_{2}}}}{3}} \left| {{{S}_{2}} - {{S}_{1}}} \right|} \right)} \right] - 4\sqrt {3{{A}_{1}}} , \\ \end{gathered} $
(31)
$\begin{gathered} \frac{{d{{A}_{2}}}}{{dt}} = - \frac{8}{3}{{A}_{2}}\left[ {Uk\sin k{{S}_{2}} + \frac{{2\sqrt 3 }}{3}A_{1}^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}} \right. \times \\ \times \,\,\left. {\exp \left( { - \sqrt {\frac{{{{A}_{1}}}}{3}} \left| {{{S}_{2}} - {{S}_{1}}} \right|} \right)} \right] - 4\sqrt {3{{A}_{2}}} , \\ \end{gathered} $
(32)
$\frac{{dU}}{{dt}} = \frac{{8\sqrt 3 }}{{3\pi }}{{k}^{2}}\left( {A_{1}^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}\sin k{{S}_{1}} + A_{2}^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}\sin k{{S}_{2}}} \right).$

Здесь A1,2 – амплитуды солитонов, а S1,2 – положения их центров относительно подошвы синусоидальной несущей волны, а экспоненциальные члены в уравнениях (28)–(31) обусловлены влиянием соседних солитонов друг на друга, максимумы которых отстоят друг от друга на расстояние |S2 – S1|. На рис. 21–23 показан в качестве примера один из вариантов численного решения системы уравнений (28)–(31), когда амлитуда несущей синусоидальной волны считается заданной, так что последнее уравнение системы (32) можно отбросить.

Рис. 21.

Начальное условие для системы уравнений (28)–(31).

Рис. 22.

Временные зависимости амплитуд солитонов (на цветном рисунке амлитуды солитонов отличаются цветом – см. электронную версию статьи).

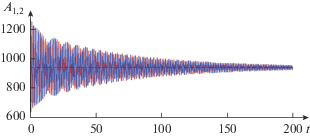
Рис. 23.

Положение и амплитуды солитонов на несущей волне (показаны фрагменты графиков вблизи подошвы волны).

На рис. 21 показано начальное условие в виде двух солитонов разной амплитуды A1 = 1000 и A2 = 1250, расположенных на синусоидальной волне длиной Λ = 100 и амплитудой U = 60 и отстоящих от минимума вправо и влево на единицу. После относительно короткого интервала времени (после одного–двух столкновений) амплитуды солитонов становятся близкими даже, если вначале они сильно отличались. После этого солитоны, взаимодействуя с несущей волной, постепенно приближаются к состоянию равновесия, приобретая равные амплитуды (см. рис. 22), но располагаясь на некотором расстоянии друг от друга.

На рис. 23 показаны взаимные положения солитонов на несущей волне в различные моменты времени; при t = 300 солитоны уже находятся практически в положении покоя.

Таким же образом можно рассматривать и более сложные комплексы из нескольких солитонов, взаимодействующих друг с другом и несущей длинной волной. В чем-то похожий процесс наблюдался в экспериментах при возбуждении солитонов стоячей волной в волновых лотках и электромагнитных линиях передачи [67–69].

4. ВЗАИМНОЕ ВЛИЯНИЕ ВРАЩЕНИЯ ЗЕМЛИ И НЕОДНОРОДНОСТИ ОКЕАНА НА ДИНАМИКУ СОЛИТОНОВ

Динамика солитонов КдВ

Как изложено выше, солитоны КдВ постепенно затухают из-за радиационных потерь, обусловленных влиянием кориолисовой дисперсии. Однако при распространении волны из открытого океана к берегу, когда глубина океана постепенно уменьшается, в игру вступает фактор неоднородности, приводящий к увеличению амплитуды волны. В отсутствии вращения зависимость амплитуд линейных и нелинейных волн от расстояния в прибрежной зоне давно изучена (см., например, [70–72]). В частности, хорошо известно, что амплитуда солитонов КдВ поверхностных волн при плавном изменении глубины водоема увеличивается обратно пропорционально глубине, A ~ h–1, тогда как амплитуда линейных волн изменяется с глубиной по закону Грина A ~ h–1/4.

Совместное воздействие переменной глубины и вращения Земли на динамику внутренних уединенных волн в Южно-Китайском море впервые рассматривалось в работе [73] на основе обобщенного уравнения Островского с переменными коэффициентами, а также в рамках полных уравнений гидродинамики стратифицированной жидкости. С помощью численных расчетов было показано, что совместные эффекты вращения и неоднородности приводят к возникновению вторичных волновых пакетов за лидирующей уединенной волной. В этой же работе рассматривалось влияние отдельных факторов таких, как различной интенсивности вращение и величины градиента подъема дна на форму волн и формирование вторичных возмущений за фронтом основной волны. Вторичный волновой пакет представлял собой образование, состоящее из нескольких связанных уединенных волн, напоминающее солибор – бездиссипативную ударную волну с осцилляторной структурой.

Впоследствие совместное влияние неоднородности (переменной глубины водоема) и вращения Земли на динамику поверхностных и внутренних уединенных волн изучалось в работах [74, 75]. В частности, в работе [75] было показано, что при определенных профилях дна солитон КдВ, благодаря конкурирующему влиянию неоднородности и вращения, может распространяться к берегу, сохраняя неизменной свою амплитуду; соответствующие профили дна вычислены как для поверхностных, так и для внутренних волн. В первом случае профиль дна имеет особенно простой вид:

(33)
$h(x) = {{h}_{0}}{{\left( {1 + \frac{x}{{2L}}} \right)}^{{ - 2}}},\,\,\,\,L = \frac{g}{{{{f}^{2}}}}\sqrt {\frac{{3{{A}_{0}}}}{{4{{h}_{0}}}}} ,$
где A0 и h0 амплитуда солитона и глубина водоема соответственно на определенном расстоянии от берега.

При распространении солитона в океане с таким профилем глубины его длительность уменьшается так, что он постепенно превращается в игольчатую уединенную волну, как показано на рис. 24. Данный рисунок получен путем прямого численного расчета в рамках уравнения Островского с указанным профилем дна (33). Из этого рисунка хорошо видно, что в соответствии с предсказаниями теории, амплитуда лидирующего солитона остается неизменной, тогда как его длительность уменьшается. При этом на промежуточном этапе в согласии с работой [73] за солитоном возникает структура, напоминающая солибор (см. линию 2 на рис. 24). При дальнейшем приближении к берегу из головной части солибора формируется вторичный солитон, который укрепляется на гребне длинной волны, излучаемой лидирующим солитоном (см. линию 3 на рис. 24). Полная энергия лидирующего солитона при такой трансформации, естественно, убывает.

Рис. 24.

Профили поверхностной уединенной волны на различных глубинах при ее приближении к берегу. Линия 1 показывает исходный КдВ солитон на глубине h = 500 м; линия 2 изображает лидирующий солитон той же амплитуды, что и исходный на глубине h = 329 м; при этом видно образование вдали за солитоном солибора. Линия 3 показывает лидирующий солитон на глубине h = 225 м и вторичный солитон малой амплитуды, сформировавшийся на гребне длинной волны, излученной головным солитоном.

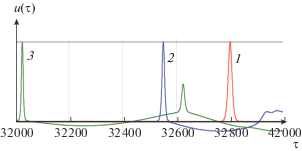
Специфический процесс трансформации солитона с сохранением амплитуды при указанном выборе глубины согласно уравнению (33) в чем-то схож с трансформацией линейных волн на безотражательных профилях дна, широко исследуемых в последнее время (см., например, [76] и имеющиеся там ссылки). Подробное описание процесса трансформации солитона с конкретными оценками и приложениями к волнам в океане можно найти в указанных публикациях [74, 75].

Динамика солитонов огибающей

В разделе 2 был описан процесс эвлюции солитона КдВ во вращаюшемся океане, который завершался формированием солитона огибающей. Однако, как показано в работе [77], в неоднородном океане с переменной глубиной может наблюдаться в некотором смысле обратный процесс, когда солитон огибающей малой амплитуды с большим числом периодов несущей волны может превратиться в одиночную волну. Так, например, если солитон огибающей внутренней волны, описываемый нелинейным уравнением Шредингера, распространяется к берегу в двухслойной жидкости с глубины H = 500 м вдоль пикноклина, расположенного на глубине h = 50 м, то в случае плавного линейного изменения полной глубины с расстоянием его амплитуда адиабатически растет до некоторых пор, а потом резко убывает, как показано на рис. 25 (см. линию 1). Резкое убывание амплитуды солитона связано с тем, что нелинейный коэффициент в уравнении Островского для внутренних волн в двухслойной жидкости обращается в ноль, когда толщины слоев становятся равными (см. уравнение (3)).

Рис. 25.

Зависимость амплитуды солитона огибающей A(x) от расстояния (линия 1) в двухслойной жидкости с линейным убыванием полной глубины водоема. Линия 2 показывает зависимость скорости солитона V(x) от расстояния, линия 3 – зависимость длительности огибающей ΔT(x), линия 4 – период несущей волны σ(x), а линия 5 – число периодов несущей волны N(x) внутри огибающей. Все переменные нормированы на их исходные значения на глубине H = 500 м.

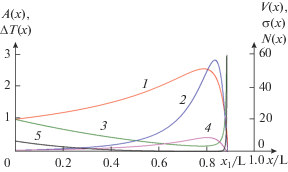
На рис. 26 можно видеть результат численного расчета динамики солитона огибающей с начальной амплитудой 2 м. Расчет выполнен в рамках уравнения Островского с переменными параметрами при линейном убывании толщины нижнего слоя с расстоянием h2(x) = h2(0)(1 – x/L); при этом L = 106 м, а толшина верхнего слоя остается постоянной, h1 = 50 м.

Рис. 26.

Форма солитона огибающей на различных расстояниях от берега. На рис. (a) расстояние до берега L; на рис. (б) расстояние 0.5L; на рис. (в) расстояние 0.3 L.

Как видно из этого рисунка, амплитуда солитона по мере приближения к берегу увеличивается вдвое, длительность огибающей при этом существенно сокращается, а период несущей волны увеличивается. В результате первоначальный солитон огибающей трансформируется в одиночную нестационарную волну, представляющую собой, по существу, бризер.

ЗАКЛЮЧЕНИЕ

В данном обзоре кратко описаны основные свойства уравнения Островского, широко используемого в океанологии (а также и в других разделах физики), и представлены результаты работ последних лет. За прошедшие 40 лет после опубликования основопологающей работы Островского [8] стало понятно, что данное уравнение оказалось удачной универсальной моделью в теории волн. Число публикаций, посвященных данному уравнению, уже превысило 105 и продолжает расти. Многие математические аспекты, связанные с этим уравнением, уже исследованы достаточно полно, но до сих пор нет полной ясности относительно его интегрируемости. Более того, не известно ни одного точного решения уравнения Островского даже в классе стационарных волн.

Как было показано в работах [10, 78], характер дисперсии для внутренних волн во вращающемся океане со сдвиговыми течениями может кардинально измениться, так что в этом случае уравнение Островского с “аномальной дисперсией” содержит решения в виде стационарных уединенных волн и их связанных комплексов. Этот вопрос заслуживает подробного изучения и выявления океанских зон, где реализуются условия существования таких режимов.

Предстоит еще подробный анализ решений обобщенного уравнения Кадомцева–Петвиашвили–Островского (5), описывающего двумерные в горизонтальной плоскости волновые возмущения. Первые шаги в этом направлении уже были сделаны в основном для достаточно редкой версии уравнения с “аномальной дисперсией” [79–83]; в частности, как показано в работе [81], данное уравнение допускает решения в виде уединенных волн, локализованных во всех направлениях и имеющих степенные асимптотики вдоль направления движения по x и экспоненциально спадающие в поперечном направлении, по y, что согласуется с численными результатами работы [79]. Здесь еще открыто широкое поле деятельности применительно к уравнению с нормальной океанской дисперсией (отметим одну из первых работ в этом направлении [84]). Это же относится к двумерному уравнению Бенджамина–Оно с вращением (6) [28], которое до сих пор незаслуженно мало изучалось (затухание солитонов Бенджамина–Оно, обусловленное вращением жидкости, в одномерном случае рассматривалось в работе [59]).

Имеющиеся данные многочисленных наблюдений внутренних волн в океане показывают, что часто их амплитуды таковы, что упоминавшиеся в данном обзоре слабонелинейные уравнения для их описания совершенно непригодны (см., например, [85]). В этом случае необходимо пользоваться либо полными уравнениями гидродинамики стратифицированной вращающейся жидкости, либо развивать новые модельные уравнения. В первом случае приходится использовать численные решения, пригодные для описания конкретных ситуаций с заданной гидрологией и начальными условиями, что ограничивает общность изучаемых эффектов. Вместе с тем, этот подход уже широко применяется, а имеющиеся программы и современные вычислительные средства вполне пригодны для обработки больших объемов информации (см., например, [73]). У некоторых исследователей возникает даже соблазн отказаться от построения приближенных модельных уравнений и сосредоточить усилия на разработке эффективных численных программ. Однако работа по развитию модельных уравнений, способных описывать сильнонелинейные волновые процессы, по-прежнему, ведется (см., например, [57, 86], а также обзор [21]), а выводы, полученные из модельных уравнений с успехом конкурируют с численными расчетами в рамках полнонелинейных уравнений гидродинамики. Более того, ряд эффектов, найденных в рамках модельных уравнений, потом с успехом используется в качестве подсказки для их поиска в полных уравнениях (так, например, были найдены бризеры внутренних волн [87]).

Наконец, отметим, что прямых наблюдений влияния вращения Земли на динамику поверхностных или внутренних волн в океане до сих пор на удивление мало. Имеются лишь скорее косвенные подтверждения важности учета эффектов вращения на динамику таких волн [88, 89]. В этом отношении теория волн во вращающемся океане существенно обгоняет накопление наблюдательных данных. Можно осторожно надеяться, что отставание экспериментальной базы от теоретической в этой области океанологии будет постепенно сокращаться.

Данный обзор написан автором по заказу редакции к 85-летию Л.А. Островского, чье имя носит обсуждавшееся здесь уравнение. Л.А. Островский продолжает активно работать в данной области, а также и в других областях физики. Пользуясь случаем, автор поздравляет Льва Ароновича с “полуюбилеем” и желает ему здоровья и дальнейшей творческой активности.

Работа выполнена при поддержке со стороны Государственной программы научной активности Министерства Образования и Науки Российской Федерации (гранта № 5.1246.2017/4.6), а также гранта Президента РФ по поддержке ведущих научных Школ РФ (НШ-2685.2018.5).

Список литературы

  1. Zabusky N.J., Kruskal M.D. Interaction of “solitons” in a collisionless plasma and the recurrence of initial states // Phys. Rev. Lett. 1965. V. 15. P. 250–243.

  2. Карпман В.И. Нелинейные волны в диспергирующих средах. М.: Наука, 1973. 175 с. (Engl. transl.: Karpman V.I. Nonlinear waves in dispersive media. Pergamon Press: Oxford, 1975.)

  3. Gardner C.S., Greene J.M., Kruskal M.D., Miura R.M. Method for solving the Korteweg–de Vries equation // Phys. Rev. Lett. 1967. V. 19. P. 1095–1097.

  4. Скотт А., Чжу Ф., Маклафлин Д. Солитон – новое понятие в прикладных науках // ТИИЭР. 1973. № 61. С. 79–123. (Scott A.C., Chu F.Y.F., McLaughlin D.W. The soliton: A new concept in applied science. Proc. IEEE. 1973. V. 61. P. 1443–1483.)

  5. Абловиц М., Сигур Х. Солитоны и метод обратной задачи. М.: Мир, 1987. 479 с. (Ablowitz M.J., Segur H. Solitons and the inverse scattering transform. SIAM: Philadelphia, 1981.)

  6. Кадомцев Б.Б., Петвиашвили В.И. Об устойчивости уединенных волн в слабо диспергирующих средах // Докл. АН СССР. 1970. Т. 192. № 4. С. 753–756. (Kadomtsev B.B., Petviashvili V.I. On the stability of solitary waves in weakly dispersive media // Sov. Phys. Doklady. 1970. V. 15. P. 539–541.)

  7. Петвиашвили В.И., Похотелов O.A. Уединенные волны в плазме и атмосфере. М.: Энергоатомиздат, 1989. 200 с. (Petviashvili V.I., Pokhotelov O.V. Solitary waves in plasmas and in the atmosphere. Gordon and Breach, Philadelphia, 1992.)

  8. Островский Л.А. Нелинейные внутренние волны во вращающемся океане // Океанология. 1978. Т. 18. № 2. С. 181–191. (Engl. transl.: Ostrovsky L.A. Nonlinear internal waves in a rotating ocean // Oceanology. 1978. V. 18. P. 119–125.)

  9. Grimshaw R., Pelinovsky E., Poloukhina O. Higher order Korteweg–de Vries models for internal solitary waves in a stratified shear flow with a free surface // Nonlin. Processes in Geophys. 2002. V. 9. P. 221–235.

  10. Alias A., Grimshaw R.H.J., Khusnutdinova K.R. Coupled Ostrovsky equations for internal waves in a shear flow // Phys. Fluids. 2014. V. 26. 126603.

  11. Vakhnenko V.O. High-frequency soliton-like waves in a relaxing medium // J. Math. Phys. 1999. V. 40. P. 2011–2020.

  12. Obregon M.A., Stepanyants Yu.A. Oblique magneto-acoustic solitons in rotating plasma // Phys. Lett. A. 1998. V. 249. № 4. P. 315–323.

  13. Fogaça D.A., Fariello R., Navarra F.S., Stepanyants Y.A. Evolution of non-stationary pulses in a cold magnetized quark-gluon plasma // CNSNS, 2020 (to be published). (ArXiv, 2676191 [hep-ph] 3 May 2019, https://arxiv.org/abs/1810.01991)

  14. Козлов С.А., Сазонов С.В. Нелинейное распространение импульсов длительностью в несколько колебаний светового поля в диэлектрических средах // ЖЭТФ. 1997. Т. 111. № 2. С. 404–418.

  15. Hunter J.K. Numerical solution of some nonlinear dispersive wave equations. In: Computational Solutions of Nonlinear Systems of Equations, Lectures in Applied Mathematics, ed. E.L. Allgower, K. Georg, AMS, Providence. 1990. V. 26. P. 301–316.

  16. Yagi D., Kawahara T. Strongly nonlinear envelope soliton in a lattice model for periodic structure // Wave Motion. 2001. V. 34. P. 97–107.

  17. Литвак А.Г., Миронов В.А., Скобелев С.А. Динамика самовоздействия сверхкоротких электромагнитных импульсов // Письма в ЖЭТФ. 2005. Т. 82. С. 119–123.

  18. Бенилов Е.С., Пелиновский Е.Н. К теории распространения волн в нелинейных флуктуирующих средах без дисперсии // ЖЭТФ. 1988. Т. 94. С. 175–185.

  19. Grimshaw R.H.J., Ostrovsky L.A., Shrira V.I., Stepanyants Yu.A. Long nonlinear surface and internal gravity waves in a rotating ocean // Surveys in Geophysics. 1998. V. 19. P. 289–338.

  20. Apel J., Ostrovsky L.A., Stepanyants Y.A., Lynch J.F. Internal solitons in the ocean and their effect on underwater sound // J. Acoust. Soc. Am. 2007. V. 121. P. 695–722.

  21. Ostrovsky L.A., Pelinovsky E.N., Shrira V.I. and Stepanyants Y.A. Beyond the KDV: Post-explosion development // Chaos. 2015. V. 25. № 9. 097620.

  22. Holloway P.E., Pelinovsky E., Talipova T. A generalized Korteweg–de Vries model of internal tide transformation in the coastal zone // J. Geophys. Res. C. 1999. V. 104. P. 18.333–18.350.

  23. Schäfer T., Wayne C.E. Propagation of ultra-short optical pulses in cubic nonlinear media // Physica D. 2004. V. 196. P. 90–105.

  24. Руденко О.В. Одномерная модель уравнений типа Хохлова–Заболотской для волн в фокальной области кубичной и квадратично-кубичной нелинейных сред // Доклады Академии Наук. 2017. Т. 475. № 5. С. 503–507. (Rudenko O.V. One-dimensional model of KZ-type equations for waves in the focal region of cubic and quadratically-cubic nonlinear media // Doklady Mathematics. 2017. V. 96. P. 399–402.

  25. Erofeev V., Kolesov D., Leonteva A. Nonlinear waves in an elastic guide interacting with an elastic-inertial foundation // MATEC Web of Conferences. 2018. V. 224. 02044.

  26. Grimshaw R. Evolution equations for weakly nonlinear, long internal waves in a rotating fluid // Stud. Appl. Math. 1985. V. 73. P. 1–33.

  27. Grimshaw R., Melville W.K. On the derivation of the modified Kadomtsev–Petviashvili equation // Stud. Appl. Math. 1989. V. 80. P. 183–202.

  28. Grimshaw R. Evolution equations for long nonlinear internal waves in stratified shear flows // Stud. Appl. Math. 1981. V. 65. P. 159–188.

  29. Бреховских Л.М., Гончаров В.В. Введение в механику сплошных сред. М.: Наука, 1982. 335 с.

  30. Yang J. Nonlinear Waves in Integrable and Nonintegrable Systems. Philadelphia, SIAM, 2010. 430 p.

  31. Khusnutdinova K., Stepanyants Y., Tranter M. The influence of the nonlinear dispersion on the shapes of solitary waves // Phys. Fluids. 2018. V. 30. 022104, 20 p.

  32. Островский Л.А., Потапов А.И. Введение в теорию модулированных волн. М.: Физматлит, 2003. 400 с. (Ostrovsky L.A., Potapov A.I. Modulated waves: Theory and applications. 1999, London, Johns Hopkins University Press, Baltimore.)

  33. Zakharov V.E., Ostrovsky L.A. Modulation instability: The beginning // Physica D. 2009. V. 238. P. 540–548.

  34. Grimshaw R., Helfrich K. Long-time solutions of the Ostrovsky equation // Stud. Appl. Math. 2008. V. 121. P. 71–88.

  35. Whitfield A.J., Johnson E.R. Rotation-induced nonlinear wavepackets in internal waves // Phys. Fluids. 2014. V. 26. 056606, 22 p.

  36. Whitfield A.J., Johnson E.R. Wave-packet formation at the zero dispersion point in the Gardner-Ostrovsky equation // Phys. Rev. E. 2015. V. 91. 051201(R).

  37. Nikitenkova S.P., Singh N., Stepanyants Y.A. Modulational stability of weakly nonlinear wavetrains in media with small- and large-scale dispersions // Chaos. 2015. V. 25. 123113, 9 p.

  38. Grimshaw R.H.J. Adjustment processes and radiating solitary waves in a regularised Ostrovsky equation // Eur. J. Mech. B/Fluids. 1999. V. 18. P. 535–543.

  39. Khusnutdinova K.R., Tranter M.R. D’Alembert-type solution of the Cauchy problem for the Boussinesq–Klein–Gordon equation // Stud. Appl. Math. 2019. V. 142. P. 551–585.

  40. Benilov E.S. On surface waves in a shallow channel with an uneven bottom // Stud. Appl. Math. 1992. V. 87. P. 1–14.

  41. Grimshaw R.H.J., Helfrich K., Johnson E.R. The reduced Ostrovsky equation: Integrability and breaking // Stud. Appl. Math. 2012. V. 129. P. 414–436.

  42. Stepanyants Y.A. On stationary solutions of the reduced Ostrovsky equation: Periodic waves, compactons and compound solitons // Chaos, Solitons and Fractals. 2006. V. 28. P. 193–204.

  43. Johnson E.R., Grimshaw R.H.J. Modified reduced Ostrovsky equation: Integrability and breaking // Phys. Rev. E. 2013. V. 88. 021201.

  44. Leonov A.I. The effect of the Earth’s rotation on the propagation of weak nonlinear surface and internal long oceanic waves // Ann. NY Acad. Sci. 1981. V. 373. Р. 150–159.

  45. Галкин В.М., Степанянц Ю.А. О существовании стационарных уединенных волн во вращающейся жидкости // ПММ. 1991. Т. 55. № 6. С. 1051−1055. (Galkin V.M., Stepanyants Yu.A. On the existence of stationary solitary waves in a rotating fluid // Appl. Math. and Mech. 1991. V. 55. № 6. P. 939–943.)

  46. Островский Л.А., Степанянц Ю.А. Нелинейные волны во вращающейся жидкости. В кн. “Нелинейные волны. Физика и астрофизика”, М.: Наука, 1993, С. 132–153. (English version: Ostrovsky L.A., Stepanyants Yu.A. Nonlinear surface and internal waves in rotating fluids. In: Nonlinear Waves. 3. Physics and Astrophysics, Springer–Verlag, 1990. Р. 106–128.)

  47. Gilman O.A., Grimshaw R., Stepanyants Yu.A. Approximate analytical and numerical solutions of the stationary Ostrovsky equation // Stud. Appl. Math. 1995. V. 95. № 1. P. 115–126.

  48. Chen G-Y., Boyd J.P. Analytical and numerical studies of weakly nonlocal solitary waves of the rotation-modified Korteweg–de Vries equation // Physica D. 2001. V. 155. P. 201–222.

  49. Boyd J.P., Chen G-Y. Five regimes of the quasi-cnoidal, steadily translating waves of the rotation-modified Korteweg–de Vries (“Ostrovsky”) equation // Wave Motion. 2002. V. 35. P. 141–155.

  50. Горшков К.А., Островский Л.А., Папко В.В. Взаимодействие и связанные состояния солитонов как классических частиц // ЖЭТФ. 1976. Т. 71. № 2. С. 585–593.

  51. Gorshkov K.A., Ostrovsky L.A., Stepanyants Yu.A. Dynamics of soliton chains: From simple to complex and chaotic motions. In: Long-Range Interactions, Stochasticity and Fractional Dynamics, eds. Albert C.J. Luo and Valentin Afraimovich, Springer, 2010, P. 177–218.

  52. Grimshaw R.H.J., He J.-M., Ostrovsky L.A. Terminal damping of a solitary wave due to radiation in rotational systems // Stud. Appl. Math. 1998. V. 101. C. 197–210.

  53. Obregon M., Stepanyants Y. On numerical solution of the Gardner–Ostrovsky equation // Math. Model. Natural Phenom. 2012. V. 7. № 2. P. 113–130.

  54. Grimshaw R., Stepanyants Y., Alias A. Formation of wave packets in the Ostrovsky equation for both normal and anomalous dispersion // Proc. Roy. Soc. A. 2016. V. 472. 20150416, 20 p.

  55. Grimshaw R., Helfrich K. The effect of rotation on internal solitary waves // IMA J. Appl. Math. 2012. V. 77. P. 326–339.

  56. Grimshaw R.H.J., Helfrich K.R., Johnson E.R. Experimental study of the effect of rotation on nonlinear internal waves // Phys. Fluids. 2013. V. 25. 056602.

  57. Helfrich K. Decay and return of internal solitary waves with rotation // Phys. Fluids. 2007. V. 19. 026601.

  58. Whitfield A.J., Johnson E.R. Whitham modulation theory for the Ostrovsky equation // Proc. R. Soc. A. 2016. V. 473. 20160709.

  59. Grimshaw R., Smyth N., Stepanyants Y. Decay of Benjamin–Ono solitons under the influence of dissipation // Wave Motion. 2018. V. 78. P. 98–115.

  60. Obregon M., Raj N., Stepanyants Y. Dynamics of Gardner solitons under the influence of the Earth’ rotation // Chaos. 2018. V. 28. 033106, 11 p.

  61. Gilman O.A., Grimshaw R., Stepanyants Yu.A. Dynamics of internal solitary waves in a rotating fluid // Dyn. Atmos. and Oceans. 1996. V. 23. № 1–4. P. 403–411.

  62. Ostrovsky L.A., Stepanyants Y.A. Interaction of solitons with long waves in a rotating fluid // Physica D. 2016. V. 333. P. 266–275.

  63. Gorshkov K.A., Ostrovsky L.A. Interaction of solitons in nonintegrable systems: direct perturbation method and applications // Physica D. 1981. V. 3. P. 428−438.

  64. Ostrovsky L.A., Gorshkov K.A. Perturbation theories for nonlinear waves. In: Christiansen P., Soerensen M. (eds.) Nonlinear science at the down at the XXI century, Amsterdam, Elsevier, 2000. P. 47−65.

  65. Grimshaw R., Smyth N., Stepanyants Y. Interaction of a Benjamin–Ono soliton with a long wave in a rotating ocean // Physica D. 2020 (to be published). ArXiv: 1911.02751 [nlin.PS] 7 Nov 2019.

  66. Ostrovsky L.A., Stepanyants Y. Complex dynamics of solitons in rotating fluids. In: The Many Facets of Complexity Science, eds. Volchenkov D., Springer, 2019.

  67. Chester W., Bones J.A. Resonant oscillations of water waves // Proc. Roy. Soc. A. 1968. V. 306. P. 23–39.

  68. Ezersky A.B., Polukhina O.E., Brossard J., Marin F., Mutabazi I. Spatiotemporal properties of solitons excited on the surface of shallow water in a hydrodynamic resonator // Phys. Fluids. 2006. V. 18. 067104, 12 p.

  69. Горшков К.А., Островский Л.А., Папко В.В. Параметрическое усиление и генерация импульсов в нелинейных распределенных системах // Изв. В-УЗов, Радиофизика. 1973. Т. 16. С. 1195–1204.

  70. Massel S.R. Hydrodynamics of the coastal zone. Amsterdam: Elsvier, 1989. 336 p.

  71. Пелиновский Е.Н. Гидродинамика волн цунами. Н. Новгород: ИПФ РАН, 1996. 276 с.

  72. Talipova T.G., Kurkina O.E., Rouvnskaya E.V., Pelinovsky E.N. Propagation of solitary internal waves in two-layer ocean of variable depth // Izvestiya Atmos Ocean Phys. 2015. V. 51. P. 89–97.

  73. Grimshaw R., Guo C., Helfrich K., Vlasenko V. Combined effect of rotation and topography on shoaling oceanic internal solitary waves // J. Phys. Oceanogr. 2014. V. 44. P. 1116–1132.

  74. Ostrovsky L.A., Helfrich K.R. Some new aspects of the joint effect of rotation and topography on internal solitary waves // J. Phys. Oceanogr. 2019. V. 49. P. 1639–1649.

  75. Stepanyants Y.A. The effects of interplay between the rotation and shoaling for a solitary wave on variable topography // Stud. Appl. Math. 2019. V. 142. P. 465–486.

  76. Pelinovsky E., Talipova T., Didenkulova I., Didenkulova E. (Shurgalina). Long traveling interfacial waves in a two-layer fluid of variable depth // Stud. Appl. Math. 2019. V. 142. № 4. P. 513–527.

  77. Stepanyants Y.A. Dynamics of internal envelope solitons in a rotating fluid of a variable depth // Fluids. 2019. V. 4. 56, 12 p.

  78. Гримшоу Р. Модели нелинейных длинных внутренних волн во вращающемся океане // Фунд. Прикл. Гидрофиз. 2013. Т. 6. № 3. С. 4–13.

  79. Stepanyants Y.A., Ten I.K., Tomita H. Lump solutions of 2D generalised Gardner equation. In: “Nonlinear Science and Complexity”, Proceedings of the Conference, Beijing, China, 7–12 August 2006, 264–271. Eds. Luo A.C.J., Dai L. and Hamidzadeh H.R., World Scientific, 2006, 556 p. http://www.worldscibooks. com/chaos/6334.html

  80. Chen R.M., Hur V.M., Liu Y. Solitary waves of the rotation-modified Kadomtsev–Petviashvili equation // Nonlinearity. 2008. V. 21. P. 2949–2979.

  81. Esfahani A. Decay properties of the traveling waves of the rotation-generalized Kadomtsev–Petviashvili equation // J. Phys. A: Math. Theor. 2010. V. 43. 395201, 13p.

  82. Esfahani A., Levandosky S. Stability of solitary waves of the Kadomtsev–Petviashvili equation with a weak rotation // SIAM J. Math. Anal. 2017. V. 49. P. 5096–5133.

  83. Clarke S., Gorshkov K., Grimshaw R., Stepanyants Y. Decay of Kadomtsev–Petviashvili lumps in dissipative media // Physica D. 2018. V. 366. P. 43–50.

  84. Grimshaw R., Tang S. The rotation-modified Kadomtsev–Petviashvili equation: An analytical and numerical study // Studies Appl. Math. 1990. V. 83. P. 223–248.

  85. Stanton T.P., Ostrovsky L.A. Observations of highly nonlinear internal solitons over the continental shelf // Geophys. Res. Lett. 1998. V. 25. P. 2695–2698.

  86. Ostrovsky L.A., Grue J. Evolution equations for strongly nonlinear internal waves // Phys. Fluids. 2003. V. 15. P. 2934–2948.

  87. Lamb K.G., Polukhina O., Talipova T., Pelinovsky E., Xiao W., Kurkin A. Breather generation in fully nonlinear models of a stratified fluid // Phys. Rev. E. 2007. V. 75. № 4. 046306.

  88. Gerkema T. A unified model for the generation and fission of internal tides in a rotating ocean // J. Marine Res. 1996. V. 54. P. 421–450.

  89. Li Q., Farmer D.M. The generation and evolution of nonlinear internal waves in the deep basin of the South China Sea // J. Phys. Oceanogr. 2011. V. 41. P. 1345–1363.

  90. Johnson E.R. Wave packets in the anomalous Ostrovsky equation // Phys. Rev. E. 2019. V. 100. 043109, 5 p.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Физика атмосферы и океана

Архивы выпусков Информация о журнале Отправить рукопись в журнал