Известия РАН. Физика атмосферы и океана, 2020, T. 56, № 1, стр. 43-54

ВВЕДЕНИЕ

Климатические изменения последних лет сопровождаются особенно резким сокращением площади и толщины морского льда в Арктике и, как следствие, аномальным выделением тепла над остающейся открытой в предзимний и начальный зимний периоды поверхностью Баренцева и отчасти Карского морей [1]. Известно, что потепление в Арктике последних двух десятилетий неожиданно сопровождалось чередой суровых зим как на Евразийском континенте, так и в Северной Америке, но остается открытым вопрос о причинах этой экстремальности и вклада в нее атмосферного блокирования (см. также раздел “Холодные зимы последних лет” в [2]). Простейшее объяснение этому обстоятельству заключается в том, что при потеплении в Арктике происходит уменьшение меридионального градиента температуры между экватором и Северным полюсом. Как следствие – в соответствии с уравнением термического ветра – уменьшается интенсивность зональной циркуляции атмосферы и вместе с этим уменьшается перенос в зимний период относительно теплого воздуха с океанов на восток вглубь континентов. При этом также увеличивается степень меридиональности атмосферной циркуляции, что способствует затоку холодного арктического воздуха в средние широты. Согласно [2], формирование аномально холодных погодных режимов над Северной Евразией в последние десятилетия связано с характерной структурой в виде антициклонической аномалии над Баренцевым морем и южнее его, приводящей к блокированию западного зонального переноса¹¹. Начиная с работы [4], достигнут консенсус относительно динамических “путей” (pathways), ведущих в недавние десятилетия от отрицательных аномалий морского льда и положительных аномалий температуры воздуха над Баренцево-Карским морем (в течение осени) к низким температурам в Северной Америке и Евразии в середине и конце зимы. Было предложено два динамических пути: тропосферный путь, в основном действующий осенью до начала зимы, и стратосферный путь, действующий в конце зимы. Тропосферный путь связан с форсированием тропосферных цугов планетарных волн, которые могут интерферировать с уже существующими планетарными волнами Россби и в итоге вести к увеличению вероятности блокирования над Скандинавией в начале зимы [5]. На втором пути аномалии морского льда и суровые зимы на континентах динамически связаны через полярную стратосферу и ослабление стратосферного полярного вихря [6]. Этот стратосферный путь может инициироваться и усилиться за счет увеличения сибирского снежного покрова в октябре месяце [7]. Возникает вопрос, есть ли прямая динамическая связь между аномальным выделением тепла в Арктике и теми изменениями характеристик крупномасштабной атмосферной циркуляции, что способствовали бы упомянутым процессам? В работе [8] была высказана идея нелинейного отклика атмосферной циркуляции над Баренцевым и Карским морями на степень покрытия его ледовым покровом. При полностью покрытыми льдом морями циркуляция атмосферы над ними циклоническая. Она сменяется на антициклоническую при частично покрытыми льдом морями, а затем снова становится циклонической при полностью свободными ото льда морями. Этот эффект был продемонстрирован как на численных расчетах с помощью модели ECHAM5, так и проинтерпретирован теоретически. Последнее представляет наибольший интерес в плане данной работы. Именно, в [8] рассмотрен баланс тепла в планетарном пограничном слое и выписаны явно условия динамического и термодинамического равновесия на его верхней границе. Следуя [9], при расчете вертикальной скорости на верхней границе планетарного (экмановского) пограничного слоя в [8] учитывалась бароклинность атмосферы. При этом имеется в виду, что приземный нагрев создает горизонтальные градиенты температуры воздуха, которые в силу уравнения термического ветра влияют на конвергенцию (дивергенцию) воздуха в пограничном слое, а значит и на вертикальную скорость на его верхней границе. Согласно авторам [8], именно эффект бароклинности ответственен за нелинейный отклик атмосферной циркуляции на изменения ледовой обстановки над Баренцевым и Карским морями.

В данной работе мы еще раз независимо рассмотрим вопрос о динамическом отклике атмосферы высоких широт на аномальный нагрев с поверхности и будем использовать для этой цели двумерную бароклинную модель атмосферы [10]. Эта модель обобщает классическую модель баротропной сжимаемой по горизонтали атмосферы [11] на случай учета (хотя и в схематическом виде) процессов усвоения притоков тепла и его превращения в работу по преодолению сил трения. Модель [10] получается путем усреднения уравнений гидротермодинамики по высоте в предположении, что компоненты скорости ветра, а также потенциальная температура слабо зависят от высоты и меняются лишь по горизонтали. Тем самым, строго говоря, нарушается динамический баланс между полями скорости и температуры, поддерживаемый вертикальными циркуляциями и математически выражаемый уравнением термического ветра. Об этом затруднении писал еще Теннекес [12], которому принадлежит одна из первых формулировок двумерной модели атмосферы с учетом горизонтальной плавучести в поле силы Кориолиса. Постоянство потенциальной температуры с высотой может быть объяснено действием двух факторов: во-первых, сильным вертикальным механическим перемешиванием благодаря большим скоростям ветра (что также выравнивает с высотой и скорость ветра); во-вторых, интенсивной конвекцией от источника тепла на поверхности. Есть также основания полагать, что сильное конвективное перемешивание по вертикали имеет своим следствием выравнивание скорости ветра с высотой и концентрацию сдвига скорости вблизи поверхности земли. В арктических широтах подобные условия возникают тогда, когда холодный воздух с температурой существенно ниже нуля градусов по Цельсию натекает на открытую поверхность воды. При этом хорошо перемешанный слой может достигать высоты в 1–2 километра, однако в целях упрощения задачи и из методических соображений, мы вначале рассмотрим случай, когда вся атмосфера перемешана по вертикали. Затем, во второй части работы будет обрисован случай, когда хорошо перемешанный слой имеет конечную толщину, малую по сравнению с высотой однородной атмосферы. Потенциальная температура в этом слое может (слабо) меняться по горизонтали под действием притоков тепла, однако она всегда остается меньшей, чем потенциальная температура вышележащего слоя воздуха, т.е. условие глобальной статической устойчивости по вертикали выполнено. В океанологии, многослойные модели, основанные на обобщениях модели “мелкой воды” на случай учета изменений плотности по горизонтали, предлагались, например, в [13]. Они активно используются в теоретических исследованиях и в настоящее время (напр. [14]); сходные модели для атмосферы (хотя и более идеализированные, чем в настоящей работе) предлагались, например, в [15].

Исходим из уравнений гидродинамики, взятых в квазистатическом приближении и записанных для простоты в декартовой системе координат $\left( {x,\,y,\,z} \right)$, где ось $x$ направлена на восток, ось $y$ – на север и ось $z$ – вверх:

В этих уравнениях ${\mathbf{v}} = \left( {u,v} \right)$ – вектор горизонтальной скорости ветра, $w$ – вертикальная скорость, $\nabla = \left( {{\partial \mathord{\left/ {\vphantom {\partial {\partial x}}} \right. \kern-0em} {\partial x}},{\partial \mathord{\left/ {\vphantom {\partial {\partial y}}} \right. \kern-0em} {\partial y}}} \right)$ – двумерный оператор Гамильтона, ${\mathbf{k}}$ – единичный вектор, направленный вертикально вверх, $\rho $ – плотность воздуха, $p$ – давление, $T$ – температура, $R$ – газовая постоянная, ${{c}_{p}}$ – удельная теплоемкость при постоянном давлении, $f$ – параметр Кориолиса, $g$ – ускорение свободного падения, ${\mathbf{F}}$ – вектор силы турбулентного вязкого трения, $Q$ – притоки тепла в расчете на единицу объема; ${{\text{D}} \mathord{\left/ {\vphantom {{\text{D}} {{\text{D}}t}}} \right. \kern-0em} {{\text{D}}t}} = {\partial \mathord{\left/ {\vphantom {\partial {\partial t}}} \right. \kern-0em} {\partial t}}$ + + ${\mathbf{v}} \cdot \nabla + w{\partial \mathord{\left/ {\vphantom {\partial {\partial z}}} \right. \kern-0em} {\partial z}}$ – символ полной (индивидуальной) производной по времени. Система уравнений (1)–(5) является полной, если вектор ${\mathbf{F}}$ выражен в терминах скорости ${\mathbf{v}}$ и поле притоков тепла $Q$ является известной функцией координат и времени. В дальнейшем нас интересуют приложения к арктической атмосфере, где параметр Кориолиса меняется очень мало, и поэтому мы считаем его постоянным по величине и ограничиваемся приближением $f$ – плоскости. Отметим, что это приближение не является необходимым и делается для облегчения логики рассуждений. Аналогичное приближение использовалось в работе [11].

МОДЕЛЬ ДВУМЕРНОЙ БАРОКЛИННОЙ АТМОСФЕРЫ

Следуя [11, 10 ], усредним уравнения (1)–(5) по толще атмосферы, считая вектор скорости ${\mathbf{v}} = \left( {u,v} \right)$ и потенциальную температуру $\theta = T{{\left( {{{{{p}_{{00}}}} \mathord{\left/ {\vphantom {{{{p}_{{00}}}} p}} \right. \kern-0em} p}} \right)}^{{{R \mathord{\left/ {\vphantom {R {{{c}_{p}}}}} \right. \kern-0em} {{{c}_{p}}}}}}},$ где ${{p}_{{00}}} = {{10}^{3}}\,\,{\text{гПа,}}$ независящими от высоты. Методика осреднения подробно описана в [11, 10 ], а также воспроизведена в [16, 17]. Именно, вводим операторы осреднения по высоте $\hat {A} = \int_0^\infty {A{\text{d}}z} {\kern 1pt} ,$ $\bar {B} = {{\int_0^\infty {B\rho } {\kern 1pt} {\text{d}}z} \mathord{\left/ {\vphantom {{\int_0^\infty {B\rho } {\kern 1pt} {\text{d}}z} {\int_0^\infty \rho {\kern 1pt} {\text{d}}z}}} \right. \kern-0em} {\int_0^\infty \rho {\kern 1pt} {\text{d}}z}}$ ≡ ${{\int_0^\infty {B\rho } {\kern 1pt} {\text{d}}z} \mathord{\left/ {\vphantom {{\int_0^\infty {B\rho } {\kern 1pt} {\text{d}}z} {\hat {\rho }}}} \right. \kern-0em} {\hat {\rho }}}$ и из уравнений (1)–(3) после ряда операций находим, что

Здесь ${{{\hat {D}}} \mathord{\left/ {\vphantom {{{\hat {D}}} {{\text{D}}t}}} \right. \kern-0em} {{\text{D}}t}} = {\partial \mathord{\left/ {\vphantom {\partial {\partial t}}} \right. \kern-0em} {\partial t}} + {\mathbf{v}} \cdot \nabla $ – символ полной производной по времени при горизонтальном (двумерном) движении и $\hat {\rho } = {{{{p}_{0}}} \mathord{\left/ {\vphantom {{{{p}_{0}}} g}} \right. \kern-0em} g},$ где ${{p}_{0}}$ – приземное давление. Чтобы привести к осредненному (редуцированному) виду уравнения (4) и (5), следуем [16, 17] и выпишем выражение для $\hat {p}$, воспользовавшись уравнением состояния (5), определением потенциальной температуры и условием ее постоянства с высотой:

В этом уравнении ${{\hat {\rho }}_{{00}}} \equiv {{{{p}_{{00}}}} \mathord{\left/ {\vphantom {{{{p}_{{00}}}} g}} \right. \kern-0em} g}$ и $\kappa = {{{{с}_{p}}} \mathord{\left/ {\vphantom {{{{с}_{p}}} {{{c}_{v}}}}} \right. \kern-0em} {{{c}_{v}}}},$ где ${{c}_{v}}$ – удельная теплоемкость при постоянном объеме. Уравнение (8) является частным случаем политропного уравнения с показателем политропы $n = {{\left( {2\kappa - 1} \right)} \mathord{\left/ {\vphantom {{\left( {2\kappa - 1} \right)} \kappa }} \right. \kern-0em} \kappa }.$ Случаю несжимаемой жидкости отвечает предел $\kappa \to \infty ,$ когда $n \to 2 - .$ Беря логарифмическую полную производную по времени от уравнения (8), используя уравнение (4), а также определение потенциальной температуры, будем иметь

При выводе (9) также использовалось уравнение (7). Уравнения (6), (7) и (9) образуют полную систему уравнений движения двумерной бароклинной атмосферы [10]. Работа [10] нашла быстрый отклик в работах [18, 19]. В частности, в [19] линеаризованные относительно состояния покоя уравнения (6), (7) и (9) (при ${\mathbf{\hat {F}}} = 0$) использовались для решения обобщенной задачи об адаптации полей давления и скорости в присутствии источников тепла. Близкая по духу к [10] климатическая модель была предложена в [20].

Непосредственно проверяется, что уравнение баланса энергии для уравнений (6), (7) и (9) имеет вид

Под знаком частной производной по времени стоит сумма $e$ кинетической и полной потенциальной энергии: $e = \hat {\rho }\left( {{{{{{\mathbf{v}}}^{2}}} \mathord{\left/ {\vphantom {{{{{\mathbf{v}}}^{2}}} 2}} \right. \kern-0em} 2}} \right) + \hat {\rho }{{с}_{p}}\bar {T}.$ Энергия генерируется при наличии положительной корреляции между полем $\hat {p}$ и средним по столбу воздуха полем объемных источников тепла, отнесенных к давлению воздуха $\overline {\left( {{Q \mathord{\left/ {\vphantom {Q p}} \right. \kern-0em} p}} \right)} .$

Следующий шаг состоит во введении в уравнения (6), (7) и (9) квазигеострофического приближения. Это можно делать несколькими способами. Один из них состоит в следующем. Используя уравнение $\hat {p} = \hat {\rho }R\bar {T},$ которое следует из (5), перепишем (9) с учетом (7) в виде

Соответственно, уравнение (6) примет вид

Введем квазигеострофическое приближение в уравнения (7), (10) и (11), взятые в адиабатическом приближении, а слагаемые с диссипацией и притоками тепла допишем позже. Вводим постоянные средние значения термодинамических переменных и малые отклонения от них по формулам: $\hat {\rho } = \left\langle {\hat {\rho }} \right\rangle + \hat {\rho }{\kern 1pt} ',$ $\bar {T} = \left\langle {\bar {T}} \right\rangle + \bar {T}{\kern 1pt} '.$ Приближенно имеем

где $\xi = {{\hat {\rho }{\kern 1pt} '} \mathord{\left/ {\vphantom {{\hat {\rho }{\kern 1pt} '} {\left\langle {\hat {\rho }} \right\rangle }}} \right. \kern-0em} {\left\langle {\hat {\rho }} \right\rangle }},$ $\eta = {{\bar {T}{\kern 1pt} '} \mathord{\left/ {\vphantom {{\bar {T}{\kern 1pt} '} {\left\langle {\bar {T}} \right\rangle }}} \right. \kern-0em} {\left\langle {\bar {T}} \right\rangle }}$ и $c_{1}^{2} = R\left\langle {\bar {T}} \right\rangle .$ Представим поле скорости в виде суммы соленоидальной и малой потенциальной компоненты, ${\mathbf{v}} = {\mathbf{k}} \times \nabla \psi + \nabla \phi ,$ где $\psi $ – функция тока и $\phi $ – потенциал скорости. Применим к (12) операции вихря и дивергенции, получаем линейное уравнение геострофического баланса $f{{\nabla }^{2}}\psi = c_{1}^{2}{{\nabla }^{2}}\left( {\xi + \eta } \right)$ и после простых преобразований приходим от (12)–(14) к уравнениям где ${{L}_{{{\kern 1pt} 1}}} = {{{{c}_{1}}} \mathord{\left/ {\vphantom {{{{c}_{1}}} f}} \right. \kern-0em} f}$ и J означает якобиан. Уравнения (15) и (16) можно записать более компактно, сделав замену переменных $f\sigma = f\eta - \frac{{\kappa - 1}}{{2\kappa - 1}}L_{1}^{{ - 2}}\psi ,$

В левой части (17) появился масштаб Обухова ${{L}_{0}} = {{{{c}_{0}}} \mathord{\left/ {\vphantom {{{{c}_{0}}} f}} \right. \kern-0em} f}$ [11], где $c_{0}^{2} = R\left\langle {{{T}_{0}}} \right\rangle $ и $\left\langle {{{T}_{0}}} \right\rangle $ – средняя приземная температура, связанная со средней температурой атмосферы $\left\langle {\bar {T}} \right\rangle $ соотношением $\left\langle {\bar {T}} \right\rangle \frac{{2\kappa - 1}}{\kappa } = \left\langle {{{T}_{0}}} \right\rangle $. Как показывает прямая выкладка, $\sigma = \frac{\kappa }{{2\kappa - 1}}\frac{{\theta {\kern 1pt} '}}{{\left\langle \theta \right\rangle }}.$ Уравнения (17) и (18) могли бы быть получены непосредственно из уравнений (6)–(9) путем квазигеострофического разложения последних, но это требует определенного искусства аппроксимаций. Использованный обходной путь более “алгоритмичен”, и мы предпочитаем его. Отметим, что в переменных $\left( {\xi ,\,\sigma } \right)$ линейное уравнение квазигеострофического баланса имеет вид $f{{\nabla }^{2}}\psi = c_{0}^{2}{{\nabla }^{2}}\left( {\xi + \sigma } \right).$

В адиабатическом приближении система уравнений (17) и (18) обладает законами сохранения энергии

и так называемых инвариантов Казимира (казимиров) где введено обозначение $\Pi = {{\nabla }^{2}}\psi - L_{0}^{{ - 2}}\psi $ для потенциальной завихренности, которая сохраняется в баротропной атмосфере [11]; $\Phi $ и $\Gamma $ – произвольные дифференцируемые функции.

Представляет определенный интерес записать уравнения (17) и (18) в форме уравнений Намбу [21, 22], используя для этого две функции Гамильтона:

Вычисляя вариации этих функционалов

имеем выражения для вариационных производных $\psi = - {{\delta \mathcal{H}} \mathord{\left/ {\vphantom {{\delta \mathcal{H}} {\delta \Pi }}} \right. \kern-0em} {\delta \Pi }},$ $\Pi = - {{\delta \mathcal{H}} \mathord{\left/ {\vphantom {{\delta \mathcal{H}} {\delta \psi }}} \right. \kern-0em} {\delta \psi }},$ $\sigma = {{\delta \mathcal{G}} \mathord{\left/ {\vphantom {{\delta \mathcal{G}} {\delta \Pi }}} \right. \kern-0em} {\delta \Pi }},$ $\Pi = {{\delta \mathcal{G}} \mathord{\left/ {\vphantom {{\delta \mathcal{G}} {\delta \sigma }}} \right. \kern-0em} {\delta \sigma }}.$ Поэтому для произвольного функционала уравнения (17) и (18) записываются в форме уравнений Намбу где квадратные скобки обозначают скобку Намбу для данной задачи. Многоточием отмечен тот факт, что для того чтобы скобка Намбу была совершенно антисимметрична, т.е. меняла бы знак при перестановке любых двух функционалов и, следовательно, обращалась бы в нуль при равенстве любых двух функционалов, к выписанному интегралу добавляются еще два, полученные циклической перестановкой функционалов. Из выписанного уравнения автоматически следуют законы сохранения ${{{\text{d}}\mathcal{H}} \mathord{\left/ {\vphantom {{{\text{d}}\mathcal{H}} {{\text{d}}t}}} \right. \kern-0em} {{\text{d}}t}} = {{{\text{d}}\mathcal{G}} \mathord{\left/ {\vphantom {{{\text{d}}\mathcal{G}} {{\text{d}}t}}} \right. \kern-0em} {{\text{d}}t}} = 0.$ Таким образом, приведен еще один пример задачи в геофизической гидродинамике, допускающей запись в форме уравнений Намбу. Отметим, что уравнения (17) и (18) могут быть альтернативно записаны в форме так называемых скобок Намбу II рода [23], когда для построения скобок используются функционалы $\mathcal{H}$, $\mathcal{K} = \left( {{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}} \right)\iint {{\kern 1pt} {{\Pi }^{2}}}{\kern 1pt} {\text{d}}x{\text{d}}y$ и $\mathcal{L} = \iint {{\kern 1pt} \sigma }{\kern 1pt} {\text{d}}x{\text{d}}y.$ При этом потенциальная энстрофия $\mathcal{K}$ не является интегралом движения и используется как чисто конструкционный элемент. Скобка Намбу II рода допускает непосредственный предельный переход $\sigma \to 0$ к случаю баротропной атмосферы [11], где $\mathcal{K}$ уже является интегралом движения.

При учете экмановского трения, аномальных притоков тепла и радиационного выхолаживания по Ньютону уравнения (17) и (18) приобретают вид

где $\mu = {{f{\kern 1pt} {{h}_{E}}} \mathord{\left/ {\vphantom {{f{\kern 1pt} {{h}_{E}}} {2H}}} \right. \kern-0em} {2H}},$ причем ${{h}_{E}}$ – толщина экмановского пограничного слоя и $H$ – высота однородной атмосферы, и $\Lambda $ – постоянная радиационного выхолаживания²². Безразмерный параметр $0 \leqslant \gamma \leqslant 1$ введен для того, чтобы хотя бы частично учесть, что экмановское трение определяется геострофической скоростью на верхней границе экмановского пограничного слоя, и эта скорость при наличии горизонтального градиента потенциальной температуры отличается от средней по толще атмосферы геострофической скорости ветра. Речь идет об эффекте термического ветра, которым мы пренебрегли при выводе уравнений (6), (7) и (9), но пытаемся косвенно учесть при параметризации эффекта экмановского трения. Сходная система уравнений, но исходящая из (15) и (16) (также с учетом орографии и бета-эффекта) приведена в [25]. Предельный случай $\gamma = 1$ в (19) отвечает полному учету эффекта термического ветра, а предельный случай $\gamma = 0$ полному пренебрежению этим эффектом. В последнем случае уравнения (19) и (20) обладают лишь тривиальным (нулевым) стационарным решением при ненулевых притоках тепла. При $\gamma \ne 0$ нетривиальное стационарное решение существует для всех переменных задачи при постоянном во времени источнике тепла $\hat {Q} = \frac{{\kappa - 1}}{{2\kappa - 1}}\overline {\left( {\frac{Q}{p}} \right)} {\kern 1pt} .$ Предположим, что $\hat {Q}$ имеет простую осесимметричную форму, например, $\hat {Q} = \frac{{\kappa - 1}}{{2\kappa - 1}}{{\overline {\left( {\frac{Q}{p}} \right)} }_{0}}{{J}_{0}}\left( {kr} \right),$ где ${{J}_{0}}$ – функция Бесселя нулевого порядка и $r$ – радиальная координата (расстояние до центра тепловой аномалии). При этом ограничиваемся такими расстояниями до оси симметрии, когда функция Бесселя положительна, т.е. $r \leqslant \mathcal{R}{\text{,}}$ где $k\mathcal{R} = {{\mu }_{1}}$ и ${{\mu }_{1}} \approx 2.4$ – первый нуль функции ${{J}_{0}}$. Якобианы в (19) и (20) обращаются в нуль, если решение задачи ищется в виде $\left( {\psi ,\sigma } \right)$ = $\left( {{{\psi }_{0}},{{\sigma }_{0}}} \right){{J}_{0}}\left( {kr} \right)$. При этом ${{\nabla }^{2}}\psi = - {{k}^{2}}\psi $ и мы получаем стационарное решение (19) и (20) вида где $k_{0}^{2} \equiv L_{0}^{{ - 2}}.$ Как это следует из геострофического соотношения $f{{\psi }_{0}} = c_{0}^{2}\left( {{{\sigma }_{0}} + {{\xi }_{0}}} \right)$, относительное возмущение приземного давления равно ${{\xi }_{0}} = - \left( {1 - \gamma } \right){{\sigma }_{0}}.$ Наконец, из определения потенциальной температуры следует, что относительное возмущение приземной температуры (оно совпадает с относительным возмущением средней температуры столба воздуха в иэнтропической по высоте атмосфере) равно ${{\eta }_{0}} = \left( {2\kappa - 1} \right){{\kappa }^{{ - 1}}}{{\sigma }_{0}}$ + $\left( {\kappa - 1} \right){{\kappa }^{{ - 1}}}{{\xi }_{0}}$, и поэтому ${{\eta }_{0}} = \left( {1 + \gamma \left( {\kappa - 1} \right){{\kappa }^{{ - 1}}}} \right){{\sigma }_{0}}.$

Отметим, что если при $\gamma = 0$ решать задачу с нулевыми начальными условиями, включая в момент времени $t = 0$ постоянный приток тепла $\hat {Q} = \frac{{\kappa - 1}}{{2\kappa - 1}}{{\overline {\left( {\frac{Q}{p}} \right)} }_{0}}{{J}_{0}}\left( {kr} \right),$ то при $t > 0$ будет иметь место нестационарный процесс генерации, а затем релаксации к нулю поля слабой антициклонической завихренности, который описывается следующим решением уравнений (19) и (20) для функции тока

Отметим, что при $0 < \gamma < 1$ решение задачи с нулевыми начальными условиями также имеет характер “всплеска” антициклональной завихренности, однако потом происходит релаксация к стационарному состоянию, которое описывается первым соотношением (20а).

По определению объемного притока тепла $\int_0^\infty {Q{\kern 1pt} dz} = H$, где $H$ – сумма потоков явного и скрытого тепла через открытую поверхность моря. Чтобы в исходной трехмерной модели атмосферы не нарушалась нейтральная стратификация, считается, что ${Q \mathord{\left/ {\vphantom {Q p}} \right. \kern-0em} p}$ не зависит от высоты. Теперь элементарная выкладка дает, что ${{\overline {\left( {{Q \mathord{\left/ {\vphantom {Q p}} \right. \kern-0em} p}} \right)} }_{0}} = {{{{H}_{0}}} \mathord{\left/ {\vphantom {{{{H}_{0}}} {\hat {p}}}} \right. \kern-0em} {\hat {p}}} = {{{{H}_{0}}} \mathord{\left/ {\vphantom {{{{H}_{0}}} {\left( {R\hat {\rho }\bar {T}} \right)}}} \right. \kern-0em} {\left( {R\hat {\rho }\bar {T}} \right)}},$ где ${{H}_{0}}$ – амплитуда потоков тепла. В качестве оценки принимаем, что ${{H}_{0}}\sim 10\,\,{\text{Вт}}\,{{{\text{м}}}^{{ - 2}}}$, а также используем значения $R = 287\,\,{{{\text{м}}}^{2}}\,{{{\text{с}}}^{{ - 2}}}\,{{{\text{К}}}^{{ - 1}}},$ $\bar {T} = 250\,\,{\text{К,}}$ $\hat {\rho } \approx {{10}^{4}}\,\,{\text{кг}}\,{{{\text{м}}}^{{ - 2}}},$ ${{\Lambda }^{{ - 1}}} = 2 \times {{10}^{6}}\,\,{\text{c}}$ (≈23 сут), $\frac{{\kappa - 1}}{{2\kappa - 1}} = \frac{2}{9},$ f = 1.46 × 10^–4 c^–1. Получается, что относительные возмущения ${{\eta }_{0}}$ и ${{\xi }_{0}}$ составляют соответственно по порядку величины $ + 6 \times {{10}^{{ - 3}}}{\kern 1pt} $ и $ - 6 \times \left( {1 - \gamma } \right) \times {{10}^{{ - 3}}},$ т.е. в абсолютных единицах над аномалией притоков тепла развиваются положительная аномалия приземной температуры порядка 2 К и отрицательная аномалия приземного давления, составляющая долю от 6 гПа, если $\gamma $ близко к единице.

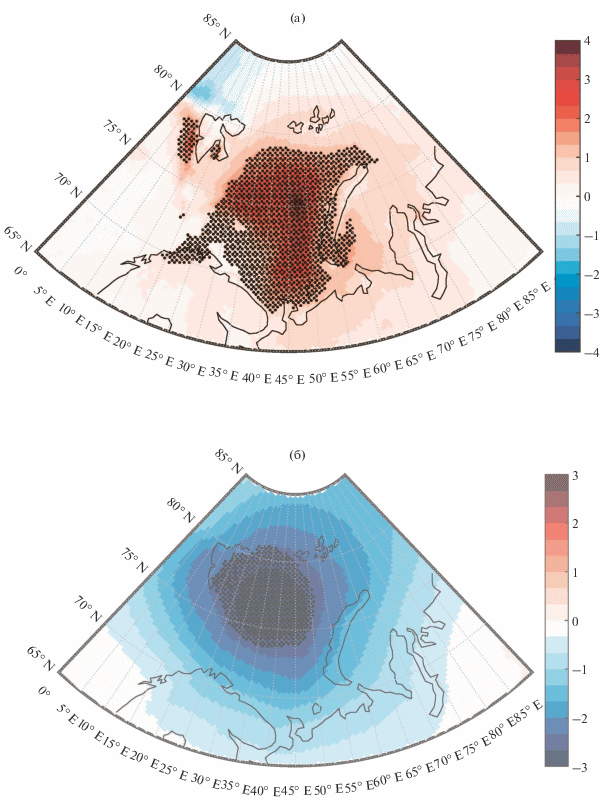
Сказанное выше иллюстрируется любезно предоставленным М.Г. Акперовым рис. 1а, 1б, где показаны композиты разности “Высокий минус низкий зимний приток Атлантических водных масс” над акваториями Баренцева и частично Карского морей для (а) приземной температуры воздуха и (б) давления на уровне моря за январь-март месяцы. Композиты получены на основе модельных расчетов с последней версией региональной климатической модели HIRHAM-NAOSIM [26]. Композиты на рис. 1а, 1б в целом неплохо, учитывая всю схематичность двумерной бароклинной модели, согласуются с нашими оценками. Также в наших расчетах в среднем по толще атмосферы возникает достаточно слабая антициклоническая циркуляция с завихренностью, равной по абсолютной величине $\sim 4.5 \times {{10}^{{ - 6}}}{\kern 1pt} \,\,{{{\text{c}}}^{{ - 1}}}$ (если ${{k}^{2}}\sim 10k_{0}^{2}$ и $\gamma $ близко к единице). Поскольку значения максимума аномалии притока тепла могут превышать ${{H}_{0}}\sim 10\,\,{\text{Вт}}\,{{{\text{м}}}^{{ - 2}}}$, то к полученному значению следует относиться как к оценке снизу. Особенностью предложенной модели является то, что она предсказывает падение приземного давления в области нагрева, но одновременно возникновение слабой антициклонической циркуляции в среднем по толще атмосферы. Это происходит из-за того, что в области аномалии нагрева возникает максимум температуры и, как следствие, происходит более медленное, чем в окружающей атмосфере падение давления с высотой, приводящее к антициклонической циркуляции в более высоких слоях атмосферы, и эта антициклоническая циркуляция превалирует при осреднении по толще атмосферы.

ДВУХСЛОЙНАЯ МОДЕЛЬ АТМОСФЕРЫ С ГОРИЗОНТАЛЬНОЙ БАРОКЛИННОСТЬЮ

Представленная выше модель отличается простотой и наглядностью, но она идеализирована в том отношении, что в ней вся атмосфера перемешана по вертикали и аномальный нагрев воздействует на всю ее толщу, хотя в арктической атмосфере его воздействие сосредоточено в нижних слоях тропосферы. Поэтому может представить интерес модель атмосферы, где прилегающий к поверхности перемешанный по вертикали слой имеет толщину порядка 1–2 километра, т.е. много меньше высоты однородной атмосферы. Впервые подобная модель была предложена и реализована в работе [27]. В реальной атмосфере этот перемешанный слой ограничен сверху устойчиво стратифицированным слоем воздуха, в котором потенциальная температура растет с высотой. Однако мы считаем, что верхний слой атмосферы характеризуется постоянством во всем его объеме потенциальной температуры, значение которой всегда выше, чем у потенциальной температуры в нижнем слое, где она под действием притоков тепла может меняться от одного столба воздуха к другому. Таким образом, условие глобальной статической устойчивости атмосферы по вертикали выполнено. В каждом из слоев скорость ветра постоянна с высотой, но меняется от одного слоя к другому. Полагаем, что нижний слой имеет верхнюю границу, описываемую уравнением $z = \zeta \left( {x,y,t} \right),$ потенциальная температура столбов воздуха в нем есть $\theta \left( {x,y,t} \right)$, а постоянная потенциальная температура верхнего слоя равна $\Theta $. Индексом “1” помечаем остальные переменные, относящиеся к верхнему слою, и индексом “2” – к нижнему. Выполняя операции усреднения по слоям, аналогично тому, как это было сделано для всей толщи атмосферы, получим

В этих уравнениях

где ${{\hat {\rho }}_{1}} = {{{{p}_{h}}} \mathord{\left/ {\vphantom {{{{p}_{h}}} g}} \right. \kern-0em} g},$ ${{\hat {\rho }}_{2}} = {{\left( {{{p}_{0}} - {{p}_{h}}} \right)} \mathord{\left/ {\vphantom {{\left( {{{p}_{0}} - {{p}_{h}}} \right)} g}} \right. \kern-0em} g}$ и ${{p}_{h}}$ – давление на поверхности раздела между слоями. Потенциальная температура в нижнем слое меняется согласно уравнению

Система уравнений замыкается уравнением для геопотенциала $g\zeta $ на поверхности раздела

которое следует из усредненного по нижнему слою уравнения гидростатики. Уравнения (21)–(28) образуют полную систему, если заданы притоки тепла в правой части (27). Хотя эти уравнения могут быть приспособлены к численной реализации, аналитическое их исследование в общем виде весьма громоздко и упрощается, когда оба слоя имеют одинаковую массу: $\left\langle {{{{\hat {\rho }}}_{1}}} \right\rangle = \left\langle {{{{\hat {\rho }}}_{2}}} \right\rangle .$

Анализ уравнений упрощается и в интересующем нас случае, когда нижний слой тонкий, т.е. $\varepsilon = {{{{{\hat {\rho }}}_{2}}} \mathord{\left/ {\vphantom {{{{{\hat {\rho }}}_{2}}} {{{{\hat {\rho }}}_{1}}}}} \right. \kern-0em} {{{{\hat {\rho }}}_{1}}}} \ll 1,$ и в задаче существует малый параметр. В этом случае выражения (26) и (28) факторизуются

откуда следует, что в этом приближении $g\zeta \approx {{{{{\hat {p}}}_{2}}} \mathord{\left/ {\vphantom {{{{{\hat {p}}}_{2}}} {{{{\hat {\rho }}}_{1}}}}} \right. \kern-0em} {{{{\hat {\rho }}}_{1}}}}.$ Как и в случае однослойной модели, вводим средние температуры верхнего и нижнего слоев по формулам ${{\hat {p}}_{{1,2}}} = R{{\bar {T}}_{{1,2}}}{{\hat {\rho }}_{{1,2}}}.$ Правые части уравнений (21) и (23) записываются в виде

Как и выше, полагаем ${{\hat {\rho }}_{{1,2}}} = \left\langle {{{{\hat {\rho }}}_{{1,2}}}} \right\rangle + \hat {\rho }_{{1,2}}^{'},$ ${{\bar {T}}_{{1,2}}}$ = $ = \left\langle {{{{\bar {T}}}_{{1,2}}}} \right\rangle + \bar {T}_{{1,2}}^{'}$ и вводим обозначения ${{\xi }_{{1,2}}} = {{\hat {\rho }_{{1,2}}^{'}} \mathord{\left/ {\vphantom {{\hat {\rho }_{{1,2}}^{'}} {\left\langle {{{{\hat {\rho }}}_{{1,2}}}} \right\rangle }}} \right. \kern-0em} {\left\langle {{{{\hat {\rho }}}_{{1,2}}}} \right\rangle }},$ ${{\eta }_{{1,2}}} = {{\bar {T}_{{1,2}}^{'}} \mathord{\left/ {\vphantom {{\bar {T}_{{1,2}}^{'}} {\left\langle {{{{\bar {T}}}_{{1,2}}}} \right\rangle }}} \right. \kern-0em} {\left\langle {{{{\bar {T}}}_{{1,2}}}} \right\rangle }}.$ С учетом постоянства потенциальной температуры в верхнем слое, очевидно, имеем ${{\eta }_{1}} = \frac{{\kappa - 1}}{\kappa }{{\xi }_{1}}.$ Теперь с асимптотической точностью, считая ${{\left\langle {{{{\hat {\rho }}}_{2}}} \right\rangle } \mathord{\left/ {\vphantom {{\left\langle {{{{\hat {\rho }}}_{2}}} \right\rangle } {\left\langle {{{{\hat {\rho }}}_{1}}} \right\rangle }}} \right. \kern-0em} {\left\langle {{{{\hat {\rho }}}_{1}}} \right\rangle }} = \varepsilon \ll 1,$ приходим к геострофическим соотношениям

Здесь введены обозначение $a_{1}^{2} = R\Theta {{\left( {{{\left\langle {{{{\hat {\rho }}}_{1}}} \right\rangle } \mathord{\left/ {\vphantom {{\left\langle {{{{\hat {\rho }}}_{1}}} \right\rangle } {{{{\hat {\rho }}}_{{00}}}}}} \right. \kern-0em} {{{{\hat {\rho }}}_{{00}}}}}} \right)}^{{\frac{{\kappa - 1}}{\kappa }}}}$ и $a_{2}^{2} = R\left\langle \theta \right\rangle {{\left( {{{\left\langle {{{{\hat {\rho }}}_{1}}} \right\rangle } \mathord{\left/ {\vphantom {{\left\langle {{{{\hat {\rho }}}_{1}}} \right\rangle } {{{{\hat {\rho }}}_{{00}}}}}} \right. \kern-0em} {{{{\hat {\rho }}}_{{00}}}}}} \right)}^{{\frac{{\kappa - 1}}{\kappa }}}}.$ Линеаризуем уравнения неразрывности (22) и (24), берем операцию вихря от уравнений движения (21) и (23), учитывая при этом (29) и (30), и исключаем из уравнений неразрывности и вихря горизонтальную дивергенцию скорости в обоих слоях. Подставляем второе соотношение (31) в получившееся для верхнего слоя уравнение и, наоборот, подставляем первое соотношение (31) в получившееся уравнение для нижнего слоя. Наконец, пользуясь определением потенциальной температуры нижнего слоя и делая замену переменных $\chi = {{\eta }_{2}} - \frac{{\kappa - 1}}{\kappa }a_{2}^{{ - 2}}{{\psi }_{2}},$ мы с асимптотической точностью по параметру $\varepsilon $ приходим на первом этапе к системе уравнений

При этом в первом уравнении (31) переменная ${{\eta }_{2}}$ без потери точности может быть заменена на $\chi $. В уравнении (33) введено краткое обозначение $\delta = {{a_{1}^{2}} \mathord{\left/ {\vphantom {{a_{1}^{2}} {a_{2}^{2} > 1}}} \right. \kern-0em} {a_{2}^{2} > 1}}.$ В правую часть уравнения (33) добавлено экмановское трение, причем толщину экмановского слоя необходимо соотносить со средней толщиной нижнего слоя $\left\langle \zeta \right\rangle $, так что в (33) $\mu = {{{{h}_{E}}} \mathord{\left/ {\vphantom {{{{h}_{E}}} {\left( {2\left\langle \zeta \right\rangle } \right)}}} \right. \kern-0em} {\left( {2\left\langle \zeta \right\rangle } \right)}}.$ Также в (34) учтено радиационное выхолаживание с постоянной $\Lambda $. Кроме того, в (32) и (33) введено слагаемое, описывающее вертикальный турбулентный обмен импульсом между слоями. Соответствующий коэффициент считается малым, $\lambda \ll \mu .$ При этом учтено, что тонкий нижний слой имеет относительную массу $\varepsilon $.

Продолжаем асимптотическую процедуру разложения уравнений (32)–(34) по малому параметру $\varepsilon $. Поскольку притоки тепла, экмановское и внутреннее трение приложены к тонкому нижнему слою, то все члены в правой части уравнения (33) имеют фактически порядок ${{\varepsilon }^{{ - 1}}}$. Поэтому в первом приближении по $\varepsilon $ левой частью уравнения (33) можно пренебречь и положить ее равной нулю. Вычисляя из получившегося уравнения ${{\partial {{\psi }_{2}}} \mathord{\left/ {\vphantom {{\partial {{\psi }_{2}}} {\partial t}}} \right. \kern-0em} {\partial t}} + J\left( {{{\psi }_{1}},\,{{\psi }_{2}}} \right)$ и подставляя в (32), после непосредственных преобразований будем иметь

При преобразовании якобиана и диссипативных членов в правой части (32а) использовалось, что приближенно ${{\psi }_{1}} = \delta {{\psi }_{2}} + \left( {{{\varepsilon a_{2}^{2}} \mathord{\left/ {\vphantom {{\varepsilon a_{2}^{2}} f}} \right. \kern-0em} f}} \right)\chi ,$ т.е. считалось, что ${{\xi }_{2}}$ и ${{\xi }_{1}}$ имеют один порядок величины. При $\lambda = 0,$ когда $\gamma = 1,$ экмановское трение в точности определяется функцией тока ${{\psi }_{2}}$ геострофического ветра в нижнем слое; ср. (33). При $\lambda > 0,$ учитывая тем самым обмен импульсом между слоями и, соответственно, влияние циркуляции в верхнем слое на процессы в экмановском пограничном слое, мы в согласии с анализом уравнения (19) имеем значения $\gamma $ немного меньшие единицы.

Соответственно, уравнение (34) записывается в виде

Уравнения (32а) и (34а) образуют полную систему уравнений, если заданы притоки тепла в правой части (34а). По найденному решению функция тока в нижнем слое диагностически выражается из соотношения $\delta {{\psi }_{2}} = {{\psi }_{1}} - \left( {{{\varepsilon a_{2}^{2}} \mathord{\left/ {\vphantom {{\varepsilon a_{2}^{2}} f}} \right. \kern-0em} f}} \right)\chi .$ Уравнения (32а) и (34а) близки к уравнениям (19) и (20). В адиабатическом и невязком приближении и при $\delta = 1$ они совпадают по форме с уравнениями (17) и (18) за исключением множителя $\varepsilon $ в первом слагаемом в правой части (32а). Появление при $\delta > 1$ якобиана в правой части (32а) – прямое следствие учета глобальной статической устойчивости в используемой двухслойной модели атмосферы. В адиабатическом и невязком приближении и при $\delta > 1$ закон сохранения энергии имеет тот же вид, что и (17а), однако теряется свойство сохранения интеграла от произведения ${{\nabla }^{2}}{{\psi }_{1}} - \left( {{{{{f}^{2}}} \mathord{\left/ {\vphantom {{{{f}^{2}}} {a_{1}^{2}}}} \right. \kern-0em} {a_{1}^{2}}}} \right){{\psi }_{1}}$ на произвольную функцию $\chi $; ср. (18а). Путем переопределения масштаба времени $t = \delta t{\kern 1pt} '$ левая часть (34а) записывается как полная производная по времени. Однако при этом в якобиане в левой части (32а) перед вихрем скорости ${{\nabla }^{2}}{{\psi }_{1}}$ появляется множитель $\delta $. В статье [25] обсуждается, как аналогичный, больший единицы, множитель возникает в уравнениях (15) и (16), если принять, что исходное движение атмосферы эквивалентно-баротропно, т.е. скорость ветра меняется с высотой по величине, но не по направлению.

При стационарных притоках тепла уравнения (32а) и (34а) имеют ненулевое стационарное решение. Если поле притоков тепла, подобно тому, как в предыдущем разделе, имеет вид $\hat {Q} = \frac{{\kappa - 1}}{\kappa }{{\overline {\left( {\frac{Q}{p}} \right)} }_{0}}{{J}_{0}}\left( {kr} \right)$ и решение (32а) и (34а) ищется в виде $\left( {{{\psi }_{1}},\chi } \right)$ = $\left( {{{\psi }_{{10}}},{{\chi }_{0}}} \right){{J}_{0}}\left( {kr} \right),$ то будем иметь

Этим решениям отвечает поле функции тока в нижнем слое и поле приземного давления соответственно вида

Полагая ${{\Lambda }^{{ - 1}}}\sim 2 \times {{10}^{6}}\,\,{\text{c,}}$ ${{\overline {\left( {{Q \mathord{\left/ {\vphantom {Q p}} \right. \kern-0em} p}} \right)} }_{0}} \approx {{{{H}_{0}}} \mathord{\left/ {\vphantom {{{{H}_{0}}} {\left( {{{p}_{0}}\left\langle h \right\rangle } \right)}}} \right. \kern-0em} {\left( {{{p}_{0}}\left\langle h \right\rangle } \right)}},$ где ${{H}_{0}}\sim 10\,\,{\text{Вт}}\,{{{\text{м}}}^{{ - 2}}}$ – амплитуда потока тепла на поверхности,${{p}_{0}} \approx {{10}^{3}}\,\,{\text{гПа}}$ – приземное давление воздуха и $\left\langle h \right\rangle \sim 2 \times {{10}^{3}}\,\,{\text{м}}$, мы из (35) получим, что ${{\chi }_{0}}\sim 2.9 \times {{10}^{{ - 2}}}.$ Как следствие, амплитуда возникающей в верхнем слое антициклонической циркуляции при ${{k}^{2}}\sim 10\left( {{{{{f}^{2}}} \mathord{\left/ {\vphantom {{{{f}^{2}}} {a_{2}^{2}}}} \right. \kern-0em} {a_{2}^{2}}}} \right)\sim {{10}^{{ - 12}}}\,\,{{{\text{м}}}^{{ - 2}}},$ $\varepsilon \approx 0.2$ и $\gamma \sim 0.8{\kern 1pt} - {\kern 1pt} 0.9$ равна $ - {{k}^{2}}{{\psi }_{{10}}}\sim - 7.2 \times {{10}^{{ - 6}}}\,\,{{{\text{c}}}^{{ - 1}}}.$ При этом, если $\delta \approx 1.2,$ то в нижнем слое возникает крайне слабая циклоническая циркуляция с амплитудой ${{k}^{2}}{{\psi }_{{20}}}\sim 1.0 \times {{10}^{{ - 6}}}\,\,{{{\text{c}}}^{{ - 1}}},$ и мы также имеем, что ${{\xi }_{{10}}} + \varepsilon {{\xi }_{{20}}}\sim - 1.0 \times {{10}^{{ - 3}}},$ см. (36). Получается значительный положительный отклик в приземной температуре воздуха (~7–8 K), небольшое понижение приземного давления в центре нагрева (~1 гПа), достаточно заметный антициклональный отклик атмосферной циркуляции в основной толще атмосферы и очень слабая циклоническая циркуляция в нижнем, нагреваемом слое воздуха.

ЗАКЛЮЧИТЕЛЬНЫЕ ЗАМЕЧАНИЯ

Установление антициклонической циркуляции над Баренцевым и Карским морями ведет к ослаблению западного зонального переноса в более низких широтах и может способствовать формированию блокирующей этот перенос вихревой пары – антициклонической аномалии на севере и циклонической аномалии на юге. Раз сформировавшись, эта вихревая пара “стационирует” в основном западном потоке [28] и в ее тылу осуществляется заток очень холодных арктических воздушных масс на евразийский континент, что ведет там к суровым зимам (ср. [2]). Безусловно, предложенная в работе теоретическая схема очень идеализирована, однако, как представляется, она качественно верно описывает отклик атмосферной циркуляции на аномальные условия нагрева над Арктическим бассейном. Представленные в работе две модели имеют много общего, но обладают и определенными различиями, особенно, что касается параметризации притоков тепла и их вертикального распределения. Обе модели показывают возникновение четко выраженной антициклонической циркуляции над областью нагрева. В обеих моделях это напрямую связано с эффектом экмановского трения³³. Поэтому выводы работы говорят, в том числе, о крайней важности надлежащей параметризации эффекта планетарного пограничного слоя в моделях атмосферы и об очень большой чувствительности моделей к таким параметризациям, особенно при моделировании крупномасштабной циркуляции атмосферы над Арктикой при различном (в разных моделях) представлении физических процессов, определяющих взаимодействие “атмосфера–морской лед–океан”, которое осуществляется мелкомасштабными процессами, в частности, турбулентностью в атмосферном пограничном слое [30].

Работа выполнена при поддержке Российского Научного Фонда (грант № 18-47-06203). Автор признателен В.Н. Крупчатникову и И.И. Мохову за полезные обсуждения. Особая благодарность М.Г. Акперову за предоставленные иллюстрации к статье (рис. 1а, 1б). В 2019 году исполняется 70 лет с момента опубликования выдающейся работы А.М. Обухова [11], и автор был бы рад, если бы данная статья могла быть приуроченной к этой дате.