Известия РАН. Физика атмосферы и океана, 2020, T. 56, № 2, стр. 210-223

1. ВВЕДЕНИЕ

Задачи описания и прогноза динамики ветровых морских волн нацелены на обеспечение безопасности судоходства и использования прибрежных акваторий, а также являются составной частью проблемы моделирования климата. В частности, нормативы строительства судов и морских плавучих и стационарных сооружений основаны на представлениях о вероятностных распределениях волновых нагрузок. Из-за относительно небольшого числа данных прямых измерений для построения вероятностной картины ветровых волн, особенно экстремальных, полученные экспериментальные зависимости экстраполируются в область редких событий, либо используются теоретические модели.

Появившаяся возможность моделировать нерегулярные морские волны и накапливать статистические данные посредством прямого численного моделирования подчеркивалась в работах [1, 2]. Она стала не только результатом совершенствования компьютерной техники, но и возникновения новых способов решения “почти полных” уравнений потенциальной гидродинамики. В частности, псевдоспектральный алгоритм высокого порядка (High Order Spectral Method, HOSM) был сформулирован сразу в двух публикациях [3, 4]. Последующее сравнение этих двух версий подхода показало преимущество второй [4]: она соответствует разложению исходного гамильтониана системы, согласованному по асимптотическому порядку в предположении слабой нелинейности [1]. В [1, 5] было показано, что метод HOSM совпадает по формулировке с динамическими спектральными уравнениями Захарова [6] (когда оба подхода записаны с учетом не выше чем 4-волновых взаимодействий), но существенно быстрее их для моделирования на компьютере. Несмотря на существующую критику HOSM, связанную с невозможностью одинаково хорошо описывать волны очень широкого спектра (поскольку описание волн разных масштабов вблизи поверхности с помощью разложения в ряд Тейлора имеет разную точность, см. [7] и раздел 2 ниже), этот подход расчета динамики гравитационных волн сейчас очень популярен. Он реализован несколькими исследовательскими группами за рубежом для исследования модельных задач, включая расчет ансамблей нерегулярных волн. Отметим здесь только открытый код HOSM, разработанный и постоянно улучшаемый группой из г. Нант (Франция) [8]. В литературе можно найти множественные сравнения результатов численного моделирования методом HOSM с лабораторными результатами, которые демонстрируют очень хорошее соответствие. Эффекты обрушения волн не могут описываться в рамках модели HOSM напрямую и должны учитываться посредством параметризации. Затухание волн и воздействие ветра могут описываться с помощью введения в уравнения неконсервативных членов.

Сравнение результатов динамического и кинетического подходов в [9] выявило заметное расхождение между решением усредненных по фазам уравнений Хассельмана, динамических уравнений Захарова и решением исходных уравнений Эйлера методом HOSM (во всех случаях решение ограничивалось учетом не выше чем 4-волновых взаимодействий). В частности, расхождение проявилось в эволюции четвертого статистического момента для смещения поверхности, эксцесса. Это важное отличие, поскольку эксцесс контролирует долю больших отклонений поверхности от состояния равновесия и тем самым определяет степень экстремальности волнения.

Прямое численное моделирование является многообещающим средством для решения новых сложных задач. Учет фазовых корреляций волн, возникающих при нелинейных неустойчивостях, делает прямое моделирование эффективным подходом к исследованию аномально высоких волн (т.н. “волн-убийц”): их динамики, роли и проявления в реалистичных полях морских волн. Термин “волны-убийцы” может пониматься широко [10–12], в настоящем исследовании для определения волн-убийц используется амплитудный критерий, что высота волны-убийцы H не менее чем в 2 раза превышает значительную высоту волн H_s,

Для вычисления H_s нами в этой работе используется среднеквадратичное смещение поверхности σ в предположении выполнения соотношения H_s = 4σ. В настоящее время расчет морского волнения на площади порядка сотни кв. км может выполняться методом HOSM с опережающей скоростью [13]. Соответственно, помимо возможности накапливать статистические данные, прямое численное моделирование рассматривается как инструмент оперативного краткосрочного прогноза волновой обстановки и уклонения от опасных волн [12–15]. Наконец, расчет модельных задач в рамках полных уравнений позволяет определить рамки применимости слабонелинейных решений, описывающих процессы возникновения и эволюции аномально высоких волн (например [16–18]).

Очевидно, что прямое численное моделирование непригодно для описания морских волн на слишком больших масштабах из-за неполных данных о волнах и ветре, неучтенных эффектов и накопления ошибки. Обсуждение места детерминистского (фазоразрешающего) моделирования морских волн можно найти в [19]. В качестве оценки применимости фазоразрешающих моделей (горизонта детерминистского прогноза) можно использовать теоретический результат [20] – до порядка 10³ волновых периодов для типичной крутизны волн в море; это время соответствует примерно 3 ч для волн с периодом 10 с. И хотя можно ожидать, что при некоторых специфических условиях (например, распространение зыби) волны более предсказуемы, другие эффекты (обрушение волн, неучтенные течения и ветер и т.д.) должны способствовать, наоборот, более быстрой стохастизации волн. Можно опираться на практическое наблюдение, что детерминистское описание пригодно как минимум для разгонов в существующих волновых лотках, то есть, до порядка 10² длин волн. Таким образом, масштаб эволюции, когда можно надеяться на хорошее описание фаз волн, по порядку величины примерно соответствует типичной длительности записей волн (волнограмм), 20 мин, связанной с условным временем квазистационарности морских волн. Отметим, что прямое моделирование пригодно и на бòльших временах, только уже после усреднения по фазам.

Неизбежным недостатком любого численного моделирования являются принятые идеализации, которые могут привести к невозможности описания физических механизмов или появлению нефизичных артефактов. Обрушение волн является очевидным физическим явлением, несомненно важным для описания волн большой амплитуды. В то же время этот эффект труден для моделирования, его учет в быстрых кодах типа HOSM возможен только посредством параметризации. Самомодуляция волн на поверхности глубокого моря является регулярным эффектом, способным генерировать экстремальные (в том числе, обрушающиеся) морские волны [21–24]. Для значительности эффекта модуляционной неустойчивости волны должны быть крутыми: волны с небольшой крутизной ε неустойчивы относительно очень длинных возмущений (~ε^–1 длин волны) и растут очень медленно (~ε^–2 периодов). В этой работе крутизна будет определяться через значительную высоту H_s и волновое число k_p, соответствующее пику спектра волновых векторов, ε = k_pH_s/2. По мере роста модуляции амплитуда и крутизна волн увеличиваются, так что цуги, состоящие из 5–10 волн с начальной крутизной ε ≈ 0.1, могут достигать порога обрушения за несколько десятков периодов [16]. Введение искусственной параметризации обрушений может вносить изменения в динамику волн, заметные уже на временах порядка 20 мин [25], хотя можно ожидать, что в статистическом смысле заметные отличия проявляются на бòльших временах.

В этой статье приводится описание собственных численных экспериментов по фазоразрешающему моделированию трехмерных нерегулярных волн на поверхности глубокого моря в рамках подхода HOSM. Приводятся результаты расчета эволюции статистических моментов смещения поверхности, распределения вероятностей высот волн. Обсуждаются геометрические характеристики и продолжительности событий волн-убийц, которые оказываются отличными от характерных для “обычных” волн.

2. МЕТОД РЕШЕНИЯ УРАВНЕНИЙ ГИДРОДИНАМИКИ

Авторами был реализован собственный код решения исходных уравнений гидродинамики методом HOSM [4] в предположении потенциальности движения жидкости. Система уравнений гидродинамики [6] состоит из двух граничных условий (2) и (3) на свободной поверхности z = η(x, y, t), уравнения Лапласа (4) в толще воды –h ≤ z ≤ η(x, y, t), и условия непротекания на плоском дне z = –h (5),

Здесь φ(x, y, z, t) есть потенциал скорости движения жидкости, а его значения на поверхности описываются функцией Φ(x, y, t) = φ(x, y, z = η, t); g – ускорение свободного падения. В пределе бесконечно большой глубины условие (5) заменяется на требование спадания потенциала φ при z → → –∞. В настоящей работе рассчитывались уравнения в предположении бесконечно глубокой воды; эффектами диссипации и ветровой накачки пренебрегалось.

Система уравнений (2)–(3) для полей на поверхности η(x, y, t) и Φ(x, y, t) оказалась бы замкнутой, если бы не слагаемые вертикальной скорости ∂φ/∂z. В методе HOSM используется разложение потенциала скорости в ряд Тейлора вблизи невозмущенной поверхности воды, что позволяет свести переменную область, занятую жидкостью, –h ≤ z ≤ η, к неизменной, –h ≤ z ≤ 0. Потенциал скорости ищется в виде ряда членов разных порядков малости φ = φ⁽¹⁾ + φ⁽²⁾ + …. Вертикальная структура функций φ^(m)(x, y, z, t) задается решением уравнения Лапласа и не изменяется на каждом шаге интегрирования, что делает код быстрым. Аналогично раскладывается в ряд и функция вертикальной скорости на поверхности, ∂φ/∂z|_{z = η} = W⁽¹⁾ + W⁽²⁾ + …. Слагаемые в (2) и (3), включающие вертикальную производную от потенциала скорости на поверхности воды, определяются в соответствии со следующей процедурой:

Формулы в последней строке уравнений (6) позволяют итерационным способом находить компоненты потенциала φ^(m) по заданному потенциалу на поверхности Φ и затем компоненты вертикальной скорости W^(m) на поверхности.

Существенно, что HOSM не является полностью нелинейным подходом; он позволяет учитывать до M + 1 нелинейных волновых взаимодействий; представление (6) обеспечивает учет только слагаемых, соответствующих разложению гамильтониана до заданного порядка (см. в [4]). Число слагаемых M в разложении Тейлора является параметром метода. На практике параметр M ограничен соображениями скорости вычислений, размера используемой памяти компьютера, сходимости разложения Тейлора. Для расчета волн на глубокой воде чаще всего ограничиваются порядком M = 3, что позволяет учитывать доминирующие четырехволновые нелинейные процессы, включая модуляционную неустойчивость. Строго говоря, такой код не может описывать волны, достигающие порога обрушения, но способен моделировать нелинейные процессы, включая приводящие к эволюции волновых спектров.

Для интегрирования уравнений во времени линейная и нелинейная части уравнений (2) и (3) разделяются. Линейная часть на каждом шаге схемы считается с использованием точного аналитического решения, а для решения нелинейной части применяется метод Рунге–Кутты 4-го порядка с фиксированным шагом по времени. Выбор параметров вычислений был ранее произведен в нашей работе [25]. Для моделирования поверхности 50 × 50 волн используется 2¹⁰ × 2¹⁰ точек в физическом пространстве и вдвое больше точек по каждому направлению в Фурье пространстве (для процедуры де-алейзинга, de-aliasing). Хорошую сходимость решения на 20 мин эволюции обеспечивает шаг по времени, равный 160 итерациям на 1 характерный период волны. Для купирования обрушений волн используется спектральный фильтр, аналогичный [26] (см. обсуждение его использования в [25]), подавляющий коротковолновые компоненты Фурье. Он применяется на каждом шаге по времени.

3. МОДЕЛИРОВАНИЕ РЕАЛИСТИЧНЫХ МОРСКИХ ВОЛН

Для численного моделирования реалистичных морских волн начальные условия η(x, y, t = 0) и Φ(x, y, t = 0) задавались в виде линейной суперпозиции гармонических функций, поля периодичны вдоль горизонтальных осей координат Ox и Oy. При этом предполагалось соотношение между η и Φ, соответствующее линейному решению уравнений гидродинамики. Для каждой гармоники Фурье задавалась случайная фаза. Абсолютная величина каждой пространственной гармоники Фурье (k_x, k_y) определялась согласно нормальному распределению с амплитудой, соответствующей выбранным спектрам частот S(ω) и углов D(χ). При этом предполагалось выполнение линейного дисперсионного соотношения между волновыми векторами и частотами волн

Таким образом, начальные реализации волн могли несколько отличаться друг от друга формой спектра Фурье и энергией.

Для моделирования был выбран энергетический спектр JONSWAP

Он содержит 3 ключевых параметра: T_p = 10 с – пиковая частота волнения, связанная с циклической частотой ω_p = 2π/T_p; H_s – значительная высота волн (определяющая в совокупности с другими параметрами величину α в (8)) и пиковатость γ (степень узости спектра вблизи пика). Для оценки крутизны волн ε = k_pH_s/2 можно использовать линейное дисперсионное соотношение (7), откуда k_p = ${{\omega _{p}^{2}} \mathord{\left/ {\vphantom {{\omega _{p}^{2}} g}} \right. \kern-0em} g}$ ≈ 0.040 рад/м. Угловое распределение D(χ) энергетического спектра задавалось в соответствии с функцией cos² по формуле

Поскольку начальное условие для нелинейных уравнений задается в соответствии с линейным решением, на начальном этапе моделирования производится медленное “включение” нелинейной части уравнений [27]. В результате происходит адиабатическое перестроение изначально линейных волн в близкое нелинейное решение, избавляющее от появления “паразитных” волн с комбинационными волновыми векторами (см. подробно в [28]). В наших расчетах переходный начальный период занимал 20 периодов волн, 200 с.

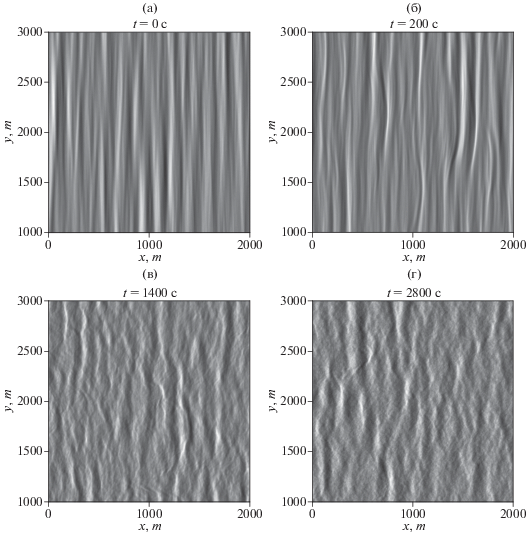
На рис. 1 приведен пример взволнованной поверхности в начальный момент времени t = 0 для условий H_s = 7 м (ε ≈ 0.14), γ = 3 и θ = 12°, а также несколько моментов позднее – до 280T_p. Расчет выполнялся с использованием параметра схемы M = 3. Моделировалась поверхность размером примерно 8 на 8 км, соответствующая области 50 на 50 длин волн, на рисунке показана только ее часть. Можно заметить качественные различия между поверхностями при t = 0 (рис. 1а) и после “включения” нелинейности t = 200 с (рис. 1б): из-за нелинейности фронты волн начинают искажаться, их гребни убегают вперед. После продолжения расчета до 1400 с (20 мин эволюции со “включенной” нелинейностью, рис. 1в) картина волн еще более изменяется: гребни волн в поперечном направлении укорачиваются, общая картина волн становится более сложной. Изменение характеристик волн происходит и на бóльших временах, хотя оно уже не столь явно заметно (ср. рис. 1в, 1г).

4. ЭВОЛЮЦИЯ СПЕКТРАЛЬНЫХ И СТАТИСТИЧЕСКИХ ХАРАКТЕРИСТИК ВОЛН

Эволюция характеристик одной реализации волн при условиях H_s = 6 м (ε ≈ 0.12), γ = 3 и θ = = 12° с параметром схемы M = 3 в течение более часа физического времени показана на рис. 2. Первые 200 с расчета занимает подготовительный этап “включения” нелинейности. В это время полная механическая энергия системы может изменяться на величину порядка 1%. После t = 200 с расчет почти консервативен, изменение энергии за все последующее время моделирования в течение 400T_p составил 0.15%. На рис. 2 хорошо заметны изменения характеристик волн в интервале 0 < t < 200 c (в первую очередь – статистических моментов смещения поверхности на рис. 2б и рис. 2в). Представленные на рис. 2 характеристики вычислялись по формулам

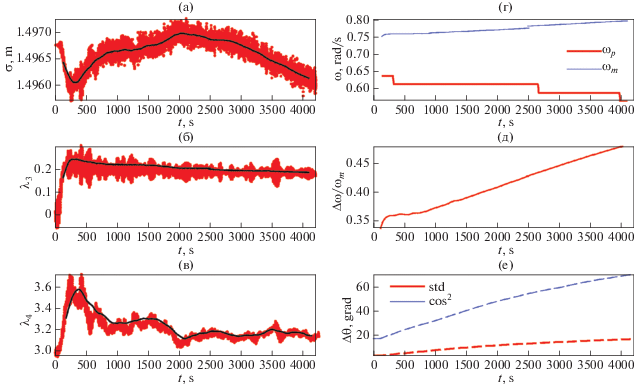
Выражения (10) представляют со второго по четвертый статистические моменты для смещения поверхности; интегрирование в (10) производится по всей поверхности, занимаемой волнами. На рис. 2а–2в точками показаны моментальные значения каждые 0.5 с, а линиями – результат усреднения в окне 25T_p.

Для нахождения средней частоты и ширины частотного спектра интегрирование в (11) производится по области частот ω > 0, при этом энергетический частотный спектр S(ω) ищется на основе выборок последовательностей моментальных поверхностей η(x, y). Каждая выборка имеет длительность примерно 250 с и производится с частотой 0.5 с. Частота ω_p соответствует пику S(ω) в данный момент времени. Энергетический спектр по углам S(χ), |χ| ≤ π, определяется посредством интегрирования моментального спектра волновых векторов. Доминирующее направление распространения волн соответствует χ = 0. Характерная ширина углового спектра определяется двумя способами (12) – как второй момент θ_std и аппроксимацией функцией cos² (см. (9)), ${{\theta }_{{{\text{co}}{{{\text{s}}}^{{\text{2}}}}}}}.$

Как следует из рис. 2a, среднеквадратичное отклонение сохраняется с хорошей точностью на всем времени счета, даже на начальной стадии t < < 200 с. Третий статистический момент λ₃ (асимметрия, рис. 2) вырастает во время подготовительной стадии и затем медленно и в среднем монотонно убывает, что свидетельствует об уменьшении степени нелинейности волн, несмотря на сохранение дисперсии σ. Четвертый статистический момент λ₄ (эксцесс, рис. 2в), показывает наличие быстрой динамики в начале расчета, затем его значение уменьшается за время более сотни периодов и далее остается примерно одинаковым с заметными медленными осцилляциями. Отметим, что эксцесс λ₄ часто используют для оценки вероятности экстремальных волн, его вычисление не требует непосредственного определения высот волн. По определению (10) для случайного Гауссового процесса λ₄ = 3; эксцесс может расти как за счет связанных нелинейных волновых компонент (то есть, из-за отклонения формы волны от синусоидальной), так и за счет возникновения фазовых корреляций между гармониками. По результатам на рис. 2в можно говорить, что в интервале времен до порядка 700 с имеет место аномально высокая вероятность возникновения высоких волн с плохо локализованным максимумом при t ≈ 400 с. Такого рода переходный процесс при задании начального условия с узким частотным и узким угловым спектром отмечался в литературе многократно [21, 22, 29–33]; он связан с модуляционной неустойчивостью волн (см. в нашем обзоре [34]) и приводит к значительной фазовой корреляции в квартетах волн [35] и резкому повышению вероятности волн большой амплитуды.

Эволюция спектральных характеристик приведена на рис. 2г–2е. Построены те величины, которые наблюдаются по измерениям в море: пиковая и средняя частота волн, ширина частотного и углового спектров, определенных через преобразования Фурье во времени и в пространстве. Пиковая частота изменяется скачками на рис. 2г из-за значительной дискретности частотного спектра, она уменьшается со временем (downshifting). При этом средняя частота ω_m наоборот, растет, что свидетельствует о перекачке энергии в более короткие масштабы. Пиковые и средние значения волновых чисел ведут себя схожим образом (графики не показаны). Ширины частотного и углового спектров также монотонно растут во времени. Рост частоты ω_m и относительной ширины частотного спектра Δω/ω_m происходит примерно по линейному закону. Ширина углового спектра, определенная через аппроксимацию функцией cos², растет быстрее, чем определенная через второй момент (рис. 2е, ее значение изначально несколько превышало 12° в данной реализации).

За более чем часовой расчет показатели на рис. 2 не вышли на какие-либо равновесные значения, в отличие от ситуации строго коллинеарных волн [34], где статистические моменты и спектры волн после переходной стадии стремились к квази-стационарным. Такое различие подтверждает вырожденность ситуации плоской геометрии волн (одна горизонтальная координата) [36, 37]. Можно предположить из рис. 2е, что ширины углового спектра имеют тенденцию к насыщению (что наблюдалось в численном моделировании зыби в рамках кинетических уравнений в [38]), но на приведенных временах расчета этот вывод не определенный. Также проводилось численное моделирование, стартуя из изначально еще более узкого углового спектра, θ = 5°. В нем наблюдалась качественно схожая с рис. 2 медленная динамика статистических и спектральных характеристик волн. Наоборот, при исходно широком угловом спектре θ = 62° для высот H_s = 3.5 м и H_s = 7 м заметной стадии сильного изменения параметров волн в начале расчета не наблюдалось. Характеристики волн медленно эволюционировали, качественно схоже с предыдущими случаями. Сдвиг пиковой частоты ω_p в длинноволновый диапазон (downshift) наблюдался только в случае более интенсивных волн H_s = 7 м (ε ≈ 0.14).

Для оценки роли нелинейности более высокого порядка было выполнено сравнение результатов двух численных экспериментов, проведенных с использованием разных значений параметра M. Одна и та же реализация волн была рассчитана в эксперименте с использованием параметра нелинейности схемы M = 3 (учет не выше 4-волновых взаимодействий) и в эксперименте c M = 4 (с учетом 5-волновых взаимодействий). Известно, что 5-волновые взаимодействия ответственны за формирование подковообразных структур на двумерной поверхности [39]. Они также предлагались как возможный механизм образования т.н. “Новогодней волны” [40, 41]. При этом в большинстве существующих базовых моделей морских волн и приведенных в литературе вычислительных экспериментах эффектами 5-волновых взаимодействий пренебрегается.

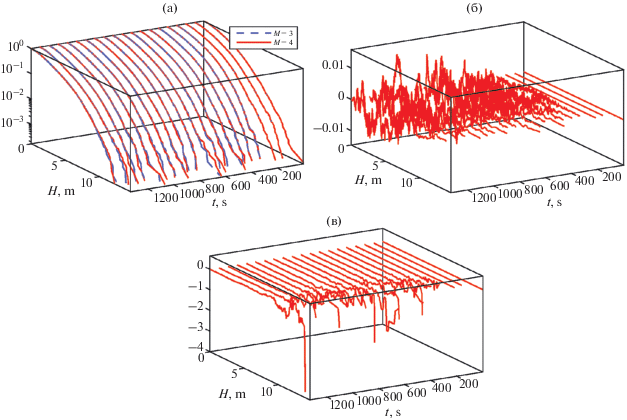
За 20 мин эволюции заметных различий в значениях тех же характеристик волн, что построены на рис. 2, для M = 3 и M = 4 выявлено не было. Дополнительно было проведено сравнение функций распределения высот для этих двух симуляций волн. Строились моментальные функции вероятности превышения высот P(H) для 64 продольных разрезов поверхности по формуле

где n нумерует высоту H_n индивидуальной волны в ансамбле из сортированных по высоте N волн. Эти распределения P₃(H) и P₄(H) для условий H_s = = 7 м (ε ≈ 0.14), γ = 6 и θ = 62° построены на рис. 3а в полулогарифмических координатах для двух соответствующих экспериментов: “стандартного” с параметром M = 3 и более точного с параметром M = 4. Различия распределений (P₃ –P₄) в интервале умеренных высот несущественны и носят случайный характер (рис. 3б). В области экстремальных значений высот расхождения также имеют нерегулярный характер, но явно прослеживается тенденция, что в рамках расчета с учетом 5-волновых взаимодействий экстремальные волны оказываются несколько выше, чем в рамках моделирования, ограниченного 4-волновыми взаимодействиями. Это различие хорошо видно на зависимостях относительной разницы (P₃ – P₄)/P₃, приведенных на рис. 3в. Схожая картина наблюдалась и в случае более узкого углового спектра, H_s = 5 м (ε ≈ 0.10), γ = 6 и θ = 12°.

5. АСИММЕТРИЯ АНОМАЛЬНО ВЫСОКИХ ВОЛН

Наиболее известная асимметрия нелинейных волн на глубокой воде, вертикальная, заключается в значительно более высоких гребнях по сравнению с ложбинами относительно среднего уровня, что соответствует типичному профилю нелинейной волны Стокса. Ранее в наших работах по численному моделированию строго коллинеарных волн (θ = 0°) со спектром JONSWAP была обнаружена асимметрия между высотами передних и задних склонов высоких волн, наблюдавшаяся только в случае значительной нелинейности волн [42, 43]. Если волны характеризовались небольшой крутизной (например, ε ≈ 0.07 при H_s = 3.5 м, γ = 3 и θ = 0°), то ложбины спереди и сзади гребня оказывались в среднем одинаковыми по глубине. В случае волн с большей средней крутизной (в частности, ε ≈ 0.14 при H_s = 7 м, γ = 3 и θ = 0°) более глубокие ложбины располагались преимущественно позади высоких гребней. Эта асимметрия экстремальных волн в сильно нелинейных волновых полях была найдена как в ситуации бесконечно глубокой воды, так и на не слишком мелкой воде (для безразмерных глубин k_ph > 2, см. в [43]). Такую асимметрию ложбин экстремальных волн можно было обнаружить по различию в хвостах распределений высот волн, выделенных по пересечению среднего уровня воды вниз и вверх (up-crossing и down-crossing, см. в [44]), а также напрямую по анализу моментальных снимков волн или записей смещения поверхности в одной точке. Разная глубина ложбин у характерной формы “волны-убийцы” отмечалась в [26] по результатам численного моделирования трехмерных волн на глубокой воде. Разное число “волн-убийц” было выделено методами up-crossing и down-crossing в натурных записях в водах Бразилии [45]. В двух последних работах типичная геометрия волн-убийц определялась для всего ансамбля волн, удовлетворяющих критерию (1), накопленного при различных условиях.

Анализ форм высоких волн, схожий с выполненным в [42, 43], был проделан в настоящей работе по результатам моделирования эволюции трехмерных волн для разных условий (было использовано по 7 реализаций для каждого случая). Популяция волн-убийц определялась на основе 128 продольных разрезов моментальных снимков поверхности воды (вдоль доминирующего направления движения волн Ox), следуя критерию (1). На рис. 4 собраны диаграммы распределения числа обнаруженных аномально высоких волн по характерным формам. Различались 4 формы волн-убийц: по вертикальной асимметрии (соотношение высоты гребня и глубины наибольшей ложбины впереди или позади гребня) и по горизонтальной асимметрии (соотношение высот волн, определенных для данного гребня и ложбин впереди и позади гребня). Буквы L, A, E в кодировке экспериментов (левые нижние углы диаграмм на рис. 4) означают, соответственно, расчет линейных уравнений (верхний ряд на рис. 4), случай небольшой нелинейности (ε ≈ 0.07, средний ряд) и большой нелинейности (ε ≈ 0.12–0.14, нижний ряд). Ширина углового спектра θ указана в нижнем индексе кодировки. Верхний индекс показывает значение пиковатости γ. В скобках указано общее число волн, выделенных согласно критерию (1).

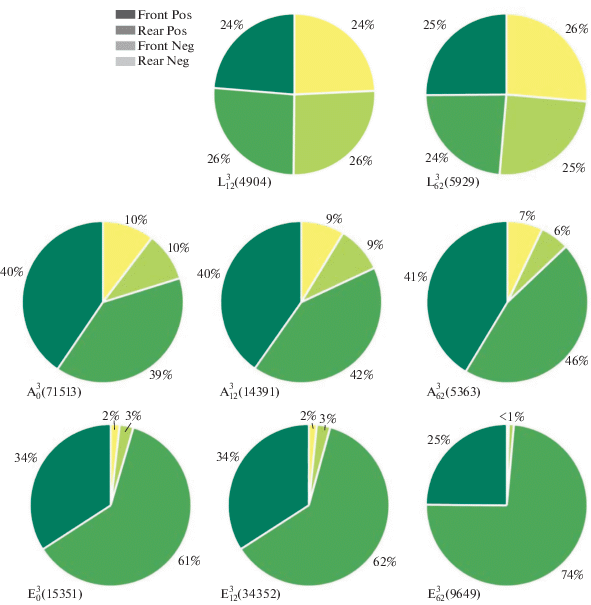
Для условий, характеризуемых в среднем умеренной нелинейностью (средний ряд на рис. 4), проявляется вертикальная асимметрия волн Стокса: преобладает доля экстремальных волн с высоким гребнем; ложбины спереди и сзади экстремального гребня в среднем одинаковой глубины. Этот вывод практически не зависит от ширины углового спектра. Для более крутых волн (нижний ряд на рис. 4) кроме асимметрии, характерной для волн Стокса, существенна горизонтальная асимметрия: ложбины позади волн-убийц в большинстве случаев более глубокие, чем спереди. При увеличении ширины углового спектра оба типа асимметрии усиливаются: число волн с экстремальными ложбинами практически равно нулю, а 3/4 от всего количества волн-убийц составляют волны с экстремально высоким гребнем и более глубокой ложбиной позади. Тенденция усиления и вертикальной, и горизонтальной асимметрии экстремальных волн с ростом ширины углового спектра прослеживается и в случае умеренной нелинейности (средний ряд на рис. 4). Для контроля процедуры обработки и оценки статистической погрешности результатов были выполнены аналогичные вычисления для таких же ансамблей полей волн, эволюция которых рассчитывалась по линейной теории. Для них все 4 типа форм волн равновероятны. Исходя из этого, из распределений в верхнем ряду на рис. 4 следует, что погрешность в определении долей волн составляет 1–2% для выборок порядка 5 тыс. волн. Потому точность пропорций, представленных на других диаграммах на рис. 4 для существенно большего числа волн можно оценить как не хуже 1%.

Дополнительно был проведен анализ геометрических свойств волн-убийц в условиях большей пиковатости, γ = 6, при сильной нелинейности и узком частотном спектре, H_s = 6 м (ε ≈ 0.12), θ = 12°. Полученное распределение оказалось аналогично случаю ${\text{E}}_{{12}}^{3},$ так что зависимости характерной формы волны-убийцы от параметра пиковатости не обнаружено.

6. ПРОДОЛЖИТЕЛЬНОСТИ СОБЫТИЙ “ВОЛН-УБИЙЦ”

По результатам численного моделирования возможно пронаблюдать развитие экстремальных событий в динамике. В частности, одним из простейших параметров, характеризующих динамику волн-убийц, является их “время жизни”, определяемое как непрерывный промежуток времени, когда выполняется условие (1). Вычисляемая таким образом продолжительность событий – не очень хороший параметр, поскольку может зависеть от небольших вариаций эволюции волн. В частности, интервал времени, когда критерий (1) выполняется для некоторой области взволнованной поверхности, может прерываться, если волны даже на очень короткое время чуть ниже, чем определено в (1). В [42] было предложено объединять волны-убийцы, происходящие в близкие моменты времени в близлежащих точках пространства в одно событие, и рассматривать продолжительности именно таких событий. Подобное определение времени жизни волны-убийцы T_RW остается неоднозначным (в частности, требуется определить новые критерии для определения порога “близких” событий), но представляется физически более разумным и статистически устойчивым. По результатам моделирования однонаправленных волн в работах [42, 43] продолжительности волн-убийц оказались неожиданно большими, до 10 минут. Такой результат предположительно связывался с упоминавшейся выше вырожденностью динамики коллинеарных волн и формированием долгоживущих интенсивных солитоноподобных групп [46]. Однако в недавних исследованиях трехмерных волн-убийц [47, 48] экстремальные события также оказались очень длительными (десятки периодов), что противоречит общепринятому представлению о волнах-убийцах как об очень кратковременных явлениях. Здесь нужно уточнить, что оценка продолжительности волны-убийцы сильно зависит от способа наблюдения. По результатам измерений в одной точке оно будет всегда меньше, чем в случае наблюдения очевидцем, способным следить за движением волн в пространстве на некотором расстоянии от него. В случае возможности неограниченно долгого отслеживания динамики волн в численном эксперименте время жизни волн-убийц может быть еще дольше.

На рис. 5 построены распределения вероятности продолжительности волн-убийц (по формуле, аналогичной (13), где вместо Н использовалась величина T_RW) по данным расчетов различных условий, в том числе, трех значений ширин угловых спектров: строго коллинеарные волны θ = 0°, волны с узким разбросом по направлениям, θ = 12° и с широким угловым спектром, θ = 62°. Кодировка экспериментов совпадает с использованной на рис. 4. В одно событие объединялись аномально высокие волны, возникающие в пределах 2.5 периодов и 2.5 длин доминантной волны друг от друга в сопровождающей системе координат. Подробности способа выделения событий волн-убийц и вычисления длительности событий можно найти в [48], в настоящей работе использованы дополненные данные численного моделирования. Распределения построены на основании разного количества событий, поэтому для разных условий достигнуты разные максимальные периоды повторяемости экстремальных значений T_RW. Нужно учитывать, что количество наиболее продолжительных событий мало, поэтому их вероятность определяется с малой достоверностью.

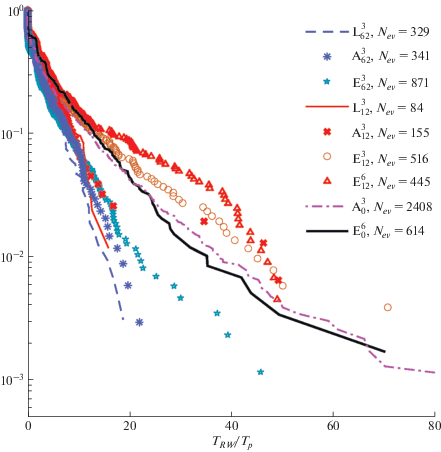
Из зависимостей, представленных на рис. 5, можно сделать вывод, что в случае коллинеарных волн (${\text{A}}_{0}^{3},$${\text{E}}_{0}^{3}$), действительно, волны-убийцы живут аномально долго. В то же время, в случае узкого углового спектра и большой интенсивности волн $\left( {{\text{E}}_{{12}}^{3}} \right)$ волны-убийцы имеют схожее распределение вероятности T_RW. При росте пиковатости $\left( {{\text{E}}_{{12}}^{6}} \right),$ т.е., более узком частотном спектре, вероятность продолжительных событий возрастает. Хвосты этих распределений (области наиболее долгоживущих волн-убийц с достоверной статистикой) спадают медленнее, чем области наиболее частых экстремальных событий, что говорит о наличии когерентных структур. В случае широкого спектра $\left( {{\text{E}}_{{62}}^{3}} \right)$ значимого отличия функции распределения времен жизни волн-убийц от контрольного линейного случая не обнаружено, они спадают почти экспоненциально, близко к результатам линейной теории ${\text{L}}_{{12}}^{3},$ ${\text{L}}_{{62}}^{3}.$ Похоже ведет себя и распределение для волн с узким угловым спектром, но небольшой нелинейностью (A₁₂³).

Таким образом, абсолютного верхнего предела, явно ограничивающего максимальную продолжительность существования волн-убийц, не найдено. Наблюдаемый максимум времен жизни связан с конечным размером ансамбля. В случае достаточно узкого углового спектра (не обязательно нулевого) и высокой в среднем нелинейности волн имеются признаки трехмерных когерентных структур, живущих аномально долго и рождающих экстремальные волны.

7. ЗАКЛЮЧЕНИЕ

Прямое численное моделирование нелинейных уравнений гидродинамики для поверхностных потенциальных гравитационных волн использовано для исследования морских волн со спектром JONSWAP в предположении несущественности действия ветра и эффектов диссипации (на временах расчета). Начальные условия выбирались в таком диапазоне параметров, когда нелинейность волн важна и проявляется не только в специфической форме волн, но и в эволюции усредненных характеристик. В то же время эпизоды обрушения волн из-за большой крутизны редки и вносят малый вклад в изменение волновой энергии и динамику волн. Эффекты обрушения были купированы с помощью спектрального фильтра. Большая часть вычислений выполнена в предположении достаточности учета только 3- и 4-волновых взаимодействий (для таких условий выполнено подавляющее большинство расчетов нерегулярных морских волн в литературе – в рамках модели HOSM, либо спектральных уравнений Захарова). Сопоставительное моделирование с учетом нелинейных взаимодействий более высокого порядка, 5-волновых, не показало отличий в эволюции статистических и спектральных моментов. В то же время, высоты наиболее экстремальных волн в рамках более аккуратной модели оказываются несколько выше.

Получено, что при изначально узком угловом спектре волн после переходной стадии наступает медленное поступательное изменение статистических и спектральных характеристик волн, не достигающее стационарных значений как минимум за 1 ч эволюции (для доминирующего периода волн 10 с и характерной крутизны k_pH_s/2 ≈ 0.12). Угловой спектр, спектр частот и волновых чисел уширяются, пиковые значения волнового числа и частоты уменьшаются. При исходно широком угловом спектре заметной переходной стадии не наблюдается, характеристики волн медленно эволюционируют, качественно схоже с предыдущим случаем.

Кроме вертикальной асимметрии, свойственной волнам Стокса на глубокой воде и усиливающейся с ростом нелинейности, экстремальным волнам оказывается свойственна асимметрия ложбин: в моменты, когда выполняется условие на высоту волны-убийцы (1), ложбины позади гребней в среднем глубже, чем спереди. Эта асимметрия усиливается при увеличении нелинейности волн и росте ширины углового спектра, так что у трех четвертей волн-убийц в поле крутых волн с широким угловым спектром (k_pH_s/2 ≈ 0.14, θ = 62°) высота гребня больше глубины ложбины и задняя ложбина глубже передней. При росте ширины углового спектра несколько усиливается и вертикальная асимметрия. Зависимости степени асимметрии волн-убийц от пиковатости, контролирующей ширину пика спектра, не обнаружено.

Определены длительности существования областей двумерной поверхности, характеризуемых последовательно возникающими волнами очень большой высоты. Из-за отслеживания движения этих областей в пространстве их времена жизни оказываются значительно дольше, чем по измерениям в одной точке. Распределения вероятности волн-убийц становятся отличными от экспоненциальных, когда растет нелинейность волн, уменьшаются ширины частотного и углового спектров. Более длительные события становятся аномально частыми, что свидетельствует о возникновении локализованных когерентных волновых структур с большой энергией. По результатам выполненного моделирования времена жизни волн-убийц ограничены только размером статистического ансамбля.

Исследование роли эффектов нелинейности высокого порядка выполнено в рамках проекта РНФ 19-12-00253. Остальные исследования проведены при поддержке гранта РНФ 16-17-00041.