Известия РАН. Физика атмосферы и океана, 2020, T. 56, № 6, стр. 689-699
Простое описание турбулентного переноса в стратифицированном сдвиговом потоке применительно к описанию термогидродинамики внутренних водоемов
И. А. Соустова a, Ю. И. Троицкая a, b, Д. С. Гладских a, c, e, *, Е. В. Мортиков c, d, e, Д. А. Сергеев a
a Институт прикладной физики Российской академии наук
603950 Нижний Новгород, ул. Ульянова, 46, Россия
b Институт физики атмосферы им. А.М. Обухова Российской академии наук
119017 Москва, Пыжевский пер., 3, Россия
c Научно-исследовательский вычислительный центр Московского государственного университета им. М.В. Ломоносова
119991 Москва, ГСП-1, Ленинские горы, 1, стр. 4, Россия
d Институт вычислительной математики им. Г.И. Марчука Российской академии наук
119333 Москва, ул. Губкина, 8, Россия
e Московский центр фундаментальной и прикладной математики
Москва, Россия
* E-mail: daria.gladskikh@gmail.com
Поступила в редакцию 22.05.2020
После доработки 22.07.2020
Принята к публикации 05.08.2020
Аннотация
Предложена параметризация турбулентного числа Прандтля, полученная на основе модели турбулентного переноса в стратифицированной жидкости, учитывающей двустороннюю трансформацию кинетической и потенциальной энергий турбулентных пульсаций. Проведены численные эксперименты, направленные на исследование влияния предложенной параметризации на характерные особенности термогидродинамических процессов во внутренних водоемах.
ВВЕДЕНИЕ
К настоящему времени установлено [1–4], что внутренние водоемы играют важную роль в процессах взаимодействия атмосферы и деятельного слоя суши. При этом известно, что процессы мелкомасштабного турбулентного перемешивания в приповерхностном слое океана и внутренних водоемов играют ключевую роль как при разработке глобальных моделей климата [5–8], так и при создании региональных моделей прогноза погоды [9, 10]. Современные глобальные океанические модели не разрешают мелкомасштабные процессы турбулентного перемешивания в приповерхностном слое океана. Поэтому эти процессы учитываются за счет параметризаций коэффициентов турбулентного обмена – турбулентной вязкости и диффузии, связывающих турбулентные потоки массы, импульса, плавучести и т.д. с характеристиками средних крупномасштабных полей скорости, плотности (температуры) и других параметров. Значения этих коэффициентов существенным образом зависят от состояния границы раздела воды и воздуха, плотностной стратификации и других факторов. В большей части современных численных моделей при описании процессов турбулентного перемешивания в океане и внутренних водоемах приходится решать уравнения в частных производных для осредненного течения; появляющиеся в этих уравнениях члены турбулентного переноса (напряжения Рейнольдса) определяются в соответствии с принятыми гипотезами турбулентного замыкания, например градиентными, позволяющими связать напряжения Рейнольдса с градиентами средней скорости (или любой другой скалярной переносимой субстанции [11]). Наиболее широко используемыми при моделировании турбулентных процессов во внутренних водоемах являются одномерные (по вертикали) модели, что связано с их вычислительной простотой. К таким моделям можно отнести и так называемые k [12, 13] и k-ε [14, 15] схемы, в которых рассматриваются эволюционные уравнения для кинетической энергии турбулентных флуктуаций ($k = \frac{1}{2}\left\langle {u_{i}^{'}u_{i}^{'}} \right\rangle $, где $u_{i}^{'}$ – турбулентные флуктуации i-той компоненты скорости), либо используется дополнительное уравнение для скорости ее (плотности кинетической энергии) диссипации (ε). Отметим, что введение дополнительного уравнения для ε связано с тем, что в k модели с единственным уравнением для кинетической энергии турбулентных флуктуаций (см., например, [16]) в выражения для коэффициентов турбулентной вязкости ${{K}_{m}}$, турбулентной теплопроводности ${{K}_{h}}$, а также скорости диссипации $\varepsilon $ входит неизвестная величина – внешний линейный масштаб турбулентности L. Так, согласно гипотезе Колмогорова–Прандтля [12], ${{K}_{h}} = {{c}_{\mu }}\sqrt k L,~$ $~\varepsilon = \frac{{C{{k}^{{3/2}}}}}{L}{\text{\;}},$ при этом определение L в случае сложных течений затруднительно. Решение уравнений в k-ε модели при больших числах Рейнольдса в условиях локальной изотропной турбулентности позволяет определить распределение линейных масштабов турбулентности $L = \frac{{{{k}^{{\frac{3}{2}}}}}}{\varepsilon }.$ Важно отметить, что при расчете переноса тепла в рамках стандартной k-ε модели полагается, что турбулентное число Прандтля, $~$связывающее коэффициенты турбулентной вязкости и диффузии $\left( {{{{\Pr }}_{T}} = {{{{K}_{m}}} \mathord{\left/ {\vphantom {{{{K}_{m}}} {{{K}_{h}}}}} \right. \kern-0em} {{{K}_{h}}}}} \right),$ постоянно.
Применимость k-ε схемы может быть расширена с использованием дополнительных алгебраических соотношений, учитывающих, например, действие сил плавучести, анизотропию турбулентности и т.д. В последнее время появились и более сложные модели, позволяющие учесть, например, разницу в эволюции различных компонент напряжений Рейнольдса (например, [17]). Это, в свою очередь, требует перехода к более сложным схемам замыкания турбулентных напряжений Рейнольдса более высокого порядка. Однако получаемые при этом уравнения позволяют учесть и проанализировать ряд интересных особенностей, возникающих в турбулентных течениях при наличии сил плавучести, горизонтальных движений во внутренних водоемах, анизотропии и т.д.
Особенностью мелкомасштабной турбулентности в океанах, морях и внутренних водоемах является то, что она, как правило, находится под действием двух факторов – плотностной стратификации и сдвига скорости, что необходимо учитывать при построении ее статистической теории. Как показано в [18] учет расслоения плотности, зависящей только, например, от температуры, приводит к появлению в уравнениях энергетического баланса так называемого динамического (или потокового) числа Ричардсона ${\text{R}}{{{\text{i}}}_{f}} = - g\frac{{\left\langle {\rho {\kern 1pt} 'u_{i}^{'}} \right\rangle }}{{\left\langle {u_{i}^{'}u_{j}^{'}} \right\rangle {{V}_{{0z}}}}},$ (здесь $\left\langle {\rho {\kern 1pt} 'u_{i}^{'}} \right\rangle $ – поток массы, $\left\langle {u_{i}^{'}u_{j}^{'}} \right\rangle $ – поток импульса, ${{V}_{{0z}}}$ – сдвиг скорости), характеризующего роль сил Архимеда и осредненного сдвигового движения в балансе турбулентной энергии. В частности, в [18] показано, что незатухающая турбулентность возможна лишь при ${\text{R}}{{{\text{i}}}_{f}} < {\text{R}}{{{\text{i}}}_{f}}_{{{\text{кр}}}} < 1$ или, с учетом определения коэффициентов турбулентной вязкости и турбулентной диффузии, условие существования незатухающей турбулентности сводится к ${\text{Ri}} < {\text{P}}{{{\text{r}}}_{T}}$, где $~{\text{Ri}} = \frac{{{{N}^{2}}}}{{V_{{0z}}^{2}}},$ ($N$ – частота Брента–Вяйсяля) – градиентное число Ричардсона. Однако есть некоторые основания полагать, что число Прандтля $~{\text{P}}{{{\text{r}}}_{T}}$ не остается постоянным, и при изменении градиентного числа Ричардсона Ri может быть настолько велико, что динамическое число Ричардсона ${\text{R}}{{{\text{i}}}_{f}}$ остается меньше критического значения, и турбулентность существует [18]. В частности, экспериментальные измерения в атмосфере, верхнем слое океана и в лаборатории [18–21] показывают, что даже при сильно устойчивой стратификации число Прандтля может принимать большие значения, т.е. коэффициент турбулентной диффузии тепла оказывается значительно меньше, чем коэффициент турбулентной вязкости, а, следовательно, турбулентность может существовать и при больших значениях градиентного числах Ричардсона. Из сказанного выше следует, что вопрос о зависимости ${\text{P}}{{{\text{r}}}_{T}}\left( {{\text{Ri}}} \right)$ представляется важным для изучения возможности поддержания турбулентности слабыми сдвигами в стратифицированной жидкости, характерными и для океана, и для внутренних водоемов.
Существует достаточное количество работ, в которых исследуются особенности полуэмпирических моделей турбулентного замыкания [11–14] для стратифицированных сдвиговых течений, и в частности, вопрос о существовании турбулентности при больших числах Ричардсона. Предложены многочисленные эмпирические зависимости $~{\text{P}}{{{\text{r}}}_{T}}\left( {{\text{Ri}}} \right)$ (например, [22–25]), характеризующие, в основном, асимптотическое поведение зависимости ${\text{P}}{{{\text{r}}}_{T}}\left( {{\text{Ri}}} \right)$, но не позволяющие с достаточной точностью установить форму зависимости при промежуточных значениях ${\text{\;Ri}}$, характеризующих переход от слабых к сильным турбулентным стратифицированным сдвиговым течениям жидкости.
В настоящей работе мы предлагаем параметризацию числа Прандтля, полученную на основе модифицированной теории турбулентного замыкания в стратифицированных сдвиговых потоках, разработанной одним из авторов в 1987 году11 [28]. Процедура получения соответствующих уравнений для средних аналогична той, которая используется в кинетической теории газов [29, 30], при этом решается уравнение для одноточечной функции распределения f – так называемое кинетическое уравнение, и по известной функции распределения вычисляются напряжения Рейнольдса. Предложенный подход позволил учесть некоторые важные, но обычно пренебрегаемые эффекты, например, зависимость вертикальной анизотропии турбулентности от стратификации, неградиентную поправку к традиционному выражению турбулентного потока массы, обратный переход из потенциальной энергии турбулентных флуктуаций в кинетическую, что приводит к устранению ограничений на существование турбулентности при больших числах Ричардсона.
Полученную зависимость числа Прандтля мы рассматриваем в рамках численного моделирования термогидродинамического режима внутренних водоемов с применением трехмерной термогидростатической модели [31, 32], ранее верифицированной в работе [33], где также приведено сравнение с более широко известной одномерной (по вертикали) моделью LAKE, используя модификацию k-ε схемы, позволяющую учесть особенности турбулентного перемешивания в стратифицированных водоемах. Показано, что аналогичная параметризация числа Прандтля может быть получена и в рамках модифицированной k-ε схемы, учитывающей взаимную трансформацию кинетической и потенциальной энергии турбулентности.
ОСНОВНЫЕ ПОЛОЖЕНИЯ МОДЕЛИ ТУРБУЛЕНТНОГО ПЕРЕНОСА В СТРАТИФИЦИРОВАННОМ СДВИГОВОМ ПОТОКЕ
Кратко остановимся на основных результатах модели [28]. Основная проблема, возникающая при вычислении средних значений гидродинамических величин, связана с адекватной аппроксимацией так называемого “интеграла столкновений” (слагаемые, связанные с пульсациями давления и пульсационными компонентами вязких сил). Как показано в [28], для получения общих выражений турбулентных потоков импульса, плотности, энергии и других гидродинамических величин удается решить уравнение для одноточечной функции распределения f при ряде предположений. После нахождения функции распределения вычисляются напряжения Рейнольдса по формулам теории вероятностей. При этом для турбулентных потоков импульса $\left\langle {u_{i}^{'}u_{j}^{'}} \right\rangle $ и массы $\left\langle {\rho {\kern 1pt} 'u_{i}^{'}} \right\rangle $, а также потоков кинетической энергии $\left\langle {\sum\nolimits_{j = 1}^3 {u_{i}^{{'{\kern 1pt} 2}}u_{j}^{'}} } \right\rangle $ и дисперсии флуктуаций плотности $\left\langle {\sum\nolimits_{j = 1}^3 {{{\rho }^{{'{\kern 1pt} 2}}}u_{j}^{'}} } \right\rangle $ были получены следующие выражения:
(1)
$\left\langle {u_{i}^{'}u_{j}^{'}} \right\rangle = {{V}^{2}}{{\delta }_{{ij}}} - LV\left( {\frac{{\partial \left\langle {{{u}_{i}}} \right\rangle }}{{\partial {{x}_{j}}}} + \frac{{\partial \left\langle {{{u}_{j}}} \right\rangle }}{{\partial {{x}_{i}}}}} \right),$(2)
$\left\langle {\rho {\kern 1pt} 'u_{i}^{'}} \right\rangle = - LV\left( {\frac{{\partial \left\langle \rho \right\rangle }}{{\partial {{x}_{i}}}} + {{g}_{i}}\frac{{\left\langle {{{\rho }^{{'2}}}} \right\rangle }}{{{{V}^{2}}{{\rho }_{0}}}} - \frac{{g{{\beta }_{i}}}}{{{{V}^{2}}{{\rho }_{0}}}}} \right),$(3)
$\left\langle {\mathop \sum \limits_{j = 1}^3 u_{j}^{{'2}}u_{i}^{'}} \right\rangle = - 5LV\frac{{\partial {{V}^{2}}}}{{\partial {{x}_{i}}}},\,\,\,\,~\left\langle {{{\rho }^{{'2}}}u_{i}^{'}} \right\rangle = - LV\frac{{\partial \left\langle {{{\rho }^{{'2}}}} \right\rangle }}{{\partial {{x}_{i}}}}.$Здесь $L$ – характерный внешний масштаб турбулентности, $V$– характерный масштаб скорости, $\vec {g}$ – ускорение свободного падения, ${{\beta }_{i}}$ – компоненты вектора $\overrightarrow {\beta ,} $ характеризующего пульсации давления в стратифицированной жидкости (см. далее).
Заметим, что в выражение для потока массы (2) входит дополнительное слагаемое $~{{g}_{i}}\frac{{\left\langle {{{\rho }^{{'2}}}} \right\rangle }}{{{{V}^{2}}{{\rho }_{0}}}} - \frac{{g{{\beta }_{i}}}}{{{{V}^{2}}{{\rho }_{0}}}}$, что приводит к ряду существенных отличий от результатов, полученных в рамках обычных градиентных моделей [34]. Для статистически однородного поля флуктуаций плотности компоненты вектора $\overrightarrow {~\beta } $ имеют вид ${{\beta }_{x}} = {{\beta }_{y}} = 0,$ $~{{\beta }_{z}} = \left\langle {{{\rho }^{{'2}}}} \right\rangle R,~$ где $R$– параметр анизотропии:
Приведенные выше выражения позволяют получить замкнутую модель турбулентного течения в стратифицированной жидкости в виде уравнений для средних: скорости $\left\langle {\vec {u}} \right\rangle $, плотности $\left\langle \rho \right\rangle $, а также кинетической энергии турбулентности $k$ и дисперсии пульсаций плотности $\left\langle {{{\rho }^{{'2}}}} \right\rangle $:
(4.1)
$\begin{gathered} \frac{{\partial \left\langle {{{u}_{i}}} \right\rangle }}{{\partial t}} + \left\langle {{{u}_{j}}} \right\rangle \frac{{\partial \left\langle {{{u}_{i}}} \right\rangle }}{{\partial {{x}_{j}}}} + \frac{1}{{{{\rho }_{0}}}}\frac{{\partial \left\langle p \right\rangle }}{{\partial {{x}_{i}}}} + {{g}_{i}}\frac{{\left\langle \rho \right\rangle - {{\rho }_{0}}}}{{{{\rho }_{0}}}} = \\ = \frac{\partial }{{\partial {{x}_{j}}}}\left( {L\sqrt k \left( {\frac{{\partial \left\langle {{{u}_{i}}} \right\rangle }}{{\partial {{x}_{j}}}} + \frac{{\partial \left\langle {{{u}_{j}}} \right\rangle }}{{\partial {{x}_{i}}}}} \right)} \right), \\ \end{gathered} $(4.2)
$\begin{gathered} \frac{{\partial \left\langle \rho \right\rangle }}{{\partial t}} + \left\langle {{{u}_{i}}} \right\rangle \frac{{\partial \left\langle \rho \right\rangle }}{{\partial {{x}_{i}}}} = \\ = 2\frac{\partial }{{\partial {{x}_{i}}}}L\sqrt k \left( {\frac{{\partial \left\langle \rho \right\rangle }}{{\partial {{x}_{i}}}} + \frac{3}{{2k{{\rho }_{0}}}}\left( {{{g}_{i}}\left\langle {{{\rho }^{{'2}}}} \right\rangle + g{{\beta }_{i}}} \right)} \right), \\ \end{gathered} $(4.3)
$\begin{gathered} \frac{{\partial k}}{{\partial t}} + \left\langle {{{u}_{i}}} \right\rangle \frac{{\partial k}}{{\partial {{x}_{i}}}} - L\sqrt k {{\left( {\frac{{\partial \left\langle {{{u}_{i}}} \right\rangle }}{{\partial {{x}_{j}}}} + \frac{{\partial \left\langle {{{u}_{j}}} \right\rangle }}{{\partial {{x}_{i}}}}} \right)}^{2}} - \frac{g}{{{{\rho }_{0}}}}L\sqrt k \,\,~ \times \\ \times \,\,\left( {\frac{{\partial \left\langle \rho \right\rangle }}{{\partial z}} + \frac{{3g}}{{2k{{\rho }_{0}}}}\left( {\left\langle {{{\rho }^{{'2}}}} \right\rangle + {{\beta }_{z}}} \right)} \right) + \frac{{C{{k}^{{3/2}}}}}{L} = \\ = \frac{5}{3}\frac{\partial }{{\partial {{x}_{i}}}}\left( {L\sqrt k \frac{{\partial k}}{{\partial {{x}_{i}}}}} \right), \\ \end{gathered} $(4.4)
$\begin{gathered} \frac{{\partial \left\langle {{{\rho }^{{'2}}}} \right\rangle }}{{\partial t}} + \left\langle {{{u}_{i}}} \right\rangle \frac{{\partial \left\langle {{{\rho }^{{'2}}}} \right\rangle }}{{\partial {{x}_{i}}}} - \\ - \,\,2\frac{{\partial \rho }}{{\partial {{x}_{i}}}}L\sqrt k \left( {\frac{{\partial \left\langle \rho \right\rangle }}{{\partial {{x}_{i}}}} + \left( {{{g}_{i}}\left\langle {{{\rho }^{{'2}}}} \right\rangle - g{{\beta }_{i}}} \right)\frac{3}{{2k{{\rho }_{0}}}}} \right) + \\ + \,\,\frac{{D{{k}^{{1/2}}}}}{L}\left\langle {{{\rho }^{{'2}}}} \right\rangle = \frac{\partial }{{\partial {{x}_{i}}}}L\sqrt k \frac{{\partial \left\langle {{{\rho }^{{'2}}}} \right\rangle }}{{\partial {{x}_{i}}}}. \\ \end{gathered} $Заметим, что в уравнениях (4.3) и (4.4) приняты колмогоровские гипотезы для учета диссипативных и диффузионных процессов. При этом скорость диссипации энергии турбулентности $\varepsilon $ и турбулентной диффузии ${{\varepsilon }_{D}}$ определяются выражениями $\varepsilon = \frac{{C{{k}^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}}}}{L}$ и ${{\varepsilon }_{D}} = \frac{{D{{k}^{{1/2}}}}}{L}\left\langle {{{\rho }^{{'2}}}} \right\rangle $, где $C\sim D = 0.09$ – эмпирические константы.
На основе предложенной модели были рассмотрены некоторые примеры взаимодействия турбулентности со сдвиговыми течениями в стратифицированной жидкости и, в частности, в [28] исследована эволюция однородной турбулентности в поле течения с постоянным сдвигом скорости. Остановимся на последней задаче подробнее, поскольку в рамках этой постановки удается проанализировать влияние взаимной трансформации кинетической и потенциальной энергий в эволюцию турбулентности при больших числах Ричардсона, а также рассчитать зависимость турбулентного числа Прандтля от числа Ричардсона.
Кратко остановимся на результатах работы [28]. Система (4) при указанных предположениях сводится к двум уравнениям для кинетической k и потенциальной $\Pi = \frac{{\left\langle {{{\rho }^{{'2}}}} \right\rangle {{g}^{2}}}}{{2{{N}^{2}}\rho _{0}^{2}}}$ энергий турбулентности и имеет вид:
(5.1)
$\begin{gathered} \frac{{dk}}{{dt}} = V_{{0z}}^{2}L\sqrt k - \\ - \,\,{{N}^{2}}L\sqrt k \left( {1 - \frac{{3\Pi }}{k}\left( {1 - R} \right)} \right) - \frac{{C{{k}^{{3/2}}}}}{L}, \\ \end{gathered} $(5.2)
$\frac{{d\Pi }}{{dt}} = {{N}^{2}}L\sqrt k \left( {1 - \frac{{3\Pi }}{k}\left( {1 - R} \right)} \right) - \frac{{D{{k}^{{1/2}}}\Pi }}{L}.$Прежде всего, анализ системы (5) показал, что в системе имеются стационарные значения кинетической и потенциальной энергий:
(6)
$\begin{gathered} k = {{k}_{2}} = \frac{{V_{{0z}}^{2}{{L}^{2}}}}{{2C}}f\left( {{\text{Ri}}} \right), \\ \Pi = {{\Pi }_{2}} = \frac{{V_{{0z}}^{2}{{L}^{2}}}}{C} - {{k}_{2}}, \\ \end{gathered} $которые устанавливаются за время ${{t}_{1}}\sim {1 \mathord{\left/ {\vphantom {1 {{{V}_{{0z}}}}}} \right. \kern-0em} {{{V}_{{0z}}}}}\sqrt {C~} $ (см. рис. 1), где $f\left( {{\text{Ri}}} \right) = 1 - \left( {4 - 3R~} \right){\text{Ri}}$ + + ${{\left( {1 - {\text{Ri}}{{{\left( {4 - 3R} \right)}}^{2}} + 12\left( {1 - R} \right){\text{Ri}}} \right)}^{{1/2}}}$ – функция числа Ричардсона.
Рис. 1.
Зависимость безразмерной кинетической $\bar {k} = {k \mathord{\left/ {\vphantom {k {{{k}_{x}}}}} \right. \kern-0em} {{{k}_{x}}}},$ ${{k}_{x}} = {{({{V}_{{0z}}})}^{2}}{{{{L}^{2}}} \mathord{\left/ {\vphantom {{{{L}^{2}}} C}} \right. \kern-0em} C}$ (сплошная линия) и потенциальной ${\bar {П}} = {{\text{П}} \mathord{\left/ {\vphantom {{\text{П}} {{{{\text{П}}}_{x}}}}} \right. \kern-0em} {{{{\text{П}}}_{x}}}},$ ${{{\text{П}}}_{x}} = {{({{V}_{{0z}}})}^{2}}{{{{L}^{2}}} \mathord{\left/ {\vphantom {{{{L}^{2}}} C}} \right. \kern-0em} C}$ (пунктирная линия) энергий турбулентности от безразмерного времени $\bar {t} = {t \mathord{\left/ {\vphantom {t {{{t}_{x}}}}} \right. \kern-0em} {{{t}_{x}}}},$ ${{t}_{x}} = {1 \mathord{\left/ {\vphantom {1 {{{V}_{{0z}}}\sqrt C }}} \right. \kern-0em} {{{V}_{{0z}}}\sqrt C }}$ при различных значениях числа Ричардсона ${\text{Ri}}$: (а) ${\text{Ri}} = 0.5,$ (б) ${\text{Ri}} = 5.$ Параметр анизотропии $~R = 0.5$ в обоих случаях.
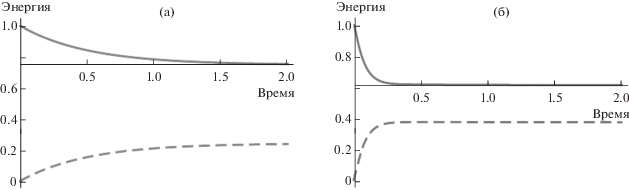
Из системы (5) ясно, что градиентное слагаемое $\left( { - {{N}^{2}}L\sqrt k } \right)$ в выражении для потока плавучести описывает переход энергии из кинетической в потенциальную (устойчивая стратификация гасит турбулентность). Дополнительное слагаемое $~\left( {\frac{{3{\text{П}}{{N}^{2}}L\left( {1 - R} \right)}}{{\sqrt k }}} \right)\sim ~\left\langle {{{\rho }^{{'2}}}} \right\rangle ,$ связанное с неградиентной добавкой в потоке массы, имеет противоположный градиентному знак и описывает обратный переход энергии из потенциальной в кинетическую за счет работы силы плавучести. При этом, если число Ричардсона велико (${\text{Ri}}~\,\, \gg 1)$ (см. рис. 1), то за достаточно короткое время $t{{~}_{2}}\,\,\sim \left( {\frac{{\sqrt k }}{{{{N}^{2}}L}}} \right) \ll {{t}_{1}};$ $~\left( {\frac{{t{{~}_{2}}}}{{{{t}_{1}}}} = {\text{R}}{{{\text{i}}}^{{ - 1}}}} \right)$ происходит уравновешивание доли энергии турбулентных флуктуаций, переходящей из кинетической в потенциальную и наоборот за счет работы силы плавучести. Это означает, что при больших числах Ричардсона достаточно быстро устанавливается определенное соотношение между кинетической и потенциальной энергиями турбулентности $~k = {\text{3П}}\left( {1 - ~R} \right)$; при этом дальнейшая эволюция турбулентности не зависит от числа Ричардсона [см. 28].
Приведенные выше результаты позволяют вычислить турбулентное число Прандтля в стационарном состоянии. По определению:
При этом из системы (6) получаем возрастающую зависимость числа Прандтля от числа Ричардсона:
(7)
$\begin{gathered} {\text{P}}{{{\text{r}}}_{T}}\left( {{\text{Ri}}} \right) = \\ = ~\frac{{\left( {4 - 3R~} \right){\text{Ri}} + 1 + {{{\left( {{{{\left( {\left( {4 - 3R} \right){\text{Ri}} + 1} \right)}}^{2}} - 4{\text{Ri}}} \right)}}^{{\frac{1}{2}}}}}}{2}. \\ \end{gathered} $Важно подчеркнуть некую универсальность зависимости ${\text{P}}{{{\text{r}}}_{T}}\left( {{\text{Ri}}} \right)$, которая определяется величиной $~\frac{{{\text{3П}}}}{k}\left( {1 - R} \right)$, связанной с переходом части потенциальной энергии в кинетическую, причем при ${\text{Ri}}~\,\, \gg 1$:
(8)
${\text{P}}{{{\text{r}}}_{T}}\left( {{\text{Ri}}} \right) = \,\,~\left( {4 - 3R~} \right){\text{Ri}}.$Отметим, что выражения (7–8) сохраняют свой вид и в рамках k-ε модели, когда для коэффициента вихревой вязкости используется выражение ${{K}_{m}} = {{c}_{\mu }}\sqrt k L,~$ и, соответственно, для масштаба турбулентности $L = C\frac{{{{k}^{{\frac{3}{2}}}}}}{\varepsilon }.$ Если при этом воспользоваться традиционной аппроксимацией скорости диффузии турбулентных пульсаций скалярной величины (см., например, [16]), то для скорости диссипации потенциальной энергии турбулентных флуктуаций можно воспользоваться выражением ${{\varepsilon }_{{\text{П}}}} = {{R}_{1}}\varepsilon \frac{{\text{П}}}{k}$ при R1 = 1 (что означает равенство временных масштабов пульсаций скорости и скалярной величины). Тогда выражения (6) преобразуются к виду:
Поскольку полученная выше (см. (7–8)) параметризация числа Прандтля зависит только от отношения П/k, из (*.2) следует ее справедливость и для расширенной k-ε модели.
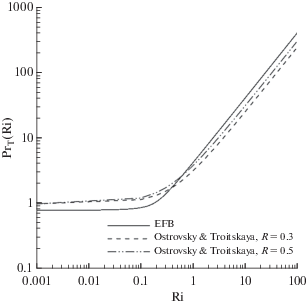
Таким образом, из (7–8) ясно, что условие поддержания турбулентности в стратифицированной жидкости $~{\text{Ri}} \ll {\text{P}}{{{\text{r}}}_{T}}$ выполняется при любом ${\text{Ri}}$, т.е. порога генерации по числу Ричардсона нет. Отметим, что асимптотическая зависимость (7–8) согласуется с результатами в работах ([27, 35]), где представлены параметризации с неограниченным ростом Прандтля. Сопоставление с моделью EFB группы С.С. Зилитинкевича представлено на рис. 2.
В следующем разделе будет продемонстрирован результат использования полученной параметризации турбулентного числа Прандтля (7) в идеализированных расчетах термогидродинамики внутренних водоемов.
ПРИМЕНЕНИЕ ПРЕДЛОЖЕННОЙ ПАРАМЕТРИЗАЦИИ В МОДЕЛИ ТЕРМОДИНАМИЧЕСКОГО РЕЖИМА ИДЕАЛИЗИРОВАННОГО ВНУТРЕННЕГО ВОДОЕМА
Для оценки влияния параметризации турбулентного числа Прандтля на процессы перемешивания во внутренних водоемах в настоящей работе использовалась трехмерная гидростатическая RANS (Reynolds-Averaged Navier-Stokes) модель, разрабатываемая в НИВЦ МГУ на основе единого гидродинамического кода, объединяющего как RANS, так и DNS- (Direct Numerical Simulation), LES- (Large-Eddy Simulation) подходы для расчета геофизических турбулентных течений при высоком пространственном и временном разрешении (см., например, [31–33]).
Численная модель включает уравнения гидродинамики в стратифицированном турбулентном вращающемся слое жидкости в приближении мелкой воды, а также уравнение для переноса тепла с учетом горизонтальной и вертикальной диффузии:
(9.1)
$\begin{gathered} \frac{{\partial u}}{{\partial t}} = ~ - A\left( u \right) + {{D}_{H}}\left( {u,~{{{\lambda }}_{m}}} \right) + {{D}_{z}}\left( {u,~{{K}_{m}} + {\nu }} \right) - \\ - \,\,g\frac{{\partial \eta }}{{\partial x}} - ~\frac{g}{{{{\rho }_{0}}}}\frac{\partial }{{\partial x}}\int\limits_z^\eta {\rho dz{\kern 1pt} '} \,\, + fv, \\ \end{gathered} $(9.2)
$\begin{gathered} \frac{{\partial v}}{{\partial t}} = ~\,\, - A\left( v \right) + {{D}_{H}}\left( {v,~{{{\lambda }}_{m}}} \right) + \\ + \,\,{{D}_{z}}\left( {v,~{{K}_{m}} + {\nu }} \right) - g\frac{{\partial \eta }}{{\partial y}} - ~\frac{g}{{{{{\rho }}_{0}}}}\frac{\partial }{{\partial y}}\int\limits_z^\eta {{\rho }dz{\kern 1pt} '} \,\, - fu, \\ \end{gathered} $(9.3)
$\nabla \cdot {\mathbf{u}} = \frac{{\partial u}}{{\partial x}} + \frac{{\partial v}}{{\partial y}} + \frac{{\partial w}}{{\partial z}} = 0,$(9.4)
$\frac{{\partial T}}{{\partial t}} = ~ - A\left( T \right) + {{D}_{H}}\left( {T,~{{{\lambda }}_{h}}} \right) + {{D}_{z}}\left( {T,~{{K}_{h}} + {\chi }{\kern 1pt} '} \right),$Здесь ${\mathbf{u}} = \left( {u,v,w} \right)$ – вектор скорости, $\eta $ – отклонение свободной поверхности от равновесного состояния, f – параметр Кориолиса, T – температура, ρ – плотность; ${{K}_{m}}~$(λm) и ${{K}_{h}}$ (λh) – коэффициенты вертикальной (горизонтальной) турбулентной вязкости и температуропроводности соответственно; ν, χ' – коэффициенты молекулярной вязкости и температуропроводности, z – вертикальная координата, проходящая от дна водоема z = –H(x, y) до поверхности, а t – время. Также здесь $A\left( q \right)$ – оператор адвекции:
а ${{D}_{H}}\left( {q,~{\lambda }} \right)$ и ${{D}_{z}}\left( {q,~K} \right)$ – операторы горизонтальной и вертикальной диффузии с коэффициентами ${\lambda }$ и К соответственно:
Для описания процессов вертикального турбулентного перемешивания (расчета коэффициентов ${{K}_{m}}$ и ${{K}_{h}}$) используется двухпараметрическая, так называемая стандартная k-ε модель (см., например, [22]), в которой используются прогностические уравнения для кинетической энергии турбулентности и скорости ее диссипации:
(10.1)
$\frac{{\partial k}}{{\partial t}} = \,\,~\frac{\partial }{{\partial z}}\left( {\frac{{{{K}_{m}}}}{{{{{\delta }}_{{\text{k}}}}}} + {\nu }} \right)\frac{{\partial k}}{{\partial z}} + P + B - {\varepsilon },~$(10.2)
$\begin{gathered} \frac{{\partial \varepsilon }}{{\partial t}} = ~\frac{\partial }{{\partial z}}\left( {\frac{{{{K}_{m}}}}{{{{{\delta }}_{{\varepsilon }}}}} + {\nu }} \right)\frac{{\partial {\varepsilon }}}{{\partial z}} + \\ + \,\,\frac{{\varepsilon }}{k}\left( {{{C}_{{1{\varepsilon }}}}P - {{C}_{{2{\varepsilon }}}}{\varepsilon } + {{C}_{{3{\varepsilon }}}}B} \right), \\ \end{gathered} $(10.4)
${{K}_{h}} = ~\,\,{{C}_{{{\varepsilon },T}}}\frac{{{{k}^{2}}}}{\varepsilon } = \frac{{{{C}_{{{\varepsilon },T}}}}}{{{{C}_{{\varepsilon }}}}}{{K}_{m}} = {\text{Pr}}_{T}^{{ - 1}}{{K}_{m}}.$Здесь слагаемое $P$ соответствует генерации энергии турбулентности за счет сдвига скорости, а B описывает генерацию или потребление энергии за счет действия сил плавучести, ${{{\delta }}_{k}},{\text{\;\;}}{{{\delta }}_{{\varepsilon }}}$ – турбулентные числа Шмидта для ТКЭ и скорости диссипации, соответственно, а ${{C}_{{1{\varepsilon }}}}$, ${{C}_{{2{\varepsilon }}}}$, ${{C}_{{3{\varepsilon }}}}$ – эмпирические константы, ${{C}_{{\varepsilon }}}$ и ${{C}_{{{\varepsilon },T}}}$ – функции устойчивости для импульса и скалярных величин, полагаемые в стандартной k-ε модели постоянными.
Заметим, что для однородного и стационарного турбулентного потока с учетом выражений для источников энергии турбулентности P и G из (10.2) следует выражение:
Учитывая формулы (**.1) для ε2/k2 и (**.2) для П/k, выражающие эти величины через число Ричардсона Ri, получим, что константы k-ε модели не являются независмыми, а связаны соотношением, зависящим от Ri:
В частности, учитывая асимптотику функции f(Ri) при Ri → ∞, получим соотношение между константами вида:
Эта особенность учитывалась при выборе констант k-ε-модели, использованной при проведении расчетов.
Что касается численных методов, используемых при расчетах, то для дискретизации системы уравнений по пространству применяются консервативные конечно-разностные схемы второго порядка точности, а для интегрирования по времени – полунеявная аппроксимация [20].
Для оценки влияния параметризации турбулентного числа Прандтля на описание процессов турбулентного перемешивания в этой модели нами были проведены численные эксперименты двух типов. В обоих случаях рассматривались идеализированные водные объекты с прямоугольным сечением и параметрами, характерными для реальных озер и водохранилищ: глубина 10 м, температура поверхности 20°C с начальным градиентом ${{\partial T} \mathord{\left/ {\vphantom {{\partial T} {\partial {\text{z}}}}} \right. \kern-0em} {\partial {\text{z}}}} = 1.5$°C/м, частота Брента–Вяйсяля (частота плавучести): $N = 4 \times {{10}^{{ - 2}}}$ c–1. В рамках первого эксперимента было проведено сопоставление расчетов по стандартной k-ε схеме, в которой полагалось постоянное значение числа Прандтля ${{\Pr }_{{{{T}_{0}}}}} = 1.25.$ Такое значение согласуется с оценками ${\text{P}}{{{\text{r}}}_{{{{T}_{0}}}}}$ при ${\text{Ri}} \approx 0$ по данным лабораторных исследований и прямого численного моделирования [36, 37] и, как правило, используется в расчетах циркуляции во внутренних водоемах с нейтральной (или близкой к ней) стратификацией (см., например, [38]). Во второй серии численных экспериментов проводилось сопоставление расчетов при использовании модернизированной k-ε модели со стандартной при значении числа Прандтля ${{\Pr }_{{{{T}_{0}}}}} = 1$, что согласно приведенной выше параметризации (7) соответствует случаю ${\text{Ri}} \to 0$. Также рассматривалось влияние величины потока импульса на поверхности и сил вращения на процессы перемешивания в обоих замыканиях. В первом эксперименте ветровой форсинг полагался одномерным: компоненты скорости трения: $u* = 0.00316~$ м/с, $v* = 0{\text{\;}}$ м/с, значение параметра анизотропии R в формуле ${\text{P}}{{{\text{r}}}_{T}}\left( {{\text{Ri}}} \right)$ равно 0.5. Во втором – форсинг был увеличен: $u* = v* = 0.00316$ м/с, рассматривались значения параметра R равные 0.2 и 0.7.
Ниже представлены результаты расчета основных характеристик термогидродинамического режима перемешивания идеализированного внутреннего водоема: вертикальное распределение температуры и кинетической энергии в первом эксперименте (рис. 3), эти же характеристики, а также их градиенты (рис. 4 и 5) во втором эксперименте, а также профили изменения числа Ричардсона в процессе перемешивания (рис. 6).
Рис. 3.
Вертикальное распределение (а) температуры, °С, (б) кинетической энергии турбулентности, м2/с2 в первом эксперименте.
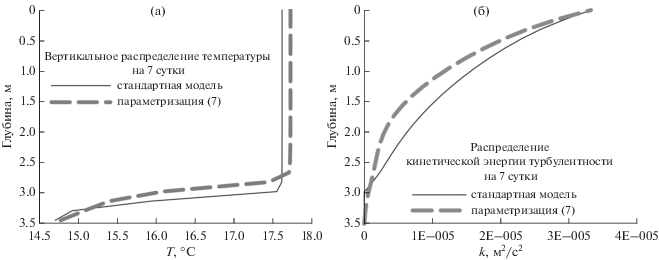
Рис. 4.
Вертикальное распределение (а) температуры, (б) градиента температуры во втором эксперименте.
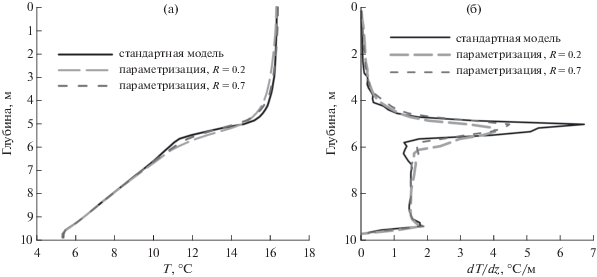
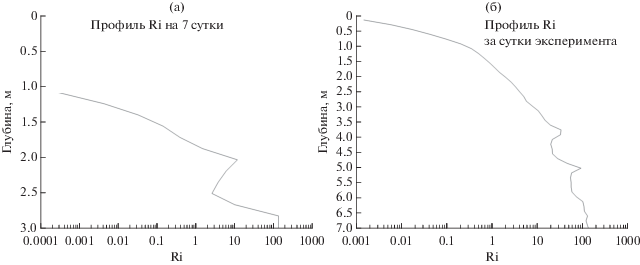
Рис. 5.
Вертикальное распределение (а) турбулентной кинетической энергии, (б) градиента турбулентной кинетической энергии во втором эксперименте.
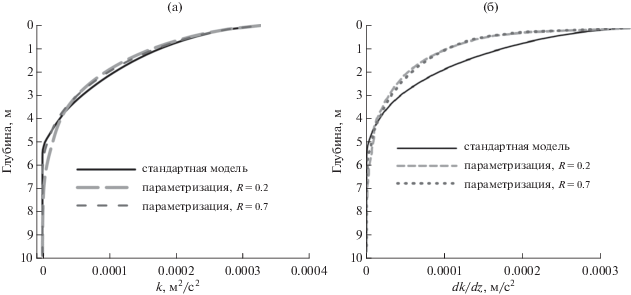
Рис. 6.
Профиль числа Ричардсона (а) в первом эксперименте на 7 сутки, (б) во втором эксперименте по окончании 1 суток.
Результаты расчетов c параметризацией показывают чувствительность основных характеристик перемешивания: вертикального распределения температуры, профиля коэффициента теплопроводности к параметризации ${\text{P}}{{{\text{r}}}_{T}}\left( {{\text{Ri}}} \right)$. В процессе численного эксперимента число Ричардсона Ri меняется значительно в диапазоне от ~0.001 до ~100, достигая уже на глубине около 2.5–3 м значения 10. При этом кинетическая энергия плавно меняется по всей глубине области перемешивания. Важно подчеркнуть, что учет параметризации приводит к сглаживанию всех резких изменений в вертикальных распределениях турбулентной кинетической энергии, температуры и толщины слоя скачка. Полученные результаты связаны с особенностями данной параметризации, из которой следует существование турбулентности при значениях ${\text{Ri}} \gg 1$.
Изменение входных данных при расчете (значение форсинга, параметра анизотропии) также влияют на характерные параметры перемешивания. Но эти изменения ожидаемы и не носят принципиального характера (меняется время формирования, глубина и толщина скачка температуры) для данной модели. Изменение значений скорости трения в основном влияет на время формирования перемешанного слоя (в, частности, процессы перемешивания происходят быстрее при увеличении u*, см. также расчеты в работе [20]).
Следует отметить, что чувствительность модели к используемой параметризации ${\text{P}}{{{\text{r}}}_{T}}\left( {{\text{Ri}}} \right)$ (особенно в области больших градиентов) представляется важной в задачах воспроизведения концентраций биохимический примесей во внутренних водоемах и описания газообмена с атмосферой (см. [39]). В настоящей работе мы ограничились рассмотрением термически стратифицированный среды в отсутствии примесей, однако в моделях внутренних водоемов, включающих перенос биохимических составляющих, турбулентные числа Шмидта, описывающие подобие между процессами турбулентной диффузии скаляра и турбулентным переносом импульса, как правило, полагаются равными турбулентному числу Прандтля (см., например, [40]). Таким образом, можно ожидать, что использование параметризации ${\text{P}}{{{\text{r}}}_{T}}\left( {{\text{Ri}}} \right)$ может влиять на перенос биохимических примесей в небольших внутренних водоемах, в частности, через термоклин. В свою очередь, данные измерений [41] показывают, что сезонные изменения в коэффициенте экстинкции проникающей коротковолновой радиации для водоемов в северных широтах напрямую связаны с вертикальным распределением концентраций органических веществ, влияющих на оптическую проницаемость среды. Результаты численного моделирования при воспроизведении сезонной изменчивости и, в частности, времени формирования ледяного покрова [41], сильно чувствительны к параметризациям данных процессов и потому требуют детального изучения с помощью полных моделей, включающих описание радиационных процессов и переноса биохимических примесей.
ВЫВОДЫ
В настоящей работе предложена параметризация турбулентного числа Прандтля, полученная на основе модели турбулентного замыкания [28], учитывающей двустороннюю трансформацию кинетической и потенциальной энергий турбулентных пульсаций. Характерной особенностью предложенной параметризации является входящее в нее отношение потенциальной энергии турбулентных флуктуаций П к кинетической k, которое, в свою очередь, определяет неградиентную добавку в выражении для среднего потока массы. Полученная параметризация находится в хорошем качественном соответствии со сравнительно недавно полученной моделью С.С. Зилитинкевича с соавторами [26, 27]. Параметризация внедрена в формулу коэффициента турбулентной теплопроводности k-ε модели с целью корректного учета устойчивой стратификации при расчете термогидродинамического режима внутренних водоемов.
Результаты расчетов позволяют сделать вывод о том, что описание вертикального перемешивания во внутренних водоемах даже в идеализированной постановке чувствительно к параметризации турбулентного числа Прандтля. Важно подчеркнуть, что учет параметризации приводит к сглаживанию всех резких изменений в вертикальных распределениях турбулентной кинетической энергии, температуры и толщины слоя скачка. Это связано с особенностями данной параметризации, справедливой в широком диапазоне изменения чисел Ричардсона (в частности, и при больших значениях ${\text{Ri}} \gg 1$), в то время как расчеты по стандартной модели с постоянным значением числа Прандтля предполагают наличие критического значения динамического (потокового) числа Ричардсона, в окрестности которого теряют смысл ряд гипотез полуэмпирической теории турбулентности [18].
Полученный результат свидетельствует о целесообразности проведения дополнительных лабораторных и натурных измерений соответствующих коэффициентов турбулентной вязкости и диффузии с целью выбора обоснованных параметризаций турбулентного числа Прандтля при расчете сезонной и межгодовой динамики стратифицированных внутренних водоемов.
Работа выполнена в рамках проектов РФФИ 18-05-00292, 18-05-60299 и 20-05-00776, а также в рамках грантов Президента Российской Федерации для государственной поддержки молодых российских ученых МК-1867.2020.5 и МД-1850.2020.5.
Список литературы
Persson T. Evaporation and heat-flux aggregation in heterogeneous boreal, landscape. Disser. for deg. of Doctor of Philos. Uppsala University. 2004. 48 p.
Eerola K., Rontu L., Kourzeneva E., Pour H.K., Duguay C. Impact of partly ice-free Lake Ladoga on temperature and cloudiness in an anticyclonic winter situation – a case study using a limited area model // Tellus A. 2014. V. 66. P. 1–17.
Степаненко В.М., Микушин Д.Н. Численное моделирование мезомасштабной динамики атмосферы и переноса примеси над гидрологически неоднородной поверхностью // Вычислительные технологии. 2008. Т. 13. № 3. С. 104–110.
Степаненко В.М., Миранда П.М., Лыкосов В.Н. Численное моделирование мезомасштабного взаимодействия атмосферы и гидрологически неоднородной суши // Вычислительные технологии. 2006. Т. 11. № 3. С. 118–127.
Tsuang B.-J., Tu C.-J., Arpe K. Lake parameterization for climate models // Max Planck Institute for Meteorology. Hamburg. 2001. Report No. 316. 72 p.
Mironov D., Terzhevik A., Beyrich F., Golosov S., Haise E., Kirillin G., Kourzeneva E., Ritter B., Schneider N. Parameterization of lakes in numerical weather prediction: description of a lake model, single-column tests, and implementation into the limited-area NWP model // Bound. Lay. Meteor. 2006. Spec. issue. 56 p.
Long Z. et al. Northern Lake Impacts on Local Seasonal Climate // Journal of Hydrometeorology. 2007. V. 8. № 4. P. 881–896.
Ljungemyr P., Gustafsson N., Omstedt A. Parameterization of lake thermodynamics in a high-resolution weather forecasting model // Tellus A. 1996. V. 48. P. 608–621.
Mackay M. Modeling the regional climate impact of boreal lakes // Geophysical Research Abstracts. 2006. V. 8. 05405.
Hostetler S.W., Bates G.T., Giorgi F. Interactive coupling of a lake thermal model with a regional climate model // J. Geophys. R. 1993. V. 98D. P. 5045–5057.
Монин А.С., Яглом А.М. Статистическая гидромеханика. Часть 1. / Под ред. Г.С. Голицына. М.: Наука, 1965. С. 333.
Монин А.С., Яглом А.М. Статистическая гидромеханика. Часть 1. / Под ред. Г.С. Голицына. М.: Наука, 1965. С. 318–325.
Степаненко В.М. Численное моделирование взаимодействия атмосферы с водоемами суши. Дисс. на соиск. уч. ст. к. ф-м. н. 2007. 159 с.; С. 27–28.
Mellor C.L., Yamada T. A hierarchy of turbulence closure models for planetary boundary layers // J. Atmos. Sci. 1974. V. 31. P. 1791–1806.
Лыкосов В.Н. О проблеме замыкания моделей турбулентного пограничного слоя с помощью уравнений для кинетической энергии турбулентности и скорости ее диссипации // Изв. АН СССР. Физика атмосферы и океана. 1992. Т. 28. С. 696–704.
Rodi W. Turbulence Models for Environmental Problems’ / in Kollmann, W. (ed.), Prediction Methods for Turbulent Flows, Hemisphere Publ. Co. London. 1980. P. 259–349.
Яковенко С.Н. Бюджет уравнений для напряжений Рейнольдса в области турбулентности, возникающей при обрушении внутренних волн // Вестник Новосиб. гос. ун-та. Серия: Физика. 2012. Т. 7. Вып. 4. С. 87–95.
Монин А.С., Яглом А.М. Статистическая гидромеханика. Часть 1. / Под ред. Г.С. Голицына. Москва: Наука. 1965. С. 338–437.
Kondo B., Curry J.A. Heat and momentum transfer under strong stability in the atmocpheric surface layer // J. Atmos. Sci. 2000. V. 57. P. 1417–1423.
Strang E.J., Fernando H.J. Vertical mixing and transports through a stratified shear layer // J. Phys. Oceanogr. 2001. V. 31. P. 2026–2048.
Stretch D.D., Rot J.W. et al. Transient mixing events in stably stratified turbulence // 14th Australasian FluidMech.Conference. 2001. Australia.
Kantha L., Clayson S. An improved mixed layer model for geophysical applications // J. Geophys. Res. 1994. V. 99 (C12). P. 25235–25266.
Mellor G., Yamada T. Development of a turbulence closure model for geophysical problems // Rev. Of Geophys. And Space Physics. 1982. V. 20(4). P. 851–875.
Baas P., de Roode S., Lenderink G. The scaling behaviour of a turbulent kinetic energy closure model for stably stratified conditions // Boundary-Layer Meteorology. 2008. V. 127. P. 17–36.
Schumann U., Gerz T. Turbulent mixing in stably stratified shear flows // J. Applied Meteorology. 1996. V. 34. P. 33–48.
Zilitinkevich S.S., Elperin T., Kleeorin N., Rogachevskii I. Energy- and Flux-Budget (EFB) turbulence closure models for stably-stratified flows. Part I: Steady-state, homogeneous regimes // Bound.-Layer Meteorol. 2007. V. 125. P. 167–191.
Zilitinkevich S.S., Elperin T., Kleeorin N., Rogachevskii I. and Esau I. A Hierarchy of Energy- and Flux-Budget (EFB) Turbulence Closure Models for Stably-Stratified Geophysical Flow // Bound.-Layer Meteorol. 2013. V. 146. P. 341–373.
Островский Л.А., Троицкая Ю.И. Модель турбулентного переноса и динамика турбулентности в стратифицированном сдвиговом потоке // Изв. АН СССР. Физика атмосферы и океана. 1987. № 3. С. 1031–104.
Lundgren T.S. Distribution functions in the statistical theory of turbulence // Phys. Fluids. 1967. V. 10 (969).
Власов А.А. Статистические функции распределения / Москва, Изд-во Наука. 1966, 356 с.
Mortikov E.V. Numerical simulation of the motion of an ice keel in stratified flow // Izv. Atmos. Ocean.Phys. 2016. V. 52. P. 108–115.
Mortikov E.V., Glazunov A.V., Lykosov V.N. Numerical study of plane Couette flow: turbulence statistics and the structure of pressure-strain correlations // Russian J. Numerical Analysis and Mathematical Modelling. 2019. V. 34. № 2. P. 1–14.
Гладских Д.С., Степаненко В.М., Мортиков Е.В. О влиянии горизонтальных размеров внутренних водоемов на толщину верхнего смешанного слоя // Водные ресурсы. 2019. 18 стр. (принята к печати)
Монин А.С., Озмидов Р.В. Океанская турбулентность / Л.: Гидрометеоиздат, 1981. С. 26–29, 237–240.
Sukoriansky S., Galperin B., Perov V. A quasi-normal scale elimination model of turbulence and its application to stably stratified flows // Nonlinear Process. Geophys. 2006. V. 13. P. 9–22.
Li D. Turbulent Prandtl number in the atmospheric boundary layer – where are we now? // Atmos. Res. 2019. V. 216. № 1. P. 86–105.
Kays W. Turbulent Prandtl number – where are we? // J. Heat Transfer. 1994. V. 116. P. 284–295.
Goudsmit G.-H., Burchard H., Peeters F., Wuest A. Application of k-eps turbulence models to enclosed basins: The role of internal seiches // J. Geophys. Res. 2002. V. 107(C12), P. 3230.
Karpowicz M., Ejsmont-Karabin J. Effect of metalimnetic gradient on phytoplankton and zooplankton (Rotifera, Crucstacea) communities in different trophic conditions // Environ. Monit. Assess. 2017. V. 189. № 8. P. 367.
Heiskanen J.J., Mammarella I., Ojala A., Stepanenko V., Erkkila K.-M., Miettinen H., Sandstrom H., Eugster W., Lepparanta M., Jarvinen H., Vesala T., Nordbo A. Effects of water clarity on lake stratification and lake-atmosphere heat exchange // J. Geophys. Res. Atmos. 2015. V. 120. № 5. P. 7412–7428.
Stepanenko V., Mammarella I., Ojala A., Miettinen H., Lykosov V., Vesala T. LAKE 2.0: a model for temperature, methane, carbon dioxide and oxygen dynamics in lakes // Geosci. Model Dev. 2016. V. 9. № 5. P. 1977–2006.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Физика атмосферы и океана