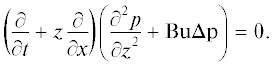1. На главную
  2. Электронные версии
  3. Известия РАН. Физика атмосферы и океана
  4. T. 56, № 6, 2020

Известия РАН. Физика атмосферы и океана, 2020, T. 56, № 6, стр. 676-688

О влиянии трения и диффузии плавучести на динамику геострофических океанских течений с линейным вертикальным профилем скорости

Н. П. Кузьмина a, *, С. Л. Скороходов b, **, Н. В. Журбас a, Д. А. Лыжков a

a Институт океанологии им. П.П. Ширшова РАН
117997 Москва, Нахимовский проспект, 36, Россия

b ФИЦ “Информатика и Управление” РАН
119333 Москва, ул. Вавилова, 44, Россия

* E-mail: kuzmina@ocean.ru
** E-mail: sskorokhodov@gmail.com

Поступила в редакцию 15.04.2020
После доработки 26.06.2020
Принята к публикации 05.08.2020

Полный текст (PDF)

Аннотация

Рассмотрена спектральная задача типа Орра–Зоммерфельда для описания неустойчивых возмущений океанских геострофических течений с линейным вертикальным профилем скорости с учетом вертикальной диффузии плавучести и трения. Численные решения получены для различных значений безразмерных параметров задачи. Проведено сравнение расчетов спектров собственных значений и инкрементов роста неустойчивых возмущений с расчетами аналогичной задачи для идеальной жидкости. Показывается, что: а) диссипация расширяет диапазон волновых чисел неустойчивых возмущений; б) диссипация может увеличивать инкременты роста бароклинных возмущений; в) возмущения, обусловленные неустойчивостью критического слоя, могут нарастать быстрее бароклинных возмущений; г) течения с шириной, равной радиусу Россби и меньше этого масштаба могут быть неустойчивы; в зонах узких течений или фронтов развиваются практически круглые (осесимметричные) неустойчивые возмущения (субмезомасштабные вихри).

Ключевые слова: фронты, неустойчивость геострофических течений, трение, диффузия плавучести, задача на собственные значения, интрузии, вихри

1. ВВЕДЕНИЕ

Настоящая работа является продолжением исследований влияния вертикальной диффузии плавучести и импульса на 3D неустойчивость геострофических течений конечного поперечного масштаба в рамках уравнения эволюции потенциального вихря в квазигеострофическом приближении [1–5]. Однако если в перечисленных работах изучалась неустойчивость течения с вертикальным параболическим профилем скорости, то в настоящей работе представлен анализ устойчивых и неустойчивых возмущений для течения с линейным вертикальным профилем (постоянным вертикальным сдвигом скорости), которое является типичным для океана. Применительно к описанию интрузионного расслоения в океане анализ неустойчивых мод такого течения проводился, как правило, в рамках 2D нестационарных агеострофических моделей с учетом трения и диффузии плавучести (см., например, [6]), причем в некоторых моделях учитывалась и двойная диффузия [7–10] или дифференциальное перемешивание [11–13]. Для описания вихрей и крупномасштабных интрузий рассматриваются 3D-модели неустойчивых возмущений, которые более сложны, так как сводятся к обыкновенным дифференциальным уравнениям с переменными коэффициентами. Для исследования образования циклонов и антициклонов в атмосфере использовались модели в приближении идеальной жидкости [14–16]. Первым, кто провел анализ влияния диссипативных процессов на неустойчивость течения с линейным вертикальным профилем скорости в полубезграничной по вертикали области, был Майлз [17]. На основе аналитического решения уравнения эволюции квазигеострофического потенциального вихря при больших модифицированных числах Пекле и Рейнольдса было получено, что вертикальные диффузия плавучести и трение не оказывают существенного влияния на бароклинную неустойчивость течения. Однако следует отметить, что диапазон значений безразмерных параметров в такой задаче применительно к океану может быть достаточно широк [2, 5], поэтому аналитическое решение задачи при больших модифицированных числах Пекле и Рейнольдса следует рассматривать как частный случай неустойчивости геострофических течений с учетом диссипации. Так, например, анализ неустойчивых мод в модели [5] показал, что диссипативные процессы могут оказывать влияние не только на расширение спектра неустойчивых возмущений, но и на инкременты роста неустойчивых бароклинных мод. В связи с этим представляется важным провести анализ неустойчивости течения с линейным вертикальным профилем скорости на основе численного решения задачи в широком диапазоне изменения безразмерных параметров. Сравнение решений такой задачи с аналогичной задачей в приближении идеальной жидкости может быть полезно для более глубоко понимания механизмов возникновения неустойчивости в области коротковолновых возмущений и анализа влияния образования интрузий и вихрей на изменчивость температуры, солености и плотности во фронтальных зонах океана.

2. МОДЕЛЬНАЯ ЗАДАЧА

Для исследования методом малых возмущений неустойчивости зонального геострофического течения с вертикальным линейным профилем скорости в ограниченном по вертикали слое мы будем ориентироваться на линейное уравнение потенциального вихря в квазигеострофическом приближении с учетом вертикальной диффузии плавучести и вертикального трения. Такое уравнение для течения с параболическим вертикальным профилем было выведено и подробно обсуждалось в [2, 3, 5]. Для скорости основного потока с линейным вертикальным профилем оно выводится аналогично, и без учета β-эффекта имеет вид:

(1)
$\begin{gathered} ~\left( {\frac{\partial }{{\partial t}} + z\frac{\partial }{{\partial x}}} \right)\left( {\frac{{{{\partial }^{2}}p}}{{\partial {{z}^{2}}}} + {\text{Bu}} \cdot {\Delta p}} \right) = \\ = \,\,\frac{1}{{\text{R}}}\left( {\frac{{{{\partial }^{4}}p}}{{\partial {{z}^{4}}}} + {\text{Pr}}{\kern 1pt} \cdot {\text{Bu}}\frac{{{{\partial }^{2}}\Delta p}}{{\partial {{z}^{2}}}}} \right), \\ \end{gathered} $
где $p$ – возмущение давления, ${\text{R}} = {{sH_{0}^{3}} \mathord{\left/ {\vphantom {{sH_{0}^{3}} {\left( {KL} \right)}}} \right. \kern-0em} {\left( {KL} \right)}}$ = = ${{{\text{Pe}}{{H}_{0}}} \mathord{\left/ {\vphantom {{{\text{Pe}}{{H}_{0}}} L}} \right. \kern-0em} L}$, ${\text{Pe}} = {{{\tilde {U}}{{H}_{0}}} \mathord{\left/ {\vphantom {{{\tilde {U}}{{H}_{0}}} K}} \right. \kern-0em} K}$ – число Пекле (аналог числа Рейнольдса), $K$– коэффициент вертикальной диффузии плавучести, s – положительная константа, характеризующая величину вертикального сдвига скорости, Ũ – максимальная скорость течения в слое, ${\text{Bu}} = {{H_{0}^{2}N_{0}^{2}} \mathord{\left/ {\vphantom {{H_{0}^{2}N_{0}^{2}} {\left( {{{f}^{2}}{{L}^{2}}} \right)}}} \right. \kern-0em} {\left( {{{f}^{2}}{{L}^{2}}} \right)}}$ – число Бургера (см., например, [18]), ${{N}_{0}}$ – частота плавучести в фоновом равновесном состоянии, $L$ – горизонтальный поперечный масштаб зонального геострофического течения, ${{H}_{0}}$ – вертикальный масштаб слоя, $f$ – параметр Кориолиса, ${\text{Pr}}$ – число Прандтля, $\Delta p = \frac{{{{\partial }^{2}}p}}{{\partial {{x}^{2}}}} + \frac{{{{\partial }^{2}}p}}{{\partial {{y}^{2}}}}$. Ось x направлена на восток (зональная координата), ось y – на север (меридиональная координата), $0 \leqslant y \leqslant L$, и ось $z$ – вверх, $0 \leqslant z \leqslant {{H}_{0}}$. Скорость зонального течения направлена вдоль координаты x, $U\left( z \right) = sz.$

Безразмерные переменные вводились по формулам: $x* = {x \mathord{\left/ {\vphantom {x L}} \right. \kern-0em} L}$, $y* = {y \mathord{\left/ {\vphantom {y L}} \right. \kern-0em} L}$, $z* = {z \mathord{\left/ {\vphantom {z {{{H}_{0}}}}} \right. \kern-0em} {{{H}_{0}}}},$ $t* = {{t{\tilde {U}}} \mathord{\left/ {\vphantom {{t{\tilde {U}}} L}} \right. \kern-0em} L},$ где ${\tilde {U}} = s{{H}_{0}}$, $p* = {p \mathord{\left/ {\vphantom {p {{{p}_{0}}}}} \right. \kern-0em} {{{p}_{0}}}},$ $v* = {v \mathord{\left/ {\vphantom {v {{{v}_{0}}}}} \right. \kern-0em} {{{v}_{0}}}},$ а ${{p}_{0}}$ и ${{v}_{0}}$ – размерные константы $\left[ {{{p}_{0}}} \right] = {{{\text{м}}}^{2}}\,{{{\text{с}}}^{{ - 2}}}$, $\left[ {{{v}_{0}}} \right] = {\text{м}}{{{\text{с}}}^{{ - 1}}}$, которые удовлетворяют соотношению ${{v}_{0}} = {{{{p}_{0}}} \mathord{\left/ {\vphantom {{{{p}_{0}}} {fL}}} \right. \kern-0em} {fL}}$ (звездочки, которыми отмечены безразмерные переменные, в (1) опущены). При выводе уравнения (1) полагалось, что число Экмана и число Кибеля–Россби много меньше единицы.

Для анализа устойчивых и неустойчивых возмущений зонального геострофического течения мы будем опираться на уравнение (1) и следующие граничные условия:

(2)
$\begin{gathered} \frac{{{{\partial }^{2}}p}}{{\partial t\partial z}} - \frac{{\partial p}}{{\partial x}} = \frac{1}{{\text{R}}}\frac{{{{\partial }^{3}}p}}{{\partial {{z}^{3}}}},\,\,\,\,z = 0, \\ \left( {\frac{\partial }{{\partial t}} + \frac{\partial }{{\partial x}}} \right)\frac{{\partial p}}{{\partial z}} - \frac{{\partial p}}{{\partial x}} = \frac{1}{{\text{R}}}\frac{{{{\partial }^{3}}p}}{{\partial {{z}^{3}}}},\,\,\,\,z = 1, \\ \end{gathered} $
(3)
$\frac{{\partial p}}{{\partial x}} = 0,\,\,\,\,y = 0,\,\,\,\,y = 1,$
(4)
$\frac{{{{\partial }^{2}}p}}{{\partial {{z}^{2}}}} = 0,\,\,\,\,z = 0,\,\,\,\,z = 1.$

Условия (2) и (4) есть условия равенства нулю на верхней и нижней границе слоя вертикальной скорости и потоков плавучести соответственно. Условие (3) означает равенство нулю меридиональной компоненты скорости возмущения на боковых границах среднего геострофического течения. Отметим, что члены в правой части уравнения (1) описывают влияние на динамику возмущений диссипативных процессов, причем первый член в скобке в правой части (1) описывает влияние вертикальной диффузии плавучести, а второй член – влияние вертикального трения. В случае идеальной жидкости уравнение (1) значительно упрощается:

(5)

Граничными условиями для решения уравнения (5) являются равенства нулю меридиональной и вертикальной скоростей на боковых границах и вертикальных границах слоя соответственно:

(6)
$\begin{gathered} \frac{{{{\partial }^{2}}p}}{{\partial t\partial z}} - \frac{{\partial p}}{{\partial x}} = 0,\,\,\,\,z = 0, \\ \left( {\frac{\partial }{{\partial t}} + \frac{\partial }{{\partial x}}} \right)\frac{{\partial p}}{{\partial z}} - \frac{{\partial p}}{{\partial x}} = 0,\,\,\,\,z = 1, \\ \end{gathered} $
(7)
$\frac{{\partial p}}{{\partial x}} = 0,\,\,\,\,y = 0,\,\,\,\,y = 1.$

Исследование неустойчивости геострофических течений применительно к атмосфере в рамках уравнений (5)–(7) представлено в известной работе Иди [19].

Следуя стандартному подходу исследования неустойчивости геострофических течений (см., например, [18]), решение (1)–(4) будем искать в виде бегущего вдоль зональной координаты волнового возмущения: $p = F\left( z \right){{e}^{{ik\left( {x - ct} \right)}}}{\text{sin}}\left( {\pi ny} \right)$. Здесь мы ограничимся случаем $n = 1$: масштаб возмущения в меридиональном направлении равен масштабу фронта или течения (максимально растущая мода). Подставляя такое решение в (1)–(4), получим спектральную задачу на собственные значения:

(8)
$\begin{gathered} \left( {z - c} \right)\left( {\frac{{{{d}^{2}}F}}{{d{{z}^{2}}}} - {\text{Bu}}\left( {{{k}^{2}} + {{\pi }^{2}}} \right)F} \right) = \\ = \frac{1}{{ik{\text{R}}}}\left( {\frac{{{{d}^{4}}F}}{{d{{z}^{4}}}} - {\text{BuPr}}\left( {{{k}^{2}} + {{\pi }^{2}}} \right)\frac{{{{d}^{2}}F}}{{d{{z}^{2}}}}} \right), \\ \end{gathered} $
(9)
$\begin{gathered} - c\frac{{dF}}{{dz}} - F = \frac{1}{{ik{\text{R}}}}\frac{{{{d}^{3}}F}}{{d{{z}^{3}}}},\,\,\,\,z = 0, \\ \left( {1 - c} \right)\frac{{dF}}{{dz}} - F = \frac{1}{{ik{\text{R}}}}\frac{{{{d}^{3}}F}}{{d{{z}^{3}}}},\,\,\,\,z = 1, \\ \end{gathered} $
(10)
$\frac{{{{d}^{2}}F}}{{d{{z}^{2}}}} = 0,\,\,\,\,z = 0,\,\,\,\,z = 1,$
где $k$ – безразмерное волновое число вдоль координаты $x$, $с = {{с}_{1}} + i \cdot {{c}_{2}}$ – комплексная фазовая скорость, $i$ – мнимая единица. Возмущения растут со временем, то есть являются неустойчивыми, если ${{c}_{2}} > 0$.

Спектральная задача в случае идеальной жидкости имеет следующий вид:

(11)
$\left( {z - c} \right)\left( {\frac{{{{d}^{2}}F}}{{d{{z}^{2}}}} - {\text{Bu}}\left( {{{k}^{2}} + {{\pi }^{2}}} \right)F} \right) = 0,$
(12)
$\begin{gathered} - c\frac{{dF}}{{dz}} - F = 0,\,\,\,\,z = 0, \\ \left( {1 - c} \right)\frac{{dF}}{{dz}} - F = 0,\,\,\,\,z = 1. \\ \end{gathered} $

Уравнение (11) отличается от основного уравнения, рассмотренного в [19] для исследования неустойчивости течения: в этой работе анализировалось уравнение для вертикальной скорости возмущений. Аналогичное нашему представление задачи Иди [19] можно найти, например, в [20].

Задача (11), (12) решается явно. Отметим, что нормальные дискретные моды данной задачи, анализу которых была посвящена работа [19], не описывают всего класса решений: решениями данной задачи являются также сингулярные нормальные моды непрерывного спектра при $c = z$ в уравнении (11), которые важны не только для описания эволюции начального возмущения согласно уравнению (5), но и для изучения взаимодействия различных мод (см., например, [21, 22]). В настоящей работе для изучения влияния диссипации на динамику возмущений мы будем сравнивать собственные значения задач (8)–(10) и (11), (12) для нормальных дискретных мод.

Отметим, что уравнение (8) является известным уравнением Орра–Зоммерфельда [23]. Однако задача (8)–(10) существенно отличается от задачи Орра–Зоммерфельда (см., например, [2, 3, 5]). Различия в физической постановке указанных задач может привести и к различным решениям.

3. РЕЗУЛЬТАТЫ РАСЧЕТОВ МОДЕЛЬНОЙ ЗАДАЧИ (8)–(10). СРАВНЕНИЕ С РЕШЕНИЯМИ ЗАДАЧИ В ПРИБЛИЖЕНИИ ИДЕАЛЬНОЙ ЖИДКОСТИ

Для поиска собственных функций (СФ) и собственных значений (СЗ) модельной задачи (8)–(10) использовался высокоточный метод численного решения уравнения 4-го порядка с малым параметром при старшей производной, разработанный ранее для решения задачи Орра-Зоммерфельда [24, 25]. Данный метод был модифицирован с учетом граничных условий (9), (10), которые отличны от граничных условий задачи Орра–Зоммерфельда и включают искомый спектральный параметр в качестве множителя. Для эффективности решения настоящей задачи в широком диапазоне изменения волнового числа при проведении расчетов использовались асимптотические разложения при $k \to 0$ [26], что позволило уменьшить время численного счета и получить собственные значения (СЗ) с большой точностью при произвольно малом изменении волнового числа.

Решениями уравнения (8), как и уравнения Орра–Зоммерфельда, являются непрерывно дифференцируемые функции. Для конкретных значений волнового числа $k$ и параметров задачи, ${\text{Bu}}$, ${\text{Pr}}$ и ${\text{R}}$, существует счетное множество дискретных СЗ задачи (8)–(10). Для удобства анализа СЗ представляют в координатных осях ${{c}_{1}}$, $~{{c}_{2}}$ и называют спектром собственных значений. Естественно, что полезно сравнить спектры СЗ задачи (8)–(10) и задачи (11), (12). В настоящей работе нас будут также интересовать распределения СЗ для двух указанных задач в координатных осях ${{c}_{1}}$, $~{{c}_{2}}$ при непрерывном изменении волнового числа $k$, или траектории СЗ (см., например, [24]). Дополнительно будут представлены инкременты роста неустойчивых мод для различных значений параметров задач (8)–(10) и (11), (12) и некоторые примеры графиков СФ для задачи (8)–(10).

Остановимся кратко на решении задачи (11), (12). Общим гладким решением уравнения (11) является функция:

(13)
$F = A{{e}^{{{\delta }z}}} + B{{e}^{{ - {\delta }z}}},$
где ${{{\delta }}^{2}} = {\text{Bu}}\left( {{{k}^{2}} + {{\pi }^{2}}} \right);$ A, B – константы.

Подставляя эту функцию в граничное условие (12), легко найти следующее выражение для СЗ:

(14)
${{c}_{{1,2}}} = 0.5 \pm \sqrt {0.25 + {{\delta }^{{ - 2}}} + \frac{{1 + {{e}^{{2{\delta }}}}}}{{\delta \left( {1 - {{e}^{{2{\delta }}}}} \right)}}} .$

Из равенства (14) можно получить условие возникновения неустойчивости в приближении идеальной жидкости, $\delta < 2.399$ (см., например, [20]), которое позволяет оценивать значение волнового числа отсечения неустойчивости для различных значений параметра Bu.

3.1. Сравнение спектров и траекторий собственных значений задач (11), (12) и (8)–(10)

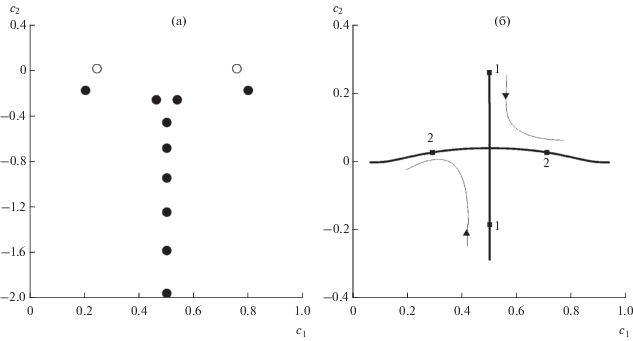
Для конкретных значений волнового числа $k$ и параметра ${\text{Bu}}$ задачи (11), (12) в соответствии с выражением (14) существует только два СЗ (рис. 1а). При изменении величины $k$ от малых до больших значений существуют только две траектории, характеризующие устойчивые (${{с}_{2}} < 0$), неустойчивые (${{с}_{2}} > 0$) и нейтральные (${{с}_{2}} = 0$) возмущения (рис. 1б). Фазовая скорость устойчивых и неустойчивых возмущений не зависит от волнового числа и равна ${{с}_{1}} = 0.5$, в то время как фазовые скорости нейтральных возмущений различны для разных волновых чисел. Коротковолновое отсечение неустойчивости наступает для значения числа Бургера, ${\text{Bu}} = 0.0001$, при $k \approx 240$.

Рис. 1.

Примеры спектра (а) и траекторий СЗ (б) для идеальной жидкости, рассчитанные для Bu = 0.0001. Спектр СЗ дан для k = 10 (белый кружок – неустойчивое возмущение, черный кружок – устойчивое возмущение). Траектории СЗ представлены для диапазона волновых чисел $0 \leqslant k \leqslant 1000$. Цифрами на траекториях отмечены точки, в которых $k = 1$ (1), $k = 200$ (2), $k = 300$ (3), $k = 800$ (4). Стрелками обозначены направления вдоль траекторий в сторону увеличения волнового числа.

Примеры спектра СЗ и двух первых траекторий задачи (8)–(10) представлены на рис. 2: только на этих траекториях наблюдаются неустойчивые СЗ, и, следовательно, именно эти траектории следует сопоставлять с траекториями в приближении идеальной жидкости (рис. 1б). (Подробнее с различными траекториями устойчивых СЗ и их описанием можно ознакомиться в работе [27].)

Рис. 2.

Примеры спектра (а) и траекторий СЗ (б) для диссипативной жидкости, рассчитанные для Bu = 0.0001. Спектр СЗ дан для k = 500 (белые кружки – неустойчивые возмущения, черные кружки – устойчивые возмущение). Две первые траектории СЗ представлены для диапазона волновых чисел $0.01 \leqslant k \leqslant 2500$. Цифрами на траекториях отмечены точки, в которых $k = 100$ (1), $k = 400$ (2).

Сравнение траекторий на рис. 1 и 2 показывает, что диапазон волновых чисел неустойчивых возмущений увеличился, причем неустойчивые возмущения при высоких значениях волнового числа характеризуются различной фазовой скоростью. Такие неустойчивые возмущения в отличие от возмущений с постоянной фазовой скоростью ${{с}_{1}} = 0.5$ (бароклинная неустойчивость) следует отнести к неустойчивости критического слоя, которая может возникать при равенстве фазовой скорости возмущения и скорости среднего потока [17] (см. также раздел 4.2.). Коротковолновое отсечение неустойчивости в данном случае наступает для значения числа Бургера, ${\text{Bu}} = 0.0001$, при $k \approx 1100$. Различие в фазовых скоростях неустойчивых возмущений помогает выделять тот или иной тип неустойчивости, что особенно важно при рассмотрении в задаче (8)–(10) случаев, когда параметр Bu близок к единице (см. ниже).

3.2. Инкременты роста неустойчивых возмущений для задач (8)–(10) и (11), (12).

Здесь мы будем представлять расчеты зависимости $k{{c}_{2}}$ от волнового числа $k$ для различных значений параметров ${\text{Bu}}$, ${\text{R}}$, ${\text{Pr}}$ задачи (8)–(11). Данные параметры задачи являются независимыми, однако, применительно к океану, они могут лежать в определенных диапазонах изменчивости (см. [2, 5]). Ниже будут приведены лишь некоторые результаты выполненных численных расчетов.

Для удобства представления результатов целесообразно рассматривать широкие и узкие течения (или фронты). Будем считать широкими течениями такие течения, для которых ${\text{Bu}} < 0.1$, то есть ширина течения превышает радиус Россби более чем в три раза: $L > {{10}^{{0.5}}}{{L}_{R}},$ где ${{L}_{R}} = {{NH} \mathord{\left/ {\vphantom {{NH} f}} \right. \kern-0em} f}$. К узким течениям будем относить течения, для которых выполняется неравенство: ${\text{Bu}} \geqslant 0.1$.

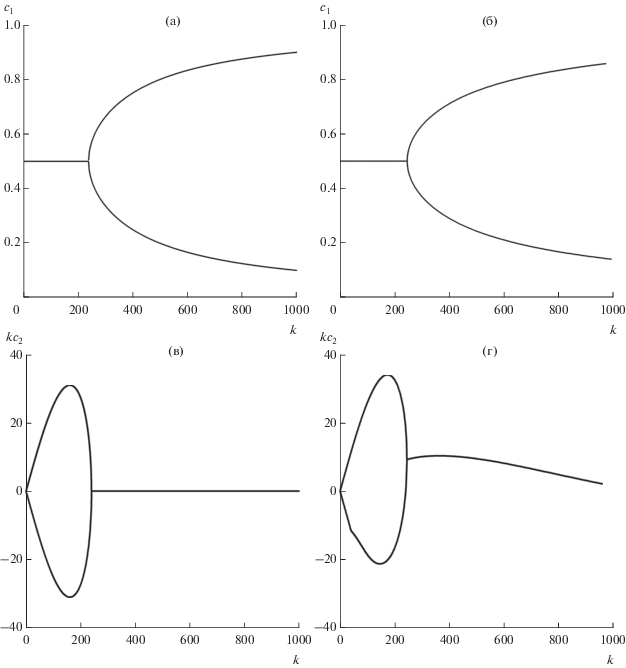
3.2.1. Широкие течения. В приближении идеальной жидкости зависимость $k{{c}_{2}}$ от $k$ для двух траекторий (то есть для отрицательных и положительных значений ${{c}_{2}})$ симметрична относительно оси $k$ (рис. 3в), причем максимальный инкремент роста $k{{c}_{2}} \approx 31$ наблюдается при $k \approx 161$ для Bu = = 0.0001. С учетом диссипации симметрия относительно оси k отсутствует (рис. 3г), а максимальный инкремент роста несколько увеличивается $k{{c}_{2}} \approx 34$ и наблюдается при $k \approx 170$.

Рис. 3.

Зависимости фазовой скорости ${{с}_{1}}$ и инкремента роста $k{{c}_{2}}$ от волнового числа $k$ при Bu = 0.0001: (а, в) идеальная задача; (б, г) диссипативная задача, Pr = 1, R = 1.

В дальнейшем мы будем представлять зависимости $k{{c}_{2}}$ от $k$ для идеальной и диссипативной задач, используя траекторию, на которой при $k \to 0$ мнимая часть СЗ положительна, то есть ${{c}_{2}} > 0$ (правые траектории на рис. 1б и 2б).

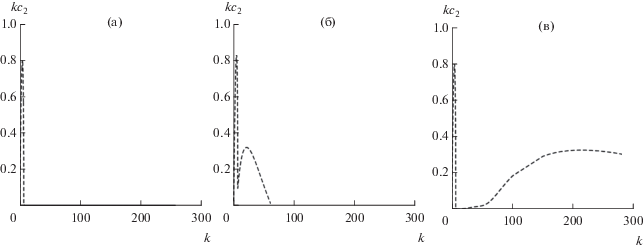
В рамках задачи (8)–(10) при Bu = 0.0001, ${\text{R}} = 1$ инкременты роста бароклинных возмущений (${{c}_{1}} = 0.5$) растут с увеличением числа Прандтля, а волновое число, соответствующее максимально растущему бароклинному возмущению, смещается в область более высоких волновых чисел (рис. 4а). Второй максимум зависимости $k{{c}_{2}}$ от $k$, соответствующий растущему возмущению из-за неустойчивости критического слоя, также увеличивается с ростом ${\text{Pr}}$, но не превышает первый максимум (рис. 4а). Ситуация меняется с увеличением параметра ${\text{R}}$. Так при ${\text{R}} = 10$ первый максимум (бароклинная неустойчивость) незначительно растет с увеличением числа Прандтля (рис. 4б). Второй максимум (неустойчивость критического слоя) более чувствителен к изменению числа Прандтля и при ${\text{Pr}} = 30$ превышает амплитуду первого максимума (рис. 4б).

Рис. 4.

Инкременты роста $k{{c}_{2}}$ (${{c}_{2}} > 0$ ) в зависимости от волнового числа $k$ для различных значений параметров R и Pr при Bu = 0.0001: а) R = 1; б) R = 10.

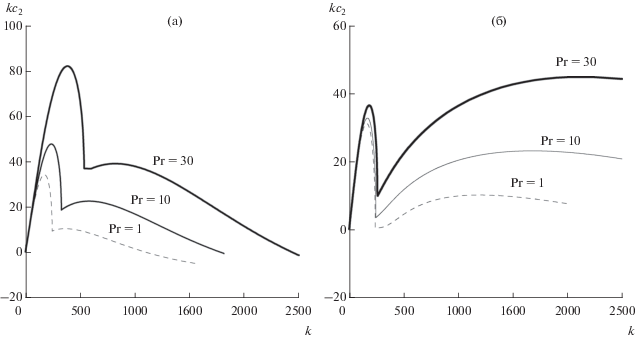
При Bu = 0.01 (умеренно широкие течения) неустойчивость критического слоя отсутствует даже при R = 10, инкремент роста максимально неустойчивого возмущения превышает соответствующий инкремент роста в случае идеальной жидкости, причем диапазон изменения волнового числа неустойчивых бароклинных возмущений (${{c}_{1}} = 0.5$) значительно возрастает с увеличением числа Прандтля (рис. 5а).

Рис. 5.

Инкременты роста $k{{c}_{2}}$ (${{c}_{2}} > 0$ ) в зависимости от волнового числа $k$ для различных значений параметров R и Pr при Bu = 0.01: а) R = 10, б) R = 100, пунктирная кривая. Сплошная кривая соответствует идеальному случаю.

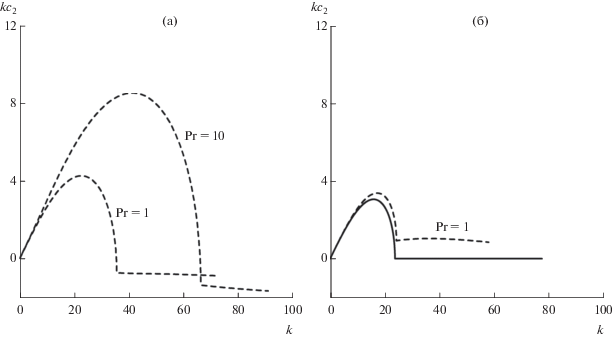
При значении R = 100 возникает неустойчивость критического слоя, а инкременты роста бароклинных возмущений близки к инкрементам роста в случае идеальной жидкости (рис. 5б).

Результаты расчетов задачи (8)–(10) показывают, что диссипация может увеличивать инкременты роста бароклинных возмущений и расширять диапазон изменчивости волнового числа растущих со временем бароклинных мод. При больших значениях параметра R (при ${\text{R}} \to \infty $), бароклинные возмущения удовлетворительно описываются в приближении идеальной жидкости.

Согласно расчетам, возникновение неустойчивости критического слоя зависит от двух параметров R и Bu: чем ближе горизонтальный масштаб течения к радиусу деформации Россби, тем больше должно быть значение параметра R для возникновения неустойчивых возмущений с фазовой скоростью ${{с}_{1}} \ne 0.5$ (см. рис. 4 и 5).

Максимально растущее возмущение в случае неустойчивости критического слоя характеризуется высоким волновым числом, то есть горизонтальным масштабом значительно меньшим радиуса деформации Россби (субмезомасштабные возмущения [5]). Инкременты роста таких возмущений могут превышать инкременты роста бароклинных возмущений при некоторых значениях параметров R и Pr.

Вертикальные структуры СФ для максимально растущих бароклинной моды и моды критического слоя существенно различны: на вертикальных профилях растущих возмущений критического слоя наблюдаются аномалии с масштабом меньше вертикального масштаба слоя (рис. 6).

Рис. 6.

Производные по z СФ задачи (8)–(10), соответствующие растущим со временем возмущениям плотности, при Bu = 0.0001, R = 1, Pr = 1: а) бароклинное максимально растущее возмущение; б) максимально растущее возмущение, обусловленное неустойчивостью критического слоя. Пунктирные кривые – Im (dF/dz), сплошные кривые – Re (dF/dz).

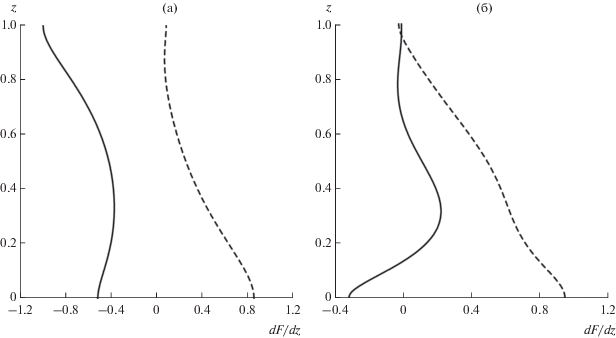
3.2.2. Узкие течения. Из условия возникновения неустойчивости в приближении идеальной жидкости следует, что течения с поперечным масштабом, равным радиусу деформации Россби (${\text{Bu}} = 1$), являются устойчивыми. Совершенно иной результат получен на основе решения задачи (8)–(10): диссипация способствует неустойчивости узких фронтов или течений, причем в зависимости от значения параметра R на узких фронтах могут возникать как неустойчивые бароклинные возмущения, так и растущие возмущения критического слоя (рис. 7). Так при Bu = 1, R = 10, (в представленных расчетах полагалось, что число Прандтля равно единице) максимально растущее возмущение следует отнести к бароклинному возмущению, ${{c}_{1}} = 0.5$ (см. рис. 7а, 7в; пунктирные кривые). Для течения с поперечным масштабом меньше радиуса деформации Россби (Bu = 1.5) максимально растущие возмущения при значениях R = 100 и R = 1000 имели фазовую скорость, отличную от 0.5 (см. рис. 7б, 7г), поэтому такие возмущения следует связывать с неустойчивостью критического слоя. При некоторых значениях параметра R на узких фронтах могут возникать два максимума на зависимости $k{{c}_{2}}\left( k \right)$ (рис. 7а, 7в; кривые 2), то есть, как и в случае широких течений, на узких фронтах могут наблюдаться одновременно бароклинные возмущения и возмущения, обусловленные неустойчивостью критического слоя. В широком диапазоне изменения параметра R в зонах узких фронтов могут развиваться практически круглые (осесимметричные) неустойчивые возмущения (с равными поперечным и продольным масштабами). Такие возмущения можно отнести к субмезомасштабным вихрям (см. раздел 4.3).

Рис. 7.

Фазовые скорости и инкременты роста в зависимости от волнового числа при Pr = 1, Bu = 1 (а, в) и Bu = 1.5 (б, г) задачи (8)–(10). Графики на фрагментах (а) и (в) построены на основе расчетов при R = 10 (кривые 1), R = 100 (кривые 2) и при R = 10000 (кривые 3). Графики на фрагментах (б) и (г) соответствуют R = 100 (кривые 1) и R = 1000 (кривые 2).

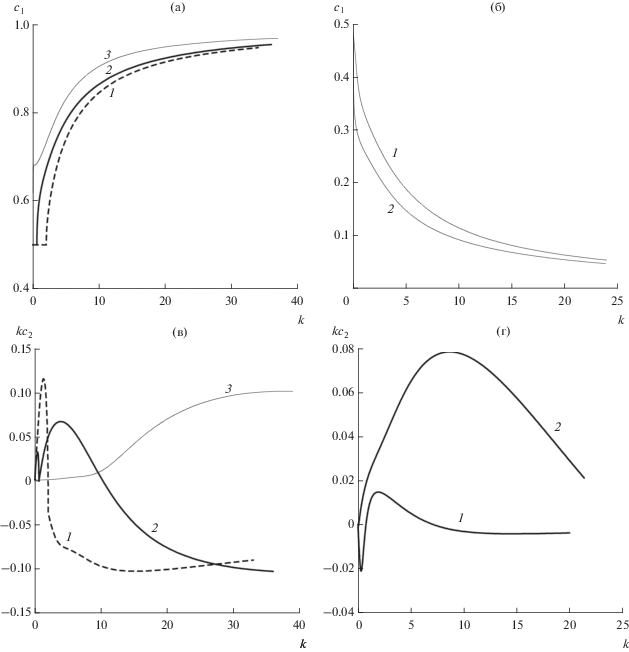
Бароклинные возмущения на умеренно узких течениях или фронтах, то есть при 0.1 ≤ Bu < < (2.399/π)2, как и на широких фронтах хорошо описываются в приближении идеальной жидкости при ${\text{R}} \to \infty $. Так, например, при Bu = 0.1 и R = = 10 000 инкремент роста и волновое число максимально растущего бароклинного возмущения диссипативной задачи равны с большой точностью соответствующим характеристикам максимально растущего возмущения в приближении идеальной жидкости (рис. 8). Однако в приближении идеальной жидкости теряются решения, которые описывают неустойчивые возмущения критического слоя при высоких значениях волнового числа (рис. 8в).

Рис. 8.

Инкременты роста в зависимости от волнового числа при Bu = 0.1: а) идеальная жидкость; б) диссипативная жидкость, R = 100; в) диссипативная жидкость, R = 10 000.

4. АНАЛИЗ ПОЛУЧЕННЫХ РЕЗУЛЬТАТОВ

Здесь мы кратко проанализируем некоторые результаты, полученные в предыдущем разделе, а также обсудим ряд вопросов, которые касаются специфики рассмотренных задач.

4.1. О влиянии диффузии плавучести и трения на рост бароклинных возмущений

Зависимости фазовых скоростей и инкрементов роста от волнового числа неустойчивых возмущений в течениях с линейным и параболическим [5] вертикальными профилями скорости имеют различия и сходства. Так, в случае течения с параболическим вертикальным профилем скорости существуют длинноволновые неустойчивые возмущения с фазовой скоростью, превышающей максимальную скорость течения [1–5]. В рамках же задачи (8)–(10) на основе расчетов в широком диапазоне параметров получено, что фазовые скорости неустойчивых возмущений лежат в диапазоне: $0 < {{с}_{1}}\left( k \right) < 1$, то есть не превышают максимальную скорость течения (см. также оценки в [3]). Сходными чертами в обоих случаях является то, что диссипация расширяет диапазон волновых чисел неустойчивых бароклинных возмущений.

Тот факт, что диффузия плавучести и трение при числе Прандтля, не равном единице, могут способствовать развитию 2D неустойчивости геострофического течения, впервые был отмечен в [6]. Однако неустойчивость Макинтайра [6] при Pr > 1, которую следует относить к бароклинной симметричной неустойчивости (см., например, [9, 28]), имеет существенные отличия от 3D бароклинной неустойчивости. Различия обуславливаются не только структурой неустойчивых возмущений, но и физическими причинами возникновения неустойчивости. Так, в случае 2D возмущений геострофического течения вертикальная стратификация, характеризующаяся частотой Вяйсяля–Брента фонового состояния, является фактором, способствующим неустойчивости, и, наоборот, является стабилизирующим фактором в случае 3D возмущений. Отметим также, что бароклинная неустойчивость, обусловленная диссипативными растущими модами задачи (8)–(10), при некоторых значениях гидрологических параметров характеризуется более высокими инкрементами роста по сравнению с инкрементами роста задачи (11), (12). Такой эффект может быть связан с тем, что вертикальные диффузия плавучести и трение способствуют переходу доступной потенциальной энергии в кинетическую энергию возмущений.

4.2. О неустойчивости критического слоя

В рамках задачи Орра–Зоммерфельда неустойчивость критического слоя возникает только для течения Пуазейля (течение с параболическим вертикальным профилем скорости) при очень больших числах Рейнольдса, в то время как течение Куэтта (течение с линейным вертикальным профилем скорости) устойчиво (см., например, [24]). Впервые доказательство неустойчивости течения Пуазейля получил Гейзенберг в 1924 г. (см., например, [23]) на основе аналитического анализа уравнения Орра–Зоммерфельда. Этот результат был подтвержден значительно позднее на основе численного решения задачи [23]. Вопрос о том, почему возникает неустойчивость течения Пуазейля при исчезающе малой вязкости, обсуждался в ряде работ (см., например, [23, 29]). Объяснение сводится к предположению, что сила трения, влияя на возмущения скорости, выстраивает фазы возмущений определенным образом, при котором происходит переход кинетической энергии среднего течения в кинетическую энергию возмущений.

Задача (8)–(10), а также задача, рассмотренная в [5], отличаются от задачи Орра–Зоммерфельда не только тем, что высокий порядок исходных уравнений обусловлен диффузией плавучести, а не трением, но и граничными условиями и безразмерными параметрами. Именно поэтому неустойчивость критического слоя возникает на широких течениях как с параболическим [5], так и с линейным профилем скорости даже при R = 1 (см. раздел 3.2.1). Разумно связывать образование неустойчивости критического слоя с влиянием диффузии плавучести на фазы возмущений. Действительно, сравнение рис. 1б и 2б показывает, что неустойчивость критического слоя развивается в области тех волновых чисел, которым соответствовали в случае идеальной жидкости нейтральные возмущения с фазовой скоростью, зависимой от волнового числа. По аналогии с задачей Орра–Зоммерфельда мы можем предположить, что диффузия плавучести выстраивает (или выравнивает) фазы возмущений таким образом, что происходит переход кинетической энергии среднего потока в кинетическую энергию возмущений.

В заключение этого подраздела отметим следующее обстоятельство. Сравнение задачи (8)–(10) с задачей Орра–Зоммерфельда позволяет дать достаточно обоснованную интерпретацию того, что растущие со временем возмущения на высоких волновых числах и с фазовой скоростью, зависимой от волнового числа, следует относить к неустойчивости критического слоя. Разумно предположить, что при числе Кибеля–Россби, равном единице, то есть, когда агеострофические эффекты влияют на динамику фронтов, неустойчивость критического слоя также может быть важным механизмом образования растущих возмущений: так, например, наклонную моду (oblique mode), полученную в модели [30], скорее всего, следует отнести к неустойчивости критического слоя. Насколько типична неустойчивость критического слоя применительно к океану, еще предстоит выяснить. Однако, по мнению авторов, неустойчивость критического слоя может явиться важным механизмом образования субмезомасштабных вихрей и интрузий, а также играть существенную роль в генерации двумерной квазигеострофической турбулентности.

4.3. О применимости модельных расчетов к описанию образования вихрей и интрузий в океане

Как правило, результаты моделирования 3D неустойчивости геострофических течений применяют к описанию образования вихрей. Однако в некоторых случаях модельные результаты целесообразно применять и к описанию образования крупных интрузий. Прежде всего, под интрузиями в океане понимают квазипериодическое по вертикали распределение температуры, солености и плотности (расслоение термо-халоклина), которое определяет изопикнический и диапикнический обмен во фронтальных зонах (см., например, [31, 32]). Интрузионное расслоение чаще всего связывают с действием двойной диффузии, если температура и соленость фонового состояния либо спадают, либо увеличиваются с глубиной [33]. Однако, например, в Евразийском бассейне Арктики в зонах бароклинных фронтов наблюдается интенсивное интрузионное расслоение при средней абсолютно устойчивой стратификации (температура падает, а соленость увеличивается с глубиной). Малое возмущение в такой ситуации может расти благодаря действию дифференциального перемешивания [12]. Альтернативная точка зрения на образование расслоения в условиях абсолютно устойчивой стратификации была высказана в [5]: неустойчивые возмущения геострофического потока с параболическим вертикальным профилем (как бароклинные, так и возмущения критического слоя) могут иметь вертикальную структуру с квазипериодической компонентой. В случае потока с линейным вертикальным профилем скорости сложная вертикальная структура СФ с аномалиями, которые имеют масштаб меньше толщины слоя, наблюдается только для возмущений критического слоя (см. рис. 6). Такие особенности профилей можно интерпретировать как образование тонкой структуры в ограниченном по вертикали слое.

К наиболее важному результату, полученному на основе расчетов задачи (8)–(10), можно отнести результат о неустойчивости течений с шириной, равной радиусу деформации Россби (Bu = 1) или меньше этого масштаба (Bu = 1.5; см. раздел 3.2.2). В зонах узких фронтов могут развиваться практически круглые неустойчивые возмущения. Когда Bu > 1, такие возмущения описывают субмезомасштабные вихри, которые, как полагают, возникают вследствие неустойчивости течения с горизонтальным сдвигом скорости [34]. Таким образом, решения задачи (8)–(10) позволяют расширить точку зрения на механизмы образования субмезомасштабных структур.

В заключение этого раздела оценим время образования максимально растущих возмущений в зонах течений различной ширины. Учитывая, что наша модель корректна при малых числах Экмана, разумно считать, что вертикальный коэффициент диффузии плавучести при Pr = 1 не должен значительно превышать значения 0.01 ${{{\text{м}}}^{2}}\,{{{\text{с}}}^{{ - 1}}}$ для толщины слоя порядка 100 м. В термоклине, в зонах перемежающейся турбулентности, коэффициенты диффузии плавучести могут быть на порядок или несколько порядков меньше (подробнее см. [5]). Таким образом, параметр R в зависимости от масштабов течения, скорости основного потока и коэффициента диффузии плавучести может лежать в широком диапазоне изменчивости. Для широкого течения, Bu = 0.0001(${{N}_{0}} = {{10}^{{ - 3}}}$ c–1, $f = {{10}^{{ - 4}}}$ c–1, ${{Н}_{0}}$ = 100 м, L = 100 км), и R = 1 ($K = {{10}^{{ - 3}}}\,\,{{{\text{м}}}^{2}}\,{{{\text{с}}}^{{ - 1}}}$), Pr = 1, получим, что ${1 \mathord{\left/ {\vphantom {1 T}} \right. \kern-0em} T}\sim {{10}^{{ - 6}}}$ c–1 (T – время увеличения амплитуды начального бароклинного возмущения в e раз) при максимальной скорости основного потока Ũ = 1 см c–1. С увеличением скорости потока время роста неустойчивых возмущений уменьшается: при Ũ = = 10 см c–1 и тех же значений Bu, R, Pr имеем ${1 \mathord{\left/ {\vphantom {1 T}} \right. \kern-0em} T}\sim {{10}^{{ - 5}}}$ c–1. Для узких фронтов при Bu = 1, R = = 100, Pr = 1, ${{Н}_{0}} = 100\,\,{\text{м}}$ и для типичных значений N0, f получим приблизительно такие же оценки времени увеличения амплитуды начального возмущения, обусловленного неустойчивостью критического слоя. Данные оценки времени роста неустойчивых возмущений существенно меньше оценок времени роста в задаче [5], в которой необходимо было учитывать строгое ограничение на величину вертикального сдвига скорости основного потока кроме ограничения, связанного с квазигеострофическим приближением: 1/T $ \gg $ f.

5. ОСНОВНЫЕ ВЫВОДЫ

Рассмотрена спектральная задача типа Орра-Зоммерфельда для описания неустойчивых возмущений океанских геострофических течений с линейным вертикальным профилем скорости с учетом вертикальной диффузии плавучести и трения. Представлены расчеты собственных значений, инкрементов роста неустойчивых мод, собственных функций максимально растущих возмущений в широком диапазоне изменения параметров задачи. Проведено сравнение с аналогичной задачей для идеальной жидкости. Получено, что: а) диссипация расширяет диапазон волновых чисел неустойчивых возмущений; б) диссипация может увеличивать инкременты роста бароклинных возмущений; в) инкременты роста возмущений, обусловленных неустойчивостью критического слоя, могут превышать инкременты роста бароклинных возмущений; г) течения с шириной, равной радиусу Россби и меньше этого масштаба, могут быть неустойчивыми; в зонах узких течений развиваются практически круглые (осесимметричные) неустойчивые возмущения (субмезомасштабные вихри); д) бароклинные неустойчивые возмущения в области широких течений удовлетворительно описываются в приближении идеальной жидкости при больших значениях модифицированных чисел Пекле и Рейнольдса.

Работа выполнена в рамках государственного задания Института океанологии им. П.П. Ширшова РАН (тема № 0149-2019-0013)

Авторы признательны анонимному рецензенту за полезные замечания.

Список литературы

  1. Кузьмина Н.П. Об одной гипотезе образования крупномасштабных интрузий в Арктическом бассейне // Фундам. прикл. гидрофиз. 2016. Т. 9. № 2. С. 15–26.

  2. Kuzmina N.P. Generation of large-scale intrusions at baroclinic fronts: an analytical consideration with a reference to the Arctic ocean // Ocean Science. 2016. V. 12. P. 1269–1277. https://doi.org/10.5194/os-12-1269-2016

  3. Кузьмина Н.П., Скороходов С.Л., Журбас Н.В., Лыжков Д.А. О неустойчивости геострофического течения с линейным вертикальным сдвигом скорости на масштабах интрузионного расслоения // Изв. РАН. Физика атмосферы и океана. 2018. Т. 54. № 1. С. 54–63.

  4. Журбас Н.В. О спектрах собственных значений в модельной задаче описания образования крупномасштабных интрузий в Арктическом бассейне (на англ. яз.) // Фундам. прикл. гидрофиз. 2018. Т. 11. № 1. С. 40–45.

  5. Кузьмина Н.П., Скороходов С.Л., Журбас Н.В., Лыжков Д.А. Описание возмущений океанских геострофических течений с линейным вертикальным сдвигом скорости с учетом трения и диффузии плавучести // Изв. РАН. Физика атмосферы и океана. 2019. Т. 55. № 2. С. 73–85.

  6. McIntyre M.E. Diffusive destabilization of the baroclinic circular vortex // Geophys. Fluid Dyn. 1970. V. 1(1–2). P. 19–57.

  7. Кузьмина Н.П., Родионов В.Б. О влиянии бароклинности на образование термохалинных интрузий в океанских фронтальных зонах // Изв. АН СССР. Физика атмосферы и океана. 1992. Т. 28. № 10–11. С. 1077–1086.

  8. May B.D., Kelley D.E. Effect of baroclinicity on double-diffusive interleaving // J. Phys. Oceanogr. 1997. V. 27. P. 1997–2008.

  9. Kuzmina N.P., Zhurbas V.M. Effects of Double Diffusion and Turbulence on Interleaving at Baroclinic Oceanic Fronts // J. Phys. Oceanogr. 2000. V. 30. P. 3025–3038.

  10. Kuzmina N.P. On the parameterization of interleaving and turbulent mixing using CTD data from the Azores Frontal Zone // J. Mar. Syst. 2000. V. 23. P. 285–302.

  11. Merryfield W.J. Intrusions in Double-Diffusively Stable Arctic Waters: Evidence for Differential mixing? // J. Phys. Oceanogr. 2002. V. 32. P. 1452–1439.

  12. Кузьмина Н.П., Журбас Н.В., Емельянов М.В., Пыжевич М.Л. Применение моделей интерливинга для описания интрузионного расслоения на фронтах глубинной полярной воды Евразийского бассейна (Арктика) // Океанология. 2014. Т. 54. С. 594–604.

  13. Kuzmina N., Rudels B., Zhurbas V., Stipa T. On the structure and dynamical features of intrusive layering in the Eurasian Basin in the Arctic Ocean // J. Geophys. Res. 2011. V. 116, C00D11. https://doi.org/10.1029/2010JC006920

  14. Eady E.T. Long waves and cyclone waves// Tellus. 1949. V. 1(3). P. 33–52.

  15. Charney J.G. The Dynamics of Long Waves in a Baroclinic Westerly Current // J. Meteorology. 1947. V. 4. № 5. P. 135–162.

  16. Green J.S.A. A problem in baroclinic stability // Quat. J. Royal. Meteorol. Soc. 1960. V. 86. № 368. P. 237–251.

  17. Miles J.W. Effect of Diffusion on Baroclinic Instability of the Zonal Wind // J. Atmos. Sci. 1965. V. 22. P. 146–151.

  18. Cushman-Roisin B. Introduction to the Geophysical Fluid Dynamics. Englewood Cliffs, NJ: Prentice Hall, 1994. 320 p.

  19. Eady E.T. Long waves and cyclone waves // Tellus. 1949. V. 1(3). P. 33–52.

  20. Океанология. Физика океана. Том 2. / Под ред. Каменковича В.М., Монина А.С.: “Наука”, 1978. 456 с.

  21. Farrell B.F. The initial growth of disturbances in a baroclinic flow // J. Atmos. Sci. 1982. V. 39. P. 1663–1686.

  22. Калашник М.В. О резонансном и квазирезонансном возбуждении бароклинных волн в модели Иди // Изв. РАН. Физика атмосферы и океана. 2015. Т. 51. № 6. С. 648–657.

  23. Lin C.C. The Theory of Hydrodynamic Stability. Cambridge University Press, 1955. 155 p.

  24. Скороходов С.Л. Численный анализ спектра задачи Орра–Зоммерфельда // ЖВМ и МФ. 2007. Т. 47. № 10. С. 1672–1691.

  25. Скороходов С.Л. Точки ветвления собственных значений оператора Орра–Зоммерфельда // ДАН. 2007. Т. 416. № 5. С. 600–605.

  26. Скороходов С.Л., Кузьмина Н.П. Аналитико-численный метод решения задачи типа Орра–Зоммерфельда для анализа неустойчивости течений в океане // ЖВМ и МФ. 2018. Т. 58. № 6. С. 976–992.

  27. Скороходов С.Л., Кузьмина Н.П., Спектральный анализ модельных течений типа Куэтта применительно к океану// ЖВМ и МФ. 2019. Т. 59. № 5. С. 867–888.

  28. Калашник М.В. К теории симметричной и несимметричной устойчивости зональных геострофических течений // Изв. РАН. Физика атмосферы и океана. 2001. Т. 37. № 3. С. 418–421.

  29. Stern M.E. Ocean circulation physics. Academic press, 1975. 246 p.

  30. Smyth W.D. Instabilities of a Baroclinic, Double Diffusive Frontal Zone // J. Phys. Oceanogr. 2008. V. 38. P. 840–861.

  31. Федоров К.Н. Физическая природа и структура океанических фронтов. Ленинград: Гидрометеоиздат, 1983. 296 с.

  32. Журбас В.М., Кузьмина Н.П., Озмидов Р.В., Голенко Н.Н., Пака В.Т. О проявлении процесса субдукции в термохалинных полях вертикальной тонкой структуры и горизонтальной мезоструктуры во фронтальной зоне Азорского течения // Океанология. 1993. Т.33. № 3. С. 321–326.

  33. Stern M.E. Lateral mixing of water masses // Deep Sea Res. 1967. Part A. V. 14. P. 747–753.

  34. Munk W., Armi L. Spirals on the sea: A manifestation of upper-ocean stirring, In: From Stirring to Mixing in a Stratified Ocean // Proceedings of the 12th 'Aha Huliko’a Hawaiian Winter Workshop, 2001. P. 81–86.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Физика атмосферы и океана

Архивы выпусков Информация о журнале Отправить рукопись в журнал