Известия РАН. Физика атмосферы и океана, 2021, T. 57, № 2, стр. 156-162
К учету верхних слоев атмосферы при моделировании орографических возмущений в тропосфере
В. Н. Кожевников *
МГУ им. М.В. Ломоносова
119991 Москва, Ленинские горы, 1, стр. 2, Россия
* E-mail: kozhvn@mail.ru
Поступила в редакцию 24.10.2020
После доработки 27.11.2020
Принята к публикации 09.12.2020
Аннотация
Рассматривается проблема верхних граничных условий при моделировании явления обтекания гор движущейся атмосферой. Используется двумерная стационарная нелинейная аналитическая модель. В трехслойном натекающем потоке скорость не зависит от высоты, а вертикальные градиенты температуры изменяются послойно. Нижний слой представляет тропосферу, средний – нижнюю стратосферу, верхний – всю верхнюю неограниченную по высоте атмосферу. Исследуется, как изменения устойчивости среднего слоя влияют на отражение волновой энергии от верхних слоев и в итоге на возмущения в тропосфере. Подтверждается, что отражение энергии особенно возрастает, когда градиент температуры в среднем слое приближается к сухоадиабатическому, поскольку при этом исчезает упругость среды по отношению к вертикальным смещениям частиц воздуха. Показывается, что даже в этом случае отражение энергии не полное и поэтому резонанс по Лонгу в атмосфере невозможен.
При моделировании обтекания гор главное внимание обычно обращают на постановку нижнего граничного условия, т.е. правильный учет взаимодействия движущейся атмосферы с неровностями земли. При этом недостаточное внимание уделяется тому, что на распространение возникающих волн оказывают влияние существующие в атмосфере неоднородности изменения плотности по вертикали. В рамках среднего масштаба главными среди них являются неоднородности, связанные с глобальным разделением атмосферы на слои по величине вертикального градиента температуры, т.е. с разделением ее на тропосферу, стратосферу и вышележащие слои. Будем данную проблему рассматривать в рамках нелинейного моделирования, т.е. при учете немалости возмущений скорости. Крайние варианты учета этих неоднородностей реализуются в двух моделях: открытой, в которой предполагается, что энергия возмущений на больших высотах свободно распространяется вверх, и закрытой, в которой атмосфера сверху ограничена поверхностью, полностью отражающей энергию вниз. К примеру, в наших исследованиях [1, 2] используется открытая аналитическая модель. Первым закрытую аналитическую нелинейную однослойную модель обтекания использовал Лонг [3]. В ряде моделей влияние верхних слоев учитывается постановкой некоторого искусственного условия на фиксированном достаточно далеком уровне высоты. Приближенность такой постановки не всегда надежно обосновывается и проверяется при проведении расчетов.
В работе [3] не только теоретически, но и экспериментально показано, что возмущения в канале являются “захваченными” и не затухают вниз по потоку за неровностями нижней границы. Определяется это тем, что волновая энергия возмущений полностью отражается от верхней границы канала. Основные свойства возмущений при этом определяются внутренним числом Фруда в натекающем потоке, которое дается соотношениями:
(1)
${{F}_{i}} = {U \mathord{\left/ {\vphantom {U {\left( {NH} \right)}}} \right. \kern-0em} {\left( {NH} \right)}},\,\,\,\,{{N}^{2}} = \frac{g}{\Theta }\frac{{d\Theta }}{{dz}} = g\frac{{{{\gamma }_{a}} - \gamma }}{{{{T}_{1}}}},$(2)
${{F}_{i}} = \frac{1}{{n\pi }} - \frac{1}{{\left( {n + 1} \right)\pi }},\,\,\,\,n = {\text{1}},{\text{2}},{\text{3}}, \ldots $В любом таком диапазоне при увеличении высоты горы возмущения растут и при превышении некоторого значения ${{h}_{0}}$(${{F}_{i}}$) над горами появляются роторы или даже области “опрокидывания траекторий” (в ряде публикаций их стали называть областями разрыва волнового поля). При переходе из диапазона с одним значением числа $n$ в диапазон со значением ($n$ + 1) значения ${{h}_{0}}$ быстро уменьшаются, так что уровень возмущений остается высоким при меньших значениях высоты горы. При фиксированном значении высоты $h$ зависимость от ${{F}_{i}}$ в любом диапазоне имеет один максимум. Если учесть, что число Фруда пропорционально скорости потока $U,$ то получается, что внутри диапазона (2) возмущения могут как нарастать при увеличении скорости потока, так и ослабевать. Наличие такой двоякой зависимости может служить признаком того, что верхние слои полностью отражают волновую энергию вниз.
При приближении величины ${{F}_{i}}$ к граничным значениям 1/($n$π) решение задачи перестает существовать при любой высоте горы $h$ и одновременно начинают выполняться соотношения
(3)
$H = n\left( {{{{{\lambda }_{c}}} \mathord{\left/ {\vphantom {{{{\lambda }_{c}}} 2}} \right. \kern-0em} 2}} \right),\,\,\,\,{{\lambda }_{c}} = 2\pi \frac{U}{N},$Ценные результаты по рассматриваемой проблеме получены в работе Дюрана [6]. Здесь исследовалось обтекание горы двухслойным потоком с помощью открытой численной модели. Как и в [1, 2], рассматривался вариант, когда в натекающем потоке скорость не меняется с высотой, в слоях постоянны частоты Брента–Вяйсяля, и задача сводится к решению уравнения Гельмгольца для возмущений функции тока. Нижний слой имел толщину в несколько км, верхний был неограниченным по высоте; слои резко различались по значениям частоты $N.$ Было установлено, что в нижнем слое амплитуды возмущений резко возрастали, когда частота в нем ${{N}_{1}}$ в два раза превышала частоту ${{N}_{2}}$ в верхнем слое. В двух рассмотренных при этом примерах амплитуды волн особенно возрастали, когда толщина нижнего слоя увеличивалась так, что стало удовлетворяться условие резонанса по Лонгу (3). Автор сделал вывод, что усиление возмущений определяется очень сильным отражением энергии от верхнего слоя, но не исследовал, почему именно верхний слой столь сильно отражает энергию. Автор кроме условия (3) привлекает к анализу установленного факта результаты исследований проблемы в рамках линейной теории [7], т.е. теории, опирающейся на предположение о малости возмущений поля скорости. Эта теория приводила к соотношению качественно подобному (3), но количественно другому. Нет сомнений, что именно условию (3) следует оказывать предпочтение, поскольку оно получено без предположения о малости возмущений компонент скорости. При выполнении условия (3) решение задачи в [6] не теряло смысла, т.е. резонанса не возникало, а имело место только резкое усиление волн. Это свидетельствовало о том, что отражение от верхнего слоя не было полным.
Результаты [6] не в полной мере поняты. В частности, в [8] предпринимались попытки искать причину усиления возмущений при обтекании гор в наличии двухслойной структуры подобной [6] – вплоть до требования инверсионности температуры в слоях заметной вертикальной мощности в тропосфере. Во-первых, такие слои в атмосфере обычно имеют толщину не более нескольких сотен метров, а во-вторых, во многих работах, в частности в [1, 2, 5], показано, что весьма серьезные возмущения при обтекании гор имеют место и при отсутствии таких слоев и при обычных значениях градиента температуры (порядка 6 градусов на км).
В настоящей работе при исследовании поставленной проблемы будет использоваться аналитическая, стационарная, двумерная, открытая модель [1, 2]. В модели натекающий поток атмосферы предполагается трехслойным, скорость в слоях постоянной и равной $U,$ градиенты температуры послойно постоянными и равными ${{\gamma }_{j}}.$ Нижний слой в модели имеет толщину 10 км и представляет тропосферу, средний задается толщиной в 2.5 км, а верхний – неограниченным по вертикали. Постановка задачи отличается от известной модели Лонга в том, что в ней гидростатическая устойчивость среды учитывается не через градиент плотности, а через разность градиентов температуры ${{\gamma }_{a}} - \gamma .$ Решение задачи для произвольной формы горы строится при использовании фурье-преобразований и приводит к соответствующим интегральным соотношениям. Форму горы удается учитывать с точностью до десятков метров по высоте. Динамика и кинематика взаимодействия потоков в слоях учитывается приближенно за счет предположения о близости поверхностей раздела к горизонталям. Свойства невозмущенного натекающего потока определяются заданием скорости, градиентов температуры и температуры на земле. Всего было рассмотрено 5 вариантов задания этих параметров. Результаты иллюстрируются рисунками и табл. 1.
Таблица 1
| Вариант | ${{\gamma }_{2}}$ | ${{\lambda }_{c}}$ | ${{z}_{{\min }}}$ | ${{z}_{{\max }}}$ | Dz |
|---|---|---|---|---|---|
| 1 | 0 | 5.20 | 3.5 | 5.3 | 1.8 |
| 2 | 7.5 | 5.20 | 2.6 | 5.1 | 2.5 |
| 3 | 8 | 5.20 | 2.25 | 5.5 | 3.25 |
| 4 | 7.5 | 5.00 | 2.7 | 5.07 | 2.35 |
| 5 | –1 | 5.20 | 2.79 | 4.67 | 1.88 |
На рис. 1 представлены результаты расчетов траекторий движения частиц воздуха над неровностями границы, представляющими двумерные особенности рельефа гор Крыма. Для определенности траектории будем отождествлять по значениям их высот в натекающем потоке ${{z}_{0}}$ в км. Частицы воздуха вдоль траекторий двигаются слева направо. Задаваемая форма рельефа на данном и остальных рисунках практически не отличима от траектории с ${{z}_{0}}$= 0. Рельеф Крыма для исследования был выбран, с одной стороны, потому что именно для этого района нами накоплен солидный банк результатов наблюдений и расчетов (см. [1 (работы в списке публикаций № 12, 28–30, 34, 41), 2]), а с другой, потому что данный рельеф за счет наличия высокого и крутого подветренного склона обладает особенной силой возмущения атмосферы (см. [1, 9]). Поверхности раздела слоев на рисунке показываются двумя линиями с высотами, различающимися в натекающем потоке на 0.1 км. Исходные значения параметров расчета даются над рисунком, значения высот ${{z}_{0}}$ – под ним. Здесь и везде далее для краткости будем подразумевать, что скорость дается в м/c, $\gamma $ – в град/км, ${{\lambda }_{c}}$ – в км и $N$ – в 1/c. В данном варианте в тропосфере градиент $\gamma $ = +6, в среднем слое равен 0 и в верхнем – +3. Соответствующие значения частот $N$ при этом равнялись в тропосфере 0.0121 и в среднем слое – 0.0205. Этот вариант можно считать иллюстрацией характера обтекания для типичного распределения частот $N$ между тропосферой и нижней стратосферой, т.е. когда значения частот возрастают примерно на 70%. Верхний слой в модели представляет верхнюю атмосферу, очевидно, приближенно, но для рассматриваемой проблемы это вполне допустимо.
Рис. 1.
Траектории движения частиц воздуха при обтекании гор для варианта 1 (${{\gamma }_{2}}$ = 0).
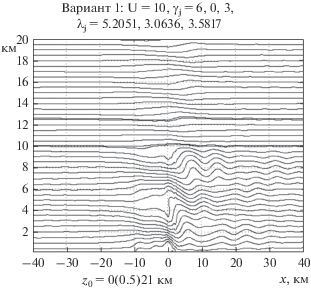
Возмущения в тропосфере над горами, как и в предыдущих аналогичных расчетах [1, 2], весьма интенсивны. Об этом свидетельствует появление развитой роторной зоны в средней тропосфере, а так же появление нескольких областей серьезного сгущения траекторий, где в разы возрастает скорость ветра. Особенности формы рельефа сказываются в форме смещений траекторий непосредственно над горами и в ближней подветренной зоне. Ниже по потоку смещения частиц становятся почти гармоническими. Усиление возмущений определяется как высотой, так и крутизной гор, и для этого, как видим, не требуется, чтобы устойчивость воздуха была заметно больше обычной или имелись заметные по мощности слои с повышенной устойчивостью. Следует заметить, что поверхности раздела почти горизонтальны, и, значит, решение надежно учитывает условия не только на нижней, но и на верхних границах. Возмущения становятся почти не заметными перед горами на расстояниях более 10 км. Ниже по потоку возмущения остаются заметными на существенно больших удалениях от гребня гор, причем быстрее всего по потоку они ослабевают у земли.
Следующие два варианта расчетов были проведены при резком уменьшении частоты Брента–Вяйсяля в среднем слое с целью лучшего осмысления важных результатов [6]. Полученные траектории движения частиц представлены на рис. 2 и 3. Здесь по сравнению с предыдущим примером изменяется только один параметр натекающего потока, а именно градиент ${{\gamma }_{2}}.$ Он задается соответственно равным 7.5 и 8, и это приводит к последовательному уменьшению значений ${{N}_{2}}$ по сравнению с нижним слоем до уровней 0.0102 и 0.0091. Это уменьшение несколько меньше, чем в [6], но вполне достаточно для рассмотрения поставленной проблемы. На рис. 4 (вариант 4) иллюстрируется результат расчета, выполненного с целью выяснения того, как изменяются возмущения, когда мы приближаемся к выполнению условия резонанса (3). На рис. 5 (вариант 5) дан результат расчета для случая, когда градиент температуры в среднем слое не увеличивается, а уменьшается. Это позволило проанализировать, как влияет на возмущения в тропосфере не ослабление, а более типичное в природе усиление устойчивости среднего слоя. На всех рисунках в аналогичной форме представлены траектории движения. Они позволяют судить о пространственных изменениях в зависимости от параметров натекающего потока таких характеристик возмущений, как амплитуды волн, особенности роторных циркуляций, возмущений поля скоростей, температуры и т.д. (см. [1, 2, 5]). Однако в данной работе имеет смысл остановиться исключительно на вопросах, связанных с проблемой отражения энергии от верхних слоев, т.е. сосредоточиться на следующих результатах.
Рис. 2.
Траектории движения частиц воздуха при обтекании гор для варианта 2 (${{\gamma }_{2}}$ = 7.5).
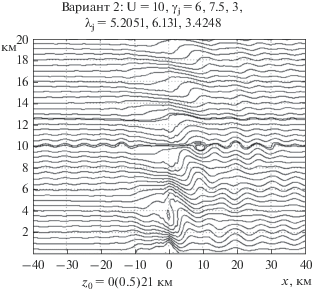
Рис. 3.
Траектории движения частиц воздуха при обтекании гор для варианта 3 (${{\gamma }_{2}}$ = 8).
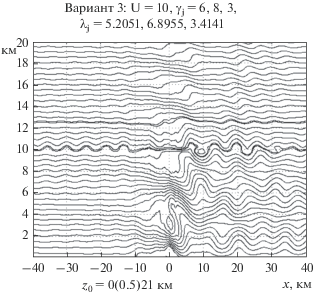
Рис. 4.
Траектории движения частиц воздуха при обтекании гор для варианта 4 (${{\gamma }_{1}}$ = 5.65).
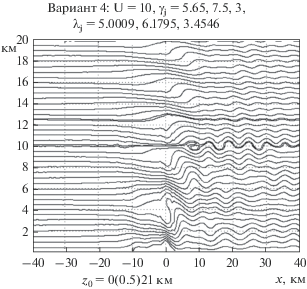
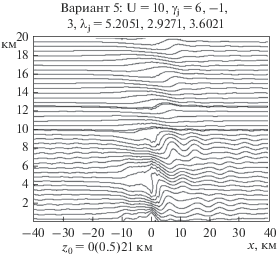
Рис. 5.
Траектории движения частиц воздуха при обтекании гор для варианта 5 (${{\gamma }_{2}}$ = –1.0).
1. Сравнение траекторий на рис. 1 и 2–4 подтверждает вывод [6] о том, что возмущения в нижнем слое должны сильно возрастать, когда в вышележащем слое значения частоты $N$ заметно уменьшаются по сравнению со значением в нижнем слое. Если в первом варианте роторная зона еще не включала полностью замкнутых вихрей, то теперь они появляются в развитом виде. Степень возрастания амплитуд возмущений характеризуют также данные таблицы. Здесь представлены характеристики экстремальных вертикальных смещений частиц воздуха, двигающихся вдоль траектории с ${{z}_{0}}$ = 4. Данные первых 3 строк позволяют рассмотреть прямую зависимость усиления возмущений при увеличении значений ${{\gamma }_{2}},$ при этом: ${{\lambda }_{c}}$ – масштаб Лира в нижнем слое, ${{z}_{{\min }}}$ – минимальный уровень опускания частиц воздуха, ${{z}_{{\max }}}$ – максимальный уровень подъема и Dz – общий размах их смещений в км. Как видим, Dz может возрастать почти в 2 раза. Усиление возмущений также проявляется в увеличении плотности степени сгущения траекторий – в особенности у границ роторов. Это позволяет оценивать величину и пространственное распределение возмущений обеих компонент скорости ветра.
2. Резкое возрастание возмущений в вариантах 2 и 3 по сравнению с вариантом 1 произошло при изменении только градиента температуры в среднем слое. Поэтому, очевидно, что это определяется именно увеличением отражения волновой энергии от среднего слоя.
3. В вариантах 2, 3 поверхности раздела достаточно возмущены, чтобы поставить под сомнение качество удовлетворения верхних граничных условий при решении поставленной задачи. В варианте 3 (${{\gamma }_{2}}$ = 8) величина ${{N}_{2}}$ в среднем слое минимальна и равна 0.75 значения ${{N}_{1}},$ а не 0.5, как было в [6]. Приближения к коэффициенту 0.5 можно было бы достичь двумя путями: либо уменьшая в нижнем слое ${{\gamma }_{1}},$ либо приближая значения градиента температуры в среднем слое к сухоадиабатическому градиенту ${{\gamma }_{a}}.$ В обоих случаях возмущения были бы еще значительнее, чем в вариантах 2, 3, причем не только в нижнем слое, но и на его верхней границе. Одновременно в таком случае нижний слой не мог бы представлять типичную тропосферу, а наличие слоя со столь малой устойчивостью на уровнях стратосферы было бы еще менее реальным. В работе [6] рассматриваемая проблема исследовалась чисто в теоретическом аспекте, в настоящем анализе выбор значений градиентов был сделан с целью, чтобы, с одной стороны, избежать слишком больших возмущений на нижней поверхности раздела, а с другой – приблизиться к учету реальных характеристик атмосферы. Важно также подчеркнуть, что расчеты были проведены для нескольких вариантов уменьшения частоты в среднем слое, и все они дали одинаковый результат. Значит, тенденция усиления возмущений и ее пропорциональность уменьшению частоты ${{N}_{2}}$ установлена надежно, а факт некоторого возмущения поверхности раздела, по-видимому, не может изменить сделанного вывода.
4. Представленные на рис. 1–3 результаты показывают, что при серьезном уменьшении частоты ${{N}_{2}}$, в среднем слое подветренные волны почти перестают затухать вниз по потоку за горами. Если на рис. 1 волны исчезали на удалениях около 25 км, то теперь они остаются заметными до 40 км. Подобное поведение возмущений ранее многие не только отмечали, но и объясняли усилением отражения волновой энергии от верхних слоев (см., например, [1, 3, 5]). Данное свойство дополнительно свидетельствует, что при уменьшении частоты $N$ в среднем слое мы приближаемся к варианту течения в канале с полным отражением волновой энергии от верхней границы. Для лучшего понимания сказанного, заметим следующее. Уменьшение частоты $N$ в среднем слое связано не просто с увеличением градиента ${{\gamma }_{2}}$ в нем, а с приближением его значений к ${{\gamma }_{a}}.$ Это означает, что мы имеем дело с уменьшением гидростатической устойчивости воздуха в среднем слое или, иначе говоря, с приближением этого слоя к состоянию, которое называют состоянием “безразличного равновесия”. Полезнее в нашем случае такой переход трактовать переходом к меньшей волновой упругости. При этом данная упругость связана не со сжимаемостью воздуха, а с появлением силы плавучести у частиц воздуха при быстрых (почти адиабатических) смещениях по высоте. Именно эта упругость является необходимым условием для появления внутренних гравитационных волн. Подобный анализ проводился нами ранее в [10], где было обращено внимание на то, что при $\gamma $ > ${{\gamma }_{a}}$ у уравнения Гельмгольца существуют только затухающие решения, а при $\gamma $ = ${{\gamma }_{a}}$ решение имеет не волновой, а потенциальный характер. Отсюда становится понятным, почему именно заметное уменьшение частоты $N$ в среднем слое препятствует распространению внутренних гравитационных волн выше. Важно, что это свойство не зависит от других параметров задачи, а уровень отражения энергии зависит от разности ${{\gamma }_{a}} - \gamma $ и, видимо, от толщины среднего слоя.
5. Амплитуды волн в верхних слоях в первом варианте заметно меньше, чем в остальных, хотя отражение волновой энергии вниз в последних случаях, как было выяснено, напротив, больше. Противоречия в этом нет, поскольку, как отмечалось и ранее в [1], величина этих амплитуд в первую очередь зависит от высоты волн на поверхностях раздела. Последние же определяются тем, с какими фазами приходят к этим уровням волны снизу.
6. Условие резонанса (3) было получено в закрытой модели с жесткой горизонтальной границей. В открытых моделях поверхности раздела не жесткие и роль условия (3) требует осмысления. Величину $n$ в (3) можно изменять путем изменения величины масштаба Лира в тропосфере. Она одинакова в первых трех вариантах и равна 5.20. При проведении расчетов по варианту 4 параметры задачи были изменены по сравнению с вариантом 2 только за счет изменения $\gamma $ в тропосфере, а именно прежнее значение ${{\gamma }_{1}}$ = 6 было уменьшено до 5.65. При этом значение масштаба Лира в тропосфере стало равным 5.0009. В итоге, если в варианте 2 (а так же 1, 3) в соотношении (3) вместо целого $n$ фигурировало число 3.84, то теперь оно стало равным 4.0003, и условие резонанса оказалось практически выполненным. Характеристики верхних слоев не изменялись и, значит, следовало ожидать, что отражение от них оставалось неизменным. Однако результаты, представленные на рис. 4, не показали даже признаков приближения к резонансу. Напротив, вертикальные смещения частиц воздуха, двигающихся вдоль траектории ${{z}_{0}}$ = 4, как показывает таблица, даже немного уменьшились. Тем самым доказано, что резонанс невозможен даже при столь сильном отражении волновой энергии, какой имеет место при наличии вверху слоя с очень малой устойчивостью и толщиной 2.5 км. Этот результат получен при использовании аналитической модели [1, 2], приближенно учитывающей условие на нижней границе слабоустойчивого слоя, но тот же результат получен и по численной модели [6], учитывающей указанное условие точно.
7. Проведенные по вариантам 1–4 расчеты позволили провести оценку того, как выглядит отражение энергии от среднего слоя, когда градиент ${{\gamma }_{2}}$ в нем принимает значение 0 или увеличивается до значений 7.5 и 8. При этом показано, что отражение возрастает, когда ${{\gamma }_{2}}$ > 6 и приближается к ${{\gamma }_{a}}.$ Однако эта закономерность имеет скорее теоретический нежели практический интерес, поскольку достаточно мощные слои с малой устойчивостью на заметных высотах в атмосфере не встречаются. Практический интерес представляют изменения уровня отражения при изменениях значения ${{\gamma }_{2}}$ в другую сторону. Чтобы оценить, что происходит с отражением при меньших значениях градиента температуры, был рассмотрен вариант 5 задания параметров натекающего потока, когда ${{\gamma }_{2}}$ в среднем слое был задан отрицательным и равным –1. Полученная картина движений показана на рис. 5. Сравнивая ее с данными рис. 1, нетрудно видеть, что возмущения почти не изменились, точнее, несколько возросли. Тот же вывод мы получим, если сравним данные, представленные на первой и последней строках таблицы выше. Важнее отметить, что возмущения остаются по-прежнему существенно меньшими, чем при больших ${{\gamma }_{2}}.$ Следовательно, отражение от среднего слоя в реальной атмосфере заметно отличается от полного.
Проведенные расчеты показали необходимость учитывать следующее.
1. Динамика взаимодействия возмущений в тропосфере с возмущениями в вышележащих слоях не менее важна, чем динамика взаимодействия с поверхностью земли.
2. Отражение волновой энергии от верхних слоев атмосферы, по-видимому, близко к максимуму, когда гидростатическая устойчивость в них близка к безразличной.
3. Отражение волновой энергии от реальной стратосферы меньше максимума.
4. Максимальное отражение всегда меньше полного и, значит, резонанс по Лонгу в атмосфере исключен.
Список литературы
Кожевников В.Н. Возмущения атмосферы при обтекании гор. М.: “Научный Мир”, 1999. 160 с.
Кожевников В.Н. Моделирование атмосферных возмущений над горами Крыма // Изв. РАН. Физика атмосферы и океана. 2019. Т. 55. № 4. С. 49–57.
Long R.R. Some aspects of the flow of stratified fluids. III. Continuous density gradients // Tellus. 1955. V. 7. № 3.
Lyra G. Theorie der stationaren Leewellenstromung in freien Atmosphare // Z. Angew. Math. und Mech. 1943. V. 23. № 1. P. 1–28.
Кожевников В.Н. Обзор современного состояния теории мезомасштабных орографических неоднородностей поля вертикальных токов // Тр. ЦАО. 1970. Вып. 98. С. 3–40.
Durran D.R. Another look at downslope windstorms. Part I: On the development of analogs to supercritical flow in an infinitely deep, continuously stratified fluid // J. Atmos. Sci. 1986. V. 43. P. 2527–2543.
Гилл А. Динамика атмосферы и океана. М.: “Мир”. 1986. Т. 1–2.
Шестакова А.А., Моисеенко К.Б., Торопов П.А. Гидродинамические аспекты эпизодов Новороссийской боры 2012–2013 гг. // Изв. РАН. Физика атмосферы и океана. 2015. Т. 51. № 4. С. 1–13.
Кожевников В.Н., Лосев А.С. О построении модели обтекания при точном выполнении граничного условия на цилиндрическом профиле. // Вестн. МГУ. Сер. 3. Физика. Астрономия. 1982. Т. 23. № 5. С. 43–50.
Кожевников В.Н. Орографические возмущения воздушного потока. Дис. ... канд. физ.-мат. наук. М.: МГУ, Физический факультет, 1965. С. 1–223.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Физика атмосферы и океана


