Известия РАН. Физика атмосферы и океана, 2021, T. 57, № 2, стр. 199-211

1. ВВЕДЕНИЕ

Морские брызги являются неотъемлемым элементом приводного слоя атмосферы при сильном и ураганном ветре. Взвешенные в воздухе капли участвуют в обмене влагой, теплом и импульсом с атмосферой, тем самым изменяя общий поток, поступающий из океана. Однако количественные оценки влияния капель на потоки, поступающие из океана в атмосферу, представляют значительную проблему, в виду неопределенности статистических характеристик капель [1]. Так, функция генерации брызг, определяющая количество капель, инжектируемых с поверхности воды в воздушный поток в единицу времени с единицы площади, у разных авторов имеет разброс до 6 порядков [2]. Причинами такой неопределенности являются непреодолимые сложности при натурных измерениях и слабая изученность механизмов генерации брызг. В последнее время в [3, 4] на основе лабораторных экспериментов было показано, что при ураганных скоростях ветра основным механизмом образования брызг является дробление по типу “парашют”. Количественные оценки потоков импульса и тепла, представленные в [5], показывают, что учет брызг, генерируемых “парашютами”, приводит к немонотонной зависимости коэффициента аэродинамического сопротивления поверхности океана от скорости ветра и увеличению потока энтальпии, поступающего в атмосферу. Однако остается открытым вопрос о переносе статистики “парашютов”, полученной в результате лабораторного моделирования, на натурные условия. Главным отличием натурных и лабораторных условий является ветровой разгон. В [4] учет разгона был осуществлен путем перехода к ветро-волновому числу Рейнольдса, ${\text{R}}{{{\text{e}}}_{B}} = {{u_{*}^{2}} \mathord{\left/ {\vphantom {{u_{*}^{2}} {{{\omega }_{p}}\nu }}} \right. \kern-0em} {{{\omega }_{p}}\nu }},$ введенному в [6], где ${{u}_{*}}$ – динамическая скорость в воздухе, ${{\omega }_{p}}$ – частота пика волн в спектре поверхностного волнения, ν – кинематическая вязкость воздуха. В связи с трудностями проведения натурных экспериментов при штормовых условиях, нет возможности проверить эту гипотезу на практике. Для пересчета лабораторных данных необходимо ввести критерии подобия, выбор которых может быть основан на теоретических представлениях о механизме генерации брызг по типу “парашют”.

К настоящему времени хорошо изучено дробление по типу “парашют” капель и струй в поперечных потоках [7–10]. Критерий подобия, который определяет режим такого процесса, – число Вебера, $We = \frac{{{{\rho }_{a}}{{U}^{2}}D}}{{{{\rho }_{w}}\sigma }},$ где ${{\rho }_{a}},$ ${{\rho }_{w}}$ – плотности воздуха и воды, $U$ – скорость набегающего потока, $D$ – размер объекта дробления, $\sigma $ – коэффициент поверхностного натяжения. В случае дробления капель или струй размер объекта – величина очевидная. В случае дробления поверхности воды под действием ветра этим размером может стать масштаб начального возмущения, дальнейшее развитие которого приведет к формированию “парашюта”. Идея, лежащая на поверхности, состоит в том, что этот масштаб можно оценить, как длину волны возмущения, развивающегося на поверхности воды под действием воздушного потока за счет линейной гидродинамической неустойчивости. В случае коротких волн, динамика которых определяется балансом сил капиллярного и гидродинамического давления, этот масштаб имеет порядок ${\sigma \mathord{\left/ {\vphantom {\sigma {{{U}^{2}}}}} \right. \kern-0em} {{{U}^{2}}}}$ (см. [8]). Однако такая зависимость противоречит эксперименту [4, 11], в котором наблюдалась более медленная зависимость размеров “парашютов” от скорости воздушного потока.

В настоящей работе рассматривается нелинейная стадия развития возмущений на потоке и получены оценки масштабов возникающий при этом возмущений. Предложена гипотеза о том, что формирование возвышений поверхности воды, из которых в дальнейшем образуются “парашюты”, связано с неустойчивостью ветрового дрейфового течения, обусловленной нелинейным резонансным взаимодействием триплета волн, одна из которых распространяется вдоль потока, а две другие – под одинаковым углом по обе стороны от основного течения (см. рис. 2).

При слабонелинейном взаимодействии резонансных триплетов происходит либо обмен энергией между гармониками, либо, если взаимодействие происходит в активной среде, может наблюдаться взрывной рост [12–14].

Резонансное трехволновое взаимодействие собственных волн также исследовалось в гидродинамике [15], в том числе в присутствии средних течений. При этом в работах [16–18] было показано, что в присутствии внешнего потока трехволновое взаимодействие может приводить к взрывной неустойчивости. В [18] взрывной рост амплитуд объяснялся присутствием в системе волн с разным знаком энергии [19]. В то же время для течения в пограничном слое, рассмотренном в [16, 17], существовали волны только одного знака энергии, а усиление всех трех волн происходило за счет энергии основного потока, которая передавалась возмущениям внутри критического слоя.

В настоящей работе для моделирования турбулентного дрейфового течения использовался кусочно-непрерывный профиль скорости, который учитывает резкое изменение скорости дрейфового течения в вязком подслое и его слабое изменение в турбулентном слое, где профиль скорости логарифмический. Для описания турбулентного переноса использовалась градиентная аппроксимация турбулентных напряжений с коэффициентом эффективной вязкости, ${{\nu }_{{{\text{эф}}}}} = {{\nu }_{w}} + {{\nu }_{t}},$ где ${{\nu }_{w}}$ – кинематическая вязкость воды, а ${{\nu }_{t}}$ – турбулентная вязкость. В данном исследовании используется упрощенная кусочно-постоянная модель эффективной вязкости, в которой в вязком подслое ${{\nu }_{{{\text{эф}}}}} = {{\nu }_{w}},$ а в области турбулентного течения ${{\nu }_{{{\text{эф}}}}}$ постоянная величина много большая ${{\nu }_{w}}.$

Данная работа имеет следующую структуру. В разделе 2 для полного профиля скорости получено дисперсионное соотношение для волн, распространяющихся под произвольным углом к потоку. В параграфе 3 показана возможность выполнения трехволнового синхронизма для волн на скачке завихренности в воде, и установлено, что ветровой поток не оказывает существенного влияния на выбранную моду. Раздел 4 посвящен выводу трехволновых уравнений с учетом взаимодействия внутри критического слоя, нелинейности уравнений движения и кинематических граничных условий. В разделе 5 представлено сравнение результатов моделирования и экспериментальных данных о дроблении по типу “парашют”, полученных в [4].

2. ЛИНЕЙНОЕ ДИСПЕРСИОННОЕ СООТНОШЕНИЕ ДЛЯ ВОЛНОВЫХ ВОЗМУЩЕНИЙ В СИСТЕМЕ ВЕТРОВОГО И ДРЕЙФОВОГО ТЕЧЕНИЙ

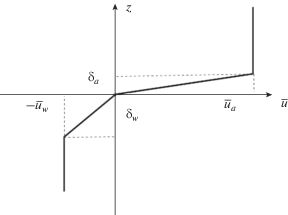
Рассмотрим ветровой поток над поверхностью воды и вызванное им дрейфовое течение в воде. Профиль скорости в воздухе, который представляет собой турбулентный пограничный слой, состоит из нескольких участков: вязкого подслоя, где скорость меняется линейно, переходного слоя и турбулентной области, где скорость меняется по логарифмическому закону. Дрейфовое течение в воде имеет аналогичную структуру. При этом динамические скорости воздушного потока, ${{u}_{*}},$ и ветрового дрейфового течения, ${{u}_{{w*}}},$ связаны условием равенства касательных напряжений, $\tau = {{\rho }_{a}}u_{*}^{2}$ = ${{\rho }_{w}}u_{{w*}}^{2}.$

В настоящей работе используется упрощенная модель профиля скорости (рис. 1) в виде кусочно-непрерывной функции (3), (4). Такой модельный профиль скорости учитывает резкое изменение скорости в вязком подслое и его слабое изменение в логарифмическом слое. В качестве характерной толщины слоев в воздухе и воде, $~{{\delta }_{a}}$ и ${{\delta }_{w}},$ выбирались толщины буферных слоев, вне которых течение считалось полностью турбулентным, а именно,

где ${{\rho }_{{w,a}}}$ – плотность воды и воздуха, ${{u}_{*}}$ – динамическая скорость в воздухе, ${{\nu }_{w}}$ – молекулярная вязкость воды. Скорости сдвига в воздухе и в воде, ${{\bar {u}}_{a}}$ и ${{\bar {u}}_{w}},$ принимались равными (см. [20])

Используя ${{\delta }_{w}},$ ${{\bar {u}}_{w}}$ из (1), (2), перейдем от размерных переменных, обозначенных индексом “d”, к безразмерным с индексом “nd”:

где $~\lambda \ll 1,$ $\mu \gg 1,$ $\sqrt \lambda \mu \sim 1.$

Определим модельный профиль скорости в безразмерных переменных в воздухе как

и в воде

Здесь и далее компоненты скорости вдоль направлений ${{\vec {x}}_{0}},~{{\vec {y}}_{0}},~{{\vec {z}}_{0}}$ обозначаются как $u,~{v},~w,$ а индекс “nd” опущен.

Прежде всего исследуем собственные волны рассматриваемой системы в рамках модели идеальной несжимаемой жидкости, когда ее движение в воздухе и воде описывается безразмерным уравнением Эйлера

где $G = \frac{{g{{\delta }_{w}}}}{{\bar {u}_{w}^{2}}}$ – безразмерное ускорение свободного падения, ${{\hat {\rho }}_{w}} = 1,$ ${{\hat {\rho }}_{a}} = \lambda ,$ и условием несжимаемости

При этом на границе раздела слоев выполняются динамические граничные условия, а именно, непрерывность нормальных напряжений:

Поскольку рассматриваются короткие волны, то в условии непрерывности нормального напряжения учитывается капиллярное давление. Здесь ${{\Delta }_{ \bot }} = \frac{{{{\partial }^{2}}}}{{\partial {{x}^{2}}}} + \frac{{{{\partial }^{2}}}}{{\partial {{y}^{2}}}},$ ${\Sigma } = \frac{{\sigma }}{{\bar {u}_{w}^{2}{{\delta }_{w}}}}$ – безразмерный коэффициент поверхностного натяжения, ${{\eta }_{a}},{{\eta }_{0}},{{\eta }_{w}}$ – смещения границ раздела слоев при $z = \sqrt \lambda \mu ,0, - 1.$ Также на границе раздела слоев выполняются кинематические граничные условия:

Представим поле скорости в виде основного течения ${{\bar {u}}_{{a,w}}}{{\vec {x}}_{0}}$ и возмущения ${{{\vec {v}}}_{{a,w}}}$

которое убывает при удалении от границы

Будем считать, что возмущение основного потока мало и имеет амплитуду порядка ε, где $\varepsilon \ll 1.$ Тогда, используя метод многих масштабов, будем искать решение (5) с подстановкой (9) в виде разложения по степеням ε

где $Q = ({{u}_{{a,w}}},{{{v}}_{{a,w}}},{{w}_{{a,w}}},{{p}_{{a,w}}},{{\eta }_{{a,0,w}}}).$

В нулевом порядке по ε из (5) следует, что $p_{a}^{{\left( 0 \right)}}\left( z \right) = - \lambda Gz;$ $p_{w}^{{\left( 0 \right)}}\left( z \right) = - Gz.$

Решение задачи в линейном приближении дает дисперсионное соотношение и структуру полей свободных собственных мод системы. Рассмотрим возмущение основного течения в виде свободной гармонической волны, т.е.

Перейдем к системе координат, в которой направление оси абсцисс ${{\vec {x}}_{j}}$ совпадает с направлением распространения волны (например, ${{\vec {x}}_{1}}$ на рис. 2) с помощью следующего преобразования

где ${{k}_{{jx}}} = {{k}_{j}}\cos {{\alpha }_{j}},$ ${{k}_{{jy}}} = {{k}_{j}}\sin {{\alpha }_{j}},$ ${{\alpha }_{j}}$ – угол между направлением распространения j-ой волны и основным потоком. В этой системе координат волна не зависит от поперечной координаты ${{y}_{j}}.$ Компоненты возмущения скорости вдоль ${{x}_{j}},$ ${{y}_{j}}$ обозначим как $\hat {u}_{j}^{{\left( 1 \right)}},$ ${\hat {v}}_{j}^{{\left( 1 \right)}}.$

В первом порядке по ε для возмущения (11) в системе координат (12) уравнения движения (5) с учетом (9) записываются как

Линеаризованные граничные условия имеют вид:

1) динамические условия

2) кинематические условия

Из системы (13) следует, что

Из системы (13) легко получить, что возмущение вертикальной скорости $w_{{a,{{w}_{j}}}}^{{\left( 1 \right)}}$ в каждом из слоев удовлетворяет уравнению Гельмгольца, которое означает отсутствие возмущений завихренности внутри слоев с нулевой или постоянной невозмущенной завихреностью в идеальной жидкости:

Из (18) и условия отсутствия возмущения на бесконечности (10) следует, что

Используя (16)–(20), из граничных условий (14)–(15) получаем однородную систему алгебраических уравнений в виде

где $X_{j}^{{{{{(1)}}^{T}}}}$ = ($\eta _{{{{a}_{j}}}}^{{\left( 1 \right)}},$ $\eta _{j}^{{\left( 1 \right)}},$ $\eta _{{{{w}_{j}}}}^{{\left( 1 \right)}},$ $V_{{2a - j}}^{{(1)}},$ $V_{{1a - j}}^{{(1)}},$ $V_{{1a + j}}^{{(1)}},$ $V_{{1w - j}}^{{(1)}},$ $V_{{1w + j}}^{{(1)}},$ $V_{{2w + j}}^{{(1)}}$), а ${{M}_{j}}({{\omega }_{j}},{{k}_{j}},{{\alpha }_{j}})$ – матрица размером 9 × 9. Из условия $\det {{M}_{j}} = 0$ получаем дисперсионное соотношение в виде: где

Поскольку (22) представляет собой уравнение 4-го порядка по ${{\omega }_{j}},$ в системе существуют 4 моды (рис. 3), из которых две соответствуют гравитационно-капиллярным поверхностным волнам, модифицированным течением, и две – волнам на скачке завихренности в воздухе и воде.

3. УСЛОВИЕ РЕЗОНАНСНОГО СИНХРОНИЗМА ДЛЯ ТРЕХВОЛНОВОГО ВЗАИМОДЕЙСТВИЯ В СИСТЕМЕ ВЕТРОВОГО И ДРЕЙФОВОГО ТЕЧЕНИЙ

Исследуем возможность выполнения условий трехволнового синхронизма для триплета волн, изображенного на рис. 2. Косые волны пронумеруем как “1”, “2”, а продольной волне присвоим индекс “3” (для нее ${{\alpha }_{3}} = 0$). Ограничим рассмотрение случаем, когда ${{\alpha }_{{1,2}}} = \pm \alpha ,$ ${{k}_{1}} = {{k}_{2}} = k$ и ${{\omega }_{1}} = {{\omega }_{2}} = \omega ,$ тогда условие трехволнового резонанса примет вид

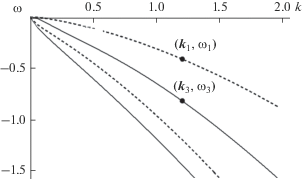
Численное решение дисперсионного уравнения (22) показывает, что при любом значении скорости трения в воздухе ${{u}_{*}}$ условия (23) выполняются для целого диапазона углов $\alpha ,$ причем в трехволновом синхронизме могут участвовать разные собственные моды (пример, рис. 4a, 4б).

Заметим, что при резонансном трехволновом взаимодействии как волн на скачке завихренности (рис. 4a), так и гравитационно-капиллярных (рис. 4б) существуют критические слои, причем для первого случая он лежит в воде в области $ - 1 \leqslant z \leqslant 0,$ а для второго – в воздухе в области $0 \leqslant z \leqslant \sqrt \lambda \mu .$ Согласно [16], [17], в критическом слое может происходить нелинейная передача энергии от основного течения возмущениям, следствием которой может стать взрывной рост амплитуд возмущений. Как показано в [17], интенсивность этого взаимодействия обратно пропорциональна коэффициенту кинематической вязкости. Так как ${{\nu }_{w}} \ll {{\nu }_{a}},$ то можно ожидать наиболее быстрого роста возмущений моды на скачке завихренности дрейфового течения. В связи с этим в настоящем исследовании основное внимание уделяется изучению резонансного взаимодействия триплета именно этой моды (рис. 4a).

Важно отметить, что аэродинамическое давление на поверхности воды оказывает слабое влияние на рассматриваемую моду. Действительно, учет воздушного потока приводит к появлению в дисперсионном соотношении (22) малых слагаемых $\left( { \propto \lambda ,~\frac{{{{\nu }_{w}}}}{{{{\nu }_{a}}}}} \right),$ поэтому в дальнейших рассуждениях ветровой поток не учитывался, и течение считалось двухслойным с профилем скорости (4).

Отметим, что в [21] была исследована устойчивость горизонтального подповерхностного течения воды с кусочно-непрерывным профилем скорости по отношению к гармоническим возмущениям, распространяющимся параллельно потоку. Было показано, что в линейном приближении возмущения оказываются устойчивыми, в то время как учет второго порядка приводит к взрывной неустойчивости гравитационно-капиллярных волн вследствие резонансного взаимодействия волн с разным знаком энергии.

В настоящей работе рассмотрена более универсальная модель течения воды, в которой принималось во внимание влияние вязкости. Вне вязкого подслоя учитывались турбулентные напряжения с помощью введения эффективной вязкости, ${{\nu }_{{{\text{эф}}}}} = {{\nu }_{w}} + {{\nu }_{t}},$ где ${{\nu }_{w}}$ – кинематическая вязкость воды, а ${{\nu }_{t}}$ – турбулентная вязкость. В связи с резким отличием ${{\nu }_{w}}$ от ${{\nu }_{t}}$ в вязком подслое и области турбулентного течения, использовалась упрощенная кусочно-постоянная модель эффективной вязкости:

где ${{\nu }_{w}},$ ${{\nu }_{t}}$ – молекулярная и турбулентная вязкость воды, причем ${{\nu }_{w}} \ll \,\,~{{\nu }_{t}}.$ В безразмерных переменных ${\text{R}}{{{\text{e}}}_{w}} = \frac{{{{{\bar {u}}}_{w}}{{\delta }_{w}}}}{{{{\nu }_{w}}}},$ ${\text{R}}{{{\text{e}}}_{t}} = \frac{{{{{\bar {u}}}_{w}}{{\delta }_{w}}}}{{{{\nu }_{t}}}}$ и ${\text{R}}{{{\text{e}}}_{w}} \gg ~\,{\text{R}}{{{\text{e}}}_{t}} \gg 1.$

При ${\text{R}}{{{\text{e}}}_{w}} \gg 1$ в области $ - 1 \leqslant z \leqslant 0$ решение невязкой задачи справедливо всюду, кроме трех слоев, два из которых расположены при $z = 0,$ $z = - 1$ и имеют масштаб ${{\delta }_{{{\text{R}}{{{\text{e}}}_{w}}}}} = O({{\left( {k{\text{R}}{{{\text{e}}}_{w}}} \right)}^{{{{ - 1} \mathord{\left/ {\vphantom {{ - 1} 2}} \right. \kern-0em} 2}}}}),$ а третий при $z = {{z}_{с}},$ где скорость основного потока, $\bar {u}\left( {{{z}_{с}}} \right),$ равна фазовой скорости возмущения, $c = {\omega \mathord{\left/ {\vphantom {\omega k}} \right. \kern-0em} k},$ имеет размер ${{\delta }_{с}} = O({{\left( {k{\text{R}}{{{\text{e}}}_{w}}} \right)}^{{{{ - 1} \mathord{\left/ {\vphantom {{ - 1} 3}} \right. \kern-0em} 3}}}}).$ Оценки, представленные в приложении, показывают, что учет конечного значения величины ${\text{R}}{{{\text{e}}}_{w}}$ в окрестности $z = 0$ приводит к появлению добавочной скорости, имеющей порядок $O\left( {{\text{Re}}_{w}^{{ - 1}}} \right).$ На границе двух вязких жидкостей при $z = - 1$ должно выполняться условие прилипания и равенства касательных напряжений, однако при ${\text{R}}{{{\text{e}}}_{w}} \gg {\text{Re}}_{t}^{2}$ касательным напряжением в верхнем слое можно пренебречь (см. приложение). Таким образом, при ${\text{R}}{{{\text{e}}}_{w}} \gg {\text{Re}}_{t}^{2} \gg 1$ вязкость в верхней области необходимо учитывать только в критическом слое, а вне него жидкость можно считать невязкой.

В новой постановке задачи течение в нижней области описывается уравнением Навье–Стокса, а в верхней области по-прежнему справедливо уравнение Эйлера (индекс “w” в дальнейшем опущен)

где $\vec {V} = \bar {u}~{{\vec {x}}_{0}} + {\vec {v}}.$ Кроме того, поскольку нижний слой теперь вязкий, появляется дополнительное граничное условие при $z = - 1 + {{\eta }_{w}}$ непрерывности касательного напряжения, и в уравнении непрерывности нормального напряжения возникает добавочное слагаемое. В результате динамические граничные условия для двуслойной жидкости, одна из которых вязкая, имеют вид:

Кинематические граничные условия остаются без изменений

Как и при рассмотрении полного профиля скорости, решая линеаризованную задачу, все переменные можно выразить через смещения $\eta _{{{{0}_{j}}}}^{{\left( 1 \right)}},$ $\eta _{{{{w}_{j}}}}^{{\left( 1 \right)}}$ и возмущение вертикальной скорости $w_{j}^{{\left( 1 \right)}},$ однако, поскольку течение в нижней области вязкое, $w_{j}^{{\left( 1 \right)}}$ при $ - \infty \leqslant z \leqslant - 1$ вместо (16) должно удовлетворять уравнению Орра–Зоммерфельда. В результате

Из (27) и отсутствия возмущений на бесконечности следует, что

где ${{\beta }_{j}} = \sqrt {1 - \frac{{i{\text{R}}{{{\text{e}}}_{t}}({{\omega }_{j}} + {{k}_{j}}\cos {{\alpha }_{j}})}}{{k_{j}^{2}}}} .$

Проводя выкладки, аналогичные представленным в параграфе 2, получаем однородную систему алгебраических уравнений в виде

где $X_{j}^{{{{{(1)}}^{T}}}}$ = ($\eta _{{{{0}_{j}}}}^{{\left( 1 \right)}},$ $\eta _{{{{w}_{j}}}}^{{\left( 1 \right)}},$ $V_{{1 - j}}^{{\left( 1 \right)}},$ $V_{{1 + j}}^{{\left( 1 \right)}},$ $V_{{2 + j}}^{{\left( 1 \right)}},$ $V_{{2{{{\beta }}_{j}}}}^{{\left( 1 \right)}}$), а ${{L}_{j}}({{\omega }_{j}},{{k}_{j}},{{\alpha }_{j}},{\text{R}}{{{\text{e}}}_{t}})$ – матрица размером 6 × 6. Из условия равенства нулю определителя ${{L}_{j}}$ находим дисперсионное соотношение, которое при ${\text{R}}{{{\text{e}}}_{t}} \gg 1$ можно разложить в ряд Тейлора, и тогда оно примет вид: где ${{\mathcal{D}}_{w}}\left( {{{\omega }_{j}},{{k}_{j}},{{\alpha }_{j}}} \right)$ определено в (22). Численное решение дисперсионного уравнения (30) показывает, что, как в случае (22), при любом значении скорости трения в воздухе ${{u}_{*}}$ условия (23) выполняются для целого диапазона углов α. Пример выполнения условий трехволнового синхронизма показан на рис. 5.

4. ТРЕХВОЛНОВОЕ ВЗАИМОДЕЙСТВИЕ С УЧЕТОМ НЕЛИНЕЙНОСТИ ГРАНИЧНЫХ УСЛОВИЙ И ВЯЗКОСТИ В КРИТИЧЕСКОМ СЛОЕ

Для получения системы трехволнового взаимодействия в уравнениях движения (24) и граничных условиях (25)–(26) необходимо сохранить слагаемые второго порядка малости. Кроме того, в порядке ε² появляется вихревая составляющая скорости, обусловленная нелинейностью. В итоге возмущение вертикальной скорости во втором приближении определим, как

где ${{\omega }_{{{{j}_{r}}}}} = {\text{Re}}({{\omega }_{j}}),$ ${{\omega }_{{{{j}_{i}}}}} = Im({{\omega }_{j}}),$ а слагаемое с ${{W}_{j}}(z)$ есть частное решение неоднородных уравнений движения второго порядка, отличное от нуля в области $ - 1 \leqslant z \leqslant 0.$ Заметим, что во втором приближении $w_{j}^{{\left( 2 \right)}},$ ${{W}_{j}}$ не зависят от времени, а вид функции $w_{j}^{{\left( 2 \right)}}$ совпадает с $w_{j}^{{\left( 1 \right)}}$ (формула (28)). Речь о том, как определить ${{W}_{j}}(z)$, пойдет ниже.

Запишем граничные условия в системе координат (10) во втором порядке малости:

1) динамические условия

где ${{\left\langle \ldots \right\rangle }_{j}}$ – умножение на $\exp \left[ { - i{{k}_{j}}{{x}_{j}} + i{{\omega }_{j}}t} \right]$ и усреднение.

2) кинематические условия

Из уравнений движения (22) и условия несжимаемости во втором порядке находим, что

Используя (34)–(35), из граничных условий (32)–(33) для j-ой волны получаем неоднородную систему уравнений в виде

где ${{L}_{j}}$ та же матрица, что была в линейном приближении и detL_j = ${{\mathcal{D}}_{w}}\left( {{{\omega }_{j}},{{k}_{j}},{{\alpha }_{j}}} \right)$ + ${\text{Re}}_{t}^{{ - 1}}{{\mathcal{D}}_{1}}$ $\left( {{{\omega }_{j}},{{k}_{j}},{{\alpha }_{j}},{\text{R}}{{{\text{e}}}_{t}}} \right)$ = = 0, $X_{j}^{{(2)}}$ совпадет с $X_{j}^{{(1)}}$ с точностью до замены индексов 2 → 1. Первое слагаемое в правой части (36) отвечает за медленное изменение амплитуды j-ой волны, второе – за нелинейность граничных условий, третье – за появление вихревой скорости ${{W}_{j}}.$

Поскольку ${{\omega }_{j}},$ ${{k}_{j}}$ удовлетворяют дисперсионному соотношению для разрешимости системы (36), для каждой из волн правая часть должна быть ортогональна собственному вектору, ${{u}_{j}},$ соответствующей сопряженной однородной задачи. Таким образом, получаем:

Для определения коэффициентов, входящих в уравнение (37), необходимо использовать решение линейной задачи $X_{j}^{{(1)}}.$ Так как столбец $X_{j}^{{(1)}}$ определен с точностью до множителя, без ограничения общности рассмотрим такую норму $X_{j}^{{(1)}},$ что $w_{j}^{{\left( 1 \right)}}(0) = 1.$ Собственный вектор ${{u}_{j}}$ нормируем так, что первая компонента равна 1. В этом случае выражение для первого слагаемого (35) примет вид

Перейдем к вопросу определения ${{W}_{j}}(z).$ Величину ${{W}_{j}}(z)$ можно попытаться найти из уравнений движения в невязком пределе, тогда получим, что

В этом случае при ${\text{R}}{{{\text{e}}}_{t}} \gg {\text{R}}{{{\text{e}}}_{w}} \gg 1$ для каждой из волн интеграл (38) будет иметь полюс высокого порядка в критическом слое при $z = ~{{z}_{с}},$ который оказывается общим для всех волн. Для устранения особенности необходимо учитывать вязкость в критическом слое $~{{z}_{с}} - {{\delta }_{с}} \leqslant z \leqslant {{z}_{с}} + {{\delta }_{с}},$ а вне критического можно использовать невязкое решение (39).

Решение вязкой задачи для чисто сдвигового течения детально изложено в [16]. Для рассматриваемой задачи критический слой также лежит в области линейного профиля скорости, поэтому все математические выкладки полностью совпадают с [16] с точностью до замены ${{e}^{{ - {{k}_{j}}{{z}_{0}}}}} \to w_{j}^{{\left( 1 \right)}}({{z}_{с}})$ и ${1 \mathord{\left/ {\vphantom {1 \nu }} \right. \kern-0em} \nu } \to {\text{R}}{{{\text{e}}}_{w}}.$ Итоговое выражение (38) для косых волн имеет вид

При выводе (40) учитывается, что основную роль в (38) играет именно критический слой, а интегрирование по области вне критического слоя не дает существенного вклада.

Для продольной волны, как показано в [16], интегрирование в (38) по критическому слою с использованием вязкого решения дает 0. В итоге, (38) определяется интегрированием невязкого решения (39), при этом контур интегрирования необходимо деформировать так, чтобы он лежал под особенностью $z = ~{{z}_{с}},$ т.е.

где ${{\gamma }_{{w3}}}$ – комплексное число, зависящее от ${{k}_{j}},~{{\omega }_{j}},~\alpha .$

Определение второго и третьего слагаемых в уравнении (37) осуществляется напрямую. Выражение для них мы опустим ввиду громоздкости и неинформативности. Проведение преобразований в рассматриваемой модели осуществлялось в системе компьютерной алгебры Wolfram Mathematica.

В итоге, условия разрешимости (37) могут быть записаны в виде системы уравнений, описывающих модуляцию амплитуд волн ${{A}_{j}},$ которая имеет вид

где учтено, что ${{A}_{1}} = {{A}_{2}},$ ${{{\Lambda }}_{j}}$ – комплексные числа, зависящие от ${{k}_{j}},~{{\omega }_{j}},~\alpha ,$${\text{R}}{{{\text{e}}}_{w}},$${\text{R}}{{{\text{e}}}_{t}}.$

5. СРАВНЕНИЕ РЕШЕНИЯ МОДЕЛЬНОЙ ЗАДАЧИ И ЭКСПЕРИМЕНТАЛЬНЫХ ДАННЫХ

Для случая $Im~{{\omega }_{j}} = 0$ подробный анализ системы (42) приведен в статье [16], в которой показано, что при ${{e}^{{i{\text{\;Arg}}~{{{\Lambda }}_{1}}{{{\Lambda }}_{3}}}}} \ne - 1$ решение системы (42) растет взрывным образом (как $ \propto \frac{1}{{t - {{t}_{0}}}},$ где ${{t}_{0}}$ – время развития неустойчивости). В настоящей задаче также реализуется подобный сценарий, так что амплитуды всех волн неограниченно возрастают (рис. 6). Стоит отметить, что взаимодействующие волны имеют один и тот же знак энергии, а рост амплитуд возмущений, как и в [16, 17], обусловлен передачей энергии внутри критического слоя, который является общим для всех трех волн.

Каждой из волн возмущения соответствует двумерное смещение границы раздела воды и воздуха ${{\eta }_{{{{0}_{j}}}}},$ и рост амплитуды возмущений также приводит к увеличению смещения ${{\eta }_{{{{0}_{j}}}}}.$ В результате суперпозиции смещений поверхности воды, обусловленных продольной и косыми волнами, образуется трехмерная структура (рис. 7). На рис. 6 и 7 отражены важные особенности рассматриваемой модели. Во-первых, резкий рост амплитуды при $t$ близком к ${{t}_{0}}.$ Во-вторых, образование трехмерных структур, у которых продольный и поперечный масштабы – величины одного порядка.

Динамика рассмотренной структуры похожа на начальный этап явления дробления типа “парашют” [4]. На рис. 8а–8д схематично показаны характерные стадии развития “парашюта”.

Подчеркнем, что “парашюты” представляют собой локализованные объекты, в то время как в рассматриваемой модели возмущение носит периодический характер. Однако нужно учесть, что при фиксированном значении скорости трения в воздухе, ${{u}_{*}},$ трехволновый синхронизм выполняется для целого диапазона углов, $\Delta \alpha ,$ причем разным углам соответствуют разные волновые числа и частоты. Как следствие, интервалу $\Delta \alpha $ соответствует некоторый диапазон волновых чисел, $\Delta k,$ и резонансных частот, $\Delta \omega ,$ то есть спектр неустойчивых возмущений оказывается широкополосным. На рис. 9 показано, что разным значениям $\alpha $ соответствуют различные временные масштабы развития неустойчивости, причем существует диапазон углов $\Delta \alpha ,$ для которых это время остается практически тем же самым, что также указывает на широкополосный характер возмущения.

Временному спектру, имеющему характерный масштаб $\Delta \omega ,$ соответствует возмущение с временным масштабом

Аналогично, оценим поперечный масштаб возмущений как

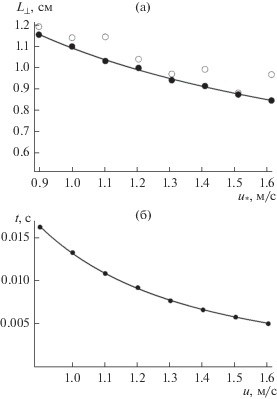
где ${{k}_{ \bot }} = k\cos \alpha .$ Полученные зависимости ${{L}_{ \bot }}$ и $t$ от динамической скорости ветра ${{u}_{*}}$ представлены на рис. 10a, 10б. Аппроксимируя их степенной функцией, получим где ${{L}_{ \bot }}$ в сантиметрах, $t$ в миллисекундах, ${{u}_{*}}$ в м/с.

Как указано выше, взрывной рост амплитуд волн возмущения также приводит к росту смещения водной поверхности и образованию трехмерных выступов. По нашему предположению, именно эти возвышения являются начальной стадией явления дробления по типу “парашют” (рис. 8а, 8b), причем поперечному размеру “парашюта” соответствует зависимость (45.1), а время жизни “парашюта” должно иметь такой же порядок, что и время образования возмущений поверхности воды (45.2). Согласно [4], средний диаметр “парашюта” в момент начала надувания, $\left\langle {{{D}_{1}}} \right\rangle ,$ и его время жизни, $\left\langle \tau \right\rangle ,$ зависят от динамической скорости как

где $\left\langle {{{D}_{1}}} \right\rangle $ в сантиметрах, $\left\langle \tau \right\rangle $ в миллисекундах, ${{u}_{*}}$ в м/с.

Количественные значения поперечного масштаба, определяемые (45.1) и (46.1), близки, хотя (46.1) имеет более резкую зависимость от динамической скорости. Однако если вместо аппроксимации (46.1) сравнивать результаты моделирования непосредственно с экспериментальными данными из [4] (рис. 10a), то увидим более точное соответствие. Характерные временные масштабы, определяемые (45.2) и (46.2), имеют одинаковую зависимость от динамической скорости. Отличие коэффициентов может быть обусловлено тем, что $\left\langle \tau \right\rangle $ представляет собой время надувания “парашюта” от стадии (в) до (д) рис. 8, в то время как величина $t$ (45.2) определяет временной интервал от стадии (a) до (в) рис. 8.

Подчеркнем, что основное влияние на итоговую зависимость характерных временных и пространственных параметров возмущения (45.1) и (45.2) оказывают завихренность, ${{Г}_{w}} = \frac{{{{{\bar {u}}}_{w}}}}{{{{\delta }_{w}}}},$ и толщина пограничного слоя, ${{\delta }_{w}},$ которые фигурируют в формулах (43)–(44).

6. ЗАКЛЮЧЕНИЕ

Представленный выше анализ показал, что для кусочно-непрерывного профиля дрейфовой скорости в воде могут быть выполнены условия трехволнового синхронизма. При этом во втором порядке малости возникает взрывной рост амплитуд всех трех волн, который происходит за счет энергии основного потока, которая, как и в [16], передается внутри критического слоя. Характерные временные и пространственные масштабы, определяемые в рамках этой модели, соответствуют экспериментальным данным [4]. Таким образом, возмущения, которые формируются за счет взрывной неустойчивости при трехволновом взаимодействии, могут рассматриваться в качестве начальной стадии дробления по типу “парашют”.

В данном исследовании рассматривались квазимонохроматические возмущения, с дополнительным условием равенства углов между направлением распространения и основным потоком у косых волн. В случае, когда возмущение представляет собой волновой пакет, для каждой его спектральной компоненты можно записать уравнения, аналогичные (42). Однако, при произвольном выборе направлений распространения, возникнет ряд сложностей: одна и та же спектральная компонента может быть в синхронизме сразу с несколькими парами волн. В конечном итоге, это приведет большому количеству систем по типу (42), которые будут связаны между собой за счет правых частей. Кроме того, предложенная модель не может рассматриваться как окончательная, поскольку не объясняет наблюдаемую пороговую зависимость явления дробления по типу “парашют” от динамической скорости ветра. Одним из возможных способов решения этой проблемы может стать учет затухания амплитуд возмущений вследствие вязкости, которое приведет к появлению порога по начальной амплитуде, зависящей от динамической скорости ветра. Однако останется открытым вопрос о том, какие процессы приводят к образованию этих начальных возмущений. Все это станет предметом будущих исследований.

Работа выполнена при поддержке РФФИ (проекты №№ 19-35-90053, 19-05-00249). Аналитические выкладки проводились при поддержке проекта РНФ (№ 19-17-00209) и гранта Фонда развития теоретической физики и математики “БАЗИС”. Численное решение полученной системы было выполнено при финансовой поддержке Минобрнауки России в рамках Соглашения № 075-15-2020-776.