1. На главную
  2. Электронные версии
  3. Известия РАН. Физика атмосферы и океана
  4. T. 57, № 2, 2021

Известия РАН. Физика атмосферы и океана, 2021, T. 57, № 2, стр. 212-217

О развитии волновых возмущений донной поверхности в реках и каналах

И. И. Потапов a, *, Ю. Г. Силакова a, **

a Вычислительный центр ДВО РАН
680000 Хабаровск, ул. Ким Ю Чена, 65, Россия

* E-mail: potapov2i@gmail.com
** E-mail: krat_yuliya@mail.ru

Поступила в редакцию 01.09.2020
После доработки 27.11.2020
Принята к публикации 09.12.2020

Полный текст (PDF)

Аннотация

На основе аналитической модели расхода влекомых наносов, учитывающей влияние уклонов донной поверхности, придонных нормальных и касательных напряжений на движение донного материала и аналитического решения, позволяющего определять придонные касательные и нормальные напряжения, возникающие при обтекании турбулентным потоком периодических длинных донных волн малой амплитуды, сформулирована и решена задача определения скорости роста амплитуды донной волны. Из решения задачи получена аналитическая зависимость, определяющая скорость роста амплитуды донных волн от текущего значения ее амплитуды. На примере развития периодической синусоидальной донной волны малой крутизны выполнена верификация, которая показала хорошее качественное и количественное согласование полученного решения с экспериментальными данными.

Ключевые слова: донные волны, устойчивость донной поверхности, расход влекомых наносов

ВВЕДЕНИЕ

Одной из центральных проблем при изучении русловых процессов является проблема устойчивости несвязной донной поверхности в реках и каналах. В настоящее время существует большое количество гипотез, определяющих причины, по которым происходит развитие донных волн.

Так, Дж.Ф. Кеннеди [1, 2] развитие донной неустойчивости связывал с передачей возмущений, возникающих на свободной поверхности потока при некоторых значениях числа Фруда, ко дну.

F. Engelund и J. Fredsoe [3] связывали развитие донной неустойчивости с фазовым сдвигом между максимумами средней скорости потока и придонным касательным напряжением.

В работах К.В. Гришанина [4], О.Н. Мельниковой [5], Н.А. Михайловой [6] показано, что развитию донной неустойчивости способствуют имеющиеся в турбулентном потоке пульсации соизмеримые по масштабу с глубиной потока. Экспериментальные работы Р. Бэгнольда [7], Б.А. Шуляка [8], S.E. Coleman [9] показали, что на характер развития донной неустойчивости оказывает влияние диаметр донного материала. В работе [10] в рамках линейной теории устойчивости несвязного дна канала получена аналитическая зависимость, определяющая длину донной волны в зависимости от числа Фруда гидродинамического потока и диаметра донных частиц, обобщающая ряд известных эмпирических зависимостей Р. Бэгнольда [7], Б.А. Шуляка [8], S.E. Coleman [9].

Попытки численного моделирования процесса развития донной неустойчивости в реках и каналах предпринимались в работах [11–16], основное внимание в которых уделялось физическим механизмам, приводящим к развитию донной неустойчивости под действием турбулентных потоков. Обработка данных натурного эксперимента, представленного в работе [17], позволила получить эмпирическую зависимость, позволяющую определить скорость роста амплитуды донных волн во времени.

Однако, несмотря на достаточное внимание исследователей к данной проблеме, вопрос о развитии донной неустойчивости остается в настоящее время открытым. В значительной мере это связано с тем, что при анализе развития донных волн используются феноменологические модели движения донного материала [7–9, 11, 12], что затрудняет или делает невозможным анализ процессов развития донных волн. По этой причине представляет интерес проведение анализа начального развития донных волн с использованием аналитической модели движения донного материала [18], учитывающей влияние локальных уклонов донной поверхности, придонных касательных и нормальных напряжений на движение донного материала.

При построении математической модели развития донных волн в данной работе были использованы результаты натурных экспериментальных исследований, изложенные в работе [17], в которой было показано, что эволюция донных волн имеет два важных этапа. На первом этапе ровное песчаное дно теряет устойчивость и происходит развитие амплитуды донных волн, при этом длина донных волн изменяется слабо и определяется гранулометрическим составом песка [9, 10, 19]. К концу первого этапа рост амплитуды донных волн замедляется, происходит их перекашивание и начинается активный рост длины донных волн, при слабых изменениях их амплитуды [17]. При этом процесс эволюции донных волн на втором этапе может не иметь стационарного состояния [20].

В работе на основе аналитической модели расхода влекомых наносов [18] и аналитической модели, позволяющей определить придонные касательные напряжения над периодическим дном [21], сформулирована математическая модель первого этапа, описывающая потерю устойчивости донной поверхности и развитие амплитуды донных волн. Из решения сформулированной задачи получена аналитическая зависимость, позволяющая определить скорость роста амплитуды периодических донных волн в зависимости от гидродинамических параметров потока, а также физико-механических и гранулометрических характеристик донного материала. Для синусоидальных донных волн выполнено сравнение полученного решения с экспериментальными данными [17], которое показало их хорошее качественное и количественное согласование.

МАТЕМАТИЧЕСКАЯ ПОСТАНОВКА ЗАДАЧИ

Рассмотрим математическую постановку задачи о развитии периодических донных волн при движении руслового потока над донной поверхностью ${{\zeta }_{b}} = h\sigma ,$ где $h = h\left( {{{t}_{b}}} \right)$ – безразмерная высота донной поверхности ${{\zeta }_{b}},$ $\sigma \left( \xi \right) = \sigma \left( {\xi + 1} \right)$ – периодическая безразмерная функция, определяющая форму донной волны с единичным периодом. Схема расчетной области задачи приведена на рис. 1.

Рис. 1.

Схема расчетной области: ${{\xi }_{1}},{{z}_{1}}$ – безразмерная декартовая система координат, $\xi ,z$ – расчетная криволинейная система координат.

Математическая постановка задачи о развитии донных волн в криволинейной ортогональной системе координат в безразмерной формулировке включает в себя:

– уравнение потенциала [1, 2]

(1)
$\frac{1}{{{{a}^{2}}}}\frac{{{{\partial }^{2}}\Psi }}{{\partial {{\xi }^{2}}}} + \frac{{{{\partial }^{2}}\Psi }}{{\partial {{z}^{2}}}} = 0,\,\,\,\,0 \leqslant \xi \leqslant 1,$

– уравнения, определяющие касательные и нормальные напряжения [21]

(2)
$\tau = \frac{{{{\tau }_{0}}}}{{y\left( \xi \right)}},\,\,\,\,p\left( \xi \right) = h\psi \left( \xi \right),\,\,\,\,\psi \left( \xi \right) = {{\left. {\frac{{\partial \Psi \left( {\xi ,z} \right)}}{{\partial z}}} \right|}_{{z = 0}}},$
(3)
$\begin{gathered} y\left( \xi \right) = E\int\limits_0^1 {\exp \left( {2ax} \right)} \times \\ \times \,\,\exp \left( {\frac{{6h}}{{{{\mu }_{0}}}}\left( {\psi \left( {a\xi } \right) - \psi \left( {a\left( {x + \xi } \right)} \right)} \right)} \right)dx, \\ \end{gathered} $

– уравнение расхода влекомых наносов [18]

(4)
$\begin{gathered} {{G}_{b}} = {{G}_{{b{\tau }}}} + {{G}_{{b\zeta }}} + {{G}_{{bp}}},\,\,\,\,{{G}_{{b{\tau }}}} = {{G}_{{b0}}}A, \\ {{G}_{{b{\zeta }}}} = {{G}_{{b0}}}B\frac{h}{a}\frac{{\partial \sigma }}{{\partial \xi }},\,\,\,\,{{G}_{{bp}}} = {{G}_{{b0}}}C\frac{{FrD}}{L}\frac{{\partial p}}{{\partial \xi }}, \\ \end{gathered} $

– уравнение Экснера [4]

(5)
${{S}_{d}}\sigma \frac{{\partial h}}{{\partial {{t}_{b}}}} + \frac{{\partial {{G}_{b}}}}{{\partial \xi }} = 0.$

Уравнения (1)–(5) замыкаются начальными $h\left( 0 \right) = {{h}_{0}}\left( \xi \right)$ и граничными условиями:

(6)
$z = 0{\text{:}}\,\,\Psi \left( {\xi ,0} \right) = \sigma \left( \xi \right),$
(7)
$z = 1{\text{:}}\,\,h\frac{{\partial \Psi }}{{\partial z}} \approx 0,$
(8)
$\Psi \left( {\xi ,z} \right) = \Psi \left( {\xi + 1,z} \right),$
(9)
${{G}_{b}}\left( {\xi ,z} \right) = {{G}_{b}}\left( {\xi + 1,z} \right).$

Связь безразмерных функций в уравнениях (1)–(9) с размерными определена следующим образом

$\begin{gathered} \Psi = \frac{{{{\Psi }_{H}}}}{{{{H}_{0}}}},\,\,\,\,\xi = \frac{X}{L},\,\,\,\,a = \frac{L}{H},\,\,\,\,{{z}_{0}} = \frac{{{{Z}_{0}}}}{H}, \\ z = \frac{Z}{H},\,\,\,\,h = \frac{{{{H}_{0}}}}{H},\,\,\,\,{{\mu }_{0}} = \frac{1}{{\ln \left( {{1 \mathord{\left/ {\vphantom {1 {{{z}_{0}}}}} \right. \kern-0em} {{{z}_{0}}}}} \right)}},\,\,\,\,\sigma \left( \xi \right) = \frac{{\zeta \left( {t,\xi } \right)}}{{{{H}_{0}}\left( t \right)}}, \\ {{t}_{b}} = \frac{t}{T},\,\,\,\,{{\tau }_{{\text{0}}}} = {{\rho }_{w}}u_{0}^{2},\,\,\,\,E = \frac{{2a\exp \left( { - 2a} \right)}}{{1 - \exp \left( { - 2a} \right)}}. \\ \end{gathered} $

Здесь $\Psi $ – безразмерная функция тока, ${{\Psi }_{H}}$ – функция тока, описывающая безвихревое поле скорости над периодическим дном, ${{Z}_{0}}$ – высота шероховатости дна, ${{\tau }_{{\text{0}}}}$ – напряжение на ровном дне, ${{u}_{0}}$ – динамическая скорость потока, ${{t}_{b}}$ – безразмерное время, $L$ – длина донной волны, $H$ – глубина логарифмического слоя, ${{H}_{0}}$ – амплитуда донной поверхности, $T$ – время развития амплитуды донной волны.

Коэффициенты уравнений (3), (4) определяются по следующим формулам

$\begin{gathered} {{S}_{d}} = \frac{{\left( {1 - \varepsilon } \right)}}{{\sqrt {{{\rho }_{b}}g{{d}^{3}}} }}\frac{{HL}}{T},\,\,\,\,G = {{G}_{b}}\sqrt {{{\rho }_{b}}g{{d}^{3}}} ,\,\,\,\,Fr = \frac{{{{U}^{2}}}}{{gD}}, \\ {{G}_{{b0}}} = \frac{{{{G}_{0}}}}{{y{{{\left( \xi \right)}}^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}}}},\,\,\,\,{{G}_{0}} = \frac{4}{3}\frac{{{{{\left( {F{{r}_{d}}} \right)}}^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}}}}{{\kappa tg\varphi }},\,\,\,\,F{{r}_{d}} = \frac{{u_{0}^{2}}}{{{{\rho }_{b}}gd}}, \\ A = 1 - \chi ,\,\,\,\,B = \frac{1}{{tg\varphi }}\left( {\frac{\chi }{2} + \left( {1 - \chi } \right)\frac{{1 + s}}{s}} \right),\,\,\,\,\,C = \frac{A}{{stg\varphi }}, \\ s = f{{\rho }_{b}},\,\,\,\,{{\rho }_{b}} = \frac{{{{\rho }_{s}} - {{\rho }_{w}}}}{{{{\rho }_{w}}}},\,\,\,\,\chi = \sqrt {\frac{{{{\tau }_{c}}}}{\tau }} ,\,\,\,\,{{\tau }_{c}} = {{\theta }_{c}}{{\rho }_{w}}{{\rho }_{b}}dg, \\ \end{gathered} $
где $\kappa $ – параметр Кармана, ${{\rho }_{w}},$ ${{\rho }_{s}}$ – плотности воды и донных частиц, $f$ – концентрация донных частиц в активном слое, $U$ – средняя скорость потока, $g$ – ускорение свободного падения, $d$ – диаметр частиц потока, $D$ – глубина гидродинамического потока, $\tau $ – придонное касательное напряжение, ${{\tau }_{c}}$ – напряжение, определяющее момент начала движения донных частиц, $\varepsilon $ – коэффициент пористости донных частиц, ${{G}_{b}}$ – безразмерный расход влекомых наносов, ${{\theta }_{c}} = 0.047$ – критическое число Шильдса, ${\text{tg}}\varphi = 1.15{{d}^{{{1 \mathord{\left/ {\vphantom {1 7}} \right. \kern-0em} 7}}}}$ – зависимость тангенса угла внутреннего трения от диаметра песчаных частиц [22, 23], ${{G}_{{b{\tau }}}},$ ${{G}_{{b{\zeta }}}},$ ${{G}_{{bp}}}$ – механизмы, которые определяют возникновение и развитие донных волн под влиянием придонных касательных напряжений, градиента уклона дна, градиента придонного напора соответственно.

АНАЛИЗ СКОРОСТИ РОСТА ДОННЫХ ВОЛН

Из экспериментальных данных [17] известно, что на начальном этапе развития донной волны ее длина не изменяется, начальная форма близка к синусоидальной, но при этом происходит рост амплитуды донной волны. Поэтому при исследовании развития донной волны на начальном этапе ее развития принята синусоидальная аппроксимация ее геометрической формы

(10)
$\sigma \left( \xi \right) = \frac{1}{2}\sin \left( {2\pi \xi } \right).$

С учетом геометрии (10) и граничных условий (6)–(8), решение уравнения (1) будет иметь вид

(11)
$\Psi \left( {x,z} \right) = \sigma \left( \xi \right)\exp \left( { - 2\pi \frac{z}{a}} \right),\,\,\,\,\psi \left( \xi \right) = - \frac{\pi }{a}\sin \left( {2\pi \xi } \right),$

что позволяет получить зависимости, необходимые для определения придонного напряжения $\tau $ и давления $p$

(12)
$p\left( \xi \right) = - \frac{h}{a}\pi \sin \left( {2\pi \xi } \right),\,\,\,\,\tau = \frac{{{{\tau }_{0}}}}{{y\left( \xi \right)}},$
(13)
$\begin{gathered} y\left( \xi \right) = E\int\limits_0^1 {\exp \left( {2ax} \right)} \times \\ \times \,\,\exp \left( {\frac{{6h}}{{{{\mu }_{0}}}}\frac{\pi }{a}\left( {\sin \left( {2\pi a\left( {x + \xi } \right)} \right) - \sin \left( {2\pi a\xi } \right)} \right)} \right)dx, \\ \end{gathered} $

которые необходимы для решения задачи определения скорости роста амплитуды донных волн

(14)
$\begin{gathered} \frac{{\partial h}}{{\partial {{t}_{b}}}} = - \frac{{{{G}_{0}}}}{{\sigma {{S}_{d}}}}\frac{\partial }{{\partial \xi }}\left( {\frac{1}{{y{{{\left( \xi \right)}}^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}}}}\left( {A - B\frac{h}{a}\frac{{\partial \sigma }}{{\partial \xi }} - \frac{{FrD}}{L}C\frac{{\partial p}}{{\partial \xi }}} \right)} \right), \\ h\left( 0 \right) = {{h}_{0}}. \\ \end{gathered} $

Решение задачи (14) проводилось при следующих гидродинамических, физико-механических и гранулометрических параметрах, согласованных с работой [17]: $L = 0.1$ м, $D = 0.52$ м, $H = 0.052$ м, $Fr = 0.01,$ ${{\rho }_{w}} = 1000\,\,{{{\text{кг}}} \mathord{\left/ {\vphantom {{{\text{кг}}} {{{{\text{м}}}^{{\text{3}}}}}}} \right. \kern-0em} {{{{\text{м}}}^{{\text{3}}}}}},$ ${{\rho }_{s}} = 2650\,\,{{{\text{кг}}} \mathord{\left/ {\vphantom {{{\text{кг}}} {{{{\text{м}}}^{{\text{3}}}}}}} \right. \kern-0em} {{{{\text{м}}}^{{\text{3}}}}}},$ g = = 9.81 м/с2, ${{H}_{0}} = 0.0062$ м, ${{u}_{0}} = 0.0116$ м/с, ${{\mu }_{0}} = 0.311,$ ${{Z}_{0}} = 5.424d,$ $\kappa = 0.2,$ ${{h}_{0}} = 0.001.$

Результаты решения задачи (14) приведены на рис. 2. Кривыми 1–5 представлены графики изменения скорости роста амплитуды донной волны от величины ее безразмерной амплитуды $h,$ при $\xi = 1{\text{/}}4$ для различных диаметров донных частиц $0.1 \leqslant d \leqslant 0.5\,\,{\text{мм}}{\text{.}}$

Рис. 2.

Изменение скорости роста донной волны при различных диаметрах донных частиц $d.$

Из графиков следует, что с увеличением диаметра донных частиц $d,$ увеличивается максимальная амплитуда донной волны ${{h}_{{\max }}},$ при которой скорость роста волны на первом этапе ее развития прекращается $\frac{{\partial h\left( {{{h}_{{\max }}}} \right)}}{{\partial {{t}_{b}}}} = 0$, и, согласно [17], начинается второй этап развития донной волны – рост ее длины. Отметим, что максимальная скорость роста амплитуды донной волны $\frac{{\partial h}}{{\partial {{t}_{b}}}}$ незначительно изменяется для различных $d.$

Из предположения существования монотонной зависимости между максимальной высотой донной волны и диаметром частиц [8, 9] и полученных результатов (кривые 1–5) следует, что донные волны, сложенные из частиц с малыми диметрами, растут быстрее волн, формируемых из более крупных частиц.

Для волн малой крутизны известны частные линейные зависимости между длиной волны $\lambda $ и ее высотой ${{H}_{0}}$ [8, 24]. Из решения задачи (14) можно построить зависимость ${{H}_{0}}$ от диаметров донных частиц $d,$ позволяющую проверить линейность связи $\lambda \sim {{H}_{0}}.$ Такая зависимость, представлена ниже в форме табл. 1.

Таблица 1.

Безразмерные максимальные амплитуды донной волны, полученные для различных диаметров донных частиц

d, мм  0.1 0.2 0.32 0.4 0.5
${{h}_{{\max }}}$, мм  0.022 0.04 0.059 0.072 0.089

В табл. 1 приведены значения безразмерных максимальных высот ${{h}_{{\max }}},$ найденные с помощью графиков 1–5 (рис. 2) для донных волн, получаемых при различных диаметрах частиц $d.$ Используя метод наименьших квадратов для обработки табличных данных, получена зависимость $h \approx 25{{d}^{{0.75}}},$ которая имеет следующий размерный вид ${{H}_{0}} = 2H \times 25{{d}^{{0.75}}} = 2.6{{d}^{{0.75}}}.$ Сравнивая полученную частную зависимость ${{H}_{0}} = 2.6\,{{d}^{{0.75}}}$ с зависимостью для длины донных волн $\lambda = 31.12{{d}^{{0.75}}},$ полученную S.Е. Coleman с коллегами в работе [9], можно убедиться в их линейности. Значение крутизны донной волны, получаемое из данных зависимостей $k = \frac{{{{H}_{0}}}}{\lambda } \approx 0.083$, попадает в диапазон $0.02 \leqslant k \leqslant 0.09,$ для которого получены результаты (рис. 2).

Пунктирной кривой 6 на рис. 2 представлена зависимость скорости роста амплитуды донной волны, полученная из решения задачи (15), сформулированной в работе [17] на основе обработки экспериментальных данных.

(15)
$\frac{{dh}}{{d{{t}_{b}}}} = 2Tn\left( {1 - {{{\left( {\frac{h}{{{{h}_{{\max }}}}}} \right)}}^{2}}} \right)h,\,\,\,\,h\left( 0 \right) = {{h}_{0}},$
где $T = 150\,{\text{c}},$ $n = 0.035\,{{{\text{c}}}^{{ - 1}}},$ ${{h}_{{\max }}} = 0.0596.$ Сравнение расчетной кривой 3 и кривой 6 показывает их хорошее согласование при $d = 0.32\,{\text{мм}}{\text{.}}$

Отметим, также, что решение задачи (14), для $\xi = {\text{1/}}4$ и диаметра частиц $d = 0.32\,{\text{мм,}}$ представленное на рис. 3 кривой 1, хорошо согласуется с экспериментальными данными, определенными точечным множеством [17].

Рис. 3.

Сравнение расчетного значения высоты донной волны (кривая 1), полученной в результате интегрирования скорости роста амплитуды (14) с экспериментальными данными (точечное множество) [17].

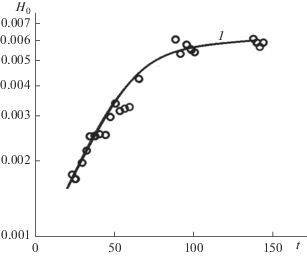
Таким образом, можно утверждать, что предложенная математическая модель развития донной неустойчивости качественно и количественно согласуется с экспериментальными данными в диапазонах, когда перекошенностью донных волн можно пренебречь.

ЗАКЛЮЧЕНИЕ

1. В работе сформулирована и решена задача определения скорости роста амплитуды периодической донной волны малой крутизны. Особенностью задачи является использование аналитической модели расхода влекомых наносов, которая учитывает влияние уклонов донной поверхности, придонных нормальных и касательных напряжений на движение донного материала и аналитической модели, позволяющей определить придонные касательные напряжения, возникающие при обтекании турбулентным потоком периодических длинных донных волн.

2. Проведен анализ полученного аналитического решения задачи для случая периодических синусоидальных донных волн в зависимости от диаметра донного материала. Показано, что диаметр донного материала слабо влияет на максимальную скорость роста волны, а волны, состоящие из более мелких частиц, растут быстрее волн состоящих из крупных частиц. Полученные решения позволили получить частную зависимость для высоты донной волны от диаметра донных частиц, которая согласуется с гипотезой о линейной связи между высотой и длиной донных волн малой крутизны. Выполненное сравнение полученного решения с экспериментальными данными показало их хорошее качественное и количественное согласование.

Работа выполнена при частичной финансовой поддержке гранта РФФИ № 18-05-00530 А и гранта РФФИ и ГФЕН № 21-57-53019.

Список литературы

  1. Kennedy J.F. The mechanics of dunes and antidunes in erodible bed channels // Fluid Mech. 1963. V. 16. № 14. P. 521–544.

  2. Kennedy J.F. The formation of sediment ripples, dune and antidunes // Annu. Rev. Fluid Mech. 1969. V. 1. P. 147–168.

  3. Engelund F. Sediment ripples and dunes // Annu. Rev. Fluid Mech. 1982. V. 4. P. 13–37.

  4. Гришанин К.В. Устойчивость русел рек и каналов. Л.: Гидрометеоиздат, 1974. 143 с.

  5. Мельникова О.Н. Динамика руслового потока: учебное пособие. М.: МАКС Пресс, 2006. 139 с.

  6. Михайлова Н.А. Перенос твердых частиц турбулентными потоками воды. Л.: Гидрометеоиздат, 1966. 236 с.

  7. Bagnold R. Motion of waves in shallow water. // Proc. R. Soc. London, Ser. А. V. 187. № 1008. 1946.

  8. Шуляк Б.А. Физика волн на поверхности сыпучей среды и жидкости. М.: Наука, 1971.

  9. Coleman S.E., Fedele J.J., Garcia M.H. Closed-conduit bed-forms initiation and development // J. Hydraulic Engineering. 2003. V. 129. № 12. P. 956–965.

  10. Крат Ю.Г., Потапов И.И. Устойчивость дна в напорных каналах // Компьютерные исследования и моделирование. 2015. Т. 7. С. 1061–1068.

  11. Tjerry S. Morphological calculation of dunes in alluvial rivers // Ph.D. Thesis. Institute of hydrodynamics and hydraulic engineering, Technical university of Denmark. 1995. P. 193.

  12. Sanne L.N. Modeling of sand dunes in steady and tidal flow // Ph.D. Thesis. Coastal and river engineering section, Technical university of Copenhagen, Denmark. 2003. P. 185.

  13. Paarlberg A.J., Dohmen-Janssen C.M., Hulscher S.J., Termes P. Modeling river dune evolution using a parameterization of flow separation // J. Geophys. Res. 2009. V. 114. P. F01014.

  14. Khosronejad A., Sotiropoulos F. Numerical simulation of sand waves in a turbulent open channel flow // J. Fluid Mech. 2014. V. 753. P. 150–216.

  15. Liu Y., Fang H., Huang L., He G. Numerical simulation of the production of three-dimensional sediment dunes // Physics of Fluids. 2019. V. 31. Iss. 9. Р. 096603.https://doi.org/10.1063/1.5108741

  16. Zgheib N., Balachandar S. Linear stability analysis of subaqueous bedforms using direct numerical simulations // Theor. Comput. Fluid Dyn. 2019. Iss. 2. P. 161–180. https://doi.org/10.1007/s00162-019-00487-x

  17. Fourriere A., Claudin Ph., Andreotti B. Bedforms in a turbulent stream: formation of ripples by primary linear instability and of dunes by nonlinear pattern coarsening // J. Fluid Mechanics. 2010. V. 649. P. 287–328.

  18. Петров А.Г., Потапов И.И. Перенос наносов под действием нормальных и касательных придонных напряжений с учетом уклона дна // Прикладная механика и техническая физика. 2014. Т. 55. № 5. С. 100–105.

  19. Крат Ю.Г., Потапов И.И. Влияние размера частиц донных наносов на длину волны донных возмущений в напорных каналах // Прикладная механика и техническая физика. 2016. Т. 57. № 3. С. 60–64.

  20. Крат Ю.Г., Потапов И.И. Модель стохастического развития донных волн // Вестн. Удмуртского университета. Математика. Механика. Компьютерные науки. 2013. Вып. 2. С. 85–91.

  21. Петров А.Г., Потапов И.И. Моделирование обтекания турбулентным потоком периодической донной поверхности // Изв. РАН. Физика атмосферы и океана. 2017. Т. 53. № 3. С. 415–421.

  22. Петров А.Г., Потапов И.И. Избранные разделы русловой динамики. М: ЛЕНАНД, 2019. 244 с.

  23. Мажидов Т.Ш. Расчетные гидравлические характеристики потоков и параметров песчано-гравийных гряд с учетом состава наносов / Дис. ... канд. техн. наук. 05.14.09. Ташкент, 1984. 275 с.

  24. Петров А.Г., Потапов И.И. О задаче русловой устойчивости Энгелунда–Фредсо // Изв. РАН. Физика атмосферы и океана. 2020. Т. 56. № 4. С. 428–432.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Физика атмосферы и океана

Архивы выпусков Информация о журнале Отправить рукопись в журнал