1. На главную
  2. Электронные версии
  3. Известия РАН. Физика атмосферы и океана
  4. T. 57, № 5, 2021

Известия РАН. Физика атмосферы и океана, 2021, T. 57, № 5, стр. 555-564

Вертикальное распределение алевритовых и песчаных частиц в ветропесчаном потоке над опустыненной территорией

Г. И. Горчаков a, *, А. В. Карпов a, **, Р. А. Гущин a, ***, О. И. Даценко a, ****, Д. В. Бунтов a, *****

a Институт физики атмосферы им. А.М. Обухова РАН
119017 Москва, Пыжевский пер., 3, Россия

* E-mail: gengor@ifaran.ru
** E-mail: karpov@ifaran.ru
*** E-mail: gushchin@ifaran.ru
**** E-mail: datsenko@ifaran.ru
***** E-mail: dbunt@mail.ru

Поступила в редакцию 12.04.2021
После доработки 07.05.2021
Принята к публикации 09.06.2021

Полный текст (PDF)

Аннотация

По данным измерений на опустыненной территории в Астраханской обл. на высотах от 3 до 15 см в условиях квазинепрерывной сальтации 23.08.11 и 01.09.2011 определены функции распределения сальтирующих частиц по размерам в диапазоне от 30 до 330 мкм, построены вертикальные профили дифференциальных счетных концентраций частиц с размерами 47.0, 85.6, 104.6, 127.7 и 156.0 мкм, которые аппроксимированы экспонентами. Показано, что в нижнем слое сальтации толщиной около 9 см масштаб высоты и логарифмический градиент концентрации не зависят от скорости ветра. Установлено, что на высотах 11 и 15 см суммарная концентрация сальтирующих частиц связана нелинейными соотношениями со скоростью ветра в приземном слое атмосферы. Для диапазона изменения скорости ветра от 6 до 11.0 м/с построены вертикальные распределения концентрации сальтирующих частиц, которые аппроксимированы кусочно-экспоненциальными профилями суммарной концентрации частиц. Получена аналитическая зависимость от скорости ветра логарифмического градиента концентрации в верхнем слое сальтации. Разработана малопараметрическая модель вертикального распределения сальтирующих частиц в диапазоне высот от 0 до 15 см. Предложены аппроксимации зависимостей от размера частиц масштаба высоты для вертикальных профилей концентрации и массового потока сальтирующих частиц.

Ключевые слова: опустынивание, ветропесчаный поток, квазинепрерывная сальтация, сальтирующие алевритовые частицы, вертикальное распределение концентрации частиц, кусочно-экспоненциальная аппроксимация, масштаб высоты, логарифмический градиент концентрации, толщина нижнего слоя сальтации, малопараметрическая модель вертикального распределения концентрации

1. ВВЕДЕНИЕ

В современную эпоху потепления климата в ряде регионов планеты возможно ускорение процессов опустынивания и аридизации [1, 2 ] , что приведет к повышению содержания в атмосфере пылевого аэрозоля и усилению его радиационных эффектов. На опустыненных территориях основным механизмом эмиссии минерального пылевого аэрозоля является воздействие ветропесчаного потока на подстилающую поверхность (sandblasting) [3, 4], в котором основным процессом является сальтация [5–10] – скачкообразное перемещение песчинок. В аридных регионах существенный вклад вносит конвективно обусловленный вынос пылевого аэрозоля в атмосферу [11–16].

По данным измерений на опустыненной территории в Астраханской обл. функции распределения сальтирующих частиц по размерам [17] с помощью фотоэлектрического счетчика [18] показано, что в ветропесчаном потоке кроме сальтирующих частиц песчаной фракции с размерами больше 100 мкм и фракции частиц минеральной пыли (пылевой аэрозоль) с размерами меньше примерно 10 мкм, которые в геологии относят к обломочным породам [19], присутствует алевритовая фракция сальтирующих частиц с размерами примерно от 30 до 100 мкм (алеврит также относится к обломочным породам [19]). Отметим, что в [9] в качестве примера показана траектория сальтирующей частицы с аэродинамическим диаметром около 65 мкм, полученная с использованием скоростной видеосъемки на опустыненной территории в Астраханской обл.

Большинство исследований механизмов сальтации и эмиссии пылевого аэрозоля выполнено в ветровых каналах [20–25], где невозможно адекватно воспроизвести все особенности взаимодействия атмосферы с песчаной подстилающей поверхностью.

Ветропесчаный поток на опустыненных территориях отличается аномально высокой электризацией [26–29]. Удельный заряд сальтирующих частиц может достигать +(50–60) мкКл/кг [10, 26, 29].

На интенсивность сальтации сильно влияют турбулентные и конвективные процессы в пограничном слое атмосферы [30–33]. Из [34, 35] следует, что турбулентность сильнее влияет на динамику сальтирующих алевритовых частиц (по сравнению с динамикой песчаных частиц), что обусловлено их меньшей инерционностью.

На процессы в ветропесчаном потоке также влияет образование ряби (рифелей) и мелкой ряби на подстилающей поверхности [8, 36–38], что может привести к возникновению квазипериодических вариаций интенсивности сальтации [9, 38]. Поэтому необходимы дальнейшие исследования процесса сальтации непосредственно на опустыненных территориях.

Целью настоящей работы является количественная характеристика вертикального распределения сальтирующих алевритовых и песчаных частиц в условиях квазинепрерывной или неперемежающейся (almost non-intermittent) сальтации [39] на опустыненной территории при вариациях скорости ветра в приземном слое атмосферы по данным измерений функции распределения сальтирующих частиц по размерам или дифференциальных счетных концентраций сальтирующих частиц, включая (1) построение и аппроксимацию средних вертикальных профилей концентрации сальтирующих алевритовых и песчаных частиц, а также вертикального профиля суммарной концентрации, (2) анализ зависимостей от скорости ветра суммарной концентрации частиц в нижнем и верхнем слоях сальтации, (3) построение и аппроксимацию вертикального профиля суммарной концентрации сальтирующих частиц в верхнем и нижнем слоях сальтации для различных значений скорости ветра и (4) оценку толщины нижнего слоя сальтации. Предложена малопараметрическая модель вертикального распределения сальтирующих частиц в слое от 0 до 15 см, которая обобщает полученные в данной работе результаты. Предложены аппроксимации зависимостей от размера частиц параметров вертикального распределения концентрации и массового потока сальтирующих частиц с использованием опубликованных данных [22].

Следует отметить, что на вертикальное распределение сальтирующих частиц влияет режим сальтации [39] и эоловые формы рельефа или морфология подстилающей поверхности, включая дюны, барханы и рябь [7, 8, 37, 38]. В настоящей работе использованы данные измерений на опустыненной территории вблизи р. Волги с плоским рельефом без барханов и дюн и без растительности в период с 16.08 по 01.09.2011. Представлены результаты измерений 23.08.2011 и 01.09.2011 в условиях квазинепрерывной сальтации, которые можно сопоставить с результатами исследований сальтации в ветровых каналах [22–25].

2. ИСПОЛЬЗУЕМЫЕ ДАННЫЕ

В работе использованы результаты измерений с временным разрешением 1 с суммарной концентрации N и дифференциальных счетных концентраций сальтирующих частиц g(D) = dN(D)/dlnD, где D – размер частицы и N(D) – накопленная концентрация частиц, в диапазоне размеров от 30 до 330 мкм с разрешением по размерам Δ lnD = 0.1, что соответствует изменению примерно на 10% в каждом интервале размеров, на высотах 3, 11 и 15 см с помощью фотоэлектрического счетчика сальтирующих частиц [18] на опустыненной территории в Астраханской обл. [17, 40] 23.08.2011 в период с 12:05 до 15:05. Данные измерений на высоте 7 см в рассматриваемый период не использовались в связи с погрешностями в работе соответствующего канала фотоэлектрического счетчика. При восстановлении вертикальных профилей концентраций сальтирующих частиц использовались данные измерений в периоды времени с 11:05 до 12:05 и с 15:06 до 16:06, когда проводились синхронные измерения для всех каналов счетчика [40] на высоте 6 см. Использовались также данные измерений для дифференциальных счетных концентраций сальтирующих частиц на высотах 3, 7, 15 см 01.09.2011 в период с 13:10 до 14:10.

В приземном слое атмосферы на высоте 2 м измерялись компоненты скорости ветра и температура воздуха с временным разрешением 0.1 с с помощью акустической метеостанции Метео-2 (Институт оптики атмосферы, г. Томск). Средние значения скорости ветра в приземном слое атмосферы в периоды проведения измерений 23.08 и 01.09.2011 были равны 7.55 и 8.05 м/с соответственно. Вероятность значений скорости ветра меньше пороговой скорости сальтации (5.0–5.1 м/с) в периоды проведения измерений не превышала 2% [33, 40], что достаточно для реализации режима квазинепрывной сальтации.

В [22] для пяти образцов песчаного грунта с средними размерами песчинок от 150 до 550 мкм в ветровом канале выполнены измерения вертикальных распределений концентрации и массового потока сальтации. Полученные в [22] результаты использованы нами при аппроксимации зависимостей от размера частиц масштаба высоты для указанных распределений.

3. ВЕРТИКАЛЬНЫЕ ПРОФИЛИ КОНЦЕНТРАЦИЙ АЛЕВРИТОВЫХ И ПЕСЧАНЫХ ЧАСТИЦ

В [17] по данным измерений функции распределения сальтирующих частиц по размерам на опустыненной территории в Астраханской обл. 23.08.2011 в период с 12:05 до 15:05 получено вертикальное распределение суммарной концентрации частиц N(z), где z – высота, которое с удовлетворительной точностью аппроксимируется экспонентой в диапазоне высот от 3 до 15 см

(1)
$N(z) = {{N}_{0}}\exp \{ {{ - z} \mathord{\left/ {\vphantom {{ - z} {{{z}_{N}}}}} \right. \kern-0em} {{{z}_{N}}}}\} ,$
где N0 = 2725 дм-3, масштаб высоты zN = 3.16 см и логарифмический градиент концентраций (ЛГК) ${{\gamma }_{N}} = d\ln {{N(z)} \mathord{\left/ {\vphantom {{N(z)} {dz}}} \right. \kern-0em} {dz}} = - z_{N}^{{ - 1}} = - 0.316\,\,{\text{с}}{{{\text{м}}}^{{ - 1}}}.$

В ряде работ zN называют толщиной слоя сальтации. Отметим, что полная толщина слоя сальтации существенно больше zN.

По данным измерений функции распределения частиц по размерам g(D) 23.08.2011 в указанный период времени на высоте 3, 11 и 15 см построены вертикальные профили дифференциальных счетных концентраций частиц (рис. 1) с средними размерами 47.0 (1), 85.6 (2), 104.6 (3), 127.7 (4) и 156.0 мкм (5). Использованы также полученные ранее [40] зависимости концентраций сальтирующих на высоте 6 см частиц разных размеров от скорости ветра в приземном слое атмосферы. Погрешность привязки шкалы фотоэлектрического счетчика частиц в абсолютных единицах при D = 100 мкм составляет примерно ±5 мкм. Подробные значения центров интервалов частиц (с шириной $\Delta \ln D$ = 0.1) приведены для характеристики используемого разбиения диапазона размеров частиц на интервалы с указанной выше шириной.

Рис. 1.

Зависимость от высоты дифференциальных счетных концентраций сальтирующих частиц с размерами 47.0 (1), 85.6 (2), 104.6 (3), 127.7 (4) и 156.0 мкм (5) по данным измерений 23.08.11 в период с 12:05 по 15:05 на опустыненной территории в Астраханской обл.

Полученные вертикальные распределения дифференциальных счетных концентраций g(D) с удовлетворительной точностью аппроксимируются экспоненциальными профилями [41]

(2)
$g{\kern 1pt} *(z,D) = g_{0}^{*}(D)\exp \{ {{ - z} \mathord{\left/ {\vphantom {{ - z} {{{z}_{D}}}}} \right. \kern-0em} {{{z}_{D}}}}\} $

c ЛГК, равными 0.30 (1), 0.307 (2), 0.314 (3), 0.327 (4), 0.347 (5) см–1 для значений D от 47.0 до 156.0 мкм.

Анализ показал, что зависимость ЛГК γD(D) = = $ - z_{D}^{{ - 1}}$ от размера частиц D аппроксимируется соотношением

(3)
${{\gamma }_{D}}(D) = - 0.30 - 0.075{{(\ln D - 3.85)}^{3}}.$

Максимальное значение масштаба высоты zD достигается при D = 47 мкм, что может быть обусловлено влиянием турбулентных пульсаций вертикальной компоненты скорости ветра на траектории сальтирующих частиц [42]. При одинаковых концентрациях вблизи подстилающей поверхности алевритовых частиц с размером 47 мкм и песчаных частиц с размером 156 мкм на высоте 15 см концентрация алевритовых частиц в два раза больше концентрации песчаных частиц.

4. СТАТИСТИЧЕСКИЕ СВЯЗИ КОНЦЕНТРАЦИЙ ЧАСТИЦ В НИЖНЕМ И ВЕРХНЕМ СЛОЯХ САЛЬТАЦИИ СО СКОРОСТЬЮ ВЕТРА

В [40] показано, что суммарная концентрация сальтирующих частиц на высоте 6 см связана соотношением линейной регрессии со скоростью ветра в приземном слое атмосферы (на высоте 2 м) ${{N}_{6}} = {{K}_{6}}(V - {{V}_{0}})$, где V – скорость ветра, V0 – пороговая скорость сальтации и K6 – коэффициент пропорциональности.

Анализ данных измерений концентрации частиц N3 на высоте 3 см показал, что 23.08.2011 в период с 12:05 до 15:05 имела место линейная корреляция между N3 и скоростью ветра на высоте 2 м (рис. 2а), которая описывается соотношением линейной регрессии.

(4)
${{N}_{3}} = {{K}_{3}}(V - {{V}_{0}}),$
где K3 = 415 дм–3 м–1 c и V0 = 5.0 м/с (коэффициент корреляции между N3 и V равен 0.83).

Рис. 2.

Корреляционные связи со скоростью ветра в приземном слое атмосферы концентраций сальтирующих частиц на высотах 3 см (а), 11 см (б) и 15 см (в) (1-аппроксимации).

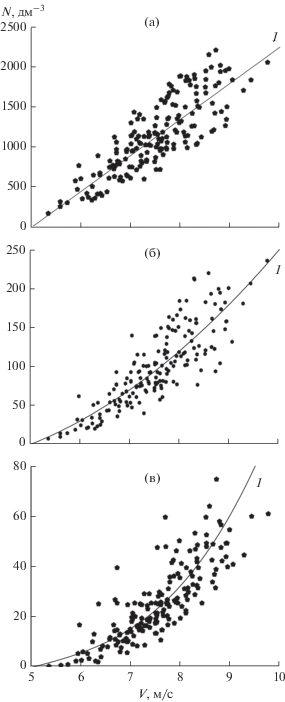
Корреляционная связь между концентрацией частиц на высоте 11 см и разностью V – V0 оказалась нелинейной (рис. 2б)

(5)
${{N}_{{11}}} = K_{{11}}^{{(1)}}(V - {{V}_{0}}) + K_{{11}}^{{(2)}}{{(V - {{V}_{0}})}^{2}},$
где $K_{{11}}^{{(1)}}$ = 23.9 дм–3 м–1 с и $K_{{11}}^{{(2)}}$ = 3.5 дм–3 м–2 с2.

Нелинейная связь между концентрацией сальтирующих частиц на высоте 15 см и разностью V – V0 (рис. 2в) заметно отличается от корреляционной связи (5)

(6)
${{N}_{{11}}} = K_{{15}}^{{(1)}}(V - {{V}_{0}}) + K_{{15}}^{{(2)}}{{(V - {{V}_{0}})}^{3}},$
где $K_{{15}}^{{(1)}}$ = 5.2 дм–3 м–1 с и $K_{{15}}^{{(2)}}$ = 0.625 дм–3 м–3 с3.

В частности, вклад в N15 нелинейной составляющей при V = 9.0 м/с достигает 65%.

Из вышеизложенного следует, что в верхнем слое сальтации на траектории сальтирующих частиц сильно влияет турбулентность, и это влияние растет с увеличением высоты и скорости ветра, что неизбежно приводит к зависимости формы вертикальных профилей концентрации сальтирующих частиц от скорости ветра.

5. ВЛИЯНИЕ ВЕТРА НА ВЕРТИКАЛЬНОЕ РАСПРЕДЕЛЕНИЕ САЛЬТИРУЮЩИХ ЧАСТИЦ

Полученные нами зависимости от скорости ветра концентраций частиц в нижнем и верхнем слоях сальтации позволили восстановить вертикальные распределения сальтирующих частиц в диапазоне высот от 3 до 15 см при изменении скорости ветра от 5.5 до 10.0 м/с по данным измерений 23.08.2011 в период от 12:05 до 15:05 и от 5.5 до 11.0 м/с по данным 01.09.2011 в период от 13:10 до 14:10.

На рис. 3 показаны вертикальные распределения концентраций сальтирующих частиц для значений скорости ветра в приземном слое атмосферы 6.0 (1), 7.0 (2), 8.0 (3), 9.0 (4) и 10.0 м/с (5), построенные по данным измерений 23.08.2011, на высотах 3, 11 и 15 см (с использованием информации о зависимости скорости ветра концентрации частиц на высоте 6 см [40]), а на рис. 4 аналогичные распределения концентрации для значений скорости ветра 6.0 (1), 7.0 (2), 8.0 (3), 9.0 (4), 10.0 (5) и 11.0 (6) по данным измерений 01.09.2011 на высотах 3, 7, 11 и 15 см.

Рис. 3.

Вертикальные профили суммарной концентрации сальтирующих частиц для значений скорости ветра в приземном слое атмосферы 6.0 (1), 7.0 (2), 8.0 (3), 9.0 (4) и 10.0 м/с (5) по данным измерений 23.08.11 в период с 12:05 по 15:05 на опустыненной территории в Астраханской обл. (E и F – точки пресечения экстраполяций вертикальных профилей концентрации в слоях А и В для значений скорости ветра 10.0 и 6.0 м/с).

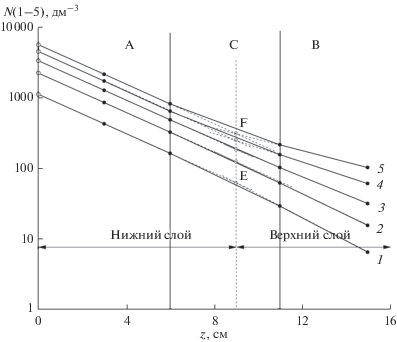
Рис. 4.

Вертикальные профили суммарной концентрации сальтирующих частиц для значений скорости ветра в приземном слое атмосферы 6.0 (1), 7.0 (2), 8.0 (3), 9.0 (4), 10.0 (5) и 11.0 м/с (6) по данным измерений 01.09.2011 в период с 13:10 по 14:10 на опустыненной территории в Астраханской обл. (E и F – точки пресечения экстраполяций вертикальных профилей концентрации в слоях А и В для значений скорости ветра 11.0 и 6.0 м/с).

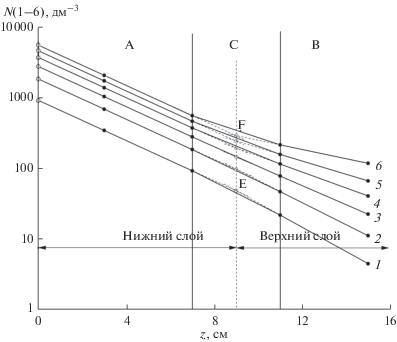
На рис. 3 выделены диапазоны высоты от 0 до 6 см (A), от 11 до 15 см (B) и от 6 до 11 см (С), а на рис. 4 диапазоны от 0 до 7 см (A), от 11 до 15 см (B) и от 7 до 11 см (С).

Анализ данных измерений показал, что в слое от 3 до 6 см ЛГК (γА) в пределах погрешности измерений не зависит от скорости ветра и равен –0.315 см–1, что практически совпадает с ЛГК для полной концентрации сальтирующих частиц (–0.316 см–1) [33]. Согласно данным измерений 01.09.2011 ЛГК в слое от 3 до 7 см γА = = –0.328 см–1 [41].

Учитывая линейную зависимость концентрации частиц в нижнем слое сальтации от скорости ветра [40, 41], вертикальное распределение частиц в слое А будем аппроксимировать экспоненциальным профилем

(7)
${{N}_{A}}(z,V) = {{K}_{A}}(V - {{V}_{0}})\exp \{ {{\gamma }_{A}}z\} ,$
где KA = 1070 и 788 дм–3 м–1 с для 23.08 и 01.09.2011 соответственно.

Независимость масштаба высоты и ЛГК от скорости ветра и динамической скорости была ранее установлена по данным измерений в ветровых каналах на высотах от 0.5 до 5.0 см [25] и от 1 до 10 см [22], а также по данным полевых измерений [43]. В нашей работе [9] по данным скоростной видеосъемки в диапазоне высот от 2 до 38 мм (с разрешением по высоте 2 мм) продемонстрирована пригодность экспоненциальной аппроксимации вертикального профиля концентрации сальтирующих частиц вблизи подстилающей поверхности. Таким образом, полученные нами профили допускают экспоненциальную экстраполяцию в диапазоне высот от 0 до 3 см.

Нетрудно видеть, что в слое B (от 11 до 15 см) ЛГК зависит от скорости ветра. Вертикальные распределения концентрации частиц в этом слое можно аппроксимировать экспонентами

(8)
${{N}_{B}}(z,V) = {{N}_{0}}(V)\exp \{ {{\gamma }_{B}}(V)z\} .$

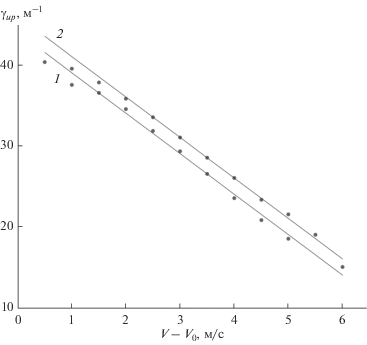
На рис. 5 представлены результаты определения γB по данным измерений 23.08 (1) и 01.09.2011 (2) для V от 6.0 до 11.0 м/с (с шагом 1 м/с) и с учетом результатов, полученных в [41], для V от 5.5 до 10.5 м/с (с шагом 1 м/с). Полученные зависимости (рис. 5) аппроксимируется линейными функциями

(9)
${{\gamma }_{B}}(V) = {{\gamma }_{0}} + {{k}_{\gamma }}(V - {{V}_{0}}),$
где γ0 = –44 (1) и –46 м–1 (2), kγ = 45 м–2 с и V0 = = 5.0 м/с. В среднем γB = –45 м–1 = –0.45 см–1. Отметим, что погрешность определения γB увеличивается при V близких к V0.

Рис. 5.

Логарифмический градиент концентрации частиц в верхнем слое сальтации по данным измерений 23.08.2011 (1) и 01.09.2011 (2).

При восстановлении вертикальных профилей концентрации сальтирующих частиц целесообразно использовать кусочно-экспоненциальную аппроксимацию, взяв за основу экспоненциальные аппроксимации профилей в слоях A и B. Экстраполируя указанные аппроксимации в слой С, найдем точки пересечения для выбранных нами значений скорости ветра (в частности, точки E и F на рис. 3 и 4), которые находятся на уровне примерно 9 см для 23.08.2011 (рис. 3) и на уровне 8.5–9 см для 01.09.2011 (рис. 4). Это позволяет выделить нижний слой сальтации толщиной 9 см с постоянным ЛГК γlw = γA и верхний слой сальтации, расположенный выше 9 см с ЛГК, зависящим от скорости ветра, ${{\gamma }_{{up}}}(V) = {{\gamma }_{B}}(V)$.

В верхнем слое сальтации профиль концентрации аппроксимируется экспонентой

(10)
$\begin{gathered} {{N}_{{up}}}(z,V) = \\ = {{K}_{A}}(V - {{V}_{0}})\exp (9{{\gamma }_{A}})\exp \{ {{\gamma }_{B}}(V)(z - 9)\} . \\ \end{gathered} $

Совокупность аппроксимаций (7), (9) и (10) представляет собой малопараметрическую модель вертикального распределения концентрации сальтирующих частиц для диапазона изменения скорости ветра от V0 до 11.0 м/с.

6. ЗАВИСИМОСТЬ ОТ РАЗМЕРА ЧАСТИЦ МАСШТАБА ВЫСОТЫ ДЛЯ ВЕРТИКАЛЬНЫХ РАСПРЕДЕЛЕНИЙ КОНЦЕНТРАЦИИ И МАССОВОГО ПОТОКА САЛЬТАЦИИ

Вертикальные распределения концентрации и массового потока сальтирующих частиц были измерены в ветровом канале на высотах от 1 до 10 см для пяти образов песчаного грунта с размерами частиц 100–200, 200–300, 300–400, 400–500 и 500–600 мкм (средние размеры 150, 250, 350, 450 и 550 мкм) и для пяти значений скорости воздушного потока на оси канала 10, 12, 14, 16 и 18 м/с [22] (динамическая скорость не определялась).

Вертикальные профили массовых концентраций и массовых потоков частиц аппроксимировались экспонентами с масштабами высоты zm и zf с-оответственно. Отметим, что для отдельных профилей наблюдались заметные отклонения от экспоненциальных аппроксимаций. Среднее значение масштаба высоты zm для профиля концентрации увеличивается примерно от 4 до 7 см с ростом среднего размера частиц от 150 до 550 мкм.

Для описания зависимости zm(D) нами предложена линейная аппроксимация (1 на рис. 6).

(11)
$\ln {{z}_{m}} = 0.4\ln D - 0.59,$
Рис. 6.

Зависимости от размера частиц масштаба высоты для концентрации (1) и массового потока сальтации (2).

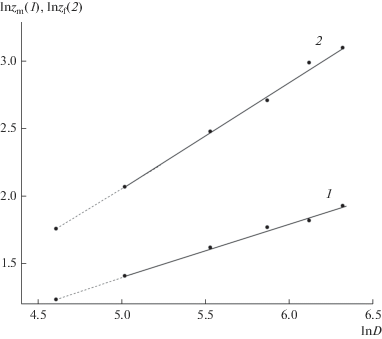
которой соответствует степенная функция zm = = 3.24D0.4. Экстраполяция полученной зависимости в точку D = 100 мкм приводит к значению zm = = 3.45 см, которое примерно на 10% больше масштаба высоты для профиля суммарной концентрации сальтирующих частиц на опустыненной территории в Астраханской обл. по данным измерений 23.08.2011 (zN = 3.16 см).

Представленная на рис. 6 зависимость масштаба высоты zf для профиля массового потока сальтирующих частиц аппроксимируется соотношением

(12)
$\ln {{z}_{f}} = 0.8\ln D - 1.92$

или соответствующей степенной функцией zf = = 0.147D0.8. Для D = 100 мкм масштаб высоты zf = = 5.85 см, который превышает zm для D = 100 мкм в 1.7 раза.

Полученные аппроксимации позволяют получить соотношение между масштабами высоты zm и zf :

(13)
$\ln {{z}_{f}} = 2\ln {{z}_{m}} - 0.74.$

Соотношение (13) можно использовать для оценки вертикального распределения массового потока сальтирующих частиц.

7. ЗАКЛЮЧЕНИЕ

Выполнено экспериментальное исследование вертикального распределения сальтирующих алевритовых и песчаных частиц в ветропесчаном потоке. По данным измерений на опустыненной территории в Астраханской обл. в условиях квазинепрерывной сальтации на высотах от 3 до 15 см определены функции распределения сальтирующих частиц по размерам в диапазоне от 30 до 330 мкм, восстановлены вертикальные распределения счетных концентраций частиц с размерами 47, 85.6, 104.6, 127.7 и 156 мкм, которые с удовлетворительной точностью аппроксимируются экспоненциальными профилями. Предложена аппроксимация зависимости от размера частиц в диапазоне от 47 до 156 мкм логарифмического градиента концентрации. Отмечено, что концентрация песчаных частиц с размером 156 мкм в слое от 0 до 15 см убывает в два раза быстрее концентрации алевритовых частиц с размером 47 мкм.

Проанализированы статистические связи между скоростью ветра в приземном слое атмосферы на высоте 2 м и суммарной концентрацией частиц в нижнем и верхнем слоях сальтации. В верхнем слое сальтации в отличие от нижнего корреляционные связи концентрации частиц со скоростью ветра оказались нелинейными.

По данным измерений на опустыненной территории в Астраханской обл. 23.08.2011 и 01.09.2011 построены вертикальные распределения концентрации сальтирующих частиц в слое от 3 до 15 см для диапазона изменения ветра в приземном слое атмосферы от 6.0 до 11.0 м/с. Предложена кусочно-экспоненциальная аппроксимация вертикальных профилей концентрации сальтирующих частиц. Показано, что в нижнем слое сальтации на опустыненной территории логарифмический градиент концентрации не зависит от скорости ветра.

Получена и аппроксимирована зависимость от скорости ветра логарифмического градиента концентрации в верхнем слое сальтации. Определена толщина нижнего слоя сальтации (около 9 см). Предложена малопараметрическая модель вертикального распределения концентраций сальтирующих частиц в слое от 0 до 15 см для диапазона изменения скорости ветра от пороговой скорости сальтации до 11.0 м/с.

По опубликованным данным получены зависимости от размера сальтирующих частиц масштаба высоты вертикальных распределений концентрации и массового потока частиц и соотношение между масштабами высоты для указанных профилей. Получена оценка масштаба для массового потока частиц с размерами 100 мкм, близкими к модальному размеру частиц на опустыненной территории в Астраханской обл.

Работа выполнена при финансовой поддержке РФФИ (грант № 19-05-00758).

Список литературы

  1. IPCC. Special Report “Global Warming of 1.5°C”. 2018.

  2. Золотокрылин А.Н. Климатическое опустынивание. М.: Наука, 2003. 247 с.

  3. Miller R., Tegen I., Perlwitz J. Surface radiative forcing by soil dust aerosol and the hydrologic cycle // J. Geophys. Res. 2004. V. 109. DO4203.

  4. Alfaro S.C., Gaudichet A., Gomes L., Maille M. Modeling the size distribution of a soil aerosol produced by sandblasting // J. Geophys. Res. 1997. V. 102. P. 11239–11249.

  5. Bagnold R.A. The Physics of Blown Sand and Desert Dunes. London: Methuen, 1941. 265 p.

  6. Shao Y. Physics and Modeling of Wind Erosion. N.Y.: Springer, 2000. 393 p.

  7. Kok J.F., Parteli E.J.R., Michaels T.I., Karam D.B. The physics of wind-blown sand and dust // Rep. Prog. Phys. 2012. V. 75. 106901. P. 1–119.

  8. Семенов О.Е. Введение в экспериментальную метеорологию и климатологию песчаных бурь. Алматы: КазНИИЭК, 2011. 580 с.

  9. Горчаков Г.И., Карпов А.В., Копейкин В.М., Злобин И.А., Бунтов Д.В., Соколов А.В. Исследование динамики сальтирующих песчинок на опустыненных территориях // Докл. АН. 2013. Т. 452. № 6. С. 669–676.

  10. Горчаков Г.И., Карпов А.В., Копейкин В.М., Соколов А.В., Бунтов Д.В. Влияние силы Сэфмана, подъёмной силы и электрической силы на перенос частиц в ветропесчаном потоке // Докл. АН. 2016. Т. 467. № 3. С. 336–341.

  11. Ju T., Li X., Zhang H., Song Y. Comparison of two different dust emission mechanisms over the Horqin Sandy Land area: Aerosols contribution and size distributions // Atmosph. Environment. 2018. V. 176. P. 82–90.

  12. Chkhetiani O.G., Gledzer E.B., Artamonova M.S., Iordanskii M.A. Dust resuspension under weak wind conditions: direct observations and model // Atmos. Chem. Phys. 2012. V. 12. P. 5147–5162.

  13. Klose M., Shao Y. Stochastic parameterization of dust emission and application to convective atmospheric conditions // Atmos. Chem. Phys. 2012. V. 12. P. 7309–7320.

  14. Вазаева Н.В., Чхетиани О.Г., Максименков А.О Организованная валиковая циркуляция и перенос минеральных аэрозолей в атмосферном пограничном слое // Изв. РАН. Физика атмосферы и океана. 2019. Т. 55. № 2. С. 17–31.

  15. Горчаков Г.И., Карпов А.В., Гущин Р.А. Турбулентные потоки пылевого аэрозоля на опустыненной территории // Докл. РАН. Наука о Земле. 2020. Т. 494. № 2. С. 53–57.

  16. Малиновская Е.А., Чхетиани О.Г. Об условиях ветрового выноса частиц почвы // Вычислительная механика сплошных сред. 2020. Т. 13. № 2. С. 175–188.

  17. Горчаков Г.И., Бунтов Д.В., Карпов А.В., Копейкин В.М., Мирсаитов С.Ф., Гущин Р.А., Даценко О.И. Алевритовая фракция сальтирующих частиц в ветропесчаном потоке на опустыненной территории // Докл. РАН. Науки о Земле. 2019. Т. 488. № 2. С. 193–196.

  18. Бунтов Д.В., Гущин Р.А., Даценко О.И. Четырехканальный фотоэлектрический счетчик сальтирующих песчинок // Оптика атмосферы и океана. 2018. Т. 31. № 6. С. 485–488.

  19. Pettijohn F.G. Sedimentary Rocs. N.Y.: Harper, 1957. 526 p.

  20. White B.R., Schulz J.C. Magnus effect in saltation // J. Fluid Mech. 1977. V. 81. № 3. P. 497–512.

  21. Zheng X.J., Huang N., Zhou Y.H. Laboratory measurement of electrification of wind-blown Sands and simulation of its effect on sand saltation movement // J. Geophys. Res. 2003. V. 108. № D10. 4322.

  22. Liu X., Dong Z. Experimental investigation of the concentration profile of a blowing sand cloud // Geomorphology. 2004. V. 60. P. 371–382.

  23. Huang N., Zheng X.-J., Zhou Y.-H., Scott Van Pelt R. Simulation of wind-blown sand movement and probability density function of liftoff velocities of sand particles // J. Geophys. Res. 2006. V. 111. D20201.

  24. Rasmussen K.R., Sorensen M. Vertical variation of particle speed and flux in aeolian saltation: Measurement and modeling // J. Geophys. Res. 2008. V. 113. FO2S12.

  25. Creyssels M., Dupont P., El Moctar A., Valance A., Cantat I., Jenkins J.T., Pasini J.M., Rasmussen K.R. Saltating particles in a turbulent boundary layer: experiment and theory // J. Fluid Mech. 2009. V. 625. P. 47–74.

  26. Schmidt D.S., Schmidt R.A., Dent Y.D. Electrostatic force on saltating sand // J.Geophys.Res. 1998. V. 103. № D8. P. 8997–9001.

  27. Kok J.F., Renno N.O. Electrostatics in wind-blown sand // Phys. Rev. Lett. 2008. V. 100. № 1. 01450L.

  28. Горчаков Г.И., Ермаков В.И., Копейкин В.М., Исаков А.А., Карпов А.В., Ульяненко А.В. Электрические токи сальтации в ветропесчаном потоке // Докл. АН. 2006. Т. 410. № 2. С. 259–262.

  29. Горчаков Г.И., Копейкин В.М., Карпов А.В., Бунтов Д.В., Соколов А.В. Удельный заряд сальтирующих песчинок на опустыненных территориях // Докл. АН. 2014. Т. 456. № 4. С. 476–480.

  30. Li B., McKenna Neuman C. Boundary-layer turbulence characteristics during aeolian saltation // Geophys. Res. Lett. 2012. V. 39. LII402.

  31. Martin R.L., Barchyn T.E., Hugenholtz C.H., Jerolmack D.J. Timescale dependence of aeolian sand flux observation under atmospheric turbulence // J. Geophys. Res. 2011. V. 117. DI6205.

  32. Liu D., Ishizuka M., Mikami M., Shao Y. Tutrbulent characteriostics of saltation and uncertain of saltation model parameters // Atmos. Chem. Phys. 2018. V. 18. P. 7595–7606.

  33. Gorchakov G.I. Buntov D.V., Karpov A.V., Kopeikin V.M., Mirsaitov S.F., Gushchin R.A., Datsenko O.I. Vertical profile of saltating particle concentration over semidesert area // IOP Conference Series: EES 606. 2020. EESE6061. EESE6061015.

  34. Карпов А.В., Гущин Р.А., Даценко О.И. Анализ вариаций скорости переноса сальтирующих песчинок // Оптика атмосферы и океана. 2017. Т. 30. № 03. С. 227–232.

  35. Karpov AV., Gorchakov G.I., Gushchin R.A., Datsenko O.I. Aleurite particle saltation modeling // Proc. SPIE 11208. 2020. 112084Y.

  36. Tong D., Huang N. Numerical simulation of saltating particles in atmospheric boundary layer over flat bed sand ripples // J. Geophys. Res. 2012. V. 117. DI6205.

  37. Gordon M., McKenna Neuman C. A study of particle splash on developing ripple forms for two bed materials // Geomorphology. 2011. V. 129. P. 79–91.

  38. Горчаков Г.И., Карпов А.В., Кузнецов Г.А., Бунтов Д.В. Квазипериодическая сальтация в ветропесчаном потоке на опустыненной территории // Оптика атмосферы и океана. 2016. Т. 29. № 6. С. 472–477.

  39. Горчаков Г.И., Шукуров К.А. Флуктуации концентрации субмикронного аэрозоля в конвективных условиях // Изв. РАН. Физика атмосферы и океана. 2003. Т. 39. № 1. С. 85–97.

  40. Горчаков Г.И., Бунтов Д.В., Карпов А.В., Копейкин В.М., Мирсаитов С.Ф., Гущин Р.А., Даценко О.И. Влияние ветра на распределение сальтирующих частиц по размерам // Оптика атмосферы и океана. 2019. Т. 32. № 10. С. 848–855.

  41. Горчаков Г.И., Карпов А.В., Гущин Р.А., Даценко О.И., Бунтов Д.В. Вертикальные профили концентраций сальтирующих частиц на опустыненной территории // Докл. РАН. Науки о Земле. 2021. Т. 496. № 2. С. 211–214.

  42. Kok J.F., Renno N.O. A comprehensive numerical model of steady state saltation (COMCALT) // J. Geophys. Res. 2009. V. 114. D17204.

  43. Namikas S.L. Field measurement and numerical modelling of aeolian mass flux distributions on a sandy beach // Sedimentology. 2003. V. 50. P. 303–326.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Физика атмосферы и океана

Архивы выпусков Информация о журнале Отправить рукопись в журнал