Известия РАН. Физика атмосферы и океана, 2021, T. 57, № 5, стр. 575-594
Особенности индуцированной ветровыми волнами турбулентности в воде по измерениям в ветро-волновом канале
В. Г. Полников a, Ф. Цяо b, И. А. Репина a, c, d, *
a Институт физики атмосферы им. А.М. Обухова РАН
119017 Москва, Пыжевский пер., 3, Россия
b First Institute of Oceanography of Ministry of Natural Resources
266061 Qingdao, Xianxialing road, 6, China
c Научно-исследовательский вычислительный центр МГУ им. М.В. Ломоносова
119991 Москва, Ленинские горы, 1, стр. 4, ГСП-1, Россия
d Московский центр фундаментальной и прикладной математики
Москва, Россия
* E-mail: repina@ifaran.ru
Поступила в редакцию 26.11.2020
После доработки 13.04.2021
Принята к публикации 09.06.2021
Аннотация
В ветро-волновом канале выполнены измерения трех компонент скорости ui (i = x, y, z) на трех горизонтах в воде при наличии ветровых волн. Цель исследования заключается в определении степени анизотропии индуцированной ветровыми волнами турбулентности и скорости ее диссипации ε в зависимости от параметров системы. Для этого рассчитаны стандартные отклонения Ϭi и частотные спектры Si(f) для компонент измеренных течений, а также ϬiF и SiF(f) для турбулентных составляющих течений, в которых отфильтрованы волновые движения. Установлено: а) турбулентность не является изотропной; б) соотношение стандартных отклонений имеет вид σx > σy > σz и σxF > σyF > σzF; в) более 70% кинетической энергии содержится в турбулентных составляющих флуктуаций течений. Для горизонтальных компонент скорости, их спектры близки по форме и интенсивности. В области частот ниже частоты пика спектра волн fp спектры Si(f) всех компонент течений имеют степенной закон спадания с показателем –1.7 ± 0.1. В области частот f > 2fp, спектры Sx(f) и Sy(f ) близки по интенсивности и имеют тот же закон спадания, но интенсивности спектров вертикальной компоненты Sz(f) почти на порядок слабее, а сами спектры Sz(f), при наличии степенного хвоста, имеют закон спадания “–2.0 ± 0.1”. Такие участки спектров трактуются как аналоги колмогоровских спектров. По интенсивности спектров Sz(f) определены величины скорости диссипации турбулентности ε. Построены полуэмпирические параметризации зависимости siF и ε от параметров волн и глубины горизонта измерения, обсуждаются их отличия от известных и возможные механизмы формирования особенностей формы спектров Si(f).
1. ВВЕДЕНИЕ
Исследования характеристик турбулентности, обусловленной присутствием волновых движений в верхнем слое воды, представляет собой отдельное направление общей тематики изучения турбулентности. Такие исследования имеют длинную историю, хорошо представленную в предыдущей работе авторов [1], посвященной описанию турбулентности, наведенной механическими волнами в воде. По этой причине широкое введение в тему, обозначение ее значимости и история подобных исследований здесь будут опущены. Далее, выделяя наиболее важные результаты предшествующих работ, в порядке введения мы отметим лишь наиболее важные понятия и мало изученные аспекты турбулентности, индуцированной волнами, на решение которых нацелена эта работа.
Во-первых, уточним, что турбулентность, как “хаотическая система вихрей с непрерывным распределением размеров” (Гл.VII в [2]), предполагает отсутствие выделенных масштабов движений в их частотном или пространственном спектре. При этом наличие участков степенного спадания спектров с частотой вида
(в значимой области частот Ω) дает основание для сопоставления эмпирики с теоретическими моделями. Часто такие участки трактуются как колмогоровские спектры [2, 3], что позволяет определять скорость диссипации кинетической энергии турбулентности (СДТ) ε как один из ее главных параметров, допускающих сравнение с теорией [3].
Поэтому описание турбулентности в фиксированной точке часто выполняется на языке частотных спектров компонент течений Si(f) (i = x, y, z), а не в терминах конкретных реализаций временного ряда компонент скорости ui(t) (например, [1–10]). В таком случае оценки стандартных отклонений σi для компонент скорости ui(t), характеризующие степень ее анизотропии, определяются через спектры по формуле [3]
(2)
$\sigma _{i}^{{}} = {{\left( {\int\limits_{{{f}_{{\min }}}}^{{{f}_{{{\text{max}}}}}} {{{S}_{i}}(f)} df} \right)}^{{1/2}}},$в которой пределы интегрирования задаются областью расчетов спектров Si(f).
В присутствие волн, наличие индуцированной ими турбулентности проявляется в частотном спектре компонент измеренных на глубине z течений Si(f, z) в виде отклонений от теоретического спектра компонент орбитальных скоростей волновых движений SiW(f, z), проникающих на заданную глубину z [10]. Именно такое описание турбулентности принято и в данной работе. Существуют и другие механизмы возникновения турбулентности, обусловленные не только орбитальным волновым движением, но, в частности, гидродинамической неустойчивостью и сдвиговыми эффектами. Но в настоящей работе они не учитываются. Далее спектры компонент, в которых волновые движения отфильтрованы, будут обозначаться как SiF(f), а стандартные отклонения для таких компонент течений, определяемые по формуле (2) через SiF(f), – как σiF.
Во-вторых, напомним, что турбулентность, индуцированная волнами в воде, физически обусловлена гидродинамической неустойчивостью волновых орбитальных движений при больших числах Рейнольдса, которые, в данном случае, задаются соотношением [11 , 12]:
(3)
${\text{Re}} = {{a_{0}^{2}{{\omega }_{p}}} \mathord{\left/ {\vphantom {{a_{0}^{2}{{\omega }_{p}}} \nu }} \right. \kern-0em} \nu } > {{10}^{3}},$В частности, нас будет интересовать характер и степень анизотропии наведенной ветровыми волнами турбулентности на языке стандартных отклонений σiF, а также форма спектров компонент течений Si(f) и наличие в них участков степенного хода вида (1) с целью определения СДТ ε, включая зависимости σiF и ε от параметров волнения и глубины измерений, что обусловлено причинами их недостаточной изученности.
В-третьих, действительно, многочисленная литература в рассматриваемой области (см., например, [1, 5, 8, 12, 15–17]) свидетельствует о неоднозначности в оценке характера анизотропии вызванных волнами флуктуаций скорости течений. Есть примеры [15, 16], когда стандартные отклонения поперечной горизонтальной компоненты турбулентной составляющей скорости σy превышают таковые для продольной компоненты – σx. Наблюдаются и обратные соотношения [1, 17]. Имеются данные о полной изотропии турбулентности как непосредственно под волнами [8], так и глубоко под ними [4, 5]. При этом в указанных работах вопрос фильтрации волновых движений специально не обсуждался, хотя его изучению посвящено значительное число работ (см., например, [10, 18–21]).
По-видимому, проблема указанной неоднозначности в оценках степени анизотропии индуцированной волнами турбулентности кроется в методике выделения самих турбулентных составляющих, т.е. в методике фильтрации волновых движений. Ее совершенствование позволит продвинуться в понимании особенностей анизотропии течений, наведенных волнами в воде. Так, в работе [4] вопрос “линейной фильтрации” волновых компонент на основе потенциальной теории в линейном приближении был лишь затронут. В работах [10, 18] были приведены рабочие формулы для выполнения указанной линейной фильтрации, включая функции когерентности рядов возвышений поверхности и наведенных течений. На их основе в [10] получены оценки спектров турбулентных составляющих течений, правда, только в их высокочастотной области спектра, т.е. вне области пика. В работе [1] было показано, что прямое привлечение формул, предложенных в [10], именно в области пика на практике оказалось малоэффективным для механических волн на воде. Дальнейшее развитие методов фильтрации описано в работах [19–21], однако предлагаемые там методы излишне громоздки. Поэтому в [1] был предложен феноменологический подход к фильтрации, обеспечивающий монотонность спадания спектра турбулентных составляющих, близкий к результатам современных методов фильтрации [20, 21]. Его описание весьма громоздко и требует отдельного раздела, представленного далее.
И, наконец, важно разобраться в вопросе анизотропии наведенной волнами турбулентности на языке различия форм частотных спектров для горизонтальных и вертикальной компонент поля скорости: Sx(f), Sy(f) и Sz(f).
Ранее, как в лабораторных исследованиях [8, 12], выполненных в различных каналах при наличии механических волн, так и в натурных измерениях в присутствии ветровых волн [4–6] было показано, что спектры Sx(f) и Sz(f) демонстрируют в области высоких частот степенные участки вида Sx,z(f) ~ f –5//3. С использованием гипотезы “замороженной турбулентности” Тейлора, эти результаты трактуются авторами в рамках модели турбулентности Колмогорова–Обухова (КО) [2]. Такая трактовка позволила им получить оценки СДТ ε и даже найти частные зависимости ε(${{a}_{0}}$) [7] и ε(z) [8].
Теоретическое обоснование указанной трактовки спектров течений, наведенных волнами, на языке частотных спектров S(f) было предложено намного раньше в широко известной работе Ламли и Террея [22]. Впоследствии этот подход стал активно применяться, начиная с классических работ [4, 5], в которых рассчитывались спектры компонент скорости течений Sx,z(f), генерированных обрушивающимися ветровыми волнами в озере Онтарио. Полученные в натурных условиях спектры для горизонтальной и вертикальной компонент скорости Sx(f) и Sz(f) были идентичны по форме и интенсивности (например, [4]). Такое подобие форм Sx(f) и Sz(f) свидетельствует в пользу изотропии турбулентности, наведенной обрушивающимися ветровыми волнами. Однако этот факт в работах [4–6, 10], равно как и во множестве аналогичных работ, выполненных в ветро-волновых каналах [8, 12, 17], детально не обсуждался; поэтому он явно требует дополнительной проверки для различных условий волнообразования.
По форме спектров важно, что еще в работе [4] было показано наличие в спектрах компонент скорости Sx(f) и Sz(f) двух диапазонов участков вида $S(f)\sim {{f}^{{ - 5/3}}}$ : а) высокочастотный участок, имеющий место при f > 2fp (ВЧ-ветвь турбулентности); и б) низкочастотный участок, расположенный при f < 0.5fp (НЧ-ветвь), где fp – частота пика спектра ветровых волн. Такой эффект был теоретически обоснован в работе [22] как результат конвекции колмогоровского спектра $S(k)\sim {{k}^{{ - 5/3}}}$ (k – волновое число) наведенными течениями, хотя его физические аспекты не были достаточно убедительно представлены. Подробнее этот вопрос мы обсудим в разделе дискуссии 5.
Для колмогоровских степенных участков частотного спектра вида S(f) ~ f–5//3, в работах [4–6, 8, 9, 22] и многих других реализована техника применения гипотезы “замороженной турбулентности”, позволяющая определять СДТ ε по интенсивности хвоста спектра S(f). С ее использованием, в [5] была найдена первая полноразмерная зависимость ε от высоты волн на поверхности воды ${{a}_{0}}$, скорости трения $u{\text{*}}$ и глубины измерений z вида
(4)
$\varepsilon = {\text{const}}{\kern 1pt} {{{{a}_{0}}u_{*}^{3}} \mathord{\left/ {\vphantom {{{{a}_{0}}u_{*}^{3}} {{{z}^{2}}}}} \right. \kern-0em} {{{z}^{2}}}},$справедливая в диапазоне глубин от 2 до 10 высот волн ${{a}_{0}}$. В дальнейшем результат (4) был неоднократно подтверждeн как в натурных [6], так и в лабораторных условиях [9].
Вместе с тем, по данным наших лабораторных измерений течений, вызванных механическими волнами [1], было установлено два других факта: а) отсутствие изотропии наведенной турбулентности; б) отличие в ВЧ-области формы спадания спектров вертикальной компоненты Sz(f) от закона “–5/3”. При этом, как и в работе [5], спектры продольных компонент турбулентных флуктуаций скорости Sx(f) и Sy(f), действительно, идентичны по форме и интенсивности и имеют две ветви: НЧ- и ВЧ-ветвь, в которых они демонстрируют законы спадания “–5/3”. Установлено, однако, что даже на глубинах z < –10 см это происходит не всегда, а только для достаточно высоких волн с амплитудами a0 ≥ 2 см. Но всегда соотношение СтО σiF, после фильтрации волновых составляющих, задается формулой σxF ≈ σyF≥ (2–3)σzF, т.е. имеется сильная анизотропия турбулентности между горизонтальной и вертикальной плоскостями.
Кроме того, оказалось, что спектры вертикальной компоненты скорости течений Sz(f) в НЧ-области (при f < 0.5fp) имеют тот же закон спадания: Sz(f) ~ f –5//3, но в ВЧ-области, т.е. при f > 2fp, они демонстрируют закон спадания “–2”, характерный для лагранжевой турбулентности [2, 3]. В таком случае частотный спектр скорости течений может быть представлен в виде [3]
позволяющим легко определить СДТ ε, а затем и ее зависимость от параметров системы. На основании оценок ε, полученных с использованием соотношения (5), в [1] показано, что в случае механических волн указанная зависимость хорошо параметризуется формулой вида (ось OZ направлена вверх)
(6)
$\varepsilon = {{c}_{\varepsilon }}[a_{0}^{2}f_{p}^{3}]({a \mathord{\left/ {\vphantom {a z}} \right. \kern-0em} z})\exp ({{c}_{{\Delta f}}}{{k}_{p}}z)$при определенном подборе подгоночных безразмерных констант ${{c}_{\varepsilon }}$ и ${{c}_{{\Delta f}}}$, где величина ${{c}_{{\Delta f}}}$ связана с шириной спектра течений Δf на горизонте z (см. детали в [1]). Существенное различие зависимостей (4) и (6), как по степени амплитуд ${{a}_{0}}$, так и от глубины измерений z, на наш взгляд, обусловлено различной природой исследуемых волн (ветровые и механические).
Отметим, что полученные в [1] результаты по анизотропии стандартных отклонений течений не соответствуют теоретическим расчетным результатам работ [14–16], а горизонтально-вертикальная анизотропия форм спектров не соответствует эмпирическим результатам работ [4, 5, 8, 12]. Эти различия, несомненно, требуют дополнительных исследований, направленных на проверку, уточнение и подтверждение перечисленных выше результатов [1]. Один из вариантов таких исследований выполняется в данной работе.
В свете сказанного выше, здесь решаются следующие задачи: 1) оценка и детальное описание степени анизотропии индуцированной волнами турбулентности на языке стандартных отклонений; 2) оценка и детальное описание различия форм спектров для горизонтальных и вертикальной компонент скорости турбулентных течений. Для этой цели привлекаются данные собственных лабораторных измерений течений, наведенных ветровыми волнами.
2. ХАРАКТЕРИСТИКИ ИЗМЕРЕНИЙ
Измерения выполнялись в ветро-волновом канале Первого института океанографии КНР с размерами 32 × 1 × 2 м3. Детальное описание устройства в целом приведено в работах [1, 24] и здесь опускается по причине ограниченности места.
Для волновых измерений использовались емкостные волновые датчики (WG), расположенные в точках Р1, Р2, Р4, соответствующих разгонам волн 8, 12 и 20.5 м. Вблизи точек Р1, Р2 и Р4 располагались три акустических доплеровских велосиметра (ADV) и трубки Пито для измерения скорости течения и профиля ветра соответственно. Исследовались ситуации с ветровыми волнами для пяти вариантов режима вентилятора, обеспечивающего скорость ветра W в центре воздушной части канала, равную 4, 6, 8, 10 и 12 м/с. Измерения параметров ветра, волн и течений проводились при установлении стационарного состояния системы (более 5 мин работы вентилятора).
Записи волнения имели длительность 10 мин и частоту дискретизации 50 Гц. Параллельно проводилась визуальная регистрация степени обрушений волн в процентах, как отношение числа обрушившихся гребней к их общему числу, прошедшему за 1–2 мин через участок наблюдений порядка трех–пяти доминантных длин волн (1.5–2 м).
Три компоненты скоростей течений ui (i = x, y, z) измерялись ADV на горизонтах: z = –10, –20 и –30 см (ось OZ направлена вверх с началом отсчета на среднем уровне воды). Частота измерений составляла 100 Гц, при значениях глубин z = –10, –20 см, и 128 Гц, при z = –30 см, что вызвано техническими причинами.
Обработка данных измерений проводилась в оболочке MATLAB. Для оценки частотных спектров S(f)) (частота f задается в Гц) использовался метод авто-регрессии (АР), обеспечивающий минимальную погрешность [23]. В силу большой длительности рядов, 95% доверительные интервалы спектров в билогарифмических координатах составляют всего [+10%, –12%], что соответствует стандартным отклонениям для спектральных интенсивностей примерно 3–4%.
3. ПАРАМЕТРЫ ВОЛН И ТЕЧЕНИЙ
Генератором изучаемых течений являются ветер и волны, поэтому о них потребуется определенная информация. Принимая во внимание, что средний ветер W и связанная с ним скорость трения $u{\text{*}}$ влияют на течения в водной толще лишь косвенно – через волны и вертикальный поток горизонтального импульса, для краткости изложения здесь мы не будем на них останавливаться.
В этом разделе основное внимание будет уделено следующим вопросам: 1) форма спектров и параметры ветровых волн в точке измерений Р2 = = 12 м; 2) форма спектров измеренных компонент скорости течений, наведенных волнами; 3) метод фильтрации орбитальных волновых движений в спектрах компонент скорости; 4) оценки стандартных отклонений измеренных и фильтрованных компонент скорости в точке Р2 на различных горизонтах, обозначаемых как ${{\sigma }_{i}}$ и ${{\sigma }_{{iF}}}$; 5) параметризация стандартных отклонений турбулентных пульсаций скорости ${{\sigma }_{{iF}}}$ как функции параметров системы в точке Р2.
3.1. Параметры ветровых волн
Форма спектров и параметры ветровых волн представляют самостоятельный интерес, поэтому они были предварительно изучены и с определенной степенью детализации описаны в недавней работе авторов [24]. Здесь будет приведена лишь часть информации о ветровых волнах, активно используемая далее. Для дальнейшего важно отметить следующее.
Во-первых, с ростом силы ветра W и разгона волн X, интенсивность спектров ветровых волн Sη(f) и их средняя амплитуда на поверхности ${{a}_{0}}$, определяемая формулой
закономерно растут, а частота пика спектра fp (или доминантная частота) – уменьшается. Зависимости ${{a}_{0}}(W,X)$ и ${{f}_{p}}(W,X)$, называемые законами роста ветровых волн на ограниченном разгоне, описаны, например, в [24, 25]. Согласно законам роста, величина амплитуды волн ${{a}_{0}}$ на фиксированном разгоне X линейно связана с ветром. В терминах скорости трения $u{\text{*}}$, эта связь задается соотношением
(8)
${{a}_{0}} = {\text{const}}\,u{\text{*}}{{({X \mathord{\left/ {\vphantom {X g}} \right. \kern-0em} g})}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}},$которое позволяет исключить параметр $u{\text{*}}$ из списка переменных, участвующих в параметризациях характеристик турбулентности, построение которых является одной из задач работы.
Во-вторых, как показано в [24], форма спектра установившихся ветровых волн в энергонесущей области частот (0.5fp < f < 2fp) при различных ветрах W остается неизменной (как известно, она близка к форме JONSWAP [25, 26]). Поэтому и форма спектров орбитальных скоростей волнения, проникающих в воду на глубину z, также слабо зависит от величины W. Этот факт позволяет не учитывать ширину спектра при параметризации характеристик индуцированной турбулентности, в отличие от случая механических волн [1]. Однако, как и в работе [1], относительная интенсивность обрушений Br, определяемая в данном эксперименте визуально как отношение числа обрушившихся гребней к их общему числу, также является параметром решаемой задачи.
В итоге, в поисках параметризации характеристик турбулентности основную роль играют лишь параметры волнения: амплитуда волн ${{a}_{0}}$, частота пика fp (или ее аналог в радианах ${{\omega }_{p}} = 2\pi {{f}_{p}}$), волновое число пика ${{k}_{p}} = {{\omega _{p}^{2}} \mathord{\left/ {\vphantom {{\omega _{p}^{2}} g}} \right. \kern-0em} g}$, средняя крутизна волн $\delta = {{a}_{0}}{{k}_{p}}$ и интенсивность обрушений гребней волн Br.
Все указанные параметры волн (кроме Br) однозначно следуют из спектров волнения, точность оценки которых, как отмечено в разделе 2, обеспечивает погрешности их определения не более 5%. С целью исключения повторения, все параметры волн приводятся далее только в сводных табл. 1 и 2 для эмпирических характеристик турбулентности и их параметризаций.
Таблица 1.
Параметризация стандартных отклонений компонент турбулентных течений в точке Р2 = 12 м
| Ветер | Параметры волнения | Эмпирические стандартные отклонения σiFem и их параметризация (14) σiFpar(обе – в см) |
|||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| z = –10 см | z = –20 см | z = –30 см | |||||||||
| W, м/с | a0, см | fp, Гц | kp, 1/м | δ, б/р | Br, % | σxFem | σzFem | σxFem | σzFem | σxFem | σzFem |
| σxFpar | σzFpar | σxFpar | σzFpar | σxFpar | σzFpar | ||||||
| 4 | 0.53 | 3.51 | 49.5 | 0.26 | 0 | 1.56 | 0.87 | 1.45 | 0.86 | 0.76 | 0.47 |
| 1.5 | 0.8 | 1.0 | 0.5 | 0.6 | 0.3 | ||||||
| 6 | 0.77 | 2.89 | 33.6 | 0.26 | 0 | 1.82 | 1.01 | 1.61 | 1.02 | 0.84 | 0.94 |
| 2.1 | 1.1 | 1.5 | 0.8 | 1.1 | 0.6 | ||||||
| 8 | 1.01 | 2.64 | 28.0 | 0.28 | 5 | 2.83 | 1.45 | 2.34 | 1.48 | 1.13 | 0.89 |
| 2.7 | 1.5 | 1.9 | 1.14 | 1.3 | 0.86 | ||||||
| 10 | 1.33 | 2.32 | 21.6 | 0.29 | 10 | 3.39 | 1.94 | 2.79 | 1.88 | 1.77 | 1.22 |
| 3.4 | 1.91 | 2.4 | 1.6 | 1.7 | 1.3 | ||||||
| 12 | 1.65 | 2.06 | 17.1 | 0.28 | 20 | 3.44 | 2.34 | 2.37 | 1.78 | 1.70 | 1.45 |
| 3.5 | 2.2 | 2.5 | 1.8 | 1.8 | 1.5 | ||||||
Примечание. Оценки экспериментальных стандартных отклонений σiFem и их параметризаций σiFpar по формулам (14), (15) размещены одни над другими. Параметрические значения σiFpar выделены полужирным курсивом.
Таблица 2.
Экспериментальные и параметрические оценки СТД
| Ветер вентилятора |
Точка измерения Р1 = 8 м | |||||
|---|---|---|---|---|---|---|
| Глубина измерения | ||||||
| z = –10 см | z = –20 см | z = –30 см | ||||
| Значения СДТ, 10–5 м2/с3 | ||||||
| W, м/с | ε | ${{\varepsilon }_{{par}}}$ | ε | ${{\varepsilon }_{{par}}}$ | ε | ${{\varepsilon }_{{par}}}$ |
| 4 | – | – | – | |||
| 6 | – | – | – | |||
| 8 | – | – | – | |||
| 10 | 2.5 | 1.6 | – | 0.6 | – | 0.3 |
| 12 | 3.0 | 2.6 | 1.5 | 1.0 | 0.8 | 0.5 |
| Точка измерения Р2 = 12 м | ||||||
| 4 | – | – | – | |||
| 6 | – | – | – | |||
| 8 | 1.2 | 1.4 | – | 0.5 | – | 0.3 |
| 10 | 2.5 | 2.3 | – | 1.0 | 0.3 | 0.5 |
| 12 | 3.5 | 3.2 | 1.5 | 1.3 | 0.8 | 0.8 |
| Точка измерения Р4 = 20.5 м | ||||||
| 4 | – | – | – | |||
| 6 | – | – | – | |||
| 8 | 1.2 | 2.4 | – | 1.0 | – | 0.6 |
| 10 | 2.5 | 4.4 | – | 1.9 | – | 1.1 |
| 12 | 6.0 | 6.6 | 4.0 | 3.0 | 0.8 | 1.8 |
Примечание. Знак “–” означает отсутствие участков вида (17) в спектрах ${{S}_{z}}(f)$. Колонки ${{\varepsilon }_{{par}}}$ соответствуют оценкам СДТ по параметрической формуле (20) (даны полужирным курсивом).
3.2. Форма спектров измеренных компонент скорости течений
Типичные формы спектров ${{S}_{i}}(f)$для измеренных компонент скорости ui (i = x, y, z) приведены на рис. 1а, 1б и 2а, 2б, 2в. Они имеют следующие эмпирические особенности.
Рис. 1.
Спектры компонент скорости течений: ${{S}_{x}}(f)$ (сплошная), ${{S}_{y}}(f)$ (штриховая) и ${{S}_{z}}(f)$ (пунктирная), в точке Р2 = 12 м для глубины z = –10 см. а) ветер W = 4 м/с ; б) ветер W = 8 м/с. Числа возле отрезков жирных линий означают закон спадания спектров по формуле (1).
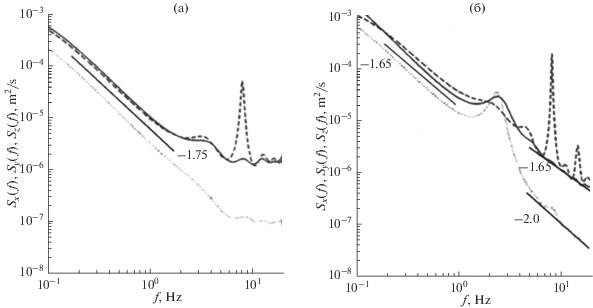
Во-первых, наблюдается существенное различие интенсивностей спектров для горизонтальных и вертикальной компонент скорости, ${{S}_{x}}(f)$, ${{S}_{y}}(f)$ и ${{S}_{z}}(f)$. При этом интенсивности спектров ${{S}_{x}}(f)$ и ${{S}_{y}}(f)$ близки друг к другу, но в разы превышают интенсивность ${{S}_{z}}(f)$, достигая в ВЧ-области ( f > 2fp) превышения на порядок. Согласно определению стандартных отклонений по формуле (2), сказанное свидетельствует о сильной анизотропии стандартных отклонений рядов измеряемых компонент скорости ${{\sigma }_{i}}$ (см. далее п. 3.4).
Во-вторых, в НЧ-области (f < 0.5fp), спектры всех компонент скорости течений ${{S}_{x}}(f)$, ${{S}_{y}}(f)$, ${{S}_{z}}(f)$ имеют одинаковую форму, близкую к виду
В-третьих, при достаточно сильных ветрах (W ≥ 8 м/с), в ВЧ-области спектры горизонтальных компонент скорости, ${{S}_{x}}(f)$, ${{S}_{y}}(f)$, спадают по закону (9), а спектры вертикальной компоненты скорости, ${{S}_{z}}(f)$, как правило, спадают по закону “–2.0”:
Но закон спадания (10) наблюдается не всегда, а только при ветре W ≥ 8 м/с и не на всех горизонтах (рис. 2а, 2б, 2в). Все случаи выполнения закона (10) для ${{S}_{z}}(f)$ в ВЧ-области будут приведены далее в сводной табл. 2 раздела 4, посвященного детальному описанию указанных особенностей.
Рис. 2.
Зависимости интенсивности спектра ${{S}_{z}}(f)$ в точке Р2 от параметров системы: а) от скорости ветра W = 4, 8, 12 м/с на глубине z = –10 см; б) от глубины z = –10, –20, –30 см для ветра W = 8 м/с; в) от глубины z для ветра W = 12 м/с. Отрезки прямых с числами при них обозначают степень спадания спектров по формуле (1).
В-четвертых, совокупность спектров течений для всех ветров и горизонтов показывает, что при малых ветрах (W ≤ 8 м/с) пик спектра волновых скоростей на частоте fp слабо проявляется в спектрах компонент течений (рис. 1а) даже на горизонте z = –10 см, не говоря о более глубоких горизонтах. При этом наличие острых пиков в спектре поперечной компоненты скорости ${{S}_{y}}(f)$(см. рис. 1а, 1б) при частотах f > (3–4)fp (которая в нашем случае должна иметь чисто турбулентный характер, т.е. без пиков в спектре) явно связано с поперечными биениями, обусловленными боковыми границами канала. Далее эти пики в спектре ${{S}_{y}}(f)$ игнорируются.
Вместе с тем, при скорости ветра W более 8 м/с, пик на частоте fp в спектрах компонент течений ${{S}_{x}}(f)$ и ${{S}_{z}}(f)$ все-таки начинает заметно проявляться, причем сильнее именно в спектре вертикальной компоненты скорости ${{S}_{z}}(f)$ (рис. 1б). Наличие таких пиков в спектрах течений показывает необходимость выполнения процедуры фильтрации орбитальных волновых движений, нужной для определения интенсивности непосредственно турбулентных пульсаций.
3.3. Метод фильтрации орбитальных волновых движений
Поскольку фильтрация волновых движений является одним из сложнейших вопросов обработки данных, не получивших своего окончательного решения, здесь мы уделим ему особое внимание, рассмотрев несколько вариантов решений из работ [10, 18, 19].
Следуя работе [10], представим компоненту отклонения измеренной скорости течения ${{u}_{i}}^{'}$ от его среднего значения ${{U}_{i}} = \left\langle {{{u}_{i}}(t)} \right\rangle $ в виде
где ${{u}_{{iW}}}$ – волновая составляющая скорости, а $u_{{iT}}^{{}}$ – турбулентная. В рамках традиционного предположения об отсутствии корреляции между этими составляющими спектр флуктуаций скорости течений ${{S}_{{u_{i}^{'}}}}(\omega ,z) \equiv {{S}_{i}}(\omega ,z)$ на глубине z имеет представлениеВ (12) ${{S}_{{iW}}}(\omega ,z)$ – спектр компонент орбитальных волновых движений, а $S_{{iT}}^{{}}(\omega ,z)$ – искомый спектр i-той компоненты турбулентных флуктуаций скорости. В рамках потенциальной теории, для спектра ${{S}_{{iW}}}(\omega ,z)$ на глубине z справедливо представление [10]
(13)
$\begin{gathered} {{S}_{{iW}}}(\omega ,z) = \\ = \,\,{{\omega }^{2}}{{S}_{\eta }}(\omega )\exp [{{ - 2{{\omega }^{2}}\left| z \right|} \mathord{\left/ {\vphantom {{ - 2{{\omega }^{2}}\left| z \right|} g}} \right. \kern-0em} g}]{{I}_{i}}[{{S}_{\eta }}(\omega ,\theta )], \\ \end{gathered} $в котором ${{S}_{\eta }}(\omega )$ – одномерный спектр временного ряда возвышений поверхности η(t), а ${{I}_{i}}[{{S}_{\eta }}(\omega ,\theta )]$ – зависящий от i-той компоненты орбитальной скорости волн интеграл по углу $\theta $ от двумерного частотно-углового спектра волн на поверхности ${{S}_{\eta }}(\omega ,\theta )$ (детали см. в [10]). Согласно (12), искомый спектр турбулентных пульсаций скорости $S_{{iT}}^{{}}(\omega ,z)$ следует из спектра измеряемой скорости ${{S}_{i}}(\omega ,z)$ за вычетом теоретического слагаемого ${{S}_{{iW}}}(\omega ,z)$. Это и есть так называемая “линейная фильтрация” [5, 10].
Зная спектр волнения на поверхности ${{S}_{\eta }}(f)$ и полагая для простоты рассмотрения i = z (тогда ${{I}_{i}}[{{S}_{\eta }}(\omega ,\theta )]$ = 1), сопоставим расчетные спектры орбитальных скоростей волнения ${{S}_{z}}_{W}(f,z) \equiv {{S}_{W}}(f,z)$ со спектрами компонент измеряемых течений ${{S}_{x}}(f)$ и ${{S}_{z}}(f)$ (рис. 3а). Из рис. 3а видно, что интенсивность спектра волновых скоростей ${{S}_{W}}(f,z)$ в области частоты пика fp превышает уровень спектров измеряемых течений, но вне энергонесущей полосы частот, 0.5fp < f < 2fp, она пренебрежима по сравнению с ${{S}_{{x,z}}}(\omega ,z)$. Кроме того, по своей ширине волновой спектр ${{S}_{W}}(f,z)$ почти полностью перекрывает ширину доминантного пика в спектрах компонент течений ${{S}_{x}}(f)$ и ${{S}_{z}}(f)$ в указанной энергонесущей полосе частот. Эти факты приводят к тому, что простое вычитание спектра ${{S}_{W}}(f,z)$ из спектра наблюдаемых течений ${{S}_{{x,z}}}(f,z)$, согласно (12), физически неполноценно, т.к. итоговые значения спектра турбулентных пульсаций $S_{{x,zT}}^{{}}(f,z)$ становятся отрицательными, а его форма – резко немонотонной.
Рис. 3.
а) спектры компонент измеряемых течений Sx(f) (сплошная), Sz(f) (штриховая) и теоретический спектр орбитальный скоростей волн Sw(f) (пунктирная) для ветра W = 10 м/с и глубины z = –10 см; отрезки линий с цифрами отражают закон спадания спектров в ВЧ-области по формуле (1). б) спектры SxF(f) (сплошная), а SzF(штриховая) после фильтрации волновых движений в спектрах измеряемых течений Sx(f), Sz(f) (жирные линии панели а).
Заметим, что в приведенном виде указанные численные факты установлены впервые, а их трактовки приводят к следующим заключениям.
Во-первых, превышение пика спектра волновых скоростей ${{S}_{W}}(f,z)$(на глубине z) над уровнем пика спектров измеряемых течений ${{S}_{{x,z}}}(f,z)$, видимо, обусловлено нарушением применимости потенциального приближения и отсутствием учета нелинейности волн и вязкости жидкости. Во-вторых, указанное соотношение пиков спектров ${{S}_{W}}(f,z)$ и ${{S}_{{x,z}}}(f,z)$, возможно, связано с уширением спектров волновых течений за счет их нелинейности и непотенциальности. Заметим, что аналогичный эффект был зафиксирован для механических волн [1], хотя в ранних работах, при разработке процедуры фильтрации, этот эффект нигде отмечен не был [10, 18–21].
В работе [18] приведенная выше процедура оценивания спектра турбулентных движений ${{S}_{{iT}}}(f,z)$ была модифицирована путем расчета функции когерентности $R_{i}^{2}(f,z)$ (далее, метод функции когерентности – МФК) между рядами возвышений поверхности η(t) и флуктуациями компонент течений ${{u}_{i}}^{'}(t,z)$, задаваемых соотношением (11),
(14)
$R_{i}^{2}(f,z) = {{{{{\left| {\eta (f)u{{{_{i}^{'}}}^{*}}(f,z)} \right|}}^{2}}} \mathord{\left/ {\vphantom {{{{{\left| {\eta (f)u{{{_{i}^{'}}}^{*}}(f,z)} \right|}}^{2}}} {{{S}_{\eta }}(f){{S}_{{u_{i}^{'}}}}(f,z)}}} \right. \kern-0em} {{{S}_{\eta }}(f){{S}_{{u_{i}^{'}}}}(f,z)}}.$В таком случае, при тех же предположениях о статистической независимости слагаемых в (11) и условии линейной связи между возвышениями η(t) и волновыми скоростями ${{u}_{{iW}}}(t)$ (типа (13)), формула (14) дает искомое решение (см. детали в [18])
С ее использованием и была получена часть результатов в [10], без привлечения прямых расчетов ${{S}_{W}}(f,z)$ и соотношений (12), (13).
В порядке критики МФК здесь стоит отметить, что условие линейной связи между рядами η(t) и ${{u}_{{iW}}}(t)$ уже само по себе должно давать решение для спектра турбулентности $S_{{iT}}^{{}}(\omega ,z)$ через уравнения (12), (13), и тогда привлечение функции когерентности излишне. Но если волновые движения нелинейны, то и функция когерентности (14) чисто математически не приводит к решению (15), т.к. числитель в (14) не переходит в выражение ${{S}_{\eta }}(f){{S}_{{iW}}}(f,z)$, как это происходит в случае линейной связи между рядами η(t) и ${{u}_{{iW}}}(t,z)$ [18]. Поэтому МФК чреват значительными количественными неточностями.
И действительно, в нашем случае расчет функции $R_{i}^{2}(f)$ показал, что максимальное значение $R_{i}^{2}(f)$ для i = z, x составляет всего около 0.52 и 0.45 соответственно даже для глубины z = –10 см при ветре W = 10 м/с. Согласно (15) и рис. 3а, это приводит к спектру турбулентных составляющих с “горбом” в области частоты пика fp. Кстати, именно такие “горбатые” спектры турбулентности $S_{{iT}}^{{}}(\omega ,z)$ были представлены в работах [5, 20], что вызывало у самих авторов вопросы по их трактовке.
Более совершенный, хотя и очень трудоемкий, метод тройной декомпозиции (МТД) был предложен
в работе [19]. В кратком изложении он заключается в том, что в разложении (11) волновые составляющие
${{u}_{{iW}}}(t)$ представляются в виде суммы потенциальных движений ${{u}_{{iWp}}}(t)$ и непотенциальных (вихревых) волновых движений ${{u}_{{iWr}}}(t)$, задаваемых через ротор функции тока. Конкретная временная реализация ${{u}_{{iWp}}}(t)$, на заданной глубине, напрямую вычисляется в потенциальном приближении из нелинейных
уравнений Эйлера по заданной реализации возвышений η(t), а затем она вычитается из реализации измеренных флуктуаций скорости: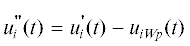 
. Предполагается, что новый ряд флуктуаций скорости 
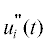содержит лишь вихревую компоненту волновой скорости ${{u}_{{iWr}}}(t)$ и искомую турбулентную составляющую $u_{{iT}}^{{}}(t)$, спектр которой находится изложенным выше МФК. При необходимости, реализация вихревой
компоненты ${{u}_{{iWr}}}(t)$ также может быть рассчитана из уравнений для функции тока [19].
МТД лишен недостатка прямого применения МФК к соотношению (11), но и он имеет ряд существенных ограничений на вычисление составляющих ${{u}_{{iWp}}}(t)$ и ${{u}_{{iWr}}}(t)$, а также чреват отсутствием учета нелинейной связи между ${{u}_{{iWr}}}(t)$ и η(t), и возможной статистической связи ${{u}_{{iWr}}}(t)$ и ${{u}_{{iT}}}(t)$, принятыми в МФК (см. детали в [19]). Следовательно, каждый их перечисленных выше методов фильтрации сохраняет в себе определенную долю неоднозначности в определении интенсивности $S_{{iT}}^{{}}(f)$, особенно в области частоты пика волн fp, и по этой причине не может быть признан совершенным.
Для дальнейшего важно, что применение МТД приводит к существенному сглаживанию “горба” в спектре турбулентности $S_{{iT}}^{{}}(f)$, порой вплоть до его исчезновения (см. рис. 6 из [20] и рис. 4 из [21]). Именно такой результат фильтрации достигается путем феноменологического “отсечения” доминантного пика в спектре измеренных течений, предложенном в [1] (см. детали ниже). В этом плане упомянутые результаты “точного” МТД фактически придают “методу отсечения” достаточное математическое обоснование. Соответствуя результатам МТД, феноменологический метод отсечения доминантного пика в спектре ${{S}_{{{{u}_{i}}}}}(f,z)$ наиболее эффективно обеспечивает монотонное спадание спектра турбулентности в соответствии с его теоретическим определением [2]. При этом важно отметить, что любой метод фильтрации спектра волновых скоростей ${{S}_{W}}(f,z)$ из спектра измеряемых течений ${{S}_{{x,z}}}(f,z)$ практически не затрагивает интенсивности спектра турбулентности в НЧ и ВЧ-областях, определенных выше в разделе 3.2 и представляющих основной интерес для оценок СДТ.
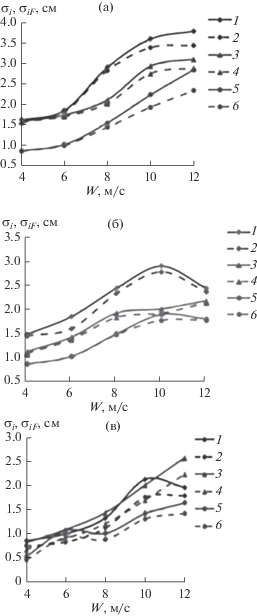
Рис. 4.
Стандартные отклонения измеренных течений σi и их турбулентных составляющих σiF, для случая ветровых волн м в точке Р2 = 12 м. а) глубина z = = –10 см; б) глубина z = –20 см; в) глубина z = –30 см. Линии: 1 – σx; 2 – σxF; 3 – σy; 4 – σyF; 5 – σz; 6 – σzF.
Фильтрация волновых компонент методом отсечения легко осуществима следующим программным образом. 1) за уровень отсечения берется значение спектра на частоте fL, соответствующей точке минимума линии спектра измеряемых течений ${{S}_{i}}(f)$, расположенной ниже частоты его пика fp (см. рис. 3б); 2) для частот f > fL уровень “фильтрованного” спектра остается постоянным вплоть до частоты fH, на которой уровень исходного спектра течений ${{S}_{i}}({{f}_{H}})$ становится равным ${{S}_{i}}({{f}_{L}})$; 3) в областях частот f < fL и f > fH интенсивность спектра ${{S}_{i}}(f,z)$ остается прежней, т.к. в них спектр волновых движений ${{S}_{W}}(f,z)$ на порядок ниже спектра течений. Если доминантный пик волновых течений в спектрах компонент скорости не выражен, например, как в спектрах ${{S}_{x}}(f)$ и ${{S}_{z}}(f)$ на рис. 1а, то для таких спектров их фильтрация не выполняется, поскольку в таком случае она не требуется по физике дела. Если в спектре ${{S}_{i}}(f,z)$ нет минимума перед доминантным пиком, за начало отсечения берется точка максимальной кривизны линии спектра, как это сделано в работе [1].
Опыт показывает, что, как правило, fL≥ 0.5fp, а fH < 1.5fp . Эти границы, кстати, хорошо согласуются с оценками границ области значимости функции когерентности рядов возвышений η(t) с рядами компонент измеренных течений $u_{i}^{'}(t)$, которые, согласно [10], задаются соотношением $R_{i}^{2}(f) \geqslant 0.25$. В принятой фильтрации интенсивность турбулентности в области частот [fHi – fLi] имеет приближенное значение, но формально, как показано выше, точно она не может быть определена всеми известными методами фильтрации. В силу малости области [fHi – fLi] по сравнению с областью определения спектра, указанное приближение в величине “фильтрованного” спектра слабо влияет на конечные результаты оценок стандартных отклонений и никак не влияет на степенные участки “фильтрованных” спектров.
Примеры “фильтрованных” спектров, обозначаемых далее как SiF(f), приведены на рис. 3б жирными линями: SxF(f) – сплошная линия, а SzF(f) – штриховая. Стрелками указаны нижние (fLx и fLz) и верхние границы (fHx и fHz) области фильтрации для спектров SxF(f) и SzF(f). Далее именно такие спектры рассматриваются в качестве спектров турбулентности.
Предлагаемая процедура фильтрации волновых движений, во-первых, проста и физически правомерна как адекватное техническое упрощение теоретической фильтрации МТД. Во-вторых, и это главное, она правильно передает интенсивности реальных турбулентных движений в НЧ- и ВЧ-областях, в которых, как явно видно из рис. 3а, орбитальные волновые движения пренебрежимо малы. В формальном, математическом смысле, “фильтрованные” спектры SiF(f) в НЧ- и ВЧ-областях можно отождествлять со спектрами турбулентности: т.е. принимать, что SiT(f) ≡ SiF(f). Такое описание не искажает физики дела и позволяет использовать НЧ- и ВЧ-области спектров измеренных течений ${{S}_{i}}(f)$ для дальнейшего анализа скорости диссипации турбулентности.
В итоге, спектры турбулентности SiF(f ) содержат две ветви: НЧ- и ВЧ-ветвь, разделенные областью постоянной интенсивности SiF( f), вызванной фильтрацией волновых движений по всей ширине доминантного пика спектра течений. Как и ранее [1], под шириной пика спектра исходных течений ${{S}_{i}}(f)$ здесь и далее будет приниматься частотная ширина участка спектра [fHi – fLi], что и закрывает вопрос фильтрации волновых движений в случае присутствия ветровых волн.
Более подробное изложение этого вопроса, выполненное совместно с детальным анализом свойств МФК и МТД, предложенных в [18, 19], требует отдельного, специального изложения.
3.4. Стандартные отклонения компонент скорости на различных горизонтах
Величины стандартных отклонений измеренных и фильтрованных компонент скорости, ${{\sigma }_{i}}$и ${{\sigma }_{{iF}}}$, характеризуют степень анизотропии соответствующих течений. Здесь они определяются по формуле спектрального анализа (2), через спектры i-той компоненты скорости Si(f) и спектры фильтрованных компонент скорости SiF(f) соответственно. Полученные таким образом оценки ${{\sigma }_{i}}$и ${{\sigma }_{{iF}}}$для точки наблюдения P2 = 12 м приведены на рис. 4. Их совместный анализ позволяет заключить следующее.
Во-первых, всегда имеет место соотношение σx > σy > σz. Как правило, величины σx и σy значительно (почти в 1.5–2 раза) больше σz. Таким образом, налицо имеет место существенная анизотропия интенсивности флуктуаций полных (измеренных) компонент скорости наведенных течений.
Стандартные отклонения отфильтрованных компонент скорости ${{\sigma }_{{iF}}}$ в значительной степени сохраняют указанный выше характер анизотропии стандартных отклонений полных течений ${{\sigma }_{i}}$. Отметим, что в отличие от механических волн, здесь нет четкого разделения анизотропии по плоскостям.
Во-вторых, степень указанной анизотропии существенно снижается с глубиной, т.е. с увеличением глубины наблюдается рост изотропизации течений (см., например, рис. 5 в для глубины измерений z = –30 см).
В-третьих, отношение (${{\sigma }_{{iF}}}$/${{\sigma }_{i}}$)2 показывает, что во всех рассмотренных случаях доля энергии турбулентности наведенных течений очень высока (порядка и более 70%). Это отношение для вертикальной компоненты несколько выше, чем для горизонтальных компонент, и эта разница растет с ростом ветра W (и высоты волн). В частности, при W ≥ 8 м/с, для вертикальной компоненты скорости uz доля турбулентной энергии составляет, в среднем, порядка 90%, в то время как в горизонтальных компонентах ux,y энергетическая доля турбулентности составляет порядка 70–90%, хаотически изменяясь в этих пределах с глубиной.
Следует отметить, что все перечисленные особенности анизотропии индуцированной ветровыми волнами турбулентности сохраняются и в других точках наблюдений.
3.5. Параметризация стандартных отклонений турбулентных пульсаций
Регулярность зависимости величин стандартных отклонений индуцированной турбулентности ${{\sigma }_{{iF}}}$ от параметров волнения позволяет построить их параметризации.
Следуя идеологии работы [1], получим параметризации значений стандартных отклонений компонент турбулентных составляющих течений ${{\sigma }_{{xF}}}$ и ${{\sigma }_{{zF}}}$ как функции параметров ветровых волн: a, f, k, δ, глубины z и степени обрушений Br. Параметризация стандартных отклонений поперечной компоненты ${{\sigma }_{{yF}}}$ требует отдельного рассмотрения в дальнейшем (если понадобится).
Из соображений размерности, в терминах параметров системы: ${{a}_{0}}$,${{f}_{p}}$, ${{k}_{p}}$, δ, Br, z и величины g, искомую параметризацию можно записать в виде
(14)
${{\sigma }_{{iF}}} = {{c}_{{0i}}}\delta [{{f}_{p}}{{a}_{0}}]\exp ( - {{c}_{{1i}}}{{k}_{p}}\left| z \right|),$в которой остается подобрать подгоночные константы${{c}_{{0i}}}$ и ${{c}_{{1i}}}$.
Методом подбора были получены следующие значения параметров
и
(15б)
${{c}_{{0x}}} = 5.2;~\,\,\,{{c}_{{1x}}} = (0.1 + {{Br} \mathord{\left/ {\vphantom {{Br} 2}} \right. \kern-0em} 2})~\,\,{\text{для}}~\,\,{{\sigma }_{{xF}}}.$Поясним, что вхождение параметра обрушений Br в параметр c1x обусловлено двумя факторами (см. рис. 4). Во-первых, при значениях W ≥ 10 м/с имеет место заметный спад σxF с ростом ветра W (и амплитуды волн ${{a}_{0}}$). А, во-вторых, изменения величины ${{k}_{p}}$оказываются недостаточными для передачи спада σxF с глубиной при росте W; в то время как σzF спадает с z по экспоненте с фиксированным коэффициентом (15а). Включение параметра Br в параметр c1x показателя экспоненты в (14) позволяет параметризовать указанные особенности стандартных отклонений горизонтальной скорости турбулентности, отличающие ее от стандартных отклонений вертикальной компоненты.
Цифровые результаты сопоставления эмпирических значений для ${{\sigma }_{{xF}}}$ и ${{\sigma }_{{zF}}}$ в точке измерения Р2 = 12 м и величины их параметризаций по формулам (14), (15) представлены в табл. 1 совместно с параметрами волнения и ветра, используемыми для идентификации вариантов измерений. Нетрудно убедиться, что для значений ветра W ≥ 8 м/с, когда интенсивность турбулентности более высокая (и определяется надежнее), параметризация (14), (15) справедлива со средней ошибкой порядка или менее 10%.
Отметим, что наличие параметризаций измеряемых характеристик турбулентности представляет определенный практический интерес как ориентир для проверки достоверности теоретических построений, типа моделей [13–15]. Предполагается, что на данный момент более точная параметризация ${{\sigma }_{{iF}}}$ не требуется, в виду ее пионерского характера и возможности последующих уточнений. На этом основании можно считать, что формулы (14), (15) закрывают поставленную в работе задачу описания анизотропии турбулентности, наведенной ветровыми волнами.
4. ОЦЕНКИ СКОРОСТИ ДИССИПАЦИИ ТУРБУЛЕНТНОСТИ
4.1. Общие положения
Как известно [2, 3], наличие степенных законов спадания спектров течений дает основание для их трактовки в качестве колмогоровских спектров, что открывает возможность определения такой важной характеристики как скорость диссипации кинетической энергии турбулентности ε [4–9]. Однако в случае турбулентности, индуцированной волновыми движениями, а не стационарными потоками жидкости, ситуация значительно усложняется.
Действительно, как уже отмечалось выше в разделах 3.2, 3.3, спектры турбулентных горизонтальных и вертикальной компонент скорости SiF(f) имеют две области – низкочастотную (НЧ‑область частот: f < 0.5fp) и высокочастотную (ВЧ-область частот: f > 2fp). В НЧ-области спектры имеют закон спадания, близкий к f –5/3, а в ВЧ-области этот закон спадания сохраняется только для спектров горизонтальных компонент скорости SxF(f ) и SyF(f ), в то время как спектр вертикальной компоненты SzF(f) спадает по закону, близкому к f –2. Оставляя обсуждение причин такой разницы для раздела 5, остановимся на вопросе о возможности получения из этих спектров оценки скорости диссипации кинетической энергии турбулентности (СДТ) ε. Для простоты записи далее букву F в нижних индексах спектров будем опускать.
Несмотря на имеющую место в нашем случае явную анизотропию турбулентности, будем “априорно” полагать, что форма степенных спектров Si(f) для каждой из компонент скорости может трактоваться в рамках теории КО [2, 3], т.е. она однозначно связана с таким параметром системы, как СДТ. При этом частотные спектры с законами спадания f –5/3 вполне уместно связывать с классической колмогоровской турбулентностью, вызванной стационарными потоками жидкости. В таком случае, как было обосновано в работе [22] и апробировано в работах [4–9], в рамках гипотезы “замороженной турбулентности” Тейлора СДТ можно получить из соотношения
(16)
$\varepsilon = {{{{C}_{0}}{{{[S(\omega ,z){{\omega }^{{5/3}}}]}}^{{3/2}}}} \mathord{\left/ {\vphantom {{{{C}_{0}}{{{[S(\omega ,z){{\omega }^{{5/3}}}]}}^{{3/2}}}} {/{{U}_{{\text{T}}}}(z)}}} \right. \kern-0em} {/{{U}_{{\text{T}}}}(z)}},$Однако ни один из теоретических подходов, представленных, например, в [13–15, 22], не дает ответа на вопрос: как получить оценку ε для спектра вида $S(f) \sim {{f}^{{ - 2}}}$ (поскольку такой спектр ранее не фиксировался). “Феноменологическое” решение этого вопроса было предложено в предыдущей работе [1], что и позволяет решить поставленную задачу.
4.2. Методы оценки СТД
Прежде всего, отметим, что согласно теории [22], в формуле (16) в качестве скорости тейлоровского переноса “замороженной турбулентности” UТ(z) (на глубине z) априорно предлагается в НЧ-области использовать среднюю скорость дрейфа Ud(z), а в ВЧ-области – амплитуду орбитальной скорости волн Uw(z), соответствующую доминантной частоте волновых движений. И хотя прямое теоретическое обоснование такого выбора в работе [22] отсутствует, на практике в качестве тейлоровской скорости переноса UТ формально можно применять оба варианта. Но на этом пути, конкретно в нашем случае, возникают проблемы.
Так, для спектров вида $S(f) \sim {{f}^{{ - 5/3}}}$ в НЧ-области рекомендуется в качестве скорости переноса UТ использовать скорость дрейфа Ud. Такой подход был реализован, например, в работах [4–6] для натурных данных и в [8, 9] для случая течений, индуцированных обрушивающимися ветровыми волнами в канале при сильных ветрах (W = = 12–25 м/с). Однако в рассматриваемом здесь эксперименте оказалось, что использование скорости дрейфа Ud по техническим причинам невозможно, т.к. эмпирические оценки средней измеренной скорости течений U = $\left\langle {{{u}_{x}}} \right\rangle ,$ отождествляемые со скоростью дрейфа Ud, проявляют хаотическую изменчивость в зависимости от величины ветра или глубины горизонта. Например, величина Ud при изменении величин W или z может менять знак или быть больше для более глубоких горизонтов. Ненадежность таких результатов вызвана, видимо, тем, что в нашем эксперименте скорость ветра W была сравнительно мала (W ≤ 12 м/с), а характерные для данного канала возвратные течения на горизонтах измерений z сопоставимы по величине с дрейфом Ud(z), наведенным волнами и ветром. По этой причине использование оценок Ud ≡ $\left\langle {{{u}_{x}}} \right\rangle $ в модели “замороженной” турбулентности является проблематичным, а результаты оценок Ui(z) здесь не обсуждаются. По-видимому, вопрос оценки СТД в НЧ-области спектров течений, в случае слабых ветров и слабо обрушивающихся волн, требует дополнительных исследований в условиях малости возвратных течений (см. также раздел 5).
Для спектров вида $S(f) \sim {{f}^{{ - 5/3}}}$, в ВЧ-области авторы [22] рекомендовали использовать в качестве тейлоровского переноса UТ орбитальную скорость доминантных волн Uw. Такое предложение нам представляется недостаточно обоснованным теоретически. Поэтому его применение здесь не проводится и переносится на рассмотрение в дальнейшем. Более подобно этот вопрос обсуждается в разделе 5.
В итоге, в ВЧ-области, в плане задачи получения оценок ε, остается только спектр вида $S(f) \sim {{f}^{{ - 2}}}$, наблюдающийся для вертикальной компоненты скорости. Как показал опыт работы [1], для такой формы спектра задача имеет решение, заключающееся в следующем.
Форма спектра $S(f) \sim {{f}^{{ - 2}}}$ известна в гидродинамике как спектр лагранжевой турбулентности [2, 3]. Согласно формулировке, приведенной в [3], лагранжева турбулентность описывает случайные блуждания частицы в фазовом пространстве (ускорений), вызванные внешней силой с дельта-образной временной корреляцией. В таком случае ускорение частицы имеет спектр белого шума, а спектр скорости имеет форму $S(f) \sim {{f}^{{ - 2}}}$ [3]. В указанной трактовке такая турбулентность соответствует броуновскому движению или, иными словами, турбулентной диффузии частицы.
Для спектров вида $S(f) \sim {{f}^{{ - 2}}}$ в эйлеровой системе координат теория отсутствует. Но, поскольку наблюдаемый в точке спектр вертикальной компоненты скорости вида ${{S}_{z}}(f) \sim {{f}^{{ - 2}}}$ абсолютно совпадает со спектром лагранжевой турбулентности, можно предположить гипотезу об их аналогии, согласно которой спектр течений ${{S}_{z}}(f)$ в фиксированной точке измерений обусловлен воздействием на вертикальные перемещения хаотизированных орбитальных волновых движений, разрушенных их гидродинамической неустойчивостью. Приняв эту гипотезу, с учетом размерности частотного спектра скорости и СТД, для ${{S}_{z}}(f)$ можно выписать соотношение, содержащее величину ε
в котором безразмерная константа ${{C}_{p}}$ считается фиксированной для имеющейся геометрии системы, т.е. она неизменна для всех значений W и z. Учитывая нормировочный характер этой величины, можно принять, что
Такой феноменологический подход позволяет оценивать СДТ по оценкам спектра ${{S}_{z}}(f)$. Подробнее вопрос его обоснованности обсуждается в разделе 5.
4.3. Оценки СДТ и их параметризация
Применение формулы (17) для оценивания величины ε очевидно. Зафиксировав некоторую частоту fF в области участка спектра вида (17), например, fF = 10 Гц, по графику спектра определяем величину ${{S}_{z}}({{f}_{F}}) = {{S}_{z}}(10\,\,{\text{Hz}}) \equiv {{S}_{{10}}}$ и получаем оценку
(19)
$\varepsilon = {{f_{F}^{2}{{S}_{{10}}}} \mathord{\left/ {\vphantom {{f_{F}^{2}{{S}_{{10}}}} {{{C}_{p}}}}} \right. \kern-0em} {{{C}_{p}}}} = f_{F}^{2}{{S}_{{10}}}.$Для всех случаев, когда спектры вертикальной компоненты ${{S}_{z}}(f)$ в ВЧ-области имеют форму (17) (см. примеры на рис. 1 и 2), с использованием соотношения (19) получены искомые оценки величины ε, приведенные в табл. 2.
Последующий анализ эмпирических оценок ${{\varepsilon }_{{}}}$ из табл. 2, с привлечением сведений о параметрах волн из табл. 1, показывает, что параметризация величины СДТ, построенная из размерных соображений, может быть представлена формулой
(20)
${{\varepsilon }_{{par}}} = {{c}_{\varepsilon }}[a_{0}^{2}f_{p}^{3}]({{{{a}_{0}}} \mathord{\left/ {\vphantom {{{{a}_{0}}} z}} \right. \kern-0em} z})\exp ( - {{c}_{2}}{{k}_{p}}\left| z \right|)$при значениях подгоночных параметров
Экспонента в (20), уточняющая линейный спад ${{\varepsilon }_{{}}}$ с глубиной, добавлена из феноменологических соображений, основанных на потенциальной теории волн.
Оценки ${{\varepsilon }_{{par}}}$, полученные по формулам (20), (21), приведены в табл. 2 полужирным курсивом совместно с эмпирическими оценками ${{\varepsilon }_{{}}}$ для удобства сравнения. Как видно, при больших значениях W и малых горизонтах z, для которых эмпирические значения ε наиболее достоверны, параметризация (20), (21) соответствует эмпирике со средней ошибкой менее или порядка 30%. Поиск более точного соответствия для имеющихся данных здесь уже не целесообразен, поскольку сама ошибка эмпирических оценок ε составляет от 20 до 30%, нарастая по мере увеличения глубин. Представляется, что с указанной точностью параметризация (20), (21) вполне пригодна для проверки теоретических моделей типа [13–15], что и закрывает вторую задачу работы.
5. ОБСУЖДЕНИЕ
Остановимся на вопросах, решение которых до конца не ясно и представляет интерес для дальнейших исследований. К ним относятся: 1) причины различия формы спектров для горизонтальных и вертикальной компонент скорости наведенных течений; 2) обоснованность рекомендаций работы [22] по выбору тейлоровской скорости переноса UТ “замороженной турбулентности”; 3) обоснованность параметризации наблюдаемых спектров (10) в виде ${{S}_{z}}(f) = {{C}_{p}}\varepsilon {{f}^{{ - 2}}}$ и выбор величины ${{C}_{p}}$; 4) точность оценивания величины $\varepsilon $; 5) сравнение оценок $\varepsilon $, полученных в разных работах.
5.1. Напомним, что различия формы спектров для горизонтальных и вертикальной компонент скорости впервые были получены в предыдущей работе авторов [1], где рассматривались течения в том же канале, наведенные механическими волнами. Поэтому полученные здесь аналогичные результаты, фактически, уже свидетельствуют об их системности, требующей системного обоснования.
Следуя общей идеологии [2–4], степенные участки спектров турбулентных течений, индуцированных волнами, трактуются как аналоги колмогоровских спектров, обусловленных передачей кинетической энергии из области частот доминантных орбитальных волновых движений вниз и вверх по частотам. Такая трактовка эмпирических степенных спектров, например, была принята в [4–9]. Ввиду отсутствия достаточной теоретической разработанности вопроса, природа формирования и причины различия таких потоков вверх и вниз по спектру турбулентности, индуцированной волнами, пока не ясны. По крайней мере, теоретические модели формирования спектров наведенной волнами турбулентности, приводящие к появлению модельных спектров компонент течений вида $S(f) \sim {{f}^{{ - 5/3}}}$, не говоря уже о спектрах вида $S(f) \sim {{f}^{{ - 2}}}$, пока отсутствуют. Сейчас можно лишь предполагать, что разница законов спадания спектров для горизонтальных и вертикальной компонент (в ВЧ-области) обусловлена различной механикой формирования волнами турбулентных движений в различных плоскостях.
Чтобы обосновать возможность появления указанного различия, следует, вначале, хотя бы указать на возможные причины принципиального отличия динамики горизонтальных и вертикальных движений. На наш взгляд, такие причины могут заключаться в следующем.
Во-первых, общеизвестно [27–29], что в горизонтальной плоскости волны на воде всегда генерируют определенное среднее сдвиговое течение ${\mathbf{U}} = ({{U}_{d}}(z),0,0)$, будь то Стоксов или ветровой дрейф ${{U}_{d}}(z)$. Но в вертикальной плоскости среднего течения нет, если не считать слабого возвратного течения, неизбежного для замкнутых водоемов [28, 29]. Во-вторых, в вертикальной плоскости всегда есть направленный вверх градиент среднего горизонтального течения ${\mathbf{G}} = (0,0,{{\partial U{}_{d}(z)} \mathord{\left/ {\vphantom {{\partial U{}_{d}(z)} {\partial z}}} \right. \kern-0em} {\partial z}})$, а в горизонтальной плоскости градиент среднего течения настолько мал, что на масштабах локальной турбулентности им можно пренебречь [27–29]. Эти два различия геометрии движений в горизонтальной и вертикальной плоскостях, возможно, и приводят к различию форм спектров для горизонтальных и вертикальной компонент скорости течений, наведенных волнами. Окончательный ответ на рассматриваемый вопрос требует детального теоретического исследования.
На данный момент можно предложить следующую феноменологическую модель рассматриваемых процессов. Запишем скорость орбитального волнового движения в виде Uw = = $({{U}_{w}}\cos (\varphi ),0,{{U}_{w}}\sin (\varphi ))$, где переменная φ означает волновую фазу и принято упрощенное представление о двухмерности волн. Естественно считать, что характер неустойчивости орбитальных движений, порождающих мелкомасштабную турбулентность, может существенно меняться в зависимости от того, как направление скорости орбитальных движений ${{{\mathbf{U}}}_{w}}$ соотносится с направлением среднего течения ${\mathbf{U}}$ в горизонтальной плоскости (по течению или против), или с направлением градиента средней скорости G в вертикальной плоскости (по градиенту или против). Согласно механике волн на течениях [26–28], в фазе φ, когда волновые орбитальные движения ${{{\mathbf{U}}}_{w}}$ направлены по течению ${\mathbf{U}}$, должно происходить укрупнение (“растягивание”) масштаба флуктуаций волновой скорости частиц, т.е. перенос энергии в низкие частоты. И наоборот – в противофазе. По аналогии с этим, в вертикальной плоскости направление орбитальных движений ${{{\mathbf{U}}}_{w}}$ в направлении градиента ${\mathbf{G}}$ (в сторону увеличения скорости переноса U(z)) может приводить к уменьшению (“сжатию”) масштаба флуктуаций волновой скорости, т.е. к переносу энергии вверх по частотам. И наоборот – в противофазе.
Таким образом, различие указанных соотношений направлений может порождать наблюдаемые эмпирически две ветви турбулентности: НЧ- и ВЧ-ветвь (рис. 1а, 1б, 2а, 2б). Остается, однако, неясной причина совпадения формы НЧ- и ВЧ‑ветвей спектров течений в горизонтальной плоскости и их различия в вертикальной плоскости (см. раздел 3.2). При этом если допустить, что спектры вида $S(f) \sim {{f}^{{ - 5/3}}}$ являются потоковыми (колмогоровскими), то в любом случае, в формуле (16) в качестве тейлоровской скорости переноса турбулентности UT должна выступать не отдельно скорость дрейфа Ud или скорость орбитального движения Uw, а их комбинация, например, Uw ± Ud. А в ВЧ-спектре вертикальной компоненты скорости вида ${{S}_{z}}(f) = C{{f}^{{ - 2}}}$ роль скорости переноса вообще не понятна, т.к. среднего потока нет. Вполне вероятно, что величину размерной константы С будет определять комбинация градиентов скоростей Ud и Uw.
Перечисленные здесь предположения дают возможные направления для поиска объяснений причин различия в формировании наблюдаемых спектров. Но их окончательное обоснование требует дополнительного как экспериментального, так и теоретического изучения.
5.2. Если трактовать формы вида $S(f) \sim {{f}^{{ - 5/3}}}$ как традиционные колмогоровские спектры (подобно работам [4–9]), то возникает вопрос о выборе тейлоровской скорости “замороженной турбулентности” UТ. Казалось бы, что ответ на этот вопрос дан в работе [22], где в НЧ-области рекомендуется использовать скорость дрейфа Ud, а в ВЧ-области – орбитальную скорость доминантных волн Uw. Поскольку НЧ-ветвь турбулентности нами в работе не рассматривается (см. начало раздела 4.2), обсудим далее только анализ ВЧ-ветви спектров компонент скорости.
Внимательное прочтение работы [22] показывает, что указанное в ней предложение выбора скорости переноса UТ недостаточно обоснованно теоретически и является, скорее, “априорным”. В пользу сказанного говорит наличие таких априорных постулатов теории [22], как: изотропия турбулентности; изначальное постулирование спектра течений вида ${{S}_{u}}(k) \sim {{k}^{{ - 5/3}}}$, которому просто неоткуда появиться без учета механизма хаотизации орбитальных движений; вольное применение допплеровского соотношения $\omega = kU$, используемого безотносительно направления компоненты скорости. Имеется и ряд математических несостыковок, например, в формулах (2.3) и (2.6). Кроме того, как постулирование изотропии, так и полученное в итоге соотношение интенсивностей НЧ- и ВЧ-ветвей колмогоровских участков спектра течений (формула 6.1 в [22]), явно не подтверждаются эмпирически (см., например, рис. 1б и 2а, 2б, 2в).
Сказанное здесь и в предыдущем разделе 5.1 заставляет сомневаться в предложении работы [22] использовать орбитальную скорость доминантных волн Uw в качестве скорости переноса турбулентности UT для ВЧ-ветви спектра скоростей. Именно по этим двум причинам указанная рекомендация работы [22] нами не применялась, а вопрос анализа ВЧ-ветви спектров горизонтальных компонент скорости Sx(f ) и Sy(f ) с законом спадания “–5/3”, равно как и трактовки НЧ-ветви для спектра Sz(f ), следует перенести на перспективу их дальнейшего изучения.
5.3. Что касается ВЧ-ветви спектра Sz(f ) вида ${{S}_{z}}(f) \sim {{f}^{{ - n}}}$, следует отметить, что близкий результат, с показателем спадания спектра 2 < n < 3 был отмечен еще в работе [10], где он никак не обсуждался. Нам представляется, что нет никаких причин, запрещающих представление нашего результата в виде (17), т.е. ${{S}_{z}}(f) = {{C}_{p}}\varepsilon {{f}^{{ - 2}}}$. Формальная аналогия с турбулентной диффузией, постулированная в разделе 4.2, вполне позволяет предложить механизм формирования спектра (17) как результат флуктуаций вертикального перемещения частиц жидкости через точку измерения, хаотически подталкиваемых случайными импульсами, индуцированными неустойчивостью волновых орбитальных движений. Согласно феноменологическому построению, предложенному в разделе 5.1, такое движение диффузного типа должно происходить только в фазе, когда орбитальная скорость направлена вверх, т.е. вдоль вертикального градиента сдвиговой горизонтальной скорости.
В принятой нами феноменологической параметризации ВЧ-ветви спектра Sz(f) вида ${{S}_{z}}(f) = {{C}_{p}}\varepsilon {{f}^{{ - 2}}}$ возникает необходимость постулирования величины ${{C}_{p}}$, функциональное представление которой через параметры системы пока неизвестно. Если принять, что соотношение (17) полностью соответствует механизму турбулентной диффузии, то, согласно формуле (1.1.19) из книги [3], величина ${{C}_{p}}$ должна иметь порядок единицы. На этом основании, учитывая предлагаемый здесь феноменологический уровень описания процесса, для простоты получения оценок СДТ, нами принято значение ${{C}_{p}}$ = 1. Дальнейшие исследования должны будут показать степень соответствия полученных величин ε тем оценкам, которые уже были получены в аналогичных исследованиях в ветро-волновых каналах, например, в работах [1, 7–9]. В этом вопросе немаловажную роль играют как точность определения значений ε, так и близость физических условий выполнения различных экспериментов.
5.4. Относительно точности определения величины ε следует заметить, что этот вопрос ранее практически нигде не обсуждался [4–9]. Во многом он зависит от метода и техники получения оценок спектральной плотности компонент скорости течений Si(f). В нашем случае, как отмечено в разделе 2, статистическая ошибка в оценках интенсивности спектров Si(f) составляет всего около 5%. Однако ошибка в оценке показателя степени n в форме аппроксимации ${{S}_{z}}(f) = C{{f}^{{ - n}}}$ определяется геометрией линии оценки спектра ${{S}_{z}}(f)$ (см. рис. 2а, 2б, 2в).
Анализ всей совокупности оценок показывает, что изрезанность линии спектра ${{S}_{z}}(f)$в НЧ-области очень мала (рис. 1 и 2). Потому для НЧ-ветви спектра ошибка оценки СДТ будет складываться из ошибки оценки интенсивности самого спектра, имеющей порядок 5%, и ошибки определения тейлоровской скорости ${{U}_{{\text{T}}}}(z)$, если пользоваться формулой (16) (в данной работе не выполнялось). Но уже для ВЧ-ветви спектра изрезанность этой части линии спектра ${{S}_{z}}(f)$ и реальные отклонения среднеквадратичного наклона спектра ${{S}_{z}}(f)$ от формы (17), даже по простой формуле (19), приводят к ошибке порядка 20–30% для оценки величины ε, что задается точностью определения уровня ${{S}_{{10}}}$, используемого в формуле (19). Поэтому эмпирические оценки ε, приведенные в табл. 2, несут в себе итоговую ошибку не менее 30%.
5.5. И наконец, для полноты рассмотрения, сопоставим наши оценки ε c таковыми из цитированных работ. При этом, с целью соблюдения требования близости экспериментальных условий, будем сравнивать только измерения СДТ в каналах [1, 7, 8].
5.5.1. Вначале сравним зависимости ε от параметров системы ${{a}_{0}}$ и $u{\text{*}}$, привлекая параметризацию $\varepsilon ({{a}_{0}},{{f}_{p}},z)$ из формулы (20). Как и в случае механических волн [1], для ветровых волн величина ε, согласно (20), пропорциональна $a_{0}^{3}$. Этот результат соответствует оценкам зависимости величины $\varepsilon $ от амплитуды волн поверхности воды ${{a}_{0}}$ из работы [7]. Однако оценка зависимости $\varepsilon ({{u}_{*}})$ требует пересчета формулы (20).
С учетом законов роста волн [24], имеют место соотношения: ${{a}_{0}} \sim u{\text{*}}$ и ${{f}_{p}} \sim u_{*}^{{ - 1/3}}$. Тогда параметризация (20) дает зависимость $\varepsilon \sim u_{*}^{2}$, что несколько отличается от результата (4), полученного, например, в [5, 9]. Такое различие объясняется различием условий эксперимента (различные возраст волн, глубина измерений и степень их обрушений), что может быть проверено в дальнейших экспериментах.
Что же касается зависимости $\varepsilon $ от глубины z, форма (20) при малых z близка к виду ε ~ z–1, установленному в работах [6] и [8] для уровней $z \leqslant {{a}_{0}}$, а при $z \geqslant (5 - 6){{a}_{0}}$, она близка к экспоненциальной зависимости, известной из работ [6, 30].
Отмеченные соответствия говорят о правдоподобии полученных здесь результатов.
5.5.2. Сопоставим теперь сами величины ε. Начнем с того, что в нашем эксперименте для ветровых волн высотой a0 = 2–3 см и частотой пика fp ≈ 1.7 Гц, для глубины z = –10 cм, получены оценки εPw≈ 6 × 10–5 м2 с–3 (здесь и далее нижние индексы при ε введены для различения оценок по фамилии первого автора работы и типу волнения: w – ветровые волны, m – механические). Для тех же параметров волн и глубин в работе [1] для механических волн со спектром типа JONSWAP, типичным для спектра ветровых волн, получены оценки εPm ≈ 10–4 м2 с–3. Как видно, при сопоставимых параметрах системы (a0, fp и z), полученные оценки величины СДТ вполне сопоставимы в пределах их точности.
В работе [7] для монохроматических волн в канале, при тех же значениях a0 и частоте пика fp = = 1.5 Гц, для глубины измерений z = –4 см получена оценка εBm ≈ 10–3 м2 с–3, что на порядок выше нашей оценки εPm. Однако, с учетом зависимости ε(z) по формуле параметризации (20), пересчет оценки εPm (из [1], для механических волн) увеличивает ее почти на порядок: εPm(z = –4 см) ≈ 8 × × 10–4 м2 с–3. Это приводит к сближению разницы величин εPm и εBm до 20%, что находится в пределах эмпирических ошибок.
В работе [8] оценки СТД были выполнены для сильно обрушивающихся механических волн с крутизной δ = 0.4 в диапазоне глубин (0.5–1.5)a0 при фиксированных значениях a0 ≈ 4 см и fp =1.2 Гц. В частности, для глубины измерения z = –a0 ≈ –4 см полученное в [8] значение εLm ≈ 2 × 10–4 м2 с–3 (см. рис. 5 из [8]) на полпорядка превышает нашу оценку εPw ≈ 6 × 10–5 м2 с–3. Однако ее пересчет по формуле (20) на указанные значения a0, fp и z дают оценку εPm(z = –4 см, a0 ≈ 4 см, fp =1.2 Гц, δ = 0.4) ≈ ≈ 3 × 10–4 м2 с–3, что сокращает различие εPw и εLm до уровня менее ошибок самих оценок.
Как видно, выполненное сравнение наших оценок ε с таковыми из других работ, близких по условиям измерений, показывает, во-первых, их близость к уже известным результатам; а во-вторых, работоспособность и эффективность использования параметризации (20); что и завершает дискуссию по результатам работы.
6. ЗАКЛЮЧЕНИЕ
С целью выделения турбулентных составляющих скорости в измеренных течениях предложена феноменологическая процедура фильтрации волновых компонент путем отсечения доминантного пика в спектрах измеренных течений ${{S}_{i}}(f)$ (i = x, y, z) в области частоты волн fp (раздел 3). Такой прием вполне соответствует результатам применения “точного” метода фильтрации по работам [19–21].
Полученные спектры турбулентности ${{S}_{{iF}}}(f)$ в области частот f < 0.5fp (НЧ-область) и при f > 2fp (ВЧ-область) совпадают со спектрами измеренных течений ${{S}_{i}}(f)$, что позволяет использовать их для дальнейшего анализа характеристик турбулентности.
Стандартные отклонения компонент измеренных и фильтрованных течений, σi, и σiF, рассчитанные через спектры ${{S}_{i}}(f)$ и ${{S}_{{iF}}}(f)$ по стандартной формуле (2), демонстрируют существенную анизотропию наведенных течений как до, так и после фильтрации.
Установлено: а) всегда имеет место соотношение σx > σy > σz, и, как правило, величины σy и σx значительно (в 1.5–2 раза) больше σz; б) ${{\sigma }_{{iF}}}$ сохраняют характер анизотропии стандартных отклонений полных течений ${{\sigma }_{i}}$; в) степень указанной анизотропии снижется с глубиной; г) отношение квадратов (${{\sigma }_{{iF}}}$/${{\sigma }_{i}}$)2 показывает, что в случае ветровых волн доля энергии турбулентности наведенных течений составляет порядка и более 70%.
С целью сопоставления эмпирики с теорией, для σiF предложена их параметризация (14, 15). Особенности а)–г) ${{\sigma }_{{iF}}}$ и их параметризация установлены впервые.
Установлен эффект различной формы степенного спадания частотных спектров ${{S}_{i}}(f)$ для горизонтальных и вертикальной компонент скорости турбулентности, индуцированной ветровыми волнами. В НЧ- и ВЧ-областях, спектры турбулентных компонент скорости ${{S}_{x}}(f)$ и ${{S}_{y}}(f)$ спадают по закону “–5/3”. Спектр вертикальной компоненты скорости ${{S}_{z}}(f)$ в НЧ-области всегда спадает по тому же закону “–5/3”, но в ВЧ-области, при ветрах W ≥ 8 м/с, для течений на глубинах z ≥ –30 см реализуется закон спадания “–2”. т.е. ${{S}_{z}}(f) \sim {{f}^{{ - 2}}}$. Для течений, индуцированных ветровыми волнами, этот эффект эмпирически установлен впервые.
На феноменологическом уровне предложена модель, позволяющая указать на возможные причины различного механизма формирования турбулентности для горизонтальных и вертикальной компонент течений, наведенных волновыми орбитальными движениями (раздел 5.1).
Для ВЧ-области спектров вертикальной компоненты скорости вида ${{S}_{z}}(f) \sim {{f}^{{ - 2}}}$ феноменологически сформулирована гипотеза об аналогии между турбулентными движениями в вертикальной плоскости и турбулентной диффузией, порождаемой стохастическими некоррелированными флуктуациями орбитальной скорости (на фазе ее направления по градиенту среднего сдвигового течения $U(z)$, см. раздел 5.1).
В таком случае, из размерных соображений спектр ${{S}_{z}}(f) \sim {{f}^{{ - 2}}}$ представлен формулой (17): ${{S}_{z}}(f) = {{C}_{p}}\varepsilon {{f}^{{ - 2}}}$ (${{C}_{p}}$ = 1), на основании которой получены оценки величины СДТ ε, приведенные в табл. 2. С учетом сведений о параметрах ветровых волн, для найденных оценок СДТ получена их аналитическая параметризация (20), пригодная для сравнений эмпирики и теории.
На основании предложенной параметризации проведено сравнение полученных оценок ε с таковыми из работ [1, 7, 8], в которых имели место близкие условия эксперимента. Показано хорошее количественное согласие между всеми оценками ε, что свидетельствует в пользу применимости предложенной параметризации (20).
Список литературы
Полников В.Г., Цяо Ф. Характеристики турбулентности, индуцированной механическими волнами в лотке // ЖЭТФ. 2021. Т. 159. № 1.
Монин А.С., Яглом А.Я. Статистическая гидромеханика. М.: Наука. 1967. Ч. 2. 630 с.
Голицын Г.С. Статистика и динамика природных процессов и явлений. М: Красанд. 2013. 398 с.
Kitaigorodskii S.A., Donelan M.A., Lumley J.L. et al. // Wave-turbulence interaction in the Upper Ocean. Pt. II. J. Phys. Oceanogr. 1983. V. 13. № 11. P. 1988–1999.
Terray E.A., Donelan M.A., Agrawal Y.C.et al. Estimates of kinetic energy dissipation under breaking waves // J. Phys. Oceanogr. 1996. V. 26. P. 792–807.
Soloviev A., Lukas R. Observation of wave-enhanced turbulence in the near-surface layer of the ocean during TOGA COARE // Deep-Sea Res. 2003. V. 50. P. 371–395.
Babanin A.V., Haus B.K. On the existence of water turbulenceinduced by non-breaking surface waves // J. Phys. Oceanogr. 2009. V. 39. P. 2675–2679.
Lee J.H., Monty J.P., Elsnab J. et al. Estimation of Kinetic Energy Dissipation from Breaking Waves in the Wave Crest Region // J. Phys. Oceanogr. 2017. V. 47. № 5. P. 1145–1159.
Полников В.Г., Байдаков Г.А., Троицкая Ю.И. Скорость диссипации турбулентности в слое воды под ветровыми волнами по данным лабораторного эксперимента // Изв. РАН. ФАО. 2019. Т 55. № 5. С. 127–137.
Ефимов В.В., Христофоров Г.Н. Спектры и характеристики статистической взаимосвязи пульсаций скорости в верхнем слое моря и поверхностного волнения // Изв. АН СССР. ФАО. Т. 7. № 12. С. 1290–1310.
Babanin A.V. On a wave-induced turbulence and a wave-mixed upper ocean layer // Geophys. Res. Lett. 2006. V. 33. P. L20605.
Alberello A., Onorato M., Frascoli F., Toffoli A. Observation of turbulence and intermittency in wave-induced oscillatory flows // Wave Motion. 2019. V. 84. P. 81–89. https://doi.org/10.1016/j.wavemoti.2018.10.003
Benilov A.Y. On the turbulence generated by the potential surface waves // J. Geophys. Res. 2012. V. 117. C00J30.
Babanin A.V., Chalikov D. Numerical investigation of turbulence generation in non-breaking potential waves // J. Geophys. Res. 2012. V. 117. C00J17.
Tsai W.T., Chen S.M., Lu G.H. Numerical Evidence of Turbulence Generated by Nonbreaking Surface Waves // J. Phys. Oceanogr. 2015. V. 45. № 3. P. 174–180.
Savelyev I.B., Maxeiner E., Chalikov D. Turbulence production by nonbreaking waves: Laboratory and numerical simulations // J. Geophys. Res. 2012. V. 117. C00J13.
Полников В.Г., Байдаков Г.А. Особенности профилей течений, потока импульса и скорости диссипации турбулентности в ветро-волновом канале// Изв. РАН. ФАО. 2020. Т. 56. № 2. С. 234–244.
Бенилов А.Ю., Филюшкин Б.Н. Приложение методов линейной фильтрации к анализу флуктуаций в поверхностном слое моря // Изв. АН СССР. ФАО. 1970. Т. 6. № 8. С. 810–819.
Thais L., Magnaudet J. A triple decomposition of the fluctuating motion below laboratory wind water waves // J. Geophys. Res. 1995. V. 100(C1). P. 741–755.
Thais L., Magnaudet J. Turbulent structure beneath surface gravity waves sheared by the wind // JFM. 1996. V. 338. P. 313–344.
Oh S-H., Mizutani N., Suh K.-D. Investigation of decomposition methods of turbulent flow field beneath wind waves // Proc. Coastal Engineering 2006. 2007. V. 251.
Lumley J.L., Terray E.A. Kinematics of turbulence convected by a random wave field // J. Phys. Oceanogr. 1983. V. 13. P. 2000–2007.
Kay S.M. Modern Spectral Estimation, Theory and Application. Englewood Cliffs, NJ: Prentice Hall, New Jersey. 1988, 540 p.
Полников В.Г., Цяо Ф., Ма Х., Чанг Ш. Новые эффекты эволюции спектра волн в лотке // Письма в ЖЭТФ. 2020. Т. 111. № 8. С. 501–508.
Komen G.I., Cavaleri L., Donelan M. et al. Dynamics and Modelling of Ocean Waves, London: Cambridge University Press, 1994.1994, 554 p.
Филлипс О.М. Динамика верхнего слоя океана. Л.: Гидрометеоиздат, 1980. 320 с.
Bremer T. S., Breivik Ø. Stokes drift // Phil. Trans. R. Soc. 2017. V. A 376: 20170104.
Longuet-Higgins M. Mass transport in water waves // Philos. Trans. Roy. Soc. London. 1953. V. 245A. P. 535–581.
Longo S. Wind-generated water waves in a wind tunnel: Free surface statistics, wind friction and mean air flow properties // Coastal Eng. 2012. V. 61. P. 27–41.
Anis A., Moum J.N. Surface wave–turbulence interactions: Scaling ε(z) near the sea surface // J. Phys. Oceanorg. 1995. V. 25. P. 2025–2045.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Физика атмосферы и океана
Пн.-пт.: 10.00-19.00