1. На главную
  2. Электронные версии
  3. Известия РАН. Физика атмосферы и океана
  4. T. 58, № 1, 2022

Известия РАН. Физика атмосферы и океана, 2022, T. 58, № 1, стр. 37-51

Исследование особенностей распространения атмосферных волн, генерируемых тропосферными источниками и вариациями приземного давления

С. П. Кшевецкий a, c, Ю. А. Курдяева b, *, С. Н. Куличков c

a Балтийский государственный университет им. И. Канта
236041 Калининград, Ал. Невского 14, Россия

b Калининградский филиал Института земного магнетизма, ионосферы и распространения радиоволн РАН
236010 Калининград, Пионерская 61, Россия

c Институт физики атмосферы им. А.М. Обухова РАН
119017 Москва, Пыжевский пер., 3, Россия

* E-mail: yakurdyaeva@gmail.com

Поступила в редакцию 23.06.2021
После доработки 24.09.2021
Принята к публикации 07.10.2021

Полный текст (PDF)

Аннотация

В работе теоретически изучается генерация и распространение волн от модельных тропосферных тепловых метеорологических источников. Предполагается, что источником волн являются процессы нагрева/охлаждение газа при фазовых переходах воды на тропосферных высотах. В аналитической части исследования выведены уравнения, описывающие генерацию и распространение акустических и внутренних гравитационных волн по отдельности. Показано, что мощности парциальных источников акустических и внутренних гравитационных волн всегда примерно совпадают, независимо от частоты волн, и генерация внутренних гравитационных волн не может происходить без генерации акустических, и наоборот. Получены явные аналитические выражения для генерируемых волн. Вследствие резонансных свойств атмосферы, высокочастотные источники генерируют преимущественно акустические волны. Низкочастотные источники генерируют преимущественно внутренние гравитационные волны, если они работают достаточное время для проявления резонансных свойств атмосферы. С помощью численных экспериментов исследован вопрос об ошибке, которая вносится, если тропосферный источник заменен поверхностным, в котором колебания давления на поверхности – зарегистрированные колебания давления, вызванные тропосферным источником. Показано, что если тропосферный источник работает на частотах инфразвуковых волн, то создаваемые в верхней атмосфере волновые картины от тропосферного источника и от поверхностных колебаний давления практически идентичны. В случае тропосферного источника на частотах внутренних гравитационных волн, амплитуда волн от поверхностного давления может быть завышена не более чем вдвое. Показано, что по колебаниям давления на поверхности Земли можно построить скорректированный поверхностный источник давления, учитывающий сдвиг фаз у интерферирующих волн, распространяющихся в верхнюю атмосферу. Это дает существенное уточнение расчета волн от метеорологических источников на основе данных о колебаниях атмосферного давления.

Ключевые слова: моделирование, акустико-гравитационные волны, внутренние гравитационные волны, акустические волны, верхняя атмосфера, тропосфера, термосфера, метеорология

1. ВВЕДЕНИЕ

Многочисленные исследования [1–6] пространственно-временных вариаций атмосферных и ионосферных параметров указывают на связь между возмущениями в верхних слоях атмосферы и вертикальным распространением акустико-гравитационных волн (АГВ) из нижней атмосферы. Атмосферные волны, генерируемые различными источниками в тропосфере, достигая высот термосферы, отдают свой импульс и энергию и влияют на общую циркуляцию в атмосфере и на распределение температуры газа с высотой [7, 8]. Диссипирующие волны могут быть источником различных неустойчивых процессов, создавать струйные течения и изменять тепловой баланс в верхних слоях атмосферы [1, 9–11], а также влиять на движение плазмы и, как следствие, на распространение радиоволн [12, 13].

Физические механизмы генерации акустико-гравитационных волн на тропосферных высотах различны [3, 14–17]. Одним из мощных энергетических источников АГВ являются процессы выделения/поглощения тепла при фазовых переходах воды в атмосфере при образовании и эволюции облаков [18, 19] и формировании других метеорологических явлений. Нагрев атмосферы этим тепловыделением может приводить атмосферный газ в движение, и может вызывать различные последствия, в том числе нарушение статической устойчивости атмосферы с последующим развитием неустойчивых процессов. Это обусловливает большое разнообразие, сложную эволюцию, и, как следствие, трудность описания детальной структуры этих явлений.

При численном исследовании распространения АГВ от метеорологических явлений часто возникает проблема задания реалистичных источников волн, связанная с существенным недостатком детальной экспериментальной информацией о них вследствие сложной трехмерной структуры многих метеорологических явлений и их большого разнообразия. Генерация волн при протекании метрологических процессов приводит к изменению приземного давления. В работах [20–22] впервые было предложено использовать экспериментальные данные о колебаниях давления на поверхности Земли, записанные на сети микробарографов, для расчета волн, распространяющихся от метеорологических явлений в верхнюю атмосферу. Поскольку задача о распространении волн от колебания давления на границе необычна для гидродинамики, в [23, 24] была сформулирована математическая постановка гидродинамической задача о распространении волн от колебаний давления на границе. Была доказана корректность предложенной постановки задачи, а также был предложен и протестирован численный метод для решения этой задачи. В [20, 21] впервые была решена задача о распространении волн от экспериментально наблюдаемых колебаний давления на поверхности Земли во время прихода атмосферного фронта.

Данная работа посвящена математическому изучению вопроса о связи задачи о генерации волн тропосферными метеорологическими источниками с задачей о генерации волн волнообразными изменениями давления у поверхности Земли. Вначале аналитически рассматривается общая задача о генерации АГВ в изотермической атмосфере локальным тепловым источником на тропосферных высотах и исследуются типы волн, которые может генерировать такой тепловой тропосферный источник. Теоретически показано, что генерация внутренних гравитационных волн тепловым источником не может происходить без генерации этим же источником инфразвуковых волн, и наоборот. Вычислены парциальные источники инфразвуковых волн и внутренних гравитационных волн по тепловому источнику. Показано, что мощности этих парциальных источников примерно равны друг другу.

В работе численно исследовано распространение инфразвуковых и внутренних гравитационных волн, генерируемых модельным локальным тепловым тропосферным источником сравнительно небольшого размера. Небольшие размеры модельного источника связаны с тем, что практически любой произвольный тепловой источник сложной формы можно представить в виде суммы локальных небольших источников. Таким образом, достаточно произвольная задача о нагреве источником тепла математически сводится к изучаемой задаче о нагреве небольшим источником. Колебания давления на поверхности Земли от рассматриваемого модельного источника записываются для дальнейшего использования. Они применяются далее при расчете распространения волн от колебаний давления на нижней границе и являются аналогом экспериментально наблюдаемых волноподобных вариаций давления на поверхности Земли. Будет проведено сравнение результатов расчетов волн непосредственно от тропосферного источника и от записанных колебаний давления на поверхности Земли. Далее будет предложено, как скорректировать поверхностный источник давления, чтобы он точнее описывал волны, возникающие от тропосферного источника.

2. АНАЛИТИЧЕСКОЕ ИССЛЕДОВАНИЕ ЗАДАЧИ О РАСПРОСТРАНЕНИИ ВОЛН ОТ ТРОПОСФЕРНОГО ТЕПЛОВОГО ИСТОЧНИКА

Тропосферные метеорологические события разнообразны по морфологии, времени существования и высоте локализации [25, 26]. Тропосферный тепловой источник находится в узком приземном слое толщиной 12 км у поверхности Земли. Рассмотрим двумерную задачу о распространении волн от тропосферного теплового источника. Упрощение задачи до двумерной не вносит принципиальных изменений в проводимый анализ, но значительно облегчает её исследование. Вблизи поверхности Земли амплитуда волн обычно мала из-за большой плотности газа и ветер у поверхности Земли обычно слабый. Поэтому при аналитическом анализе генерации волн тропосферным источником можно воспользоваться уравнениями линейной теории волн [27] и не учитывать ветер:

(1)
$\begin{gathered} {{\left( {{{\rho }_{0}}\Psi } \right)}_{t}} + {{\left( {{{\rho }_{0}}U} \right)}_{x}} + {{\left( {{{\rho }_{0}}W} \right)}_{z}} = 0, \\ {{\left( {{{\rho }_{0}}U} \right)}_{t}} + {{\rho }_{0}}gH{{\left( {\Psi + \Phi } \right)}_{x}} = 0, \\ {{\left( {{{\rho }_{0}}W} \right)}_{t}} + {{({{\rho }_{0}}gH\left( {\Psi + \Phi } \right))}_{z}} + {{\rho }_{0}}g\Psi = 0, \\ {{\left( {{{\rho }_{0}}\Phi } \right)}_{t}} + \left( {\gamma - 1} \right)\left( {{{{\left( {{{\rho }_{0}}U} \right)}}_{x}} + {{{\left( {{{\rho }_{0}}W} \right)}}_{z}}} \right) + \\ + \,\,\frac{\alpha }{H}{{\rho }_{0}}W = {{\rho }_{0}}f\left( {x,z,t} \right). \\ \end{gathered} $
Здесь $\Psi = \frac{{\rho \left( {x,z,t} \right) - {{\rho }_{0}}\left( z \right)~}}{{{{\rho }_{0}}\left( z \right)}}$ – волновая добавка к фоновой температуре, $\Phi = \frac{{T\left( {x,z,t} \right) - {{T}_{0}}\left( z \right){\text{\;}}}}{{{{T}_{0}}\left( z \right)}}$ – волновая добавка к фоновому распределению плотности атмосферного газа ${{\rho }_{0}}\left( z \right)$, $H\left( z \right)$ – высота однородной атмосферы, $\alpha = \left( {\gamma - 1 + \gamma \frac{{dH\left( z \right)}}{{dz}}} \right)$, $\gamma $– показатель адиабаты, – ускорение свободного падения, $U,W$– компоненты массовой скорости газа вдоль горизонтальной оси $x$ и вертикальной оси $z$. Остальные обозначения традиционны. В правой части системы уравнений записан тепловой источник $f\left( {x,z,t} \right)$. Мы предполагаем, что источник учитывает нагрев/охлаждение газа при фазовых переходах воды в атмосфере. Очевидно, изменение температуры газа приводит газ в сложное движение.

Дополним систему уравнений (1) естественным нижним граничным условием

(2)
$W\left( {x,z = 0,t} \right) = 0.$

Рассматривается случай, когда атмосферы изотермическая: фоновое распределение температуры газа с высотой ${{T}_{0}}\left( z \right){\text{\;}}$ не зависит от высоты $z$ и фоновая плотность изменяется с высотой экспоненциально ${{\rho }_{0}}\left( z \right) = {{\rho }_{{00}}}{\text{exp}}\left( { - \frac{z}{H}} \right)$. Общее решение рассматриваемой задачи можно записать в виде разложения по системе собственных базисных функций задачи. Для удобства, запишем систему уравнений (1) в виде одного матричного уравнения

(3)
${{\rho }_{0}}\frac{{\partial \lambda }}{{\partial t}} + \hat {L}\lambda = {{\rho }_{0}}\left( z \right)F\left( {x,z,t} \right).$
Здесь

(4)
$\hat {L}\lambda = \left( {\begin{array}{*{20}{c}} {{{{\left( {{{\rho }_{0}}U} \right)}}_{x}} + {{{\left( {{{\rho }_{0}}W} \right)}}_{z}}} \\ {{{\rho }_{0}}gH{{{\left( {\Psi + \Phi } \right)}}_{x}}} \\ {{{{({{\rho }_{0}}gH\left( {\Psi + \Phi } \right))}}_{z}} + {{\rho }_{0}}g\Psi } \\ {\left( {\gamma - 1} \right)\left( {{{{\left( {{{\rho }_{0}}U} \right)}}_{x}} + {{{\left( {{{\rho }_{0}}W} \right)}}_{z}}} \right) + \frac{\alpha }{H}{{\rho }_{0}}W} \end{array}} \right),$
(5)
$F\left( {x,z,t} \right) = \left( {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} 0 \\ 0 \\ 0 \end{array}} \\ {f\left( {x,z,t} \right)} \end{array}} \right),\,\,\,\,~\lambda \left( {x,z,t} \right) = \left( {\begin{array}{*{20}{c}} {\Psi \left( {x,z,t} \right)} \\ {U\left( {x,z,t} \right)} \\ {W\left( {x,z,t} \right)} \\ {\Phi \left( {x,z,t} \right)} \end{array}} \right).$

В случае, когда тепловой источник не работает и $F\left( {x,z,t} \right) = 0$, система уравнений (1) при нижнем граничном условии (2) имеет систему собственных частных решений вида

(6)
$\chi \left( {x,z,t,k,m,\omega } \right) = \tilde {\chi }\left( {x,z,t,k,m,\omega } \right)\frac{1}{{\sqrt {2\pi } }}{{e}^{{ - i\omega t}}},$
где

(7)
$\begin{gathered} \tilde {\chi }\left( {x,z,t,k,m,\omega } \right) = \left( {\begin{array}{*{20}{c}} {\tilde {\Psi }} \\ {\tilde {U}} \\ {\tilde {W}} \\ {\tilde {\Phi }} \end{array}} \right) = \varepsilon \frac{1}{{\sqrt {2\pi } }}{{e}^{{\frac{z}{{2H}}}}}{{e}^{{ikx}}} \times \\ \times \,\,\left( {\begin{array}{*{20}{c}} {\left( {A\sin ~\left( {mz} \right) + B\cos ~\left( {mz} \right)} \right)} \\ {\frac{{gHk}}{\omega }\left( {\left( {A + C} \right)\sin \left( {mz} \right) + \left( {B + D} \right)\cos \left( {mz} \right)} \right)} \\ {\sin \left( {mz} \right)} \\ {\left( {C\sin ~\left( {mz} \right) + D\cos ~\left( {mz} \right)} \right)} \end{array}} \right), \\ \end{gathered} $
(8)
$\begin{gathered} A = - \frac{1}{2}i\left( {\frac{{2\gamma gH{{k}^{2}} - 2gH{{k}^{2}} - {{\omega }^{2}}}}{{\omega h\left( { - {{\omega }^{2}} + \gamma ~gH{{k}^{2}}} \right)}}} \right),~ \\ B = \frac{{i\omega m}}{{ - {{\omega }^{2}} + ~gH{{k}^{2}}}}, \\ C = - \frac{1}{2}i\frac{{\left( { - {{\omega }^{2}} + ~2gH{{k}^{2}}} \right)\left( {\gamma - 1} \right)}}{{\omega h\left( { - {{\omega }^{2}} + \gamma ~gH{{k}^{2}}} \right)}},~ \\ D = \frac{{i\omega m\left( {\gamma - 1} \right)}}{{ - {{\omega }^{2}} + ~\gamma gH{{k}^{2}}}}.~ \\ \end{gathered} $

Нормировочный множитель $\varepsilon $ в (7) будет определен позже. Частота $\omega $ определяется дисперсионным соотношением:

(9)
$\begin{array}{*{20}{c}} {\omega _{{A,G}}^{2} = \frac{{\gamma gH}}{2}\left( {{{k}^{2}} + {{m}^{2}} + \frac{1}{{4{{H}^{2}}}}} \right) \times } \\ { \times \,\,\left( {1 \pm \sqrt {1 - \frac{{4\left( {\gamma - 1} \right){{k}^{2}}}}{{{{\gamma }^{2}}{{H}^{2}}{{{\left( {{{k}^{2}} + {{m}^{2}} + {1 \mathord{\left/ {\vphantom {1 {(4{{H}^{2}})}}} \right. \kern-0em} {(4{{H}^{2}})}}} \right)}}^{2}}}}} } \right).} \end{array}$

Дисперсионное соотношение имеет четыре ветви, две из которых соответствуют акустическим волнам и две внутренним гравитационным волнам. То есть, при фиксированных компонентах $k$ и $m$ волнового вектора имеется четыре частных решения, два из которых соответствует акустическим волнам и два внутренним гравитационным волнам, распространяющимся в противоположные стороны.

Столбцы-функции $\tilde {\chi }\left( {z,k,m,\omega } \right)~$ образуют базис, и решение задачи (1) можно записать в виде разложения по этому базису:

(10)
$\begin{gathered} \lambda ~\left( {x,z,t} \right) = \int\limits_{ - \infty }^\infty {\int\limits_0^\infty {\left[ {{{A}^{ + }}\left( {k,m,t} \right)\tilde {\chi }\left( {z,k,m,{{\omega }_{A}}\left( {k,m} \right)} \right)} \right.} } + \\ + \,\,{{A}^{ - }}\left( {k,m,t} \right)\tilde {\chi }\left( {z,k,m, - {{\omega }_{A}}\left( {k,m} \right)} \right) + \\ + \,\,{{G}^{ + }}\left( {k,m,t} \right)\tilde {\chi }\left( {z,k,m,{{\omega }_{G}}\left( {k,m} \right)} \right) + \\ + \,\,{{G}^{ - }}\left( {k,m,t} \right)\tilde {\chi }\left. {\left( {z,k,m, - {{\omega }_{G}}\left( {k,m} \right)} \right)} \right]dkdm, \\ \end{gathered} $
где функции ${{A}^{ + }}\left( {k,m,t} \right)$, ${{A}^{ - }}\left( {k,m,t} \right)$, ${{G}^{ + }}\left( {k,m,t} \right)$, ${{G}^{ - }}\left( {k,m,t} \right),$ удовлетворяют сиcтеме незацепляющихся обыкновенных дифференциальных уравнений, которые с учетом источника волн ($F\left( {x,z,t} \right)~\, \ne ~\,0)$ выглядят следующим образом:

(11)
$\begin{gathered} \frac{{d{{A}^{ \pm }}\left( {k,m,t} \right)}}{{dt}} \pm i{{\omega }_{A}}{{A}^{ \pm }}\left( {k,m,t} \right) = F_{A}^{ \pm }\left( {k,m,t} \right), \\ \frac{{d{{G}^{ \pm }}\left( {k,m,t} \right)}}{{dt}} \pm i{{\omega }_{G}}{{G}^{ \pm }}\left( {k,m,t} \right) = F_{G}^{ \pm }\left( {k,m,t} \right). \\ \end{gathered} $

Уравнения (11) описывают генерацию и распространение акустических и внутренних гравитационных волн в спектральном представлении. Для источников этих волн $F_{A}^{ \pm }\left( {k,m,t} \right)$, $F_{G}^{ \pm }\left( {k,m,t} \right)$ выводятся выражения

(12)
$\begin{gathered} F_{A}^{ \pm }\left( {k,m,t} \right) = \tilde {\chi }\left( {x,z,t,k,m, \pm {{\omega }_{A}}\left( {k,m} \right)} \right),F\left( {x,z,t} \right), \hfill \\ F_{G}^{ \pm }\left( {k,m,t} \right) = \tilde {\chi }\left( {x,z,t,k,m, \pm {{\omega }_{G}}\left( {k,m} \right)} \right),F\left( {x,z,t} \right). \hfill \\ \end{gathered} $

Здесь скалярное произведение двух произвольных столбцов ${{\lambda }_{1}},~{{\lambda }_{2}}$, представляющих два решения системы (3), определяется формулой

(13)
$\begin{gathered} \left\langle {{{\lambda }_{1}},~{{\lambda }_{2}}} \right\rangle = \mathop \smallint \limits_{ - \infty }^\infty \mathop \smallint \limits_0^\infty {{\rho }_{0}}\left( z \right) \times \\ \times \,\,\left( {{{U}_{1}}{{U}_{2}} + {{W}_{1}}{{W}_{2}} + gH\left( z \right)\frac{{\left( {{{\Psi }_{1}} + {{\Phi }_{1}}} \right)\left( {{{\Psi }_{2}} + {{\Phi }_{2}}} \right)}}{\gamma }} \right. + \\ \left. { + \,\,gH\left( z \right)\frac{{\left( {{{\Phi }_{1}} - \left( {\gamma - 1} \right){{\Psi }_{1}}} \right)\left( {{{\Phi }_{2}} - \left( {\gamma - 1} \right){{\Psi }_{2}}} \right)}}{{\gamma \alpha \left( z \right)}}} \right)dzdx. \\ \end{gathered} $

Нормировочный множитель в (7) равен

$\varepsilon = \sqrt {\frac{1}{{{{\rho }_{{00}}}\tilde {\chi }\left( {x,z,t,k,m,\omega } \right),\tilde {\chi }\left( {x,z,t,k,m,\omega } \right)}}} .$

Решение уравнений (11) имеет вид

(14)
$\begin{gathered} {{A}^{ \pm }}\left( {k,m,t} \right) = \\ = \exp \left( { \mp i{{\omega }_{A}}t} \right)\mathop \smallint \limits_0^t \exp \left( { \pm i{{\omega }_{A}}t{\kern 1pt} '} \right)F_{A}^{ \pm }\left( {k,m,t{\kern 1pt} '} \right)dt{\kern 1pt} ', \\ {{G}^{ \pm }}\left( {k,m,t} \right) = \\ = \exp \left( { \mp i{{\omega }_{G}}t} \right)\mathop \smallint \limits_0^t \exp \left( { \pm i{{\omega }_{G}}t{\kern 1pt} '} \right)F_{G}^{ \pm }\left( {k,m,t{\kern 1pt} '} \right)dt{\kern 1pt} '. \\ \end{gathered} $

Из представленных формул видно, что базисные функции изменяются с высотой для акустических и гравитационных волн примерно одинаково. Поэтому мощности источников ${{F}_{A}}$, ${{F}_{G}}$ всегда примерно совпадают, независимо от частоты источника $F$. Однако это важное наблюдение не означает, что амплитуды генерируемых акустических и гравитационных волн будут одинаковыми. Если тепловой источник ассоциируется с метеорологическими процессами, то он имеет характерное время изменения большее обратной частоты Вяйясяля-Брента $N~\,\, = ~\sqrt {\frac{{\gamma - 1}}{\gamma }gH} ~$ [28]. В этом случае значение интеграла в (14) для акустических волн зарезается быстрооциллирующей экспонентой $\exp \left( { \pm i{{\omega }_{A}}t{\kern 1pt} '} \right)$ в подинтегральном выражении. Зарезание не сильное, поэтому амплитуда генерируемых акустических волн может быть оценена как амплитуда источника $F_{A}^{ \pm }\left( {k,m,t{\kern 1pt} '} \right)$, умноженная на $\left| {\frac{1}{{{{\omega }_{A}} - \sigma }}} \right|$, где $\sigma $ – характерная частота источника: $\frac{{\max \left| {F_{A}^{ \pm }\left( {k,m,t{\kern 1pt} '} \right)} \right|~}}{{{{\omega }_{A}} - \sigma }}$.

Если частота источника попадает в спектр частот внутренних гравитационных волн, то амплитуда внутренних гравитационных волн может линейно нарастать со временем, пока источник работает. В реальности метеорологические источники обычно непериодические и амплитуда гравитационных волн оценивается как произведение амплитуды источника на время работы источника.

Таким образом, тепловые метеорологические источники, работающие на частотах меньших частоты Вяйсяля–Брента, генерируют преимущественно внутренние гравитационные волны. При этом инфразвуковые волны тоже обязательно генерируются. Они имеют амплитуду меньшую, чем амплитуда гравитационных волн, но достаточную, чтобы эти волны было нельзя игнорировать.

Возбуждение инфразвуковых волн низкочастотным тепловым источником происходит потому, что у гравитационных волн колебания температуры и плотности согласованы, что определено поляризационными соотношениями (7). Тепловой источник локально изменяет лишь температуру. Чтобы возникла гравитационная волна, необходимо обеспечить согласованное колебание плотности. Генерация сопутствующих акустических волн во время возникновения гравитационных волн позволяет достичь согласования колебаний температуры и плотности. Генерация внутренних гравитационных волн тепловым источником всегда сопровождается генерацией акустических волн, и наоборот.

Если тепловой источник работает на частотах акустических волн, то такой источник, кроме акустических волн также генерирует внутренние гравитационные волны. Амплитуда таких дополнительно генерируемых гравитационных волн меньше амплитуды акустических волн, но достаточна, чтобы такую генерацию гравитационных волн нельзя было игнорировать.

3. ПОСТАНОВКА ЗАДАЧИ О РАСПРОСТРАНЕНИИ ВОЛН ОТ ЛОКАЛЬНОГО ТРОПОСФЕРНОГО ИСТОЧНИКА ТЕПЛА

Аналитическое исследование спектра волн, генерируемых локальным тропосферным источником тепла, выполнено для изотермической атмосферы. Для исследования волн в неизотермической атмосфере будет применена численная модель “AtmoSym” [27, 29], которая позволяет решать задачи распространения волн от различных начальных возмущений и источников волн в диапазоне высот 0–500 км над территорией с горизонтальным масштабом до нескольких тысяч километров.

Общая идея предлагаемых численных экспериментов иллюстрируется на рис. 1. На рис. 1 схематически показано распространение волн от тропосферного источника тепла. Амплитуда волн на этих высотах обычно мала из-за большой плотности газа на тропосферных высотах. Поэтому для анализа генерируемых волн можно использовать понятия линейной теории волн. Источник излучает волну $\Delta {{P}_{{downward}}}~\left( {x,~z,~t} \right)$ вниз с такой же амплитудой, как и у волны $\Delta {{P}_{{upward}}}~\left( {x,~z,~t} \right)$, которая распространяется вверх. Волна $\Delta {{P}_{{downward}}}~(x,~z,~t)$, распространяющаяся вниз от тропосферного источника, достигает поверхности Земли, и отражается от нее. Амплитуда отраженной волны $\Delta {{P}_{{reflected}}}~\left( {x,~z,~t} \right)$ равна амплитуде падающей волны, и поэтому регистрируемое на поверхности Земли волнообразное колебание давления $\Delta P~\left( {x,~z\,~ = ~\,0,~t} \right)$ равно удвоенному по амплитуде колебанию давления, создаваемому падающей волной:

(15)
$\begin{gathered} \Delta P~\left( {x,~z~\,\, = 0,~t} \right) = \Delta {{P}_{{downward}}}~\left( {x,~z = 0,t} \right) + \\ + \,\,\Delta {{P}_{{reflected}}}~\left( {x,~z = 0,~t} \right), \\ \Delta {{P}_{{downward}}}~\left( {x,~z = 0,t} \right) = \Delta {{P}_{{reflected}}}~\left( {x,~z = 0,~t} \right) = \\ = \frac{1}{2}\Delta P~\left( {x,~z\,~ = ~\,0,~t} \right). \\ \end{gathered} $
Рис. 1.

Схематичная картина распространения волн от тропосферного источника тепла.

Верхней атмосферы достигает сумма волн, представляющая собою результат интерференции волны $\Delta {{P}_{{upward}}}~\left( {x,~z,~t} \right)$, распространяющейся непосредственно от источника, и волны $\Delta {{P}_{{reflected}}}~\left( {x,~z,~t} \right)$, отраженной от поверхности Земли. Когда рассчитываются волны от вариаций давления $\Delta P~\left( {x,~z\,~ = ~\,0,~t} \right)$ на поверхности Земли, то происходит замена волны $\Delta {{P}_{{upward}}}~\left( {x,~z,~t} \right)$, идущей непосредственно от тропосферного источника, на еще одну отраженную волну $\Delta {{P}_{{reflected}}}~\left( {x,~z,~t} \right)$. При этом, очевидно, вносится некоторая ошибка, которая требует изучения.

Волны $\Delta {{P}_{{upward}}}~\left( {x,~z,~t} \right)$ и $\Delta {{P}_{{reflected}}}~\left( {x,~z,~t} \right)$ проходят различные пути до верхней атмосферы. Поэтому можно предположить, что основное отличие волны $\Delta {{P}_{{upward}}}~\left( {x,~z,~t} \right)$ от $\Delta {{P}_{{reflected}}}~\left( {x,~z,~t} \right)$ сводится к тому, что эти волны имеют различные фазы. Это различие в фазах, если оно существенно, может быть учтено. Тогда функция ${{\varphi }_{p}}\left( {x,~t} \right)$, описывающая вариации давления во вводимом граничном источнике, не равна $\Delta P~\left( {x,~z~\, = \,~0,~t} \right)$, но в то же время не сильно от неe отличается и строится по $\Delta P~\left( {x,~z\,~ = \,~0,~t} \right)$ для учета различия фаз у интерферирующих волн.

Предложенный выше модельный тропосферный источник тепла, имитирующий нагрев/охлаждение атмосферного газа при фазовых переходах воды в атмосфере, можно записать в виде

(16)
$f\left( {x,~z,~t} \right) = \left\{ {\begin{array}{*{20}{c}} {S\exp \left( { - {{{\left( {\frac{{x - {{x}_{0}}}}{{{{D}_{x}}}}} \right)}}^{2}} - {{{\left( {\frac{{z - {{z}_{0}}}}{{{{D}_{z}}}}} \right)}}^{2}}} \right)(1 - {{e}^{{ - \frac{t}{\tau }}}})} \\ 0 \end{array}} \right.\sin \left( {\omega t} \right)\,\,\,\,\begin{array}{*{20}{c}} {0 \leqslant t \leqslant 1~\,\,{\text{ч}}} \\ {t > 1\,\,~{\text{ч}}} \end{array}.$

Здесь параметр ${{x}_{0}}$ определяет расположение источника в расчетной области, ${{z}_{0}}$ = 6 км, ${{D}_{x}}$ = = 2 км, ${{D}_{z}}$ = 1.5 км, $\tau $ = 300 сек. Параметры ${{z}_{0}}$, ${{D}_{x}}$, ${{D}_{z}}$ задают расположение и размеры модельного источника тепла. Предполагается, что эти параметры примерно соответствуют размеру и расположению типичного небольшого облака, поскольку конденсация паров воды не только влечет выделение тепла, но и сопровождается образованием облаков. Параметр $\tau $ = 300 секунд введен для медленного включения источника, чтобы подавить возможные переходные процессы. $S$ – амплитуда источника.

Действие тепловых источников со сложной конфигурацией или больших размеров можно понимать как одновременное действие нескольких тепловых источников вида (16). Поэтому изучение решения задачи о волнах от одного простого источника вида (16) представляется достаточным для понимания общего случая.

При исследовании генерации и распространения инфразвука будет использован модельный источник, работающий на частоте ${{\omega }} = {{2{{\pi }}} \mathord{\left/ {\vphantom {{2{{\pi }}} {3~\,\,{\text{минуты}}}}} \right. \kern-0em} {3~\,\,{\text{минуты}}}}$. В исследовании генерации и распространения внутренних гравитационных волн будет задан источник (16) с частотой ${{\omega }} = {{2{{\pi }}} \mathord{\left/ {\vphantom {{2{{\pi }}} {30\,\,~{\text{минут}}}}} \right. \kern-0em} {30\,\,~{\text{минут}}}}$. Данные частоты взяты из предположения, что возможные другие источники, работающие на других частотах и потенциально интересные для данного исследования, качественно действуют так же. Кроме этого, небольшие размеры источника позволяют записывать другие, более сложные источники, как суперпозицию источников, рассмотренных выше. Таким образом, задача о волнах от сложного источника сводится к задаче о волнах от рассматриваемых простых источников.

3.1. Уравнения численной модели, начальные и граничные условия

Используемая численная модель атмосферы высокого разрешения “AtmoSym” основана на решении системы нелинейных двумерных гидродинамических уравнений для атмосферного газа в поле тяжести и детально описана в работе [24].

Зависимость параметров среды (вязкости, теплопроводности, фоновой плотности, фоновой температуры) от вертикальной координаты $z$ в численной модели берется из эмпирической модели атмосферы [30]. Оптимальная вычислительная сетка неоднородная по вертикали и строится программой автоматически на основе реальной стратификации среды.

Верхние граничные условия типичны для моделей термосферы, и задаются на высоте h = 500 км:

(17)
${{\left. {\frac{{\partial T}}{{\partial z}}} \right|}_{{z = h}}} = 0,\,\,~{{\left. {\frac{{\partial U}}{{\partial z}}} \right|}_{{z = h}}} = 0,\,\,{{\left. {\frac{{\partial V}}{{\partial z}}} \right|}_{{z = h}}} = 0,\,\,{{\left. W \right|}_{{z = h}}} = 0.$

Граничные условия по горизонтали в численной модели задаются в следующем виде

(18)
$\begin{gathered} T~\left( {x\,\,~ = \,\,~0,~z,~t} \right) = ~\,\,T~\left( {x\,\,~ = \,\,~L,~z,~t} \right),~ \\ \rho \left( {x~\,\, = \,\,~0,~z,~t} \right) = \,\,~\rho \left( {x\,\,~ = \,\,~0,~z,~t} \right), \\ ~W\left( {x\,\,~ = \,\,~0,~z,~t} \right) = \,\,~W\left( {x~\,\, = \,\,~L,~z,~t} \right),~ \\ U\left( {x~\,\, = \,\,~0,~z,~t} \right) = \,\,~ - U\left( {x\,\,~ = \,\,~L,~z,~t} \right). \\ \end{gathered} $

Такие граничные условия предложены в [22]. Эти условия позволяют имитировать убегание волн за горизонтальные границы области в случае симметрии задачи. В любом случае, ширина $L$ расчетной области выбирается достаточно большой, чтобы граничные условия (18) по горизонтали не влияли на решение задачи.

При численном моделировании распространения волн от локального теплового источника будут решены две близкие задачи. В первой задаче в численных расчетах будет задаваться модельный тропосферный источник тепла $f\left( {x,~z,~t} \right)$, аппроксимированный формулой (16). Нижние граничные условия для задачи распространения волн от тропосферного источника $f\left( {x,~z,~t} \right)$ стандартны для задач диссипативной модели атмосферы и имеют вид

(19)
$\begin{gathered} U\left( {x,~z~\,\, = \,\,~0,~t} \right) = \,\,~0,~~\,\,\,\,W\left( {x,~z~\,\, = \,\,~0,~t} \right) = ~\,\,0,~ \\ ~T\left( {x,~z~\,\, = \,\,~0,~t} \right)~\,\, = ~\,\,{{T}_{0}}\left( 0 \right). \\ \end{gathered} $

Поскольку исследуется распространение волн от тропосферного источника тепла, то начальные условия соответствуют отсутствию волн в начальный момент времени:

(20)
$\begin{gathered} U~\left( {x,~y,~z,~t~\,\, = \,\,~0} \right) = 0,~\,\,\,\,~W~\left( {x,~y,~z,~t~\,\, = \,\,~0} \right) = 0,{\text{\;}} \\ \rho ~\left( {x,~y,~z,~t~\,\, = \,\,~0} \right) = {{\rho }_{0}}\left( z \right),~\,\,\,\,~T~\left( {x,~y,~z,~t~\,\, = \,\,~0} \right) = {{T}_{0}}\left( z \right). \\ \end{gathered} $

Вторая задача использует данные о колебаниях давления на поверхности Земли, полученные из решения первой задачи и имеющие смысл аналога экспериментальных наблюдений. Далее будет произведено сравнение результатов решения обеих задач друг c другом.

Во второй постановке задачи тропосферный источник тепла отсутствует и $f\left( {x,~y,~t} \right) = 0$. Но вместо него имеется граничный источник ${{\varphi }_{p}}\left( {x,t} \right)$, определяющий вариации давления на поверхности Земли. Таким образом, нижние граничные условия для второй задачи имеют вид:

$U\left( {x,~z~\,\, = ~\,\,0,~t} \right)~\,\, = \,\,~0,~\,\,\,~\frac{{\partial W\left( {x,~z~\,\, = \,\,~0,~t} \right)~}}{{\partial z}}\,\,~ = \,\,~0,$
(21)
$\begin{gathered} T~\left( {x,~z~\,\, = \,\,~0,~t} \right) = \,\,~{{T}_{0}}\left( 0 \right), \\ P\,\left( {x,~z\,\,~ = \,\,~0,~t} \right) = ~\,\,{{P}_{0}}\left( 0 \right) + {{\varphi }_{p}}\left( {x,t} \right). \\ \end{gathered} $

Здесь ${{\varphi }_{p}}\left( {x,t} \right)$ – функция, описывающая волноподобные колебания давления на нижней границе и ${{P}_{0}}\left( 0 \right)$ – фоновое давление на поверхности Земли. Доказательство корректности такой постановки задачи дано в [23, 24]. В статьях [21, 22 ] решалась задача о распространении волн от вариаций давления, экспериментально наблюдаемых на сети микробарографов.

Предлагаемые задачи связаны через функцию ${{\varphi }_{p}}\left( {x,t} \right)$ в (21). В простейшем случае ${{\varphi }_{p}}\left( {x,t} \right)$ – это записанные вариации давления $\Delta P\left( {x,~z~\,\, = \,\,~0,~t} \right)$ на нижней границе, полученные из решения первой задачи, где $f\left( {x,~y,~t} \right) \ne 0$. Такая постановка задач позволяет выяснить, возможно ли по записанным вариациям давления $\Delta P\left( {x,~z~\,\, = \,\,~0,~t} \right)$ вычислить те же волны, которые распространяются от тропосферного источника $f\left( {x,~y,~t} \right)$. В более сложном случае, функция ${{\varphi }_{p}}\left( {x,t} \right)$ не совпадает с записанными вариациями давления $\Delta P\left( {x,~z\,\,~ = \,\,~0,~t} \right)$, но вычисляется по этим вариациям давления и учитывает фазовые поправки.

4. ВОЛНЫ ОТ ТРОПОСФЕРНОГО ИСТОЧНИКА ТЕПЛА НА ЧАСТОТАХ ИНФРАЗВУКОВЫХ ВОЛН

Теоретическое исследование показало, что любой источника тепла генерирует инфразвуковые волны. Поэтому в первую очередь рассмотрим генерацию волн тропосферным источником тепла, работающим на частотах инфразвуковых волн.

На рис. 2a, 2в показано возмущение поля температуры, возникающее вследствие работы тропосферного источника тепла $f\left( {x,z,t} \right)~$ (16) с периодом $T\,\,~ = ~\,\,3$ минуты для моментов времени t = 0.25 ч и t = 1 ч. Источник с таким периодом излучает в основном инфразвуковые волны. В нижнем ряду на рис. 2б, 2г показаны результаты аналогичных расчетов, выполненных с $f\left( {x,z,t} \right) = 0$, где в качестве граничного источника волновых колебаний ${{\varphi }_{p}}\left( {x,t} \right)$ в (19) берется ${{\varphi }_{p}}\left( {x,t} \right) = \Delta P\left( {x,z~\,\, = 0,t} \right).$ Функция $\Delta P\left( {x,z = 0,t} \right)$ будет получена в ходе решения задачи с тропосферным источником $f\left( {x,~z,~t} \right)$ и является аналогом экспериментально наблюдаемых вариаций давления на поверхности Земли. В данном случае эти вариации приземного давления вычислены с помощью численного решения задачи распространении волн от тропосферного источника тепла.

Рис. 2.

Поля возмущений температуры для t = 0.5 ч (а, б) и для t = 1 ч (в, г). Волновая картина (а, в) от источника $f\left( {x,z,t} \right)$, период колебаний источника T = 3 мин. Волновая картина (б, г) от записанных вариаций давления на нижней границе.

Видно, что волновая картина, возникающая от граничного источника ${{\varphi }_{p}}\left( {x,t} \right) = \Delta P\left( {x,z{\text{\;}} = 0,t} \right)$, похожа на волновую картину от тропосферного источника. На небольших временах амплитуда волн от тропосферного источника превышает амплитуду волн от поверхностного источника, на временах около часа соотношение амплитуд противоположное. Различие в амплитудах волн от тропосферного и поверхностного источников во время работы источника иногда достигает 30%. После выключения источника, амплитуда волн довольно быстро падает, и быстрее спадает от поверхностного источника.

Основное отличие волновых картин от тропосферного и поверхностного источников, вероятно, объясняется так же, как и в случае генерации внутренних гравитационных волн. Генерация волн источником, работающим на частотах внутренних гравитационных волн, обсуждается ниже.

Обращает на себя внимание значительная амплитуда сгенерированных инфразвуковых волн на рис. 2б, 2г. Такая амплитуда объясняется тем, что время работы источника значительно больше периода колебаний источника. Это позволяет резонансным свойствам атмосферы проявиться в полной мере. В обсуждаемом далее случае генерации волн на частотах внутренних гравитационных волн отношение частоты осцилляций источника ко времени его работы значительно больше, что, соответственно, приводит к меньшей результирующей амплитуде.

Хорошее совпадение волновых картин от тропосферного и от граничного источников показывает, что задачу о волнах от тропосферного источника над поверхностью Земли, работающего на частотах инфразвуковых волн, можно успешно заменить задачей о распространении волн от поверхностного источника, в которой на границе заданы экспериментально наблюдаемые волновые колебания давления.

Тропосферные источники тепла обычно находятся на высоте несколько километров над поверхностью Земли и имеют сложную пространственно-временную структуру. Это делает затруднительным получение детальной экспериментальной информации об этих источниках. Использование граничного источника волн вместо прямого задания тропосферного источника имеет преимущество при численных исследованиях генерируемых волн. Давление на поверхности Земли экспериментально регистрируется сетями микробарографов или его можно получить другими способами. Это позволяет при выполнении численных исследований волн, генерируемых метеорологическими источниками, использовать экспериментальную наблюдательную информацию о колебаниях давления на поверхности Земли.

5. ГЕНЕРАЦИЯ И РАСПРОСТРАНЕНИЕ ВОЛН ОТ ТРОПОСФЕРНОГО НИЗКОЧАСТОТНОГО ИСТОЧНИКА ТЕПЛА

Рассмотрим генерацию волн тропосферным источником тепла, работающим на частотах внутренних гравитационных волн с последующим распространением в верхнюю атмосферу. На рис. 3 показан результат численного расчета возникновения и распространения волнового возмущения температуры в области высот $0 \leqslant z < 100$ км, полученный вследствие работы тропосферного источника тепла (16) с периодом T = 30 минут для моментов времени t = 0.23 ч, t = 0.5 ч, t = 1 ч, t = 1.6 ч.

Период рассматриваемого модельного источника больше частоты Вяйсяля–Брента, то есть источник работает на частотах внутренних гравитационных волн. Известно, что скорость вертикального распространения внутренних гравитационных волн значительно меньше скорости звука. Однако на рис. 3 наблюдается довольно быстрое появление внутренних гравитационных волн на больших высотах. Механизм этого явления будет рассмотрен ниже.

Рис. 3.

Поле возмущений температуры в интервале высот 0 ≤ z < 100 км, создаваемое тропосферным тепловым низкочастотным источником f(x, z, t) с периодом T = 30 мин в моменты времени t = 0.23 ч (а), t = = 0.5 ч (б), t = 1 ч (в), t = 1.6 ч (г).

Достигается такой эффект за счет парного появления акустических и внутренних гравитационных волн при работе монохроматического источника внутренних гравитационных волн, что будет показано ниже. Рассмотрим уравнения (11), описывающую генерацию акустических и внутренних гравитационных волн. Эти уравнения написаны для коэффициентов при волновых гармониках, определяющих пространственную структуру волн: волновые гармоники определены при $0 \leqslant z < \infty $. Волновые гармоники – это решение системы уравнений в виде функций $\tilde {\Psi },~\,\tilde {U},\,~\tilde {W},\,~\tilde {\Phi }$, которые зависят от пространственных координат согласно формулам (7), (8). Эти уравнения (11) показывают, что волна может генерироваться источником $f\left( {x,z,t} \right)$ не только строго в районе источника, но и за его пределами.

В уравнениях (11) присутствуют источники акустических и гравитационных волн $F_{A}^{ \pm }~(k,~m,~t)$, $F_{G}^{ \pm }~\left( {k,~m,~t} \right)$, записанные в k-представлении в виде разложения по волновым модам $\tilde {\chi }\left( {z,k,m,\omega \left( {k,m} \right)} \right)$, зависящим от координат и являющимся столбцами из компонент $\tilde {\Psi },~\tilde {U},~\tilde {W},~\tilde {\Phi }$. Если перейти в обычное координатное представление, то мы получим те же источники в виде $F_{A}^{ \pm }~(x,~z,~t$), $F_{G}^{ \pm }~(x,~z,~t$) в зависимости от координат. Эти источники определены для всех четырех функций, фигурирующих в задаче, то есть, являются столбцами. Очевидно, для компонент столбцов справедливо:

(22)
$\begin{gathered} F_{{A,\Psi }}^{ + }~\left( {x,~z,~t} \right) + F_{{A,\Psi }}^{ - }\left( {x,~z,~t} \right) + \\ + \,\,F_{{G,\Psi }}^{ + }~\left( {x,~z,~t} \right) + F_{{G,\Psi }}^{ + }\left( {x,~z,~t} \right)~\,\, = \,\,~0,~ \\ F_{{A,U}}^{ + }~\left( {x,~z,~t} \right) + F_{{A,U}}^{ - }\left( {x,~z,~t} \right) + \\ + \,\,F_{{G,U}}^{ + }~\left( {x,~z,~t} \right) + F_{{G,U}}^{ + }\left( {x,~z,~t} \right)~\,\, = \,\,~0,~ \\ F_{{A,W}}^{ + }~\left( {x,~z,~t} \right) + F_{{A,W}}^{ - }\left( {x,~z,~t} \right) + F_{{G,W}}^{ + }~\left( {x,~z,~t} \right) + \\ + \,\,F_{{G,W}}^{ + }\left( {x,~z,~t} \right) = \,\,~0, \\ F_{{A,\Phi }}^{ + }~\left( {x,~z,~t} \right) + F_{{A,\Phi }}^{ - }\left( {x,~z,~t} \right) + F_{{G,\Phi }}^{ + }~\left( {x,~z,~t} \right) + \\ + \,\,F_{{G,\Phi }}^{ + }\left( {x,~z,~t} \right)~\,\, = ~f\left( {x,~z,~t} \right). \\ \end{gathered} $

Здесь в левой части уравнений (20) записаны компоненты столбцов $F_{A}^{ \pm }~(x,~z,~t)$, $F_{G}^{ \pm }~\left( {x,~z,~t} \right)$. Уравнения для скоростей в (22) удовлетворяют $F_{{A,U}}^{ \pm }(x,z,t)$ = =  $~F_{{G,U}}^{ \pm }~\left( {x,~z,~t} \right)$ = $F_{{A,W}}^{ \pm }(x,z,t)$ $F_{{G,W}}^{ \pm }~\left( {x,~z,~t} \right) = 0$.

Функции-источники $F_{{A,\Psi }}^{ \pm }~\left( {x,~z,~t} \right),~$ $F_{{G,\Psi }}^{ \pm }~\left( {x,~z,~t} \right),~$ $F_{{A,\Phi }}^{ \pm }~\left( {x,~z,~t} \right),$ $F_{{G,\Phi }}^{ \pm }~\left( {x,~z,~t} \right)$ выражаются через источник тепла $f\left( {x,z,t} \right)$ довольно сложными интегральными формулами, но в ряде случаев эти выражения упрощаются. Для иллюстрации рассмотрим случай, когда эти выражения имеют довольно простой вид. А именно, в приближении длинных волн, когда ${{k}^{2}} \ll {{m}^{2}} + \frac{1}{{4{{H}^{2}}}}$, имеем

(23)
$\begin{gathered} F_{{A,\Phi }}^{ + }~\left( {x,~z,~t} \right) = F_{{A,\Phi }}^{ - }\left( {x,~z,~t} \right) = \frac{{\gamma - 1}}{{2\gamma }}f\left( {x,z,t} \right), \\ F_{{G,\Phi }}^{ + }~\left( {x,~z,~t} \right) = F_{{G,\Phi }}^{ - }\left( {x,~z,~t} \right) = \frac{1}{{2\gamma }}f\left( {x,z,t} \right), \\ F_{{A,\Psi }}^{ \pm }~\left( {x,~z,~t} \right) = - F_{{G,\Psi }}^{ \pm }\left( {x,~z,~t} \right) = \\ = \frac{1}{2}\left( {f\left( {x,z,t} \right) - \mathop \smallint \limits_{ - \infty }^z f\left( {x,z{\kern 1pt} ',t} \right)dz{\kern 1pt} '\frac{1}{H}} \right). \\ \end{gathered} $

Соотношения (23) представлены в [31, 32]. Эти соотношения были выведены для решения задачи с начальным температурным возмущением, но задача с начальным возмущением и задача с источником математически связаны [31, 32]. Соотношения (23) записаны в том же виде, как были выведены, для бесконечной атмосферы. Для данной задачи естественно считать, что $f\left( {x,z,t} \right) = 0$ при $z < 0$, и тогда соотношения (23) справедливы и для полу-бесконечной атмосферы.

Формулы (23) показывают, что волны генерируются не только в районе источника тепла, но и выше источника тепла. Важно, что источники плотности $F_{{A,\Psi }}^{ \pm }~\left( {x,~z,~t} \right)$ и $F_{{G,\Psi }}^{ \pm }\left( {x,~z,~t} \right)$имеют противоположные знаки для акустических и внутренних гравитационных волн. Это объясняется тем, что суммарный источник массы отсутствует.

Акустическая и гравитационная волны от источника тепла всегда генерируются в паре. Этот эффект парного образования волн связан с тем, что у гравитационной волны температура и плотность связаны поляризационными соотношениями, что аналитически было показано выше. Тропосферный источник тепла изменяет только температуру газа. Поэтому, чтобы гравитационная волна возникла, одновременно должна возникнуть акустическая волна, компенсирующая изменение плотности среды, производимое гравитационной волной. Причем это изменение плотности, как показывает формула (23), имеет место не только в районе локализации источника, но и выше его. Это и обусловливает эффект довольно быстрого проникновения внутренних гравитационных волн от источника тепла на большие высоты.

На рис. 4 показаны волновые возмущения температуры, создаваемые тропосферным тепловым источником $f\left( {x,~z,~t} \right)~$ с периодом $T~\,\, = ~\,\,30$ мин, в моменты времени t = 0.5 ч, t = 1 ч, t = 1.5 ч, t = 2.16 ч. Наклоны фазового фронта говорят о том, что на рисунках преобладают гравитационные волны, за исключением первых двух рисунков (рис. 4а, 4б), на которых в центральных частях рисунков заметный вклад принадлежит также инфразвуковым волнам.

Рис. 4.

Поле волновых возмущений температуры атмосферы, создаваемое тропосферным тепловым низкочастотным источником $f\left( {x,z,t} \right)$ с периодом T = 30 мин в моменты времени t = 0.5 ч (а), t = 1 ч (б), t = 1.5 ч (в), t = 2.16 ч (г).

На рис. 5а показана зависимость колебаний возмущения температуры от времени на нижней границе. Колебания плотности на нижней границе ведут себя со временем аналогично. Вместе колебания температуры и колебания плотности создают колебания давления на нижней границе, которые будут использованы далее в качестве граничного условия при решении задачи о распространения волн от колебаний давления на нижней границе.

Рис. 5.

Зависимость возмущения температуры на нижней границе от времени (а) и на нижней границе вблизи источника (б).

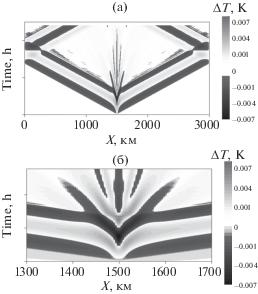
Из рис. 5а видно, что возмущение на границе состоит из двух расходящихся волнообразных возмущений, исключая центральную часть области. Скорость горизонтального распространения этих волнообразных возмущений примерно 250 м/с. Примерно через 1.6 ч эти расходящиеся волнообразные возмущения достигают горизонтальных границ расчетной области.

Постоянная горизонтальная скорость и неизменная форма двух расходящихся волн, говорят о возможных проявлениях волноводных свойств атмосферы у поверхности Земли. Действительно, в [33] изучались атмосферные квазиволноводы, где волна захватывается стратификацией, и распространяется горизонтально, где у поверхности Земли и был обнаружен квазиволновод с похожими параметрами. Скорость распространения вычисленной в [33] первой квазиволноводной моды была примерно = 271 м/с, что близко к 250 м/с. Различия могут объясняться различиями в деталях стратификации в данной работе и в [32]. На рис. 5б показана центральная часть графика 5а. Волна на рис. 5б является суммой падающей и отраженных волн, равных по амплитуде.

5.1. Распространение внутренних гравитационных волн от вариаций приземного давления

Сравнение распространения инфразвуковых волн от тропосферного и граничного источников показало хорошее совпадение волновых картин. Известно, что неизотермической атмосфере с реалистичной стратификацией высот верхней атмосферы достигают только инфразвуковые волны, распространяющиеся под небольшими углами к вертикали. Эти волны распространяются быстро. Инфразвуковые волны, излученные под большими углами к вертикали, меняют постепенно направление распространения вследствие роста температуры с высотой выше 100 км, либо даже отражаются к поверхности Земли [34]. На распространение внутренних гравитационных волн значительно сильнее влияют особенности стратификации, что усложняет волновую картину.

На рис. 6 последовательно показаны волновые возмущение поля температуры, полученные путем расчета волн от поля вариаций давления на поверхности Земли. Используемые в качестве граничного источника вариации давления на поверхности Земли вычислены при решении предыдущей задачи о распространении волн от тропосферного низкочастотного теплового источника с периодом T = 30 мин.

Рис. 6.

Поле волновых возмущений температуры атмосферы, создаваемых низкочастотными вариациями поля давления в моменты времени t = 0.5 ч (а), t = = 1 ч (б), t = 1.5 ч (в), t = 2.16 ч (г).

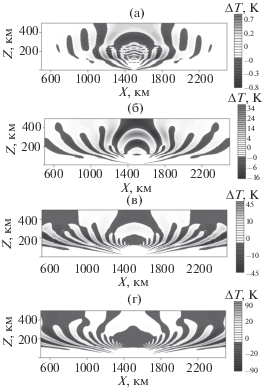
Отчетливо видно, что волны, рассчитанные от вариаций поля давления на поверхности Земли, отличаются примерно вдвое завышенной амплитудой. Многие авторы отмечали [11, 35–37], что трудно определить порядок амплитуды волн, достигающих верхнюю атмосферу, при моделировании распространения волн от тропосферных источников в верхнюю атмосферу. В то же время многие другие параметры волн (частота, скорость распространения, масштабы) уверенно определяются по информации о тропосферных источниках. Поэтому ошибка в амплитуде волн в два раза приемлема и её можно оценить, а результат уточнить. Важно, что можно использовать экспериментальные данные о вариациях давления у поверхности Земли для расчета параметров волн, генерируемых метеорологическими источниками.

5.1.1. Конструирование улучшенного поверхностного источника по данным о вариациях давления на поверхности Земли и расчет волн от источника

Рассмотрим возможные причины полученного расхождения результатов расчета волн от низкочастотного тропосферного источника и от вариаций давления на поверхности Земли. Схематический рис. 1 показывает, что верхнюю атмосферу достигают волны как непосредственно от источника, так и отраженные от поверхности Земли. Эти волны интерферируют. При интерференции амплитуда результирующей волны обычно примерно равна максимальной амплитуде интерферирующих волн, исключая случай, когда интерферирующие волны когерентны. В представленных расчетах волн от вариаций давления волна, распространяющаяся вверх непосредственно от источника, заменяется еще одной волной, отраженной от поверхности Земли. Это тот особый случай, когда интерферирующие волны когерентные, и в этом исключительном случае амплитуда результирующей волны удваивается по отношению к интерферирующим волнам. Поэтому, чтобы скорректировать амплитуду волн, нужно, прежде всего, постараться учесть разницу в фазах интерферирующих волн, достигающих верхнюю атмосферу. Это разница в фазах примерно равна удвоенному времени распространения волн от источника до поверхности Земли.

Попробуем оценить сдвиг фазы $\Delta {{\phi }_{G}}$ между гравитационной волной, распространяющейся вверх непосредственно от источника, и отраженной волной. Очевидно, что $\Delta {{\phi }_{G}} = \frac{{2H}}{{{{c}_{{vert}}}}}$, где $H$ – высота центра источника, а ${{c}_{{vert}}}$ – скорость вертикального распространгения волн. Скорость ${{c}_{{vert}}}$ можно примерно определить как ${{c}_{{vert}}}$ $ \approx {\text{\;}}20$ м/с, и поэтому функцию ${{\varphi }_{p}}\left( {x,~t} \right)$ можно в этом случае записать как

(24)
$\begin{gathered} {{\varphi }_{p}}\left( {x,~t} \right) = 0.5~\Delta P\left( {x,~z = 0,~t} \right) + \\ + \,\,0.5~\eta ~\left( {x,~t + \Delta {{\phi }_{G}}\left( {1 - \exp \left( { - \frac{t}{\tau }} \right)} \right)} \right) + \\ + \,\,0.5\left( {\Delta P\left( {x,~z = 0,~t + ~\Delta {{\phi }_{A}}} \right) - \eta ~\left( {x,~t + \Delta {{\phi }_{A}}} \right)} \right), \\ \eta ~\left( {x,~t} \right) = \frac{1}{{2{{T}_{A}}}}\mathop \smallint \limits_{t - {{T}_{A}}}^{t + {{T}_{A}}} \Delta P\left( {x,~z = 0,~t{\kern 1pt} '} \right)dt{\kern 1pt} '. \\ \end{gathered} $

В формуле (24) во второй из интерферирующих волн приблизительно выделен вклад внутренних гравитационных волн и вклад акустических волн. Введенная функция $\eta {\text{\;}}\left( {x,{\text{\;}}t} \right)$ представляет гравитационную составляющую волны, которая получена с помощью локального усреднения по времени функции $\Delta P\left( {x,z = 0,t} \right)$. Интервал усреднения $2{{T}_{A}}$ = 300 с, что примерно соответствует максимальному периоду акустических волн. Множитель $\left( {1 - \exp \left( { - \frac{t}{\tau }} \right)} \right)$ в (24) введен в сдвиге фазы гравитационной волны $\eta {\text{\;}}\left( {x,{\text{\;}}t} \right)$, чтобы подавить возможные переходные процессы, $\tau = 300$ с. Функция $\left( {\Delta P\left( {x,{\text{\;}}z = 0,{\text{\;}}t} \right) - \eta {\text{\;}}\left( {x,{\text{\;}}t} \right)} \right)$ представляет вклад акустической волны во второй из интерферирующих волн. По аналогии с гравитационными волнами, в эту функцию тоже введен сдвиг фазы $\Delta {{\phi }_{А}} = \frac{{2H}}{{{{c}_{{vert}}}}}$ ≈ 36 с, учитывающий, что реальный тропосферный источник находится выше поверхности Земли на высоте $H\,~ = ~\,6$ километров.

На рис. 7 показаны волновые вариации давления, соответствующие такому поверхностному источнику (24). Сравнение рис. 4 и рис. 7 показывает, что совпадение волновых картин неплохое. За исключением первых результатов рис. 4 и на рис. 7, построенных для моментов времени, не превышающих два периода волны. Несмотря на это, на этих рисунках различие в амплитудах не превышает $25\% $ и форма волн схожая. На рис. 7а амплитуда волны еще маленькая, волна в верхней атмосфере только формируется. Очевидно, погрешности сказываются на волне малой амплитуды ощутимее. Введенный в численных расчетах распространения волн от граничного источника сдвиг по времени $\Delta {{\phi }_{G}} = 10~$ мин оправдан на больших временах и учитывает сдвиг фаз между интерферирующими в верхней атмосфере волнами, но на малых временах он может приводить к тому, что одна из волн прибудет на большие высоты несколько преждевременно. На небольших временах значительный вклад вносят акустические волны, которые также присутствуют в спектре.

Рис. 7.

Поле волновых возмущений температуры атмосферы, создаваемых низкочастотными модифицированными вариациями поля давления (22) в моменты времени t = 0.5 ч (а), t = 1 ч (б), t = 1.5 ч (в), t = 2.16 ч (г).

Анализ волновой картины показал, что даже грубый учет сдвига фаз между интерферирующими волнами существенно улучшил совпадение результатов расчетов волн от колебаний давления на границе с прямыми расчетами волн от тропосферного источника. Очевидно, можно точнее учесть сдвиг фаз между интерферирующими волнами. Скорость вертикального распространения волн зависит от волновых чисел и, соответственно, сдвиг фаз реально тоже от них зависит. Это не учтено в предложенной простой модели граничного источника. Можно также более точно учесть структуру тропосферного источника, и не ограничиваться только введением высоты $H$ источника. Однако усложнение модели граничного источника должно оправдываться какими-то конкретными соображениями. Для оценки амплитуды волн, генерируемых метерологическими событиями и достигающих верхней атмосферы, использование простой модели граничного источника оправданно. Важно, что оценка параметров волн, достигающих верхнюю атмосферу, может быть получена на основе экспериментальных данных о вариациях давления на поверхности Земли.

6. ЗАКЛЮЧЕНИЕ

Практический интерес к вопросу о генерации волн граничным источником обусловлен важностью исследования распространения атмосферных волн в верхнюю атмосферу от реалистичных тропосферных источников. Часто экспериментальной информации о тропосферных источниках недостаточно для определения параметров генерируемых, в особенности для вычисления амплитуды генерируемых волн. Экспериментальная информация о колебаниях давления на поверхности Земли нередко имеется, или может быть получена, и еe можно использовать для анализа волн от метеорологических источников. Поэтому вопрос о возможности замены одной задачи на другую представляется практически оправданным.

В работе аналитически рассмотрена общая задача о генерации АГВ в изотермической атмосфере локальным источником тепла на тропосферных высотах. Источник моделирует нагрев атмосферы фазовыми переходами воды. Изучен спектр генерируемых источником волн. Показано, что генерация внутренних гравитационных волн этим источником не может происходить без генерации инфразвуковых волн, и наоборот. Получены оценки амплитуд генерируемых волн.

Выполнено численное моделирование распространения инфразвуковых и внутренних гравитационных волн от локального источника тепла в неизотермической атмосфере. Численное решение задачи о волнах от тропосферного источника тепла дало данные о колебаниях давления на поверхности Земли. Записанные колебания давления использованы как граничные источники в задаче о генерации волн вариациями давления на поверхности Земли. Проведено сравнение решений обеих решенных задач.

Результаты численного исследования распространения инфразвуковых и внутренних гравитационных волн от локального тропосферного источника тепла и от граничного источника показали:

– если тропосферный источник работает на частотах инфразвуковых волн, то решения задач о волнах от тропосферного источника и от регистрируемых колебаний поверхностного давления совпадают с достаточной точностью для многих практических приложений;

– если источник работает на частотах внутренних гравитационных волн, то амплитуда волн от поверхностного источника обычно превышает амплитуду волн от тропосферного источника. Если источник находится высоко, то амплитуда может быть превышена вдвое. Расхождение амплитуд меньше, если тропосферный источник находится недалеко от поверхности Земли. Форма волн в решениях обоих задач в любом случае схожа.

Это расхождение амплитуд волн в сравниваемых задачах объясняется тем, что в случае с тропосферным источником верхней атмосферы достигают как волны, распространяющиеся непосредственно от источника, так и волны отраженные от поверхности Земли. Эти волны интерферируют и амплитуда результирующей волны определяется этой интерференцией. Волны, отраженные от поверхности Земли, имеют амплитуду равную половине экспериментально измеряемого давления. Замена задачи о волнах от тропосферного источника на задачу о волнах от регистрируемых колебаний давления эквивалентна тому, что одна из интерферирующих волн (распространяющаяся вверх от тропосферного источника) заменяется на волну, отраженную от поверхности Земли. В этом случае обе интерферирующие волны имеют одинаковые фазы, интерферирующие волны когерентны, и амплитуда результирующей волны в два раза больше амплитуды интерферирующих волн. В случае же реального тропосферного источника интерференция волн может давать амплитуду примерно равную амплитуде интерферирующих волн, поскольку фазы интерферирующих волн различны. Различие фаз интерферирующих волн зависит от высоты, на которой расположен тропосферный источник. Чем выше источник, тем больше проявляется различие рассматриваемых задач.

Проведенный анализ позволил построить по данным колебаний давления на поверхности Земли скорректированный граничный источник, который примерно учитывает сдвиг фаз между интерферирующими волнами. Сдвиг фаз оценен по высоте тропосферного источника. Такая модификация формулы для задаваемого приповерхностного давления дает существенное улучшение точности волновой картины и точности расчета амплитуды волн.

Полученной точности достаточно для оценки переноса энергии и импульса волн в верхнюю атмосферу и для параметризации влияния акустико-гравитационных волн в моделях общей циркуляции атмосферы. Развитый подход позволяет привлечь для выполнения расчетов волн от метеорологических источников экспериментальные данные о вариациях давления на поверхности Земли.

Работа была выполнена при финансовой поддержке грантом Российского научного фонда № 21-17-00208 (Ю.А. Курдяева: разделы 2, 3, 4) и № 21-17-00021 (С.Н. Куличков раздел 1, 5). Разделы 1-6 выполнены С.П. Кшевецким.

Список литературы

  1. Fritts D.C., Vadas S.L. et al. Wan and variable forcing of the middle atmosphere by gravity waves // J. Atmos. Sol.-Terr. Phys. 2006. V.68. P. 247–265.

  2. Ploogonven R., Snyder Ch., Inertial Gravity Waves Spontaneously Generated by Jets and Fronts. Part I: Different Baroclinic Life Cycles // J. Atmospheric Sciences. 2007. V. 64. P. 2502–2520.

  3. Plougonven R., Zhang F. Internal gravity waves from atmospheric jets and fronts // Rev. Geophys. 2014. V. 52. P. 1–37.

  4. Черниговская М.А., Сутырина Е.Н., Ратовский К.Г. Метеорологические эффекты ионосферной возмущенности над Иркутском по данным вертикального радиозондирования // Современные проблемы дистанционного зондирования Земли из космоса. 2014. Т. 11(2). С. 264–274.

  5. Borchevkina O., Karpov I., Karpov M. Meteorological Storm Influence on the Ionosphere Parameters // Atmosphere. 2020 V. 11. № 9. 1017. https://doi.org/10.3390/atmos11091017

  6. Boška J., Šauli P. et al. Diurnal variation of the gravity wave activity at midlatitudes of the ionospheric F region // Studia Geophysica et Geodaetica. 2003. V. 47. № 3. P. 579–586. https://doi.org/10.1023/A:1024763618505

  7. Ebel A. Contributions of gravity waves to the momentum, heat and turbulent energy budget of the upper mesosphere and lower thermosphere // J. Atmospheric and Terrestrial Physics. 1984. V. 46. P. 727–737. https://doi.org/10.1016/0021-9169(84)90054-0

  8. Alexander M.J., Pfister L. Gravity wave momentum flux in the lower stratosphere over convection // Geophysical Research Letter. 1995. V. 22. № 15. P. 2029–2032.

  9. Kshevetskii S.P., Gavrilov N.M. Vertical propagation, breaking, and effects of nonlinear gravity waves in the atmosphere // J. Atmos. Solar-Terr. Phys. 2005. V. 67. P. 10141030.

  10. Karpov I., Kshevetskii S. Numerical study of heating the upper atmosphere by acoustic-gravity waves from a local source on the Earth’s surface and influence of this heating on the wave propagation conditions // J. Atmospheric and Solar-Terrestrial Physics. 2017. V. 164. https://doi.org/10.1016/j.jastp.2017.07.019

  11. Snively J.B., Pasko V.B. Breaking of thunderstorm-generated gravity waves as a source of short-period ducted waves at mesopause altitudes // Geophys. Res. Lett. 2003. V. 30(24). P. 2254. https://doi.org/10.1029/2003GL018436

  12. Klimenko M. et al. Ionospheric Effects of the Sudden Stratospheric Warming in 2009: Results of Simulation with the First Version. 2018. V. 12. P. 760–770. https://doi.org/10.1134/S1990793118040103

  13. Григорьев Г.И. Акустико-гравитационные волны в атмосфере Земли (обзор) // Изв. вузов. Радиофизика. 1999. Т. 42(1). С. 3–24.

  14. Коваль А.В., Гаврилов Н.М. Параметризация воздействия орографических волн на общую циркуляцию средней и верхней атмосферы // Ученые записки Российского государственного гидрометеорологического университета. 2011. Т. 20. С. 71–75.

  15. Artru J. et al. Ionospheric detection of gravity waves induced by tsunamis // Geophys. J. Int. 2005. V. 160. P. 840–848. https://doi.org/10.1111/j.1365-246X.2005.02552.x

  16. Bourdillon A. et al. HF radar detection of infrasonic waves generated in the ionosphere by the 28 March 2005 Sumatra earthquake // J. Atmospheric and Solar-Terrestrial Physics. 2014. V. 109. P. 75–79. https://doi.org/10.1016/j.jastp.2014.01.008

  17. Chum J., Skripnikova K., Base J. Atmospheric infrasound observed during intense convective storms on 9–10 July 2011, J. Atmospheric and Solar Terrestrial Physics. 2015. V. 122. P. 66–74. https://doi.org/10.1016/j.jastp.2014.10.014

  18. Blanc E., FargesT., Le Pichon A. et al. Ten year observations of gravity waves from thunderstorms in western Africa // J. Geophysical Research: Atmospheres. 2014. V. 119. P. 6409–6418.

  19. Pierce A.D., Coroniti S.C. A mechanism for the generation of acoustic-gravity waves during thunder-storm formation // Nature. 1966. V. 210. P. 1209–1210.

  20. Kurdyaeva Y., Kulichkov S., Kshevetskii S. et al. Propagation to the upper atmosphere of acoustic-gravity waves from atmospheric fronts in the Moscow region // Annales Geophysicae. 2019. V. 37(3). P. 447–454. https://doi.org/10.5194/angeo-37-447-2019

  21. Курдяева Ю.А., Куличков С.Н., Кшевецкий С.П. и др. Вертикальное распространение акустико-гравитационных волн от атмосферных фронтов в верхнюю атмосферу // Изв. РАН. Физика атмосферы и океана. 2019. Т. 55(4). С. 3–12. https://doi.org/10.31857/S0002-35155543-12

  22. Kshevetskii S., Kurdyaeva Y., Kulichkov S. et al. Simulation of Propagation of Acoustic-Gravity Waves Generated by Tropospheric Front Instabilities into the Upper Atmosphere // Pure Appl. Geophys. 2020. V. 177. P. 5567–5584. https://doi.org/10.1007/s00024-020-02569-y.

  23. Курдяева Ю.А., Кшевецкий С.П. Гаврилов Н.М. и др. Исследование корректности задачи о распространении нелинейных акустико-гравитационных волн в атмосфере от переменного давления на нижней границе // Сибирский журн. вычислительной математики. 2017. Т. 20(4). С. 393–412.

  24. Kurdyaeva Y.A., Kshevetskii S.P., Gavrilov N.M. et al. Correct Boundary Conditions for the High-Resolution Model of Nonlinear Acoustic-Gravity Waves Forced by Atmospheric Pressure Variations // Pure Appl. Geophys. 2018. V. 175. P. 3639–3652. https://doi.org/10.1007/s00024-018-1906-x

  25. Погосян X.П. Циклоны. Л.: Гидрометеоиздат, 1976, 148 с.

  26. Wallace J.M., Hobbs P.V. Atmospheric science: An introductory survey, 92, Academic Press, New York, 2006, p. 483.

  27. Kshevetskii S.P. Modeling of propagation of internal gravity waves in gases // Comput. Math. Math. Phys. 2001. V. 41(2). P. 273–288.

  28. Госсард Э., Хук У. Волны в атмосфере. Москва: Мир, 1978, 531 с.

  29. AtmoSym Model of Atmospheric Processes, 2016. http://atmos.kantiana.ru/ (accessed on 14 March, 2021).

  30. Picone J.M., Hedin A.E., Drob D.P. et al. NRLMSISE-00 Empirical model of the atmosphere: statistical comparisons and scientific Isssues // J. Geophys.Res. 2002. V. 107(A12). P. 1468, https://doi.org/10.1029/2002JA009430

  31. Кшевецкий С.П. О длинных акустико-гравитационных волнах в атмосфере с произвольной стратификацией по плотности // Известия РАН. Физ. атмосферы и океана. 1992. Т. 28(5). С. 558–559.

  32. Брежнев Ю.В., Кшевецкий С.П., Лебле С.Б. Линейная инициализация линейных полей // Известия АН. Физика атмосферы и океана. 1994. Е. 30(1). С. 86–90.

  33. Кшевецкий С.П. Квазиволноводные моды внутренних гравитационных волн в атмосфере // Изв. РАН. Физика атмосферы и океана. 2003. Т. 39(2). С. 244–253.

  34. Drobzheva Ya., Krasnov V. The acoustic field in the atmosphere and ionosphere caused by a point explosion on the ground // J. Atmos. and Solar-Terr. Phys. 2003. V. 65(3). P. 369–377.

  35. Miller D.V. Thunderstorm induced gravity waves as a potential hazard to commercial aircraft // Presented at the American Meteorological Society 79th Annual conference, American Meteorological Society. 1999.

  36. Fovell R., Durran D., Holton J.R. Numerical simulation of convectively generated stratospheric gravity waves // J. Atmospheric Sciences. 1992. V. 49(16). P. 1427–1442.

  37. Кшевецкий С.П., Куличков С.Н. Влияние внутренних гравитационных волн от конвективных облаков на атмосферное давление и пространственное распределение возмущений температуры // Изв. РАН. Физика атмосферы и океана. 2015. Т. 51(1). С. 52–59.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Физика атмосферы и океана

Архивы выпусков Информация о журнале Отправить рукопись в журнал