1. На главную
  2. Электронные версии
  3. Известия РАН. Физика атмосферы и океана
  4. T. 58, № 4, 2022

Известия РАН. Физика атмосферы и океана, 2022, T. 58, № 4, стр. 384-395

К теории симметричной неустойчивости периодических по времени течений с точным учетом силы Кориолиса

М. В. Курганский *

Институт физики атмосферы им. А.М. Обухова РАН
119017 Москва, Пыжевский пер., 3, Россия

* E-mail: kurgansk@ifaran.ru

Поступила в редакцию 14.02.2022
После доработки 21.03.2022
Принята к публикации 11.04.2022

Полный текст (PDF)

Аннотация

Исследована симметричная (инерционная) параметрическая неустойчивость периодических по времени течений с линейным профилем скорости, с точным учетом силы Кориолиса в задаче. Показана возможность неустойчивости при меньших сдвигах скорости, чем на это указывает критерий инерционной устойчивости стационарного течения такой же амплитуды скорости. Наиболее содержательные результаты получаются в пределе малой плотностной стратификации среды, что выполняется в хорошо перемешанных по вертикали конвективных слоях атмосферы, в глубоких слоях океана, а также может иметь прямое отношение к лабораторному эксперименту.

Ключевые слова: симметричная неустойчивость, инерционная неустойчивость, сила Кориолиса, периодические течения, параметрический резонанс

1. ВВЕДЕНИЕ

Исследование симметричной неустойчивости сдвиговых потоков относительно возмущений, зависящих от координаты в направлении, ортогональном основному потоку, было положено классическими работами [1, 2] (см. [3]), но восходит еще к работам Гельмгольца по устойчивости “чисто зональной циркуляции атмосферы” (см. написанный И.А. Кибелем §2 в гл. XI книги [4]). В настоящее время симметричная, и в частности чисто инерционная, неустойчивость вновь привлекает внимание исследователей, поскольку эта неустойчивость встречается чаще и имеет большее значение для геофизических сред, таких как атмосфера и океан, чем раньше считалось. В частности, в [5, 6] указано, что то, что до сих пор в экваториальной атмосфере считалось проявлением внутренних гравитационных волн, на самом деле связано с реализацией механизма инерционной неустойчивости. В атмосфере симметричная неустойчивость может возникать и иметь значение в струйных течениях (с их субтропической, антициклонической, стороны) [7–9], в атмосферных фронтах [10], в тропических ураганах [11] и в целом в приэкваториальной атмосфере [12]. Большое значение симметричная неустойчивость имеет для океана (напр., [13]). Учет кривизны линий тока в критериях симметричной устойчивости океанических фронтальных зон дан в [14]. В целях сопоставления с другими типами неустойчивости, отметим, что традиционная бароклинная неустойчивость относительно возмущений, зависящих от координаты вдоль основного потока [15], реализуется при числах Ричардсона ${\text{Ri}}$ (много) больших единицы. Симметричная неустойчивость реализуется при числах Ричардсона в диапазоне $\frac{1}{4} < {\text{Ri}} < 1$. Согласно [16, 17], скорость роста неустойчивых симметричных возмущений наивысшая при $0.25 < {\text{Ri}} < 0.95$. Наконец, вертикальная сдвиговая неустойчивость реализуется при ${\text{Ri}} < \frac{1}{4}$. С симметричной неустойчивостью может быть сопряжено образование роллов (облачных улиц), когда холодный арктический воздух натекает на теплую поверхность моря (см. [18]). Облачные улицы также наблюдаются на гораздо более высоких уровнях (“улицы перистых облаков”) и часто ассоциируются со струйными течениями [18, 19]. В таких случаях механизм симметричной неустойчивости может иметь значение (там же). Как отмечено в [20–22], существенное влияние на развитие инерционной (симметричной) неустойчивости оказывает полный учет силы Кориолиса (отказ от “традиционного” приближения), что может иметь наибольший эффект в приэкваториальной области атмосферы, а также в океане. Симметричная неустойчивость фронтальных зон в океане, а также возможность полного учета силы Кориолиса в задаче обсуждаются в недавней работе [23]. Можно ожидать большую роль, которую инерционная (симметричная) неустойчивость играет в атмосфере таких быстро вращающихся планет, как Юпитер, Сатурн, Уран и Нептун [24].

Имеются еще недостаточно изученные задачи, связанные с симметричной (инерционной) неустойчивостью. В частности, представляет интерес исследование симметричной неустойчивости потоков со сдвигами скорости, зависящими от времени по периодическому закону, например, за счет действия вынуждающих приливных сил или же либрации, как в лабораторном эксперименте или на других планетах (и их спутниках) [25, 26]. Представляет также интерес продолжить исследование симметричной устойчивости с точным учетом силы Кориолиса (ср. [20–23]). Здесь возможен учет произвольной ориентации основного потока относительно меридиана (ср. [27]), а также учет диссипации и анализ зависимости результатов от числа Прандтля и, особенно, от термической релаксации (ср. [12]). Помимо решения задач собственно теории симметричной устойчивости, сказанное открывают новые пути исследования механизмов волнообразования в геофизических средах и, в конечном счете, механизмов генерации турбулентности в них. При исследовании устойчивости сдвиговых течений, которые периодически зависят от времени, в работе используется теория Флоке и аналогия задачи с параметрической неустойчивостью колебаний маятника [28].

2. ПОСТАНОВКА ЗАДАЧИ

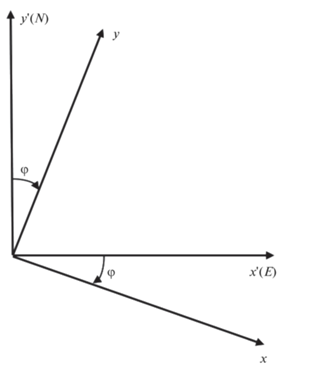
Рассмотрим движение атмосферы на обобщенной $f$-плоскости, где сила Кориолиса учитывается точным образом. Основной поток, устойчивость которого исследуется, может составлять угол $\varphi $ с зональным направлением (рис. 1). В географических $\left( {x{\kern 1pt} ',y{\kern 1pt} ',z} \right)$ координатах, в которых ось $x{\kern 1pt} '$ направлена на восток (E), $y{\kern 1pt} '$ на север (N), а $z$ вертикально вверх, вектор планетарной завихренности имеет вид $2\Omega = 2{{\Omega }_{z}}{\mathbf{k}} + 2{{\Omega }_{{y'}}}{\mathbf{j}}{\kern 1pt} ' \equiv f{\kern 1pt} {\mathbf{k}} + \tilde {f}{\kern 1pt} {\mathbf{j}}{\kern 1pt} '$. Здесь $\Omega $ вектор угловой скорости вращения Земли с компонентами $\left( {0,{{\Omega }_{{y'}}},{{\Omega }_{z}}} \right)$, ${\mathbf{j}}{\kern 1pt} '$ и ${\mathbf{k}}$ единичные вектора в направлении осей $y{\kern 1pt} '$ и $z$ соответственно, $f$ и $\tilde {f}$ называются соответственно параметром Кориолиса и (зачастую, но не всегда) вторым параметром Кориолиса. Считаем параметры $f$ и $\tilde {f}$ положительными (Северное полушарие). В “традиционном” приближении вкладом слагаемых с $\tilde {f}$ в уравнениях движения пренебрегают. Преобразуя к системе координат $\left( {x,y,z} \right)$, повернутой по часовой стрелке вокруг оси $z$ на угол $\varphi $ относительно $\left( {x{\kern 1pt} ',y{\kern 1pt} ',z} \right)$ координат, будем иметь

$\begin{gathered} 2\Omega = 2{{\Omega }_{z}}{\mathbf{k}} - 2{{\Omega }_{{y'}}}\sin {\kern 1pt} \varphi {\kern 1pt} {\kern 1pt} {\mathbf{i}} + 2{{\Omega }_{{y'}}}\cos {\kern 1pt} \varphi {\kern 1pt} {\mathbf{j}} \equiv \\ \equiv f{\kern 1pt} {\mathbf{k}} - \tilde {f}{\kern 1pt} \sin {\kern 1pt} \varphi {\kern 1pt} {\kern 1pt} {\mathbf{i}} + \tilde {f}{\kern 1pt} \cos \varphi {\kern 1pt} {\kern 1pt} {\mathbf{j}}, \\ \end{gathered} $
где ${\mathbf{i}}$ и ${\mathbf{j}}$ суть единичные векторы в направлении осей $x$ и $y$ соответственно.

Рис. 1.

Схема используемой в статье системы координат; подробности даны в тексте.

В приближении Буссинеска в случае вязкой и теплопроводной среды и предполагая, что поле скорости ${\mathbf{v}} = \left( {u,v,w} \right)$, поле плавучести $b$ и поле редуцированного давления $\pi $ не зависят от $x$ координаты, имеем полную систему уравнений

(1а)
$\begin{gathered} \frac{{{\text{D}}u}}{{{\text{D}}t}} - f{\kern 1pt} v + \tilde {f}{\kern 1pt} \cos {\kern 1pt} \varphi {\kern 1pt} w = \nu {{\nabla }^{2}}u + F, \\ \frac{{{\text{D}}v}}{{{\text{D}}t}} + fu + \tilde {f}{\kern 1pt} \sin {\kern 1pt} \varphi {\kern 1pt} w = - \frac{{\partial \pi }}{{\partial y}} + \nu {\kern 1pt} {{\nabla }^{2}}v, \\ \end{gathered} $
(1б)
$\begin{gathered} \frac{{{\text{D}}w}}{{{\text{D}}t}} - \tilde {f}{\kern 1pt} \cos {\kern 1pt} \varphi u - \tilde {f}{\kern 1pt} \sin {\kern 1pt} \varphi {\kern 1pt} v = - \frac{{\partial \pi }}{{\partial z}} + b + \nu {\kern 1pt} {{\nabla }^{2}}w, \\ \frac{{{\text{D}}b}}{{{\text{D}}t}} = \kappa {{\nabla }^{2}}b + G,\,\,\,\,\frac{{\partial v}}{{\partial y}} + \frac{{\partial w}}{{\partial z}} = 0, \\ \end{gathered} $

если заданы источники импульса $F$ и плавучести $G$. Оператор полной производной по времени имеет вид ${{\text{D}} \mathord{\left/ {\vphantom {{\text{D}} {{\text{D}}t}}} \right. \kern-0em} {{\text{D}}t}} = {\partial \mathord{\left/ {\vphantom {\partial {\partial t}}} \right. \kern-0em} {\partial t}}$ + $v\left( {{\partial \mathord{\left/ {\vphantom {\partial {\partial y}}} \right. \kern-0em} {\partial y}}} \right)$ + $w\left( {{\partial \mathord{\left/ {\vphantom {\partial {\partial z}}} \right. \kern-0em} {\partial z}}} \right)$; ${{\nabla }^{2}} = {{{{\partial }^{2}}} \mathord{\left/ {\vphantom {{{{\partial }^{2}}} {\partial {{y}^{2}}}}} \right. \kern-0em} {\partial {{y}^{2}}}}$ + ${{{{\partial }^{2}}} \mathord{\left/ {\vphantom {{{{\partial }^{2}}} {\partial {{z}^{2}}}}} \right. \kern-0em} {\partial {{z}^{2}}}}$ – двумерный оператор Лапласа. Коэффициенты кинематической вязкости $\nu $ и температуропроводности $\kappa $ (молекулярной и/или турбулентной) в (1) считаются постоянными и для простоты одинаковыми в вертикальном и горизонтальном направлениях.

Вводим функцию тока, полагая $v = - {{\partial \psi } \mathord{\left/ {\vphantom {{\partial \psi } {\partial z}}} \right. \kern-0em} {\partial z}}$, $w = {{\partial \psi } \mathord{\left/ {\vphantom {{\partial \psi } {\partial y}}} \right. \kern-0em} {\partial y}}$, и переменную $m = u - f{\kern 1pt} y + \tilde {f}{\kern 1pt} \cos {\kern 1pt} \varphi z$, называемую геострофическим моментом. При этом ${{\partial m} \mathord{\left/ {\vphantom {{\partial m} {\partial y}}} \right. \kern-0em} {\partial y}}$ = ${{\partial u} \mathord{\left/ {\vphantom {{\partial u} {\partial y}}} \right. \kern-0em} {\partial y}} - f$ и ${{\partial m} \mathord{\left/ {\vphantom {{\partial m} {\partial z}}} \right. \kern-0em} {\partial z}}$ = ${{\partial u} \mathord{\left/ {\vphantom {{\partial u} {\partial z}}} \right. \kern-0em} {\partial z}} + \tilde {f}{\kern 1pt} \cos {\kern 1pt} \varphi $. Теперь система (1) путем исключения давления $\pi $ записывается в виде системы трех уравнений

(2а)
$\frac{{\text{D}}}{{{\text{D}}t}}{{\nabla }^{2}}\psi = \tilde {f}{\kern 1pt} \cos {\kern 1pt} \varphi {\kern 1pt} \frac{{\partial m}}{{\partial y}} + f\frac{{\partial m}}{{\partial z}} + \frac{{\partial b}}{{\partial y}} + \nu {\kern 1pt} {{\nabla }^{4}}\psi ,$
(2б)
$\begin{gathered} \frac{{\text{D}}}{{{\text{D}}t}}m = \nu {{\nabla }^{2}}m + F,\,\,\,\,\frac{{\text{D}}}{{{\text{D}}t}}b = \kappa {\kern 1pt} {{\nabla }^{2}}b + G, \\ \frac{{\text{D}}}{{{\text{D}}t}} = \frac{\partial }{{\partial t}} + \frac{{\partial \left( {\psi ,...} \right)}}{{\partial \left( {y,z} \right)}}, \\ \end{gathered} $

Методически полезно начать с невязкого и нетеплопроводного случая, когда $\nu = \kappa = 0$ и F = G = = 0. Система (2) при этом имеет стационарное решение $\bar {m} = \bar {m}\left( {y,z} \right)$, $\bar {b} = \bar {b}\left( {y,z} \right)$, $\bar {\psi } = 0$. Функции $\bar {m}\left( {y,z} \right)$ и $\bar {b}\left( {y,z} \right)$, связаны обобщенным уравнением термического ветра

(3)
$\tilde {f}{\kern 1pt} \cos {\kern 1pt} \varphi {\kern 1pt} \frac{{\partial{ \bar {m}}}}{{\partial y}} + f\frac{{\partial{ \bar {m}}}}{{\partial z}} + \frac{{\partial{ \bar {b}}}}{{\partial y}} = 0.$

Рассмотрим устойчивость такого стационарного решения, налагая на него малые возмущения $m = \bar {m} + m{\kern 1pt} '$, $b = \bar {b} + b{\kern 1pt} '$, $\psi = \psi {\kern 1pt} '$ и линеаризуя уравнения относительно штрихованных величин. Полагаем, что $\bar {m} = \left( {{{\partial{ \bar {m}}} \mathord{\left/ {\vphantom {{\partial{ \bar {m}}} {\partial y}}} \right. \kern-0em} {\partial y}}} \right)y$ + $\left( {{{\partial{ \bar {m}}} \mathord{\left/ {\vphantom {{\partial{ \bar {m}}} {\partial z}}} \right. \kern-0em} {\partial z}}} \right)z$, $\bar {b} = \left( {{{\partial{ \bar {b}}} \mathord{\left/ {\vphantom {{\partial{ \bar {b}}} {\partial y}}} \right. \kern-0em} {\partial y}}} \right)y$ + $\left( {{{\partial{ \bar {b}}} \mathord{\left/ {\vphantom {{\partial{ \bar {b}}} {\partial z}}} \right. \kern-0em} {\partial z}}} \right)z$, где все четыре частные производные постоянны. Аддитивные константы не учитываем. Ищем решение в виде $\left( {\psi {\kern 1pt} ',m{\kern 1pt} ',b{\kern 1pt} '} \right)$ = = $\left( {\hat {\psi },\hat {m},\hat {b}} \right)$$\exp \left\{ {{\text{i}}\left( {py + qz - \sigma t} \right)} \right\}$ и с учетом (3) приходим к дисперсионному соотношению (характеристическому уравнению)

(4)
$\begin{gathered} {{\sigma }^{2}}\left( {{{p}^{2}} + {{q}^{2}}} \right) = \left( {\tilde {f}{\kern 1pt} \cos {\kern 1pt} \varphi \frac{{\partial{ \bar {m}}}}{{\partial z}} + \frac{{\partial{ \bar {b}}}}{{\partial z}}} \right){{p}^{2}} + \\ + \,\,\left( { - f\frac{{\partial{ \bar {m}}}}{{\partial y}}} \right){{q}^{2}} + 2f\frac{{\partial{ \bar {m}}}}{{\partial z}}pq. \\ \end{gathered} $

Условие устойчивости заключается в положительной определенности квадратичной формы в правой части (4), что эквивалентно выполнению трех неравенств

(5)
$\begin{gathered} \tilde {f}{\kern 1pt} \cos {\kern 1pt} \varphi \frac{{\partial{ \bar {m}}}}{{\partial z}} + \frac{{\partial{ \bar {b}}}}{{\partial z}} > 0,\,\,\,\, - f\frac{{\partial{ \bar {m}}}}{{\partial y}} > 0, \\ \left( {\tilde {f}{\kern 1pt} \cos {\kern 1pt} \varphi \frac{{\partial{ \bar {m}}}}{{\partial z}} + \frac{{\partial{ \bar {b}}}}{{\partial z}}} \right)\left( { - f\frac{{\partial{ \bar {m}}}}{{\partial y}}} \right) - {{f}^{2}}{{\left( {\frac{{\partial{ \bar {m}}}}{{\partial z}}} \right)}^{2}} > 0. \\ \end{gathered} $

Первое неравенство в (5) обобщает обычное условие статической устойчивости, однако теперь допускается возможность в устойчивом случае малых отрицательных значений $\frac{{\partial{ \bar {b}}}}{{\partial z}}$, если только слагаемое $\tilde {f}{\kern 1pt} \cos {\kern 1pt} \varphi \left( {{{\partial{ \bar {m}}} \mathord{\left/ {\vphantom {{\partial{ \bar {m}}} {\partial z}}} \right. \kern-0em} {\partial z}}} \right)$ положительно и достаточно велико. Второе неравенство в (5) есть классическое условие инерционной устойчивости $f\left( {f - {{\partial{ \bar {u}}} \mathord{\left/ {\vphantom {{\partial{ \bar {u}}} {\partial y}}} \right. \kern-0em} {\partial y}}} \right) > 0$; примечательно, что в нем не присутствует второй параметр Кориолиса. Третье неравенство (5) обобщает традиционное условие симметричной бароклинной устойчивости, которое в безразмерной форме имеет вид $1 + {\text{Ro}} - {\text{R}}{{{\text{i}}}^{{ - 1}}} > 0$ (ср. [12, 14]), где ${\text{Ro}}$ = = ${{f}^{{ - 1}}}\left( { - {{\partial{ \bar {u}}} \mathord{\left/ {\vphantom {{\partial{ \bar {u}}} {\partial y}}} \right. \kern-0em} {\partial y}}} \right)$ и ${\text{Ri}} = {{\left( {{{\partial{ \bar {b}}} \mathord{\left/ {\vphantom {{\partial{ \bar {b}}} {\partial z}}} \right. \kern-0em} {\partial z}}} \right)} \mathord{\left/ {\vphantom {{\left( {{{\partial{ \bar {b}}} \mathord{\left/ {\vphantom {{\partial{ \bar {b}}} {\partial z}}} \right. \kern-0em} {\partial z}}} \right)} {{{{\left( {{{\partial{ \bar {u}}} \mathord{\left/ {\vphantom {{\partial{ \bar {u}}} {\partial z}}} \right. \kern-0em} {\partial z}}} \right)}}^{2}}}}} \right. \kern-0em} {{{{\left( {{{\partial{ \bar {u}}} \mathord{\left/ {\vphantom {{\partial{ \bar {u}}} {\partial z}}} \right. \kern-0em} {\partial z}}} \right)}}^{2}}}}$ числа Россби и Ричардсона, соответственно. В нашем случае это условие включает полный учет силы Кориолиса, что не позволяет его записать в столь же компактной безразмерной форме.

В устойчиво стратифицированной земной атмосфере средних широт значение ${{\partial{ \bar {b}}} \mathord{\left/ {\vphantom {{\partial{ \bar {b}}} {\partial z}}} \right. \kern-0em} {\partial z}} \equiv {{N}^{2}}$, где $N$ – частота Брента–Вяйсяля, на два порядка превосходит значения $f\sim \tilde {f}$. Здесь для крупномасштабных движений горизонтального масштаба $L\sim {{N{{H}_{0}}} \mathord{\left/ {\vphantom {{N{{H}_{0}}} f}} \right. \kern-0em} f}$, где ${{H}_{0}}$ – высота однородной атмосферы определяющая вертикальный масштаб движений, поправки в (5) за счет отказа от традиционного приближения имеют относительный порядок величины ${{\tilde {f}} \mathord{\left/ {\vphantom {{\tilde {f}} N}} \right. \kern-0em} N} = O\left( {{{{10}}^{{ - 2}}}} \right)$. Для движений среднего (мезо-) масштаба эти поправки могут достигать порядка величины $O\left( {{{{10}}^{{ - 1}}}} \right)$. Для глубоководной части океана, в его абиссальной зоне, для очень слабо стратифицированных водных масс c периодами колебаний ${{T}_{b}} = {{2{{\pi }}} \mathord{\left/ {\vphantom {{2{{\pi }}} N}} \right. \kern-0em} N}$ между примерно шестью часами и сутками [29], может оказаться ситуация, когда ${{N}^{2}}$ и ${{\tilde {f}}^{2}}$ отличаются на порядок величины или даже менее. Здесь учет второго параметра Кориолиса может быть существенным [20, 21; 30, гл. 1, §3]. К примеру, когда вертикальный сдвиг скорости равен нулю, то наряду с условием ${{\tilde {f}}^{2}}{\kern 1pt} {{\cos }^{2}}{\kern 1pt} \varphi + {{N}^{2}} > 0$, обобщающим условие статической устойчивости, имеется условие инерционной устойчивости $f\left( {f - {{\partial{ \bar {u}}} \mathord{\left/ {\vphantom {{\partial{ \bar {u}}} {\partial y}}} \right. \kern-0em} {\partial y}}} \right) > 0$, а также более ограничивающее величину горизонтального сдвига скорости условие симметричной бароклинной устойчивости $f[f - (1 + {{{{{\tilde {f}}}^{2}}{\kern 1pt} {{{\cos }}^{2}}{\kern 1pt} \varphi } \mathord{\left/ {\vphantom {{{{{\tilde {f}}}^{2}}{\kern 1pt} {{{\cos }}^{2}}{\kern 1pt} \varphi } {{{N}^{2}}}}} \right. \kern-0em} {{{N}^{2}}}})$$\left( {{{\partial{ \bar {u}}} \mathord{\left/ {\vphantom {{\partial{ \bar {u}}} {\partial y}}} \right. \kern-0em} {\partial y}}} \right)] > 0$.

3. УСТОЙЧИВОСТЬ ПЕРИОДИЧЕСКОГО ПО ВРЕМЕНИ ТЕЧЕНИЯ С ЛИНЕЙНЫМ ПРОФИЛЕМ СКОРОСТИ

Обратимся к задаче об устойчивости периодического во времени основного потока $\bar {m} = \bar {m}\left( {y,z,t} \right)$, $\bar {b} = \bar {b}\left( {y,z,t} \right)$, $\bar {\psi } = 0$, линейного по $y$ и $z$, с учетом вязкости и теплопроводности среды в общем случае. При этом уравнения (2) тождественно удовлетворятся путем надлежащего выбора функций $F$ и $G$. Сразу исходим из системы уравнений, линеаризованных относительно возмущений, наложенных на основное течение

(6а)
$\frac{\partial }{{\partial t}}{{\nabla }^{2}}\psi {\kern 1pt} ' = \tilde {f}{\kern 1pt} \cos {\kern 1pt} \varphi {\kern 1pt} {\kern 1pt} \frac{{\partial m{\kern 1pt} '}}{{\partial y}} + f\frac{{\partial m{\kern 1pt} '}}{{\partial z}} + \frac{{\partial b{\kern 1pt} '}}{{\partial y}} + \nu {{\nabla }^{4}}\psi {\kern 1pt} ',$
(6б)
$\frac{\partial }{{\partial t}}m{\kern 1pt} '\,\, - \frac{{\partial \psi {\kern 1pt} '}}{{\partial z}}\frac{{\partial{ \bar {m}}}}{{\partial y}} + \frac{{\partial \psi {\kern 1pt} '}}{{\partial y}}\frac{{\partial{ \bar {m}}}}{{\partial z}} = \nu {\kern 1pt} {{\nabla }^{2}}m{\kern 1pt} ',$
(6в)
$\frac{\partial }{{\partial t}}b{\kern 1pt} ' - \frac{{\partial \psi {\kern 1pt} '}}{{\partial z}}\frac{{\partial{ \bar {b}}}}{{\partial y}} + \frac{{\partial \psi {\kern 1pt} '}}{{\partial y}}\frac{{\partial{ \bar {b}}}}{{\partial z}} = \kappa {{\nabla }^{2}}b{\kern 1pt} '.$

В этих уравнениях

(7а)
$\begin{gathered} {{\partial{ \bar {m}}} \mathord{\left/ {\vphantom {{\partial{ \bar {m}}} {\partial y}}} \right. \kern-0em} {\partial y}} = {{\partial{ \bar {u}}} \mathord{\left/ {\vphantom {{\partial{ \bar {u}}} {\partial y}}} \right. \kern-0em} {\partial y}} - f = - \alpha {\kern 1pt} \cos {\kern 1pt} \omega t - f, \\ {{\partial{ \bar {m}}} \mathord{\left/ {\vphantom {{\partial{ \bar {m}}} {\partial z}}} \right. \kern-0em} {\partial z}} = {{\partial{ \bar {u}}} \mathord{\left/ {\vphantom {{\partial{ \bar {u}}} {\partial z}}} \right. \kern-0em} {\partial z}} + \tilde {f}{\kern 1pt} \cos {\kern 1pt} \varphi = - \beta {\kern 1pt} \cos {\kern 1pt} \omega t + \tilde {f}{\kern 1pt} \cos {\kern 1pt} \varphi , \\ \end{gathered} $
(7б)
${{\partial{ \bar {b}}} \mathord{\left/ {\vphantom {{\partial{ \bar {b}}} {\partial y}}} \right. \kern-0em} {\partial y}} = \left( {\alpha \tilde {f}{\kern 1pt} \cos {\kern 1pt} \varphi + \beta f} \right)\cos {\kern 1pt} \omega t.$

Соотношение (7б) соответствует (3). Считается, что ${{\partial{ \bar {b}}} \mathord{\left/ {\vphantom {{\partial{ \bar {b}}} {\partial z}}} \right. \kern-0em} {\partial z}} \equiv {{N}^{2}} = const$; $\alpha $ и $\beta $ – амплитуды сдвигов скорости и $\omega $ – угловая частота.

Приведем уравнения (6) с учетом (7) к безразмерному виду, вводя безразмерные переменные (помечаются крышечками сверху) (y, z) = $L\left( {\hat {y},\hat {z}} \right)$, $t = {{\omega }^{{ - 1}}}\hat {t}$, $\psi {\kern 1pt} ' = {{L}^{2}}f\hat {\psi }$, $m{\kern 1pt} ' = L\omega {\kern 1pt} \hat {m}$, $b{\kern 1pt} ' = L\omega f\hat {b}$, R = = L2ω/ν, $S = {{{{L}^{2}}\omega } \mathord{\left/ {\vphantom {{{{L}^{2}}\omega } \kappa }} \right. \kern-0em} \kappa }$, а также полагая $\delta = {{\tilde {f}{\kern 1pt} \cos {\kern 1pt} \varphi } \mathord{\left/ {\vphantom {{\tilde {f}{\kern 1pt} \cos {\kern 1pt} \varphi } f}} \right. \kern-0em} f}$, $A = {{{{f}^{2}}} \mathord{\left/ {\vphantom {{{{f}^{2}}} {{{\omega }^{2}}}}} \right. \kern-0em} {{{\omega }^{2}}}}$, $B = {{{{N}^{2}}} \mathord{\left/ {\vphantom {{{{N}^{2}}} {{{\omega }^{2}}}}} \right. \kern-0em} {{{\omega }^{2}}}}$, $\varepsilon = {\alpha \mathord{\left/ {\vphantom {\alpha f}} \right. \kern-0em} f}$, $\tilde {\varepsilon } = {\beta \mathord{\left/ {\vphantom {\beta f}} \right. \kern-0em} f}$. Параметр $\varepsilon $ имеет смысл числа Россби ${\text{Ro}}$. Отношение ${B \mathord{\left/ {\vphantom {B A}} \right. \kern-0em} A} = {{{{N}^{2}}} \mathord{\left/ {\vphantom {{{{N}^{2}}} {{{f}^{2}}}}} \right. \kern-0em} {{{f}^{2}}}}$ иногда называется параметром стратификации [18]. Здесь $L$ – пространственный масштаб, который произволен, но фиксирован. В невязкой и нетеплопроводной задаче уравнения безразличны (автомодельны) к его выбору. Это уже не так в вязкой и теплопроводной среде, где $L$ входит в определение чисел Рейнольдса $R$ и Пекле $S$, которые связаны посредством числа Прандтля $\Pr = {\kern 1pt} {\kern 1pt} {\nu \mathord{\left/ {\vphantom {\nu \kappa }} \right. \kern-0em} \kappa }$. Отметим, что получающиеся безразмерные уравнения инварианты относительно перемасштабирования $L \to k{\kern 1pt} L$, $\nu \to {{k}^{2}}\nu $, $\kappa \to {{k}^{2}}\kappa $, где $k$ произвольное число и $\Pr = const$. Выпишем эти уравнения, опуская крышечки над переменными

(8а)
$\left( {\frac{\partial }{{\partial t}} - \frac{1}{R}{{\nabla }^{2}}} \right){{\nabla }^{2}}\psi - \delta {\kern 1pt} {\kern 1pt} \frac{{\partial m}}{{\partial y}} - \frac{{\partial m}}{{\partial z}}{\kern 1pt} - \frac{{\partial b}}{{\partial y}} = 0,$
(8б)
$\begin{gathered} \left( {\frac{\partial }{{\partial t}} - \frac{1}{R}{{\nabla }^{2}}} \right)m + A\left( {1 + \varepsilon {\kern 1pt} \cos {\kern 1pt} t} \right)\frac{{\partial \psi }}{{\partial z}} + \\ + \,\,A\left( {\delta - \tilde {\varepsilon }{\kern 1pt} \cos {\kern 1pt} t} \right)\frac{{\partial \psi }}{{\partial y}} = 0, \\ \end{gathered} $
(8в)
$\left( {\frac{\partial }{{\partial t}} - \frac{1}{S}{{\nabla }^{2}}} \right)b - A\left( {\varepsilon \delta + \tilde {\varepsilon }} \right)\cos {\kern 1pt} t\frac{{\partial \psi }}{{\partial z}} + B\frac{{\partial \psi }}{{\partial y}} = 0.$

В общем случае путем исключения $m$ и $b$ из системы (8) получается уравнение третьего порядка по времени, которое сводится к уравнению второго порядка по времени в случае $\Pr = 1$, как это применимо при учете мелкомасштабной (турбулентной) вязкости и теплопроводности в атмосфере и океане. Если искать решение задачи в виде $\psi = \Psi \left( t \right)$$\exp \left[ {{\text{i}}\left( {py + qz} \right)} \right]$ и ввести оператор $\mathcal{L} = {\partial \mathord{\left/ {\vphantom {\partial {\partial t}}} \right. \kern-0em} {\partial t}}$ + ${{R}^{{ - 1}}}\left( {{{p}^{2}} + {{q}^{2}}} \right) \equiv {\partial \mathord{\left/ {\vphantom {\partial {\partial t}}} \right. \kern-0em} {\partial t}}$ + ${{S}^{{ - 1}}}\left( {{{p}^{2}} + {{q}^{2}}} \right)$, то это уравнение записывается в виде

(9а)
${{\mathcal{L}}^{2}}\Psi + \left( {{{\Delta }^{2}} + {\rm E}{\kern 1pt} \cos {\kern 1pt} t} \right)\Psi = 0,$
(9б)
$\begin{gathered} {{\Delta }^{2}} = \frac{{A{{{\left( {p\delta + q} \right)}}^{2}} + B{{p}^{2}}}}{{{{p}^{2}} + {{q}^{2}}}}, \\ {\rm E} = A\frac{{\varepsilon {{q}^{2}} - 2\tilde {\varepsilon }pq - \tilde {\varepsilon }{\kern 1pt} \delta {{p}^{2}}}}{{{{p}^{2}} + {{q}^{2}}}}, \\ \end{gathered} $

что близко совпадает по форме с уравнением Матье. Общий случай $\Pr \ne 1$ кратко обсуждается в Приложении. Используя аналогию задачи с параметрической неустойчивостью колебаний маятника [28], решение (9) ищется методом Флоке в виде

$\Psi = \sum\limits_{n = - \infty }^\infty {{{a}_{{n + {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}\exp \left[ {{\text{i}}\left( {n + {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}} \right)t + \mu {\kern 1pt} t} \right]} ,$
где используются возмущения с удвоенной периодичностью по времени; $\mu $ является, вообще говоря, комплексным числом. Подставляя в (9) приходим к трехточечному рекуррентному соотношению

(10)
$\begin{gathered} \frac{1}{2}{\rm E}{{a}_{{n - {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}} + \left\{ {{{{\left[ {\mu + {\text{i}}\left( {n + \frac{1}{2}} \right) + {{R}^{{ - 1}}}{\kern 1pt} \left( {{{p}^{2}} + {{q}^{2}}} \right)} \right]}}^{2}} + {{\Delta }^{2}}} \right\} \times \\ \times \,\,{{a}_{{n + {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}} + \frac{1}{2}{\rm E}{{a}_{{n + {3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}} = 0. \\ \end{gathered} $

Начнем со случая, когда ${{R}^{{ - 1}}} = {{S}^{{ - 1}}} = 0$ и выполняется принцип смены устойчивости [31], т.е. на нейтральной кривой устойчивости $\mu = 0$. Переписывая (10) в виде

$\begin{gathered} {{a}_{{n - {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}} - {{\gamma }_{{n + {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}{{a}_{{n + {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}} + {{a}_{{n + {3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}} = 0, \\ {{\gamma }_{{n + {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}} = {{2\left[ {{{{\left( {n + \frac{1}{2}} \right)}}^{2}} - {{\Delta }^{2}}} \right]} \mathord{\left/ {\vphantom {{2\left[ {{{{\left( {n + \frac{1}{2}} \right)}}^{2}} - {{\Delta }^{2}}} \right]} {\rm E}}} \right. \kern-0em} {\rm E}}, \\ \end{gathered} $

и решая получившуюся бесконечную систему уравнений методом непрерывных дробей, получаем стандартным образом условие ее разрешимости (ср. [32])

(11)
${{\gamma }_{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}} - \frac{1}{{{{\gamma }_{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}} - \frac{1}{{{{\gamma }_{{{5 \mathord{\left/ {\vphantom {5 2}} \right. \kern-0em} 2}}}} - ...}}}} = \pm 1.$

Ограничиваясь в (11) подходящей дробью самого низкого порядка, имеем ${{\gamma }_{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}} \approx \pm 1$, или Δ2 – ‒ $\frac{1}{4} \approx \mp \frac{1}{2}{\rm E}$. Параметрическая неустойчивость при сколь угодно малом значении $\left| {\rm E} \right|$ возникает, когда ${{\Delta }^{2}} - \frac{1}{4} \approx 0$. Отметим, что при $\left| {\rm E} \right| \ll 1$ величина бесконечной непрерывной дроби в (11) надежно аппроксимируется значением ${{\gamma }_{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}$ и полученное решение является очень хорошим приближением к точному решению задачи.

Критические для неустойчивости значения $\left| {\rm E} \right|$ получаются при учете (турбулентной) вязкости и теплопроводности. Ограничимся случаем $R \gg 1$ и решаем задачу приближенным методом, апеллирующим к теории возмущений. На первом этапе пренебрегаем действием диссипативных факторов и вычисляем инкремент роста неустойчивых возмущений в консервативной задаче, исходя из вытекающего из (10) соотношения

(12)
$\begin{gathered} \frac{1}{2}{\rm E}{{a}_{{n - {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}} + \left\{ {{{{\left[ {\mu + {\text{i}}\left( {n + \frac{1}{2}} \right)} \right]}}^{2}} + {{\Delta }^{2}}} \right\}{{a}_{{n + {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}} + \\ \\ + \,\,\frac{1}{2}{\rm E}{{a}_{{n + {3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}} = 0. \\ \end{gathered} $

Действуя методом Галеркина и ограничиваясь в первом приближении двумя ненулевыми амплитудами ${{a}_{{ - {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}$ и ${{a}_{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}$, имеем систему двух уравнений с двумя неизвестными

$\left[ {{{{\left( {\mu \pm \frac{1}{2}{\text{i}}} \right)}}^{2}} + {{\Delta }^{2}}} \right]{{a}_{{{{ \pm 1} \mathord{\left/ {\vphantom {{ \pm 1} 2}} \right. \kern-0em} 2}}}} + \frac{1}{2}{\rm E}{{a}_{{ \mp {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}} = 0.$

Требование равенства нулю определителя этой системы приводит к биквадратному уравнению

${{\mu }^{4}} + \left( {2{{\Delta }^{2}} + \frac{1}{2}} \right){{\mu }^{2}} + {{\left( {{{\Delta }^{2}} - \frac{1}{4}} \right)}^{2}} - \frac{1}{4}{{{\rm E}}^{2}} = 0,$

и корень этого уравнения μ = = $\sqrt {\sqrt {{{\Delta }^{2}} + \frac{1}{4}{{{\rm E}}^{2}}} - \left( {{{\Delta }^{2}} + \frac{1}{4}} \right)} $ > 0 отвечает неустойчивости. Это будет тогда, когда $\frac{1}{4}{{{\rm E}}^{2}}$ > ${{\left( {{{\Delta }^{2}} - \frac{1}{4}} \right)}^{2}}$, что полностью согласуется с анализом на основе метода непрерывных дробей. На втором этапе учитываем малую вязкость и теплопроводность среды. Для неустойчивости невязкий (нетеплопроводный) инкремент неустойчивости должен превосходить по величине декремент затухания за счет вязкости и теплопроводности, т.е. должно выполняться условие

(13)
$\sqrt {\sqrt {{{\Delta }^{2}} + \frac{1}{4}{{{\rm E}}^{2}}} - \left( {{{\Delta }^{2}} + \frac{1}{4}} \right)} > {{R}^{{ - 1}}}\left( {{{p}^{2}} + {{q}^{2}}} \right).$

После преобразований в пределе $R \gg 1$ и когда ${{\Delta }^{2}} = \frac{1}{4}$ получается приближенное условие $\frac{1}{4}{{{\rm E}}^{2}}$ > > ${{R}^{{ - 2}}}{{\left( {{{p}^{2}} + {{q}^{2}}} \right)}^{2}}$. Более строго уравнение нейтральной кривой устойчивости для диссипативной задачи получено в Приложении.

Рассмотрим два примера. Оба относятся к случаю плотностной стратификации, близкой к нейтральной, ${{N}^{2}} \approx 0$. Это, например, имеет место в пограничном слое над незамерзающими полярными морями при адвекции очень холодных воздушных масс [18] или, напротив, в экваториальной атмосфере при развитой проникающей конвекции. Первый пример − это когда основной поток обладает лишь горизонтальным сдвигом скорости $ - \alpha $. Тогда в размерных переменных условие неустойчивости приобретает вид

$\left| \alpha \right| > \frac{{2\nu {{{\left( {{{p}^{2}} + {{q}^{2}}} \right)}}^{2}}}}{{f{{q}^{2}}}}\omega ,$
где $p$ и $q$ теперь считаются размерными волновыми числами (что всегда можно делать в силу произвольности выбора пространственного масштаба $L$). Неравенство (14) надо рассматривать совместно с условием ${{\Delta }^{2}} = \frac{1}{4}$, которое (опять в размерных переменных) приобретает вид

(15)
$\omega = \frac{{2f\left( {p\delta + q} \right){\kern 1pt} }}{{\sqrt {{{p}^{2}} + {{q}^{2}}} }},$

Исключая $\omega $ из (14) и (15), имеем

(16)
$\begin{gathered} \left| \alpha \right| > \frac{{4\nu {{{\left( {{{p}^{2}} + {{q}^{2}}} \right)}}^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}}\left( {p\delta + q} \right)}}{{{\kern 1pt} {{q}^{2}}}} = \\ = 4\nu {{p}^{2}}\frac{{{{{\left( {{{\eta }^{2}} + 1} \right)}}^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}}\left( {\delta + \eta } \right)}}{{{\kern 1pt} {{\eta }^{2}}}} \equiv 4\nu {{p}^{2}}F\left( {\eta ;\delta } \right). \\ \end{gathered} $

В этом соотношении отсутствует явная зависимость от параметра Кориолиса $f$. Если ввести число Рейнольдса ${{\operatorname{Re} }_{\alpha }} = \left| \alpha \right|{{p}^{{ - 2}}}{{\nu }^{{ - 1}}}$, то (16) примет форму критерия Рейнольдса ${{\operatorname{Re} }_{\alpha }} > {{\left( {{{{\operatorname{Re} }}_{\alpha }}} \right)}_{{{\text{crit}}}}} = 4\,F\left( {\eta ;\delta } \right)$. Функция $F\left( {\eta ;\delta } \right)$ переменной $\eta = {q \mathord{\left/ {\vphantom {q p}} \right. \kern-0em} p}$ имеет минимум, когда $\eta = {{\eta }_{ * }}$ является корнем кубического уравнения $2{{\eta }^{3}} + \delta {{\eta }^{2}} - \eta - 2\delta = 0$, которое решается численно. Этот минимум указан в табл. 1 для нескольких избранных значений $\delta $. Отметим, что для предельных значений $\delta = 0,\infty $ в точности имеем ${{\eta }_{ * }} = {1 \mathord{\left/ {\vphantom {1 {\sqrt 2 }}} \right. \kern-0em} {\sqrt 2 }},\sqrt 2 $, соответственно. Данные табл. 1 показывают, что критические для неустойчивости значения горизонтального сдвига скорости монотонно возрастают с ростом $\delta $. Они бесконечно велики при $\delta \to \infty $ и минимальны при $\delta \to 0$. По определению, $\delta = {{\tilde {f}{\kern 1pt} \cos {\kern 1pt} \varphi } \mathord{\left/ {\vphantom {{\tilde {f}{\kern 1pt} \cos {\kern 1pt} \varphi } f}} \right. \kern-0em} f} \equiv {\text{ctg}}{\kern 1pt} {\kern 1pt} \Phi {\kern 1pt} {\kern 1pt} \cos {\kern 1pt} \varphi $, где $\Phi $ − географическая широта и угол $\varphi $ характеризует отклонение основного потока от зонального направления. Поэтому наиболее благоприятные для неустойчивости условия возникают или в высоких широтах, или когда основной поток направлен по меридиану, или когда выполняются оба эти условия. Сложная ситуация возникает на экваторе, где в общем случае неустойчивость невозможна, а в специальном случае меридионально направленного основного потока возникает неопределенность 0/0. Будем формально рассматривать наиболее благоприятный для неустойчивости случай $\delta \to 0$. Минимальное значение горизонтального сдвига скорости, при котором возникает неустойчивость, равно ${{\left| \alpha \right|}_{{\min }}} = 6\sqrt {3{\kern 1pt} {\kern 1pt} } {\kern 1pt} \nu {{p}^{2}}$. Полагая $\nu = \kappa = 10\,\,{{{\text{м}}}^{2}}{{{\text{с}}}^{{ - 1}}}$ и ${{\lambda }_{y}} = {{2{{\pi }}} \mathord{\left/ {\vphantom {{2{{\pi }}} p}} \right. \kern-0em} p}$ = 3 × 103 м, что в целом согласуется со структурой облачных улиц над полярными морями [18], получаем, что ${{\left| \alpha \right|}_{{\min }}} \approx 4.6 \times {{10}^{{ - 5}}}\,\,{{{\text{с}}}^{{ - 1}}}$. Согласно (5), неустойчивость стационарного течения с таким сдвигом скорости в средних и высоких широтах невозможна. Поэтому эффект нестационарности является принципиальным. Пусть внешняя возбуждающая сила имеет полусуточный период (солнечный полусуточный прилив; лунный полусуточный прилив имеет период в 12 часов 25 мин). Подставляя $\omega = 2\Omega $ в (15), где $\Omega $ угловая скорость вращения Земли, и ${{q}^{2}} = \frac{1}{2}{{p}^{2}}$, видим, что (15) в точности выполняется на широте $\Phi = 60^\circ $. Необходимо учесть, что если условие ${{\Delta }^{2}} = \frac{1}{4}$ выполняется лишь приближенно, то и в этом случае возможна неустойчивость, которая, впрочем, потребует более высоких значений сдвигов скорости для ее реализации. К примеру, когда $\omega = 2\Omega $, то на широте $\Phi = 70^\circ $ будем иметь ${{\Delta }^{2}} \approx 0.29$, т.е. условие ${{\Delta }^{2}} = \frac{1}{4}$ с определенной точностью (порядка $16\% $), но все же выполняется.

Таблица 1.  

Значения безразмерной функции $F\left( {\eta ;\delta } \right)$ в точках ее минимума в правой части (16)

δ 0 1/8 1/4 1/2 1 2 4 8 $\infty $
${{\eta }_{ * }}$ 0.7071 0.7817 0.8340 0.9077 1 1.1017 1.1991 1.2793 1.4142
$F\left( {{{\eta }_{ * }};\delta } \right)$ 2.5981 3.0342 3.4408 4.2086 5.6569 8.4171 13.7633 24.2739 $\infty $

Второму примеру отвечает поток с одним лишь вертикальным сдвигом скорости $ - \beta $. Вместо (16) будем иметь

(17)
$\begin{gathered} \left| \beta \right| > \frac{{4\nu {{{\left( {{{p}^{2}} + {{q}^{2}}} \right)}}^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}}\left( {p\delta + q} \right)}}{{{\kern 1pt} 2pq + {{p}^{2}}\delta }} = \\ = \,\,4\nu {{q}^{2}}\frac{{{{{\left( {{{\xi }^{2}} + 1} \right)}}^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}}\left( {\xi \delta + 1} \right)}}{{{\kern 1pt} 2\xi + {{\xi }^{2}}\delta }} \equiv 4\nu {{q}^{2}}F\left( {\xi ;\delta } \right). \\ \end{gathered} $

Аналогично (16), если ввести число Рейнольдса ${{\operatorname{Re} }_{\beta }} = \left| \beta \right|{{q}^{{ - 2}}}{{\nu }^{{ - 1}}}$, то (17) примет форму критерия Рейнольдса ${{\operatorname{Re} }_{\beta }} > {{\left( {{{{\operatorname{Re} }}_{\beta }}} \right)}_{{{\text{crit}}}}}$ = $4F\left( {\xi ;\delta } \right)$. Функция $F\left( {\xi ;\delta } \right)$ переменной $\xi = {p \mathord{\left/ {\vphantom {p q}} \right. \kern-0em} q}$ достигает минимума при значении $\xi = {{\xi }_{ * }}$, которое является корнем решаемого численно уравнения четвертой степени

(18)
$2{{\delta }^{2}}{{\xi }^{4}} + 7\delta {{\xi }^{3}} + \left( {4 - {{\delta }^{2}}} \right){{\xi }^{2}} - 2\delta \xi - 2 = 0,$

и указано в табл. 2 для нескольких избранных значений $\delta $. В асимптотических пределах $\delta = 0,\infty $ в точности имеем ${{\xi }_{ * }} = {1 \mathord{\left/ {\vphantom {1 {\sqrt 2 }}} \right. \kern-0em} {\sqrt 2 }}$ и поэтому соответственно $F\left( {{{\xi }_{ * }}} \right)$ = ${{\sqrt {27} } \mathord{\left/ {\vphantom {{\sqrt {27} } 4}} \right. \kern-0em} 4},{{\sqrt {27} } \mathord{\left/ {\vphantom {{\sqrt {27} } 2}} \right. \kern-0em} 2}$. Воспользуемся тем, что ${{\xi }_{ * }}$ относительно слабо зависит от $\delta $ и возьмем в начальном приближении ${{\xi }_{ * }} = {1 \mathord{\left/ {\vphantom {1 {\sqrt 2 }}} \right. \kern-0em} {\sqrt 2 }}$. Поскольку $\delta = {\text{ctg}}{\kern 1pt} \Phi {\kern 1pt} \cos {\kern 1pt} \varphi $, то условие ${{\Delta }^{2}} = \frac{1}{4}$, где $\xi = {{\xi }_{ * }} = {1 \mathord{\left/ {\vphantom {1 {\sqrt 2 }}} \right. \kern-0em} {\sqrt 2 }}$, в случае внешней силы с полусуточным периодом записывается в виде

(19)
${{\sin }^{2}}{\kern 1pt} \Phi \frac{{{{{\left( {{{{\text{ctg}}{\kern 1pt} {\kern 1pt} \Phi {\kern 1pt} \cos {\kern 1pt} \varphi } \mathord{\left/ {\vphantom {{{\text{ctg}}{\kern 1pt} {\kern 1pt} \Phi {\kern 1pt} \cos {\kern 1pt} \varphi } {\sqrt 2 }}} \right. \kern-0em} {\sqrt 2 }} + 1} \right)}}^{2}}}}{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}} = \frac{1}{4}.$
Таблица 2.

Значения безразмерной функции $F\left( {\xi ;\delta } \right)$ в точках ее минимума в правой части (17)

δ 0 1/8 1/4 1/2 1 2 4 8 $\infty $
${{\xi }_{ * }}$ 0.7071 0.6871 0.6722 0.6517 0.6303 0.6180 0.6242 0.6459 0.7071
$F\left( {{{\xi }_{ * }};\delta } \right)$ 1.2990 1.3533 1.4021 1.4875 1.6242 1.8164 2.041 2.2476 2.5981

Более точно задача решается методом итераций. Сначала из (19) при заданном $\cos \varphi $ находится значение $\delta = {\text{ctg}}{\kern 1pt} \Phi {\kern 1pt} \cos {\kern 1pt} \varphi $, которое подставляется в (18) и находится новое значение ${{\xi }_{ * }}$. Это новое значение подставляется в (19) вместо ${1 \mathord{\left/ {\vphantom {1 {\sqrt 2 }}} \right. \kern-0em} {\sqrt 2 }}$ и так далее до сходимости. Действуя этим методом и беря $\varphi = 45^\circ $, после пяти итераций находим, что $\Phi \approx 8.72^\circ $, $\delta \approx 4.61$, ${{\xi }_{ * }} \approx 0.6278$ и $F\left( {{{\xi }_{ * }};\delta } \right) \approx 2.086$. Поэтому условие (17) приобретает вид |β| > 8.344νq2. Полагая $q = {{{\pi }} \mathord{\left/ {\vphantom {{{\pi }} H}} \right. \kern-0em} H}$, где $H$ характерный вертикальный масштаб рассматриваемого слоя атмосферы (например, перемешанного слоя атмосферы, ограниченного сверху термической инверсией), который ограничивает вертикальный масштаб возмущений, переписываем условие неустойчивости в виде $\left| \beta \right| > 8.344{\kern 1pt} {\kern 1pt} {{{{\pi }}}^{2}}\nu {\kern 1pt} {{H}^{{ - 2}}}$. Полагая $H = {{10}^{3}}\,\,{\text{м}}$, ν = κ = = 10 м2 с–1, будем иметь оценку $\left| \beta \right| > 8.2 \times {{10}^{{ - 4}}}\,\,{{{\text{c}}}^{{ - 1}}}$. Наблюдаемые вертикальные сдвиги скорости $\left| \beta \right|\sim {{10}^{{ - 2}}}\,\,{{{\text{c}}}^{{ - 1}}}$ над полярными морями [18] и, например, над тропической Атлантикой [33], где формируется тропические ураганы, удовлетворяют этому условию. Удивительной чертой нашего анализа является то, что по отношению к вынуждающей силе с суточным или полусуточным периодом строго зональные движения с $\cos \varphi = 1$ являются устойчивыми, т.е. для них невозможно выполнение условия ${{\Delta }^{2}} = \frac{1}{4}$, и неустойчивость появляется лишь для движений, для которых значение $\cos \varphi $ ниже определенного порога, зависящего от периода внешней силы. В силу того, что используется приближение Буссинеска, данная модель более строго применима к океану, например тропическому. Для тех же значений параметров, что и выше, но беря $\nu = \kappa = {{10}^{{ - 4}}}\,\,{{{\text{м}}}^{2}}\,\,{{{\text{с}}}^{{ - 1}}}$ [34], получаем очень низкий порог неустойчивости $\left| \beta \right| > 8.2 \times {{10}^{{ - 9}}}\,\,{{{\text{c}}}^{{ - 1}}}$, который может превышаться в реальном океане. Отметим, что запрет на неустойчивость при углах $\varphi \approx 0^\circ $, т.е. для периодических во времени (с суточным или полусуточным периодом) океанических течений, близких к зональным, сохраняется и в этом случае. Этот запрет снимается при действии более высокочастотной вынуждающей силы, например, когда $\omega = 4{\kern 1pt} {\kern 1pt} \Omega $, т.е. речь идет о четвертьсуточном приливе, ср. [35].

Важность учета отклонения потока от зональности, т.е. учета множителя $\cos \varphi $ в выражении для “эффективного” второго параметра Кориолиса $\tilde {f}{\kern 1pt} \cos {\kern 1pt} \varphi $, демонстрируют и результаты работы [36], где показано, что отказ от традиционного приближения не влияет на расчеты симметричной устойчивости кросс-экваториального, меридионально направленного течения в Атлантическом океане, поскольку $\tilde {f}{\kern 1pt} \cos {\kern 1pt} \varphi = 0$ в этом случае.

Кратко обсудим вопрос об относительной важности (а) учета приливных модуляций и (б) отказа от традиционного приближения в задаче об устойчивости течения с вертикальным сдвигом скорости. В консервативной задаче, при точном выполнении условия параметрического резонанса ${{\Delta }^{2}} = \frac{1}{4}$ (см. выше), такое модулированное во времени течение является абсолютно неустойчивым, т.е. не существует ненулевого порогового для неустойчивости значения вертикального сдвига скорости $\left| \beta \right|$, в том числе в присутствии устойчивой плотностной стратификации. Последнее означает, что критическое для неустойчивости значение числа Ричардсона ${\text{Ri}} = {{{{N}^{2}}} \mathord{\left/ {\vphantom {{{{N}^{2}}} {{{{\left( {{{\partial{ \bar {u}}} \mathord{\left/ {\vphantom {{\partial{ \bar {u}}} {\partial z}}} \right. \kern-0em} {\partial z}}} \right)}}^{2}}}}} \right. \kern-0em} {{{{\left( {{{\partial{ \bar {u}}} \mathord{\left/ {\vphantom {{\partial{ \bar {u}}} {\partial z}}} \right. \kern-0em} {\partial z}}} \right)}}^{2}}}} \equiv $ ${{{{N}^{2}}} \mathord{\left/ {\vphantom {{{{N}^{2}}} {{{{\left| \beta \right|}}^{2}}}}} \right. \kern-0em} {{{{\left| \beta \right|}}^{2}}}}$ равно бесконечности. Однако, такое пороговое значение $\left| \beta \right|$ существует для стационарного течения и при условии, что ${{\partial{ \bar {u}}} \mathord{\left/ {\vphantom {{\partial{ \bar {u}}} {\partial z}}} \right. \kern-0em} {\partial z}} = \left| \beta \right| > 0$, оно определяется из уравнения ${{\left| \beta \right|}^{2}} + \delta f\left| \beta \right| = {{N}^{2}}$. Таким образом, отказ от традиционного приближения ведет к дестабилизации течения, понижая порог неустойчивости по сравнению с пороговым значением ${{\left| \beta \right|}^{2}} = {{N}^{2}}$ при $\delta = 0$, т.е. повышая критическое значение числа Ричардсона по сравнению с ${\text{Ri}} = 1$. Выводы, касающиеся влияния отказа от традиционного приближения на устойчивость стационарного потока с вертикальным сдвигом скорости, остаются справедливыми и при учете малой диссипации. В случае модулированного во времени основного потока малая диссипация определяет ненулевой порог неустойчивости. Соответствующее условие при числе Прандтля, равном единице, принимает форму критерия Рейнольдса, в котором критическое число Рейнольдса зависит от параметра $\delta $, ср. (17).

Определенным ограничением теории является то, что фактически не весь основной поток, а лишь его часть может испытывать периодические осцилляции. Учет этого обстоятельства ведет к усложнению теории, но не принципиальному. В этом случае необходимо в формулах (7) произвести замену $ - \alpha {\kern 1pt} \cos {\kern 1pt} \omega {\kern 1pt} t = - {{\alpha }_{0}} - {{\alpha }_{1}}{\kern 1pt} \cos {\kern 1pt} \omega t$, $ - \beta {\kern 1pt} \cos {\kern 1pt} \omega t$ = = $ - {{\beta }_{0}} - {{\beta }_{1}}{\kern 1pt} \cos {\kern 1pt} \omega t$ и $\varepsilon = {{\varepsilon }_{0}} + {{\varepsilon }_{1}}$, $\tilde {\varepsilon } = {{\tilde {\varepsilon }}_{0}} + {{\tilde {\varepsilon }}_{1}}$, где ε0 = = ${{{{\alpha }_{0}}} \mathord{\left/ {\vphantom {{{{\alpha }_{0}}} f}} \right. \kern-0em} f}$, ${{\varepsilon }_{1}} = {{{{\alpha }_{1}}} \mathord{\left/ {\vphantom {{{{\alpha }_{1}}} f}} \right. \kern-0em} f}$, ${{\tilde {\varepsilon }}_{0}} = {{{{\beta }_{0}}} \mathord{\left/ {\vphantom {{{{\beta }_{0}}} f}} \right. \kern-0em} f}$, ${{\tilde {\varepsilon }}_{1}} = {{{{\beta }_{1}}} \mathord{\left/ {\vphantom {{{{\beta }_{1}}} f}} \right. \kern-0em} f}$, а также переопределить

$\begin{gathered} {{\Delta }^{2}} = \frac{{A{{{\left( {p\delta + q} \right)}}^{2}}{\kern 1pt} + B{{p}^{2}}{\kern 1pt} + A\left( {{{\varepsilon }_{0}}{{q}^{2}} - 2{{{\tilde {\varepsilon }}}_{0}}pq - {{{\tilde {\varepsilon }}}_{0}}{\kern 1pt} {\kern 1pt} \delta {{p}^{2}}} \right)}}{{{{p}^{2}} + {{q}^{2}}}}, \\ {\rm E} = A\frac{{{{\varepsilon }_{1}}{{q}^{2}} - 2{{{\tilde {\varepsilon }}}_{1}}pq - {{{\tilde {\varepsilon }}}_{1}}{\kern 1pt} {\kern 1pt} \delta {{p}^{2}}}}{{{{p}^{2}} + {{q}^{2}}}}, \\ \end{gathered} $

ср. (9б), но на детальном анализе этого случая и возникающих здесь вариантов мы останавливаться не будем.

Скажем несколько слов относительно ситуации, когда $B \gg A$, именно ${A \mathord{\left/ {\vphantom {A B}} \right. \kern-0em} B}$ = ${{{{f}^{2}}} \mathord{\left/ {\vphantom {{{{f}^{2}}} {{{N}^{2}}}}} \right. \kern-0em} {{{N}^{2}}}}\sim {{10}^{{ - 4}}}$, и при этом $\delta \sim 1$. Теперь $A{{\left( {p\delta + q} \right)}^{2}}$ + $B{{p}^{2}} \approx B{{p}^{2}}$ в (9б), если только ${{{{p}^{2}}} \mathord{\left/ {\vphantom {{{{p}^{2}}} {{{q}^{2}}}}} \right. \kern-0em} {{{q}^{2}}}} \gg {A \mathord{\left/ {\vphantom {A B}} \right. \kern-0em} B}$, например p/q ~ 10–1, и комбинируя условие (14) и ${{\Delta }^{2}} = \frac{1}{4}$ (в заданном приближении), получаем критерий неустойчивости потока с горизонтальным сдвигом скорости в виде $\left| \alpha \right| > 4\nu \left( {{N \mathord{\left/ {\vphantom {N f}} \right. \kern-0em} f}} \right)pq$, что для рассматриваемых атмосферных условий задает высокий порог неустойчивости, превышающий тот, что для инерционной неустойчивости стационарного потока, см. (5). Схожие сложности будут и в случае потока с вертикальным сдвигом скорости, когда при $\delta \sim 1$ и указанных выше условиях критерий неустойчивости приобретает вид $\left| \beta \right| > 2\nu \left( {{N \mathord{\left/ {\vphantom {N f}} \right. \kern-0em} f}} \right){{q}^{2}}$ и для значений параметров из второго примера в этом разделе (см. выше) дает критическое значение вертикального сдвига скорости ${{\left| \beta \right|}_{{crit}}} \approx 2 \times {{10}^{{ - 2}}}\,\,{{{\text{c}}}^{{ - 1}}}$, которое не всегда может быть превзойдено. Дополнительное ограничение связано с тем, что для выполнения условия параметрического резонанса ${{\Delta }^{2}} = \frac{1}{4}$ требуется высокая частота $\omega \approx 2 \times {{10}^{{ - 3}}}\,\,{{{\text{с}}}^{{ - 1}}}$ внешней силы.

В заключение данного раздела укажем, что в рассматриваемой задаче имеется интересное приложение к относительно небольшим по размерам циклонам, которые наблюдаются в высоких широтах [37, 38]. На достаточно большом расстоянии $\mathcal{R}$ от центра циклона можно в первом приближении пренебречь кривизной линий тока и рассматривать движение в локальной правосторонней декартовой системе координат (ср. [14, 39]), где ось $х$ направлена по азимуту, ось $y$ к центру вихря и ось $z$ вверх. Движение воздуха по кругу радиуса $\mathcal{R}$ будут приводить к изменению угла $\varphi $ (см. рис. 1) с угловой частотой $\omega = {U \mathord{\left/ {\vphantom {U \mathcal{R}}} \right. \kern-0em} \mathcal{R}}$, где $U$ – средняя азимутальная скорость в вихре на радиусе $\mathcal{R}$. Ниже рассматривается простейшая постановка задачи, когда имеется только радиальный линейный сдвиг скорости, а вертикальный сдвиг скорости и эффект плавучести полагаются равными нулю, равно как и диссипативные факторы. Теперь основная безразмерная система уравнений для возмущений в обозначениях данного раздела приобретает вид

(20)
$\begin{gathered} \frac{\partial }{{\partial t}}{{\nabla }^{2}}\psi - {{\delta }_{0}}{\kern 1pt} \cos {\kern 1pt} t\frac{{\partial u}}{{\partial y}} - \frac{{\partial u}}{{\partial z}} = 0, \\ \frac{{\partial u}}{{\partial t}} + {{\delta }_{0}}A{\kern 1pt} \cos {\kern 1pt} t\frac{{\partial \psi }}{{\partial y}} + \left( {1 + \varepsilon } \right)A\frac{{\partial \psi }}{{\partial z}} = 0, \\ \end{gathered} $
где ${{\delta }_{0}} = {{\tilde {f}} \mathord{\left/ {\vphantom {{\tilde {f}} f}} \right. \kern-0em} f}$ и $A = {{{{f}^{2}}} \mathord{\left/ {\vphantom {{{{f}^{2}}} {{{\omega }^{2}}}}} \right. \kern-0em} {{{\omega }^{2}}}}$ = ${{{{f}^{2}}{{\mathcal{R}}^{2}}} \mathord{\left/ {\vphantom {{{{f}^{2}}{{\mathcal{R}}^{2}}} {{{U}^{2}}}}} \right. \kern-0em} {{{U}^{2}}}}$. Заметим, что переход к геострофическому моменту в (20) не имеет смысла. Энергия основного потока считается настолько большой, что он не меняется в результате роста возмущений. Ищем решение (20) в виде (см. также выше)

$\left\| {\begin{array}{*{20}{c}} \psi \\ u \end{array}} \right\| = \sum\limits_{n = - \infty }^\infty {\left\| {\begin{array}{*{20}{c}} {{{a}_{{n + {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}} \\ {{{b}_{{n + {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}} \end{array}} \right\|} \exp \left\{ {{\text{i}}\left[ {\left( {n + \frac{1}{2}} \right)t + py + qz} \right] + \mu t} \right\},$

и подставляя в (20) приходим к системе уравнений

$\begin{gathered} \left[ {\mu + {\text{i}}\left( {n + \frac{1}{2}} \right)} \right]\left( {{{p}^{2}} + {{q}^{2}}} \right){{a}_{{n + {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}} + {\text{i}}q{{b}_{{n + {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}} + \\ + \,\,\frac{1}{2}{\text{i}}{\kern 1pt} p{{\delta }_{0}}\left( {{{b}_{{n - {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}} + {{b}_{{n + {3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}}} \right) = 0, \\ \end{gathered} $
$\begin{gathered} \left[ {\mu + {\text{i}}\left( {n + \frac{1}{2}} \right)} \right]{{b}_{{n + {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}} + {\text{i}}Aq\left( {1 + \varepsilon } \right){{a}_{{n + {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}} + \\ + \,\,\frac{1}{2}{\text{i}}pA{{\delta }_{0}}\left( {{{a}_{{n - {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}} + {{a}_{{n + {3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}}} \right) = 0. \\ \end{gathered} $

В первом приближении ограничиваясь ненулевыми амплитудами ${{a}_{{ \pm {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}$ и ${{b}_{{{{ \pm 1} \mathord{\left/ {\vphantom {{ \pm 1} 2}} \right. \kern-0em} 2}}}}$, имеем систему четырех уравнений с четырьмя неизвестными

$\begin{gathered} \left( {\mu \pm \frac{1}{2}{\text{i}}} \right)\left( {{{p}^{2}} + {{q}^{2}}} \right){{a}_{{{{ \pm 1} \mathord{\left/ {\vphantom {{ \pm 1} 2}} \right. \kern-0em} 2}}}} + {\text{i}}q{{b}_{{{{ \pm 1} \mathord{\left/ {\vphantom {{ \pm 1} 2}} \right. \kern-0em} 2}}}} + \frac{1}{2}{\text{i}}p{{\delta }_{0}}{{b}_{{ \mp {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}} = 0, \\ \left( {\mu \pm \frac{1}{2}{\text{i}}} \right){{b}_{{{{ \pm 1} \mathord{\left/ {\vphantom {{ \pm 1} 2}} \right. \kern-0em} 2}}}} + {\text{i}}qA\left( {1 + \varepsilon } \right){{a}_{{{{ \pm 1} \mathord{\left/ {\vphantom {{ \pm 1} 2}} \right. \kern-0em} 2}}}} + \frac{1}{2}{\text{i}}pA{{\delta }_{0}}{{a}_{{ \mp {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}} = 0. \\ \end{gathered} $

Требование равенства нулю определителя этой системы приводит к биквадратному уравнению, которое записываем в символическом виде ${{\mu }^{4}} + {{p}_{2}}{{\mu }^{2}} + {{p}_{4}} = 0$, где ${{p}_{2}} > 0$. Поэтому неустойчивость реализуется, когда ${{p}_{4}} < 0$, где

$\begin{gathered} {{p}_{4}} = \frac{1}{{16}}\left[ {4A{{q}^{2}} - {{p}^{2}} - {{q}^{2}}{\kern 1pt} - {{p}^{2}}\delta _{0}^{2}A + 4Aq\varepsilon \left( {q + \frac{1}{2}p{{\delta }_{0}}} \right)} \right] \times \\ \times \,\,\left[ {4A{{q}^{2}} - {{p}^{2}} - {{q}^{2}} - {{p}^{2}}\delta _{0}^{2}A + 4Aq\varepsilon \left( {q - \frac{1}{2}p{{\delta }_{0}}} \right)} \right]. \\ \end{gathered} $

Рассмотрим случай, когда $q = \frac{1}{2}p{{\delta }_{0}}$. Здесь неустойчивость реализуется при

$\varepsilon > {{\varepsilon }_{{{\text{crit}}}}} = \frac{{{{p}^{2}} + {{q}^{2}}}}{{8A{{q}^{2}}}} = \frac{1}{2}{\text{Ro}}_{ * }^{2}\frac{{1 + \frac{1}{4}\delta _{0}^{2}}}{{\delta _{0}^{2}}},$
где ${\text{R}}{{{\text{o}}}_{ * }} = {U \mathord{\left/ {\vphantom {U {\left( {f\mathcal{R}} \right)}}} \right. \kern-0em} {\left( {f\mathcal{R}} \right)}}$ − число Россби в вихре. На широте $\Phi = 65^\circ $ при $\mathcal{R} = 3 \times {{10}^{5}}\,\,{\text{м}}$ и $U = 15\,\,{\kern 1pt} {\text{м}}\,\,{{{\text{с}}}^{{ - 1}}}$ (ср. [36, 37]), когда ${\text{R}}{{{\text{o}}}_{ * }} \approx 0.38$ и условие нашего анализа, $f{\kern 1pt} U \gg {{{{U}^{2}}} \mathord{\left/ {\vphantom {{{{U}^{2}}} \mathcal{R}}} \right. \kern-0em} \mathcal{R}}$, хотя и приближенно, но выполняется, имеем ${{\delta }_{0}} = {\text{ctg}}{\kern 1pt} \Phi \approx 0.466$. Следовательно, ${{\varepsilon }_{{{\text{crit}}}}} \approx 0.35$, в то время как стационарный вихрь с таким циклоническим сдвигом скорости инерционно устойчив. Проведенный анализ идеалистичен в том отношении, что время оборота вихря вокруг своей оси $T = {{2{{\pi }}\mathcal{R}} \mathord{\left/ {\vphantom {{2{{\pi }}\mathcal{R}} U}} \right. \kern-0em} U}$ = $4{{\pi }} \times {\text{1}}{{{\text{0}}}^{4}}\,\,{\text{с}} \approx 1.5\,\,{\text{сут}}$ лишь в два раза меньше типичной продолжительности жизни циклонов в 3 суток и в большей мере оправдан для долгоживущих вихрей, которые составляют относительно небольшую долю всех циклонов [37].

4. ЗАКЛЮЧИТЕЛЬНЫЕ ЗАМЕЧАНИЯ

В данной работе рассмотрен круг задач, касающихся симметричной (инерционной) неустойчивости модельных атмосферных и океанических течений. Эта неустойчивость носит параметрический характер, т.е. обусловлена модулирующей основной поток периодической во времени внешней силой, которая вступает в резонанс с инерционно-гравитационными волнами (ИГВ), генерируемыми основным потоком в результате потери его устойчивости. Это накладывает важные ограничения на период внешней силы и на географическую локализацию теряющего устойчивость потока. В статье сделана попытка учесть многообразие факторов, влияющих на исследуемую параметрическую симметричную неустойчивость. Это включает точный учет силы Кориолиса (отказ от “традиционного” приближения) и учет отклонения основного потока от зонального направления. Хотя развитый в работе подход позволяет в принципе учесть одновременно горизонтальный и вертикальный сдвиги скорости основного потока, их учет в приведенных в статье модельных примерах для простоты и наглядности производился по-отдельности. Аналогичным образом, учет турбулентной вязкости и температуропроводности среды производился приближенным способом и притом в предположении равенства единице турбулентного числа Прандтля, что является хорошим приближением для геофизических сред. Однако в Приложении показано, что наглядный приближенный анализ неустойчивости в основном тексте статьи совпадает с тем, что дает более строгий анализ. Там же рассмотрены два предельных случая малых и больших чисел Прандтля, допускающие приближенный анализ.

Несмотря на ряд сделанных приближений, проведенный в статье анализ свидетельствует, на наш взгляд, о том, что параметрическая симметричная (инерционная) неустойчивость возможна в реальной атмосфере и океане в достаточно широком диапазоне изменений параметров этих геофизических сред. При этом важно, что эта неустойчивость реализуется тогда, когда соответствующие стационарные движения гидродинамически устойчивы, и тем самым она вносит вклад в генерацию волн и последующей турбулентности в атмосфере и океане.

Проведенные в данной работе исследования инерционной устойчивости периодических по времени потоков имеют приложения к лабораторным экспериментам с вращающимися кольцевыми сосудами при наличии «долготной» либрации, т.е. периодического по времени изменения угловой скорости вращения боковой стенки вращающегося сосуда с жидкостью [26]. В случае узкого зазора между цилиндрическими боковыми стенками и низкочастотной либрации речь может идти об инерционной устойчивости периодического по времени течения Куэтта с линейным по радиусу профилем скорости (ср. [40]), т.е. о задаче, которая рассмотрена в данной работе для бесконечной области (или же для канала с периодическими граничными условиями).

Работа поддержана грантом Российского научного фонда (проект № 22-27-00039). Автор благодарен М.В. Калашнику, В.Н. Крупчатникову и двум анонимным рецензентам за полезные замечания, способствовавшие улучшению статьи.

Список литературы

  1. Rayleigh L. On the dynamics of revolving fluids // Proc. R. Soc. 1917. V. A 93. P. 148–154.

  2. Solberg H. Le mouvement d’inertie de L’atmosphere stable et son role dans la theorie des cyclones // Memoir presented to the Meteor. Assoc. U.G.G.I., Lisbon, Dupont Press. 1933. P. 66–82.

  3. Emanuel K.A. Inertial instability and mesoscale convective systems. Part I: Linear theory of inertial instability in rotating viscous fluids // J. Atmos. Sci. 1979. V. 36. P. 2425–2449.

  4. Динамическая метеорология. Ч.II. / Под ред. Извекова Б.И., Кочина Н.Е. Л.-М.: Гидрометеоиздат, 1937. 280 с.

  5. Rapp M., Dörnbrack A., Preusse P. Large midlatitude stratospheric temperature variability caused by inertial instability: a potential source of bias for gravity wave climatologies // Geophys. Res. Lett. 2018. V. 45. P. 10682–10690.

  6. Harvey V.L., Knox J.A. Beware of inertial instability masquerading as gravity waves in stratospheric temperature perturbations // Geophys. Res. Lett. 2019. V. 46. P. 1740–1745.

  7. Пальмен Э., Ньютон Ч. Циркуляционные системы атмосферы. Л.: Гидрометеоиздат, 1973. 616 с.

  8. Шакина Н.П. Гидродинамическая неустойчивость в атмосфере. Л.: Гидрометеоиздат, 1990. 309 с.

  9. Houghton D.D., Young J.A. A note on inertial instability // Tellus. 1970. V. 22. № 5. P. 581–583.

  10. Bennetts D.A., Hoskins B.J. Conditional symmetric instability - a possible explanation for frontal rainbands // Quart. J. Roy. Meteor. Soc. 1979. V. 105. P. 945–962.

  11. Molinari J., Vollaro D. Symmetric instability in the outflow layer of a major hurricane // J. Atmos. Sci. 2014. V. 71. P. 3739–3746.

  12. Dunkerton T.J. On the inertial stability of the equatorial middle atmosphere // J. Atmos. Sci. 1981. V. 38. P. 2354–2364.

  13. Thomas L.N., Taylor J.R., Ferrari R., Joyce T.M. Symmetric instability in the Gulf Stream // Deep-Sea Res. II. 2013. V. 91. P. 96–110.

  14. Buckingham C.E., Gula J., Carton X. The role of curvature in modifying frontal instabilities. Part I: Review of theory and presentation of a nondimensional instability criterion // J. Phys. Oceanogr. 2021. V. 51. P. 314.

  15. Eady E.T. Long waves and cyclone waves // Tellus. 1949. V. 1. № 3. P. 33–52.

  16. Stone P.H. On non-geostrophic baroclinic stability // J. Atmos. Sci. 1966. V. 23. № 4. P. 390–400.

  17. Stone P.H. On non-geostrophic baroclinic stability: part II // J. Atmos. Sci. 1970. V. 27. № 5. P. 721–726.

  18. Weber J.E. Symmetric instability of stratified geostrophic flow // Tellus. 1980. V. 32. № 2. P. 176–185.

  19. Trier S.B., Sharman R.D. Mechanisms influencing cirrus banding and aviation turbulence near convectively enhanced upper-level jet stream // Mon. Wea. Rev. 2016. V. 144. P. 3003–3027.

  20. Itano T., Maruyama K. Symmetric stability of zonal flow under full-component Coriolis force-effect of the horizontal component of the planetary vorticity // J. Meteorol. Soc. Japan. 2009. V. 87. № 4. P. 747–753.

  21. Tort M., Ribstein B., Zeitlin V. Symmetric and asymmetric inertial instability of zonal jets on the f-plane with complete Coriolis force // J. Fluid Mech. 2016. V. 788. P. 274–302.

  22. Zeitlin V. Symmetric instability drastically changes upon inclusion of the full Coriolis force // Phys. Fluids. 2018. V. 30. P. 061701.

  23. Wienkers A.F., Thomas L.N., Taylor J.R. The influence of front strength on the development and equilibration of symmetric instability. Part 1. Growth and saturation // J. Fluid Mech. 2021. V. 926. P. A6-1–A6-25.

  24. O’Neill M.E, Kaspi Y. Slantwise convection on fluid planets // Geophys. Res. Lett. 2016. V. 43. P. 10611–10620.

  25. Noir J., Hemmerlin F., Wicht J., Baca S.M., Aurnou J.M. An experimental and numerical study of librationally driven flow in planetary cores and subsurface oceans // Phys. Earth Planet. Int. 2009. V. 173. P. 141–152.

  26. Ghasemi A.V., Klein M., Harlander U., Kurgansky M.V., Schaller E., Will A. Mean flow generation by Görtler vortices in a rotating annulus with librating side walls // Phys. Fluids. 2016. V. 28. P. 056603.

  27. Manfroi A., Young W. Slow evolution of zonal jets on the beta plane // J. Atmos. Sci. 1999. V. 56. P. 784–800.

  28. Джеффрис Г., Свирлс Б. Методы математической физики. Вып. 3. М.: Мир, 1970. 344 с.

  29. van Haren H. Slow persistent mixing in the abyss // Ocean Dyn. 2020. V. 70. P. 339–352.

  30. Океанология. Физика океана. Т. 2. Гидродинамика океана / Отв. ред. Каменкович В.М., Монин А.С. М.: Наука, 1978. 455 с.

  31. Chandrasekhar S. Hydrodynamic and Hydromagnetic Stability. Dover Publications, 1981. 654 pp.

  32. Kurgansky M.V. Inertial instability of the Kolmogorov flow in a rotating stratified fluid // Fluid Dyn. Res. 2021. V. 53. P. 035502 (30pp).

  33. Aiyyer A.R., Thorncroft C. Climatology of vertical wind shear over the tropical Atlantic // J. Clim. 2006. V. 19. P. 2969–2983.

  34. Large W.G., Danabasoglu G., McWilliams J.C., Gent P.R., Bryan F.O. Equatorial circulation of a global ocean climate model with anisotropic horizontal viscosity // J. Phys. Oceanogr. 2001. V. 31. P. 518–536.

  35. Pairaud I.L., Lyard F., Auclair F., Letellier T., Marsaleix P. Dynamics of the semi-diurnal and quarter-diurnal internal tides in the Bay of Biscay. Part 1: Barotropic tides // Continental Shelf Research. 2008. V. 28. P. 1294–1315.

  36. Goldsworth F.W., Marshall D.P., Johnson H.L. Symmetric instability in cross-equatorial western boundary currents // J. Phys. Oceanogr. 2021. V. 51. P. 2049–2067.

  37. Интенсивные атмосферные вихри и их динамика / Под ред. Мохова И.И., Курганского М.В., Чхетиани О.Г. М.: ГЕОС, 2018. 482 с.

  38. Akperov M., Rinke A., Mokhov I.I., Matthes H., Semenov V.A., Adakudlu M., Cassano J., Christensen J.H., Dembitskaya M.A., Dethloff K., Fettweis X., Glisan J., Gutjahr O., Heinemann G., Koenigk T., Koldunov N.V., Laprise R., Mottram R., Nikiéma O., Scinocca J.F., Sein D., Sobolowski S., Winger K., Zhang W. Cyclone activity in the Arctic from an ensemble of regional climate models (Arctic CORDEX) // J. Geophys. Res.: Atmospheres. 2018. V. 123. P. 2537–2554.

  39. McIntyre M.E. Diffusive destabilisation of the baroclinic circular vortex // Geophys. Fluid Dyn. 1970. V. 1. P. 19–57.

  40. Kurgansky M.V., Seelig T., Klein M., Will A., Harlander U. Mean flow generation due to longitudinal librations of sidewalls of a rotating annulus // Geophys. Astrophys. Fluid Dyn. 2020. V. 114. № 6. P. 742–762.

  41. Park J., Prat V., Mathis S. Horizontal shear instabilities in rotating stellar radiation zones I. Inflectional and inertial instabilities and the effects of thermal diffusion // A&A (Astronomy & Astrophysics). 2020. V. 635. P. A133.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Физика атмосферы и океана

Архивы выпусков Информация о журнале Отправить рукопись в журнал