1. На главную
  2. Электронные версии
  3. Известия РАН. Физика атмосферы и океана
  4. T. 58, № 5, 2022

Известия РАН. Физика атмосферы и океана, 2022, T. 58, № 5, стр. 591-600

О переносе микропузырьков поверхностными волнами

О. А. Дружинин *

Институт прикладной физики РАН
603950 Нижний Новгород, ул. Ульянова 46, Россия

* E-mail: druzhinin@ipfran.ru

Поступила в редакцию 26.04.2022
После доработки 16.05.2022
Принята к публикации 09.06.2022

Полный текст (PDF)

Аннотация

Проводится прямое численное моделирование (DNS) и исследуется динамика приповерхностного водного слоя, насыщенного воздушными пузырьками, в присутствии стационарной поверхностной волны. Полные, трехмерные уравнения движения водной среды (Навье-Стокса) решаются в Эйлеровой формулировке одновременно с Лагранжевыми уравнениями движения пузырьков с учетом их воздействия на несущую фазу. Диаметры пузырьков в DNS рассматриваются в интервале от 200 до 400 микрон, что позволяет пренебречь их деформацией. Результаты показывают, что наличие вихревых следов за всплывающими пузырьками приводит к усилению турбулентных пульсаций в водной среде. Среди сил, действующих на пузырьки со стороны окружающей водной среды, определяющими являются силы плавучести, вязкого трения и Лагранжевого ускорения, в то время как подъемная сила, определяемая завихренностью несущей фазы и относительной скоростью пузырька, остается пренебрежимо малой. Показано, что горизонтальный перенос пузырьков контролируется скоростью Стоксового дрейфа, в то время как вертикальный перенос определяется скоростью всплывания пузырьков в покоящейся водной среде. На основе результатов DNS предложены параметризации вертикального и горизонтального потоков концентрации воздушной фазы.

Ключевые слова: поверхностные волны, воздушные пузырьки, турбулентность, численное моделирование

1. ВВЕДЕНИЕ

Детальное понимание физических механизмов мелкомасштабных процессов, происходящих вблизи границы раздела между атмосферой и гидросферой, важно для их корректной параметризации в крупномасштабных прогностических моделях [1, 2]. Одним из многих важных факторов, которые необходимо учитывать в моделях обмена, является наличие в приповерхностном водном слое воздушных (газовых) пузырьков.

Основным источником воздушных пузырьков в приповерхностном водном слое являются обрушающиеся (и микро-обрушающиеся) поверхностные волны [3, 4]. Источником газовых пузырьков, активно изучаемым в последнее время, являются донные выбросы метана (см. напр. [5]). Лабораторные и натурные наблюдения [3, 6–8], а также недавние численные эксперименты [9] показывают, что в то время как относительно крупные пузыри (с диаметрами d более миллиметра) быстро всплывают к поверхности и лопаются, мелкие (микро-) пузырьки (с d ~ 100 µm) пребывают в воде достаточно долго и поэтому дают основной вклад в объемную долю воздушной фазы и типичное распределение по диаметрам пузырьковой взвеси. Наблюдения показывают, что объемная доля микропузырьков в верхнем слое океана может быть значительной (до 10–5) даже при относительно слабом ветре (до нескольких м/с), что обусловливает их существенное влияние на процессы газообмена между атмосферой и гидросферой [10, 11], продукцию морского аэрозоля [12], и распространение звука [13, 14]. Таким образом, моделирование дисперсии микропузырьков в приповерхностном слое гидросферы и параметризация потоков их концентрации является весьма актуальной задачей. Одним из подходов к ее решению, используемым также в данной работе, является численное моделирование.

Численное моделирование дисперсии взвеси пузырьков вблизи взволнованной водной поверхности является непростой задачей, которая осложняется сильной геометрической нелинейностью решаемых уравнений. Прямое разрешение динамики границы раздела вода-воздух с использованием, например, метода Volume of Fluid (VoF) становится весьма “дорогим” при достаточно большом (порядка 105–106) числе пузырьков, т.к. требует значительного увеличения размеров расчетной сетки [9]. Альтернативным является подход, основанный на конформном преобразовании, переводящем волнообразную границу раздела в плоскую, и представлении микропузырьков в виде точечных частиц [15].

Целью настоящей работы является исследование динамики водного слоя вблизи взволнованной водной поверхности, насыщенного воздушными пузырьками с использованием прямого численного моделирования (DNS). Движение водной поверхности задается в виде стационарной (необрушающейся) волны Стокса. При этом предполагается, что влиянием индуцированной турбулентности на саму волну можно пренебречь. Это предположение основано на известных результатах DNS волнованной водной поверхности [16], говорящих о том, что относительный вклад турбулентных пульсаций пренебрежимо мал по сравнению с волновыми движениями, их порождающими. Также считается, что при рассматриваемой объемной доле пузырьков (порядка 10–5) их влиянием на поверхностную волну можно пренебречь. При этом, однако, учитывается влияние пузырьков на приповерхностную, индуцированную волной турбулентность, которое оказывается значительным. Используемый подход основан на алгоритме [15], где использован метод расчета динамики воздушного погранслоя над взволнованной водной поверхностью, несущего капли брызг [17], адаптированный для рассматриваемого случая приповерхностного водного слоя, насыщенного микропузырьками. Полные, трехмерные уравнения движения водной среды (Навье-Стокса) решаются в Эйлеровой формулировке одновременно с Лагранжевыми уравнениями движения пузырьков с учетом их воздействия на несущую фазу, которое моделируется с применением аппроксимации “точечных” сил [17]. Диаметры пузырьков в DNS задаются в интервале от 200 до 400 микрон (т.е. рассматриваются микропузырьки), что позволяет пренебречь их деформацией. Не рассматриваются также эффекты, связанные с растворением пузырьков воде.

2. МАТЕМАТИЧЕСКАЯ МОДЕЛЬ

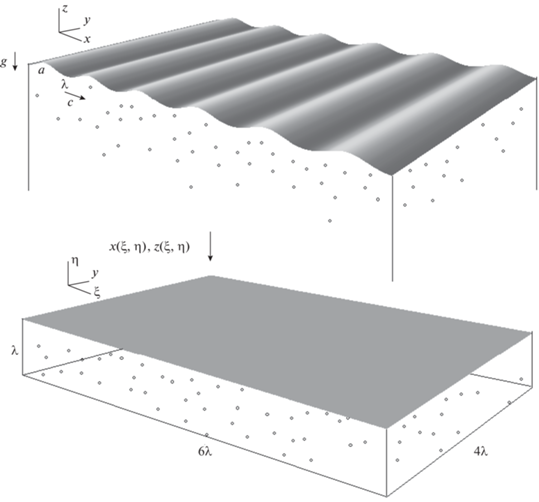
Схема численного эксперимента представлена на рис. 1. Верхняя граница области счета совпадает с водной поверхностью, на которой распространяется двумерная стационарная волна с амплитудой a, длиной λ; крутизна волны $ka = 2\pi a{\text{/}}\lambda $. В каждый рассматриваемый момент времени t в DNS используется конформное преобразование координат декартовой системы в вертикальной плоскости, $x(\xi ,\eta )$ и $z(\xi ,\eta )$, в виде:

(1)
$\begin{gathered} \xi = x + a\exp (kz)\sin k(x - ct), \hfill \\ \tilde {\eta } = z + a\exp (kz)\cos k(x - ct). \hfill \\ \end{gathered} $
Рис. 1.

Схема численного эксперимента (см. текст).

Используется дополнительно преобразование вертикальной координаты:

(2)
$\eta {\text{/}}\lambda = \tanh (\tilde {\eta }{\text{/}}\lambda ).$

Преобразования (1) и (2) переводят бесконечно глубокую область с волнообразной верхней границей в область, ограниченную верхней и нижней плоскими границами при $\eta = 0$ и $\eta = - \lambda $. Форма водной поверхности ${{z}_{s}}(x,t)$ задается неявно преобразованием (1) и с точностью до членов второго порядка малости по ka совпадает с решением для волны Стокса в виде [18]:

(3)
${{z}_{s}}(x,t) \approx - a\cos {\kern 1pt} k(x - ct) + \frac{{{{a}^{2}}k}}{2}\cos {\kern 1pt} 2k(x - ct).$

Все поля являются периодическими по горизонтальным координатам. На водной поверхности (при $\eta = 0$) ставятся условия для скорости воды согласно потенциальному решению для поверхностной волны (3) [18]:

(4)
$\begin{gathered} {{U}_{x}}(\xi ,y,0,t) = - akc{\kern 1pt} \cos {\kern 1pt} k(\xi - ct), \hfill \\ {{U}_{z}}(\xi ,y,0,t) = - akc{\kern 1pt} \sin {\kern 1pt} k(\xi - ct). \hfill \\ \end{gathered} $

На нижней границе ($\eta = - \lambda $) ставится условие (Неймана) отсутствия нормальных градиентов.

Уравнения Навье-Стокса для воды решаются численно в безразмерных переменных в виде:

(5)
$\begin{gathered} \frac{{\partial {{U}_{i}}}}{{\partial t}} + \frac{{\partial ({{U}_{i}}{{U}_{j}})}}{{\partial {{x}_{j}}}} = - \frac{{\partial P}}{{\partial {{x}_{j}}}} + \frac{1}{{\operatorname{Re} }}\frac{{{{\partial }^{2}}{{U}_{i}}}}{{\partial {{x}_{j}}\partial {{x}_{j}}}} + \sum\limits_{n = 1}^{{{N}_{b}}} {S_{i}^{n}} , \\ \frac{{\partial {{U}_{j}}}}{{\partial {{x}_{j}}}} = 0. \\ \end{gathered} $

В уравнениях (5) по повторяющимся индексам проводится суммирование, $U_{i}^{{}}$ и ${{P}_{{}}}$ – скорость и давление (i = x, y, z), $S_{i}^{n}$ – мгновенная сила, с которой n-ый пузырек воздействует на окружающую водную среду (определяемая ниже). Все переменные нормированы на масштабы скорости и длины, равные фазовой скорости и длине поверхностной волны, $с$ и $\lambda $. Число Рейнольдса определяется как

(6)
$\operatorname{Re} = \frac{{с\lambda }}{\nu },$
где $\nu $ – кинематическая вязкость воды (≈0.01 см2/с).

Динамика пузырьков описывается уравнениями для координат и скоростей в виде [19]:

(7)
$\frac{{dr_{i}^{n}}}{{dt}} = V_{i}^{n},$
(8)
$\begin{gathered} \frac{{dV_{i}^{n}}}{{dt}} = 3\frac{{DU_{i}^{n}}}{{Dt}} + \frac{{f({{{\operatorname{Re} }}_{b}})}}{\tau }\left( {U_{i}^{n} - V_{i}^{n}} \right) + \\ + \,\,\frac{1}{2}{{\varepsilon }_{{ijk}}}\left( {U_{j}^{n} - V_{j}^{n}} \right)\omega _{k}^{n} + 2g{{\delta }_{{iz}}}. \\ \end{gathered} $

В уравнениях (7), (8) $r_{i}^{n},\,V_{i}^{n}(i = x,y,z)$ – координата и скорость n-го пузырька, $U_{i}^{n}$ – локальная скорость воды, $d{\text{/}}dt = \partial {\text{/}}\partial t + V_{j}^{n}{{\partial }_{j}}$ и $D{\text{/}}Dt = \partial {\text{/}}\partial t + U_{j}^{n}{{\partial }_{j}}$ – полные производные по времени (ускорения) вдоль траектории пузырька и Лагранжевой частицы окружающей водной среды, соответственно; g – ускорение силы тяжести, $\omega _{i}^{n} = {{\varepsilon }_{{ijk}}}{{\partial }_{j}}U_{k}^{n}$ – локальная завихренность воды. В правую часть уравнения (8) включены силы, действующие на пузырек: сила, обусловленная Лагранжевым ускорением частицы воды, сила вязкого трения, подъемная сила и сила плавучести. Сила вязкого трения включает фактор

(9)
$f\left( {{{{\operatorname{Re} }}_{b}}} \right) = 1 + 0.197\operatorname{Re} _{b}^{{0.63}} + 2.6 \times {{10}^{{ - 4}}}\operatorname{Re} _{b}^{{1.38}},$
учитывающий конечность числа Рейнольдса пузырька, равного

(10)
${{\operatorname{Re} }_{b}} = \frac{{d\left| {{{U}^{n}} - {{V}^{n}}} \right|}}{\nu }.$

В силу трения входит также безразмерное время релаксации пузырька, $\tau $, (т.е. число Стокса):

(11)
$\tau = \frac{{{{d}^{2}}}}{{36\nu }}\frac{с}{\lambda }.$

Как уравнение движения пузырька (8), так и сила, $S_{i}^{n}$, формулируются исходя из предположения, что масса (воздуха) пузырька пренебрежимо мала по сравнению с массой соответствующей Лагранжевой частицы воды. С использованием аппроксимации “точечной” силы, $S_{i}^{n}$ может быть представлено в виде [17, 20]:

(12)
$S_{i}^{n} = \frac{{\pi {{d}^{3}}}}{6}\left( {\frac{{DU_{i}^{n}}}{{Dt}} + g{{\delta }_{{iz}}}} \right)\frac{{w({{r}^{n}},r)}}{{{{\Omega }_{g}}}},$
где $w({{r}^{n}},r)$ – геометрический весовой фактор, обратно пропорциональный расстоянию между пузырьком с координатой rn = (xn , yn, zn) и рассматриваемым узлом сетки с координатой r = (x, y, z), и Ωg(r) – объем ячейки сетки, внутри которой находится пузырек. Таким образом, для каждого пузырька определяются восемь весовых коэффициентов (для каждого из окружающих узлов рассматриваемой ячейки), нормированных таким образом, что их сумма равна единице. Это означает, что для каждого пузырька сумма сил, распределяемых по окружающим узлам ячейки, равна исходной силе, с которой данный пузырек действует на окружающую воду (более детальное обсуждение см. напр. в [17, 20]).

Уравнения (5) для воды в DNS решаются численно с использованием метода Адамса-Бэшфорта второго порядка точности в области 0 ≤ $\xi $ ≤ 6, ‒2 ≤ y ≤ 2, –1 ≤ $\eta $ ≤ 0 на разнесенной сетке, состоящей из 360 × 240 × 180 узлов. Используется метод расщепления, и уравнение Пуассона для давления решается методом итераций с помощью преобразования Фурье в горизонтальной плоскости и методом Гаусса по вертикальной координате. Одновременно решаются уравнения для координат и скоростей пузырьков (7) и (8). При этом локальная скорость воды в местоположении каждого пузырька определяется с помощью Эрмитовой интерполяции [21, 22].

При инициализации расчетов задается случайное, трехмерное поле скорости воды с малой амплитудой (порядка 0.1%). На верхней границе в каждый момент времени задается двумерное поле скорости, определяемое потенциальным решением для волны Стокса на глубокой воде второго порядка точности [1]. Пузырьки инжектируются случайным образом в толще воды с экспоненциально спадающем с глубиной пространственным распределением вероятности и со скоростью, равной мгновенной скорости окружающей воды. Пузырьки, достигающие поверхности, ре-инжектируются, так что полное число пузырьков поддерживается постоянным на протяжении всего времени счета. Фазово-осредненные поля течения определяются по мере установления стационарного режима (на временах порядка 200 периодов волны) осреднением по времени, поперечной координате и “оконным” усреднением по длине волны. Усреднение по времени проводится по мгновенным полям в последовательные моменты времени, в которые фаза поверхностной волны отличалась на 2π. Средние вертикальные профили получаются дополнительным осреднением по горизонтальной координате.

3. РЕЗУЛЬТАТЫ ЧИСЛЕННОГО МОДЕЛИРОВАНИЯ

DNS проводились для значения длины поверхностной волны λ = 15 cm с крутизной ka = 0.2 (амплитуда a ≈ 0.5 cm). Для задаваемой длины волны фазовая скорость, определяемая линейным дисперсионным соотношением [1], равна c ≈ ≈ 49 cm/s, и число Рейнольдса, определенное в (6), Re ≈ 73019. Диаметры пузырьков варьировались от 200 до 400 микрон, их общее число поддерживалось постоянным (от Nd = 126 × 103 для пузырьков с диаметром d = 400 µm до Nd = 106 для d = 200 µm), таким, что эквивалентная средняя концентрация соответствующего равномерного пространственного распределения пузырьков по области счета равнялась C0 ≈ 5 × 10–5.

Как показывают расчеты, после инициализации по истечении относительно короткого переходного процесса (длительностью порядка 10 периодов волны) устанавливается поле скорости в воде, которое хорошо описывается потенциальным решением (рис. 2). С течением времени, однако, вблизи поверхности возникают вихревые движения, индуцированные поверхностной волной (см. рис. 3), что обусловливает отличие поля скорости от потенциального решения вблизи поверхности. Течение становится статистически стационарным по истечении О(100) периодов волны.

Рис. 2.

Поля горизонтальной (a) и вертикальной (b) компонент фазово-осредненной скорости воды в DNS в отсутствие пузырьков. Штрихом показано потенциальное решение для поля скорости поверхностной волны на глубокой воде.

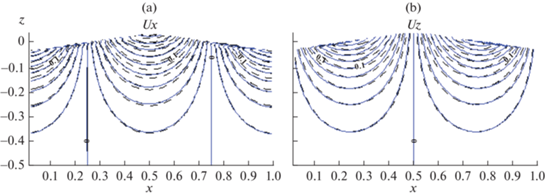
Рис. 3.

Мгновенное поле модуля завихренности ω в центральных (x, z) (a) и (y, z) (c) и в горизонтальной плоскости (x, y) при $\eta $ = –0.05 (b) в отсутствие пузырьков.

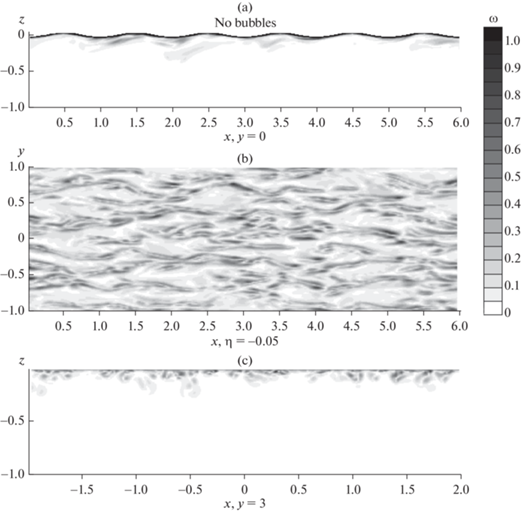
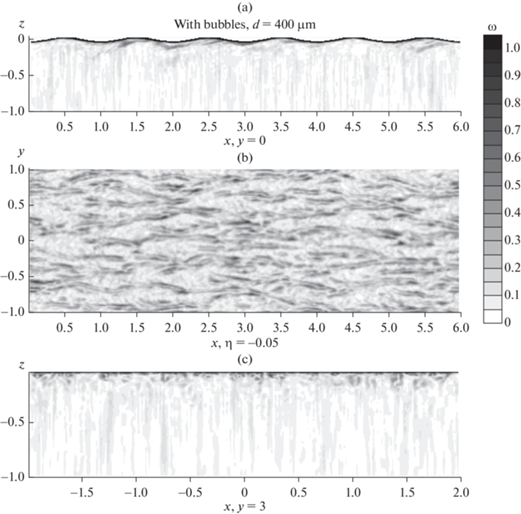
На рис. 3 и 4 представлено мгновенное поле модуля завихренности, полученное в DNS на стадии установившегося течения при значении крутизны ka = 0.2 для однофазного и двухфазного случаев, соответственно. Качественно поле завихренности на рис. 3 согласуется с результатами численного эксперимента [16], где показано, что приповерхностная, индуцированная волной, турбулентность характеризуется наличием вихревых структур, вытянутых вдоль направления распространения волны. Как видно из рис. 4, всплывающие пузырьки порождают возмущения в виде вытянутых по вертикали вихревых структур.

Рис. 4.

Мгновенное поле модуля завихренности ω в центральных плоскостях (x, z) (a) и (y, z) (c) и в горизонтальной плоскости (x, y) при $\eta $ = –0.05 (b) в DNS с пузырьками диаметром d = 400 µm.

Траектории отдельных пузырьков с диаметрами d = 400 µm и d = 200 µm представлены на рис. 5. На рисунках показаны также зависимости от глубины сил (трения, Лагранжевого ускорения и подъемной силы), действующих на пузырёк со стороны окружающей воды. Как видно из рисунков, влияние волнового движения поверхности на динамику пузырьков возрастает с уменьшением глубины и проявляется в том, что их траектории (как и силы, на них действующие) начинают осциллировать при приближении к поверхности. Вблизи поверхности (z > –0.2) траектории имеют вид раскручивающихся спиралей (рис. 5a, 5e). В обоих случаях (d = 400 µm и d = 200 µm) пузырьки дрейфуют в направлении распространения поверхностной волны. Этот дрейф в определённой степени аналогичен классическому Стоксовому дрейфу Лагранжевых частиц воды, и обусловлен экспоненциальным спаданием амплитуды горизонтальной скорости, индуцируемой поверхностной волной, с глубиной [24]. Однако, полной аналогии нет, поскольку пузырьки всплывают и “пересекают” траектории Лагранжевых частиц. В результате, более крупные пузырьки (d = 400 µm) менее подвержены горизонтальному дрейфу по сравнению с мелкими, поскольку их средняя вертикальная скорость (пропорциональная квадрату диаметра, см. выражение (10) и ниже уравнение (14) и рис. 6) почти в 4 раза превышает вертикальную скорость пузырьков с d = 200 µm. Такое поведение всплывающих пузырьков можно сравнить с явлением “пересекающихся” траекторий (или “crossing trajectories effect”), наблюдаемое при движении инерционных частиц в поле изотропной турбулентности [25], когда инерция и оседание частиц приводят к уменьшению их диффузии турбулентными пульсациями.

Рис. 5.

Траектории пузырьков с диаметрами d = 400 µm (a) и d = 200 µm (e) и зависимости от глубины x и z компонент сил (синим и красным цветом), действующих на пузырёк со стороны окружающй воды [трения Fd (b, f); Лагранжевого ускорения Fa (c, g); и подъемной силы FL (d, h)].

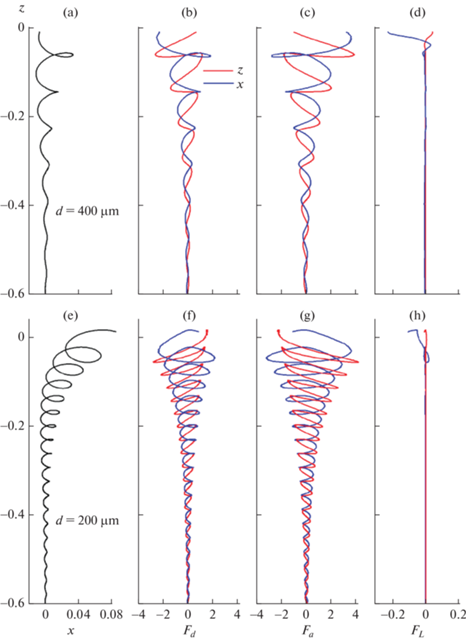
Рис. 6.

Вертикальные профили: концентрации пузырьков [C] (a), горизонтальной и вертикальной компонент её потоков, [CVx] (b) и [CVz] (c), нормированных на [C], и среднеквадратичных флуктуаций скорости воды $[U_{{x,y,z}}^{'}]$ (d, e, f). Цвета (синий, красный и сиреневый) соответствуют диаметрам пузырьков 200, 300 и 400 µm. Параметризации потоков концентрации (16), (17) (панели b, c) показаны штриховыми линями. На панелях (d–f) профили флуктуаций скорости воды в однофазном случае обозначены сплошной кривой черного цвета.

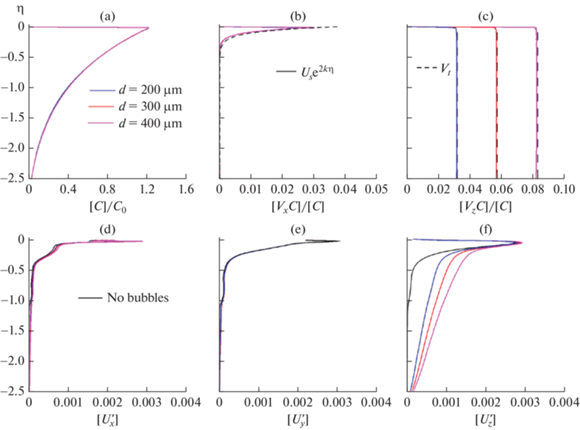
Рисунок 5 указывает на доминирующую роль сил трения и Лагранжевого ускорения воды, Fd и Fa, по сравнению с подъемной силой FL. Рисунок показывает, что силы Fd и Fa осциллируют с амплитудами, монотонно возрастающими при приближении к поверхности. Подъемная сила оказывается пренебрежимо малой по сравнению с Fd и Fa даже вблизи поверхности, в области, где развивается индуцированная волной турбулентность.

Производился расчет средних профилей концентрации пузырьков и горизонтальной и вертикальной компонент её потоков:

(13)
$\left[ C \right] = \frac{{\pi d_{{}}^{3}}}{6}\left[ {\sum\limits_{n = 1}^{{{N}_{d}}} {\frac{{w({{r}^{n}},r)}}{{{{\Omega }_{g}}}}} } \right],$
(14)
$\left[ {CV_{i}^{n}} \right] = \frac{{\pi d_{{}}^{3}}}{6}\left[ {\sum\limits_{n = 1}^{{{N}_{d}}} {\frac{{V_{i}^{n}w({{r}^{n}},r)}}{{{{\Omega }_{g}}}}} } \right],$
а также профилей среднеквадратичных флуктуаций различных компонент скорости воды

(15)
$[U_{i}^{'}] = {{\left( {[U_{i}^{2}] - {{{\left[ {{{U}_{i}}} \right]}}^{2}}} \right)}^{{1/2}}}$

На рис. 6 представлены профили концентрации (a), её потоков (b, c), и флуктуаций скорости воды (d, e, f), полученные согласно выражениям (13)–(15) для различных диаметров пузырьков. Также приводятся профили флуктуаций в однофазном случае (панели d, e, f) и параметризации потоков концентрации (панели b, c) в виде

(16)
$\left[ {C{{V}_{x}}} \right] = {{U}_{s}}[C]\exp ( - 2kz),$
(17)
$\left[ {C{{V}_{z}}} \right] = {{V}_{t}}[C],$
где Us = (ka)2 – безразмерная скорость Стоксового дрейфа на водной поверхности [1], Vt – терминальная (установившаяся) скорость всплывания пузырька в покоящейся воде. Эта скорость определяется решением уравнения
(18)
$0 = - \frac{{f({{{\operatorname{Re} }}_{b}})}}{\tau }{{V}_{t}} + 2g{{\delta }_{{iz}}},$
где ${{\operatorname{Re} }_{b}} = {{V}_{t}}d{\text{/}}\nu $. Уравнение (18) решается численно методом Ньютона [21].

Как видно из рис. 6a, концентрация пузырьков экспоненциально спадает с глубиной, что соответствует натурным наблюдениям [12]. Параметризации (16), (17) хорошо согласуются с профилями потоков концентрации (рис. 6b, 6c). Это согласие говорит о том, что перенос пузырьков в горизонтальном направлении обусловлен Стоксовым дрейфом, в то время как волновые движения практически не влияют на вертикальный перенос, который контролируется силой плавучести.

Сравнение амплитуд пульсаций в воде в однофазном и двухфазном случаях (рис. 6d–6f) показывает, что пузырьки эффективно усиливают вертикальные, индуцированные поверхностной волной, флуктуации скорости водной среды. Это усиление происходит благодаря развитию следов за всплывающими пузырьками (см. рис. 4). Рис. 6f показывает, что усиление пульсаций в водной среде растет с увеличением диаметра пузырьков.

4. ВЫВОДЫ

Проведено прямое численное моделирование (DNS) приповерхностного водного слоя, насыщенного воздушными пузырьками, в присутствии стационарной поверхностной волны. Полные, трехмерные уравнения движения водной среды (Навье-Стокса) решаются в Эйлеровой формулировке одновременно с Лагранжевыми уравнениями движения пузырьков с учетом их воздействия на несущую фазу. Диаметры пузырьков в DNS рассматриваются в интервале от 200 до 400 микрон, что позволяет пренебречь их деформацией.

Результаты показывают, что всплывающие пузырьки эффективно усиливают мелкомасштабные турбулентные пульсации в водной среде благодаря формированию за ними вихревых следов. Показано также, что определяющую роль в динамике пузырька играют силы плавучести, вязкого трения и Лагранжевого ускорения, в то время как подъемная сила, определяемая завихренностью несущей фазы и относительной скоростью пузырька, остается пренебрежимо малой. Показано, что горизонтальный перенос пузырьков контролируется скоростью Стоксового дрейфа, в то время как вертикальный поток определяется скоростью всплывания пузырьков в покоящейся водной среде. На основе полученных данных предложены параметризации вертикального и горизонтального потоков объемной доли воздушной фазы в приповерхностном водном слое.

Следует отметить, что в настоящей работе поверхностная волна считается заданной. Рассмотрение самосогласованной задачи (с учетом модификации поверхностной волны приповерхностной турбулентностью и пузырьками) остается предметом будущих исследований.

Источники финансирования: Разработка численных алгоритмов выполнена при поддержке проекта РФФИ № 20-05-00322. Обработка и теоретический анализ результатов выполнены при поддержке проекта РФФИ № 21-55-52005. Численные расчеты выполнены на кластере ИПФ РАН (проект госзадания № 0030-2022-0005).

Список литературы

  1. Филлипс О.М. Динамика верхнего слоя океана. Л.: Гидрометеоиздат, 1980. 319 с.

  2. Thorpe S.A. Dynamical processes of transfer at the sea surface // Progress in Oceanography. 1995. V. 35. P. 315–352.

  3. Kolovaev P.A. Investigation of the concentration and statistical size distribution of wind-produced bubbles in the near surface ocean layer // Oceanology. 1976. V. 15. P. 659–661.

  4. Johnson B.D., Cooke R.C. Bubble populations and spectra in coastal waters // J. Geophys. Res. 1979. V. 84. P. 3761–3766.

  5. Steinbach J., Holmstrand H., Shcherbakova K., Kosmach D., Brüchert V., Shakhova N., Salyuk A., Sapart C.J., Chernykh D., Noormets R., Semiletov I., Gustafsson Ö. Source apportionment of methane escaping the subsea permafrost system in the outer Eurasian Arctic Shelf // PNAS. 2021. V. 118. № 10. P. e2019672118.

  6. Medwin H. In situ acoustic measurements of microbubbles at sea // J. Geophys. Res. 1977. V. 82. P. 971–976.

  7. Dean G.B., Stokes M. D. Scale dependence of bubble creation mechanisms in breaking waves // Nature. 2002. V. 418. P. 839–844.

  8. Blenkinsopp C.E., Chaplin, J.R. Void fraction measurements in breaking waves // Proc. R. Soc. Lond. A . 2007. V. 463. P. 3151–3170.

  9. Deike L., Melville W.K., Popinet S. // Air entrainment and bubble statistics in breaking waves. J. Fluid Mech. 2016. V. 801. P. 91–129.

  10. Woolf D.K., Thorpe S.A. Bubbles and the air-sea exchange of gases in near-saturation conditions // Journal of Marine Research. 1991. V. 49. P. 435–466.

  11. Merlivat L., Memery L. Gas exchange across an air–water interface: experimental results and modeling of bubble contribution to transfer // J. Geophys. Res. 1983. V. 88. P. 707–724.

  12. Blanchard D.C. The ejection of drops from the sea and their enrichment with bacteria and other materials: a review // Estuaries. 1989. V. 12. P. 127–137.

  13. Farmer D.M., Lemon D.D. The influence of bubbles on ambient noise in the ocean at high wind speeds // J. Phys. Oceanogr. V. 1984. V. 14. P. 1762–1778.

  14. Buckingham M.J. Sound speed and void fraction profiles in the sea surface bubble layer // Appl. Acoust. 1997. V. 51. P. 225–250.

  15. Druzhinin O.A., Tsai W.-t. Numerical simulation of microbubbles dispersion by surface waves // Algorithms. 2022. V. 15. P. 110.

  16. Tsai W.-t., Chen S.-m., Lu G.-h. Numerical evidence of turbulence generated by non-breaking surface waves // J. Phys. Oceanogr. 2015. V. 45. P. 174–180.

  17. Druzhinin O.A., Troitskaya Yu.I., Zilitinkevich S.S. The study of droplet-laden turbulent air-flow over waved water surface by direct numerical simulation // J. Geophys. Res. Oceans. 2017. V. 122. P. 1789–1807.

  18. Gent P.R., Taylor P.A. A numerical model of the air flow above water waves // J. Fluid Mech. 1976. V. 77. P. 105–128.

  19. Mattson M., Mahesh K. Simulation of bubble migration in a turbulent boundary layer // Phys. Fluids. 2011. V. 23, P. 045107.

  20. Druzhinin O.A., Elghobashi S.E. Direct numerical simulation of bubble-laden turbulent flows using the two-fluid formulation // Phys. Fluids. 1998. V. 10. P. 685–697.

  21. Fletcher C.A.J. Computational Techniques for Fluid Dynamics. 2nd ed. Springer, 1991. P. 493.

  22. Белоцерковский О.М. Численное моделирование в механике сплошных сред. М.: Наука, 1984. 520 с.

  23. Tsai W.-t., Chen S.-m., Lu G.-h., Garbe C.S. Numerical evidence of turbulence generated by non-breaking surface waves // J. Geophys. Res.: Oceans. 2013. V. 118. P. 1–21.

  24. Bremer T.S., Breivik O. Stokes drift // Phil. Trans. R. Soc. A. 2017. V. 376. P. 20170104.

  25. Wells M.R., Stock D.E. The effect of crossing trajectories on the dispersion of particles in a turbulent flow // J. Fluid Mech. 1983. V. 136. P. 31–62.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Физика атмосферы и океана

Архивы выпусков Информация о журнале Отправить рукопись в журнал