1. На главную
  2. Электронные версии
  3. Известия РАН. Физика атмосферы и океана
  4. T. 59, № 1, 2023

Известия РАН. Физика атмосферы и океана, 2023, T. 59, № 1, стр. 33-43

К теории индивидуальных атмосферных вихрей: пример эволюции субтропического антициклона

А. В. Кислов a, *, И. В. Железнова a, **, Ю. В. Мухартова a, А. И. Несвятипаска a

a Московский государственный университет имени М.В. Ломоносова
199911 Москва, Ленинские горы, д. 1, Россия

* E-mail: avkislov@mail.ru
** E-mail: ijeleznova@gmail.com

Поступила в редакцию 06.08.2022
После доработки 07.10.2022
Принята к публикации 12.10.2022

Полный текст (PDF)

Аннотация

Физика индивидуальных атмосферных вихрей далеко не ясна, несмотря на то, что они надежно воспроизводятся современными гидродинамическими моделями. В данной работе развивается теория вихрей, стабильно существующих длительное время в некоторой области. Их структура характеризуется первой (доминирующей) естественной ортогональной функцией (ЕОФ, NOF), а динамика определяется коэффициентом при данной моде y1(t), для которого получено обыкновенное дифференциальное уравнение исходя из уравнения бюджета завихренности. Невязка явно разрешаемых факторов компенсируется параметризацией, которая строится на основе учета влияний второй и последующих мод ЕОФ-разложения. Показано, что она состоит из гауссового шума и неслучайной компоненты, которая может быть аппроксимирована с помощью кубической функции от y1(t). Для проверки развиваемой методики было использовано моделирование поведения завихренности, описывающей динамику наиболее стабильного вихря среди всех, существующих в атмосфере Земли – субтропического (Гавайского) антициклона. Для работы использованы данные реанализа ERA5. Предложенный подход к анализу индивидуальных вихрей предполагается использовать для оценки различных циркуляционных систем, выявления факторов, влияющих на их динамику в различных регионах, исследования экстремальных гидрометеорологических событий, связанных с долгоживущими вихрями.

Ключевые слова: уравнение бюджета завихренности, индивидуальный вихрь, Гавайский антициклон, ЕОФ-разложение

ВВЕДЕНИЕ

Важнейшей особенностью динамики атмосферы (и океана) является существование вихрей синоптического масштаба. Они, как целостные образования, видны на любой синоптической карте как в тропических, так и во внетропических широтах. В течение своей жизни (нескольких суток) они проходят различные стадии эволюции. Вихри меньших размеров (мезомасштаба) также непосредственно наблюдаются как индивидуальные циркуляционные особенности, но проследить их динамику сложнее из-за гораздо более короткого времени жизни. Вихри еще меньшего масштаба редко можно зафиксировать, их существование проявляется косвенно по вкладу в колмогоровский спектр.

Несмотря на то, что динамика атмосферы, включая все аспекты циклогенеза, хорошо воспроизводится численными гидродинамическими моделями, представляется привлекательной задача развития физики индивидуальных вихрей, которая известна далеко не полно. При этом одной из принципиальных проблем на этом пути является необходимость знать границы вихря в пространстве и их эволюцию во времени.

Можно пытаться очертить вихрь (например, на основе положения его последней замкнутой изобары [1]), а затем, принимая допущения о динамике этой границы, перейти к расчету его интегральных характеристик. Таким путем, интегрируя уравнения по замкнутому контуру, исследовалась энергетика циклонов еще полвека назад [2]). В некоторых случаях возможны иные упрощающие предложения. Например, для движения в плоскости, когда завихренность сосредоточена в точке, можно описать поле скорости моделью так называемого точечного вихря [3], однако для реальных атмосферных вихрей эта модель неприменима. Другой подход связан с допущением, что завихренность сконцентрирована в пространстве в форме эллипсоида, который может деформироваться (растягиваться-сжиматься и вращаться) [4–8].

Для уравнений гидродинамики в двух измерениях описание вихревой циркуляции было осуществлено на основе метода контурной динамики [9]. Их применение возможно для гораздо более общих случаев; однако уравнения деформации формы сложны, поэтому их можно решить только численно. Это снижает ценность подхода, поскольку и без этого, как отмечалось, современные численные модели могут непосредственно воспроизводить вихревую структуру течений.

Развитие теории индивидуальных вихревых систем полезно, поскольку приведет, в том числе, к пониманию природы длительно существующих так называемых блокирующих образований и сопровождающих их систем низкого давления, и, следовательно, к пониманию механизмов опасных явлений, связанных с засушливостью одних и переувлажненностью других регионов. Цель настоящей работы именно в изучении вихрей, квазистабильно существующих в определенном регионе.

Метод идентификации отдельного вихря основан на использовании для этого завихренности, динамика которой определяется уравнением бюджета завихренности, причем из-за существования вихря в заданной области в течение длительного периода точная диагностика его жидких границ не требуется. Отметим, что данное требование не является чересчур ограничительным, поскольку долгоживущие вихри, как правило, стабильно занимают определенное положение [10, 11].

Главные пространственно-временные особенности выделяются благодаря использованию разложения в ряд Фурье. В качестве базисных функций применены естественные ортогональные функции [12], вычисленные в пределах области, занимаемой квазистабильным вихрем (та же методика, но в масштабе полушария и с другими конечными целями, была реализована в [13]). Этот метод позволяет как диагностировать вихрь, так и вывести уравнения, раскрывающие механизм его эволюции как целостного образования. При этом динамика вихря во времени описывается обыкновенными дифференциальными уравнениями для коэффициентов разложения.

В рамках такого подхода вихрь рассматривается как единая структура, а анализ полученных уравнений малокомпонентной модели может позволить оценить, какие атмосферные процессы наиболее значимы. При этом проблема возникновения вихря не рассматривается, т.е. анализируется уже существующий вихрь.

Данная методика ранее была апробирована для исследования динамики малоподвижных и долгоживущих синоптических объектов умеренных широт – блокирующих антициклонов [14–16] и для анализа внетропических циклонов Дальнего Востока [17].

В настоящей работе эта методика получила дальнейшее развитие. Наиболее важным явился своеобразный параметризационный учет вклада переменных, которые не могут явным образом быть выражены. Основой для этого служит теория MTV [18–20], показывающая, что квадратично нелинейные уравнения могут быть в общем случае заменены стохастическими уравнениями, включающими аддитивный и мультипликативный шум.

Для проверки анализ был применен к исследованию самого устойчивого вихря земной атмосферы – субтропического антициклона. В качестве модельного объекта взят Гавайский антициклон, располагающийся в субтропиках северного полушария над Тихим океаном. Чтобы исключить сезонное смещение его положения, был рассмотрен только летний период.

ИСПОЛЬЗУЕМЫЕ ДАННЫЕ

Для вычислений были использованы данные реанализа Европейского центра среднесрочных прогнозов погоды ERA5 [21] с шагом по сетке 0.25° × 0.25° в регионе 165°–135° з.д. и 35°–45° с.ш. Координаты области были определены в соответствии со средним положением центральной части Гавайского антициклона в исследуемый период, чтобы максимально, насколько это возможно, исключить влияние других циркуляционных систем (рис. 1). Рассматривался июнь-август 1980 года.

Рис. 1.

Среднее поле геопотенциала на уровне 925 гПа для Гавайского антициклона за летний период 1980 года. Красным прямоугольником выделена область, для которой проводились расчеты.

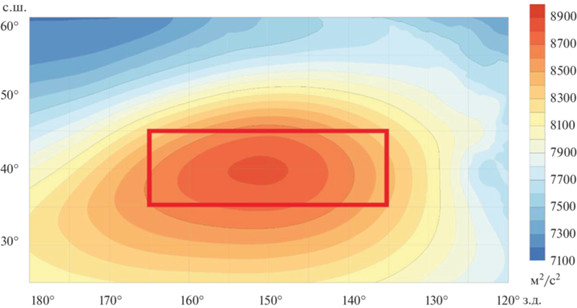
Использовались ежечасные данные о высотах геопотенциальных поверхностей 200 и 925 гПа, а также значения геопотенциала и температуры воздуха на 22 уровнях в слое от 200 до 1000 гПа. Также были использованы значения потока явного тепла и количества осадков на поверхности и значения коротковолнового и длинноволнового радиационного баланса на поверхности и на верхней границе атмосферы.

Расчеты проводились для 1, 2, 3 и 4-суточного осреднения. Суточные значения рассчитывались как арифметическое среднее, полученное из ежечасных данных. Для 2, 3 и 4-суточного осреднения были рассчитаны скользящие средние значения на основе суточных данных.

АНАЛИЗ БЮДЖЕТА ЗАВИХРЕННОСТИ

Динамику антициклона будем характеризовать завихренностью ($\xi $)

$\xi = ro{{t}_{z}}\vec {v}.$

Уравнение эволюции завихренности хорошо известно, однако мы выполним его вывод таким способом, чтобы сразу были исключены заведомо малые составляющие. Рассмотрим слой, ограниченный изобарическими поверхностями с давлением ${{p}_{1}}$ и ${{p}_{2}}$, расположенными на геопотенциальных высотах ${{H}_{1}}$ и ${{H}_{2}}$, с относительной геопотенциальной высотой $h = {{H}_{1}} - ~{{H}_{2}}$, причем ${{H}_{2}}$ находится вблизи поверхности Земли, а ${{H}_{1}}$ - в верхней тропосфере. Применим к разности геопотенциальных высот горизонтальный оператор Лапласа и умножим на $\frac{g}{f}$, где $g$ – ускорение свободного падения, а $f = 2\omega {\kern 1pt} {\text{sin}}{\kern 1pt} \varphi $ – параметр Кориолиса.

$\frac{g}{f}{{\nabla }^{2}}h = ~\frac{g}{f}{{\nabla }^{2}}{{H}_{1}} - ~\frac{g}{f}{{\nabla }^{2}}{{H}_{2}}.$
Затем, в соответствии с уравнением статики заменяем $h = \frac{{R\left\langle T \right\rangle }}{g}{\kern 1pt} \ln {\kern 1pt} \frac{{{{P}_{2}}}}{{{{P}_{1}}}}~$ (с осредненной по слою температурой $\left\langle T \right\rangle $, а R – газовая постоянная для воздуха), переходим к геострофической завихренности и, дифференцируя полученное выражение по времени, получаем выражение

(1)
$\frac{{\partial {{\xi }_{2}}}}{{\partial t}} = \frac{{\partial {{\xi }_{1}}}}{{\partial t}} - \frac{R}{f}\ln \left( {\frac{{{{p}_{2}}}}{{{{p}_{1}}}}} \right){{\nabla }^{2}}\frac{{\partial \left\langle T \right\rangle }}{{\partial t}}.$

Выразим $\frac{{\partial \left\langle T \right\rangle }}{{\partial t}}$ из уравнения бюджета внутренней энергии:

${{с}_{v}}\rho \frac{{dT}}{{dt}} + R\rho \frac{{dT}}{{dt}} - \frac{{dp}}{{dt}} = LQ - \frac{{\partial {{F}_{{R,z}}}}}{{\partial z}}.$

Заменяя, ввиду крупномасштабности рассматриваемых процессов, $\frac{{dp}}{{dt}} \approx - w\rho g$ получим:

(2)
$\frac{{\partial T}}{{\partial t}} + ~\vec {v}{{\nabla }_{h}}T + w\left( {\frac{g}{{{{c}_{p}}}} + \frac{{\partial T}}{{\partial z}}} \right) = \frac{1}{{{{c}_{p}}\rho }}LQ - \frac{1}{{{{c}_{p}}\rho }}\frac{{\partial {{F}_{{R,z}}}}}{{\partial z}}.$

Вертикальные движения (на верхней границе пограничного слоя) можно представить, используя завихренность:

$w = \xi \sqrt {\frac{{{{K}_{m}}}}{{2f}}} ,$
где ${{K}_{m}}$ – коэффициент турбулентности.

Произведем замену $\gamma = - \frac{{\partial T}}{{\partial z}}$ и ${{\gamma }_{a}} = \frac{g}{{{{c}_{p}}}}$ (сухоадиабатический градиент), выполним осреднение уравнения (2) по вертикали в пределах рассматриваемого слоя ($h$):

$\begin{gathered} \frac{{\partial \left\langle T \right\rangle }}{{\partial t}} = - \left\langle {\vec {v}{{\nabla }_{h}}T} \right\rangle - \left\langle w \right\rangle \left\langle {\left( {{{\gamma }_{a}} - \gamma } \right)} \right\rangle - \\ - \,\,\left\langle {w{\kern 1pt} *\left( {{{\gamma }_{a}} - \gamma } \right){\kern 1pt} *} \right\rangle + \frac{L}{{{{c}_{p}}\left\langle \rho \right\rangle h}}\mathop \smallint \limits_0^h Qdz - \frac{{{{F}_{{R,h}}} - {{F}_{{R,s}}}}}{{{{c}_{p}}\left\langle \rho \right\rangle h}}. \\ \end{gathered} $

Отметим, что здесь вертикальная адвекция делится на две части: одно слагаемое обозначает вертикальные движения синоптического масштаба, другое (со звездочками (*)), есть произведение отклонений от среднего по профилю значения. Это, по сути, может быть интерпретировано как вклад мелкомасштабной турбулентности в изменение температуры, и в этом случае оно описывается потоком явного тепла через нижнюю границу ($~{{P}_{s}}$).

Слагаемое, учитывающее роль скрытого тепла, выделяющегося при конденсации может быть легко определено по данным об осадках ($P$), поскольку $\left( {\int_0^h {Qdz \equiv P} } \right)$.

Подставим получившееся выражение в уравнение (1). В итоге получаем:

(3)
$\begin{gathered} \frac{{\partial {{\xi }_{2}}}}{{\partial t}} = \frac{{\partial {{\xi }_{1}}}}{{\partial t}} - \frac{R}{f}{\kern 1pt} {\text{ln}}\left( {\frac{{{{p}_{2}}}}{{{{p}_{1}}}}} \right){{\nabla }^{2}}\left\{ { - \left\langle {\vec {v}{{\nabla }_{h}}T} \right\rangle - \left\langle w \right\rangle \left\langle {\left( {{{\gamma }_{a}} - \gamma } \right)} \right\rangle + \frac{{{{P}_{s}}}}{{{{c}_{p}}\left\langle \rho \right\rangle h}} + \frac{{LP}}{{{{C}_{p}}\left\langle \rho \right\rangle h}} + {{E}_{R}}} \right\}. \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,1\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,2\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,3\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,4\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,5\,\,\,\,\,\,\,\,\,\,\,\,6 \hfill \\ \end{gathered} $

В левой части уравнения (3) находится изменение завихренности в нижней тропосфере (в нашем случае был выбран уровень 925 гПа). Первое слагаемое правой части представляет собой изменение завихренности в верхней тропосфере. Второе и третье слагаемые (под оператором Лапласа) связаны с адвекцией температуры. Четвертое слагаемое характеризует роль пятнистости теплообмена атмосферы с земной поверхностью в формировании завихренности (например, над теплым «пятном», с большим притоком тепла в атмосферу, оператор Лапласа отрицателен и, поскольку перед ним в выражении (3) стоит знак минус, то воздействие этого фактора создает положительную завихренность). Обозначим, для краткости, ${{E}_{T}} = \frac{{{{P}_{s}}}}{{{{c}_{p}}\left\langle \rho \right\rangle h}}$. Пятое слагаемое выражает роль скрытого тепла. Обозначим, для использования в дальнейшем, ${{E}_{{\text{Ф}}}} = \frac{{LP}}{{{{C}_{p}}\left\langle \rho \right\rangle h}}$. Отметим, что осадки в антициклонах малы и при исследовании блокирующего антициклона над Европейской территорией России в 2010 году [14] это слагаемое было проигнорировано. Однако при выполнении данной работы наш анализ показал, что в западной части рассматриваемого в данной статье региона (рис. 1) осадки нередки, поэтому в настоящем исследовании мы принимаем во внимание вклад этого слагаемого. Наконец, последний член $\left( {{{E}_{R}} = \frac{{{{F}_{{R,s}}} - {{F}_{{R,h}}}}}{{{{c}_{p}}\left\langle \rho \right\rangle h}}} \right)$ отражает изменение температуры слоя за счет радиационного теплообмена. Это слагаемое представим в виде разницы радиационных балансов на поверхности Земли (${{B}_{{surf}}}$) и на верхней границе атмосферы (${{B}_{{TOP}}}$), то есть ${{E}_{R}} = ~{{B}_{{surf}}} - {{B}_{{TOP}}}$. Отметим, что данное выражение не в полной мере отражает радиационный баланс рассматриваемого слоя воздуха, однако можно думать, что относительная изменчивость, нужная для правильного определения оператора Лапласа, будет воспроизведена верно. И вообще, при решении такого рода задач следует исходить из компромисса между нужными данными и теми, которые непосредственно доступны в реанализе и близки по сути.

Таким образом, мы получили дифференциальное уравнение, в левой части которого находится изменение завихренности, а в правой части уравнения представлены факторы, вызывающие ее изменения,

(4)
$\begin{gathered} \frac{{\partial {{\xi }_{2}}}}{{\partial t}} = \frac{{\partial {{\xi }_{1}}}}{{\partial t}} - \frac{R}{f}{\text{ln}}\left( {\frac{{{{p}_{2}}}}{{{{p}_{1}}}}} \right){{\nabla }^{2}} \times \\ \times \,\,\left\{ {{{A}_{T}} - \left\langle w \right\rangle \left\langle {\left( {{{\gamma }_{a}} - \gamma } \right)} \right\rangle + {{E}_{T}} + {{E}_{{\text{Ф}}}} + {{E}_{R}}} \right\}, \\ \end{gathered} $
которые можно, до некоторой степени условно, разделить на внешние и внутренние. К внешним относятся вариации завихренности в верхней тропосфере, которые действуют посредством формирования полей дивергенции потоков воздуха и адвекции завихренности. Остальные факторы (адвекция тепла по горизонтали и вертикали, притоки явного, скрытого и радиационного тепла), влияние которых выражено посредством их пространственной конфигурации, определяемой оператором Лапласа, носят совместный внутренне-внешний характер. Так, например, адвекция тепла (${{A}_{T}}$) определяется не только полем градиента температуры, в том числе вне области, охваченной вихрем, но и полем ветра, генерируемым самим вихрем.

В таком же ключе, выражения, аналогичные в главных чертах уравнению (4), были использованы для синоптического анализа во внетропических широтах [22] и в тропиках [23].

ЕОФ-АНАЛИЗ ПОЛЯ ЗАВИХРЕННОСТИ

Для исследования пространственно-временной структуры поля завихренности используется метод разложения на естественные ортогональные функции (ЕОФ):

$\xi \left( {\lambda ,\varphi ,t} \right) = \mathop \sum \limits_{i = 1}^k {{y}_{i}}\left( t \right){{V}_{i}}\left( {\lambda ,\varphi } \right),$
где $\lambda $ – долгота, $\varphi $ – широта, $t$ – время, ${{y}_{i}}\left( t \right)$ – временные коэффициенты разложения, ${{V}_{i}}\left( {\lambda ,\varphi } \right)$ – ортогональные функции (векторы) разложения, k – число базисных функций, соответствующее количеству дней во временных рядах ${{y}_{i}}\left( t \right)$ (так как в нашем случае шаг по времени равен суткам).

Заменим левую часть уравнения бюджета завихренности (4) на разложение по ЕОФ и скалярно умножим каждое слагаемое на вектор разложения ${{V}_{i}}\left( {\lambda ,\varphi } \right)$. Из-за свойства ортогональности коэффициентов Фурье, получаем уравнение:

(5)
$\begin{gathered} \frac{{d{{y}_{i}}\left( t \right)}}{{dt}} = \frac{{\partial {{\xi }_{1}}}}{{\partial t}}{{V}_{i}}\left( {\lambda ,\varphi } \right) - \frac{R}{f}{\text{ln}}\left( {\frac{{{{p}_{2}}}}{{{{p}_{1}}}}} \right){{\nabla }^{2}} \times \\ \times \,\,\left\{ {{{A}_{T}} - \left\langle w \right\rangle \left\langle {\left( {{{\gamma }_{a}} - \gamma } \right)} \right\rangle + {{E}_{T}} + {{E}_{{\text{Ф}}}} + {{E}_{R}}} \right\}{{V}_{i}}\left( {\lambda ,\varphi } \right). \\ \end{gathered} $

Его левая часть описывает эволюцию i-й моды ЕОФ-разложения вихря, правая часть содержит факторы, определяющие эти изменения.

Если структура поля завихренности изучаемого объекта может быть хорошо описана небольшим числом мод ЕОФ разложения, то для принципиального понимания того, за счет каких процессов развивается или ослабляется вихрь, можно использовать только эти первые несколько мод. Поэтому следующим этапом исследования стал ЕОФ анализ поля завихренности в интересующем нас регионе.

АНАЛИЗ ПРОСТРАНСТВЕННОЙ СТРУКТУРЫ ПОЛЯ ЗАВИХРЕННОСТИ ГАВАЙСКОГО АНТИЦИКЛОНА

Для оценки пространственной структуры поля завихренности Гавайского антициклона было выполнено разложение на естественные ортогональные функции поля завихренности на уровне 925 гПа в области 165° з.д.–135° з.д. и 35°–45° с.ш. Границы области взяты именно так потому (см. рис. 1), что севернее области резко увеличивалась дисперсия колебаний, то есть, с точки зрения стабильности картины включение этой зоны в расчетную область было нерационально, а южнее становилось неоправданно геострофическое приближение, использованное при определении завихренности в (1). Пространственная структура первых трех мод ЕОФ-разложения поля завихренности при различном временном усреднении приведена на рис. 2. Хорошо видно, что она практически не изменяется при увеличении временного сглаживания.

Рис. 2.

Пространственная структура поля завихренности на геопотенциальной поверхности 925 гПа, соответствующая первым трем модам ЕОФ-разложения по данным реанализа ERA5 с временным осреднением 1, 2, 3 и 4 дня.

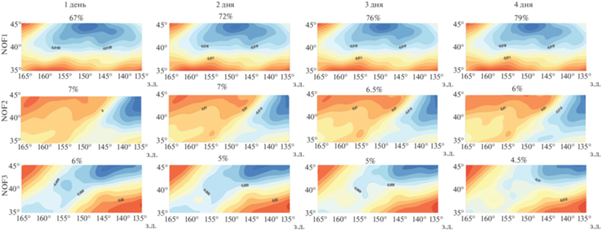
Первая мода, как видно, соответствует среднему положению Гавайского антициклона. По мере увеличения временного сглаживания отмечается рост вклада этой доминирующей моды в общую изменчивость. Так, при суточном осреднении эта структура объясняет 67% от общей изменчивости, а при 4-суточном – почти 80% (рис. 2, верхний ряд). На вторую и третью моду ЕОФ приходится всего 7 и 6% изменчивости при суточном осреднении и 6 и 4.5% при 4-суточном. Таким образом, при учете трех мод процент изменчивости достигает почти 80% при 1-суточном осреднении. Это соотвествует заявленным условиям принципиальной применимости методики ЕОФ анализа для индивидуального вихря. Так как значительных различий при увеличении временного сглаживания выявлено не было, в дальнейшем анализ будет проведен только для среднесуточных значений.

Причем, ввиду несоизмеримости вклада 1-й и последующих мод ЕОФ-разложения, внимание будет уделено первой моде.

АНАЛИЗ РОЛИ РАЗЛИЧНЫХ ФАКТОРОВ В ДИНАМИКЕ ГАВАЙСКОГО АНТИЦИКЛОНА

По данным реанализа ERA5 для рассмотренной области Тихого океана были рассчитаны слагаемые уравнения (5), спроектированные на первую моду ЕОФ-разложения.

Анализ показал, что наиболее значимыми слагаемыми, вносящими вклад в изменение завихренности, являются те, которые отражают влияние горизонтальной адвекции температуры, роль вертикальных движений и изменения завихренности в верхней тропосфере. Влияние потоков тепла и радиационного баланса менее заметно, что логично, поскольку анализ проводится над исключительно однородной поверхностью океана в субтропиках в летнее время.

Анализ полученных рядов демонстрирует отсутствие строгих зависимостей изменения завихренности в антициклоне от различных факторов. Так, например, в отдельные дни (минимум 17 июня и максимум 21 июня) хорошо согласованы с аналогичными экстремумами изменения завихренности в верхней тропосфере. Максимум 13 июля соответствует одновременно росту значений слагаемого, ответственного за адвекцию температуры и минимуму слагаемого, отражающего вертикальные движения. Для оценки характера связи изменения завихренности с проекций каждого из слагаемых уравнения (5) (за исключением слагаемого, отражающего роль скрытого потока тепла ввиду его крайне малых значений), были рассчитаны коэффициенты корреляции (табл. 1).

Таблица 1.  

Коэффициент синхронной корреляции (корреляция Пирсона) между изменением завихренности в левой части уравнения (5) и слагаемыми в правой части уравнения

dξ1/dt AT $w\left( {{{\gamma }_{a}} - \gamma } \right)$ ET ER
0.58 –0.02 –0.30 0.14 0.10

Наибольшая положительная корреляция (0.58) отмечается для слагаемого, ответственного за изменение завихренности в верхней тропосфере, что неудивительно, поскольку Гавайский максимум представляет собой высокий антициклон, и изменения циркуляции на разных уровнях во многом синхронизированы. Небольшая, но статистически значимая отрицательная корреляционная связь (–0.30) отмечается для слагаемого, относящегося к вертикальным движениям. Это отражение того, что данное слагаемое в уравнении (5) играет контролирующую роль в динамике антициклона, ограничивая его интенсивность. В самом деле, при усилении антициклона происходящее нарастание нисходящих движений создает положительный знак выражения ${{\nabla }^{2}}w$, становясь фактором отрицательной обратной связи, демпфирующим дальнейшее развитие антициклона. Роль подобных обратных связей была отмечена еще в [21].

Линейная корреляционная связь других факторов с изменением завихренности в Гавайском антициклоне оказывается незначимой. Интересно, что хотя слагаемое, ответственное за горизонтальную адвекцию температуры в слое довольно велико по абсолютным значениям, согласно корреляционному анализу оно не оказывает систематического влияния на динамику завихренности. Возможно, это связано с конкретной конфигурацией поля температуры в рассматриваемой области на разных вертикальных уровнях.

УРАВНЕНИЕ ДЛЯ КОЭФФИЦИЕНТА ${{y}_{1}}\left( t \right)$ ПРИ ПЕРВОЙ МОДЕ ЕОФ РАЗЛОЖЕНИЯ ЗАВИХРЕННОСТИ

Наша цель – получить уравнение для коэффициента ${{y}_{1}}\left( t \right)$ при первой моде ЕОФ-разложения исходя из уравнения (5), в котором два слагаемых в правой части непосредственно зависят от ${{\xi }_{2}}$. Это слагаемое с адвекцией средней по слою температуры

(6)
$\frac{R}{f}{\text{ln}}\left( {\frac{{{{p}_{2}}}}{{{{p}_{1}}}}} \right){{\nabla }^{2}}\left\{ {\left( {\vec {v}{{\nabla }_{h}}} \right)T} \right\}{{V}_{1}}\left( {\lambda ,\varphi } \right),$
так как скорость $\vec {v}$ зависит от завихренности, а также слагаемое с вертикальными движениями, поскольку мы выражаем $\left\langle w \right\rangle $ через ${{\xi }_{2}}$:

(7)
$\frac{R}{f}\ln \frac{{{{P}_{2}}}}{{{{P}_{1}}}}{{\nabla }^{2}}\left\{ {{{\xi }_{2}}\sqrt {\frac{{{{K}_{m}}}}{{2f}}} \left\langle {{{\gamma }_{a}} - \gamma } \right\rangle } \right\}{{V}_{1}}\left( {\lambda ,\varphi } \right).$

Начнем с выражения (6). Скорость $\vec {v}$ линейно зависит от ${{\xi }_{2}}$, то есть $\vec {v}$ можно представить как результат действия некоторого линейного оператора $\vec {V}\left[ {} \right]$ на функцию ${{\xi }_{2}}$: $\vec {v} = \vec {V}\left[ {{{\xi }_{2}}} \right]$. Подставим в это выражение ЕОФ-разложение завихренности ${{\xi }_{2}}$ и воспользуемся линейностью оператора $\vec {V}\left[ {} \right]$:

(8)
$\begin{gathered} \vec {v} = \vec {V}\left[ {{{\xi }_{2}}} \right] = \vec {V}\left[ {\sum\limits_{i = 1}^k {{{y}_{i}}\left( t \right){{V}_{i}}\left( {\lambda ,\varphi } \right)} } \right] = \\ = \,\,\sum\limits_{i = 1}^k {{{y}_{i}}\left( t \right)} \vec {V}\left[ {{{V}_{i}}\left( {\lambda ,\varphi } \right)} \right], \\ \end{gathered} $
где множители $\vec {V}\left[ {{{V}_{i}}\left( {\lambda ,\varphi } \right)} \right] = \left\{ {{{V}_{u}}\left[ {{{V}_{i}}\left( {\lambda ,\varphi } \right)} \right],} \right.$ $\left. {{{V}_{v}}\left[ {{{V}_{i}}\left( {\lambda ,\varphi } \right)} \right]} \right\}$ зависят только от координат, но не зависят от времени. Их необходимо найти при известной скорости ветра $\vec {v}$. Отметим, что можно было бы воспользоваться известным интегральным соотношением, связывающим скорость и завихренность (см. напр. [3]), однако его практическое применение затруднительно.

Фиксируем произвольную точку $\left( {\bar {\lambda },\bar {\varphi }} \right)$ и рассмотрим в ней временные ряды $u\left( {\bar {\lambda },\bar {\varphi },t} \right)$ и $v\left( {\bar {\lambda },\bar {\varphi },t} \right)$. Из (8) следует, что

(9)
$u\left( {\bar {\lambda },\bar {\varphi },t} \right) = \sum\limits_{i = 1}^k {{{y}_{i}}\left( t \right)a_{u}^{i}} ,\,\,\,\,v\left( {\bar {\lambda },\bar {\varphi },t} \right) = \sum\limits_{i = 1}^k {{{y}_{i}}\left( t \right)a_{v}^{i}} ,$
где $a_{u}^{i} = {{V}_{u}}\left[ {{{V}_{i}}\left( {\bar {\lambda },\bar {\varphi }} \right)} \right]$ и $a_{v}^{i} = {{V}_{v}}\left[ {{{V}_{i}}\left( {\bar {\lambda },\bar {\varphi }} \right)} \right]$ – числовые коэффициенты, которые можно оценить по известным временным рядам $u\left( {\bar {\lambda },\bar {\varphi },t} \right)$ и $v\left( {\bar {\lambda },\bar {\varphi },t} \right)$ пользуясь регрессионным анализом.

Проделывая описанную процедуру в каждом узле сетки, получаем поля ${{V}_{u}}\left[ {{{V}_{i}}\left( {\lambda ,\varphi } \right)} \right]$ и ${{V}_{v}}\left[ {{{V}_{i}}\left( {\lambda ,\varphi } \right)} \right]$ соответственно для всех $i = 1,2,...,k$, причем они оказались практически идентичными как при суточном осреднении данных, так и при осреднении по двум, трем и четырем дням.

Вернемся к получению слагаемого в выражении (6), соответствующего первой моде. Изначально временной ряд (6) содержит в себе комбинацию всех коэффициентов ${{y}_{i}}\left( t \right)$, так как скорость ${\vec {v}}$ зависит от всех мод ЕОФ-разложения. Выделим часть, содержащую только ${{y}_{1}}\left( t \right)$:

(10)
$\begin{gathered} \frac{R}{f}\ln \frac{{{{P}_{2}}}}{{{{P}_{1}}}}{{\nabla }^{2}}\left\{ {\left( {\vec {v},{{\nabla }_{h}}} \right)\left\langle T \right\rangle } \right\}{{V}_{1}}\left( {\lambda ,\varphi } \right) = \\ = \,\,\frac{R}{f}\ln \frac{{{{P}_{2}}}}{{{{P}_{1}}}}{{\nabla }^{2}}\left\{ {\left( {\sum\limits_{i = 1}^k {{{y}_{i}}\left( t \right)\vec {V}\left[ {{{V}_{i}}\left( {\lambda ,\varphi } \right)} \right]} ,{{\nabla }_{h}}} \right)\left\langle T \right\rangle } \right\}{{V}_{1}}\left( {\lambda ,\varphi } \right) = \\ = {{y}_{1}}\left( t \right)\frac{R}{f}\ln \frac{{{{P}_{2}}}}{{{{P}_{1}}}}{{\nabla }^{2}}\left\{ {\left( {\vec {V}\left[ {{{V}_{1}}\left( {\lambda ,\varphi } \right)} \right],{{\nabla }_{h}}} \right)\left\langle T \right\rangle } \right\}{{V}_{1}}\left( {\lambda ,\varphi } \right) + \\ + \,\,\left\{ {{\text{все}}\,\,{\text{остальные}}\,\,{\text{слагаемые}}} \right\}. \\ \end{gathered} $

Исходный временной ряд (содержащий все компоненты ЕОФ-разложения) для слагаемого с адвекцией температуры, а также первого слагаемого в правой части (10), приведены на рис. 3а. Первая мода достаточно хорошо описывает поведение полного временного ряда (6), причем для большего промежутка осреднения данных отклонение полного ряда от первого слагаемого уменьшается.

Рис. 3.

Временные ряды для 1 – полного (содержащего все компоненты ЕОФ-разложения) слагаемого (а) с адвекцией температуры и (б) с вертикальными движениями в правой части уравнения (5) и 2 – соответствующего слагаемого, содержащего только первую моду ЕОФ-разложения.

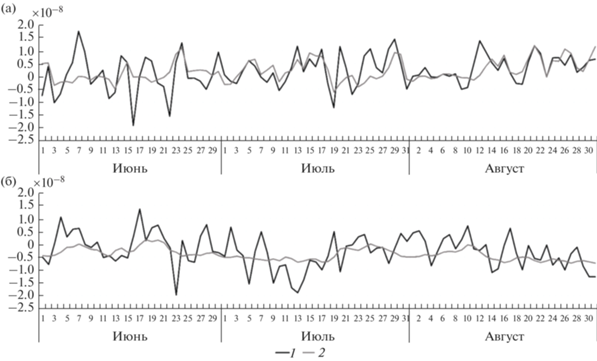
Рассмотрим теперь слагаемое с вертикальными движениями. Подставляя в выражение (7) функцию ${{\xi }_{2}}$ в виде ЕОФ-разложения, получаем:

(11)
$\begin{gathered} \frac{R}{f}\ln \frac{{{{P}_{2}}}}{{{{P}_{1}}}}{{\nabla }^{2}}\left\{ {{{\xi }_{2}}\sqrt {\frac{{{{K}_{m}}}}{{2f}}} \left\langle {{{\gamma }_{a}} - \gamma } \right\rangle } \right\}{{V}_{1}}\left( {\lambda ,\varphi } \right) = \\ = \,\,\frac{R}{f}\ln \frac{{{{P}_{2}}}}{{{{P}_{1}}}}{{\nabla }^{2}}\left\{ {\sum\limits_{i = 1}^k {{{y}_{i}}\left( t \right){{V}_{i}}\left( {\lambda ,\varphi } \right)} \sqrt {\frac{{{{K}_{m}}}}{{2f}}} \left\langle {{{\gamma }_{a}} - \gamma } \right\rangle } \right\}{{V}_{1}}\left( {\lambda ,\varphi } \right) = \\ = \sum\limits_{i = 1}^k {{{y}_{i}}\left( t \right)} \frac{R}{f}\ln \frac{{{{P}_{2}}}}{{{{P}_{1}}}} \times \\ \times \,\,{{\nabla }^{2}}\left\{ {{{V}_{i}}\left( {\lambda ,\varphi } \right)\sqrt {\frac{{{{K}_{m}}}}{{2f}}} \left\langle {{{\gamma }_{a}} - \gamma } \right\rangle } \right\}{{V}_{1}}\left( {\lambda ,\varphi } \right) = \\ = {{y}_{1}}\left( t \right)\frac{R}{f}\ln \frac{{{{P}_{2}}}}{{{{P}_{1}}}}{{\nabla }^{2}}\left\{ {{{V}_{1}}\left( {\lambda ,\varphi } \right)\sqrt {\frac{{{{K}_{m}}}}{{2f}}} \left\langle {{{\gamma }_{a}} - \gamma } \right\rangle } \right\}{{V}_{1}}\left( {\lambda ,\varphi } \right) + \\ + \,\,\left\{ {{\text{все}}\,\,{\text{остальные}}\,\,{\text{слагаемые}}} \right\}. \\ \end{gathered} $

Исходный временной ряд (7) и ряд для первого слагаемого в правой части (11) приведены на рис. 3б.

Слагаемое, соответствующее первой моде ЕОФ-разложения, описывает поведение среднего значения выражения с вертикальными движениями, причем и в данном случае отклонения от среднего уменьшаются с ростом периода осреднения.

Итак, уравнение (5) для коэффициента ${{y}_{1}}\left( t \right)$ принимает вид:

(12)
$\begin{gathered} \frac{{d{{y}_{1}}}}{{dt}} = \frac{{\partial {{\xi }_{1}}}}{{\partial t}}{{V}_{1}} + {{y}_{1}}\frac{R}{f}\ln \frac{{{{P}_{2}}}}{{{{P}_{1}}}}{{\nabla }^{2}}\left\{ {\left( {\vec {V}\left[ {{{V}_{1}}} \right],{{\nabla }_{h}}} \right)\left\langle T \right\rangle } \right\}{{V}_{1}} + \\ + \,\,{{y}_{1}}\frac{R}{f}\ln \frac{{{{P}_{2}}}}{{{{P}_{1}}}}{{\nabla }^{2}}\left\{ {{{V}_{1}}\sqrt {\frac{{{{K}_{m}}}}{{2f}}} \left\langle {{{\gamma }_{a}} - \gamma } \right\rangle } \right\}{{V}_{1}} - \\ - \,\,\frac{R}{f}\ln \frac{{{{P}_{2}}}}{{{{P}_{1}}}}{{\nabla }^{2}}\left\{ {{{E}_{T}} + {{E}_{\Phi }} + {{E}_{R}}} \right\}{{V}_{1}} + {\text{ }}{{\Psi }_{1}}{\text{(}}t{\text{),}} \\ \end{gathered} $
где слагаемое Ψ1(t) содержит все слагаемые с компонентами ЕОФ-разложения завихренности для всех мод, старше первой.

ОЦЕНКА “ШУМОВОЙ” СОСТАВЛЯЮЩЕЙ В УРАВНЕНИИ ЗАВИХРЕННОСТИ

Уравнение (12) можно проверить, оценивая, насколько адекватно слагаемые его правой части суммарно описывают изменения ${{y}_{1}}\left( t \right)$ в левой части уравнения. Однако при подстановке в уравнение данных реанализа строгого равенства правой и левой части не получается даже при учете всех мод разложения в выражениях с адвекцией температуры и вертикальными движениями. Тем более, точного равенства не получится, если пренебречь слагаемым Ψ1(t).

Несовпадение правой и левой части может объясняться тем, что мы рассматриваем уравнение только для первой моды ЕОФ-разложения, которая, хотя и является доминирующей, не объясняет всей изменчивости. Влияние других мод дает свой вклад, формируя невязку уравнения. Она особенно велика в периоды, когда роль первой моды ослабевает. Например, в период 24–27 июля доминирующей стала вторая мода ЕОФ-разложения, а в поле завихренности произошло исчезновение антициклона из рассматриваемой области. Такая ситуация противоречит первоначально сформулированному условию стабильного существования вихря в выбранной зоне. В этом плане, периоды с большой невязкой можно трактовать как промежутки, когда наше уравнение не может замыкаться по определению. В рамках данного исследования мы не исключали данные периоды из рассмотрения, чтобы продемонстрировать потенциальные ограничения метода, однако в дальнейшем, в случае рассмотрения уравнения только для первой моды ЕОФ-разложения, может быть рациональным подбирать периоды, в течение которых условие существования вихря в границах выполняется более строго, либо включить в анализ нескольких младших мод ЕОФ-разложения.

Среди прочих факторов, влияющих на наличие невязки, можно отметить тот факт, что при переходе от аналитических уравнений к численным расчетам мы делаем ряд допущений. Это, во-первых, рассмотрение геострофической завихренности. Во-вторых, шаг сетки модели (около 20–25 км), обрезает часть изменчивости при переходе от аналитических выражений к численным. С учетом этого, в уравнении (12) должен появляться добавочный член Ψ(t), включающий в себя влияние не учитываемых мод ЕОФ-разложения завихренности, явлений мелкого масштаба, а также все неучтенные погрешности.

В работах [18–20] предложена методика аппроксимации не учитываемых явно слагаемых уравнения с более высокими модами ЕОФ-разложения через оставляемые в уравнении в явном виде компоненты ЕОФ-разложения, к которым прибавляется «шумовое» слагаемое. При этом показано, что если в исходном уравнении имелась квадратичная нелинейность, то при аппроксимации отбрасываемых компонент ЕОФ-разложения неизбежно возникают как квадратичные, так и кубические слагаемые с учитываемыми явно компонентами. В нашем случае это можно интерпретировать как гипотезу о том, что наличие в недоучтенных факторах квадратичных по ${{\xi }_{2}}$ слагаемых (например, адвекции завихренности), приведет к появлению в Ψ(t) слагаемых, пропорциональных первой, второй и третьей степени ${{y}_{1}}\left( t \right)$. Это позволило искать Ψ(t) в виде:

(13)
$\begin{gathered} ~\Psi \left( t \right) = {{\alpha }_{0}} + {{\alpha }_{1}}{{y}_{1}}\left( t \right) + {{\alpha }_{2}}{{\left( {{{y}_{1}}\left( t \right)} \right)}^{2}} + \\ + \,\,{{\alpha }_{3}}{{\left( {{{y}_{1}}\left( t \right)} \right)}^{3}} + \varepsilon \left( t \right), \\ \end{gathered} $
где $\varepsilon \left( t \right)$ – шум, а числовые коэффициенты (${{\alpha }_{0}},~{{\alpha }_{1}},~{{\alpha }_{2}},{{\alpha }_{3}}$) были определены на основе регрессионного анализа. Полная аппроксимация (13) сравнивалась с редуцированным выражением:

(14)
$~\Psi \left( t \right) = {{\alpha }_{0}} + {{\alpha }_{1}}{{y}_{1}}\left( t \right) + \varepsilon \left( t \right).$

Результаты моделирования невязки приведены на рис. 4. Как кубическое выражение от $~{{y}_{1}}\left( t \right)$, так и редуцированное линейное выражение, позволяют компенсировать ненулевое среднее значение невязки. Как видно из рис.4, кубическое выражение от ${{y}_{1}}\left( t \right)$ лучше описывает поведение невязки, чем линейное. В частности, оно частично, хоть и не полностью, компенсирует всплески невязки в период с 18 по 26 июня и с 19 по 27 июля. По-видимому, они объясняются, как отмечено ранее, возрастающей ролью следующих мод ЕОФ-разложения.

Рис. 4.

Аппроксимация невязки уравнения (12) с помощью кубического и линейного выражений (13) и (14). 1 – исходная невязка, 2 – линейная аппроксимация невязки, 3 – кубическая аппроксимация невязки.

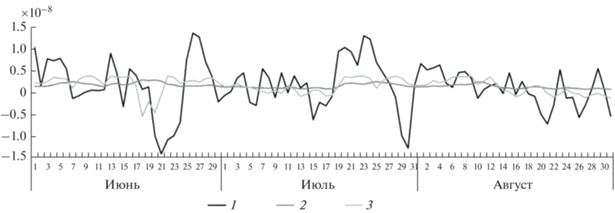
Анализ остаточного члена $\varepsilon \left( t \right)$ при кубической аппроксимации невязки показывает, что он представляет собой гауссов шум. Проверка ряда на нормальность проводилась с помощью теста Колмогорова–Смирнова (p-value = 0.61). Это представляется важным, поскольку исключает, по крайней мере, в рассматриваемом случае, возможность существования мультипликативного шума, обладающего способностью к большим нерегулярным вариациям. Возможным подтверждением правильности этого заключения является то, что ход эволюции антициклона всегда протекает гладким образом (в отличии от циклонов, где возможно резкое снижение давления до стадии тропического циклона; а “тропических антициклонов” не бывает).

ЗАКЛЮЧЕНИЕ

В ходе работы показано, что использование завихренности служит надежной характеристикой субтропического (Гавайского) антициклона, представляющего собой атмосферный вихрь, стабильно существующий в некоторой области с фиксированными границами. В эволюцию антициклона наибольший вклад вносит изменение завихренности в верхних слоях тропосферы и вертикальные движения, действующие на его развитие как отрицательная обратная связь. Непосредственное воздействие на циркуляционную систему потоков явного и скрытого тепла, а также радиационного баланса крайне невелико.

Картина динамики индивидуального вихря получается при применении уравнения бюджета завихренности, в котором для характеристики вихря использована первая естественная ортогональная функция. Ее временной коэффициент y1(t), для которого получено обыкновенное дифференциальное уравнение, комплексно определяет динамику вихря. Невязка явно разрешаемых факторов компенсируется параметризацией, которая строится на основе учета влияний второй и последующих мод ЕОФ-разложения. Показано, что она состоит из гауссова шума и неслучайной компоненты, которая может быть аппроксимирована с помощью кубической функции от временного коэффициента при первой моде.

В настоящей статье представлены данные только за один год. Это связано с тем, что здесь мы решали главным образом методические проблемы, связанные с формулировкой задачи, с использованием параметризаций, которые в такой форме применены впервые. Теперь мы видим направление работы в расширении географии, то есть в применении метода к стабильным вихрям разных регионов, и в анализе временных срезов за ряд лет. Это позволит рассмотреть различные циркуляционные системы, выявить факторы, влияющие на их динамику в различных регионах, исследовать экстремальный характер гидрометеорологических событий, связанных с долгоживущими вихрями.

Данный подход в своих принципиальных чертах полезен и при анализе долгоживущих вихревых структур океана.

Работа поддержана грантом № 075-15-2021-574 Министерства науки и высшего образования Российской Федерации, а также Московским государственным университетом имени М.В. Ломоносова в форме гранта AAAA-A16-116032810086-4 и в рамках исследовательской программы междисциплинарной научной и образовательной школы “Будущее планеты и глобальные изменения окружающей среды”.

Список литературы

  1. Rudeva I., Gulev S.K. Composite analysis of the North Atlantic extratropical cyclones in NCEP/NCAR reanalysis. // Mon. Wea. Rew. 2011. V. 139. № 5. P. 1419–1446. https://doi.org/10.1175/2010MWR3294.1

  2. Пальмен Э., Ньютон Ч. Циркуляционные системы атмосферы. Л: Гидрометиздат, 1973. 615 с.

  3. Saffman P.G. Vortex Dynamics. Cambridge University Press, Cambridge, 1992.

  4. Lamb G. Hydrodynamics. 6th Edition, Cambridge University Press, Cambridge, 1932.

  5. Cushman-Rosin B., Hell W.H., Nof D. Oscillation and Rotation of Elliptical Warm-Core Rings // Journal of the Geophysical Research. 1985. V. 90. P. 11 756–11 764. https://doi.org/10.1029/JC090iC06p11756

  6. Meacham S.M., Pankratov K.K., Shchepetkin A.F., Zhmur V.V. The Interaction of Ellipsoidal Vortices with Background Shear Flows in a Stratified Fluid. // Dynamics of Atmospheres and Oceans. 1994. V. 21. P. 167–212. https://doi.org/10.1016/0377-0265(94)90008-6

  7. Жмур В.В. Мезомасштабные вихри океана. М.: ГЕОС, 2011. 289 с.

  8. Zhmur V.V., Ryzhov E.A. and Koshel K.V. Ellipsoidal Vortex in a Nonuniform Flow: Dynamics and Chaotic Advections. // Journal of Marine Research. 2011. V. 69. P. 435–461. https://doi.org/10.1357/002224011798765204

  9. Zabusky N.J., Hughes M.N., Roberts K.V.J. Contour dynamics for the Euler equations in two-dimensions // J. Comp.Phys. 1979. V. 30, №. 1. P. 96‒106. https://doi.org/10.1016/0021-9991(79)90089-5

  10. Barriopedro D., García-Herrera R., Lupo A.R., Hernández, E. A Climatology of Northern Hemisphere blocking. // Journal of Climate. 2006. V. 19. P. 1042–1063. https://doi.org/10.1175/JCLI3678.1

  11. Mokhov I., Timazhev A.V., Lupo A.R. Changes in Atmospheric Blocking Characteristics within Euro-Atlantic Region and Northern Hemisphere as a Whole in the 21st Century from Model Simulations Using RCP Anthropogenic Scenarios. // Global and Planetary Change. 2014. V. 122. P. 265–270. https://doi.org/10.1016/j.gloplacha.2014.09.004

  12. Hannachi A., Jolliffe I.T., Stephenson D.B. Empirical orthogonal functions and related techniques in atmospheric science: A review // International Journal of Climatology: A Journal of the Royal Meteorological Society. 2007. V. 27. P. 1119–1152. https://doi.org/10.1002/joc.1499

  13. Feldstein S. The Growth and Decay of Low-Frequency Anomalies in a GCM. // Journal of the Atmospheric Sciences. 1998. V. 55. P. 415–428. https://doi.org/10.1175/1520-0469(1998)055<0415: TGADOL>2.0.CO;2

  14. Кислов А.В., Соколихина Н.Н., Семенов Е.К., Тудрий К.О. Анализ вихря как целостного образования применительно к исследованию блокирующего антициклона 2010 г // Метеорология и гидрология. 2017. № 4. С. 18–26.

  15. Кислов А.В., Соколихина Н.Н., Семенов Е.К., Тудрий К.О. Динамика зимнего высокоширотного блокирующего антициклона зимой 2012 года в Северном полушарии // Труды Гидрометеорологического научно-исследовательского центра Российской Федерации. 2017. № 363. С. 24–35.

  16. Kislov A., Sokolikhina N., Semenov E. and Tudriy K. Blocking Anticyclone in the Atlantic Sector of the Arctic as an Example of an Individual Atmospheric Vortex // Atmospheric and Climate Sciences. 2017. V. 7. P. 323–336. https://doi.org/10.4236/acs.2017.73024

  17. Семенов Е.К., Соколихина Н.Н., Татаринович Е.В. Атмосферная циркуляция в период катастрофического снегопада в Хабаровском крае 30 ноября – 2 декабря 2014 г // Метеорология и гидрология. 2018. № 1. С. 85–96.

  18. Majda A., Timofeyev I., Vanden-Eijnden E. A mathematical framework for stochastic climate models // Communications on Pure and Applied Mathematics. 2001. V. 54. P. 891–974.

  19. Majda A., Franzke C., Khouider B. An applied mathematics perspective on stochastic modelling for climate // Philosophical transactions. Series A, Mathematical, physical, and engineering sciences. 2008. V. 366. P. 2429–2455.

  20. Majda A., Franzke C., Crommelin D. Normal forms for reduced stochastic climate models // Proceedings of the National Academy of Sciences of the United States of America. 2009. V. 106. P. 3649–3653.

  21. Hersbach H., Bell B., Berrisford P., Biavati G., Horányi A., Muñoz Sabater J., Nicolas J., Peubey C., Radu R., Rozum I., Schepers D., Simmons A., Soci C., Dee D., Thépaut J-N. ERA5 hourly data on pressure levels from 1979 to present // Copernicus Climate Change Service (C3S) Climate Data Store (CDS). 2018.

  22. Петерсен С. Анализ и прогноз погоды. Ленинград: Гидрометеоиздат, 1961. 650 с.

  23. Рамедж К. Метеорология муссонов. Ленинград : Гидрометеоиздат, 1976. 335 с.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Физика атмосферы и океана

Архивы выпусков Информация о журнале Отправить рукопись в журнал