1. На главную
  2. Электронные версии
  3. Известия РАН. Физика атмосферы и океана
  4. T. 59, № 1, 2023

Известия РАН. Физика атмосферы и океана, 2023, T. 59, № 1, стр. 44-54

Приближение коротких по вертикали волн малой амплитуды в атмосфере с учетом среднего ветра

С. П. Кшевецкий a, *, Ю. А. Курдяева b, Н. М. Гаврилов c

a Балтийский государственный университет им. И. Канта
236041 Калининград, ул. Ал. Невского 14, Россия

b Калининградский филиал Института земного магнетизма, ионосферы и распространения радиоволн им. Н.В. Пушкова РАН
236016 Калининград, ул. Пионерская 61, Россия

c Санкт-Петербургский государственный университет
199034 Санкт-Петербург, Университетская наб., 7/9, Россия

* E-mail: SPKshev@gmail.com

Поступила в редакцию 17.08.2022
После доработки 29.09.2022
Принята к публикации 12.10.2022

Полный текст (PDF)

Аннотация

Методом разных масштабов построены формулы для гидродинамических полей акустико-гравитационных волн (ВГВ) с вертикальными длинами волн, малыми по сравнению с масштабами изменений фоновых полей температуры и ветра. Эти формулы эквивалентны традиционному ВКБ-приближению, но включают в явном виде вертикальные градиенты фоновых полей. Сформулированы и анализируются условия применимости полученных формул для описания распространения АГВ из тропосферы в термосферу. Одним из условий применимости приближенных формул является отсутствие особых точек (критических уровней) в уравнениях для волновых мод в анализируемом интервале высот. Для случая ветра из эмпирической модели HWM, особые точки часто располагаются ниже 200 км и характерны для внутренних гравитационных волн (ВГВ), с длинами волн порядка 10 км. С увеличением длины волны количество особых точек уменьшается. Для ВГВ с масштабами порядка или более 300 км, особые точки обычно отсутствуют. Показано, что у ВГВ с периодами менее 20 мин, распространяющихся вверх с тропосферных высот, обычно существует одна точка поворота в интервале высот от 100 до 130 км. Полученные формулы полезны, в частности, для параметризации эффектов АГВ в численных моделях атмосферной динамики и энергетики.

Ключевые слова: акустико-гравитационные волны, приближение коротких волн, приближение ВКБ, дисперсионное соотношение, критический уровень, особая точка

1 ВВЕДЕНИЕ

Акустико-гравитационные волны (АГВ), генерируемые на тропосферных высотах источниками различной природы, значительно влияют на верхнюю атмосферу и ионосферу [1–8].

В численных моделях глобальной циркуляции атмосферы динамические и тепловые эффекты АГВ учитываются с помощью параметризаций. Среди первых параметризации эффектов АГВ следует упомянуть работы [9–12]. Некоторые параметризации используют численные расчеты для наборов волновых мод, моделирующих спектр атмосферных ВГВ [13–16]. Понятие вертикального волнового числа строго вводится только для изотермической безветренной атмосферы. Для атмосферы с реалистичными профилями ветра и температуры эту характеристику можно использовать только в рамках приближения коротких по вертикальной координате волн. Наиболее полный набор коротковолновых формул для волн малой амплитуды получен в [17], что выгодно отличает их от более частных результатов [18–20]. Автор [17] свел исходную систему уравнений гидродинамики к дифференциальному уравнению Риккати и нашел его асимптотические решения, представимые в виде ряда по большому параметру. Этот вариант коротковолнового приближения часто называют приближением Вентцеля–Крамерса–Бриллюэна (ВКБ). В практических вычислениях обычно используют только первые члены ряда, и в этом приближении полученные решения фактически эквивалентны гипотезе локальной вертикальной однородности и не содержат вертикальных градиентов температуры и ветра. Годин в [17, 21] изучал дифракцию волн вдоль поверхности Земли, обусловленную тем, что в точке поворота волны отражаются.

Предметом данной статьи является не дифракция АГВ, а построение формул приближения коротких по вертикальной переменной волн, которые явно содержат вертикальные градиенты температуры и ветра и пригодны для параметризации волновых эффектов в численных моделях глобальной динамики атмосферы. Поэтому использован иной, чем в [17], вариант коротковолнового приближения, основанный на методе разных масштабов. Большое внимание уделено формулированию условий применимости полученных приближенных формул и их анализу в условиях реалистичных профилей ветра и температуры. В частности, значительное внимание уделяется поиску особых точек (критических уровней) в приближенных дифференциальных уравнениях для волновых мод, и влиянию этих точек на применимость асимптотических формул. Кроме того, также анализируется вопрос о точках поворота, и об их зависимости от параметров АГВ и параметров атмосферы.

2 УРАВНЕНИЯ ДЛЯ АГВ МАЛОЙ АМПЛИТУДЫ В АТМОСФЕРЕ С УЧЕТОМ ФОНОВОГО ВЕТРА

В данной работе рассмотрена система трехмерных линеаризованных гидродинамических уравнений для недиссипативного атмосферного газа, без учета вращения и кривизны поверхности Земли. Система уравнений имеет следующий вид:

(1)
$\begin{gathered} \frac{{\partial \psi }}{{\partial t}} + \frac{{\partial u}}{{\partial x}} + \frac{{\partial v}}{{\partial y}} + \frac{{\alpha \left( z \right) + 1}}{{\gamma H\left( z \right)}}w + \frac{{\partial w}}{{\partial z}} + \\ + \,\,\frac{{\partial \psi }}{{\partial x}}U\left( z \right) + \frac{{\partial \psi }}{{\partial y}}V\left( z \right) = 0, \\ \frac{{\partial u}}{{\partial t}} + \frac{{\partial u}}{{\partial x}}U\left( z \right) + \frac{{\partial u}}{{\partial y}}V\left( z \right) + w\frac{d}{{\partial z}}U\left( z \right) + \\ + \,\,gH\left( z \right)\left( {\frac{{\partial \psi }}{{\partial x}} + \frac{{\partial \varphi }}{{\partial x}}} \right) = 0, \\ \frac{{\partial v}}{{\partial t}} + \frac{{\partial v}}{{\partial x}}U\left( z \right) + \frac{{\partial v}}{{\partial y}}V\left( z \right) + w\frac{d}{{\partial z}}V\left( z \right) + \\ + \,\,gH\left( z \right)\left( {\frac{{\partial \psi }}{{\partial y}} + \frac{{\partial \varphi }}{{\partial y}}} \right) = 0, \\ \frac{{\partial w}}{{\partial t}} + \frac{{\partial w}}{{\partial x}}U\left( z \right) + \frac{{\partial w}}{{\partial y}}V\left( z \right) - \\ - \,\,\frac{{\alpha \left( z \right) + 1}}{\gamma }g\left( {\psi + \varphi } \right) + g\frac{d}{{\partial z}} \\ H{\text{(}}z{\text{)(}}\psi + \varphi {\text{)}} + g\psi {\text{ = 0,}} \\ \frac{{\partial \varphi }}{{\partial t}} + \frac{{\partial \varphi }}{{\partial x}}U\left( z \right) + \frac{{\partial \varphi }}{{\partial y}}V\left( z \right) + \\ + \,\,\frac{{\left( {\alpha \left( z \right) - \gamma + 1} \right)w}}{{\gamma H\left( z \right)}} + \left( {\gamma - 1} \right)\left( {\frac{{\partial u}}{{\partial x}} + \frac{{\partial v}}{{\partial y}} + \frac{{\partial w}}{{\partial z}}} \right) = 0. \\ \end{gathered} $
Здесь $u$ и $v$ – компоненты горизонтальной скорости в волне вдоль горизонтальных осей $x$ и $y$, $w$ – скорость вдоль вертикальной оси $z$. $U\left( z \right)$, $V\left( z \right)$– компоненты средней скорости $.\psi = \frac{{\rho - {{\rho }_{0}}\left( z \right)}}{{{{\rho }_{0}}\left( z \right)}}$, $\varphi = \frac{{T - {{T}_{0}}\left( z \right)}}{{{{T}_{0}}\left( z \right)}}$, где $\rho $ и $T$ – плотность и температура, а ${{\rho }_{0}}\left( z \right)$ и ${{T}_{0}}\left( z \right)$ – фоновые плотность и температура. Зависимость фоновой плотности от z описывается формулой ${{\rho }_{0}}\left( z \right) = \frac{{{{\rho }_{{00}}}}}{{H\left( z \right)}}{\text{exp}}\left( { - \int_0^z {\frac{{dz}}{{H\left( z \right)}}} } \right)$, и $\frac{{d{{\rho }_{0}}\left( z \right)}}{{dz}} = \frac{{ - \alpha \left( z \right) + 1}}{{\gamma H\left( z \right)}}{{\rho }_{0}}\left( z \right)$ и $H\left( z \right) = \frac{{R{{T}_{0}}\left( z \right)}}{{g\mu }}$ – высота однородной атмосферы. $R$ – универсальная газовая постоянная, $\mu $ – молекулярный вес, $\gamma $ – постоянная адиабаты, $g$ – ускорение свободного падения. Производными от $\mu ,\gamma ,g$ можно пренебречь. Переменная $\alpha \left( z \right) = \gamma - 1 + \gamma \frac{{dH\left( z \right)}}{{dz}} > 0$.

2.1. Уравнения и соотношения для волновых мод

Для волновых мод $ \sim {\kern 1pt} {\text{exp}}\left( {i\left( {kx + my - \omega t} \right)} \right)$ система уравнений (1) приводится к виду-i

(2)
$\begin{gathered} \frac{d}{{dz}}w\left( z \right) + \left( {\frac{{ - i\sigma \left( z \right)}}{{gH\left( z \right)\gamma }} + \frac{{ - i\left( {{{m}^{2}} + {{k}^{2}}} \right)}}{{\sigma \left( z \right)}}} \right)\frac{{p\left( z \right)}}{{{{\rho }_{0}}\left( z \right)}} - \\ - \,\,\left( {\frac{1}{{\gamma H\left( z \right)}} - \frac{{k\frac{d}{{dz}}U\left( z \right) + m\frac{d}{{dz}}V\left( z \right)}}{{\sigma \left( z \right)}}} \right)w\left( z \right) = 0, \\ \frac{d}{{dz}}p\left( z \right) + \frac{{p\left( z \right)}}{{\gamma H\left( z \right)}} + \\ + \,\,\left( { - i\sigma \left( z \right) + \frac{{ - ig\alpha \left( z \right)}}{{\gamma H\left( z \right)\sigma \left( z \right)}}} \right){{\rho }_{0}}\left( z \right)w\left( z \right) = 0, \\ \end{gathered} $
где введены функции $p\left( z \right) = {{\rho }_{0}}\left( z \right)gH\left( z \right)\left( {\phi + \psi } \right)$, и $\sigma \left( z \right) = \omega - kU\left( z \right) - mV\left( z \right)$. Остальных искомые функции явно выражаются через $p\left( z \right),w\left( z \right)$ следующим образом:

(3)
$\begin{gathered} u\left( z \right) = \frac{{ikp\left( z \right) + {{\rho }_{0}}\left( z \right)w\left( z \right)\frac{d}{{dz}}U\left( z \right)}}{{i{{\rho }_{0}}\left( z \right)\sigma \left( z \right)}}, \\ v\left( z \right) = \frac{{imp\left( z \right) + {{\rho }_{0}}\left( z \right)w\left( z \right)\frac{d}{{dz}}V\left( z \right)}}{{i{{\rho }_{0}}\left( z \right)\sigma \left( z \right)}}, \\ \psi \left( z \right) = \frac{{p\left( z \right)}}{{g{{\rho }_{0}}\left( z \right)H\left( z \right)\gamma }} + \frac{{iw\left( z \right)\alpha \left( z \right)}}{{\gamma H\left( z \right)\sigma \left( z \right)}}, \\ \varphi \left( z \right) = \frac{{\left( {\gamma - 1} \right)p\left( z \right)}}{{\gamma g{{\rho }_{0}}\left( z \right)H\left( z \right)}} - \frac{{iw\left( z \right)\alpha \left( z \right)}}{{\gamma H\left( z \right)\sigma \left( z \right)}}. \\ \end{gathered} $

3 ПРИБЛИЖЕНИЕ КОРОТКИХ ПО ВЕРТИКАЛИ ВОЛН

Можно ввести характерный масштаб ls = $ = {\text{mi}}{{{\text{n}}}_{{0 \leqslant z < \infty }}}$|H(z)/(H(z)/dz)| изменения фоновых полей $H\left( z \right),U\left( z \right),V\left( z \right).$При малых скоростях ветра ${{l}_{s}} = {\text{mi}}{{{\text{n}}}_{{0 \leqslant z < \infty }}}$|H(z)/(H(z)/dz)|. Введем характерный вертикальный масштаб волны ${{l}_{w}}$, и рассмотрим короткие вдоль вертикали волны, для которых $\epsilon = \frac{{{{l}_{w}}}}{{{{l}_{s}}}} \ll 1.$

В [30, 31, 32 построены асимптотические при $\lambda = \frac{1}{\epsilon } \to \infty $ решения матричного уравнения $y{\kern 1pt} ' = \lambda A\left( x \right)y$, где $A\left( x \right)$ – матрица размерности $\left( {2 \times 2} \right)$и $y = \left( {\frac{{{{y}_{1}}}}{{{{y}_{2}}}}} \right)$– двукомпонентный столбец.

В работах [17, 21] система уравнений типа (2) сводится к одному уравнению второго порядка, которое стандартным способом сводится к уравнению Риккати, решение которого ищется в виде разложения по большому параметру $\lambda $.

В данном исследовании будет использован другой подход, который называется методом разных масштабов [22, 23]. В рамках этого подхода, мы считаем, что функции $H,U,V,\alpha $, входящие в коэффициенты уравнений, являются медленно изменяющимися функциями переменной $z$, то есть зависят от $z$ через переменную $\xi = \epsilon z$, и имеют вид $H\left( \xi \right),U\left( \xi \right),V\left( \xi \right),\alpha \left( \xi \right)$. Тогда в уравнении (2) перед членами, содержащими $\frac{d}{{d\xi }}U\left( \xi \right)$ и $\frac{d}{{d\xi }}V\left( \xi \right)$ содержится малый параметр $\epsilon $. В отличие от [23], мы не предполагаем $\alpha \left( z \right) \approx \gamma - 1$, но предполагаем только, что $\alpha \left( z \right)$ является медленной функцией $z$. Например, на высотах в окрестности 120 км $dH\left( z \right){\text{/}}dz~$ может достигать значения 0.4, что является значительным при определении значения $\alpha \left( z \right)$.

В ходе построения теории возмущений выводится локальное дисперсионное соотношение, связывающее параметры $m,k,\omega $ и локальное вертикальное волновое число $n\left( z \right)$ волновой моды. В силу этой связи параметров возможно написание различных по форме, но эквивалентных приближенных формул для волновых мод. Это дает возможность выбрать наиболее компактные и удобные для наших целей формулы. Обычно решение строится с точностью до малых членов порядка $\epsilon $, и членами порядка ${{\epsilon }^{2}}$ пренебрегается.

Поскольку коэффициенты уравнений (2) описываются медленно изменяющимися функциями вертикальной координаты, естественно искать приближенное решение уравнений (2) в виде

(4)
$W\left( z \right) = {{A}_{w}}\left( \xi \right){{e}^{{S\left( z \right)}}},\,\,\,\,p\left( z \right) = {{\rho }_{0}}\left( z \right){{A}_{p}}\left( \xi \right){{e}^{{S\left( z \right)}}}.$

Подставляя (4) в систему уравнений (2), получим соотношения

(5)
$\begin{gathered} \left( {\frac{{ - 1}}{{H\left( \xi \right)\gamma }}\, + \,\frac{d}{{dz}}S\left( z \right) + \frac{{\left( {m\frac{d}{{d\xi }}V\left( \xi \right) + k\frac{d}{{d\xi }}U\left( \xi \right)} \right)i\epsilon }}{{\sigma \left( \xi \right)}}} \right) \times \\ \times \,\,{{A}_{w}}\left( \xi \right) + i\left( {\frac{{ - \sigma \left( \xi \right)}}{{gH\left( \xi \right)\gamma }} + \frac{{{{k}^{2}} + {{m}^{2}}}}{{\sigma \left( \xi \right)}}} \right){{A}_{p}}\left( \xi \right) + \\ + \,\,\epsilon \frac{d}{{d\xi }}{{A}_{w}}\left( \xi \right) = 0, \\ i\left( { - \sigma \left( \xi \right) + \frac{{g\alpha \left( \xi \right)}}{{gH\sigma \left( \xi \right)\gamma }}} \right){{A}_{w}}\left( \xi \right) + \\ + \,\,\left( {\frac{d}{{dz}}S\left( z \right) - \frac{{\alpha \left( \xi \right)}}{{\gamma H\left( \xi \right)}}} \right){{A}_{p}}\left( \xi \right) + \epsilon \frac{d}{{d\xi }}{{A}_{p}}\left( \xi \right) = 0. \\ \end{gathered} $

Пренебрегая в (5) малыми членами $\epsilon \frac{d}{{d\xi }}{{A}_{w}}\left( \xi \right),\epsilon \frac{d}{{d\xi }}{{A}_{p}}\left( \xi \right)$ порядка $\epsilon $, мы приходим к системе линейных однородных алгебраических уравнений относительно неизвестных ${{A}_{w}}$, ${{A}_{p}}$. Члены, пропорциональные $\epsilon $, но не содержащие производные, сохранены в упрощенных уравнениях: они не затрудняют вычисления. Условием разрешимости системы линейных однородных алгебраических для неизвестных ${{A}_{w}}$, ${{A}_{p}}$ является равенство нулю детерминанта этой системы:

(6)
$\begin{gathered} {{\sigma }^{4}}\left( \xi \right) - \left( {\left( {{{k}^{2}} + {{n}^{2}}\left( \xi \right) + {{m}^{2}}} \right)gH\left( \xi \right)\gamma + \frac{{{{{\left( {\alpha \left( \xi \right) + 1} \right)}}^{2}}g}}{{4\gamma H\left( \xi \right)}}} \right) \times \\ \times \,\,{{\sigma }^{2}}\left( \xi \right) - \left( { - \left( \xi \right)\gamma H\left( \xi \right) + \frac{{\alpha \left( \xi \right) - 1}}{2}} \right) \times \\ \times \,\,\left( {k\frac{d}{{d\xi }}U\left( \xi \right) + m\frac{d}{{d\xi }}V\left( \xi \right)} \right)g\epsilon \sigma \left( \xi \right) - \\ - \,\,\left( { - \left( \xi \right)\gamma H\left( \xi \right) + \frac{{\alpha \left( \xi \right) - 1}}{2}} \right)\left( {k\frac{d}{{d\xi }}U\left( \xi \right) + m\frac{d}{{d\xi }}V\left( \xi \right)} \right) \times \\ \times \,\,g\epsilon \sigma \left( \xi \right) + \alpha \left( \xi \right)\left( {{{k}^{2}} + {{m}^{2}}} \right){{g}^{2}} = 0. \\ \end{gathered} $

Соотношение (6) имеет смысл локального дисперсионного соотношения; это понятие обсуждалось выше. Здесь $n\left( \xi \right)$ имеет смысл локальной вертикальной компоненты волнового вектора. Ниже увидим, что $n\left( z \right)$ комплексное. Функция $\frac{d}{{dz}}S\left( z \right)$ из (5) связана с $n\left( \xi \right)$ соотношением $\frac{d}{{dz}}S\left( z \right) = \frac{1}{2}\frac{{\alpha \left( \xi \right) + 1}}{{\gamma H\left( \xi \right)}} + \left( \xi \right).$ Первое слагаемое описывает рост амплитуды волны с высотой вследствие падения плотности с высотой.

Если пренебречь в (6) членом с производными от ветра, то (6) принимает вид дисперсионного соотношения для акустико-гравитационных волн [18]. Если пренебречь производными от ветра и рассмотреть предел, то получим соотношение для коротких акустических волн, где – скорость звука [24–26]. В пределе несжимаемой жидкости $\left( {\gamma ~ \to ~\infty } \right)$, если пренебречь производными от ветра, то на частотах, малых по сравнению с частотой Брента–Вяйсяля, (6) переходит в дисперсионное соотношение для внутренних гравитационных волн в несжимаемой жидкости [18, 27, 28].

В дисперсионное соотношение (6) входит частота $\sigma \left( \xi \right)$ в нечетной, первой степени в слагаемом, пропорциональном градиентам течения. Это означает, что амплитуда волны может расти или падать на градиентах течения. Сдвиговая неустойчивость на градиентах течения широко известна, и является одним из частных проявлений этого эффекта. Амплитуда волны может расти или падать на градиентах ветра вследствие передачи энергии ветра волне, и наоборот. В рамках линейного приближения этот обмен энергией не учитывается и не виден.

Нелинейные уравнения недиссипативной гидродинамики обратимы во времени. И из существования эффекта передачи энергии сдвигового ветра волне может следовать существование обратного эффекта, когда волна создает сдвиговый ветер, даже при отсутствии диссипации.

Ниже выписана зависимость комплексной локальной вертикальной компоненты $n\left( \xi \right)$ волнового вектора от $k,m$ и частоты

(7)
$\begin{gathered} n\left( \xi \right) = \epsilon \frac{{i\left( {k\frac{d}{{d\xi }}U\left( \xi \right) + m\frac{d}{{d\xi }}V\left( \xi \right)} \right)}}{{2\sigma \left( \xi \right)}} \pm \frac{1}{{2\gamma gH\left( \xi \right)\sigma \left( \xi \right)}} \times \\ \times \,\,\left[ { - 2\left( {\alpha \left( \xi \right) - 1} \right)\left( {k\frac{d}{{d\xi }}U\left( \xi \right) + m\frac{d}{{d\xi }}V\left( \xi \right)} \right)} \right.\gamma \sigma \left( \xi \right) \times \\ \times \,\,{{g}^{2}}H\left( \xi \right)\epsilon - 4\left( {{{k}^{2}} + {{m}^{2}}} \right){{\gamma }^{2}}{{\sigma }^{2}}\left( \xi \right){{g}^{2}}{{H}^{2}}\left( \xi \right) + \\ + \,\,4\left( {\alpha \left( \xi \right)\left( {{{k}^{2}} + {{m}^{2}}} \right){{g}^{2}} + {{\sigma }^{4}}\left( \xi \right)} \right) \times \\ \times {{\left. {_{{_{{}}^{{_{{}}^{{}}}}}}^{{_{{_{{}}^{{}}}}^{{}}}}g\gamma H\left( \xi \right) - {{{\left( {\alpha \left( \xi \right) + 1} \right)}}^{2}}{{\sigma }^{2}}\left( \xi \right){{g}^{2}}} \right]}^{{1/2}}}. \\ \end{gathered} $

Малые порядка ${{\epsilon }^{2}}$ отброшены. Видно, что $n\left( \xi \right)$ – комплексное, и первый, мнимый член учитывает рост или падение амплитуды волны с высотой на градиентах течения. Остальные члены имеют более стандартный вид.

Сравнение полученного локального дисперсионного соотношения с [17] показывает, что в [17] дисперсионное соотношение выведено при $\alpha \left( z \right) \approx \left( {\gamma - 1} \right)$, в то время как в (6) $\alpha \left( z \right)$ задается точно:$\alpha \left( z \right) = \gamma - 1 + \gamma \frac{{dH\left( z \right)}}{{dz}} > 0$. На высотах около 120 км $\frac{{dH\left( z \right)}}{{dz}} \approx 0.4$, и $\alpha \approx 1.2$. Если пренебречь членом с $\frac{{dH\left( z \right)}}{{dz}}$, то $\alpha \approx 0.6$.

Обозначим $B\left( \xi \right) = - i\left( {\sigma \left( \xi \right) - \frac{{g\alpha \left( \xi \right)}}{{\gamma H\left( \xi \right)\sigma \left( \xi \right)}}} \right)$ и, используя второе уравнение системы (5), выразим ${{A}_{w}}$:

(8)
$\begin{gathered} {{A}_{w}}\left( \xi \right) = \frac{{ - \epsilon \frac{{dH\left( z \right)}}{{dz}}{{A}_{p}}\left( \xi \right)}}{{B\left( \xi \right)}} - \\ - \,\,\left( {\frac{{\left( \xi \right)}}{{B\left( \xi \right)}} - \frac{{\alpha \left( \xi \right) - 1}}{{2B\left( \xi \right)\gamma H\left( z \right)}}} \right){{A}_{p}}\left( \xi \right). \\ \end{gathered} $

Подставим выражение (8) в первое уравнение системы уравнений (5). В результате некоторых упрощений, опуская малые порядка ${{\epsilon }^{2}}$, приходим к дифференциальному уравнению для ${{A}_{p}}\left( \xi \right)$:

(9)
$\begin{gathered} \left( {\frac{{\left( {k\frac{d}{{d\xi }}U\left( \xi \right) + m\frac{d}{{d\xi }}V\left( \xi \right)} \right)\epsilon }}{{\sigma \left( \xi \right)}} + 2\epsilon \left( \xi \right)} \right)\frac{{d{{A}_{p}}\left( \xi \right)}}{{d\xi }} + \\ + \,\,D\left( \xi \right){{A}_{p}}\left( \xi \right) = 0, \\ \end{gathered} $
где

(10)
$\begin{gathered} D\left( \xi \right) = i\frac{{dn\left( \xi \right)}}{{d\xi }} - \frac{1}{{2\gamma H\left( z \right)}}\frac{{d\alpha \left( \xi \right)}}{{d\xi }} + \\ + \,\,\frac{{\left( {\alpha \left( \xi \right) - 1} \right)\left( {\alpha \left( \xi \right) - \gamma + 1} \right)}}{{2{{\gamma }^{2}}{{H}^{2}}\left( z \right)}} + \\ + \,\,\left( { - \left( \xi \right) + \frac{{\alpha \left( \xi \right) - 1}}{{2\gamma H\left( z \right)}}} \right)\frac{d}{{d\xi }}B\left( \xi \right)\left( {B{{{\left( \xi \right)}}^{{ - 1}}}} \right). \\ \end{gathered} $

Представим комплексную вертикальную компоненту волнового вектора (7) в виде n(ξ) = n1(ξ) + $ + \,\,{{n}_{2}}\left( \xi \right),$ где ${{n}_{1}}\left( \xi \right) = \epsilon \frac{{i\left( {k\frac{d}{{d\xi }}U\left( \xi \right) + m\frac{d}{{d\xi }}V\left( \xi \right)} \right)}}{{2\sigma \left( \xi \right)}}$. При действительных $k,m,\omega $, когда выражение в квадратных скобках в (7) положительно, функция ${{n}_{2}}\left( \xi \right)$ действительна, и поэтому роль вертикальной компоненты волнового вектора выполняет ${{n}_{2}}\left( \xi \right)$. Ели выражение в квадратных скобках в (7) отрицательное, то это соответствует отражению от соответствующего слоя, и волны распространяются горизонтально. Слагаемое ${{n}_{1}}\left( \xi \right)$ очевидно мнимое, и описывает изменение амплитуды волны с высотой на градиентах течения. Градиенты течения выполняют ту же роль, что и стратификация плотности, то есть приводят к изменению амплитуды волны с высотой. Однако эта зависимость существенно более сложная и зависит от параметров волны.

В линейной теории недиссипирующих атмосферных АГВ известен закон сохранения вертикального потока волнового действия (плотность волновой энергии, поделенная на частоту относительно течения) вдоль лучевой трубки в среде с плавно-меняющейся скоростью течения (см. например, [28]). Используя выражение для вертикального потока волнового действия для коротких AГВ с частотами много меньшими частоты Брента–Вяйсяля [29], можно показать, что относительная скорость изменения амплитуды волны с высотой совпадает с выражением для n1(ξ) в (7).

Решение уравнения (9) имеет вид

(11)
${{A}_{p}}\left( \xi \right) = {\text{exp}}\left( { - \mathop \smallint \limits_0^\xi \frac{{D\left( {\xi {\kern 1pt} '} \right)}}{{2\epsilon \left( {\xi {\kern 1pt} '} \right)}}d\xi {\kern 1pt} '} \right).$

Формулы приближения коротких вдоль вертикальной координаты волн полностью построены. Заметим, что в коротковолновых формулах (11) для ${{A}_{p}}\left( \xi \right)$ имеется некоторый произвол. У волновой коротковолновой моды параметры волны $k,m,\omega ,{{n}_{2}}\left( \xi \right)$ связаны дисперсионным соотношением (6). Поэтому некоторые из этих параметров могут быть выражены через другие. При этом вид формул изменится, хотя формулы будет эквивалентными. Также при интегрировании уравнения (9) можно ввести новую зависимую переменную ${{C}_{p}}\left( \xi \right) = {{A}_{p}}\left( \xi \right){\text{/}}f\left( \xi \right)$ и проинтегрировать уравнения в терминах этой переменной, а затем вернуться к ${{A}_{p}}\left( \xi \right)$. Это приведет к выражению для ${{A}_{p}}\left( \xi \right)$, которое отличалось от (11) на малые порядка $\epsilon $. То есть, возможно получить различные формулы для ${{A}_{p}}\left( \xi \right)$, но которые однако совпадают с точностью до малых следующего порядка.

4 АНАЛИЗ УСЛОВИЙ ПРИМЕНИМОСТИ ФОРМУЛ ВКБ. КРИТИЧЕСКИЕ УРОВНИ И ТОЧКИ ПОВОРОТА

Приближенные формулы написаны с использованием медленной переменной $\xi $. На этом этапе можно везде перейти обратно к обычной переменной $z$.

Согласно математической теории коротковолнового приближения [30], [31], выписанные формулы справедливы, если все коэффициенты уравнений описываются дважды-дифференцируемыми функциями, и если волны достаточно короткие вдоль вертикальной координаты $z:\epsilon \ll 1$.

Некоторые коэффициенты уравнений (2) содержат в знаменателе функцию $\sigma \left( z \right) = \omega - kU\left( z \right) - $ $ - \,\,mV\left( z \right)$, которая может принимать значение, равное нулю на некоторых высотах. При этом соответствующие коэффициенты обращаются в бесконечность. То есть, уравнения (2) могут содержать особые точки [32, 33] на высотах ${{z}_{0}}$, где $\sigma \left( {{{z}_{0}}} \right) = 0$. Если особая точка в уравнениях (2) присутствует на интервале высот от тропосферы до верхней атмосферы, то условия применимости коротковолнового приближения не выполнены на этом интервале высот, и коротковолновые формулы могут быть недостаточно точными для описания распространение волн с тропосферных высот в термосферу.

В геофизической литературе высота, на которой $\sigma \left( {{{z}_{0}}} \right) = 0$, называется критическим уровнем, и часто предполагается, что волна разрушается на критическом уровне. Далее мы будем придерживаться термина “особая точка”, поскольку он четко определен в теории линейных дифференциальных уравнений. Согласно классификации особых точек дифференциальных уравнений [32], обсуждаемая особая точка является слабой особой точкой. Поведение решения системы дифференциальных уравнений в окрестности слабой особой точки изучено. Согласно [32], решения уравнений (2) в окрестности особой точки ${{z}_{0}}$ можно записать в виде:

(12)
${{w}_{{1,2}}}\left( z \right) = {{\left( {z - {{z}_{0}}} \right)}^{{{{r}_{{1,2}}}}}}{{\tilde {w}}_{{1,2}}}\left( z \right),$
(13)
${{p}_{{1,2}}}\left( z \right) = {{\left( {z - {{z}_{0}}} \right)}^{{{{r}_{{1,2}}}}}}{{\tilde {p}}_{{1,2}}}\left( z \right),$
где
(13)
$\begin{gathered} {{r}_{{1,2}}} = \frac{1}{2} \pm \sqrt {1 - \frac{{4ga\left( {{{z}_{0}}} \right)\left( {{{k}^{2}} + {{m}^{2}}} \right)}}{{\gamma \left( {{{z}_{0}}} \right)H\left( {{{z}_{0}}} \right){{a}^{2}}\left( {{{z}_{0}}} \right)}}} , \\ a\left( {{{z}_{0}}} \right) = \frac{{d\sigma \left( {{{z}_{0}}} \right)}}{{dz}}, \\ \end{gathered} $
где функции ${{\tilde {w}}_{{1,2}}}\left( z \right)$, ${{\tilde {p}}_{{1,2}}}\left( z \right)$ представимы сходящимися в некоторой окрестности точки ${{z}_{0}}$ рядами Тейлора. Остальные функции, выписаны в (3). Эти функции бесконечны в особой точке, но сингулярность интегрируема.

Наличие слабой особой точки в уравнениях (2) еще не означает, что волна вблизи высоты особой точки разрушается вследствие больших амплитуд. В реальности амплитуды сдерживаются диссипативными процессами, не учитываемыми в данном упрощенном описании. Большие амплитуды локальны, и быстро исчезают при удалении от особой точки. Наконец, гидродинамические уравнения описывают потоки массы, энергии, импульса, которые сохраняются, хотя возможен обмен энергией волны с течением. Поэтому волна может преодолевать соответствующий уровень.

В работе [34] изучалось прохождение внутренних гравитационных волн через критический уровень в жидкости. Показано, что если число Ричардсона $R = \frac{{{{N}^{2}}}}{{U_{z}^{2} + V_{z}^{2}}}$ везде больше $\frac{1}{4}$, то волна преодолевает критический уровень, несколько ослабевая, и волна передает часть своего импульса среднему течению. Здесь $N$ – частота Вяйсяля-Брендта.

Групповая скорость акустических волн превышает скорости средних ветров, поэтому можно считать, что для акустических волн особые точки отсутствует.

Для внутренних гравитационных волн доплеровский сдвиг частоты $\Delta \left( z \right) = kU\left( z \right) + mV\left( z \right) \vee $ изображен на рис. 1 для ветров $\left( {U\left( z \right),V\left( z \right)} \right)$ из эмпирической модели горизонтального ветра HWM [35] для некоторых значений $k,m$. Высотные профили ветра построены для среднеширотной (далее обозначим как П1) и высокоширотной (далее обозначим как П2) атмосферы (рис. 1а, 1в). Экспериментальные работы [1, 36, 37] определяют периоды волн, генерируемых конвективными тропосферными процессами, в основном в промежутке от 12 минут до 3 часов. Характерная длина волны была определена в [1] около 200 км. Для оценки Δ(z) были выбраны волновые числа $k = 2\pi {\text{/}}\lambda $ и $m = - 2\pi {\text{/}}\lambda $, где $\lambda = 10,\,\,50,\,\,100,\,\,200,\,\,1000$ км.

Рис. 1.

Левая панель – зональная (штриховая линия) и меридиональная (сплошная линия) компоненты ветра эмпирической модели горизонтального ветра HWM для (а) для среднеширотной атмосферы и (в) высокоширотной атмосферы. Правая панель – $\Delta \left( z \right)$ при λ = $10,\,\,50,\,\,100,\,\,200,\,\,1000$ км для (б) для среднеширотной атмосферы и (г) высокоширотной атмосферы.

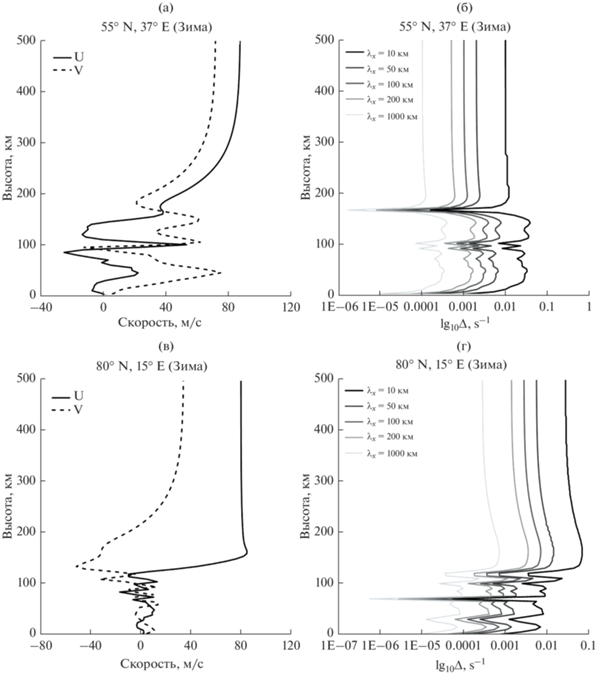
На рис. 1б, 1г представлены графики $\Delta \left( z \right)$ для волн с различными горизонтальными масштабами. Оценка максимумов $\Delta \left( z \right)$ для волн разной длины для двух выбранных вертикальных профилей горизонтального ветра представлена в табл. 1.

Таблица 1.  

Оценка сдвига частоты Δ(z) для волн разной длины для двух выбранных вертикальных профилей горизонтального ветра для среднеширотной (П1) и высокоширотной (П2) атмосферы

  $\lambda = 10$ км $\lambda = 50$ км $\lambda = 100$ км $\lambda = 200$ км $\lambda = 1000$ км
П1 (максимум), с–1 0.04 0.0078 0.004 0.002 0.0004
П2 (максимум), с–1 0.073 0.015000 0.0073 0.003674 0.00073

Мы видим, что интервал значений функции $\Delta \left( z \right)$ перекрывается с интервалом частот внутренних гравитационных волн, наблюдаемых в атмосфере. Следовательно, для внутренних гравитационных волн особые точки, определяемые уравнением σ(z) = 0, необходимо принимать во внимание.

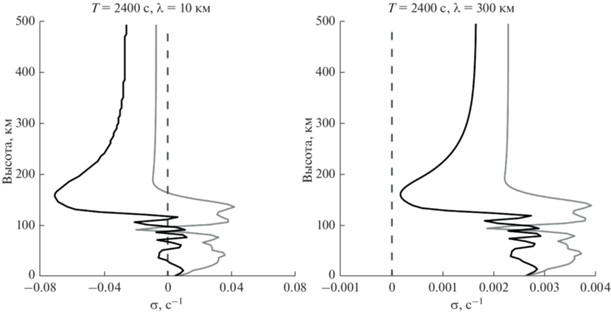
На рис. 2 даны графики $\sigma \left( z \right)$ для среднеширотной и высокоширотной атмосферы, П1 и П2. Для случая П2, количество возможных нулей равно 8, для случая П1 – около 10. В случае П2 (рис. 2), нули $\sigma \left( z \right)$ отсутствуют при $\lambda > 280$ км.

Рис. 2.

График $\sigma \left( z \right)$ для волн с частотой$\omega = 2\pi {\text{/}}2400$ c, длиной волны $\lambda = 10$ км (левая панель) и $\lambda $ = 300 км (правая панель). Серая сплошная линия построена для случая П1, черная сплошная линия - для случая П2. Серая штриховая линия обозначает ноль.

Из формулы (11) видно, что когда ${{n}_{2}}\left( z \right) = 0$, то знаменатель подынтегральной функции обращается в ноль, а сама подынтегральная функция обращается в бесконечность. Таким образом, использованное при выводе формул ВКБ-приближения предположение о том, что ${{A}_{p}}\left( \xi \right)$, ${{A}_{w}}\left( \xi \right)$ являются медленно изменяющимися функциями переменной z очевидным образом нарушается в окрестности точки, где ${{n}_{2}}\left( z \right) = 0$.

Такие точки, когда ${{n}_{2}}\left( z \right) = 0$, называются точками поворота [17, 21, 30, 38]. Точки поворота обычно интерпретируются физически как уровни, от которых волна отражается, потому что за точкой поворота волна затухает. В этом случае перед точкой поворота решение строится как суперпозиция волн, распространяющихся вверх и вниз. Коэффициенты этой суперпозиции, а также сшивание решений до и после точки поворота, обычно выводятся на основе специального асимптотического уравнения, описывающего поведение решения в переходной области ${{n}_{2}}\left( z \right) \approx 0$; это сделано, например, в работах [17, 21].

В [17, 21] доказано, что формулы ВКБ применимы, только если |$z - {{z}_{t}} \vee \gg {{\left( {{{\mu }^{{ - 2}}}2{{l}_{S}}} \right)}^{{1/3}}}$, где ${{z}_{t}}$ – высота точки поворота и $\mu $ – значение $\left| {{{n}_{2}}\left( z \right)} \right|$ вдали от точки поворота.

Влияние ветра на точку поворота в последующих оценках не учитывается. Ширину L окрестности точки поворота, в которой коротковолновые формулы не работают, можно оценить примерно как $L > 2H \approx 20{\kern 1pt} - {\kern 1pt} 60$ км. В [17, 21]. изучалась дифракция волн вдоль поверхности Земли, обусловленная тем, что в окрестности точки поворота волны отражаются вниз. Для рассмотрения этого эффекта вычисленная ширина $L$ незначительная. В вопросах параметризации волн в глобальных моделях вычисленная ширина переходной области может рассматриваться как значительная.

Для выполнения условия ${{n}_{2}}\left( z \right) = 0$ достаточно, чтобы подкоренная часть соотношения (7) была равна нулю. Обозначим подкоренную часть соотношения (7) как ${{n}_{{sqr}}}\left( z \right)$. При анализе одно из волновых чисел можно поворотом системы координат сделать равным нулю, пусто это будет $m = 0$. На рисунке 3 построен график функции ${{n}_{{sqr}}}\left( z \right)$ для различных значений $k,\omega ,$ компонентами ветра пренебрегаем. График дает представление о том, когда точка поворота существует и на каких высотах она типично располагается. Волновое число $k$ выбрано соответственно горизонтальным длинам волн ${{\lambda }_{x}}$ = 10, 100, 1000 км.

Рис. 3.

Левая панель - график функции ${{n}_{{sqr}}}\left( z \right)$ для значений $\omega $ = 6.3 × 10−6, 3.0 × 10−3, 1.9 × 10−2 с−1 (черная, серая и светло-серая сплошные линии соответственно) и $\omega = \sqrt {\frac{{q\left( {\gamma - 1} \right)}}{{2H}}} $ (малая штриховая линия) при (а) λx= 10 км, (б) λx = 100 км, (в) λx = 1000 км. Большая штриховая линия – ноль функции ${{n}_{{sqr}}}\left( z \right)$. Правая панель – увеличенные в области нуля графики левой панели.

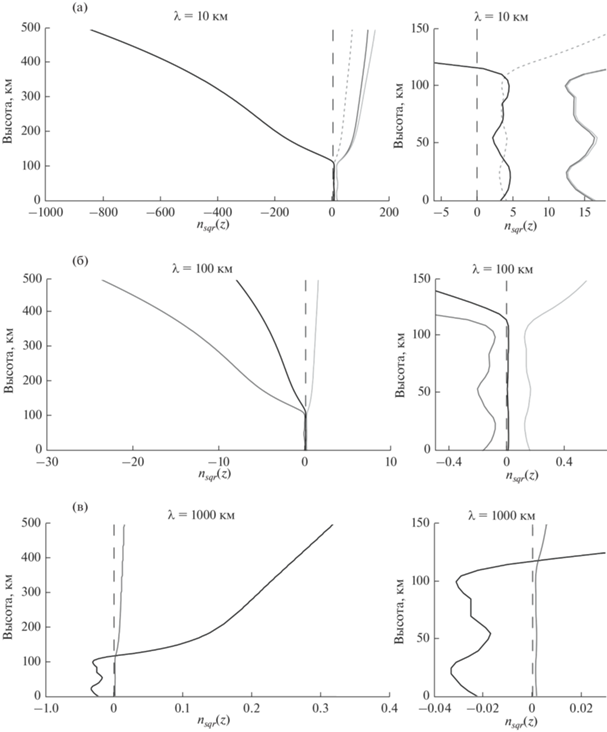
Видно, что при низких частотах на малых и средних горизонтальных масштабах волны (рис. 3а, 3б) график ${{n}_{{sqr}}}\left( z \right)$ всегда имеют одну точку ${{n}_{{sqr}}}\left( z \right) = 0$ на высотах от 110 до 130 км. Точки поворота; идущие из тропосферы волны из указанного дипазона отражаются вниз на этих высотах. На низких частотах при больших масштабах волн имеется другая точка поворота; она свидетельствует, что волны из указанного диапазона, распространяющиеся в верхней атмосфере, не проникают на тропосферные высоты.

С точки зрения параметризации эффектов волн в глобальных моделях важна только первая точка поворота. Несложно учесть, что волны из указанного диапазона не проникают выше 130 км.

5 ЗАКЛЮЧЕНИЕ

В данной работе применен метод разных масштабов для получения и анализа формул, описывающих гидродинамические поля атмосферных АГВ в приближении коротких по вертикали волн. В отличие от традиционного ВКБ-приближения, эти формулы включают в явном виде вертикальные градиенты фонового ветра и температуры. Это делает их удобными для параметризации динамических и тепловых эффектов АГВ в моделях атмосферной динамики и энергетики.

Сформулированы условия применимости приближенных формул для описания АГВ, распространяющихся с тропосферных высот до высот термосферы. Одним из условий применимости формул является отсутствие особых точек, в которых $\sigma \left( z \right) = 0$, в интервале высот от тропосферных до термосферных. При типичных профилях фонового ветра особые точки для акустических волн отсутствуют. Для ВГВ особые точки в уравнениях обычно присутствуют и их может быть несколько одновременно. Наличие особых точек характерно для более коротких волн, с горизонтальным масштабом меньше или порядка 10 км. Количество особых точек уменьшается с увеличением длины волны. Для волн с горизонтальным масштабом порядка или более 300 км особые точки обычно отсутствуют. Показано, обсуждаемые особые точки являются простыми, для которых решения в окрестности особой точки математически исследовано.

Другим условием применимости формул коротковолнового приближения является отсутствие точек поворота в интервале высот от тропосферы до верхней атмосферы.

Данное исследование выполнено при поддержке Российского научного фонда (грант 22-27-00171).

Список литературы

  1. Borchevkina O.P., Kurdyaeva Y.A., Dyakov Y.A., Karpo I.V., Golubko, G.V., Wang P.K., Golubkov M.G. Disturbances of the Thermosphere and the Ionosphere during a Meteorological Storm // Atmosphere. 2021. V. 12. P. 1384. https://doi.org/10.3390/atmos12111384

  2. Boška J., Šauli P. Observations of gravity waves of meteorological origin in the F-region ionosphere // Physics and Chemistry of the Earth. 2001. V. 26. P. 425–428. https://doi.org/10.1016/S1464-1917(01)00024-1

  3. Kumar K.V., Ajeet K.M., Kumar S., Singh R. July 22, 2009, Total Solar Eclipse induced gravity waves in the ionosphere as inferred from GPS observations over EIA // Advances in Space Research. 2016. V. 58. P. 1755–1762.

  4. Рыбнов Ю.С., Соловьев С.П. Cинхронные вариации атмосферного давления и электрического поля при прохождении солнечного терминатора // Геомагнетизм и аэрономия. 2019. Т. 59(2). С. 249–257.

  5. Захаров В.И., Куницын В.Е. Региональные особенности атмосферных проявлений тропических циклонов по данным наземных GPS-сетей // Геомагнетизм и аэрономия. 2012. Т. 52(4). С. 562.

  6. Перцев Н.Н., Шалимов С.Л. Генерация атмосферных гравитационных волн в сейсмически активном регионе и их влияние на ионосферу // Геомагнетизм и аэрономия. 1996. Т. 36(2), С. 111–118.

  7. Клименко М.В., Клименко В.В., Карпов И.В., Захаренкова И.Е. Моделирование сейсмоионосферных эффектов, инициированных внутренними гравитационными волнами // Химическая физика. 2011. Т. 30. (5). С. 41–49.

  8. Fritts D.C., Vadas S.L. et al. Wan and variable forcing of the middle atmosphere by gravity waves // Journal of Atmospheric and Solar-Terrestrial Physics. 2006. V. 68. P. 247–265.

  9. Lindzen R.S., Turbulence and stress owing to gravity wave and tidal breakdown // Journal of Geophysical Research. 1981. V. 86. P. 9707–9714.

  10. Holton J.R. The role of gravity wave induced drag and diffusion in the momentum budget of the mesosphere // Journal of the Atmospheric Sciences. 1982. V. 39. P. 791–799.

  11. Lindzen R.S., Holton J.R. A Theory of the Quasi-Biennial Oscillation // Journal of the Atmospheric Sciences. 1968. V. 25. P. 1095–1107. https://doi.org/10.1175/1520-0469(1968)025<1095: ATOTQB>2.0.CO;2

  12. Alexander M.J., Dunkerton T.J. A Spectral Parameterization of Mean-Flow Forcing due to Breaking Gravity Waves // Journal of the Atmospheric Sciences. 1999. V.56(24), P. 4167–4182.

  13. Weinstock J. Saturated and unsaturated spectra of gravity waves and scale-dependent diffusion //Journal of Atmospheric Sciences. 1990. V. 47(18). P. 2211–2226.

  14. Medvedev A.S., Klaassen G.P. Vertical evolution of gravity wave spectra and the parameterization of associated wave drag // Journal of Geophysical Research. 1995. V. 100. P. 25841–25853.

  15. Medvedev A.S., Klaassen G.P. Parameterization of gravity momentum deposition based on a nonlinear theory of wave spectra // Journal of Atmospheric and Solar-Terrestrial Physics. 2000. V. 62. P. 1015–1033.

  16. Yiğit E., Aylward A., Medvedev A.S. Parameterization of the effects of vertically propagating gravity waves for thermosphere general circulation models: Sensitivity study // Journal of Geophysical Research. 2008. V. 113. D19106. .https://doi.org/10.1029/2008jd010135

  17. Godin O. Wentzel–Kramers–Brillouin approximation for atmospheric waves // Journal of Fluid Mechanics. 2015. V. 777. P. 260–290. https://doi.org/10.1017/jfm.2015.367

  18. Gossard E.E., Hooke W.H. Waves in the atmosphere. Elsevier: Amsterdam, 1975, p. 456.

  19. Jones R.M., Georges T.M. Propagation of acoustic-gravity waves in a temperature- and wind-stratified atmosphere // Journal of the Acoustical Society of America. 1976. V. 59. P. 765–779.

  20. Fritt D.C., Alexander M.J. Gravity wave dynamics and effects in the middle atmosphere // Reviews of Geophysics. 2003. V. 41. P. 1003.

  21. Godin O.A. Diffraction of acoustic-gravity waves in the presence of a turning point // The Journal of the Acoustical Society of America. 2016. V. 140. P. 283. https://doi.org/10.1121/1.4955283

  22. Nayfeh A.H. Introduction to perturbation techniques. A Willey intersience publication. New York. 1981. 535 p.

  23. Найфэ А.Х. Методы возмущений. Москва. Мир. 1976. 456 с.

  24. Ostashev V.E., Wilson D.K. Acoustics in Moving Inhomogeneous Media. Second Edition. by CRC Press. 2019. 544 p.

  25. Brekhovskikh L.M., Godin O.A. Acoustics of Layered Media. Springer. 1998.

  26. Ostashev V.E. Equation for acoustic and gravity-waves in a stratified moving medium // Soviet Physics Acoustics. 1987. V. 33. P. 95–96.

  27. Yeh K.C. and Liu C.H. Acoustic-Gravity Waves in the Upper Atmosphere // Reviews of Geophysics and Space Physics. 1974. V. 12. P. 193–216.

  28. Лайтхилл Дж. Волны в жидкостях. Мир. М. 1981. 598 с.

  29. Gavrilov N.M., Fukao S.A. Comparison of Seasonal Variations of Gravity Wave Intensity Observed by the MU Radar with a Theoretical Model // Journal of the Atmospheric Sciences. 1999 V. 56(20). P. 3485–3494.

  30. Федорюк М.В. Асимптотические методы для линейных обыкновенных дифференциальных уравнений. Москва. Наука. 1983. 352 с.

  31. Федорюк М.В. Асимптотические методы в теории обыкновенных линейных дифференциальных уравнений // Математический сборник. 1969 Т. 79(121), № 4(8). С. 477–516.

  32. Камке Э. Справочник по обыкновенным дифференциальным уравнениям. Наука. Москва. 1976. 576 с.

  33. Смирнов В.И. Курс высшей математики. Т. 3, часть 2. М. 1974. 672 с.

  34. Booker J., Bretherton F. The critical layer for internal gravity waves in a shear flow // Journal of Fluid Mechanics. 1967. V. 27(3). P. 513–539. https://doi.org/10.1017/S0022112067000515

  35. Drob D.P., Emmert J.T., Meriwether J.W. et al. An update to the Horizontal Wind Model (HWM): The quiet time thermosphere // Earth and Space Science. 2015. V. 2. P. 301–319.

  36. Polyakova A.S., Perevalova N.P. Comparative analysis of TEC disturbances over tropical cyclone zones in the north-west Pacific Ocean // Advances in Space Research. 2013. V. 52. № 8. P. 1416–1426. https://doi.org/10.1016/j.asr.2013.07.029

  37. Куличков С.Н., Цыбульская Н.Д., Чунчузов И.П. и др. Исследования внутренних гравитационных волн от атмосферных фронтов в Московском регионе // Известия Российской академии наук. Физика атмосферы и океана. 2017. Т. 53(4). С. 455–469. https://doi.org/10.7868/S0003351517040031

  38. Дикий Л.А. Теория колебаний земной атмосферы. Ленинград. Гидрометеоиздат, 1969. 194 с.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Физика атмосферы и океана

Архивы выпусков Информация о журнале Отправить рукопись в журнал