Известия РАН. Физика атмосферы и океана, 2023, T. 59, № 2, стр. 217-229
Двухслойная модель циркуляции океана с вариационным управлением коэффициента турбулентной вязкости
В. Б. Залесный *
Институт вычислительной математики им. Г.И. Марчука РАН
119333 Москва, ул. Губкина, 8, Россия
* E-mail: vzalesny@yandex.ru
Поступила в редакцию 31.10.2022
После доработки 10.12.2022
Принята к публикации 11.01.2023
- EDN: HQJIJR
- DOI: 10.31857/S0002351523020104
Аннотация
Рассматривается развитие вариационного метода решения задачи квазигеострофической динамики в двухслойном периодическом канале. Развитие метода состоит в следующем. Во-первых, обобщается формулировка вариационной задачи: в вектор управления включается коэффициент турбулентного обмена квазигеострофического потенциального вихря (КГПВ). Во-вторых, область решения точнее описывает размеры Антарктического кругового течения (АКТ). Используя выделение зонального переноса и разложение решения в ряд Фурье, задача сводится к нелинейной системе обыкновенных дифференциальных уравнений (ОДУ) по времени. Двухсвязность области приводит к тому, что решение ОДУ должно удовлетворять дополнительному стационарному соотношению, определяющему расход АКТ. Вариационный алгоритм сводится к решению системы прямых и сопряженных уравнений, минимизирующему квадратичную погрешность стационарного соотношения. Коэффициент турбулентного обмена КГПВ определяется в процессе решения оптимальной задачи. Расчеты проводятся для периодического канала, имитирующего акваторию АКТ в Южном океане. Изучаются характеристики стационарных режимов течений при разных значениях модельных параметров. Типичной является синусоидальная циркуляция в обоих слоях с линейным переносом по ветру, зависящая от рельефа дна. В некоторых случаях под синусоидальной, в нижнем слое, формируется ячеистая циркуляция, а иногда возникает противотечение. При этом решение оптимальной задачи характеризуется низкой величиной коэффициента турбулентной вязкости и малым расходом течения в нижнем слое.
1. ВВЕДЕНИЕ
Современные задачи геофизической гидродинамики и общей циркуляции океана описываются как простыми, так и сложными физико-математическими моделями [McWilliams, 2006; Марчук, 2018а; Марчук, 2018б; Дымников, Залесный, 2019]. Простые – являются объектом математических исследований (теоремы и методы), а сложные – объектом моделирования и вычислительных экспериментов (прогнозы, ассимиляция наблюдений). К классу простых задач принадлежат, в частности, квазигеострофические модели [Pedlosky, 1970; Farhat et al., 2012; Павлушин и др., 2015; Cai et al., 2017; Ivchenko et al., 2018; Ивченко, Залесный, 2019; Chekroun et al., 2022].
Условно, в развитии всех моделей, включая квазигеострофические, можно выделить три основных направления. Первое связано с обобщением систем дифференциальных уравнений – включением дополнительных слагаемых и новых уравнений, их обоснованием и разрешимостью [Onica, Panetta, 2005; Agoshkov, Ipatova, 2010; Chen, 2019]. К нему можно отнести также изучение устойчивости и потери устойчивости течений, возникновения новых режимов, описание структуры и размерности аттракторов и т.д. [Bernier, 1994; Bernier, Chuesov, 2000; Cai et al., 2017; Дымников, Залесный, 2019; Chekroun et al., 2022]. Второе направление связано с увеличением пространственного разрешения численных моделей, поиском и испытанием новых алгоритмов решения задач супер-большой размерности, изучением свойств решений при долговременном интегрировании [Farhat et al., 2012; Дымников, Залесный, 2019]. Третье направление связано с формулировкой новых постановок задач и методов их решения: задачи с неполной информацией, в обратном времени, вариационная ассимиляция данных и т.д. [Agoshkov, Ipatova, 2010; Марчук, 2018а; Марчук, 2018б; Шутяев, 2019; Zalesny et al., 2020].
Наша работа относится к третьему направлению. В ней развивается двухслойная модель квазигеострофической циркуляции, рассмотренная ранее в [Pedlosky, 1970; Charney et al., 1981]. Квазигеострофические модели широко используются в теоретических и практических исследованиях. С их помощью развивается математическая теория, описывающая нелинейную устойчивость: динамические переходы сдвиговых течений, обусловленные бароклинной неустойчивостью; квазигеострофическую турбулентность; топологическую структуру аттракторов и т.д. Позволяя проводить длительное интегрирование с высоким пространственным разрешением, эти модели используются для расчета и анализа вихревой динамики морских циркуляций [Павлушин и др., 2015].
С физической точки зрения новизна нашей модели состоит в использовании параметризации турбулентной вязкости за счет вихревой динамики [Ivchenko et al., 2018; Ивченко, Залесный, 2019]. С вычислительной – в том, что постановка задачи и метод решения формулируются в рамках вариационного подхода, изложенного в [Залесный, 2022]. По сравнению с [Залесный, 2022] здесь внесены два основных изменения. Во-первых, обобщается формулировка вариационной задачи: в вектор управления включается коэффициент турбулентного обмена квазигеострофического потенциального вихря. Во-вторых, область решения точнее описывает размеры Антарктического кругового течения.
Следуя [Charney et al., 1981] и затем [Ivchenko et al., 2018; Ивченко, Залесный, 2019], при решении уравнений квазигеострофической циркуляции в периодическом канале используется выделение зонального переноса и разложение решения в ряды Фурье по широте, что позволяет разделить переменные. После преобразований задача сводится к нелинейной системе обыкновенных дифференциальных уравнений по времени. Численный алгоритм решения задачи формулируется в рамках вариационного усвоения данных. В отличие от [Залесный, 2022] в вектор управления наряду с начальными условиями для искомых функций (коэффициентов Фурье и бароклинной скорости течений) добавляется коэффициент турбулентного обмена КГПВ. Это позволяет в процессе решения системы оптимальности найти также коэффициент турбулентного обмена.
Дополнительная особенность задачи связана с тем, что она решается в двухсвязной области – периодическом зональном канале. Для атмосферы подобные задачи обычно рассматриваются на сфере или в двоякопериодической области. В океане наличие берегов приводит к формулировке задач в многосвязных областях [Chen, 2017; Дымников, Залесный, 2019]. Эта особенность увеличивает сложность вычислительного алгоритма не только для нелинейных, но и для линейных задач. Впервые краевые задачи данного типа, возникающие в теории упругости, были исследованы [Мусхелишвили, 1946] и получили название видоизмененная задача Дирихле. Методы и алгоритмы решения подобных задач океанологии и прикладной математики можно найти в [Каменкович, 1961; Волков, 1997; Дымников, Залесный, 2019; Chen, 2017; Chen, 2019]. Заметим, что в океанологии такие постановки задач позволяют определить расход течений между островами, в нашем случае – расход АКТ.
Основная цель данной работы связана с разработкой вариационного численного метода решения нестационарных уравнений КГПВ в периодическом канале по широте с расчетом коэффициента обмена. Основные особенности формулировки и метода решения задачи состоят в следующем. (1) Дифференциальные уравнения модели – нестационарные, включающие диффузионную параметризацию вихревого обмена КГПВ. (2) Следуя [Чарни и др., 1981], ищется частное решение, позволяющее разделить переменные и свести задачу к системе ОДУ по времени. Двухсвязность области приводит к тому, что решение ОДУ должно удовлетворять стационарному соотношению, с помощью которого определяется расход АКТ. (3) Задача для ОДУ с дополнительным соотношением решается в рамках вариационного подхода: ищется решение, удовлетворяющее системе прямых и сопряженных ОДУ – системы оптимальности [Дымников, Залесный, 2019]. На этом решении достигается минимум квадратичного функционала, или функции ценности. Функционал/ функция ценности формулируется на основе стационарного соотношения. (4) В вектор управления включаются начальные условия для решения прямой системы ОДУ: для 4-х коэффициентов Фурье и разности течений двух слоев (бароклинной скорости), а также коэффициент турбулентного обмена КГПВ. (5) В результате решения находятся восемь коэффициентов Фурье (для прямой и сопряженной систем), две бароклинные скорости (для прямого и сопряженного уравнения), сумма скоростей двух слоев (баротропная скорость) и коэффициент турбулентного обмена КГПВ.
Численные эксперименты проводятся для периодического канала, имитирующего акваторию АКТ в Южном океане. Изучаются стационарные режимы возбуждаемых ветром течений при разных значениях модельных параметров. Типичной является синусоидальная циркуляция в обоих слоях с линейным переносом по ветру, зависящая от рельефа дна. В некоторых случаях под синусоидальной в нижнем слое формируется ячеистая циркуляция, иногда сопровождаемая слабым противотечением.
1. ИСХОДНЫЕ УРАВНЕНИЯ
Исходную формулировку задачи запишем в терминах функции тока ${{\psi }_{1}},$ ${{\psi }_{2}}$ для двух слоев (1-й – верхний, 2-й – нижний) в прямоугольной периодической по x области $D$ [Ivchenko et al., 2018; Ивченко, Залесный, 2019; Залесный, 2022].
Уравнения имеют вид (здесь и далее $i = 1,\,2$)
(1.1)
$\begin{gathered} \frac{{\partial {{q}_{1}}}}{{\partial t}} + \frac{\partial }{{\partial x}}\left( { - \frac{{\partial {{\psi }_{1}}}}{{\partial y}}{{q}_{1}} - {{k}_{1}}\frac{{\partial {{q}_{1}}}}{{\partial x}}} \right) + \frac{\partial }{{\partial y}}\left( {\frac{{\partial {{\psi }_{1}}}}{{\partial x}}{{q}_{1}} - {{k}_{1}}\frac{{\partial {{q}_{1}}}}{{\partial y}}} \right) = \\ = {{\mu }_{1}}{{\Delta }^{2}}{{\psi }_{1}} + \frac{1}{{{{H}_{1}}}}\left( {\frac{{\partial {{\tau }_{y}}}}{{\partial x}} - \frac{{\partial {{\tau }_{x}}}}{{\partial y}}} \right), \\ \end{gathered} $(1.2)
$\begin{gathered} \frac{{\partial {{q}_{2}}}}{{\partial t}} + \frac{\partial }{{\partial x}}\left( { - \frac{{\partial {{\psi }_{2}}}}{{\partial y}}{{q}_{2}} - {{k}_{2}}\frac{{\partial {{q}_{2}}}}{{\partial x}}} \right) + \\ + \frac{\partial }{{\partial y}}\left( {\frac{{\partial {{\psi }_{2}}}}{{\partial x}}{{q}_{2}} - {{k}_{2}}\frac{{\partial {{q}_{2}}}}{{\partial y}}} \right) = \Delta \left( {{{\mu }_{2}}\Delta {{\psi }_{2}} - r{{\psi }_{2}}} \right), \\ \end{gathered} $(1.3)
$\begin{gathered} {{q}_{i}} = \Delta {{\psi }_{i}} + {{f}_{0}} + \beta y + \\ + \,\,{{\left( { - 1} \right)}^{i}}\alpha \frac{{{{\psi }_{1}} - {{\psi }_{2}}}}{{{{H}_{i}}}} + \left[ {1 + {{{\left( { - 1} \right)}}^{i}}} \right]\frac{{{{f}_{0}}B}}{{2{{H}_{i}}}}. \\ \end{gathered} $Для (1.1)–(1.2) поставим следующие граничные и начальные условия
(1.4)
${{\left. {{{\psi }_{i}}} \right|}_{{x = 0}}} = {{\left. {{{\psi }_{i}}} \right|}_{{x = {{L}_{x}}}}},\,\,\,\,{{\left. {\frac{{\partial {{\psi }_{i}}}}{{\partial x}}} \right|}_{{x = 0}}} = {{\left. {\frac{{\partial {{\psi }_{i}}}}{{\partial x}}} \right|}_{{x = {{L}_{x}}}}},$(1.5)
${{\left. {{{\psi }_{i}}} \right|}_{{y = 0}}} = 0,\,\,\,\,{{\left. {{{\psi }_{i}}} \right|}_{{y = L}}} = {\text{cons}}{{{\text{t}}}_{i}},$(1.6)
$\begin{gathered} {{k}_{i}}{{\left. {\frac{{\partial {{q}_{i}}}}{{\partial y}}} \right|}_{{y = 0}}} = {{k}_{i}}{{\left. {\frac{{\partial {{q}_{i}}}}{{\partial y}}} \right|}_{{y = L}}} = 0, \\ {{\mu }_{i}}{{\left. {\frac{{{{\partial }^{2}}{{\psi }_{i}}}}{{\partial {{y}^{2}}}}} \right|}_{{y = 0}}} = {{\mu }_{i}}{{\left. {\frac{{{{\partial }^{2}}{{\psi }_{i}}}}{{\partial {{y}^{2}}}}} \right|}_{{y = L}}} = 0, \\ \end{gathered} $Условия (1.5) вытекают из условий непротекания твердой стенки
Уравнения (1.1), (1.2) рассматриваются в пространственно – временной области $(0,T] \times D,$ где $t \in (0,T],$ $\left( {x,y} \right) \in D,$ а (1.3) – это дифференциальное выражение, которое следует подставить вместо ${{q}_{i}}$ в левую часть (1.1), (1.2).
2. ПРЕОБРАЗОВАНИЕ УРАВНЕНИЙ
Пусть компоненты ветра на поверхности океана заданы следующим образом
(2.1)
${{\tau }_{x}} = {{\tau }_{0}}\sin \left( {{{\pi y} \mathord{\left/ {\vphantom {{\pi y} L}} \right. \kern-0em} L}} \right),\,\,\,\,{{\tau }_{y}} = 0.$Будем искать решение (1.1)–(1.7) в виде [Чарни и др., 1981; Ivchenko et al., 2018]
(2.2)
${{\psi }_{i}} = - {{U}_{i}}y + {{\Phi }_{i}}\sin \left( {{{\pi y} \mathord{\left/ {\vphantom {{\pi y} L}} \right. \kern-0em} L}} \right),\,\,\,\,i = 1,2,$(2.3)
${{u}_{i}} \equiv - {{\left( {{{\psi }_{i}}} \right)}_{y}} = {{U}_{i}} - {\pi \mathord{\left/ {\vphantom {\pi L}} \right. \kern-0em} L}\cos \left( {{{\pi y} \mathord{\left/ {\vphantom {{\pi y} L}} \right. \kern-0em} L}} \right){{\Phi }_{i}},$(2.4)
${{v}_{i}} \equiv {{\left( {{{\psi }_{i}}} \right)}_{x}} = \sin \left( {{{\pi y} \mathord{\left/ {\vphantom {{\pi y} L}} \right. \kern-0em} L}} \right){{\Phi }_{{ix}}},$(2.5)
${{q}_{1}} = \Delta {{\psi }_{1}} + {{f}_{0}} + \beta y - \alpha {{\left( {{{\psi }_{1}} - {{\psi }_{2}}} \right)} \mathord{\left/ {\vphantom {{\left( {{{\psi }_{1}} - {{\psi }_{2}}} \right)} {{{H}_{1}}}}} \right. \kern-0em} {{{H}_{1}}}},$(2.6)
${{q}_{2}} = \Delta {{\psi }_{2}} + {{f}_{0}} + \beta y + \alpha {{\left( {{{\psi }_{1}} - {{\psi }_{2}}} \right)} \mathord{\left/ {\vphantom {{\left( {{{\psi }_{1}} - {{\psi }_{2}}} \right)} {{{H}_{2}}}}} \right. \kern-0em} {{{H}_{2}}}} + {{{{f}_{0}}B} \mathord{\left/ {\vphantom {{{{f}_{0}}B} {{{H}_{2}}}}} \right. \kern-0em} {{{H}_{2}}}},$(2.7)
$B = \sin \left( {{{\pi y} \mathord{\left/ {\vphantom {{\pi y} L}} \right. \kern-0em} L}} \right)h\left( x \right),$(2.8)
${{\Phi }_{i}} = \sum\limits_n {a_{n}^{{\left( i \right)}}\left( t \right)\cos \left( {Nx} \right)} + \sum\limits_n {b_{n}^{{\left( i \right)}}\left( t \right)sin\left( {Nx} \right)} ,$(2.9)
$h = \sum\limits_n {{{c}_{n}}\cos \left( {Nx} \right)} + \sum\limits_n {{{d}_{n}}sin\left( {Nx} \right)} ,$(2.10)
${{V}_{1}} = {{\left( {{{U}_{1}} + {{U}_{2}}} \right)} \mathord{\left/ {\vphantom {{\left( {{{U}_{1}} + {{U}_{2}}} \right)} 2}} \right. \kern-0em} 2},\,\,\,\,{{V}_{2}} = {{\left( {{{U}_{1}} - {{U}_{2}}} \right)} \mathord{\left/ {\vphantom {{\left( {{{U}_{1}} - {{U}_{2}}} \right)} 2}} \right. \kern-0em} 2},$(2.11)
$\begin{gathered} N = {{2\pi N} \mathord{\left/ {\vphantom {{2\pi N} {{{L}_{x}}}}} \right. \kern-0em} {{{L}_{x}}}},\,\,\,\,{{s}_{0}} = {{N}^{2}} + {{{{\pi }^{2}}} \mathord{\left/ {\vphantom {{{{\pi }^{2}}} {{{L}^{2}}}}} \right. \kern-0em} {{{L}^{2}}}},\,\,\,\,{{s}_{i}} = {{H}_{i}}{{s}_{0}} + \alpha , \\ n = 1,2,...,\,\,\,\,\alpha = {{f_{0}^{2}\left( {{{\rho }_{1}} + {{\rho }_{2}}} \right)} \mathord{\left/ {\vphantom {{f_{0}^{2}\left( {{{\rho }_{1}} + {{\rho }_{2}}} \right)} {\left[ {2g\left( {{{\rho }_{2}} - {{\rho }_{1}}} \right)} \right]}}} \right. \kern-0em} {\left[ {2g\left( {{{\rho }_{2}} - {{\rho }_{1}}} \right)} \right]}}, \\ \end{gathered} $Подставим (2.1)–2.6) в (1.1)–1.2) и преобразуем их, как это сделано в [Залесный, 2022]. После преобразований получим
(2.12)
$\begin{gathered} \left[ {\frac{\partial }{{\partial t}} + \left( {{{V}_{1}} + {{V}_{2}}} \right)\frac{\partial }{{\partial x}} - k\frac{{{{\partial }^{2}}}}{{\partial {{x}^{2}}}}} \right] \times \\ \times \,\,\left[ {{{H}_{1}}\left( {\frac{{{{\partial }^{2}}{{\Phi }_{1}}}}{{\partial {{x}^{2}}}} - \frac{{{{\pi }^{2}}}}{{{{L}^{2}}}}{{\Phi }_{1}}} \right) - \alpha \left( {{{\Phi }_{1}} - {{\Phi }_{2}}} \right)} \right] + \\ + \,\,\left( {\beta {{H}_{1}} + 2\alpha {{V}_{2}}} \right)\frac{{\partial {{\Phi }_{1}}}}{{\partial x}} + {{H}_{1}}\mu {{s}_{0}}\left( {\frac{{{{\partial }^{2}}{{\Phi }_{1}}}}{{\partial {{x}^{2}}}} - \frac{{{{\pi }^{2}}}}{{{{L}^{2}}}}{{\Phi }_{1}}} \right) = 0, \\ \end{gathered} $(2.13)
$\begin{gathered} \left[ {\frac{\partial }{{\partial t}} + ({{V}_{1}} - {{V}_{2}})\frac{\partial }{{\partial x}} - k\frac{{{{\partial }^{2}}}}{{\partial {{x}^{2}}}}} \right] \\ \times \left[ {{{H}_{2}}\left( {\frac{{{{\partial }^{2}}{{\Phi }_{2}}}}{{\partial {{x}^{2}}}} - \frac{{{{\pi }^{2}}}}{{{{L}^{2}}}}{{\Phi }_{2}}} \right) + \alpha \left( {{{\Phi }_{1}} - {{\Phi }_{2}}} \right) + {{f}_{0}}h} \right] + \\ + \,\,\left( {\beta {{H}_{2}} - 2\alpha {{V}_{2}}} \right)\frac{{\partial {{\Phi }_{2}}}}{{\partial x}} + {{H}_{2}}\left( {\mu {{s}_{0}} + r} \right) \times \\ \times \left( {\frac{{{{\partial }^{2}}{{\Phi }_{2}}}}{{\partial {{x}^{2}}}} - \frac{{{{\pi }^{2}}}}{{{{L}^{2}}}}{{\Phi }_{2}}} \right) = 0, \\ \end{gathered} $(2.14)
$\begin{gathered} - \frac{{3{{L}^{2}}\alpha }}{{{{\pi }^{2}}}}\frac{{\partial {{V}_{2}}}}{{\partial t}} + \frac{{2\alpha }}{{{{L}_{x}}}}\oint\limits_{{{L}_{x}}} {\frac{{\partial {{\Phi }_{1}}}}{{\partial x}}} {{\Phi }_{2}}dx - \\ - \,\,6k\alpha {{V}_{2}} + 3\left( {\frac{{{{\tau }_{0}}\pi }}{4} - k\beta {{H}_{1}}} \right) = 0, \\ \end{gathered} $(2.15)
$\frac{{3\pi {{\tau }_{0}}}}{8} = \frac{{{{f}_{0}}}}{{{{L}_{x}}}}\oint\limits_{{{L}_{x}}} {\frac{{\partial h}}{{\partial x}}} {{\Phi }_{2}}dx + \frac{3}{2}\beta k({{H}_{1}} + {{H}_{2}}).$Замечание. Соотношение (2.15) описывает стационарный баланс импульса. Импульс, внесенный в канал ветром (левая часть (2.15)) балансируется сопротивлением давления на рельефе дна за счет среднего потока (первый член правой части (2.15)) и параметризованных вихрей (второй член правой части (2.15)). В [Ivchenko et al., 2018] отмечалось, что сопротивление давления на рельефе дна – это основной механизм, обеспечивающий баланс импульса для Антарктического кругового течения.
Сформулируем вариационную постановку задачи. Среди всех возможных решений (2.12)–(2.14), зависящих от параметров ${{V}_{1}},k$ найти такие функции ${{\Phi }_{i}}\left( {t,x} \right),$ ${{V}_{2}}\left( t \right),$ которые доставляют минимум функционалу $J{\text{:}}$
(2.16)
$\begin{gathered} J \equiv \frac{1}{{2T{{L}_{x}}}}\int\limits_{{{t}_{0}}}^{{{t}_{0}} + T} {\oint\limits_{{{L}_{x}}} {\left\{ {{{f}_{0}}\frac{{\partial h}}{{\partial x}}{{\Phi }_{2}}} \right.} - } \\ {{\left. { - \frac{3}{2}\left[ {\frac{{\pi {{\tau }_{0}}}}{4} - \beta k({{H}_{1}} + {{H}_{2}})} \right]} \right\}}^{2}}dxdt \to \min . \\ \end{gathered} $Эта – задача нахождения условного минимума (2.16) в пространстве всевозможных решений (2.12)–(2.14), для которой можно применить метод множителей Лагранжа [Дымников, Залесный, 2019].
3. ЭНЕРГЕТИЧЕСКИЕ СООТНОШЕНИЯ
Умножим (2.12)–(2.15), соответственно на ${{\Phi }_{1}},{{\Phi }_{2}},$ ${{V}_{2}},$ $\left( {{{V}_{1}} - {{V}_{2}}} \right)$ и проинтегрируем их по замкнутому контуру ${{L}_{x}}{\text{:}}$ $0 \leqslant x \leqslant {{L}_{x}}.$ Складывая все уравнения, получим энергетическое соотношение для полной энергии $\Pi $
(3.1)
$\frac{{\partial \Pi }}{{\partial t}} = G + \frac{{kf_{0}^{2}{{L}^{2}}}}{{4{{H}_{2}}{{\pi }^{2}}{{L}_{x}}}}\oint\limits_{{{L}_{x}}} {h_{x}^{2}dx} - \left( {k\delta _{1}^{2} + r\delta _{2}^{2} + \mu {{s}_{0}}\delta _{3}^{2}} \right),$(3.2)
$\begin{gathered} \Pi = \frac{1}{{2{{L}_{x}}}}\oint\limits_{{{L}_{x}}} {\left[ {{{H}_{1}}\left( {\Phi _{{1x}}^{2} + \frac{{{{\pi }^{2}}}}{{{{L}^{2}}}}\Phi _{1}^{2}} \right) + } \right.} \\ + \,\,\left. {{{H}_{2}}\left( {\Phi _{{2x}}^{2} + \frac{{{{\pi }^{2}}}}{{{{L}^{2}}}}\Phi _{2}^{2}} \right) + \alpha {{{\left( {{{\Phi }_{1}} - {{\Phi }_{2}}} \right)}}^{2}} + \frac{{3{{L}^{2}}\alpha }}{{{{\pi }^{2}}}}V_{2}^{2}} \right]dx, \\ \end{gathered} $(3.3)
$\begin{gathered} \delta _{1}^{2} = \frac{1}{{{{L}_{x}}}}\oint\limits_{{{L}_{x}}} {\left[ {{{H}_{1}}\left( {\Phi _{{1xx}}^{2} + \frac{{{{\pi }^{2}}}}{{{{L}^{2}}}}\Phi _{{1x}}^{2}} \right) + {{H}_{2}}\Phi _{{2xx}}^{2} + } \right.} \frac{{{{H}_{2}}{{\pi }^{2}}}}{{{{L}^{2}}}} \times \hfill \\ \times \,\,\left. {{{{\left( {{{\Phi }_{{2x}}} - \frac{{{{f}_{0}}{{L}^{2}}}}{{2{{H}_{2}}{{\pi }^{2}}}}{{h}_{x}}} \right)}}^{2}} + \alpha {{{\left( {{{\Phi }_{{1x}}} - {{\Phi }_{{2x}}}} \right)}}^{2}} + 6\alpha V_{2}^{2}} \right]dx, \hfill \\ \end{gathered} $(3.4)
$\begin{gathered} \delta _{2}^{2} = \frac{1}{{{{L}_{x}}}}\oint\limits_{{{L}_{x}}} {{{H}_{2}}\left( {\Phi _{{2x}}^{2} + \frac{{{{\pi }^{2}}}}{{{{L}^{2}}}}\Phi _{2}^{2}} \right)} dx, \\ \delta _{3}^{2} = \frac{1}{{{{L}_{x}}}}\oint\limits_{{{L}_{x}}} {\left[ {{{H}_{1}}\left( {\Phi _{{1x}}^{2} + \frac{{{{\pi }^{2}}}}{{{{L}^{2}}}}\Phi _{1}^{2}} \right) + {{H}_{2}}\left( {\Phi _{{2x}}^{2} + \frac{{{{\pi }^{2}}}}{{{{L}^{2}}}}\Phi _{2}^{2}} \right)} \right]} dx, \\ \end{gathered} $(3.5)
$G = \frac{3}{2}\left[ {\frac{{\pi {{\tau }_{0}}}}{4}{{U}_{1}} - k\beta \left( {{{H}_{1}}{{U}_{1}} + {{H}_{2}}{{U}_{2}}} \right)} \right].$Из (3.1) имеем оценку изменения по времени полной энергии
(3.6)
$\begin{gathered} \frac{{\partial \Pi }}{{\partial t}} \leqslant \frac{3}{2}\left[ {\frac{{\pi {{\tau }_{0}}}}{4}{{U}_{1}} - k\beta \left( {{{H}_{1}}{{U}_{1}} + {{H}_{2}}{{U}_{2}}} \right)} \right] + \\ + \,\,\frac{{kf_{0}^{2}{{L}^{2}}}}{{4{{H}_{2}}{{\pi }^{2}}{{L}_{x}}}}\oint\limits_{{{L}_{x}}} {h_{x}^{2}dx} . \\ \end{gathered} $Из (3.6) видно, что энергия диссипирует пропорционально расходу АКТ (второе слагаемое правой части (3.6)) и генерируется ветром (первое слагаемое) при заданном рельефе дна (третье слагаемое). При увеличении ширины канала $L$ и номера гармоники по $x$ (интеграл от $h_{x}^{2}$ возрастает) верхняя граница изменения полной энергии увеличивается, а при увеличении длины канала ${{L}_{x}}$ и глубины нижнего слоя ${{H}_{2}}$ она уменьшается.
Предположим, что решение выходит на стационарный режим. Тогда из (3.1) следует
(3.7)
$\begin{gathered} \frac{3}{2}\left[ {\frac{{\pi {{\tau }_{0}}}}{4}{{U}_{1}} - k\beta \left( {{{H}_{1}}{{U}_{1}} + {{H}_{2}}{{U}_{2}}} \right)} \right] + \\ + \,\,\frac{{kf_{0}^{2}{{L}^{2}}}}{{4{{H}_{2}}{{\pi }^{2}}{{L}_{x}}}}\oint\limits_{{{L}_{x}}} {h_{x}^{2}dx} = k\delta _{1}^{2} + r\delta _{2}^{2} + \mu {{s}_{0}}\delta _{3}^{2}, \\ \end{gathered} $(3.8)
${{H}_{1}}{{U}_{1}} + {{H}_{2}}{{U}_{2}} \leqslant \frac{1}{\beta }\left[ {\frac{{\pi {{\tau }_{0}}}}{{4k}}{{U}_{1}} + \frac{{f_{0}^{2}{{L}^{2}}}}{{3{{H}_{2}}{{\pi }^{2}}{{L}_{x}}}}\oint\limits_{{{L}_{x}}} {h_{x}^{2}dx} } \right].$Положим в (3.7) ${{U}_{2}} = 0,$ тогда учитывая последнее слагаемое в (3.3), имеем
(3.9)
$U_{1}^{2} - \frac{1}{\alpha }\left( {\frac{{\pi {{\tau }_{0}}}}{{4k}} - \beta {{H}_{1}}} \right){{U}_{1}} - \frac{{f_{0}^{2}{{L}^{2}}}}{{6\alpha {{H}_{2}}{{\pi }^{2}}{{L}_{x}}}}\oint\limits_{{{L}_{x}}} {h_{x}^{2}dx} \leqslant 0.$Поскольку неравенство (3.9) имеет решение, скорость в нижнем слое может стремиться к нулю. Можно выписать формальную оценку сверху возникновения противотечения в нижнем слое, т.е. ${{U}_{2}} \leqslant 0.$ Из (3.7) следует, что это происходит при выполнении неравенства
(3.10)
$\begin{gathered} {{U}_{1}} \leqslant \frac{2}{{3\left( {{{\pi {{\tau }_{0}}} \mathord{\left/ {\vphantom {{\pi {{\tau }_{0}}} 4}} \right. \kern-0em} 4} - k\beta {{H}_{1}}} \right)}} \times \\ \times \,\,\left( {k\delta _{1}^{2} + r\delta _{2}^{2} + \mu {{s}_{0}}\delta _{3}^{2} - \frac{{kf_{0}^{2}{{L}^{2}}}}{{4{{H}_{2}}{{\pi }^{2}}{{L}_{x}}}}\oint\limits_{{{L}_{x}}} {h_{x}^{2}dx} } \right). \\ \end{gathered} $4. СИСТЕМА ОПТИМАЛЬНОСТИ И ВЫЧИСЛИТЕЛЬНЫЙ АЛГОРИТМ
После разложения функций ${{\Phi }_{i}},h$ в ряды Фурье по $x$ (2.8), (2.9), прямая система уравнений (2.12)–(2.15) принимает вид [Залесный, 2022]
(4.1)
$\begin{gathered} \left( {\frac{d}{{dt}} + k{{N}^{2}}} \right)\left( {{{s}_{1}}b_{n}^{{\left( 1 \right)}} - \alpha b_{n}^{{\left( 2 \right)}}} \right) - \\ - \,\,N\left[ {{{s}_{1}}\left( {{{V}_{1}} + {{V}_{2}}} \right) - \beta {{H}_{1}} - 2\alpha {{V}_{2}}} \right]a_{n}^{{\left( 1 \right)}} + \\ + \,\,\alpha N\left( {{{V}_{1}} + {{V}_{2}}} \right)a_{n}^{{\left( 2 \right)}} + \mu {{H}_{1}}s_{0}^{2}b_{n}^{{\left( 1 \right)}} = 0, \\ \left( {\frac{d}{{dt}} + k{{N}^{2}}} \right)\left( {{{s}_{2}}a_{n}^{{\left( 2 \right)}} - \alpha a_{n}^{{\left( 1 \right)}} - {{f}_{0}}{{c}_{n}}} \right) + \\ + \,\,N\left[ {{{s}_{2}}\left( {{{V}_{1}} - {{V}_{2}}} \right) - \beta {{H}_{2}} + 2\alpha {{V}_{2}}} \right]b_{n}^{{\left( 2 \right)}} \\ - \,\,N\left( {{{V}_{1}} - {{V}_{2}}} \right)(\alpha b_{n}^{{\left( 1 \right)}} + {{f}_{0}}{{d}_{n}}) + {{H}_{2}}{{s}_{0}}\left( {r + \mu {{s}_{0}}} \right)a_{n}^{{\left( 2 \right)}} = 0, \\ \end{gathered} $(4.2)
$\begin{gathered} \frac{{6\alpha {{L}^{2}}}}{\pi }\frac{{\partial {{V}_{2}}}}{{\partial t}} + 12\alpha k{{V}_{2}} + 2\alpha N\left( {a_{n}^{{\left( 1 \right)}}b_{n}^{{\left( 2 \right)}} - a_{n}^{{\left( 2 \right)}}b_{n}^{{\left( 1 \right)}}} \right) = \\ = 6\left( {\frac{{\pi {{\tau }_{0}}}}{4} - \beta k{{H}_{1}}} \right), \\ \end{gathered} $(4.3)
${{f}_{0}}N\left( {{{c}_{n}}b_{n}^{{(2)}} - {{d}_{n}}a_{n}^{{(2)}}} \right) + 3\left[ {\frac{{\pi {{\tau }_{0}}}}{4} - \beta k\left( {{{H}_{1}} + {{H}_{2}}} \right)} \right] = 0.$Решением (4.1)–(4.2) являются функции $a_{n}^{{\left( 1 \right)}},$ $b_{n}^{{\left( 1 \right)}},$ $a_{n}^{{\left( 2 \right)}},$ $b_{n}^{{\left( 2 \right)}},$ ${{V}_{2}}$ и параметры ${{V}_{1}},$ $k.$ Решение задачи должно удовлетворять интегральному соотношению (2.15).
Перепишем (4.1)–(4.2) в матричном виде
где вектор $\Psi = {{\left( {a_{n}^{{\left( 1 \right)}},b_{n}^{{\left( 1 \right)}},a_{n}^{{\left( 2 \right)}},b_{n}^{{\left( 2 \right)}},{{V}_{2}}} \right)}^{T}},$ $A,B$ – квадратные матрицы. Сформулируем вариационную постановку задачи (2.12)–2.14), (2.16).Будем искать такое решение (4.3) с неизвестными параметрами ${{V}_{1}},$ $k \equiv {{k}_{{opt}}},$ которое доставляет минимум функционалу $\Im $
(4.5)
$\begin{gathered} J = \frac{1}{{2T}}\int\limits_{{{t}_{0}}}^{{{t}_{0}} + T} {\left\{ {{{f}_{0}}\sum\limits_n {N\left( {a_{n}^{{\left( 2 \right)}}{{d}_{n}} - b_{n}^{{\left( 2 \right)}}{{c}_{n}}} \right) - } } \right.} \\ {{\left. { - \,\,3\left[ {\frac{{\pi {{\tau }_{0}}}}{4} - \beta k\left( {{{H}_{1}} + {{H}_{2}}} \right)} \right]} \right\}}^{2}}dt. \\ \end{gathered} $Отметим, что минимум среднеквадратического отклонения левой части (2.15) от нуля требуется на интервале ${{t}_{0}} \leqslant t \leqslant {{t}_{0}} + T.$ Эта задача с помощью стандартного вариационного метода сводится к системе оптимальности, включающей прямые (4.1)–(4.2) и сопряженные уравнения (см. [Залесный, 2022]).
Замечание. Сопряженные уравнения получаются умножением (4.1)–(4.2), соответственно на $a_{n}^{{\left( 1 \right)*}},$ $b_{n}^{{\left( 1 \right)*}},$ $a_{n}^{{\left( 2 \right)*}},$ $b_{n}^{{\left( 2 \right)*}},$ $V_{2}^{*},$ интегрирования их по времени от ${{t}_{0}}$ до ${{t}_{0}} + T$ и приравнивания нулю производных по $a_{n}^{{\left( 1 \right)}}\left( t \right),\,b_{n}^{{\left( 1 \right)}}\left( t \right),\,a_{n}^{{\left( 2 \right)}}\left( t \right),\,b_{n}^{{\left( 2 \right)}}\left( t \right),\,{{V}_{2}}\left( t \right)$, и по начальным и конечным данным $a_{n}^{{\left( 1 \right)}}\left( {{{t}_{0}}} \right),$ $b_{n}^{{\left( 1 \right)}}\left( {{{t}_{0}}} \right),$ $a_{n}^{{\left( 2 \right)}}\left( {{{t}_{0}}} \right),$ $b_{n}^{{\left( 2 \right)}}\left( {{{t}_{0}}} \right),$ ${{V}_{2}}\left( {{{t}_{0}}} \right),$ $a_{n}^{{\left( 1 \right)}}\left( {{{t}_{0}} + T} \right),$ $b_{n}^{{\left( 1 \right)}}\left( {{{t}_{0}} + T} \right),$ $a_{n}^{{\left( 2 \right)}}\left( {{{t}_{0}} + T} \right),$ $b_{n}^{{\left( 2 \right)}}\left( {{{t}_{0}} + T} \right),$ ${{V}_{2}}\left( {{{t}_{0}} + T} \right).$ В сопряженные уравнения добавляются также производные от (4.5) по искомым компонентам $a_{n}^{{\left( 2 \right)}},b_{n}^{{\left( 2 \right)}},k.$ Таким образом, система оптимальности включает пять прямых и пять сопряженных уравнений. Искомыми переменными являются десять функций $a_{n}^{{\left( 1 \right)}}\left( t \right),$ $b_{n}^{{\left( 1 \right)}}\left( t \right),...,$ $b_{n}^{{\left( 2 \right)*}}\left( t \right),$ $V_{2}^{*}\left( t \right)$ плюс два неизвестных параметра ${{V}_{1}}$ и ${{k}_{{opt}}}.$ Для их поиска используются компоненты градиента $\Im {\text{:}}$ ${{\left( {\partial \Im } \right)}_{{{{V}_{1}}}}},$ ${{\left( {\partial \Im } \right)}_{k}}.$
Полученная система оптимальности решается с помощью стандартной процедуры M1QN3 [Gilbert, Lemarechal, 1995]. В вектор управления решением входят начальные условия для прямой системы $a_{n}^{{\left( 1 \right)}},$ $b_{n}^{{\left( 1 \right)}},$ $a_{n}^{{\left( 2 \right)}},$ $b_{n}^{{\left( 2 \right)}},$ ${{V}_{2}}$ при $t = {{t}_{0}},$ а также искомые параметры ${{V}_{1}}$ и ${{k}_{{opt}}}.$ Для нахождения вектора управления используются семь соотношений для градиента $\Im {\text{:}}$ ${{\left( {\partial \Im } \right)}_{{a_{n}^{{\left( 1 \right)}}}}},...,{{\left( {\partial \Im } \right)}_{{{{V}_{2}}}}},$ ${{\left( {\partial \Im } \right)}_{{{{V}_{1}}}}},$ ${{\left( {\partial \Im } \right)}_{k}}.$ Алгоритм решения полученной системы оптимальности такой же, как в [Залесный, 2022], дополнительная компонента градиента ${{\left( {\partial \Im } \right)}_{k}}$ равна
(4.6)
$\begin{gathered} {{\left( {\partial \Im } \right)}_{k}} = \\ = \int\limits_{{{t}_{0}}}^{{{t}_{0}} + T} {N\left[ \begin{gathered} \left( {{{s}_{1}}a_{n}^{{\left( 1 \right)}} - \alpha a_{n}^{{\left( 2 \right)}}} \right)a_{n}^{{\left( 1 \right)*}}\, + \,\left( {{{s}_{1}}b_{n}^{{\left( 1 \right)}}\, - \,\alpha b_{n}^{{\left( 2 \right)}}} \right)b_{n}^{{\left( 1 \right)*}}\, + \\ + \,\,\left( {{{s}_{2}}a_{n}^{{\left( 2 \right)}} - \alpha a_{n}^{{\left( 1 \right)}}} \right)a_{n}^{{\left( 2 \right)*}} + \\ + \,\,\left( {{{s}_{2}}b_{n}^{{\left( 2 \right)}} - \alpha b_{n}^{{\left( 1 \right)}}} \right)b_{n}^{{\left( 2 \right)*}} + 3\beta {{H}_{1}}V_{2}^{*} \\ \end{gathered} \right]} dt. \\ \end{gathered} $Итак, по сравнению с [Залесный, 2022], в вектор управления добавлен коэффициент турбулентности k. В чем смысл этого расширения вектора управления? Коэффициент k появляется в модели в результате диффузионной параметризации вихревого потока квазигеострофического потенциального вихря [Ivchenko et al., 2018; Ивченко, Залесный, 2019]. При подобных параметризациях оценка коэффициента турбулентной вязкости k является, как правило, непростой задачей. Иногда его удается оценить лишь в некоторых пределах. Используя прямое моделирование и изменяя (сканируя) коэффициент турбулентности, его значение можно выбрать по близости решения к данным наблюдений. Иногда требуется большое число расчетов, причем величина коэффициента зависит от модели, пространственного разрешения, полноты и точности наблюдений и т.д.
Как облегчить решение задачи идентификации коэффициента k? Это можно сделать, например, в рамках вариационного подхода. Можно предположить, что k неизвестен, и поставить задачу его нахождения в результате минимизации некоторого функционала, описывающего разницу между модельным решением и данными наблюдений. Этот прием используется в 4DVAR моделях. В отличие от классического 4DVAR метода в нашем случае минимизируется не отклонение решения от данных наблюдений, а среднеквадратическое отклонение интегрального соотношения (2.15) от нуля. Напомним, что это интегральное соотношение возникает при поиске решения задачи для функции тока в двусвязной области [Ивченко, Залесный, 2018; Залесный, 2022]. Включение дополнительной компоненты в вектор управления приводит к варьированию k в итерационном процессе минимизации $\Im $ (обратно пропорционально ${{\left( {\partial \Im } \right)}_{k}}$) и в результате – к нахождению ${{k}_{{opt}}}.$ Численные эксперименты показывают, что данный прием повышает эффективность решения оптимальной задачи по сравнению с простым подбором k.
Один из практических приемов улучшения решения 4DVAR задач связан с изменением функции ценности (минимизируемого функционала). Если задача не решается или процесс поиска решения сходится медленно – следует попробовать изменить функционал. Примером может служить ε-регуляризация [Дымников, Залесный, 2019]. Если взглянуть на функционал (4.5), видно, что его величина зависит от параметра $k.$ Поскольку стационарное решение может существовать лишь при определенном выборе параметров, подбор k в процессе решения может не только улучшить сходимость решения вариационной задачи, но и ввести ее в область разрешимости или бóльшей устойчивости.
5. ЧИСЛЕННЫЕ РАСЧЕТЫ
Расчеты были проведены для периодического зонального канала протяженностью ${{L}_{x}} = 1.8 \times {{10}^{7}}$ м, шириной $L = {{10}^{6}}$ м, глубиной слоев ${{H}_{1}} = {{10}^{3}}$ и ${{H}_{2}} = 3 \times {{10}^{3}}$ м. Размеры расчетной области соответствуют бассейну Антарктического кругового течения, расположенному в Южном полушарии. В расчетах использовались следующие параметры ${{\tau }_{0}} = {{10}^{{ - 4}}}$ м2с–1, ${{f}_{0}} = - {{10}^{{ - 4}}}$ с–1, $\beta = 1.4 \times {{10}^{{ - 11}}}$ м–1с–1, $0 \leqslant \mu \leqslant 4 \times {{10}^{3}}$ м2с–1, $r = {{10}^{{ - 7}}}$ с–1, $\alpha = {{10}^{{ - 6}}}$ м–1.
Модельные параметры, как с оптимальным выбором коэффициента турбулентной вязкости (обозначается ${{k}_{{opt}}}$), так и с фиксированным (обозначается $k$), приведены в табл. 1, 2. Коэффициент турбулентной вязкости, полный расход и скорость течений приведены в следующих единицах $[k] = {{{\text{м}}}^{{\text{2}}}}{{{\text{с}}}^{{ - 1}}},$ $[{{V}_{{ACC}}}] = {\text{св}} \equiv {{10}^{6}}$ м3 с–1, VACC = $ = {{U}_{1}}{{H}_{1}} + {{U}_{2}}{{H}_{2}},$ $[{{U}_{i}}]$ = см с–1. Как и в [Залесный, 2022] оптимальная задача решалась с помощью алгоритма M1QN3 [Gilbert, Lemarechal, 1995].
Таблица 1.
Модельные параметры в первой серии расчетов, n = 1
| № | ${{c}_{n}}$ | ${{d}_{n}}$ | $k_{{opt}}^{0}$ ${{k}_{{opt}}}$ |
r | $\mu $ | $n$ | ${{U}_{1}},\,{{U}_{2}}$ ${\text{см/сек}}$ |
${{V}_{{ACC}}}$ ${\text{Св}}$ |
a1 × 104b1 × 104 | a2 × 104b2 × 104 | ${{J}_{{opt}}}$ × 1010 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 5.1 | 100 | 0 | 1100 1379 |
10–7 | 0 | 1 | 10 6 |
283 | 1.9 0.24 |
0.9 0.1 |
2 × 10–5 |
| 5.2 | 100 | 0 | 1000 1380 |
10–7 | 0 | 1 | 10 5.8 |
276 | 1.85 0.24 |
0.8 0.1 |
2 × 10–5 |
| 5.3 | 120 | 0 | 1000 1371 |
10–7 | 0 | 1 | 10 5.7 |
270 | 2.2 0.3 |
1.0 0.1 |
5 × 10–5 |
| 5.4 | 200 | 0 | 1000 1317 |
10–7 | 0 | 1 | 10 5.7 |
273 | 3.7 0.46 |
1.6 0.2 |
3 × 10–4 |
| 5.5 | 200 | 0 | 1000 1280 |
1.3 × 10–7 | 0 | 1 | 11 6.1 |
292 | 3.9 0.64 |
1.7 0.3 |
3 × 10–5 |
| 5.6 | 200 | 0 | 1000 1245 |
1.6 × 10–7 | 0 | 1 | 11 6.4 |
305 | 4.0 0.8 |
1.8 0.4 |
5 × 10–4 |
| 5.7 | 200 | 0 | 1000 1202 |
2 × 10–7 | 0 | 1 | 12 6.7 |
319 | 4.0 1.0 |
1.8 0.5 |
2 × 10–7 |
| 5.8 | 200 | 0 | 1000 1000 |
2 × 10–7 | 0 | 4 | 13 7.8 |
370 | 4.9 0.45 |
3.4 0.24 |
${{10}^{{ - 7}}}$ |
Первая серия расчетов. Первая серия расчетов (табл. 1), сделана для младшей гармоники разложения Фурье n = 1, см. (2.8), (2.9). Во всех вариантах первой серии 5.1–5.7 коэффициент турбулентной вязкости ${{k}_{{opt}}}$ находился в процессе решения системы оптимальности. Варианты отличались друг от друга тремя входными параметрами: высотой рельефа дна ${{c}_{1}}$ (${{c}_{1}}$ = 100, 120 и 200 м), коэффициентом придонного трения $r,$ и начальным приближением $k_{{opt}}^{0}$ в итерационном решении системы оптимальности. Например, в 5.2–5.7 было положено $k_{{opt}}^{0} = {{10}^{3}},$ в 5.1 $k_{{opt}}^{0} = 1.1 \times {{10}^{3}}$ (табл. 1).
Следует отметить, что невысокая изменчивость рельефа является типичной для моделей квазигеострофической циркуляции океана [Ivchenko et al., 2018]. В отличие от моделей, основанных на примитивных уравнениях, КГПВ-модели используются для качественного описания вихревой динамики и оценивать их количественные результаты следует весьма осторожно.
Замечание. При решении нелинейных систем оптимальности выбор начального приближения является непростой задачей. От него зависят как сама сходимость, так и скорость сходимости итерационного процесса, и при наличии нескольких локальных экстремумов – конечный результат. Мы не касаемся изучения данного вопроса, а просто указываем, какие параметры использованы при численном решении конкретных вариантов.
Основная цель первой серии расчетов – описать особенности стационарного решения оптимальной задачи и оценить его чувствительность к изменению параметров модели.
На рис. 1а, 1б приведены изолинии функции тока в верхнем и нижнем слое для варианта 5.1. Видно, что циркуляции в обоих слоях похожи и имеют синусоидальный вид. Отличия состоят в два раза большей интенсивности течений в верхнем слое, и наличии локальной замкнутой циркуляции в верхнем слое у северной границы.
Рис. 1
. Функция тока в верхнем слое. Вариант 5.1. По осям x, y указаны градусы по широте и долготе. ${{V}_{{ACC}}}$ = 283 Св (а); функция тока в нижнем слое. Вариант 5.1. ${{V}_{{ACC}}}$ = 283 Св (б).

Варианты 5.1–5.3 отличались друг от друга небольшим изменением начального приближения в итерационном процессе $k_{{opt}}^{0}$ и амплитуды рельефа дна. Во всех трех случаях решения оптимальной задачи – стационарны и близки. Небольшим изменениям параметров отвечают небольшие изменения полного расхода АКТ ${{V}_{{ACC}}}{\text{:}}$ от 283 до 270 Св и коэффициента ${{k}_{{opt}}}{\text{:}}$ от 1380 до 1371 м2/с. Расход АКТ в проливе Дрейка по результатам наблюдательных программ DRAKE и cDrake равен, соответственно, 141 и 173.3 Св [Xu et al., 2020]. Наша оценка завышена, но для подобного рода моделей это допустимо. Расчеты 5.4–5.7 сделаны для увеличенной амплитуды рельефа до 200 м и разных значений коэффициента придонного трения $r.$ Результаты расчетов показывают, что изменения решения также невелики. Как и в 5.1–5.3, решения – стационарны, минимизируемый функционал уменьшается почти до нуля: ${{J}_{{opt}}} \approx {{10}^{{ - 14}}} - {{10}^{{ - 16}}}.$ Коэффициент турбулентной вязкости и расход АКТ изменяются в разумных пределах $1.2 \times {{10}^{3}} \leqslant {{k}_{{opt}}} \leqslant 1.3 \times {{10}^{3}}$ м2/с, $273 \leqslant {{V}_{{ACC}}} \leqslant 319$ Св. Коэффициент ${{k}_{{opt}}}$ уменьшается при увеличении амплитуды рельефа и увеличении придонного трения. Уменьшение ${{k}_{{opt}}}$ в свою очередь приводит к увеличению расхода АКТ.
Кратко результаты первой серии можно суммировать следующим образом. (1) Расчеты показывают физически приемлемое описание характеристик АКТ. Метод позволяет не задавать, а находить коэффициент турбулентной вязкости ${{k}_{{opt}}},$ величина которого лежит в разумных пределах. (2) Чувствительность стационарного решения к небольшим изменениям входных параметров модели – невысокая. (3) Увеличение коэффициента придонного трения приводит к изменению (в данном случае уменьшению) ${{k}_{{opt}}}$ и затем остальных компонент решения. (4) Алгоритм работает быстро и позволяет вычислять стационарное решение с высокой точностью.
Вторая серия расчетов. Во второй серии расчетов был использован рельеф дна, описываемый гармоникой n = 2 с амплитудой 200 м. Входные параметры рассчитанных вариантов 5.9–5.16 находятся в таблице 2. Основная цель второй серии – уточнение алгоритмических аспектов нового метода, а также описание изменения режима циркуляции в нижнем слое – переход от синусоидальной к ячеистой структуре.
Алгоритмические аспекты нового алгоритма. Какие требования можно предъявить к предлагаемому методу? Зачем в поиск (или в само понятие) решения включать коэффициент турбулентной вязкости? Если бы требовалось приблизить модельное решение к описанию известной из наблюдений ситуации, то поиск коэффициента турбулентной вязкости был бы оправдан. Он является одним из ключевых параметров модели, определяющих конфигурацию решения, и его выбор может приблизить решение к данным наблюдений. В этом случае можно использовать стандартный метод 4-х мерного усвоения данных [Дымников, Залесный, 2019]. То есть, решая систему оптимальности, находить такое ${{k}_{{opt}}},$ при котором модельное решение минимально отклоняется от “данных наблюдений”.
В нашем случае задача несколько иная. Информации о том, какое решение нужно найти связано не с данными наблюдений, а с выполнением дополнительного условия на искомое решение. Формально, можно задавать разные $k$ в физически разумных пределах. Однако расчеты показывают, что стационарное решение задачи удается найти не для всех значений $k$ [Залесный, 2022], и его подбор (в результате сканирования) может быть не рациональным. Поэтому в данном случае включение $k$ в качестве дополнительно определяемой переменной может способствовать улучшению характеристик численного алгоритма. Вместо того, чтобы находить решение, задавая разные $k,$ можно его находить в процессе решения оптимальной задачи. Разумность этого предположения подтверждают результаты второй серии расчетов – см. варианты 5.14–5.16.
С физической точки зрения расширение понятия решения оптимальной задачи (с поиском ${{k}_{{opt}}}$) можно объяснить так. На основании гипотезы о параметризации турбулентной вязкости за счет вихревой динамики [Ivchenko et al., 2018; Ивченко, Залесный, 2019] формулируется дифференциальная форма параметризации с некоторым коэффициентом. Этот коэффициент определяется в процессе решения оптимальной задачи.
Выделим основные результаты алгоритмического характера.
(1) Система оптимальности с поиском ${{k}_{{opt}}}$ решается быстро и позволяет достаточно точно найти стационарное решение – табл. 2, варианты (5.10)–(5.14). Сравнение нового алгоритма с априори заданным $k$ показывает, что решения совпадают с высокой точностью (ср. 5.14, 5.15).
(2) В некоторых случаях видна повышенная чувствительность решения к изменению параметров $k,$ $\mu $ и начальному выбору $k_{{opt}}^{0}$ – варианты (5.9), (5.12), (5.15), (5.16) (табл. 2), а также (5.4)–(5.7) (табл. 1). Она проявляется в двух случаях: при недостаточно стационарном характере течения и кардинальной перестройки режима.
(3) Иногда (см. 5.9) решение не является “строго стационарным”. Это может быть связано с тем, что стационарная точка близка к “неустойчивой”, в окрестности которой происходит перестройка режима. Например, в варианте (5.9) функционал снижается до величины ${{J}_{{opt}}} \approx {{10}^{{ - 12}}},$ заметно большей, чем в других случаях.
(4) Имеются случаи кардинальной перестройки решения, связанные с увеличением параметров ${{k}_{{opt}}}$ (варианты 5.9, 5.14, 5.15) и $\mu $ (вариант 5.12), когда форма течения в нижнем слое переходит от синусоидальной к ячеистой. Причем, перестройка может происходить при отличии только начальных значений $k_{{opt}}^{0}{\text{:}}$ (5.9), (5.14). С физической точки зрения этот эффект можно описать так. От выбора $k_{{opt}}^{0}$ может зависеть вид предельной траектории, описывающей стационарный, квазистационарный или иной режим. В (5.9), (5.16) решение попадает в синусоидальный режим, (возможно близкий к нестационарному), а в (5.14), (5.15) – в стационарный ячеистый.
Ячеистая структура циркуляции в нижнем слое. В одном из расчетов предыдущей работы [Залесный, 2022] был получен режим циркуляции ячеистой структуры с противотечением в нижнем слое рис. 2а, 2б (в [Залесный, 2022] рисунки не приводятся). Он характеризовался снижением расхода АКТ до 52 Св. Причинами снижения расхода было увеличение номера гармоники и коэффициента придонного трения $r.$ В верхнем слое течение оставалось синусоидальным, а в нижнем возникала ячеистая структура с небольшим переносом против ветра.
Рис. 2
. Функция тока в верхнем слое. Вариант 2.4 [Залесный, 2022]. ${{V}_{{ACC}}}$ = 52 Св. Здесь ${{H}_{1}}$ = 1, ${{H}_{2}}$ = 4, ${{L}_{x}} = 4 \times {{10}^{6}},$ ${{c}_{5}}$ = 100. $k = {{10}^{3}},$ $r = {{10}^{{ - 6}}},$ $\mu $ = 1, $n$ = 5 (а); функция тока в нижнем слое. Вариант 2.4 [Залесный, 2022] (б).

В данной работе также получены режимы с ячеистой структурой. На рис. 3, 4 приведены результаты расчета вариантов 5.12 и 5.14. В обоих вариантах, отличающихся друг от друга значением $\mu $ (в 5.14 $\mu = 0,$ в 5.12 $\mu = 3 \times {{10}^{3}}$), решения близки. Если сравнивать эти случаи с вариантом 5.1, где $n = 1,$ а также 5.9–5.11 можно отметить следующее. В верхнем слое циркуляции 5.12, 5.14 синусоидальные, похожие на варианты 5.1, 5.9–5.11. В нижнем слое, однако, наблюдается принципиально иной, ячеистый режим. При этом расход АКТ значительно падает. В наших расчетах ячеистый режим возникает при увеличении ${{k}_{{opt}}}$ и $\mu ,$ но в большей степени он зависит от ${{k}_{{opt}}}$ (см. 5.15 и 5.16).
Рис. 3
. Функция тока в верхнем слое. Вариант 5.12. ${{V}_{{ACC}}}$ = 42 Св (а); функция тока в нижнем слое. Вариант 5.12. В красных тонах обозначены антициклональные, в синих – циклональные циркуляции. ${{V}_{{ACC}}}$ = 42 Св (б).
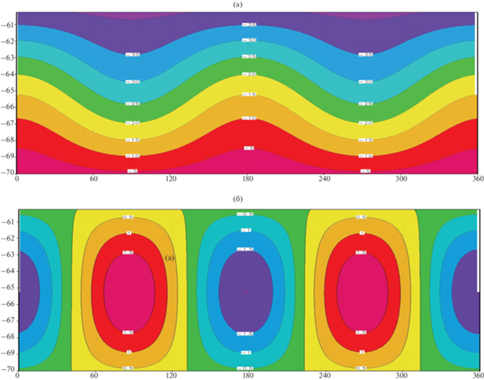
Рис. 4
. Функция тока в верхнем слое. Вариант 5.14. ${{V}_{{ACC}}}$ = 51 Св (а); функция тока в нижнем слое. Вариант 5.14. В красных тонах обозначены антициклональные, в синих – циклональные циркуляции. ${{V}_{{ACC}}}$ = 51 Св (б).

Сравнивая 5.14 (${{k}_{{opt}}} \approx 1341$) с 5.15, в котором $k$ априори задан ($k \equiv 1341$), видно, что алгоритмы дают практически одинаковый результат (табл. 2). С одной стороны это подтверждает правильность работы нового метода. С другой, – на основании расчетов с заданным $k$ (5.15, 5.16), можно заключить, что синусоидальный режим переходит в ячеистый, если $k$ лежит в интервале от 1210 до 1341 м2/с. Расход АКТ при этом уменьшается от 371 до 50.6 Св. Ячеистый режим характеризуется невысоким расходом АКТ, синусоидальной структурой в верхнем и ячеистой – в нижнем слое (рис. 4а, 4б). Скорость в верхнем слое значительно выше, чем в нижнем: ${{U}_{1}} \approx 4.6,$ ${{U}_{2}} \approx 0.2$ см/с. В верхнем слое у северной границы видны слабые циклональные ячейки циркуляции, расположенные над антициклонами нижнего слоя. Циклоны/антициклоны нижнего слоя расположены над впадинами/поднятиями рельефа дна. Экстремумы круговоротов немного смещены относительно экстремумов рельефа дна.
Таблица 2.
Модельные параметры второй серии расчетов, n = 2
| № | ${{c}_{n}}$ | ${{d}_{n}}$ | $k_{{opt}}^{0}$ ${{k}_{{opt}}}$ |
r | $\mu $ | $n$ | ${{U}_{1}},\,{{U}_{2}}$ ${\text{см/сек}}$ |
${{V}_{{ACC}}}$ ${\text{Св}}$ |
a1 × 104b1 × 104 | a2 × 104b2 × 104 | ${{J}_{{opt}}}$ × 1010 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 5.9 | 200 | 0 | 1000 1294 |
10–7 | 0 | 2 | 11 6.1 |
290 | 3.9 0.3 |
1.8 0.13 |
10–2 |
| 5.10 | 200 | 0 | 103 103 | 10–7 | 104 | 2 | 14 7.9 |
371 | 4.8 0.85 |
2.3 0.48 |
5 × 10–4 |
| 5.11 | 200 | 0 | 103 103 | 10–7 | 2 × 104 | 2 | 11 5.6 |
279 | 3.6 0.94 |
1.4 0.48 |
2 × 10–4 |
| 5.12 | 200 | 0 | 0 1393 |
10–7 | 3 × 103 | 2 | 4.2 0.005 |
42 | 1.9 0.24 |
–0.2 0.01 |
5 × 10–9 |
| 5.13 | 200 | 0 | 0 1383 |
10–7 | 4 × 103 | 2 | 4.3 0.02 |
43 | 0.6 0.01 |
–0.2 0.02 |
4 × 10–4 |
| 5.14 | 200 | 0 | 100 1341 |
10–7 | 0 | 2 | 4.6 0.2 |
51 | 1.1 –0.2 |
–0.27 0.07 |
7 × 10–7 |
| 5.15 | 200 | 0 | $k \equiv $ 1341 | 10–7 | 0 | 2 | 4.6 0.17 |
50.6 | 1.1 –0.2 |
–0.3 0.07 |
7 × 10–6 |
| 5.16 | 200 | 0 | $k \equiv $ 1282 | 10–7 | 0 | 2 | 11. 6.2 |
295 | 4.0 0.3 |
1.8 0.14 |
2 × 10–3 |
ВЫВОДЫ
Разработан новый вариационный метод решения задачи квазигеострофической динамики в двухслойном периодическом канале. Его основная новизна состоит в обобщении формулировки вариационной задачи: в вектор управления включается коэффициент турбулентного обмена квазигеострофического потенциального вихря ${{k}_{{opt}}}.$ Включение расширяет вектор-решение оптимальной задачи и позволяет вычислить значение коэффициента ${{k}_{{opt}}}.$ Используя разложение в ряды Фурье, задача сводится к эволюционной системе прямых и сопряженных уравнений для коэффициентов Фурье и бароклинной скорости ${{V}_{2}} = {{({{U}_{1}} - {{U}_{2}})} \mathord{\left/ {\vphantom {{({{U}_{1}} - {{U}_{2}})} 2}} \right. \kern-0em} 2}$ (где ${{U}_{i}}$ – скорость в $i$-том слое). Решение задачи параметрически зависит от неизвестной баротропной скорости ${{V}_{1}} = {{({{U}_{1}} + {{U}_{2}})} \mathord{\left/ {\vphantom {{({{U}_{1}} + {{U}_{2}})} 2}} \right. \kern-0em} 2}$ и коэффициента турбулентной вязкости КГПВ ${{k}_{{opt}}}.$ Следуя [Залесный, 2022], минимизируемый функционал формулируется на основе дополнительного соотношения, возникающего из-за двухсвязности области решения задачи. В отличие от [Залесный, 2022], в вектор управления вместе с начальными условиями для прямой системы и параметром ${{V}_{1}} = {{({{U}_{1}} + {{U}_{2}})} \mathord{\left/ {\vphantom {{({{U}_{1}} + {{U}_{2}})} 2}} \right. \kern-0em} 2},$ включается коэффициент турбулентного обмена КГПВ ${{k}_{{opt}}}.$
Численные эксперименты проводятся для периодического зонального канала, имитирующего акваторию Антарктического кругового течения в Южном океане. Изучаются особенности численного алгоритма и характеристики стационарных режимов течений, возникающих под действием ветра при разных значениях модельных параметров. Расчеты показывают физически приемлемое описание характеристик АКТ. Метод позволяет не задавать, а находить коэффициент турбулентной вязкости ${{k}_{{opt}}},$ величина которого лежит в разумных пределах.
Включение коэффициента турбулентной вязкости ${{k}_{{opt}}}$ в вектор управления увеличивает эффективность и точность решения оптимальной задачи. При одинаковой величине фиксированного $k = 1341$ (5.15, табл. 2) с рассчитанным (вариант 5.14, ${{k}_{{opt}}} = 100 \to 1341,$ табл. 2), алгоритмы дают одинаковые результаты. Используя алгоритм с фиксированным k, иногда трудно подобрать интервал его сканирования для поиска стационарного решения или решения заданной структуры. Новый алгоритм позволяет это сделать быстро и достаточно точно.
Расчеты показывают наличие случаев кардинальной перестройки решения. Они связаны с увеличением параметров ${{k}_{{opt}}}$ и $\mu ,$ когда форма течения в нижнем слое переходит от синусоидальной к ячеистой. Наряду с ячеистой структурой в нижнем слое режим характеризуется невысоким расходом АКТ и синусоидальной структурой течений в верхнем слое. При некоторых условиях в нижнем слое может формироваться течение противоположное направлению ветра.
Ячеистый режим может являться предвестником появления в нижнем слое слабого противотечения. Численные эксперименты позволяют описать следующую цепочку трансформаций. Интенсификация вихревой динамики, отражаемая ростом коэффициента турбулентного обмена ${{k}_{{opt}}},$ приводит к уменьшению расхода АКТ (согласно (3.8)), перестройки циркуляции в нижнем слое от синусоидальной к ячеистой, а при дальнейшем увеличении топографического сопротивления – к возникновению противотечения в нижнем слое. Указанная цепочка трансформации циркуляции в нижнем слое, включая изменения коэффициента обмена ${{k}_{{opt}}}$ и расхода АКТ, прослеживается лишь экспериментально. Из-за нелинейности исходной задачи ее трудно описать априори, Оценки, полученные при анализе энергетических соотношений являются апостериорными. Возникновение ячеистой циркуляции и, возможно, противотечения в нижнем слое вызывается ростом сопротивления на рельефе дна за счет вихревой активности – вклад второго слагаемого правой части в уравнении баланса момента (2.15) растет, вклад первого – уменьшается.
Работа выполнена при поддержке РНФ, грант № 20-11-20057.
Список литературы
Волков Е.А. О решении быстрым блочным методом видоизмененной задачи Дирихле на многосвязном многоугольнике // Труды МИАН. 1997. Т. 214. С. 135–144.
Дымников В.П., Залесный В.Б. Основы вычислительной геофизической гидродинамики. Москва: Геос, 2019. 448 с.
Залесный В.Б. Вариационный метод решения задачи о квазигеострофической циркуляции в океане // Изв. РАН. Физика атмосферы и океана. 2022. Т. 58. № 5. С. 493–503.
Ивченко В.О., Залесный В.Б. Диффузионно-ротационная параметризация вихревых потоков потенциального вихря: баротропное течение в зональном канале // Изв. РАН. Физика атмосферы и океана. 2019. Т. 55. № 1. С. 3–16.
Каменкович В.М. Об интегрировании уравнений теории морских течений в неодносвязных областях // ДАН СССР. 1961. Т. 138. № 5. С. 1076–1079.
Марчук Г.И. Избранные научные труды. Том II. Сопряженные уравнения и анализ сложных систем. Москва: РАН, 2018. 500 с.
Марчук Г.И. Избранные научные труды. Том 3. Модели и методы в задачах физики атмосферы и океана. Москва: РАН, 2018. 892 с.
Мусхелишвили Н.И. Сингулярные интегральные уравнения. М.-Л.: Гостехиздат, 1946. 448 с.
Павлушин А.А., Шапиро Н.Б., Михайлова Э.Н., Коротаев Г.К. Двухслойная вихреразрешающая модель ветровых течений в Черном море // Морской гидрофизический журн. 2015. № 5. С. 3−22.
Шутяев В.П. Методы усвоения данных наблюдений в задачах физики атмосферы и океана // Изв. РАН, Физика атмосферы и океана. 2019. Т. 55. № 1. С. 17–34.
Agoshkov V.I., Ipatova V.M. Convergence of solutions to the problem of data assimilation for a multilayer quasigeostrophic model of ocean dynamics // Russ. J. Numer. Anal. Math. Modelling. 2010. V. 25. № 2. P. 105–115.
Bernier C. Existence of attractor for the quasi-geostrophic approximation of the Navier-Stokes equations and estimate of its dimension // Adv. Math. Sci. Appl. 1994. V. 4. № 2. P. 465–489.
Bernier C., Chueshov I.D. The finiteness of determining degrees of freedom for the quasi-geostrophic multi-layer ocean model // Nonlinear Anal. Theory, Methods Appl. 2000. V. 42. № 8. P. 1499–1512.
Cai M., Hernandez M., Ong. K.W., Wang S. Baroclinic Instability and Transitions in a Two-Layer Quasigeostrophic Channel Model // arXiv:1705.07989 [physics], April 2017.
Charney J.G., Shukla J., Mo K.C. Comparison of a barotropic blocking theory with observation // J. Atmos. Sci. 1981. V. 38. P. 762–779.
Chekroun M.D., Dijkstra H., Şengül T., Wang S. Transitions of zonal flows in a two-layer quasi-geostrophic ocean model // Nonlinear Dynamics. 2022. V. 109. P. 1887–1904.
Chen Q. The Barotropic Quasi-Geostrophic Equation under a Free Surface // SIAM J. Math. Anal. 2017. V. 51. № 3. P. 1836–1867.
Chen Q. On the well-posedness of the inviscid multi-layer quasi-geostrophic equations // Discrete and continuous dynamical systems. 2019. V. 39. № 6. P. 3215–3237.
Farhat A., Panetta R.L., Titi E.S., Zian M. Long-time behavior of a two-layer model of baroclinic quasi-geostrophic turbulence // J. Mathematical Physics. 2012. V. 53. 115603.
Gilbert J.C., Lemarechal C.L. The modules M1QN3 and N1QN3. Version 2.0c (June 1995).
Ivchenko V.O., Zalesny V.B., Sinha B. Is the coefficient of eddy potential vorticity diffusion positive? Part 1: barotropic zonal channel // J. Phys. Oceanogr. 2018. V. 48. № 6. P. 1589–1607.
McWilliams J.C. Fundamentals of Geophysical Fluid Dynamics. Cambridge University Press, 2006. 299 p.
Onica C., R. Panetta L. Forced two layer beta-plane quasigeostrophic flow. Part I: Long-time existence and uniqueness of weak solutions // J. Differential Equations. 2006. V. 226. № 1. P. 180–209.
Pedlosky J. Finite-amplitude baroclinic waves // J. Atmospheric Sciences. 1970. V. 27. № 1. P. 15–30.
Xu X., Chassignet E.P., Firing Y.L., Donohue K. Antarctic Circumpolar Current transport through Drake Passage: What can we learn from comparing high-resolution model results to observations? // J. Geophysical Research: Oceans. 2020. V. 125. № 7. P. 1–16.
Zalesny V., Agoshkov V., Shutyaev V., Parmuzin E., Zakharova N. Numerical Modeling of Marine Circulation with 4D Variational Data Assimilation // J. Marine Science and Engineering. 2020. V. 8. № 7. 503.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Физика атмосферы и океана


