1. На главную
  2. Электронные версии
  3. Известия РАН. Физика атмосферы и океана
  4. T. 59, № 2, 2023

Известия РАН. Физика атмосферы и океана, 2023, T. 59, № 2, стр. 230-241

О видах неустойчивости геострофического течения с вертикальным параболическим профилем скорости

Н. П. Кузьмина a, *, С. Л. Скороходов b, **, Н. В. Журбас a, Д. А. Лыжков a

a Институт океанологии им. П.П. Ширшова РАН
117997 Москва, Нахимовский просп., 36, Россия

b ФИЦ “Информатика и Управление” РАН
119333 Москва, ул. Вавилова, 44, Россия

* E-mail: kuzmina@ocean.ru
** E-mail: sskorokhodov@gmail.com

Поступила в редакцию 20.06.2022
После доработки 28.08.2022
Принята к публикации 12.10.2022

Полный текст (PDF)

Аннотация

Проведен анализ неустойчивых возмущений геострофического течения конечного поперечного масштаба с параболическим вертикальным профилем скорости общего вида (с линейным и постоянным сдвигами скорости) в ограниченном по вертикали слое. Модель основана на уравнении потенциального вихря в квазигеострофическом приближении с учетом вертикальной диффузии импульса и массы. Уравнение и граничные условия сводились к спектральной задаче на собственные значения типа Орра–Зоммерфельда. Для поиска собственных функций и собственных значений использовался высокоточный аналитико-численный метод. Особое внимание уделялось изучению неустойчивых возмущений с фазовой скоростью, превышающей максимальную скорость потока. Такую неустойчивость следует отличать от бароклинной неустойчивости и неустойчивости критического слоя. Получено, что указанная неустойчивость может развиваться в океанских течениях при вариации параметров задачи в широком диапазоне значений, причем с увеличением числа Прандтля фазовая скорость таких возмущений увеличивается, и может существенно превышать максимальную скорость течения. Однако возникновение таких неустойчивых возмущений возможно только в случаях, когда максимум скорости течения находится внутри слоя (но необязательно в его центре). Получено также, что узкие течения (поперечный масштаб равен или меньше радиуса Россби) с параболическим вертикальным профилем могут быть неустойчивы. Максимально неустойчивые возмущения имеют приблизительно равные масштабы вдоль и поперек течения, то есть являются круглыми возмущениями. Представлено обсуждение различных видов неустойчивости геострофического течения с параболическим вертикальным профилем скорости применительно к океану.

Ключевые слова: неустойчивость океанских геострофических течений, диффузия импульса и массы, задача на собственные значения

1. ВВЕДЕНИЕ

В работах [Кузьмина, 2016; Kuzmina, 2016; Скороходов, Кузьмина, 2016; Кузьмина и др., 2018; Zhurbas, 2018; Скороходов, Кузьмина, 2018; Кузьмина и др., 2019] получено, что при неустойчивости геострофического течения с большим поперечным масштабом и с параболическим вертикальным профилем скорости возникают растущие со временем возмущения, фазовая скорость которых превышает максимальную скорость течения. Такую неустойчивость нельзя отнести к бароклинной неустойчивости и неустойчивости критического слоя (подробнее см. в [Кузьмина и др., 2018]), поэтому изучение такой неустойчивости представляет определенный интерес.

В перечисленных работах анализ устойчивых и неустойчивых возмущений зонального течения в ограниченном по вертикали слое проводился на основе уравнения потенциального вихря в квазигеострофическом приближении с учетом вертикальной диффузии импульса и массы. При этом полагалось, что течение характеризуется только линейным по вертикали сдвигом и имеет максимум скорости в центре слоя. Однако исследования [Скороходов, Кузьмина, 2021] на основе аналогичной модели динамики течения с линейным и постоянным вертикальными сдвигами и с максимумом скорости на верхней или нижней границах слоя, показали, что фазовая скорость неустойчивых возмущений не превышает максимальной скорости течения. Учитывая, что анализ неустойчивых возмущений разного масштаба важен для исследования динамики океана (в частности, для понимания процесса образования интрузий в Арктическом бассейне [Кузьмина и др., 2014; Кузьмина, 2016; Kuzmina, 2016; Скороходов, Кузьмина, 2016; Кузьмина и др., 2018; Zhurbas, 2018]), представляется целесообразным выяснить, возникают ли неустойчивые возмущения, полученные в моделях [Кузьмина, 2016; Kuzmina, 2016; Скороходов, Кузьмина, 2016; Кузьмина и др., 2018; Zhurbas, 2018; Скороходов, Кузьмина, 2018; Кузьмина и др., 2019], только в частном случае параболического течения с максимумом скорости в центре слоя, или они типичны для более общего вида течения с вертикальным параболическим профилем скорости. Данная работа посвящена, прежде всего, такому анализу. Особое внимание уделено также описанию неустойчивых возмущений в области узких течений с поперечными масштабами, равными или меньшими масштаба Россби (об узких и широких течениях или фронтах см. подробнее в [Кузьмина и др., 2020]), и обсуждению различных видов неустойчивости, которые могут возникать в зоне течения с параболическим вертикальным профилем скорости применительно к океану.

2. МОДЕЛЬНАЯ ЗАДАЧА

Для исследования методом малых возмущений неустойчивости зонального геострофического течения с вертикальным параболическим профилем скорости общего вида в ограниченном по вертикали слое мы будем опираться на линейное уравнение потенциального вихря в квазигеострофическом приближении с учетом вертикальной диффузии плавучести и трения (или диффузии массы и импульса). Впервые уравнение потенциального вихря с учетом диффузии массы и импульса для исследования неустойчивости геострофического течения с линейным вертикальным профилем скорости в полубезграничной по вертикали области было проанализировано на основе аналитических решений Майлзом [Miles, 1965]. Уравнение потенциального вихря в безразмерном виде для течения с параболическим вертикальным профилем, который имеет максимум в центре слоя, было выведено и подробно анализировалось в [Кузьмина и др., 2018; Кузьмина и др., 2019]. Для течения с вертикальным параболическим профилем общего вида оно выводится аналогично, и без учета β-эффекта сводится к следующему уравнению:

(1)
$\begin{gathered} ~\left( {\frac{\partial }{{\partial t}} + U\left( z \right)\frac{\partial }{{\partial x}}} \right)\left( {\frac{{{{\partial }^{2}}p}}{{\partial {{z}^{2}}}} + {\text{Bu}}\cdot{{\Delta }}p} \right) - U_{{zz}}^{{''}}\frac{{\partial p}}{{\partial x}} = \\ = \,\,\frac{1}{{\text{R}}}\left( {\frac{{{{\partial }^{4}}p}}{{\partial {{z}^{4}}}} + {\text{Pr}}\cdot{\text{Bu}}\frac{{{{\partial }^{2}}\Delta p}}{{\partial {{z}^{2}}}}} \right), \\ \end{gathered} $
где $p$ – возмущение давления, $U\left( z \right) = 1 - a{{z}^{2}} + bz$, $a = \frac{{{{s}_{1}}H_{0}^{2}}}{{{{U}_{0}}}}$, $b = \frac{{{{s}_{2}}{{H}_{0}}}}{{{{U}_{0}}}}$, ${{s}_{1}},~~{{s}_{2}}$ – положительные константы, характеризующие величины вертикальных линейного и постоянного сдвигов скорости, $~{{U}_{0}}$ – скорость течения в середине слоя, $2{{H}_{0}}$ – вертикальный масштаб слоя, ${\text{R}} = {{U}_{0}}H_{0}^{2}{\text{/}}\left( {KL} \right) = {\text{Pe}}{{H}_{0}}{\text{/}}L$ , ${\text{Pe}} = {{U}_{0}}{{H}_{0}}{\text{/}}K$ – число Пекле (аналог числа Рейнольдса), $K$– коэффициент вертикальной диффузии плавучести, ${\text{Bu}} = H_{0}^{2}N_{0}^{2}{\text{/}}\left( {{{f}^{2}}{{L}^{2}}} \right)$ – число Бургера (см., например, [Cushman-Roisin, 1994]), ${{N}_{0}}$ – частота плавучести в фоновом состоянии, $L$ – горизонтальный поперечный масштаб зонального геострофического течения, $f$ – параметр Кориолиса, ${\text{Pr}}$ – число Прандтля, $\Delta p = \frac{{{{\partial }^{2}}p}}{{\partial {{x}^{2}}}} + \frac{{{{\partial }^{2}}p}}{{\partial {{y}^{2}}}}$. Ось $x$ направлена на восток (зональная координата), ось y – на север (меридиональная координата), и ось $z$ – вверх. Скорость зонального течения направлена вдоль координаты x. Для определенности положим, что скорость течения на нижней границе слоя равна нулю, то есть ${{U}_{0}} = {{s}_{1}}H_{0}^{2} + {{s}_{2}}{{H}_{0}}~$, и, следовательно, $a + b = 1$.

Безразмерные переменные и искомая функция вводились по формулам: $x{\kern 1pt} * = x{\text{/}}L$, $y{\kern 1pt} * = y{\text{/}}L$, $z{\kern 1pt} * = z{\text{/}}{{H}_{0}}$ , $t{\kern 1pt} * = t{{U}_{0}}{\text{/}}L$, $p{\kern 1pt} * = p{\text{/}}{{p}_{0}}$, ${{p}_{0}}$ – размерная константа, $\left[ {{{p}_{0}}} \right] = {{{\text{м}}}^{{\text{2}}}}{\text{ }}{{{\text{с}}}^{{ - 2}}}$ (давление нормировано на отсчетную плотность). Звездочки, которыми отмечены безразмерные переменные и искомая функция, в (1) опущены.

Для анализа устойчивых и неустойчивых возмущений зонального геострофического течения мы будем опираться на уравнение (1) и следующие граничные условия:

(2)
$\begin{gathered} \left( {\frac{\partial }{{\partial t}} + \left( {1 - a{{z}^{2}} + bz} \right)\frac{\partial }{{\partial x}}} \right)\frac{{\partial p}}{{\partial z}} - \\ - \,\,\left( { - 2az + b} \right)\frac{{\partial p}}{{\partial x}} = \frac{1}{R}\frac{{{{\partial }^{3}}p}}{{\partial {{z}^{3}}}},\,\,\,\,z = \pm 1, \\ \end{gathered} $
(3)
$\frac{{\partial p}}{{\partial x}} = 0,\,\,\,\,y = 0,\,\,\,\,y = 1,$
(4)
$\frac{{{{\partial }^{2}}p}}{{\partial {{z}^{2}}}} = 0,\,\,\,\,z = - 1,\,\,\,\,z = 1.$

Условия (2) и условия (4) означают равенства нулю на верхней и нижней границах слоя вертикальной скорости и потоков плавучести соответственно. Равенства нулю меридиональной компоненты скорости возмущения на боковых границах среднего геострофического течения определяются условиями (3). Отметим, что члены в правой части уравнения (1) описывают влияние на динамику возмущений диссипативных процессов, причем первый член в скобке в правой части (1) описывает влияние вертикальной диффузии плавучести, а второй член – влияние вертикального трения. Обоснования граничных условий (4) сводятся к следующему: а) четвертый порядок уравнения (1) обусловлен учетом вертикальной диффузии плавучести; б) целесообразно рассматривать слой, на границах которого отсутствуют потоки тепла и соли (массы).

При $a = 1,~~b = 0$ (течение с параболическим профилем скорости с максимумом в центре слоя) уравнения (1)–(4) сводятся к задаче, рассмотренной в работах [Скороходов, Кузьмина, 2018; Кузьмина и др., 2019]. При $a = 0,~~b = 1$ (течение с постоянным вертикальным сдвигом скорости) уравнения (1)–(4) сводятся к аналогичной задаче [Кузьмина и др., 2020], которая рассматривалась в слое от $z = 0$ до $z = 1$.

Следуя стандартному подходу исследования неустойчивости геострофических течений (см., например, [Stern, 1975]), решение (1)–(4) будем искать в виде бегущего вдоль зональной координаты волнового возмущения: $p = F\left( z \right){{e}^{{ik\left( {x - ct} \right)}}}{\text{sin}}\left( {\pi ny} \right)$. Здесь мы ограничимся случаем $n = 1$: масштаб возмущения в меридиональном направлении равен масштабу фронта или течения (максимально растущая мода). Подставляя такое решение в (1)–(4), получим спектральную задачу на собственные значения:

(5)
$\begin{gathered} \left( {1 - a{{z}^{2}} + bz - c} \right)\left( {\frac{{{{d}^{2}}F}}{{d{{z}^{2}}}} - {\text{Bu}}\left( {{{k}^{2}} + {{\pi }^{2}}} \right)F} \right) + \\ + \,\,2aF = \frac{1}{{ik{\text{R}}}}\left( {\frac{{{{d}^{4}}F}}{{d{{z}^{4}}}} - {\text{Bu}} \cdot {\text{Pr}} \cdot \left( {{{k}^{2}} + {{\pi }^{2}}} \right)\frac{{{{d}^{2}}F}}{{d{{z}^{2}}}}} \right), \\ \end{gathered} $
(6)
$\begin{gathered} \left( {1 - a + b - c} \right)\frac{{dF}}{{dz}} - F\left( { - 2a + b} \right) = \\ = \,\,\frac{1}{{ik{\text{R}}}}\frac{{{{d}^{3}}F}}{{d{{z}^{3}}}},\,\,\,\,z = 1, \\ \end{gathered} $
(7)
$ - c\frac{{dF}}{{dz}} - F\left( {2a + b} \right) = \frac{1}{{ik{\text{R}}}}\frac{{{{d}^{3}}F}}{{d{{z}^{3}}}},\,\,\,\,z = - 1,$
(8)
$\frac{{{{d}^{2}}F}}{{d{{z}^{2}}}} = 0,\,\,\,\,z = - 1,\,\,\,\,z = 1,$
где $k$ – безразмерное волновое число вдоль координаты $x$, $с = {{с}_{1}} + i \cdot {{c}_{2}}$ – комплексная фазовая скорость, $i$ – мнимая единица. Возмущения растут со временем, то есть являются неустойчивыми, если ${{c}_{2}} > 0$.

Отметим, что уравнение (5) является аналогом известного уравнения Орра-Зоммерфельда [Lin, 1955]. Однако задача (5)–(8) существенно отличается от задачи Орра-Зоммерфельда граничными условиями (см., например, [Кузьмина и др., 2018; Zhurbas, 2018; Скороходов, Кузьмина, 2018; Кузьмина и др., 2019]). Отличительные особенности в постановке указанных задач приводят к существенным различиям в решениях.

3. РЕЗУЛЬТАТЫ РАСЧЕТОВ МОДЕЛЬНОЙ ЗАДАЧИ (5)–(8)

Для поиска собственных функций (СФ) и собственных значений (СЗ) модельной задачи (5)–(8) использовался высокоточный аналитико-численный метод решения уравнения 4-го порядка с малым параметром при старшей производной, разработанный ранее для решения задачи Орра–Зоммерфельда [Скороходов, 2007а; Скороходов, 2007б]. Данный метод был модифицирован с учетом граничных условий (6), (7), которые отличны от граничных условий задачи Орра–Зоммерфельда и включают искомый спектральный параметр в качестве множителя. Для эффективности решения настоящей задачи в широком диапазоне изменения волнового числа при проведении расчетов использовались построенные асимптотические разложения при $k \to 0$ [Скороходов, Кузьмина, 2018; Скороходов, Кузьмина, 2021], что позволило уменьшать время численного счета и получать собственные значения с большой точностью при произвольно малом изменении волнового числа.

Решениями уравнения (5), как и уравнения Орра-Зоммерфельда, являются непрерывно дифференцируемые функции. Для конкретных значений волнового числа $k$ и параметров задачи ${\text{Bu}}$, ${\text{Pr}}$, ${\text{R}}$, $a$ существует счетное множество дискретных СЗ задачи (5)–(8). Для удобства анализа СЗ представляют в координатных осях ${{c}_{1}}$, $~{{c}_{2}}$ и называют спектрами собственных значений (см., например, [Кузьмина и др., 2018; Zhurbas, 2018]). В настоящей работе нас будут, прежде всего, интересовать распределения СЗ в координатных осях ${{c}_{1}}$,$~{{c}_{2}}$ при непрерывном изменении волнового числа $k$, или, согласно общепринятой терминологии, траектории СЗ (см., например, [Скороходов, Кузьмина, 2018; Кузьмина и др., 2019; Скороходов, Кузьмина, 2021]) при различных значениях параметров задачи. Особое внимание, как уже говорилось выше, будет уделяться изучению неустойчивых возмущений с фазовой скоростью, превышающей максимальную скорость течения. Дополнительно будут представлены инкременты роста неустойчивых возмущений в зонах узких фронтов для различных значений параметров R задачи (5)–(8).

3.1. Траектории собственных значений для различных параметров задачи (5)–(8)

Метод решения общей задачи (5)–(8) существенно отличается от метода решения задачи [Скороходов, Кузьмина, 2018; Кузьмина и др., 2019], в которой рассматривался геострофический поток с максимумом в центре слоя, и решения искались в виде четных и нечетных функций. В общей задаче (5)–(8) особое внимание, с точки зрения изучения неустойчивости течения, уделялось первой и второй траекториям СЗ, на которых значения ${{c}_{2}}$ могли быть больше нуля. Естественно, что проводилась проверка корректности решений задачи (5)–(8) на основе сравнения решений двух задач при $a = 1$ в задаче (5)–(8).

На рис. 1а представлены первая и вторая траектории, рассчитанные при ${\text{Bu}} = 0.0001,~\,\,{\text{R}} = 10,~$ ${\text{Pr}} = 1,~\,\,a = 1$. Эти траектории с большой точностью совпадают с траекториями для четных и нечетных решений задачи [Скороходов, Кузьмина, 2018; Кузьмина и др., 2019]. В случае первой траектории (здесь она соответствует четным решениям) фазовая скорость неустойчивых возмущений превышает максимальную скорость потока (${\text{U}}\left( 0 \right) = 1$) для волновых чисел вплоть до $k \approx 0.5$. В случае второй траектории (соответствует нечетным решениям) превышение фазовой скорости неустойчивых возмущений над максимальной скоростью потока наблюдается вплоть до $k \approx 30$, то есть на длинах волн, значительно меньших поперечного масштаба течения. При небольшом уменьшении параметра $a$ ($a = 0.8,~~b = 0.2$) траектории незначительно меняются (рис. 1б), причем неустойчивые возмущения с фазовой скоростью, превышающей максимальную скорость потока (${\text{U}}\left( {0.125} \right) = 1.0125$), наблюдаются вплоть до тех же волновых чисел, что и при $a = 1$.

Рис. 1.

Первые (сплошные линии) и вторые (штриховые линии) траектории СЗ задачи (5)–(8) при ${\text{Bu}} = 0.0001,~~{\text{R}} = 10,~$ ${\text{Pr}} = 1$: (а) $a = 1$; (б) $a = 0.8$. Стрелками вдоль траекторий обозначены направления в сторону уменьшения волнового числа k.

Картина траекторий существенно меняется при $a = 0.5$ (рис. 2а, 2б) и тех же значениях остальных параметров, что и в рассмотренном выше случае. Фазовая скорость неустойчивых возмущений превышает максимальную скорость потока (${\text{U}}\left( {0.5} \right) = 1.125$) только, когда $k \leqslant 0.11$ (первая траектория) и $9.5 \leqslant k \leqslant 115$ (вторая траектория), причем инкремент роста возмущения при $k = 115$ (вторая траектория) значительно превышает инкремент роста возмущения при $k = 0.11$ (первая траектория). С увеличением числа Прандтля (рис. 2в, 2г) возрастают инкременты неустойчивых возмущений, и увеличивается область волновых чисел, при которых фазовая скорость неустойчивых возмущений превышает максимальную скорость потока: $~k \leqslant 1.2$ (первая траектория) и $9.5 \leqslant k \leqslant 140$ (вторая траектория).

Рис. 2.

Две первые траектории СЗ при Bu = 0.0001, R = 10, $a = 0.5$ для различных значений числа Прандтля: (а, б) Pr = 1; (в, г) Pr = 4. Точки на графиках соответствуют волновым числам: k = 0.1 (4), k = 1(3), k = 100 (2), k = 1000 (1). Первые траектории – сплошные линии, вторые траектории – штриховые линии.

Расчеты траекторий СЗ, рассмотренные выше, были выполнены для Bu = 0.0001, то есть для очень широких течений. Поэтому представляет интерес рассмотреть случай узкого течения (см. предложенные определения в [Кузьмина и др., 2020]), например, когда Bu = 1. На рис. 3а, 3б представлены первая и вторая траектории, рассчитанные при ${\text{Bu}} = 1,~$ ${\text{R}} = 1,~\,\,{\text{Pr}} = 1,\,\,a = 1$. В данном случае длинноволновые неустойчивые возмущения имеют фазовую скорость меньше максимальной скорости течения. Однако фазовая скорость неустойчивых возмущений при большем значении числа Прандтля (Pr = 4) и малых волновых числах (первая траектория) превышает максимальную скорость потока (рис. 3в).

Рис. 3.

Две первые траектории СЗ при Bu = 1, R = 1, $a = 1$ для различных значений числа Прандтля: (а, б) Pr = 1; (в, г) Pr = 4. Точки на графиках соответствуют волновым числам: k = 0.1 (4), k = 1(3), k = 100 (2), k = 1000 (1). Первые траектории – сплошные линии, вторые траектории – штриховые линии.

3.2. О влиянии изменения параметра a на фазовую скорость неустойчивых возмущений

Здесь нас будет интересовать изменение фазовой скорости неустойчивого возмущения с некоторым определенным волновым числом k при изменении параметра $a$ от 1 до 0, то есть при смещении расположения максимума скорости геострофического течения от центра слоя.

На рис. 4 представлено сравнение максимальной скорости течения с фазовой скоростью неустойчивого возмущения с волновым числом при изменении a от 1 до 0 для различных параметров Bu и чисел Прандтля (первые траектории).

Рис. 4.

Сравнение величин безразмерной максимальной скорости среднего геострофического течения вида $U = 1 - a{{z}^{2}} + bz$ (черные кружки) и фазовой скорости длинноволновых (k = 0.01) неустойчивых возмущений (крестики) при различных значениях $a$ ($a + b = 1$): (а, б) Bu = 0.0001, R = 10, Pr = 1 (а), Pr = 4 (б); (в, г) Bu = 0.1, R = 10, Pr = 1 (в), Pr = 4 (г). Результаты представлены для СЗ первых траекторий.

Представленные результаты расчетов показывают, что чем больше максимум скорости течения отклоняется от центра слоя, тем меньше различие между фазовой скоростью неустойчивого возмущения и максимальной скоростью течения. Тем не менее, диапазон изменения параметра $a$, при котором неустойчивое возмущение с волновым числом $k = 0.01$ имеет фазовую скорость, превышающую максимальную скорость потока, достаточно широк. Более того, при числах Прандтля, превышающих единицу, фазовая скорость неустойчивых возмущений может значительно превышать максимальную скорость потока. Данный результат может быть справедлив и для неустойчивых возмущений с волновым числом $k \geqslant 1$ при типичных значениях параметров задачи (см. рис. 5, а также рис. 2б, 2г).

Рис. 5.

Сравнение величин безразмерной максимальной скорости среднего геострофического течения вида $U = 1 - a{{z}^{2}} + bz$ (черные кружки) и фазовой скорости неустойчивых возмущений (крестики) для k = 1 и при различных значениях $a$ ($a + b = 1$), Bu = 0.1, Pr = 2: (а) R = 1; (б) R = 5. Результаты представлены для СЗ первых траекторий.

3.3. О неустойчивости узких течений

В [Скороходов, Кузьмина, 2019; Кузьмина и др., 2020] впервые было показано, что геострофические течения могут быть неустойчивы в случаях, когда параметр Bu равен или даже превышает единицу. В этих работах рассматривалась модель, аналогичная задаче (5)–(8), но для течения с линейным вертикальным профилем скорости. Этот результат кардинально отличается от результата, полученного в работе Иди [Eady, 1949] (см., также [Океанология, 1978]), где анализировалась устойчивость геострофического течения с линейным вертикальным профилем скорости в приближении идеальной жидкости, и было показано, что условием возникновения неустойчивости является неравенство ${{\left[ {{\text{Bu}}\left( {{{k}^{2}} + {{\pi }^{2}}} \right)} \right]}^{{0.5}}} < 2.399$ (подробнее см. [Океанология, 1978; Кузьмина и др., 2020]), то есть существует строгое ограничение на максимальное значение параметра Bu, которое меньше единицы.

Настоящий анализ показывает, что узкие геострофические течения диссипативной жидкости могут быть неустойчивы и в случае параболического вертикального профиля течения (рис. 3 и 6).

Рис. 6.

Две первые траектории СЗ при Bu = 1, R = 100, Pr = 1, $a = 1$. Точки на графиках соответствуют волновым числам: k = 0.1 (4), k = 1(3), k = 5 (2), k = 10 (1). Первая траектория (соответствует четным решениям) – сплошная линия, вторая траектория (соответствует нечетным решениям) – штриховая линия.

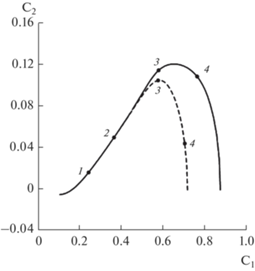
Удивительным результатом в случае узких течений при $a = 1$ и больших значениях параметра R (рис. 6) является то, что инкременты роста максимально неустойчивых возмущений первой (четные решения) и второй (нечетные решения) траекторий практически равны. Так, для четных решений максимальный инкремент роста возмущения равен $k{{c}_{2}} = 0.25098$ при $k = 4.70$, для нечетных решений имеем следующие значения: $k{{c}_{2}} = 0.25084$ при $k = 4.75$. Важно отметить, что для нечетных решений при $k = 4.7$ инкремент роста возмущения равен $k{{c}_{2}} = 0.25083$, то есть отличается от максимального инкремента всего на 0.00014. Таким образом, значения ${{с}_{1}}~\,{\text{и}}\,~{{с}_{2}}$ для четных и нечетных решений настолько близки по величине, что их траектории при больших волновых числах с большой точностью совпадают (рис. 6). Это обуславливает идентичные графики инкрементов роста в зависимости от волнового числа в зонах узких течений при больших значениях параметра R для возмущений первой (четные решения) и второй (нечетные решения) траекторий (рис. 7). Согласно рис. 7, волновые числа максимально растущих возмущений для значений параметра ${\text{R}} = 1,\,\,~10,\,\,~100$ и Bu = 1 меняются в пределах от 2-ух до приблизительно 5-ти, то есть такие возмущения можно отнести к практически круглым вихревым возмущениям. Время образования такого возмущения (увеличение амплитуды начального возмущения в e раз) при R = 100, L = 5000 м, ${{U}_{0}} = 0.03~\,\,{\text{м }}{{{\text{с}}}^{{ - 1}}}$ равно: $T\sim 0.7 \times {{10}^{6}}{\text{ с}} \approx 8$ суток.

Рис. 7.

Инкременты роста неустойчивых возмущений в зависимости от волнового числа при Bu = 1, Pr = 1, $a = 1$ и различных значениях параметра R: (а) четные решения; (б) нечетные решения; R = 1 (сплошные линии), R = 10 (штриховые линии); R = 100 (штрихпунктирные линии).

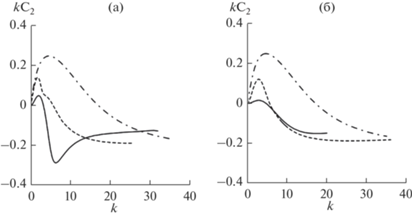
Очень узкое течение (Bu = 1.5) также может быть неустойчивым согласно расчетам, причем при R = 100 максимально растущие возмущения, соответствующие четным и нечетным решениям, имеют очень близкие по величине волновые числа и инкременты роста.

4. ОБСУЖДЕНИЕ РЕЗУЛЬТАТОВ РАСЧЕТОВ

Согласно работам [Кузьмина, 2016; Kuzmina, 2016; Скороходов, Кузьмина, 2016; Кузьмина и др., 2018; Zhurbas, 2018; Скороходов, Кузьмина, 2018; Кузьмина и др., 2019], в которых рассматривалась неустойчивость широких (Bu $ \ll $ 1) геострофических течений с максимумом скорости в центре слоя (параболический вертикальный профиль), растущие со временем возмущения с фазовой скоростью, превышающей максимальную скорость течения, возникают благодаря учету в уравнении потенциального вихря вертикальной диффузии массы и импульса. Настоящие результаты показали, что такие неустойчивые возмущения могут возникать и в области узких течений. Однако в общем случае течения с параболическим профилем такие неустойчивые возмущения возникают только тогда, когда максимум скорости течения находится внутри слоя (но необязательно в его центре).

Наиболее вероятно ожидать возникновение неустойчивых возмущений с фазовой скоростью, превышающей максимальную скорость потока, в области широких фронтов или течений (малые значения параметра Bu), причем, чем больше значение параметра R, тем меньше область волновых чисел растущих возмущений с большой фазовой скоростью. С увеличением числа Прандтля не только расширяется область волновых чисел возмущений, характеризующихся такой неустойчивостью, но наблюдается и значительное увеличение фазовой скорости возмущений по сравнению с максимальной скоростью потока. Важно также отметить, что обусловленные такой неустойчивостью возмущения, которые соответствуют СЗ первой траектории, имеют волновые числа, как правило, не превышающие единицы, в то время как возмущения, соответствующие СЗ второй траектории, могут иметь длину волны значительно меньше ширины течения.

В целом указанная неустойчивость может развиваться, согласно моделированию, при вариации параметров задачи в широком диапазоне значений.

Если сравнить данную неустойчивость с неустойчивостью критического слоя [Lin, 1955; Stern, 1975] (см. также обсуждение в работах [Кузьмина и др., 2019; Кузьмина и др., 2020]), то можно отметить, что и та и другая неустойчивость может возникать только с учетом диссипации. В отличие от неустойчивости с фазовой скоростью, превышающей максимальную скорость потока, неустойчивость критического слоя возникает на очень коротких длинах волн (при больших значениях волнового числа), причем инкременты роста ее возмущений могут при некоторых значениях параметров задачи превышать инкременты роста бароклинных возмущений [Кузьмина и др., 2019; Кузьмина и др., 2020]. Вероятно, что неустойчивость возмущений с большой фазовой скоростью возникает так же, как и неустойчивость критического слоя, из-за воздействия диссипации на фазы возмущений. Именно это и приводит к сложности понимания физики возникновения указанных видов неустойчивости в отличие, например, от некоторых случаев монотонной симметричной неустойчивости [Калашник, 2001], которая является основным механизмом образования интрузионного расслоения в океане [Stern,1967; Кузьмина, Родионов,1992; Журбас и др., 1993; Kuzmina, 2000; Kuzmina et al., 2011].

Наибольший интерес с точки зрения применения модельных результатов к океану вызывают, естественно, максимально растущие со временем возмущения. Подробное изучение максимально неустойчивых бароклинных возмущений и возмущений критического слоя в зонах течений различной ширины представлено в [Кузьмина и др., 2019; Скороходов, Кузьмина, 2021] (для течения с параболическим профилем с максимумом в центре слоя [Кузьмина и др., 2019] или на границе слоя [Скороходов, Кузьмина, 2021]) и в работе [Кузьмина и др., 2020] (для течения с линейным вертикальным профилем). В разделе 3.3 нас интересовала, прежде всего, возможность развития неустойчивости в области узкого течения с параболическим вертикальным профилем скорости с максимумом в центре слоя. Результаты расчетов показывают, что узкие течения с таким вертикальным профилем являются неустойчивыми для различных значений параметра R, причем максимально неустойчивые возмущения имеют приблизительно равные масштабы вдоль и поперек течения, то есть являются практически круглыми возмущениями. Удивительным результатом при больших значениях параметра R является то, что инкременты роста максимально неустойчивых возмущений первой (четные решения) и второй (нечетные решения) траекторий примерно равны. Это может определить достаточно сложную вертикальную структуру возмущений.

В заключение данного раздела остановимся на вопросах, касающихся постановки задачи.

По мнению авторов, задачу (1)–(4) и ее спектральный аналог (5)–(8), следует рассматривать как задачу, которая уточняет и дополняет описание неустойчивости геострофического течения в толще океана по сравнению с описаниями динамики течения в приближении идеальной жидкости. Решение такой задачи дает возможность получить новые результаты, так как уравнение потенциального вихря с учетом вертикальной диффузии плавучести является уравнением более высокого порядка по сравнению с аналогичным уравнением в приближении идеальной жидкости. Действительно, для всех неустойчивых возмущений идеальной жидкости верна теорема Ховарда о полукруге [Howard, 1961], которую в упрощенном виде можно свести к утверждению: фазовая скорость всех неустойчивых возмущений должна располагаться внутри интервала $\left[ {{{U}_{{{\text{min}}}}},{{U}_{{{\text{max}}}}}} \right]$, где ${{U}_{{{\text{min}}}}}$ и ${{U}_{{{\text{max}}}}}$ – минимальная и максимальная скорости потока соответственно (подробнее см. [Шакина, 2013]). В то время как решениями задачи (5)–(8) являются и такие неустойчивые возмущения, фазовая скорость которых выходит за правую границу этого интервала.

В представленной модели используются классические параметризации диффузии массы и импульса и граничные условия, при которых вертикальная скорость и потоки плавучести равняются нулю на горизонтальных границах (верхняя и нижняя границы слоя непроницаемы для переноса тепла и соли). Естественно, что при таких граничных условиях нельзя учесть влияние на динамику возмущений пограничных экмановских слоев, возникающих у дна и/или у поверхности. Однако известно, что трение в экмановских слоях может сужать область неустойчивых возмущений: на основе двухслойной модели описания неустойчивости геострофических течений [Педлоски, 1984] с учетом параметризации трения в экмановских слоях было получено, что трение стабилизирует длинные зональные возмущения. В связи с этим нельзя исключать, что спектр неустойчивых возмущений с фазовой скоростью, превышающей максимальную скорость потока, может быть сужен. Поэтому важно подчеркнуть, что растущие со временем возмущения с такой фазовой скоростью возникают при решении задачи (5)–(8) в широком диапазоне волновых чисел $0 < k < {{k}_{b}}$, причем правая граница этого интервала может значительно превышать единицу (см. раздел 3.1). Целесообразно отметить также, что сужение спектра неустойчивых возмущений можно получить на основе уравнения (5), если вместо граничных условий (8) формально (без необходимых физических обоснований) использовать граничные условия вида F(z) $ = 0$ при $z = \pm 1$, которые соответствуют условиям прилипания (нулевые значения горизонтальных скоростей возмущений на границах слоя). Однако и при таких граничных условиях существуют неустойчивые возмущения с фазовой скоростью, превышающей максимальную скорость потока: результаты расчетов траекторий СЗ для широких геострофических течений с вертикальным параболическим профилем скорости для частного случая $a = 1$ и обсуждение этих результатов представлены в работах [Скороходов, Кузьмина, 2018; Кузьмина и др., 2019].

5. ОСНОВНЫЕ ВЫВОДЫ

Первое. Получено, что при неустойчивости геострофического течения с параболическим вертикальным профилем скорости общего вида, максимальная скорость которого находится внутри слоя, могут возникать растущие со временем возмущения, фазовая скорость которых превышает максимальную скорость течения. Такую неустойчивость нельзя отнести к бароклинной неустойчивости и неустойчивости критического слоя. Таким образом, суммируя результаты работ [Кузьмина и др., 2019; Скороходов, Кузьмина, 2021] и настоящие расчеты, можно сказать, что в зоне течения с вертикальным параболическим профилем с учетом диссипации могут развиваться растущие со временем возмущения трех типов: бароклинные возмущения, возмущения критического слоя и возмущения, фазовая скорость которых превышает максимальную скорость потока.

Второе. Узкие течения с параболическим вертикальным профилем и поперечным масштабом, который равен или меньше радиуса деформации Россби, могут быть неустойчивыми. Максимально неустойчивые возмущения имеют приблизительно равные масштабы вдоль и поперек течения, то есть являются практически круглыми возмущениями. При $a = 1$ и больших значениях параметра R инкременты роста максимально неустойчивых возмущений первой (четные решения) и второй (нечетные решения) траекторий практически равны. Это может определить достаточно сложную вертикальную структуру возмущений.

Работа поддерживалась бюджетным финансированием Института океанологии им. П.П. Ширшова РАН (тема FMWE -2021-0001).

Авторы признательны анонимным рецензентам за полезные замечания.

Список литературы

  1. Журбас В.М., Кузьмина Н.П., Озмидов Р.В., Голенко Н.Н., Пака В.Т. О проявлении процесса субдукции в термохалинных полях вертикальной тонкой структуры и горизонтальной мезоструктуры во фронтальной зоне Азорского течения // Океанология. 1993. Т.33. № 3. С. 321–326.

  2. Калашник М.В. К теории симметричной и несимметричной устойчивости зональных геострофических течений // Изв. РАН. Физика атмосферы и океана. 2001. Т. 37, № 3. С. 418 –421.

  3. Кузьмина Н.П. Об одной гипотезе образования крупномасштабных интрузий в Арктическом бассейне// Фундаментальная и прикладная гидрофизика. 2016. Т.9. №2. С.15 –26.

  4. Кузьмина Н.П., Родионов В.Б. О влиянии бароклинности на образование термохалинных интрузий в океанских фронтальных зонах // Изв. РАН. Физика атмосферы и океана. 1992. Т. 28. № 10–11. С. 1077–1086.

  5. Кузьмина Н.П., Журбас Н.В., Емельянов М.В., Пыжевич М.Л. Применение моделей интерливинга для описания интрузионного расслоения на фронтах глубинной полярной воды Евразийского бассейна (Арктика) // Океанология. 2014. Т. 54. С. 594–604.

  6. Кузьмина Н.П., Скороходов С.Л., Журбас Н.В., Лыжков Д.А. О неустойчивости геострофического течения с линейным вертикальным сдвигом скорости на масштабах интрузионного расслоения // Изв. РАН. Физика атмосферы и океана. 2018. Т. 54. № 1. С. 54–63.

  7. Кузьмина Н.П., Скороходов С.Л., Журбас Н.В., Лыжков Д.А. Описание возмущений океанских геострофических течений с линейным вертикальным сдвигом скорости с учетом трения и диффузии плавучести// Изв. РАН. Физика атмосферы и океана. 2019. Т. 55. № 2. С. 73–85.

  8. Кузьмина Н.П., Скороходов С.Л., Журбас Н.В., Лыжков Д.А. О влиянии трения и диффузии плавучести на динамику геострофических океанских течений с линейным вертикальным профилем скорости// Изв. РАН. Физика атмосферы и океана. 2020.Т.56. № 6. С.676 – 688.

  9. Педлоски Дж. Геофизическая гидродинамика/ Под ред. Каменковича В.М., Монина А.С. М.: Мир, 1984. 812 с.

  10. Скороходов С.Л. Численный анализ спектра задачи Орра-Зоммерфельда // Журнал вычислительной математики и математической физики. 2007а. Т. 47. № 10. С. 1672–1691.

  11. Скороходов С.Л. Точки ветвления собственных значений оператора Орра-Зоммерфельда // Доклады Академии Наук. 2007б. Т. 416. № 5. С. 600–605.

  12. Скороходов С.Л., Кузьмина Н.П. Эффективный метод решения модифицированной задачи Орра-Зоммерфельда для анализа неустойчивости течений в Арктическом бассейне // Таврический вестник информатики и математики. 2016. № 3. С. 88 – 97.

  13. Скороходов С.Л., Кузьмина Н.П. Аналитико-численный метод решения задачи типа Орра-Зоммерфельда для анализа неустойчивости течений в океане // Журнал вычислительной математики и математической физики. 2018. Т. 58. № 6. С. 976–992.

  14. Скороходов С.Л., Кузьмина Н.П., Спектральный анализ модельных течений типа Куэтта применительно к океану// Журнал вычислительной математики и математической физики. 2019. Т. 59. № 5. С. 106 –127.

  15. Скороходов С.Л., Кузьмина Н.П. Спектральный анализ малых возмущений геострофических течений с параболическим вертикальным профилем скорости применительно к океану// Журнал вычислительной математики и математической физики. 2021. Т. 61. № 12. С. 2010–2023.

  16. Океанология. Физика океана. Том. 2. Гидродинамика океана / Под ред. Каменковича В.М., Монина А.С. М.: Наука, 1978. 456 с.

  17. Шакина Н. П. Лекции по динамической метеорологии. М.: Триада ЛТД, 2013. 160 с.

  18. Cushman-Roisin B. Introduction to the Geophysical Fluid Dynamics. New Jersey 07632, Englewood Cliffs: Prentice Hall, 1994. 320 p.

  19. Eady E.T. Long waves and cyclone waves // Tellus. 1949. Vol. 1 № 3. P. 33–52.

  20. Howard L.N. Note on paper of John W. Miles// Fluid Mech.1961.V.10. № 4. P. 509–512.

  21. Kuzmina, N. P. On the parameterization of interleaving and turbulent mixing using CTD data from the Azores Frontal Zone// J. Mar. Syst. 2000. V. 23. 285–302.

  22. Kuzmina, N.P. Generation of large-scale intrusions at baroclinic fronts: an analytical consideration with a reference to the Arctic Ocean // Ocean Science. 2016. V.12. P. 1269 – 1277. https://doi.org/10.5194/os-12-1269-2016

  23. Kuzmina N., Rudels B., Zhurbas V., Stipa T. On the structure and dynamical features of intrusive layering in the Eurasian Basin in the Arctic Ocean // J. Geophys. Res. 2011. Vol. 116. C00D11, https://doi.org/10.1029/2010JC006920

  24. Lin, C. C. The Theory of Hydrodynamic Stability. Cambridge University Press, 1955. 155 p.

  25. Miles, J. W. Effect of Diffusion on Baroclinic Instability of the Zonal Wind // J. Atmos. Sci. 1965. V. 22. P. 146–151.

  26. Stern, M. E. Lateral mixing of water masses// Deep Sea Res. 1967. Part A. V. 14. 747–753.

  27. Stern M. E. Ocean circulation physics. Academic press, 1975. 246 p.

  28. Zhurbas N. V. On the eigenvalue spectra for a model problem describing formation of the large-scale intrusions in the Arctic basin// Fundamentalnaya I Prikladnaya Gidrofizika. 2018. V.11. № 1. P. 40–45.https://doi.org/10.7868/S2073667318010045

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Физика атмосферы и океана

Архивы выпусков Информация о журнале Отправить рукопись в журнал