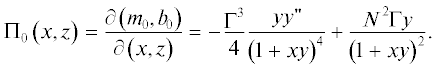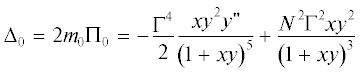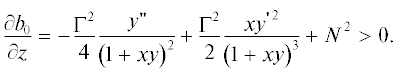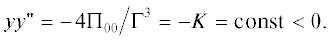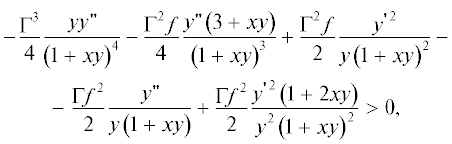Известия РАН. Физика атмосферы и океана, 2023, T. 59, № 3, стр. 251-264
Симметричная устойчивость вертикальных бароклинных вихрей с теплым ядром
М. В. Курганский *
Институт физики атмосферы им. А.М. Обухова РАН
119017 Москва, Пыжевский пер., 3, Россия
* E-mail: kurgansk@ifaran.ru
Поступила в редакцию 16.01.2023
После доработки 11.02.2023
Принята к публикации 10.03.2023
- EDN: TSAPPF
- DOI: 10.31857/S0002351523030069
Аннотация
Сделана попытка связать морфологические характеристики интенсивных конвективных вихрей, таких как (водяные) смерчи и пыльные вихри, с их гидродинамической устойчивостью. Рассмотрена симметричная устойчивость циклострофически сбалансированных вертикальных бароклинных вихрей, радиус максимального ветра которых зависит от высоты. Показана устойчивость узких, близких к цилиндрическим в своей нижней части вихрей с радиусом, который затем с возрастающей скоростью увеличивается с высотой и становится бесконечным на конечном уровне над поверхностью Земли. Напротив, более широкие вихри конической формы удовлетворяют необходимому условию неустойчивости, и высказывается гипотеза о том, что это отчасти объясняет более диффузный, неорганизованный характер подобного рода пыльных вихрей. Рассмотрена возможность постановки задачи с учетом общего вращения.
1. ВВЕДЕНИЕ
Интенсивные вертикальные вихри конвективной природы, такие как сухопутные и водяные смерчи, а также пыльные вихри могут иметь существенно различающееся морфологическое строение. К примеру, видимая под основанием материнского облака воронка сухопутного смерча (торнадо) может принимать различные формы, например: форму конуса (cone), V-образную (V-shaped) форму, форму клина (wedge), форму цилиндра (cylinder), форму песочных часов (hour-glass), форму веревки (rope) (см. [Stull, 2011], p. 577, Fig. 15.3211). Различающиеся формы имеют и воронки водяных смерчей (waterspouts) [Schwiesow, 1981]. Что касается пыльных вихрей, то в [Kurgansky et al., 2016] была предложена классификация вихрей по их форме на два основных типа. Во-первых, узкие, сосредоточенные вихри коаксиальной (цилиндрической) формы, которые простираются высоко вверх в конвективный пограничный слой (рис. 1а). Во-вторых, более широкие и менее организованные (более диффузные) вихри, имеющие в своей нижней части форму перевернутого клина и в зарождении и поддержании которых вертикальная конвекция играет, по всей видимости, меньшую роль, нежели для вихрей первого типа (рис. 1б). Эта неорганизованность, или диффузность, отчетлива видна на рис. 1б, если его сравнивать в рис. 1а. В недавней работе [Fenton et al., 2022], схоже с тем, как это было предложено в [Balme and Greeley, 2006] (Fig. 4), использована чуть более широкая классификация форм пыльных вихрей. Она включает (а) узкие, цилиндрические (“cylindrical”) вихри, сохраняющие свою постоянную толщину во всей вихревой колонне, (б) конические (“conical”) вихри, сходящиеся к одной точке или обрезанному конусу на поверхности земли, и (в) неорганизованные (“disorganized”) вихри, которые не имеют четко определенной формы. Безусловно, иногда происходит существенное изменение формы вихря, например, при его внезапном распаде (vortex breakdown), но, как правило, во время зрелой, квазиустановившейся, фазы своего существования, которая составляет подавляющую часть продолжительности жизни вихря, он сохраняет ту или иную свою форму. Оказывать определенное влияние на форму вихря может степень шероховатости подстилающей поверхности [Kurgansky et al., 2016]; также влиять на визуальную форму вихря может дисперсный состав пыли, вовлеченной в вихревое движение, в силу зависимости свойств инерционности частиц пыли от их размера [Ингель, 2021].
Рис. 1.
Две характерные морфологические формы пыльных вихрей: (а) вихри формы веревки и (б) вихри формы вазы (ср. [Schwiesow, 1981]). В то время как вихри формы (б) часто более интенсивны в нижней части, вихри формы (а) распространяются на максимальную высоту и наиболее эффективно переносят пыль вверх. Фотографии сделаны недалеко от поселка Уара (Huara) в пустыне Атакама в Чили в январе 2009 г. (см. [Kurgansky et al., 2011, 2016]).

В данной работе сделана попытка связать морфологию вертикальных конвективных вихрей с их гидродинамической устойчивостью. Конкретно, будет исследован случай симметричной неустойчивости, и если вихрь оказывается неустойчивым согласно этому анализу, то полученный результат может указывать на дезорганизованный, диффузный характер исследуемой вихревой структуры. Анализ неустойчивости будет наиболее простым в том отношении, что в основной поток, устойчивость которого исследуется, не включается аксиальное (вертикальное) поле скорости в вихре. Основанием этому, в частности, является наблюдаемая малость вертикальной скорости в пыльных вихрях по отношению к азимутальной скорости. Так, в [Balme and Greeley, 2006] указано, что вертикальная скорость $w$ в пыльных вихрях обычно составляет порядка одной четверти от максимальной азимутальной скорости ${{v}_{m}}.$ В [Ito and Niino, 2014] методом PIV (Particle Image Velocimetry) найдено, что в исследованном ими пыльном вихре ${{v}_{m}} = 16$ и $w = 6\,\,{\text{м}}\,{{{\text{с}}}^{{ - 1}}}.$ Аналогично, прямые самолетные измерения азимутальной, вертикальной и радиальной компонент скорости в водяных смерчах вблизи Флориды дали соответственно значения $25,$ $8$ и $1\,\,{\text{м}}\,{{{\text{с}}}^{{ - 1}}}$ [Leverson et al., 1977].
Данная статья состоит из трех частей. В первой части статьи на основе предыдущих работ излагается нелинейная теория симметричной устойчивости аксиально-симметричных бароклинных вихрей. Во второй, основной, части статьи полученные критерии устойчивости применяются к вертикальным аксиально-симметричным бароклинным вихрям с радиусом, меняющимся с высотой. Рассматриваются два случая: (1) узких, сосредоточенных вихрей и (2) широких, диффузных вихрей. В третьей части статьи кратко обсуждается учет силы Кориолиса в задаче.
2. КРИТЕРИЙ НЕЛИНЕЙНОЙ СИММЕТРИЧНОЙ УСТОЙЧИВОСТИ
Рассматривается аксиально-симметричное вихревое движение в атмосфере с учетом, вообще говоря, влажности воздуха. Используется приближение Буссинеска, диссипативными факторами и эффектом вращения Земли пренебрегается. Вектор скорости имеет три компоненты $\left( {u,v,w} \right)$ в рассматриваемой цилиндрической системе координат $\left( {r,\,\theta ,\,z} \right)$. Эти компоненты скорости зависят от двух координат $\left( {r,z} \right),$ где $r$ – радиальная координата, $z$ – аксиальная (вертикальная) координата. Зависимость от азимутальной координаты $\theta $ отсутствует. Диссипативные факторы не учитываем. Исходим из полной системы уравнений
(1а)
$\frac{{{\text{D}}u}}{{{\text{D}}t}} - \frac{{{{v}^{2}}}}{r} = - \frac{{\partial \pi }}{{\partial r}},\,\,\,\,\frac{{\text{D}}}{{{\text{D}}t}}\left( {vr} \right) = 0,\,\,\,\,\frac{{{\text{D}}w}}{{{\text{D}}t}} = - \frac{{\partial \pi }}{{\partial z}} + \tilde {b},$(1б)
$\frac{{{\text{D}}\tilde {b}}}{{{\text{D}}t}} + {{N}^{2}}w = 0,\,\,\,\,\frac{\partial }{{\partial r}}\left( {ru} \right) + \frac{\partial }{{\partial z}}\left( {rw} \right) = 0.$С учетом того, что $u = {{{\text{D}}r} \mathord{\left/ {\vphantom {{{\text{D}}r} {{\text{D}}t}}} \right. \kern-0em} {{\text{D}}t}},$ из уравнений (1) следует уравнение баланса энергии
(2а)
$\frac{{\text{d}}}{{{\text{d}}t}}E = 0,\,\,\,\,E = \iint {\frac{1}{2}\left( {{{{\mathbf{u}}}^{2}} + {{v}^{2}} + \frac{{{{{\tilde {b}}}^{2}}}}{{{{N}^{2}}}}} \right)}r{\text{d}}r{\text{d}}z.$Удобно, однако, выражение для энергии (2а) преобразовать, используя $w = {{{\text{D}}z} \mathord{\left/ {\vphantom {{{\text{D}}z} {{\text{D}}t}}} \right. \kern-0em} {{\text{D}}t}}$ и вводя “полную плавучесть” $b = \tilde {b} + {{N}^{2}}z,$ такую что ${{{\text{D}}b} \mathord{\left/ {\vphantom {{{\text{D}}b} {{\text{D}}t}}} \right. \kern-0em} {{\text{D}}t}} = 0.$ Теперь
(2б)
$\begin{gathered} \iint {\frac{1}{2}\frac{{{{{\tilde {b}}}^{2}}}}{{{{N}^{2}}}}}r{\text{d}}r{\text{d}}z = \iint {\frac{1}{2}\frac{{{{{\left( {b - {{N}^{2}}z} \right)}}^{2}}}}{{{{N}^{2}}}}}r{\text{d}}r{\text{d}}z = \\ = \iint {\frac{1}{2}\frac{{{{b}^{2}}}}{{{{N}^{2}}}}}r{\text{d}}r{\text{d}}z - \iint {bz}r{\text{d}}r{\text{d}}z + \iint {\frac{1}{2}{{N}^{2}}{{z}^{2}}}r{\text{d}}r{\text{d}}z. \\ \end{gathered} $Первый интеграл в правой части (2б) является сохраняющейся величиной в силу ${{{\text{D}}b} \mathord{\left/ {\vphantom {{{\text{D}}b} {{\text{D}}t}}} \right. \kern-0em} {{\text{D}}t}} = 0,$ а третий интеграл является абсолютной константой, которая может принимать бесконечные значения для неограниченной области. Поэтому в выражении для энергии необходимо учитывать лишь второй интеграл в (2б), и мы вместо (2а) приходим к более удобному для последующего анализа выражению для сохранения энергии
(2в)
$\frac{{\text{d}}}{{{\text{d}}t}}E = 0,\,\,\,\,E = \iint {\left\{ {\frac{1}{2}\left( {{{{\mathbf{u}}}^{2}} + {{v}^{2}}} \right) - bz} \right\}}r{\text{d}}r{\text{d}}z.$Кроме того, следствием уравнений (1) является бесконечный набор законов сохранения (казимиров)
(3)
$\frac{{\text{d}}}{{{\text{d}}t}}F = 0,\,\,\,\,F = \iint {\Phi \left( {m,b} \right)}{\kern 1pt} r{\text{d}}r{\text{d}}z,$(4)
$\begin{gathered} E = \iint {\left\{ {\frac{1}{2}\left( {{{{\mathbf{u}}}^{2}} + \frac{\mu }{{2x}}} \right) - bz} \right\}}{\kern 1pt} {\text{d}}x{\text{d}}z, \\ F = \iint {\Phi \left( {\mu ,b} \right)}{\kern 1pt} {\text{d}}x{\text{d}}z. \\ \end{gathered} $Применяя метод Арнольда [Арнольд, 1965] и следуя в целом работе [Калашник и Свиркунов, 1996] (см. также [Калашник и др., 2022]), но с использованием приближения Буссинеска, будем исследовать на нелинейную устойчивость установившееся во времени, циклострофически и гидростатически сбалансированное вихревое течение, отвечающее первичной (тороидальной) циркуляции в вихре
Исключая из этой системы уравнений давление ${{\pi }_{0}},$ придем к обобщению уравнения термического ветра, которое записываем с использованием зависимой переменной ${{\mu }_{0}} = m_{0}^{2} = v_{0}^{2}{{r}^{2}} = 2v_{0}^{2}x,$
(5)
$\frac{1}{{4{{x}^{2}}}}\frac{{\partial {{\mu }_{0}}}}{{\partial z}} = \frac{{\partial {{{\tilde {b}}}_{0}}}}{{\partial x}} \equiv \frac{{\partial {{b}_{0}}}}{{\partial x}}.$Наша цель найти условия, при которых значение функционала $I = E + F$ экстремально на основном течении, определяемом соотношением (5), а также условием ${{{\mathbf{u}}}_{0}} = 0.$ Для этого наложим на основное течение малые вариации $\mu = {{\mu }_{0}} + \delta \mu ,$ $b = {{b}_{0}} + \delta b,$ ${\mathbf{u}} = {{{\mathbf{u}}}_{0}} + \delta {\mathbf{u}} = \delta {\mathbf{u}},$ подставим в (4) и произведем разложение функционала $I$ по степеням этих малых вариаций. Для первой вариации функционала $I,$ с учетом того, что ${{{\mathbf{u}}}_{0}} = 0,$ будем иметь
(6)
$\frac{{\partial \Phi }}{{\partial \mu }} = - \frac{1}{{4x}},\,\,\,\,\frac{{\partial \Phi }}{{\partial b}} = z.$Вычисляя вторую вариацию, будем иметь
(7)
$\begin{gathered} {{\delta }^{2}}I = \iint {\left\{ {{{{\left( {\delta {\mathbf{u}}} \right)}}^{2}} + \frac{{{{\partial }^{2}}\Phi }}{{\partial {{\mu }^{2}}}}{{{\left( {\delta \mu } \right)}}^{2}} + 2\frac{{{{\partial }^{2}}\Phi }}{{\partial \mu {\kern 1pt} {\kern 1pt} \partial b}}\delta \mu \delta b} \right. + {\kern 1pt} } \\ \left. { + \,\,\frac{{{{\partial }^{2}}\Phi }}{{\partial {{b}^{2}}}}{{{\left( {\delta b} \right)}}^{2}}} \right\}{\text{d}}x{\text{d}}z. \\ \end{gathered} $Используя соотношения (6) для определения вторых производных функции $\Phi $ в (7), в итоге имеем
В дальнейшем используем краткое обозначение ${{\Delta }_{0}} = \frac{{\partial \left( {{{\mu }_{0}},{{b}_{0}}} \right)}}{{\partial \left( {x,z} \right)}}.$
Рассчитаем потенциальный вихрь Эртеля $\Pi = {\mathbf{\omega }} \cdot \nabla b$ для основного вихревого потока, где ${\mathbf{\omega }}$ вектор завихренности. Будем иметь
Достаточные условия устойчивости основного вихревого потока заключаются в знакоопределенности квадратичной формы в подынтегральном выражении в (7), именно
(8а)
$\frac{{{{\partial }^{2}}\Phi }}{{\partial {{\mu }^{2}}}} = \frac{1}{{4{{x}^{2}}}}\frac{{\partial {{b}_{0}}}}{{\partial z}}\Delta _{0}^{{ - 1}} > 0,\,\,\,\,\frac{{{{\partial }^{2}}\Phi }}{{\partial {{b}^{2}}}} = \frac{{\partial {{\mu }_{0}}}}{{\partial x}}\Delta _{0}^{{ - 1}} > 0,$(8б)
$\begin{gathered} \frac{{{{\partial }^{2}}\Phi }}{{\partial {{\mu }^{2}}}}\frac{{{{\partial }^{2}}\Phi }}{{\partial {{b}^{2}}}} - {{\left( {\frac{{{{\partial }^{2}}\Phi }}{{\partial \mu {\kern 1pt} \partial b}}} \right)}^{2}} = \\ = \frac{1}{{4{{x}^{2}}\Delta _{0}^{2}}}\left( {\frac{{\partial {{\mu }_{0}}}}{{\partial x}}\frac{{\partial {{b}_{0}}}}{{\partial z}} - \frac{{\partial {{\mu }_{0}}}}{{\partial z}}\frac{{\partial {{b}_{0}}}}{{\partial x}}} \right) = \frac{1}{{4{{x}^{2}}{{\Delta }_{0}}}} > 0. \\ \end{gathered} $Условие (8б) устойчивости выполнено, если ${{\Delta }_{0}} > 0.$ Если это так, то для устойчивости должны еще выполняться условия (8а). Первое из них есть условие статической устойчивости ${{\partial {{b}_{0}}} \mathord{\left/ {\vphantom {{\partial {{b}_{0}}} {\partial z}}} \right. \kern-0em} {\partial z}} > 0.$ Второе условие это классический критерий центробежной устойчивости Рэлея ${{\partial {{\mu }_{0}}} \mathord{\left/ {\vphantom {{\partial {{\mu }_{0}}} {\partial x}}} \right. \kern-0em} {\partial x}} > 0.$ На самом деле эти три критерия устойчивости, т.е. условие (8б) и условия статической и центробежной устойчивости, взаимосвязаны. Действительно, используя (5), мы можем записать
(8в)
${{\Delta }_{0}} = \frac{{\partial {{\mu }_{0}}}}{{\partial x}}\frac{{\partial {{b}_{0}}}}{{\partial z}} - \frac{{\partial {{\mu }_{0}}}}{{\partial z}}\frac{{\partial {{b}_{0}}}}{{\partial x}} = \frac{{\partial {{\mu }_{0}}}}{{\partial x}}\frac{{\partial {{b}_{0}}}}{{\partial z}} - \frac{1}{{4{{x}^{2}}}}{{\left( {\frac{{\partial {{\mu }_{0}}}}{{\partial z}}} \right)}^{2}}.$Поэтому если одновременно выполняются условия (8б) и центробежной устойчивости, то вихрь заведомо является и статически устойчивым. Альтернативно, если одновременно выполняются условия (8б) и статической устойчивости, то вихрь заведомо является и центробежно устойчивым.
3. ПРИЛОЖЕНИЕ К УЗКИМ, СОСРЕДОТОЧЕННЫМ ВИХРЯМ
В качестве приложения рассмотрим устойчивость модельного вихря с профилем скорости, который обобщает на случай бароклинного вихря профиль скорости, предложенный в [Fiedler, 1989]22
(9)
${{v}_{0}}\left( {r,z} \right) = \frac{{{{{{v}_{m}}\left( z \right)r} \mathord{\left/ {\vphantom {{{{v}_{m}}\left( z \right)r} {{{r}_{m}}\left( z \right)}}} \right. \kern-0em} {{{r}_{m}}\left( z \right)}}}}{{1 + {{{{r}^{2}}} \mathord{\left/ {\vphantom {{{{r}^{2}}} {r_{m}^{2}\left( z \right)}}} \right. \kern-0em} {r_{m}^{2}\left( z \right)}}}}.$В этой модели азимутальная скорость на каждом высотном уровне достигает максимального значения ${{v}_{m}}\left( z \right)$ на расстоянии ${{r}_{m}}\left( z \right)$ от оси вихря. Вблизи оси вихря азимутальная скорость линейно возрастает с радиусом $r,$ а на больших расстояниях от оси (на периферии вихря) она обратно пропорциональна $r.$ В выражении (9) заложено предположение о полном подобии поля скорости на различных высотных уровнях. Такой профиль скорости соответствует узким сосредоточенным вихрям; см. рис. 1(а) и рис. 2, на котором показана структура полей скорости и завихренности для узкого вихря (А), изученного в [Bluestein et al., 2004]. На каждом высотном уровне профилю скорости (9) отвечает так называемый лоренцевский профиль редуцированного давления (ср. [Kahanpää et al., 2016])
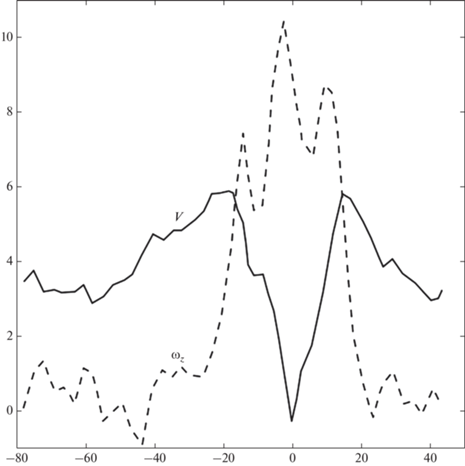
Рис. 2.
Приблизительная азимутальная компонента скорости ветра $V$ в системе отсчета движущейся с вихрем (сплошная линия; м с–1) и вертикальная завихренность ${{\omega }_{z}}$ (штриховая линия; ×10 с–1) в пыльном вихре А как функция расстояние от центра $r$ (${\text{м}}$). Отрицательные (положительные) расстояния измеряются слева (справа) от центра вихря, как это просматривается радаром. Завихренность в центре вихря оценивается как среднее значение завихренности, вычисленной справа и слева от центра; адаптировано из [Bluestein et al., 2004], см. также [Kurgansky et al., 2016].
Сузим класс возможных профилей скорости в (9), полагая, что ${{v}_{m}}\left( z \right){{r}_{m}}\left( z \right) = \Gamma = {\text{const}},$ т.е. условная граница вихревого ядра $r = {{r}_{m}}\left( z \right)$ является поверхностью постоянных значений углового момента $m = \Gamma ,$ и введем новую переменную $y\left( z \right) = {2 \mathord{\left/ {\vphantom {2 {r_{m}^{2}\left( z \right)}}} \right. \kern-0em} {r_{m}^{2}\left( z \right)}}.$ Величина $\Gamma $ считается положительной, т.е. без ограничения общности рассматривается циклоническое (против часовой стрелки, если смотреть сверху) вихревое движение. Теперь уравнение (9) записывается более кратко
и из уравнения (5) элементарной выкладкой имеемШтрих над переменной $y$ означает дифференцирование по $z.$ Интегрируя по $x$ имеем
(11)
${{b}_{0}}\left( {x,z} \right) = - \frac{{{{\Gamma }^{2}}}}{4}\frac{{y{\kern 1pt} '}}{{{{{\left( {1 + xy} \right)}}^{2}}}} + {{N}^{2}}z,$Теперь у нас есть все, чтобы рассчитать поле потенциального вихря. С учетом (10) и (11) прямая выкладка показывает, что
В рассматриваемых симметрично устойчивых циклонических вихрях $\Gamma > 0$ и потенциальный вихрь ${{\Pi }_{0}}$ положителен. В антициклонических вихрях (вращение по часовой стрелке) он отрицателен. Очевидно, имеем
и из (8в) и (13) следует, что для того, чтобы при ${{N}^{2}} = 0$ не было симметричной неустойчивости должно выполняться условие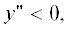 т.е. для вихря с теплым ядром скорость его расширения с высотой должна возрастать
по мере увеличения самой высоты $z.$ Из (11) вытекает, что условие Рэлея центробежной устойчивости всегда выполнено, а
условие статической устойчивости записывается в виде
т.е. для вихря с теплым ядром скорость его расширения с высотой должна возрастать
по мере увеличения самой высоты $z.$ Из (11) вытекает, что условие Рэлея центробежной устойчивости всегда выполнено, а
условие статической устойчивости записывается в виде
Отметим, что при ${{N}^{2}} = 0$ это условие заведомо выполнено, если выполняется условие симметричной устойчивости
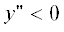 (см. также выше).
(см. также выше).
В качестве приложения полученных результатов рассмотрим семейство вихрей, в которых
радиус вихря становится бесконечным на некотором конечном уровне $z = h$ (ср. [Kurgansky, 2005, 2013]), причем ${{r}_{m}}\left( z \right) = {{r}_{0}}{{\left( {1 - {z \mathord{\left/ {\vphantom {z h}} \right. \kern-0em} h}} \right)}^{{ - \sigma }}},$ где $\sigma > 0$ и ${{r}_{m}}\left( 0 \right) = {{r}_{0}}.$ При этом $y\left( z \right) = 2r_{0}^{{ - 2}}{{\left( {1 - {z \mathord{\left/ {\vphantom {z h}} \right. \kern-0em} h}} \right)}^{{2\sigma }}}.$ Имея в виду геофизические приложения, будем рассматривать это вихревое решение в
интервале высот $0 \leqslant z < h.$ При формальном продолжении решения в область отрицательных $z$ и когда $z \to - \infty $ это решение отвечало бы концентрированной вихревой нити. Очевидно, имеем $y{\kern 1pt} ' = - 4\sigma r_{0}^{{ - 2}}{{h}^{{ - 1}}}{{\left( {1 - {z \mathord{\left/ {\vphantom {z h}} \right. \kern-0em} h}} \right)}^{{2\sigma - 1}}} < 0$ и 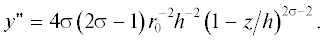 Симметрично устойчивым вихрям отвечает $0 < \sigma < {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}.$ Особым является пограничный случай $\sigma = {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2},$ когда вопрос о симметричной устойчивости требует дополнительного исследования, выходящего
за рамки данной работы. Будем рассматривать вихри, для которых $\sigma = {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2} - {{\sigma }_{1}},$ где $0 < {{\sigma }_{1}} \ll 1$ – малое положительное число. В таких вихрях плавучесть (11) возрастает при приближении
к уровню $z = h$ по степенному закону ${{\left( {1 - {z \mathord{\left/ {\vphantom {z h}} \right. \kern-0em} h}} \right)}^{{ - 2{{\sigma }_{1}}}}}$ что является определенной схематизацией эффекта температурной инверсии, ограничивающей
сверху вихревое движение. При этом потенциальный вихрь (12) изменяется $ \propto - 2{{\sigma }_{1}}{{\left( {1 - {z \mathord{\left/ {\vphantom {z h}} \right. \kern-0em} h}} \right)}^{{ - 1}}},$ т.е. он, вообще говоря, мал по величине, но при приближении к уровню $z = h$ возрастает по степенному закону. Отметим, что такой вихрь в своей нижней, видимой,
например, за счет поднятой пыли части, сравнительно мало отличается от строго цилиндрического
по форме вихря, поскольку, например, ${{r}_{m}}\left( {{h \mathord{\left/ {\vphantom {h 2}} \right. \kern-0em} 2}} \right) \approx \sqrt 2 {{r}_{0}}.$ Рисунок 3 доставляет пример такого близкого к цилиндрическому в своей нижней части, но расширяющему
кверху вихрю, который отвечает водяному смерчу.
Симметрично устойчивым вихрям отвечает $0 < \sigma < {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}.$ Особым является пограничный случай $\sigma = {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2},$ когда вопрос о симметричной устойчивости требует дополнительного исследования, выходящего
за рамки данной работы. Будем рассматривать вихри, для которых $\sigma = {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2} - {{\sigma }_{1}},$ где $0 < {{\sigma }_{1}} \ll 1$ – малое положительное число. В таких вихрях плавучесть (11) возрастает при приближении
к уровню $z = h$ по степенному закону ${{\left( {1 - {z \mathord{\left/ {\vphantom {z h}} \right. \kern-0em} h}} \right)}^{{ - 2{{\sigma }_{1}}}}}$ что является определенной схематизацией эффекта температурной инверсии, ограничивающей
сверху вихревое движение. При этом потенциальный вихрь (12) изменяется $ \propto - 2{{\sigma }_{1}}{{\left( {1 - {z \mathord{\left/ {\vphantom {z h}} \right. \kern-0em} h}} \right)}^{{ - 1}}},$ т.е. он, вообще говоря, мал по величине, но при приближении к уровню $z = h$ возрастает по степенному закону. Отметим, что такой вихрь в своей нижней, видимой,
например, за счет поднятой пыли части, сравнительно мало отличается от строго цилиндрического
по форме вихря, поскольку, например, ${{r}_{m}}\left( {{h \mathord{\left/ {\vphantom {h 2}} \right. \kern-0em} 2}} \right) \approx \sqrt 2 {{r}_{0}}.$ Рисунок 3 доставляет пример такого близкого к цилиндрическому в своей нижней части, но расширяющему
кверху вихрю, который отвечает водяному смерчу.
Рис. 3.
Водяной смерч вблизи г. Сочи 22 июля 2021 г. примерно 05:20 по Гринвичу (фото любезно предоставлено О.В. Калмыковой).

Заслуживает внимания модель симметрично устойчивого бароклинного вихря конечной высоты, в которой рост плавучести при приближении к верхнему предельному уровню $z = h$ хотя и является неограниченным, но в определенном смысле минимален, поскольку происходит по логарифмическому закону. Это модель, в которой поле потенциального вихря (12) на оси вихря принимает постоянное с высотой положительное значение ${{\Pi }_{0}}\left( {0,z} \right) = {{\Pi }_{{00}}} = {\text{const}} > 0$ (ср. [Kurgansky, 2006]), т.е.,
Уравнение (14) решается с граничными условиями: (а) $y = 0$ при $z = h$ и (б) $y{\kern 1pt} ' = - {{4{{b}_{0}}\left( {0,0} \right)} \mathord{\left/ {\vphantom {{4{{b}_{0}}\left( {0,0} \right)} {{{\Gamma }^{2}}}}} \right. \kern-0em} {{{\Gamma }^{2}}}} \equiv $ $ \equiv - {{4{{b}_{{00}}}} \mathord{\left/ {\vphantom {{4{{b}_{{00}}}} {{{\Gamma }^{2}}}}} \right. \kern-0em} {{{\Gamma }^{2}}}}$ при $z = 0$ и $x = 0;$ см. (11). Первый интеграл уравнения (14) имеет вид
где ${{y}_{0}} \equiv y\left( 0 \right).$ Произвольная постоянная $a$ в (15) определяется из граничного условия на поверхности земли, ${{8b_{{00}}^{2}} \mathord{\left/ {\vphantom {{8b_{{00}}^{2}} {{{\Gamma }^{4}}}}} \right. \kern-0em} {{{\Gamma }^{4}}}} = K{{a}^{2}} = \left( {{{4{{\Pi }_{{00}}}} \mathord{\left/ {\vphantom {{4{{\Pi }_{{00}}}} {{{\Gamma }^{3}}}}} \right. \kern-0em} {{{\Gamma }^{3}}}}} \right){{a}^{2}},$ т.е. $a = \pm \sqrt {{2 \mathord{\left/ {\vphantom {2 \Gamma }} \right. \kern-0em} \Gamma }} \left( {{{{{b}_{{00}}}} \mathord{\left/ {\vphantom {{{{b}_{{00}}}} {\sqrt {{{\Pi }_{{00}}}} }}} \right. \kern-0em} {\sqrt {{{\Pi }_{{00}}}} }}} \right).$ Делаем в уравнении (15) замену переменных ${{\eta }^{2}} = {{a}^{2}} - \ln \left( {{y \mathord{\left/ {\vphantom {y {{{y}_{0}}}}} \right. \kern-0em} {{{y}_{0}}}}} \right)$ и, извлекая квадратный корень из обеих частей (15) для вихрей с радиусом, монотонно растущим с высотой, получаемПоследнее уравнение имеет решение
(16)
$ - \sqrt {\frac{{{\pi }}}{{2K}}} {{y}_{0}}\exp \left( {{{a}^{2}}} \right)\left[ {\operatorname{erfc} \left( \eta \right) - \operatorname{erfc} \left( a \right)} \right] = z,$(17а)
$\begin{gathered} h = \sqrt {\frac{{{\pi }}}{{2K}}} {{y}_{0}}\exp \left( {{{a}^{2}}} \right)\operatorname{erfc} \left( a \right) \equiv \\ \equiv \frac{{\sqrt {{\pi }} }}{4}\frac{{{{\Gamma }^{2}}{{y}_{0}}}}{{{{b}_{{00}}}}}a\exp \left( {{{a}^{2}}} \right)\operatorname{erfc} \left( a \right). \\ \end{gathered} $С учетом (17а), деля обе части (16) на $h,$ получаем
(17б)
${\text{erfc}}\left( \eta \right) = {\text{erfc}}\left( a \right)\left( {1 - {z \mathord{\left/ {\vphantom {z h}} \right. \kern-0em} h}} \right).$Рассмотрим предельный случай малых значений потенциального вихря ${{\Pi }_{{00}}},$ когда $a \gg 1.$ В этом случае справедлива асимптотика erfc(a) ≅ $ \cong \left( {{1 \mathord{\left/ {\vphantom {1 {\sqrt {{\pi }} }}} \right. \kern-0em} {\sqrt {{\pi }} }}} \right){{a}^{{ - 1}}}\exp \left( { - {{a}^{2}}} \right)$ и приближенно имеем h ≅ $ \cong \left( {{1 \mathord{\left/ {\vphantom {1 4}} \right. \kern-0em} 4}} \right)\left( {{{{{\Gamma }^{2}}{{y}_{0}}} \mathord{\left/ {\vphantom {{{{\Gamma }^{2}}{{y}_{0}}} {{{b}_{{00}}}}}} \right. \kern-0em} {{{b}_{{00}}}}}} \right),$ т.е. ${{v}_{m}}\left( 0 \right) \cong 2b_{{00}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}{{h}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}},$ что близко согласуется с результатами в [Rennó et al., 1998]. Теперь при $z = {h \mathord{\left/ {\vphantom {h 2}} \right. \kern-0em} 2}$ из (17б) с точностью до логарифмической поправки имеем ${{y\left( {{h \mathord{\left/ {\vphantom {h 2}} \right. \kern-0em} 2}} \right)} \mathord{\left/ {\vphantom {{y\left( {{h \mathord{\left/ {\vphantom {h 2}} \right. \kern-0em} 2}} \right)} {{{y}_{0}}}}} \right. \kern-0em} {{{y}_{0}}}} \approx {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2},$ т.е. ${{r}_{m}}\left( {{h \mathord{\left/ {\vphantom {h 2}} \right. \kern-0em} 2}} \right) \approx \sqrt 2 {{r}_{0}},$ что согласуется с рассмотренной выше моделью вихря. В противоположном предельном случае больших значений потенциального вихря ${{\Pi }_{{00}}},$ когда $a \ll 1,$ асимптотически имеем $h \cong \sqrt {{{{\pi }} \mathord{\left/ {\vphantom {{{\pi }} 8}} \right. \kern-0em} 8}} \left( {{{{{\Gamma }^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}}{{y}_{0}}} \mathord{\left/ {\vphantom {{{{\Gamma }^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}}{{y}_{0}}} {\Pi _{{00}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}}} \right. \kern-0em} {\Pi _{{00}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}}} \right)$ и поэтому vm(0) ≅ $ \cong \left( {{2 \mathord{\left/ {\vphantom {2 {\sqrt[3]{{{\pi }}}}}} \right. \kern-0em} {\sqrt[3]{{{\pi }}}}}} \right)\Pi _{{00}}^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}}}{{\left[ {{{r}_{m}}\left( 0 \right)} \right]}^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}}}}{{h}^{{{2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-0em} 3}}}}.$ Здесь проявляется зависимость ${{v}_{m}}\left( 0 \right) \propto {{\left[ {{{r}_{m}}\left( 0 \right)} \right]}^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}}}},$ которая находит определенное подтверждение в наблюдательных данных о пыльных вихрях на Земле и на Марсе [Balme and Greeley, 2006]. Отметим, что асимптотический случай $a \ll 1$ может отвечать гигантским пыльным вихрям на Марсе, где важным источником плавучести служит прямой нагрев пыли Солнцем в вихревой колонне, а также влажно-конвективным вихрям на Земле, таким как смерчи над сушей и над морем, когда источником плавучести является теплота конденсации водяного пара в вихревом ядре.
4. ПРИЛОЖЕНИЕ К ШИРОКИМ, ДИФФУЗНЫМ ВИХРЯМ
В [Kurgansky, 2013] была также рассмотрена модель “перевернутого вихревого конуса”, когда ${{r}_{m}}\left( z \right) = c\left( {z + d} \right)$ и вершина конуса, представляющего границу вихревого ядра, находится в точке с координатой $z = - d$ под поверхностью земли $z = 0,$ а постоянный множитель $c$ характеризует угол раскрыва конуса. Для такого рода вихрей, имеющих форму вазы, см. рис. 1(б), профиль азимутальной скорости может представляться более общей чем (9) формулой (ср. уравнение (10) для обобщенного вихря Рэнкина в [Kurgansky et al., 2016])
(18)
${{v}_{0}}\left( {r,z} \right) = \frac{{{{{{v}_{m}}\left( z \right){{r}^{s}}} \mathord{\left/ {\vphantom {{{{v}_{m}}\left( z \right){{r}^{s}}} {r_{m}^{s}\left( z \right)}}} \right. \kern-0em} {r_{m}^{s}\left( z \right)}}}}{{1 + {{{{r}^{{1 + s}}}} \mathord{\left/ {\vphantom {{{{r}^{{1 + s}}}} {r_{m}^{{1 + s}}\left( z \right)}}} \right. \kern-0em} {r_{m}^{{1 + s}}\left( z \right)}}}},\,\,\,\,s \geqslant 1.$При $s = 1$ следует формула (9), а с увеличением $s$ в пределе $s \to \infty $ приходим к так называемому “полому вихрю” (hollow vortex), сердцевина которого находится в покое, а вся завихренность сосредоточена вблизи границы вихревого ядра при $r = {{r}_{m}}\left( z \right).$ Формула (18) является обобщением формулы (9), и она дополнительна формуле
(19)
${{v}_{0}}\left( {r,z} \right) = \frac{{{{{{v}_{m}}\left( z \right)r} \mathord{\left/ {\vphantom {{{{v}_{m}}\left( z \right)r} {{{r}_{m}}\left( z \right)}}} \right. \kern-0em} {{{r}_{m}}\left( z \right)}}}}{{{{{\left[ {1 + {{{{r}^{{2n}}}} \mathord{\left/ {\vphantom {{{{r}^{{2n}}}} {r_{m}^{{2n}}\left( z \right)}}} \right. \kern-0em} {r_{m}^{{2n}}\left( z \right)}}} \right]}}^{{{1 \mathord{\left/ {\vphantom {1 n}} \right. \kern-0em} n}}}}}},\,\,\,\,n \geqslant 1$Профиль скорости (18) при $s > 1$ соответствует широким, диффузным вихрям; см. рис. 1(б) и 4, на котором показана структура полей скорости и завихренности для широкого интенсивного пыльного вихря (B), изученного в [Bluestein et al., 2004].
Теперь, если ${{v}_{m}}\left( z \right){{r}_{m}}\left( z \right) = \Gamma = {\text{const}},$ то в прежних обозначениях вместо (10) имеем
Непосредственно проверяется, что обобщенное уравнение термического ветра (5) выполнено.
На оси вихря при ${{N}^{2}} = 0$ условие гидростатической устойчивости 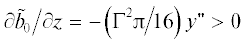 заведомо не выполнено, поскольку в данном случае
заведомо не выполнено, поскольку в данном случае 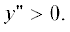 Также, вообще говоря, во всем вихревом потоке не выполнено и условие симметричной
бароклинной устойчивости ${{\Pi }_{0}} > 0.$
Также, вообще говоря, во всем вихревом потоке не выполнено и условие симметричной
бароклинной устойчивости ${{\Pi }_{0}} > 0.$
Сказанное может вносить вклад в объяснение того обстоятельства, что конические пыльные
вихри (вихри формы вазы, см. рис. 1б) имеют в определенной степени неорганизованный, диффузный характер. Однако, если
имеется фоновая устойчивая стратификация атмосферы, то условие гидростатической устойчивости
заключается в выполнении неравенства 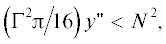 которое в случае “перевернутого вихревого конуса” когда
которое в случае “перевернутого вихревого конуса” когда 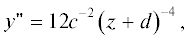 принимает вид ${{\left( {z + d} \right)}^{4}} > \left( {{{3{{\pi }}} \mathord{\left/ {\vphantom {{3{{\pi }}} 4}} \right. \kern-0em} 4}} \right){{\Gamma }^{2}}{{c}^{{ - 2}}}{{N}^{{ - 2}}}$ и заведомо выполнено, если ${{d}^{4}} > \left( {{{3{{\pi }}} \mathord{\left/ {\vphantom {{3{{\pi }}} 4}} \right. \kern-0em} 4}} \right){{\Gamma }^{2}}{{c}^{{ - 2}}}{{N}^{{ - 2}}}.$ Последнее условие можно переписать в виде неравенства
принимает вид ${{\left( {z + d} \right)}^{4}} > \left( {{{3{{\pi }}} \mathord{\left/ {\vphantom {{3{{\pi }}} 4}} \right. \kern-0em} 4}} \right){{\Gamma }^{2}}{{c}^{{ - 2}}}{{N}^{{ - 2}}}$ и заведомо выполнено, если ${{d}^{4}} > \left( {{{3{{\pi }}} \mathord{\left/ {\vphantom {{3{{\pi }}} 4}} \right. \kern-0em} 4}} \right){{\Gamma }^{2}}{{c}^{{ - 2}}}{{N}^{{ - 2}}}.$ Последнее условие можно переписать в виде неравенства
Рис. 4.
То же, что и на рис. 2, но для пыльного вихря В. Адаптировано из [Bluestein et al., 2004], см. также [Kurgansky et al., 2016].
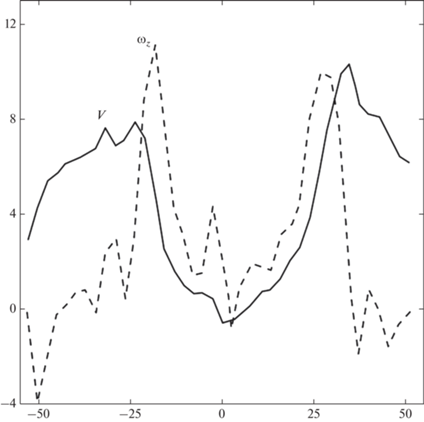
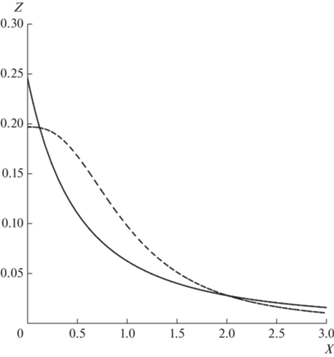
На рис. 5 показаны профили скорости, отвечающие соответственно $s = 1$ (в этом случае имеется профиль скорости (9)) и $s = 3$ в (19). Рисунки 6 и 7 дают представление о радиальных профилях давления и плавучести соответственно в вихрях с $s = 1$ (узкий сосредоточенный вихрь, ср. рис. 2) и $s = 3$ (широкий диффузный вихрь, ср. рис. 4).
Рис. 5.
Зависимость от нормированной радиальной координаты $R = {r \mathord{\left/ {\vphantom {r {{{r}_{m}}}}} \right. \kern-0em} {{{r}_{m}}}}\left( z \right)$ значения нормированной скорости ${{V}_{n}} = {{{{v}_{0}}\left( {r,z} \right)} \mathord{\left/ {\vphantom {{{{v}_{0}}\left( {r,z} \right)} {{{v}_{m}}}}} \right. \kern-0em} {{{v}_{m}}}}\left( z \right)$ для вихрей с $s = 1$ (сплошная линия) и $s = 3$ (пунктирная линия).
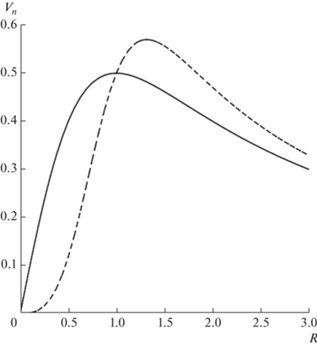
Рис. 6.
Зависимость от переменной $X = xy$ нормированного падения давления $Y = {{{{\pi }_{0}}} \mathord{\left/ {\vphantom {{{{\pi }_{0}}} {\left( {{{\Gamma }^{2}}y} \right)}}} \right. \kern-0em} {\left( {{{\Gamma }^{2}}y} \right)}}$ для вихрей с $s = 1$ (сплошная линия) и $s = 3$ (пунктирная линия).
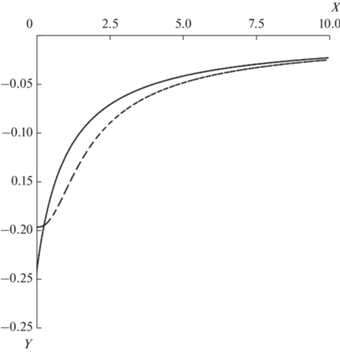
Рис. 7.
Зависимость от переменной $X = xy$ нормированной плавучести $Z = {{{{{\tilde {b}}}_{0}}} \mathord{\left/ {\vphantom {{{{{\tilde {b}}}_{0}}} {\left( { - {{\Gamma }^{2}}y{\kern 1pt} '} \right)}}} \right. \kern-0em} {\left( { - {{\Gamma }^{2}}y{\kern 1pt} '} \right)}}$ для вихрей с $s = 1$ (сплошная линия) и $s = 3$ (пунктирная линия).
Выше рассматривалась простейшая модель “перевернутого конуса” ${{r}_{m}}\left( z \right) = c\left( {z + d} \right).$ Однако, все сказанное справедливо и для более сложных и более реалистичных моделей, таких, как ${{r}_{m}}\left( z \right) = {{c}_{1}}{{\left( {z + d} \right)}^{{{\beta }}}}$ и ${{r}_{m}}\left( z \right) = {{c}_{2}}{\text{th}}\left[ {{{\left( {z + d} \right)} \mathord{\left/ {\vphantom {{\left( {z + d} \right)} \varepsilon }} \right. \kern-0em} \varepsilon }} \right],$ где $0 < \beta < 1$ и значение безразмерного показателя степени $\beta $ определяет размерность постоянной ${{c}_{1}};$ постоянные ${{c}_{2}}\,$и $\varepsilon $ имеют размерность длины.
5. УЧЕТ ОБЩЕГО ВРАЩЕНИЯ
Рассмотрим теперь более сложную задачу с учетом общего вращения. В этом случае основная система уравнений (1) принимает вид
(20а)
$\begin{gathered} \frac{{{\text{D}}u}}{{{\text{D}}t}} - \frac{{{{v}^{2}}}}{r} - fv = - \frac{{\partial \pi }}{{\partial r}}, \\ \frac{{\text{D}}}{{{\text{D}}t}}\left( {vr + f\frac{{{{r}^{2}}}}{2}} \right) = 0,\,\,\,\,\frac{{{\text{D}}w}}{{{\text{D}}t}} = - \frac{{\partial \pi }}{{\partial z}} + \tilde {b}, \\ \end{gathered} $(20б)
$\frac{{{\text{D}}\tilde {b}}}{{{\text{D}}t}} + {{N}^{2}}w = 0,\,\,\,\,\frac{\partial }{{\partial r}}\left( {ru} \right) + \frac{\partial }{{\partial z}}\left( {rw} \right) = 0.$В уравнениях (20) $f$ обозначает постоянный параметр Кориолиса. Теперь (абсолютный) удельный угловой момент принимает вид $m = vr + {{f{{r}^{2}}} \mathord{\left/ {\vphantom {{f{{r}^{2}}} 2}} \right. \kern-0em} 2}$ и $\left( {u,v,w} \right)$ служат компонентами скорости во вращающейся системе отсчета. Поскольку сила Кориолиса гироскопическая (не совершает работы), то закон сохранения энергии записывается в прежнем виде (2в), но интеграл энергии целесообразно переписать, используя следующие тождественные преобразования (ср. [Калашник и др., 2022])
(21)
${{\Delta }_{0}} = \frac{{\partial \left( {{{\mu }_{0}},{{b}_{0}}} \right)}}{{\partial \left( {x,z} \right)}} = 2{{m}_{0}}\frac{{\partial \left( {{{m}_{0}},{{b}_{0}}} \right)}}{{\partial \left( {x,z} \right)}} \equiv 2{{m}_{0}}{{\Pi }_{0}} > 0,$Теперь из обобщенного уравнения термического ветра следует, что
(23)
${{b}_{0}} = - \frac{{{{\Gamma }^{2}}}}{4}\frac{{y{\kern 1pt} '}}{{{{{\left( {1 + xy} \right)}}^{2}}}} - \frac{{\Gamma {\kern 1pt} f}}{2}\frac{{y{\kern 1pt} '}}{{y\left( {1 + xy} \right)}} + {{N}^{2}}z.$Опять из (23) вытекает, что при ${{N}^{2}} = 0$ в вихре с теплым ядром (${{\tilde {b}}_{0}} > 0$) выполняется условие $y{\kern 1pt} ' < 0,$ т.е. этот вихрь должен расширяться с высотой. Если ${{\Delta }_{0}} > 0$ (см. (21)), то как это следует из (22), условие центробежной устойчивости заведомо
выполнено, а (23) показывает, что при ${{N}^{2}} = 0$ условие статической устойчивости заведомо выполняется, когда 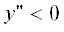 (последнее условие является достаточным, но не необходимым условием статической устойчивости,
см. также ниже). Наибольшие сложности связаны с выполнением самого условия (21), которое
также является и условием симметричной бароклинной устойчивости. С учетом (22) и (23)
в развернутой форме оно при ${{N}^{2}} = 0$ записывается в виде неравенства
(последнее условие является достаточным, но не необходимым условием статической устойчивости,
см. также ниже). Наибольшие сложности связаны с выполнением самого условия (21), которое
также является и условием симметричной бароклинной устойчивости. С учетом (22) и (23)
в развернутой форме оно при ${{N}^{2}} = 0$ записывается в виде неравенства
Раскрывая якобиан, получаем весьма громоздкое условие
которое показывает, что достаточным условием положительности потенциального вихря ${{\Pi }_{0}}$ является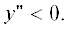 Отметим, что это условие, вообще говоря, не необходимо и наличие общего вращения
оказывает стабилизирующее действие в том смысле, что в некоторых случаях ${{\Pi }_{0}} > 0$ и при
Отметим, что это условие, вообще говоря, не необходимо и наличие общего вращения
оказывает стабилизирующее действие в том смысле, что в некоторых случаях ${{\Pi }_{0}} > 0$ и при 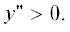 Именно, для вихрей, рассмотренных в разделе 3, возможна ситуация, когда сумма второго
и третьего членов и соответственно сумма четвертого и пятого членов в левой части
(24) положительны при
Именно, для вихрей, рассмотренных в разделе 3, возможна ситуация, когда сумма второго
и третьего членов и соответственно сумма четвертого и пятого членов в левой части
(24) положительны при 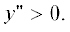 Теперь, оценивая сравнительный порядок членов в левой части (24) и нормируя на величину
(отрицательного при
Теперь, оценивая сравнительный порядок членов в левой части (24) и нормируя на величину
(отрицательного при 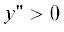 ) первого члена, так что он приобретает порядок величины $О\left( 1 \right)$, мы видим, что второй и третий член приобретают порядок величины $О\left( {{{\varepsilon }^{{ - 1}}}} \right),$ а четвертый и пятый член – $О\left( {{{\varepsilon }^{{ - 2}}}} \right),$ где $\varepsilon = {{v}_{m}}\left( z \right)r_{m}^{{ - 1}}\left( z \right){{f}^{{ - 1}}}$ – вихревое число Россби. Стабилизация общим вращением возможна, если при всех $z$ число Россби $\varepsilon $ (существенно) меньше единицы. Однако, это условие в целом не выполняется для мелкомасштабных
вихрей. Частичная стабилизация возможна в окрестности верхней границы вихря $z = h,$ где угловая скорость ${{v}_{m}}\left( z \right)r_{m}^{{ - 1}}\left( z \right)$ неограниченно уменьшается и поэтому локальное вихревое число Россби становится сколь
угодно малым. Однако, случай
) первого члена, так что он приобретает порядок величины $О\left( 1 \right)$, мы видим, что второй и третий член приобретают порядок величины $О\left( {{{\varepsilon }^{{ - 1}}}} \right),$ а четвертый и пятый член – $О\left( {{{\varepsilon }^{{ - 2}}}} \right),$ где $\varepsilon = {{v}_{m}}\left( z \right)r_{m}^{{ - 1}}\left( z \right){{f}^{{ - 1}}}$ – вихревое число Россби. Стабилизация общим вращением возможна, если при всех $z$ число Россби $\varepsilon $ (существенно) меньше единицы. Однако, это условие в целом не выполняется для мелкомасштабных
вихрей. Частичная стабилизация возможна в окрестности верхней границы вихря $z = h,$ где угловая скорость ${{v}_{m}}\left( z \right)r_{m}^{{ - 1}}\left( z \right)$ неограниченно уменьшается и поэтому локальное вихревое число Россби становится сколь
угодно малым. Однако, случай 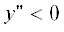 является более общим (более “грубым, робастным” (robust)) и мы будем рассматривать
именно его. Если ${{\Pi }_{0}} > 0$ и условие ${{\Delta }_{0}} > 0$ выполнено, см. (21), то, как следует из обобщенного на случай общего вращения соотношения
(8в), условие статической устойчивости заведомо выполнено.
является более общим (более “грубым, робастным” (robust)) и мы будем рассматривать
именно его. Если ${{\Pi }_{0}} > 0$ и условие ${{\Delta }_{0}} > 0$ выполнено, см. (21), то, как следует из обобщенного на случай общего вращения соотношения
(8в), условие статической устойчивости заведомо выполнено.
6. ЗАКЛЮЧИТЕЛЬНЫЕ ЗАМЕЧАНИЯ
Нами рассмотрены примеры, иллюстрирующие связь симметричной устойчивости интенсивных вертикальных вихрей с их морфологией. Именно, были рассмотрены модели двух типов вихрей. Во-первых, это модель симметрично устойчивого вихря конечной высоты, который в своей нижней части (скажем, половине высоты) мало отличим от строго цилиндрического вихря. Эта первая модель наиболее близко соответствует узким, четко структурированным, сосредоточенным пыльным вихрям и водяным смерчам. Во-вторых, это модель вихря, который по форме напоминает перевернутый конус и для которого в развитом конвективном пограничном слое, при стратификации близкой к нейтральной, не выполняется критерий симметричной устойчивости. Эта вторая модель наиболее близко соответствует широким, диффузным вихрям, имеющим в определенной степени неорганизованный характер. Для этой второй модели в работе была предложена параметризация радиальной зависимости азимутальной скорости внутри вихревого ядра с помощью кубической функции, что согласуется с наблюдаемой концентрацией вертикальной завихренности на границе вихревого ядра и наличием мелкомасштабных концентрированных вертикальных вихрей в этой зоне (ср. [Schwiesow, 1981]).
Безусловно, проведенный анализ симметричной устойчивости является технически наиболее простым, и он в том числе не учитывает возможность неустойчивости вихрей относительно азимутально-асимметричных возмущений. Учет таких возмущений является более сложной задачей на будущее. Строго говоря, нарушение критерия симметричной устойчивости означает выполнение необходимых условий неустойчивости. Однако для более простой модели бароклинного вихря в [Ooyama, 1966] показано, что невыполнение критерия симметричной устойчивости является и достаточным условием для симметричной неустойчивости (см. также [Калашник и др., 2022]). Если тот же самый вывод справедлив для нашей более сложной модели бароклинных вихрей, то это значительно усиливает выводы работы, касающиеся возможной дезорганизации широких, диффузных вихрей.
Последнее замечание относится к выбору, в качестве основного потока, лишь азимутальной компоненты скорости в вихре (так называемой, первичной или тороидальной циркуляции), полностью игнорируя вертикальную компоненту скорости (вторичную, или полоидальную циркуляцию). Это вызвано как чисто техническими трудностями, так и тем принципиальным обстоятельством, что поддержание полоидальной циркуляции в бароклинном вихре требует ненулевых диабатических притоков тепла (см. [Kurgansky, 2005, 2013]).
Автор благодарен рецензенту за полезные замечания. Работа поддержана грантом Российского научного фонда (проект № 22-27-00039).
Список литературы
Арнольд В.И. Об условиях нелинейной устойчивости плоских стационарных криволинейных течений идеальной жидкости // ДАН СССР. 1965. Т. 162. № 5. С. 975–978.
Вараксин А.Ю. Воздушные торнадоподобные вихри: математическое моделирование // ТВТ. 2017. Т. 55. № 2. С. 291–316.
Ингель Л.Х. О динамике инерционных частиц в интенсивных атмосферных вихрях // Изв. РАН. Физика атмосферы и океана. 2021. Т. 57. № 6. С. 632–640.
Калашник М.В., Свиркунов П.Н. О симметричной устойчивости состояний циклострофического и геострофического баланса в стратифицированной среде // ДАН. 1996 Т. 348. № 6. С. 811–813.
Калашник М.В., Курганский М.В., Чхетиани О.Г. Бароклинная неустойчивость в геофизической гидродинамике // УФН. 2022. Т. 192. № 10. С. 1110–1144.
Онищенко О.Г., Похотелов О.А., Астафьева Н.М., Хортон В., Федун В.Н. Структура и динамика концентрированных мезомасштабных вихрей в атмосферах планет // УФН. 2020. Т. 190. № 7. С. 732–748.
Balme M., Greeley R. Dust devils on Earth and Mars // Rev. Geophys. 2006. V. 44. P. RG3003.
Bluestein H.B., Weiss C.C., Pazmany A.L. Doppler radar observations of dust devils in Texas // Mon. Wea. Rev. 2004. V. 132. № 1. P. 209–224.
Fenton L.K., Metzger S.M., Michaels T.I., Scheidt S.P., Dorn T.C., Neakrase L.D.V., Cole B., Sprau O. Meteorological and geological controls on dust devil activity: Initial results from a field study at Smith Creek Valley, Nevada, USA // Aeolian Research. 2022. V. 59. P. 100 831.
Fiedler B.H. Conditions for laminar flow in geophysical vortices // J. Atmos. Sci. 1989. V. 46. P. 252–259.
Hess G.D., Spillane K.T. Characteristics of dust devils in Australia // J. Appl. Meteorol. 1990. V. 29. P. 498–507.
Ito J., Niino H. Particle image velocimetry of a dust devil observed in a desert // SOLA. 2014. V. 10. P. 108–111.
Kahanpää H, Newman C., Moores J., Zorzano M.-P., Martín-Torres J., Navarro S., Lepinette A., Cantor B., Lemmon M. T., Valentín–Serrano P., Ullán A., Schmidt W. Convective vortices and dust devils at the MSL landing site: annual variability // J. Geophys. Res. Planets 2016. V. 121(8). P. 1514–1549.
Kanak K.M., Lilly D.K., Snow J.T. The formation of vertical vortices in the convective boundary layer // Q. J. R. Meteorol. Soc. 2000. V. 126. P. 2789–2810.
Kurgansky M.V. A simple model of dry convective helical vortices (with applications to the atmospheric dust devil) // Dyn. Atmos. Oceans. 2005. V. 40. P. 151–162.
Kurgansky M.V. Steady-state properties and statistical distribution of atmospheric dust devils // Geophys. Res. Lett. 2006. V. 33. P. L19S06(1–4).
Kurgansky M.V. Simple models of helical baroclinic vortices // Procedia IUTAM. 2013. V. 7. P. 193–202.
Kurgansky M.V., Lorenz R.D., Renno N.O., Takemi T., Gu Z., Wei W. Dust devil steady-state structure from a fluid dynamics perspective // Space Sci. Rev. 2016. V. 203(1–4). P. 209–244.
Kurgansky M.V., Montecinos A., Villagran V., Metzger S.M. Micrometeorological conditions for dust-devil occurrence in the Atacama Desert // Boundary-Layer Meteorol. 2011. V. 138. P. 285–298.
Leverson V.H., Sinclair P.C., Golden J.H. Waterspout wind, temperature and pressure structure deduced from aircraft measurements // Mon. Wea. Rev. 1977. V. 105(6). P. 725–733.
Ooyama K. On the stability of the baroclinic circular vortex: A sufficient condition for instability // J. Atmos. Sci. 1966. V. 23. № 1. P. 43–53.
Rayleigh L. On the dynamics of revolving fluids // Proc. R. Soc. 1917. V. A 93. P. 148–154.
Rennó N.O., Burkett M.L., Larkin M.P. A simple thermodynamical theory for dust devils // J. Atmos. Sci. 1998. V. 55. P. 3244–3252.
Schwiesow R.L. Horizontal velocity structure in waterspouts // J. Appl. Meteor. 1981. V. 20. P. 349–360.
Stull R.B. Meteorology for Scientists and Engineers. 3rd ed. Univ. of British Columbia, 2011. 938 pp.
Vatistas G.H., Kozel V., Mih W.C. A simpler model for concentrated vortices // Exp. Fluids. 1991. V. 11. P. 73–76.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Физика атмосферы и океана