1. На главную
  2. Электронные версии
  3. Известия РАН. Физика атмосферы и океана
  4. T. 59, № 4, 2023

Известия РАН. Физика атмосферы и океана, 2023, T. 59, № 4, стр. 417-420

Аналитическая модель генерации завихренности, обусловленной неоднородным трением на подстилающей поверхности

Л. Х. Ингель a, c, *, А. А. Макоско b, c

a ФГБУ “НПО "Тайфун”
249038 Обнинск, ул. Победы, 4, Россия

b Российская академия наук
119991 Москва, Ленинский пр-кт, 14, Россия

c Институт физики атмосферы им. А.М. Обухова РАН
119017 Москва, Пыжевский пер., 3, Россия

* E-mail: lev.ingel@gmail.com

Поступила в редакцию 11.04.2023
После доработки 21.04.2023
Принята к публикации 26.04.2023

Полный текст (PDF)

Аннотация

В ряде публикаций последних лет обращается внимание на неоднородности подстилающей поверхности как фактор, который может способствовать зарождению и интенсификации смерчей. В работе предложена аналитическая модель генерации завихренности под влиянием горизонтально-неоднородного трения. Возникающая завихренность пропорциональна скорости фонового течения и поперечному к этому течению горизонтальному градиенту коэффициента сопротивления; зависимость от других факторов относительно слабая. Численные оценки показывают возможность эффективной генерации завихренности.

Ключевые слова: атмосферные течения, завихренность, неоднородное трение, атмосферные вихри, аналитическая модель

1. ВВЕДЕНИЕ

В ряде публикаций последних лет обращается внимание на неоднородности подстилающей поверхности как фактор, который может способствовать зарождению и интенсификации смерчей [Frazier et al, 2019; Kellner, Niyogy, 2014; Lyza, Knupp, 2018; Markert et al, 2019; Muncy, 2021; Wheatley, Trapp, 2008]. Один из возможных физических механизмов заключается в том, что при взаимодействии горизонтального течения с неоднородной подстилающей поверхностью эффективное сопротивление может быть неоднородным в поперечном к потоку направлении. Это должно приводить к возникновению горизонтального сдвига, и, следовательно, генерации вертикальной завихренности, которая, как известно, является важнейшим фактором, способствующим зарождению и интенсификации смерчей (см., например, [Dotzek et al, 2010; Miglietta, 2019]). В настоящей заметке рассмотрена относящаяся сюда простейшая аналитическая модель. Отметим, что некоторые эффекты неоднородного трения исследовались в недавней работе [Ингель, Макоско, 2023], но в ней рассматривались неоднородности поверхности и связанные с этим процессы относительно больших горизонтальных масштабов, для которых важную роль играет, в частности, учет кориолисовых ускорений. В настоящей работе рассматриваются процессы меньших масштабов с существенно иной динамикой.

2. ПОСТАНОВКА И РЕШЕНИЕ ЗАДАЧИ

В качестве фонового горизонтального течения рассматриваем некоторое обобщение плоского течения Куэтта [Ландау, Лифшиц, 1986], описываемого уравнением

(1)
$\frac{d}{{dz}}K\left( z \right)\frac{{du}}{{dz}} = 0.$
Здесь ось $z$ направлена вверх, $u$ – скорость течения (ограничиваемся рассмотрением плоскопараллельного течения вдоль одной из горизонтальных осей $x$), $K$ – эффективный коэффициент турбулентного обмена. Рассматривается горизонтальный слой среды на верхней границе которого $z = H$ задана скорость $u = U.$ Воспользуемся моделью пограничного слоя с квадратичным трением на нижней границе $z = 0$ [Галушко, Орданович, 1978; Ингель, Михайлова, 1990; Ingel, 2005]. В таких моделях предполагается, что уровень $z = 0$ соответствует не подстилающей поверхности, а, например, верхней границе приземного (приводного) слоя или уровню стандартных метеорологических наблюдений, так что на этом уровне допускается некоторое “проскальзывание”. Краевое условие на нижней границе имеет вид
(2)
$K\frac{{\partial u}}{{\partial z}} = {{c}_{D}}{{u}^{2}}\,\,\,\,{\text{при}}\,\,\,\,z = 0,$
где ${{c}_{D}}$ – безразмерный коэффициент сопротивления. Из (1) следует
(3)
$\frac{{du}}{{dz}} = \frac{C}{{K(z)}},$
где $C$ – постоянная интегрирования. Из (3) и граничного условия на поверхности $z = H$ следует

(4)
$u = U + C\int\limits_H^z {\frac{{dz{\kern 1pt} '}}{{K\left( {z{\kern 1pt} '} \right)}}} .$

С учетом (2), (3), (4), получаем уравнение для определения постоянной $C{\text{:}}$

(5)
$\begin{gathered} {{C}^{2}} - \frac{{1 + 2{{c}_{D}}UI}}{{{{c}_{D}}{{I}^{2}}}}C + \frac{{{{U}^{2}}}}{{{{I}^{2}}}} = 0, \\ I \equiv \int\limits_0^H {\frac{{dz{\kern 1pt} '}}{{K\left( {z{\kern 1pt} '} \right)}}} = H\overline {K{{{\left( z \right)}}^{{ - 1}}}} , \\ \end{gathered} $
где черта означает осреднение по $z.$ Отсюда
(6)
$C = \frac{U}{I}\frac{{1 + \varphi \pm {{{\left( {1 + 2\varphi } \right)}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}}}{\varphi },$
где безразмерный параметр $\varphi = 2{{c}_{D}}UI.$ Для профиля скорости получаем выражение

(7)
$\begin{gathered} u\left( z \right) = U\left\{ {1 - \frac{{1 + \varphi \pm {{{\left( {1 + 2\varphi } \right)}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}}}{\varphi }} \right. \times \\ \times \,\,\left. {\left[ {{{\int\limits_z^H {\frac{{dz{\kern 1pt} '}}{{K\left( {z{\kern 1pt} '} \right)}}} } \mathord{\left/ {\vphantom {{\int\limits_z^H {\frac{{dz{\kern 1pt} '}}{{K\left( {z{\kern 1pt} '} \right)}}} } {\int\limits_0^H {\frac{{dz{\kern 1pt} '}}{{K\left( {z{\kern 1pt} '} \right)}}} }}} \right. \kern-0em} {\int\limits_0^H {\frac{{dz{\kern 1pt} '}}{{K\left( {z{\kern 1pt} '} \right)}}} }}} \right]} \right\}. \\ \end{gathered} $

Решение формально оказалось неоднозначным. Но из физических соображений в (6) и (7) следует выбрать решение с отрицательным знаком перед корнем. (Решение с положительным знаком приводит к отрицательным значениям скорости в нижней части слоя. Это несовместимо с тем, что рассматриваемый слой приводится в движение положительным “форсингом” $U > 0$ на верхней границе). На нижней границе слоя $z = 0$

(8)
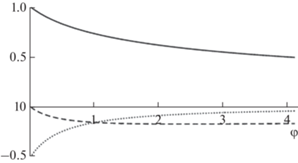
$\begin{gathered} u\left( 0 \right) = U\left[ {1 - \frac{{1 + \varphi - {{{\left( {1 + 2\varphi } \right)}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}}}{\varphi }} \right], \\ {{\left. {\frac{{du}}{{d\varphi }}} \right|}_{{z = 0}}} = \frac{U}{{{{\varphi }^{2}}}}\left[ {1 - \frac{{1 + \varphi }}{{{{{\left( {1 + 2\varphi } \right)}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}}}} \right]. \\ \end{gathered} $

На рис. 1 представлены эти функции параметра $\varphi .$ В простейшем частном случае $K = {\text{const}}$ получаем $I = {H \mathord{\left/ {\vphantom {H K}} \right. \kern-0em} K},$ $\varphi = {{2{{c}_{D}}UH} \mathord{\left/ {\vphantom {{2{{c}_{D}}UH} K}} \right. \kern-0em} K},$ и решение имеет вид

(9)
$u\left( z \right) = U\left[ {1 - \frac{{1 + \varphi - {{{\left( {1 + 2\varphi } \right)}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}}}{\varphi }\left( {1 - \frac{z}{H}} \right)} \right].$
Рис. 1.

Нормированные на $U$ зависимости от параметра $\varphi $ скорости $u\left( 0 \right)$ (сплошная линия), производной ${{\left. {{{du} \mathord{\left/ {\vphantom {{du} {d\varphi }}} \right. \kern-0em} {d\varphi }}} \right|}_{{z = 0}}}$ (пунктир) и $F\left( \varphi \right) \equiv {{\left. {\varphi ({{du} \mathord{\left/ {\vphantom {{du} {d\varphi }}} \right. \kern-0em} {d\varphi }})} \right|}_{{z = 0}}}$ (штриховая линия).

Пусть теперь трение горизонтально-неоднородно – коэффициент сопротивления ${{c}_{D}}$ зависит от поперечной к потоку горизонтальной координаты $y.$ Следовательно, от $y$ зависит и параметр $\varphi ,$ и горизонтальная скорость $u,$ что означает возникновение завихренности ${{du} \mathord{\left/ {\vphantom {{du} {dy}}} \right. \kern-0em} {dy}}.$

Очевидно,

(10)
$\begin{gathered} \frac{{du}}{{dy}} = \frac{{du}}{{d\varphi }}\frac{{d\varphi }}{{d{{c}_{D}}}}\frac{{d{{c}_{D}}}}{{dy}} = UF\left( \varphi \right)\frac{{d\ln {{c}_{D}}}}{{dy}}\left[ {{{\int\limits_z^H {\frac{{dz{\kern 1pt} '}}{{K\left( {z{\kern 1pt} '} \right)}}} } \mathord{\left/ {\vphantom {{\int\limits_z^H {\frac{{dz{\kern 1pt} '}}{{K\left( {z{\kern 1pt} '} \right)}}} } {\int\limits_0^H {\frac{{dz{\kern 1pt} '}}{{K\left( {z{\kern 1pt} '} \right)}}} }}} \right. \kern-0em} {\int\limits_0^H {\frac{{dz{\kern 1pt} '}}{{K\left( {z{\kern 1pt} '} \right)}}} }}} \right], \\ F\left( \varphi \right) = \frac{1}{\varphi }\left[ {1 - \frac{{1 + \varphi }}{{{{{\left( {1 + 2\varphi } \right)}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}}}} \right]. \\ \end{gathered} $

В частности, при $K = {\text{const}}$

(11)
$\frac{{du}}{{dy}} = UF\left( \varphi \right)\frac{{d\ln {{c}_{D}}}}{{dy}}\left( {1 - \frac{z}{H}} \right).$

Если, например, принять значения параметров $U = 15\,\,{{\text{м}} \mathord{\left/ {\vphantom {{\text{м}} {\text{с}}}} \right. \kern-0em} {\text{с}}}{\text{,}}$ $K = {\text{10}}\,\,{{{{{\text{м}}}^{{\text{2}}}}} \mathord{\left/ {\vphantom {{{{{\text{м}}}^{{\text{2}}}}} {\text{c}}}} \right. \kern-0em} {\text{c}}}{\text{,}}$ $H = {\text{200}}\,\,{\text{м,}}$ ${{c}_{D}} = {{10}^{{ - 3}}},$ то $\varphi = 0.6.$ Это значение может заметно увеличиваться в более реальных моделях с $K \ne {\text{const,}}$ учитывающих существенное ослабление турбулентного обмена у подстилающей поверхности и, следовательно, большие значения параметра $I.$ Остановимся, например, на модели [Гутман, 1969]:

$K\left( z \right) = {{K}_{0}} + \left( {{{K}_{1}} - {{K}_{0}}} \right)\left( {1 - {{e}^{{{{ - z} \mathord{\left/ {\vphantom {{ - z} h}} \right. \kern-0em} h}}}}} \right).$

Эта модель предполагает рост $K\left( z \right)$ от относительно малого значения $K = {{K}_{0}}$ при $z = 0$ до некоторого значения ${{K}_{1}}$ на уровнях, существенно выше некоторого уровня $z = h.$ В этом случае входящий в решение интеграл

(12)
$\begin{gathered} \int\limits_z^H {\frac{{dz{\kern 1pt} '}}{{K\left( {z{\kern 1pt} '} \right)}}} = \frac{h}{{{{K}_{1}}}}\ln \left[ {\frac{{{{{{K}_{0}}} \mathord{\left/ {\vphantom {{{{K}_{0}}} {{{K}_{1}}}}} \right. \kern-0em} {{{K}_{1}}}} + \exp \left( {{H \mathord{\left/ {\vphantom {H h}} \right. \kern-0em} h}} \right) - 1}}{{{{{{K}_{0}}} \mathord{\left/ {\vphantom {{{{K}_{0}}} {{{K}_{1}}}}} \right. \kern-0em} {{{K}_{1}}}} + \exp \left( {{z \mathord{\left/ {\vphantom {z h}} \right. \kern-0em} h}} \right) - 1}}} \right], \\ I \equiv \int\limits_0^H {\frac{{dz{\kern 1pt} '}}{{K\left( {z{\kern 1pt} '} \right)}}} = \frac{H}{{{{K}_{1}}}}\frac{h}{H}\ln \left[ {1 + \frac{{{{K}_{1}}}}{{{{K}_{0}}}}\left( {\exp \left( {{H \mathord{\left/ {\vphantom {H h}} \right. \kern-0em} h}} \right) - 1} \right)} \right]. \\ \end{gathered} $

Если коэффициент обмена $K\left( z \right)$ сильно убывает у нижней границы (${{K}_{0}} \ll {{K}_{1}}$), то значение интеграла $I$ в (12) может быть заметно больше величины ${H \mathord{\left/ {\vphantom {H {{{K}_{1}}}}} \right. \kern-0em} {{{K}_{1}}}},$ отвечающей случаю $K\left( z \right) = {{K}_{1}} = {\text{const}}{\text{.}}$ Например, если ${{K}_{0}} = {{10}^{{ - 2}}}$ м2/с, ${{K}_{1}} = 10$ м2/с, $h = 50$ м, $H = 200$ м, то $I > {{2H} \mathord{\left/ {\vphantom {{2H} {{{K}_{1}}}}} \right. \kern-0em} {{{K}_{1}}}}.$ Пропорционально увеличивается и оценка параметра $\varphi .$ Таким образом, $\varphi $ при рассматриваемых значениях параметров больше или порядка единицы. Как видно из рис. 1, функция $F(\varphi )$ в рассматриваемой области слабо меняется и принимает значения около 0.2.

Оценим генерацию завихренности. Если U = $ = 15\,\,{\text{м/с,}}$ ${{c}_{D}} = {\text{1}}{{{\text{0}}}^{{ - {\text{3}}}}},$ и последняя величина убывает вдвое на горизонтальных масштабах $\Delta y = 500$ м, то, согласно (10), у нижней границы генерируется завихренность ${{\partial u} \mathord{\left/ {\vphantom {{\partial u} {\partial y}}} \right. \kern-0em} {\partial y}}$ порядка $0.3 \times {{10}^{{ - 2}}}$ с–1 – величина на полтора порядка большая скорости планетарного вращения. Этот эффект будет еще значительнее при уменьшении $\Delta y.$ Но при меньших горизонтальных масштабах неоднородностей настоящая модель менее применима, поскольку не учитывает “горизонтальной” вязкости.

3. ЗАКЛЮЧЕНИЕ

Априори можно было предположить, что результат может сильно зависеть от ряда произвольных допущений, например, от значения высоты $H,$ на которой считается заданной скорость $U$, или от предполагаемого профиля коэффициента обмена $K\left( z \right).$ Но оказалось, что результат носит весьма простой, прозрачный и универсальный характер. Параметры задачи входят в безразмерный параметр $\varphi ,$ зависимость решения от которого оказалась слабой. В частности, входящий в $\varphi $ размерный параметр $I$ может меняться в довольно ограниченных пределах. Фактически генерация завихренности существенно зависит лишь от двух параметров: фоновой скорости и горизонтального градиента сопротивления (производной ${{d\ln {{c}_{D}}} \mathord{\left/ {\vphantom {{d\ln {{c}_{D}}} {dy}}} \right. \kern-0em} {dy}}$).

Список литературы

  1. Галушко В.В., Орданович А.Е. Двухслойная модель экмановского пограничного слоя атмосферы // Метеорология и гидрология. 1978. № 4. С. 33–34.

  2. Гутман Л.Н. Введение в нелинейную теорию мезометеорологических процессов. Л.: Гидрометеоиздат, 1969. 295 с.

  3. Ингель Л.Х., Макоско А.А. О механизме генерации спиральности восходящего потока, обусловленного неоднородным трением на подстилающей поверхности // Докл. РАН. Науки о Земле. 2023. Т. 508. № 2. С. 253–257.

  4. Ингель Л.Х., Михайлова Л.А. К теории экмановского пограничного слоя с нелинейными граничными условиями // Изв. AН СССР. Физика атмосферы и океана. 1990. Т. 26. № 7. С. 675–681.

  5. Ландау Л.Д., Лифшиц Е.М. Гидродинамика. М.: Наука, 1986. 733 с.

  6. Dotzek N., Emeis S., Lefebvre C., Gerpott J. Waterspouts over the North and Baltic Seas: Observations and climatology, prediction and reporting // Meteorologische Zeitschrift. 2010. V. 19. № 1. P. 115–129.

  7. Ingel L.Kh. On the nonlinear dynamics of the boundary layer of intense atmospheric vortex // Dynamics of Atmospheres and Oceans. 2005. V. 40. № 4. P. 295–304.

  8. Frazier A.E., Hemingway B.L., Brasher J.P. Land surface heterogeneity and tornado occurrence: an analysis of Tornado Alley and Dixie Alley // Geomatics, Natural Hazards and Risk. 2019. V. 10. № 1. P. 1475–1492.https://doi.org/10.1080/19475705.2019.1583292

  9. Kellner O., Niyogy D. Land surface heterogeneity signature in tornado climatology? An illustrative analysis over Indiana, 1950–2012 // Earth Interactions. 2014. V. 18. № 10. P. 1–32. https://doi.org/10.1175/2013EI000548.1

  10. Lyza A.W., Knupp K.R. A Background investigation of tornado activity across the Southern Cumberland Plateau Terrain System of Northeastern Alabama // Mon. Wea. Rev. 2018. V. 146. P. 4261–4278. https://doi.org/10.1175/MWR-D-18-0300.1

  11. Markert A., Griffin R., Knupp K., Molthan A., Coleman T. A spatial pattern analysis of land surface roughness heterogeneity and its relationship to the initiation of weak tornadoes // Earth Interactions. 2019. V. 23. № 5. P. 1–28. https://doi.org/10.1175/EI-D-18-0010.1

  12. Miglietta M.M. Waterspouts: A Review // Reference Module in Earth Systems and Environmental Sciences. 2019. 15 p.

  13. Muncy T.J. Topographic and surface roughness influences on tornadogenesis and decay [Электронный ресурс] / Thesis. College of Arts and Sciences of Ohio University. 2021. 164 p. Режим доступа: https://etd.ohiolink. edu/apexprod/rws_olink/r/ 1501/10?clear=10&p10_accession_ num=ohiou1628513174226383 (дата обращения 19.12.2022 г.).

  14. Wheatley D.M., Trapp R.J. The effect of mesoscale heterogeneity on the genesis and structure of mesovortices within quasi-linear convective systems // Mon. Wea. Rev. 2008. V. 136. P. 4220–4241.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Физика атмосферы и океана

Архивы выпусков Информация о журнале Отправить рукопись в журнал