Журнал физической химии, 2019, T. 93, № 4, стр. 632-640

ТЕРМОДИНАМИЧЕСКАЯ РАБОТА РАЗДЕЛЕНИЯ СТУПЕНИ КАСКАДА

К фундаментальным понятиям общей теории разделения относится понятие разделительной способности (ценности смеси) [1, 4, 15]. Это понятие имеет большое значение в изотопной технологии [4, 13], так как его использование позволяет оценить удельные затраты на производство продукта [4, 15] и дать сравнительную оценку эффективности процесса разделения [4, 8]. Данное понятие оказалось также практически важным для проведения некоторых расчетов экономического характера [5, 13]. В качестве показателя разделительной способности ступени (элемента) газоразделительного каскада используют функцию

где q, q' и q'' – количества молей исходной бинарной смеси и полученных фракций, x⁰, x' и x'' – соответствующие концентрации, Φ(x) – функция, которую называют разделительным потенциалом [1, 6, 7]:

Физический смысл W изучен недостаточно [7]. Предпринимались ранее [4, 6, 7] попытки объяснения W и Φ(x) с привлечением энтропии и выражений для термодинамических потенциалов по Гиббсу. В [6, 7] функцию W называют полезной работой разделения. Для случая разделения компонентов бинарной смеси и при выделении двух фракций, в соответствии с данными [6, 7], можно написать (j = n = 2):

где $\sum\nolimits_{i = 1}^n {{{x}_{i}}\ln [{{x}_{i}}{\text{/}}(1 - {{x}_{i}})]} $ – потенциал, введенный П.Г. Кузнецовым и др. [6, 7] и распространенный по аналогии с энтропийным потенциалом разделения [6, 7] на многокомпонентные смеси.

Уравнение для W можно представить также в виде [16]:

где A₀ и B₀ – количества молей компонентов A и B в исходной смеси, A₁ и B₁ – количества молей разделяемых компонентов в одной фракции, A₂ и B₂ – в другой. Соответственно имеем

Последнее уравнение для W удобно применять при исследовании ступеней многоступенчатой фракционной экстракции [17].

Однократный акт разделения характеризуют обычно коэффициентом разделения α, эффективным коэффициентом разделения β [2] и степенью деления фракций Θ:

Отсюда Обозначения p_i и q_i широко используются в жидкостной экстракции [17]. Смысл этих обозначений следует из уравнений: где ε_A и ε_B – факторы экстракции [17], k_A и k_B – факторы хроматографического удерживания [18].

Используя приведенные уравнения, найдем

При A₀ = B₀ и β = α^1/2 разделительная способность максимальна [3] (1 < β < α [2]). Если величина α близка к единице, то и значение β близко к единице. В этом случае можно использовать приближенно справедливые уравнения С учетом приведенных уравнений В оптимальном режиме симметричного разделения [5, 15] (β = α^1/2 = γ) выражение для разделительной способности принимает вид: Данное уравнение справедливо для любых значений α. Для тонкого разделения [1, 2] (α – 1 $ \ll $ 1 и Θ = 1 – Θ ≈ 0.5) имеем

Подобные соотношения были получены Дираком, Пайерлсом и Фуксом в ходе выполнения Манхеттенского проекта [15]. Для значений α, близких к единице и заметно отличающихся от единицы [1], установлена [19] связь:

где $\Re $ – разрешение пиков распределения [18, 19], характеризующее разделительную способность распределительной системы фракционирования [18], и t – число циклов (стадий) разделения. При симметричном разделении величина W максимальна и ${{\Re }^{2}}$/t является критерием оптимизации в процессе тонкого разделения [19].

Известна формула Пайерлса и Фукса [4, 15], связывающая W_уд = W/q с изменением молярной величины – энтропии смешения ∆S. По данным [4, 15, 16], для тонкого разделения компонентов смеси идеальных газов можно написать

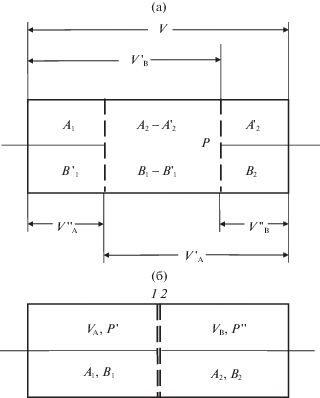
где R – газовая постоянная. Идеальный газ, как известно, теоретическая модель газа, в которой “взаимодействием” частиц газа пренебрегают. Идеальный газ может быть однокомпонентным и многокомпонентным и подчиняется уравнению состояния идеального газа. В смеси идеальных газов поведение каждого из них не зависит от присутствия остальных [12].

Гипотетические полупроницаемые мембраны и идеализированные поршни как теоретические модели достаточно широко применяются в термодинамике равновесных процессов [20–22]. В [16] описано разделительное устройство, обеспечивающее неполное равновесное (квазистатическое) разделение компонентов смеси идеальных газов. Это устройство изображено на рис. 1 (положения “а” и “б”). В данном устройстве давление (P) исходной смеси идеальных газов и выделенных фракций (P', P'') в общем случае [16] различаются (P' ≠ P'' ≠ P). Связь между W и термодинамической работой W_Т, совершаемой в предложенном устройстве при симметричном разделении (β = α^1/2 = γ), по данным [16], можно представить в следующей форме:

где T – абсолютная температура. Полученное уравнение справедливо для произвольного состава исходной смеси идеальных газов и при любых значениях α. Для значений α, близких к единице и заметно отличающихся от единицы (α ≤ 1.5) можно с известным приближением принять ƒ(α) = 0.25 и (согласно [16]) написать или Из данных соотношений следует, что величина разделительной способности пропорциональна безразмерной термодинамической работе. Следовательно, W_α возможно интерпретировать как меру совершаемой на ступени работы разделения [1] (впервые название “работа разделения” для W = q(α – 1)²/8 было предложено Юрии в 1939 г. [1, 4]).

В [16] обоснована связь

где $W_{T}^{*}$ – термодинамическая работа разделения, определяемая с использованием энтропийного потенциала разделения [15]. Полученные термодинамические соотношения отличаются от формулы Пайерлса и Фукса множителем RT/4. Термодинамически обоснованное введение этого множителя позволяет при x⁰ = 0.5 получить равенство ${{W}_{T}} = T\Delta {{S}_{{{\text{с м }}}}} = W_{T}^{*}$, что подтверждает адекватность предложенной модели (рис. 1) и согласуется с описанными в [20, 22, 23] принципами полного и неполного равновесного разделения компонентов бинарной смеси идеальных газов в цилиндре с двумя полупроницаемыми поршнями в условиях P, T = const. Введение множителя RT/4 согласуется также с уравнением полученным (для обратимого процесса) [24] на примере ступеней фракционной жидкостной экстракции из предельно разбавленных растворов. Здесь W_T – максимальная полезная работа [19, 20].

Учитывая приведенные выше данные, перейдем к термодинамическому обоснованию работы разделения многокомпонентной смеси. В качестве примера рассмотрим процесс симметричного разделения смеси идеальных газов, содержащей две пары газов AB и CD. На рис. 2 изображено гипотетическое устройство, которое позволяет, по крайней мере, в принципе осуществить равновесное разделение указанных пар. Данное устройство [11] является модификацией системы, изображенной на рис. 1, и представляет собой цилиндрический сосуд объемом V, заполненный смесью идеальных газов A, B, C и D в количествах A₀, B₀, C₀ и D₀ молей при общем давлении P. В общем случае A₀ ≠ B₀ ≠ C₀ ≠ D₀ (рис. 2). В сосуде установим четыре полупроницаемые перегородки (рис. 2а), каждая из которых имеет форму поршня [20, 22], способного перемещаться бесконечно медленно [22] и без трения. Учитывая [21–23], будем считать, что перегородка 1 проницаема для В, а перегородка 2 – для А. Существенно (и это следует особо подчеркнуть), что обе перегородки 1 и 2 свободно пропускают газы C и D. Одновременно считаем, что перегородка 3 проницаема для D, а перегородка 4 – для С, и обе перегородки 3 и 4 проницаемы для А и В, т.е. свободно пропускают эти газы. Тогда, передвигая перегородки, можно получить при симметричном разделении каждой из пар (${{\beta }_{{{\text{AB}}}}} = \alpha _{{{\text{AB}}}}^{{1/2}} = {{\gamma }_{{{\text{AB}}}}}$, ${{\beta }_{{{\text{CD}}}}} = \alpha _{{{\text{CD}}}}^{{1/2}} = {{\gamma }_{{{\text{CD}}}}}$) картину, показанную на рис. 2б. В конечном положении (как и на рис. 1) перегородки симметрично располагаются относительно центра цилиндра (V_A= V_B= V/2). Выбор пар и соответствующих перегородок осуществляется по принципу, описанному, например, в [25, 26].

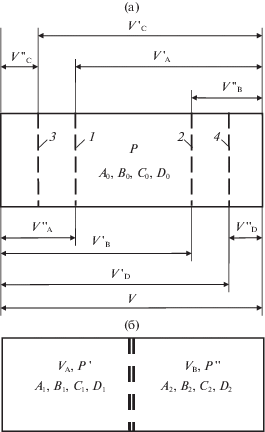
В соответствии с рис. 2, принимаем α_СD > α_AB. При одновременном выполнении равенств ${{\beta }_{{{\text{AB}}}}} = \alpha _{{{\text{AB}}}}^{{1/2}}$ и ${{\beta }_{{{\text{CD}}}}} = \alpha _{{{\text{CD}}}}^{{1/2}}$ (рис. 2) справедливы соотношения

которые следуют из группы уравнений (3). Отсюда Покажем возможность выполнения подобных равенств на одном примере [12]. В распределительных системах фракционирования [19] могут выполняться, по крайней мере, в принципе следующие соотношения: Нетрудно видеть, что при симметричном разделении (k₀ = 1 [19]) выполняются все записанные выше условия симметричного разделения. Отметим, что существует принципиальная возможность обратимого перевода разделяемого раствора в идеальное газовое состояние [20] с последующим равновесным разделением газовой смеси в системе, показанной на рис. 2, и обратимой конденсации фракций. Режим симметричного разделения при многоступенчатой экстракции обсуждается также в [17].

С учетом принятых обозначений, приведенных рисунков и данных, можно, на наш взгляд, сразу написать (для устройства на рис. 2)

где ∆U – минимальная потребная энергия, которую необходимо подводить в рассматриваемом процессе. Эту энергию целесообразно сообщать каждой паре поршней (1, 2 и 3, 4) отдельно в виде электрической работы [21]. Для тонкого разделения соответственно имеем где величина W для многокомпонентной смеси пропорциональна безразмерной термо-динамической работе W_T/RT. Таким образом, W возможно интерпретировать и как меру совершаемой на ступени термодинамической работы разделения многокомпонентной смеси.

Из данных [11] следует, что в изученном устройстве (рис. 2) давление (P) исходной многокомпонентной смеси идеальных газов и выделенных фракций (P', P'') в общем случае различаются. При A₀ = B₀ и C₀ = D₀ имеем Θ_AB = Θ_CD = 0.5 и P' = P'' = P. В этих условиях вновь выполняются равенства

Эти равенства подтверждают адекватность предложенной модели (рис. 2). Здесь ∆S_см относится к рассматриваемой многокомпонентной смеси идеальных газов (A₀ = B₀ и C₀ = D₀ [10, 11]).

В заключение раздела сумму W = W_AB + W_CD целесообразно представить в следующей обобщенной форме [26]:

Здесь [26] и $X_{i}^{'}$, $X_{i}^{{''}}$ и $X_{i}^{0}$ – соответствующая концентрация компонентов в многокомпонентной смеси идеальных газов. Более расширенная группа равенств в обобщенной форме и информация о входящих в приведенные равенства величин дана в [26]. Для бинарной смеси обобщенные равенства [26] сводятся к уравнениям (1) и (2).

ТЕРМОДИНАМИЧЕСКАЯ РАБОТА РАЗДЕЛИТЕЛЬНОГО КАСКАДА

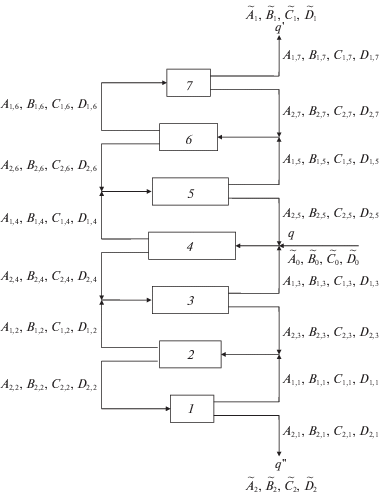
Упрощенная схема каскада изображена на рис. 3. Она включает в себя семь описанных выше ступеней равновесного разделения. Ограничимся случаем разделения эквимолярных смесей идеальных газов. С учетом содержания предыдущего раздела считаем, что каждая ступень каскада работает в режиме симметричного разделения.

Для варианта разделения в каскаде компонентов смеси А(1) и В(2) и при выделении двух фракций можно, в соответствии с данными [6, 7], написать (j = n = 2)

Отметим, что входящие в эти уравнения величины относятся уже к каскаду в целом (характеризуют питание каскада и продукты).

Уравнение для W_K можно представить также в виде:

где ${{\tilde {A}}_{0}}$ и ${{\tilde {B}}_{0}}$ – количества молей компонентов А и B в исходной (перерабатываемой) смеси (${{\tilde {A}}_{0}} = {{\tilde {B}}_{0}}$), ${{\tilde {A}}_{1}}$ и ${{\tilde {B}}_{1}}$ – количества молей разделяемых компонентов в одной фракции, ${{\tilde {A}}_{2}}$ и ${{\tilde {B}}_{2}}$ – в другой. Соответственно имеем Здесь где ${{\tilde {\alpha }}_{{{\text{AB}}}}} = \tilde {\alpha }$ – коэффициент разделения каскада [15, 24]. Используя приведенные соотношения, получим известное уравнение [4, 9, 15], определяющее максимальную разделительную способность каскада Уравнение для термодинамической работы разделения W_Т,К, также справедливое для любых значений α, по данным [24], имеет вид: Для значений α ≤ 1.5 [24] где Φ(x) – разделительный потенциал или функция Дирака–Пайерлса для каскада в целом. Соответственно Из приведенных соотношений следует, что эта разделительная способность каскада пропорциональна безразмерной термодинамической работе W_Т,K/RT. Следовательно, разделительную способность W_К можно интерпретировать как меру работы, совершаемой каскадом при симметричном разделении компонентов бинарной смеси.

Для расчета термодинамической работы разделения многокомпонентной смеси идеальных газов (A, B, C и D) воспользуемся рассмотренным в предыдущем разделе условием, согласно которому, симметричное разделение на ступенях каскада возможно более чем для одной пары компонентов разделяемой многокомпонентной смеси. Процесс разделения в каскаде охарактеризуем величинами (см. рис. 3):

где N – номер верхней ступени (${{\tilde {A}}_{0}} = {{\tilde {B}}_{0}}$, ${{\tilde {C}}_{0}} = {{\tilde {D}}_{0}}$).

В узлах каскада (рис. 3) осуществляется несмешивание по нескольким относительным концентрациям для выбранных пар компонентов смеси (т.е. по R_AB и R_CD [5]). Например, в узле перед ступенью 6 выполняются равенства

где (с учетом данных [12, 27]) Далее, в соответствии с данными [12, 27], имеем: Здесь N – число ступеней в каскаде (рис. 3). Для любой ступени каскада тонкого разделения где N – номер ступени. По данным [12, 27], для любых значений α_AB Суммируя и принимая во внимание равенства $\tilde {\alpha }_{{{\text{AB}}}}^{{1/2}} = \alpha _{{{\text{AB}}}}^{{(7 + 1)/4}} = \alpha _{{{\text{AB}}}}^{2}$ и $\ln \tilde {\alpha }_{{{\text{AB}}}}^{{1/2}} = [(7 + 1){\text{/}}2]\ln \alpha _{{{\text{AB}}}}^{{1/2}}$, найдем Аналогично получим Следовательно, и мы вновь можем записать группу равенств, подобных приведенным в конце предыдущего раздела и в [26], но отнести их уже к каскаду в целом [12, 26]. Заметим, что потенциал $\sum\nolimits_{i = 1}^n {{{X}_{i}}\left[ {{{x}_{i}}{\text{/}}(1 - {{x}_{i}})} \right]} $ отличается от “обобщенного” разделительного потенциала, приведенного в [5]. Описанный каскад, на наш взгляд, может служить “эталонным” каскадом для распределительных систем фракционирования [9, 28, 29], обеспечивая (в режиме равновесного разделения на каждой ступени) наиболее эффективное преобразование энергии в полезную работу при максимальной разделительной способности по отношению к выбранным парам компонентов смеси.

В заключение выражаем искреннюю благодарность авторам [5] за интерес, проявленный к нашим работам [10–12]. Приведенные в статье [5] данные и уравнения будут учитываться в наших дальнейших исследованиях.